BSE Odisha 10th Class Maths Solutions Geometry Chapter 1 ଜ୍ୟାମିତିରେ ସାଦୃଶ୍ୟ Ex 1(a)

Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 1 ଜ୍ୟାମିତିରେ ସାଦୃଶ୍ୟ Ex 1(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Geometry Chapter 1 ଜ୍ୟାମିତିରେ ସାଦୃଶ୍ୟ Ex 1(a)

Question 1.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
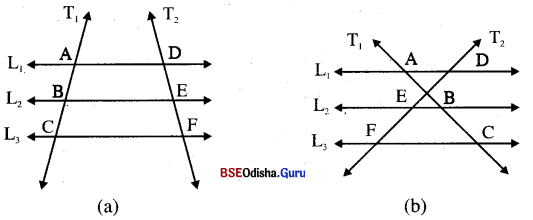
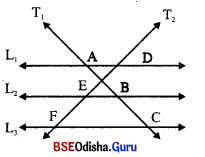
(a) ବିମ୍ନ ଟିତ୍ର (a) 6ର L₁ || L₂ || L₃ ଏର୍ଚ T₁ ଓ T₂ ଛେଦ ଦା |
(i) AB = 2 6ସ.ର୍ମି., BC = 3 6ସ.ର୍ମି. ଓ DE = 3 6ସ.ର୍ମି. 6ହ6ଲ EF = ……….|
(ii) DE = 6 6ସ.ର୍ମି., EF = 8 6ସ.ର୍ମି. ଓ BC = 6 6ସ.ର୍ମି. 6ହ6ଲ AC = ……….|

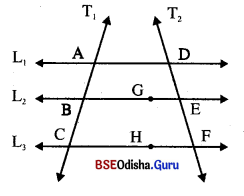
(b) ଗପଭୋକ୍ତ ତିତ୍ର (b) 6ର L₁ || L₂ || L₃ ଏବଂ T₁ ଓ T₂ ଛେଦକ |
(i) AB = 1.5 × BC ହେଲେ, \(\frac { EF }{ FD }\) = ……………..
(ii) \(\overline{\mathrm{AC}}\) ର ମଧ୍ୟବିରୁ B 6ହ6ଲ, EF ର ……… ମୁଶ 6ହରଛି FD|
Solution:
(a) (i) L₁ || L₂ || L₃ ⇒ \(\frac { AB }{ BC }\) = \(\frac { DE }{ EF }\)
⇒ \(\frac { 2 }{ 3 }\) = \(\frac { 3 }{ EF }\) ⇒ EF = \(\frac{3 \times 3}{2}\) 6 ସ.ମି. = 4.5 6ସ.ମି.

(ii) L₁ || L₂ || L₃ ଏବଂ T₁ ଓ T₂ ରୁକଚି 6ଛଦକ |
∴ \(\frac { DE }{ EF }\) = \(\frac { AB }{ BC }\) ⇒ \(\frac { 6 }{ 8 }\) = \(\frac { AB }{ 6 }\)
⇒ AB = \(\frac{6 \times 6}{8}\) = 4.5 6ସ.ମି. |
AC = AB + BC = 4.5 6ସ.ମି. + 6ସ.ମି. = 10.5 6ସ.ମି. |

(b) (i) ଏଠ।6ର L₁ || L₂ || L₃ ଏରଂ T₁ ଓ T₂ ଦୁଲଟି 6ଚ୍ଚଦକ |
\(\frac { AB }{ BC }\) = \(\frac { DE }{ EF }\) ⇒ \(\frac { 3 }{ 2 }\) = \(\frac { DE }{ EF }\)
⇒ \(\frac{3+2}{2}\) = \(\frac{\mathrm{DE}+\mathrm{EF}}{\mathrm{EF}}\) ⇒ \(\frac { DE }{ EF }\) = \(\frac { 5 }{ 2 }\) ⇒ \(\frac { EF }{ DF }\) = \(\frac { 2 }{ 5 }\)

(ii) \(\overline{\mathrm{AC}}\) ର ମଧ୍ୟ ଦିନୁ B ଅର୍ଥ।ତ୍ AB = BC
\(\frac { EF }{ FD }\) = \(\frac { BC }{ AC }\) = \(\frac{\mathrm{BC}}{\mathrm{AB}+\mathrm{BC}}\) = \(\frac { BC }{ 2BC }\) = \(\frac { 1 }{ 2 }\) ⇒ 2EF = FD>
ଅର୍ଥାତ୍ EF ଭ 2 ଣ୍ଣଣ 6ଦ୍ରଣଛି FD |

Question 2.
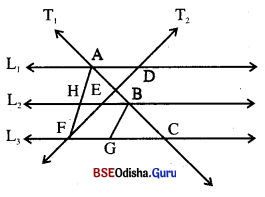
ଟିତ୍ର6ର L₁ || L₂ || L₃ ଏବଂ T₁ ଓ T₂ ଦୁଲଟି 6ଚ୍ଛଦକ | L₂ ଓ L₃ ରପ6ର ପ୍ଥଥ।କୁ6ର G ଓ H ଦିହୁ ରିଜିତ 6 ପ୍ପପତି BC = AD ଏବଂ CH = BE;

ପ୍ରମାଣ କର 6ଯ
(i) DG : EH = DE : EF
(ii) (DG + EH) : EH = DF : EF
Solution:
ଦଉ : L₁ || L₂ || L₃ ଏବଂ T₁ ଓ T₂ ଦୁକଟି 6ଚ୍ଛଦକ ଯଥାସ୍ତ6ମ L₁, L₂ ଓ L₃ କୁ A,B,C ଓ D,E,F ଦିନ୍ଦ6ର 6ଚ୍ଛଦକ6ର | L₂ ରପ6ର G ଏକ ଦିବ୍ର 6ସ୍ ପରି BG = AD ଏର୍ବ L₃ ରପ6ର H ଏକ ଦିନ୍ଦୁ 6ନ୍ଦ୍ ପରି CH = BE |
ପ୍ରାମାଣ୍ୟ :
(i) DG : EH = DE : EF
(ii) (DG + EH) : EH = DF : EF

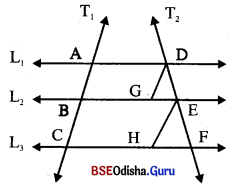
ଅକ୍ଳଜ : \(\overline{\mathrm{DG}}\) ଓ \(\overline{\mathrm{EH}}\) ଅଲ୍ଲବ ଦବାପାର |
ପ୍ତମାଣ : (i) AD = BG (ଦର) \((\overline{\mathrm{AD}} \| \overline{\mathrm{BG}})\), ∵ L₁ || L₂ (ଦର)
⇒ ABGD ଏକ ସାମାତ୍ରତିଦ ଚିତ୍ର | AB = DG
6ସଦୃପତି BEHC ଏକ ସାମାତ୍ର ଚିତ୍ର ଓ BC = EH
∴ \(\frac { DG }{ EH }\) = \(\frac { AB }{ BC }\) …(1)
ପୁନଣ୍ଡ \(\frac { AB }{ BC }\) = \(\frac { DE }{ EF }\) ⇒ \(\frac { DG }{ EH }\) = \(\frac { DE }{ EF }\) (1ରୁ) (ପ୍ରମାଣିତ)

(ii) ପୁଫରୁ ପ୍ରମାଣିର \(\frac { DG }{ EH }\) = \(\frac { DE }{ EF }\) ⇒ \(\frac{\mathrm{DG}+\mathrm{EH}}{\mathrm{EH}}\) = \(\frac{\mathrm{DE}+\mathrm{EF}}{\mathrm{EF}}\) (Componendo ଦ୍ଦାରା )
⇒ \(\frac{\mathrm{DG}+\mathrm{EH}}{\mathrm{EH}}\) = \(\frac { DF }{ EF }\) (ପ୍ରମାଣିତ)

Question 3.
ନିମ୍ନ ଚିତ୍ରରେ L₁ || L₂ || L₃ ଏବଂ T₁, ଓ T₂, ଦୁଇଟି ଛେଦକ । ଯଦି AB = BC ହୁଏ, ପ୍ରମାଣ କର ଯେ 2 BE = AD + CF |
Solution:
ଦତ୍ତ : L₁ || L₂ || L₃ ଛେଦକ T₁ ଓ T₂ , L₁, L₂, ଓ L₃, କୁ ଯଥାକ୍ରମେ A, B, C ଓ D, E, F ବିନ୍ଦୁରେ ଛେଦ କରେ ଏବଂ AB = BC |
ପ୍ରାମାଣ୍ୟ : 2BE = AD + CF
ଅକନ : E ଦିଦୁ ମଧ୍ୟ6ଦକ AC ସମାତ ତା6ଦ ଅଜିତ ବେଡା L₁ || L₃ କୁ ଯଥାକୁ6ମ X ଓ Y ଦିଦ6ର 6ଛଦକ୍ଳରୁ |

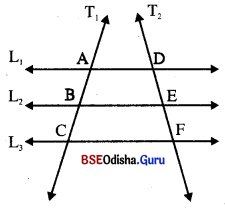
ଅଙ୍କନ : E ବିନ୍ଦୁ ମଧ୍ୟଦେଇ \(\overline{\mathrm{AC}}\)ସହ ସମାନ୍ତର ଭାବେ ଅଙ୍କିତ ରେଖା L₁ ଓ L₃, କୁ ଯଥାକ୍ରମେ X ଓ Y ବିନ୍ଦୁରେ ଛେଦକରୁ ।

Question 4.
ଚିତ୍ରରେ L₁ || L₂ || L₃, ଏବଂ T₁, ଓ T₂, ଦୁଇଟି ଛେଦକ । L₁, L₂, ଓ L₃, କୁ ଛେଦକ T₁, ଯଥାକ୍ରମେ A, B ଓ C ବିନ୍ଦୁରେ ଛେଦକରେ ଏବଂ L₁, L₂, ଓ L₃, କୁ ଛେଦକ T₂, ଯଥାକ୍ରମେ D, E ଓ F ବିନ୍ଦୁରେ ଛେଦ କରେ । DE = EF ହେଲେ, ପ୍ରମାଣ କର ଯେ, CF – AD = 2 EB । (ସୂଚନା : AF ଅଙ୍କନ କର)

Solution:
ଦତ୍ତ : L₁ || L₂ || L₃ ଏବଂ T₁, ଓ T₂, ଦୁଇଟି ଛେଦକ ଯଥାକ୍ରମେ L₁, L₂, ଓ L₃, କୁ A, B, C ଓ D, E, F ବିନ୍ଦୁରେ ଛେଦକରେ ।
ପ୍ରାମାଣ୍ୟ : CF – AD = 2EB.
ଅଙ୍କନ : \(\overline{\mathrm{AF}}\) ଅଙ୍କନ କର । B ବିନ୍ଦୁରୁ \(\overline{\mathrm{AF}}\) ସହ ସମାନ୍ତର ଭାବେ ଅଙ୍କିତ ରେଖା \(\overline{\mathrm{FC}}\) କୁ ଓ ବିନ୍ଦୁରେ ଛେଦକରୁ ।
\(\overline{\mathrm{AF}}\), L₂, କୁ H ବିନ୍ଦୁରେ ଛେଦକରୁ ।

ପ୍ରମାଣ : DE = EF (ଦଣ) ଓ \(\stackrel{\leftrightarrow}{\mathrm{BE}}\) || \(\overline{\mathrm{AD}}\) (∵ L₂ || L₁)
⇒ AH = HF,
ଦର୍ମାବ AH = HF ଓ \(\overline{\mathrm{BH}}\) || \(\overline{\mathrm{CF}}\) ⇒ AB = BC
\(\overline{\mathrm{BG}}\) || \(\overline{\mathrm{AF}}\) (ଅକo) ⇒ CG = GF ⇒ CF = 2GF △AFD 6ର H ଓ E ଯଥାକ୍6ମ \(\overline{\mathrm{AF}}\) ଓ \(\overline{\mathrm{DF}}\) ର ମଧ୍ୟଦିଦୁ
⇒ \(\overline{\mathrm{EH}}\) || \(\overline{\mathrm{AD}}\)
∴ ଦଘଣପଷ୍ଟ = CF – AD = 2GF – 2HE
= 2BH – 2HE (∵ GF = BH)
= 2(BH – HE) = 2BE = ଦାମପଖ (ପ୍ରମାଣିତ)

Question 5.

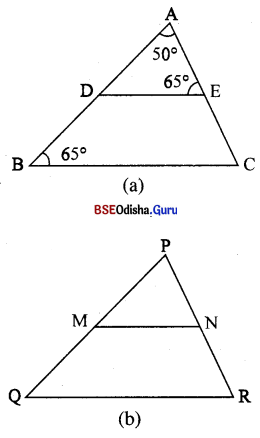
(i) ଭପରିସ୍ଥ ଚିତ୍ର (a) 6ର A – D – B ଏବଂ A – E – C | m∠DAE = 50°, m ∠AED = m∠ABC = 65° | AD = 3 6ସ.ମି., AE : EC = 2 : 1 6ଦୃ6କ, \(\overline{\mathrm{DB}}\) ଓ \(\overline{\mathrm{AB}}\) ର 6ଦିଘ୍ୟ ବ୍ଶଷଯ ଦର |
(ii) ଉପରିସ୍ଥ ବିତ୍ର (b) 6ର \(\overline{\mathrm{MN}}\) || \(\overline{\mathrm{QR}}\), NR = \(\frac { 2 }{ 5 }\) PR ଏବଂ PQ = 10 6ସ. ମି. 6ଦୃ6କ, PM ଓ QM କିଣପ୍ର କର |
(iii) କପଟାସ୍ଟ ଚିତୃ (b) 6ର PM = \(\frac { 1 }{ 2 }\) PQ, NR = 1.2 6ସ.ମି. ଓ \(\overline{\mathbf{M N}} \| \overline{\mathbf{Q R}}\) 6 ଦୁ6 କ, PR ଷ୍ଟିର କର
Solution:
(i) △ ADE 6ର m∠AD = 180° – (50° + 65°) = 65°
∠ADE ≅ ∠ABC ⇒ \(\overline{\mathrm{DE}} \| \overline{\mathrm{BC}}\)

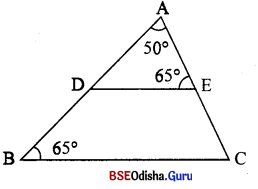
⇒ \(\frac{AD}{DB}\) = \(\frac{AE}{EC}\) = \(\frac { 2 }{ 1 }\)
⇒ \(\frac{3}{DB}\) = \(\frac { 2 }{ 1 }\) ⇒ DB = \(\frac { 3 }{ 2 }\) 6ପ.ମି. = 1.5 6ସ.ମି
AB = AD + DB = 3 6ସ.ମି. + 1.5 6ସ.ମି = 4.5 6ସ.ମି. |

(ii) \(\overline{\mathrm{MN}}\) || \(\overline{\mathrm{QR}}\) (ଦଉ)
\(\frac { PM }{ MQ }\) = \(\frac { PN }{ NR }\) ⇒ \(\frac{P M+M Q}{M Q}\) = \(\frac{\mathrm{PN}+\mathrm{NR}}{\mathrm{NR}}\)

⇒ \(\frac { PQ }{ MQ }\) = \(\frac { PR }{ NR }\) ⇒ \(\frac { 10 }{ MQ }\) = \(\frac{\mathrm{PR}}{\frac{2}{5} \mathrm{PR}}\)
⇒ \(\frac { 10 }{ MQ }\) = \(\frac { 5 }{ 2 }\)
⇒ MQ = \(\frac{10 \times 2}{5}\) 6ସ.ମି. = 4 6ସ.ମି. |
PM = PQ – MQ = 10 6ସ.ମି. – 4 6ସ.ମି. = 6 6ସ.ମି. |
∴ \(\overline{\mathrm{PM}}\) \(\overline{\mathrm{QM}}\) ର ଦେଶ ଯଥାଦୃ6ମ 6 6ସ.ମି. ଓ 4 6ସ.ମି.|

(iii) \(\overline{\mathrm{MN}}\) || \(\overline{\mathrm{QR}}\) , PM = \(\frac { 2 }{ 3 }\) PQ
⇒ MQ = PQ – PM = PQ – \(\frac { 2 }{ 3 }\) PQ = \(\frac { 1 }{ 3 }\) PQ

⇒ \(\frac { 1.2 }{ PR }\) = \(\frac{\frac{1}{3} \mathrm{PQ}}{\mathrm{PQ}}\) ⇒ \(\frac { 1.2 }{ PR }\) = \(\frac { 1 }{ 3 }\)
⇒ PR = 1.2 × 3 6ସ.ମି. = 3.6 ସେ.ମି. |
∴ \(\overline{\mathrm{PR}}\) ର 6ଦଣu = 3.6 ପେ.ପି. |

Question 6.
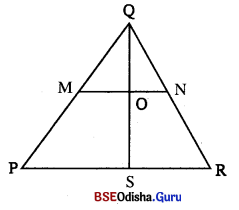
(i) △ABC 6ର, \(\overline{\mathbf{AB}}\) ଓ \(\overline{\mathbf{AC}}\) ର ମଧତିହୁ ଯଥାକ୍ର6ମ X ଓ Y 6ହ6କ, ଦଶାଥ 6ଯ \(\overline{\mathbf{X Y}} \| \overline{\mathbf{B C}}\) |
(ii) ଏକ ତ୍ରିସ୍ତକର 6ଣାଟିଏ ତାଦୃତ ମଧ୍ୟଝିହୁ 6ଦକ ଅଠ୍ୟ ଏଜ ଚାହପ୍ତତି ଅଜାଡ ସମାତର 6ରଖା, ତୃତୀୟ ବlନୁ ସମକ୍ରିଖଶ୍ନ କ6ର |
(iii) 6ଣାଟିଏ ପମ6କାଣା ତ୍ରିହ୍ନର ଦଶାବ ମଧ୍ୟବିଦୁ ଅଠ୍ୟ ଏବ୍ଲ ଗ୍ଲାସ୍ଥଗି ସମସ୍ତିଖଣ୍ଡକ6ର , ପ୍ରମାଣ କର |
Solution:

Question 7.
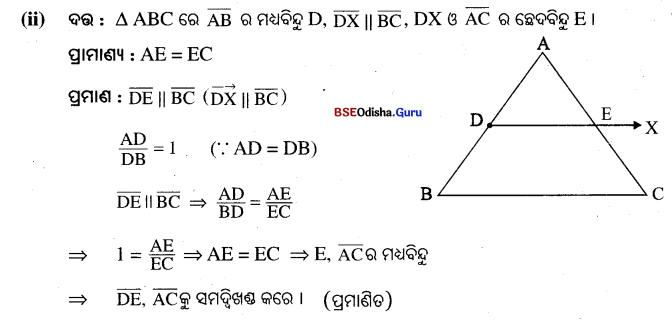
△PQR ରେ, \(\overline{\mathbf{PQ}}\) ଓ \(\overline{\mathbf{QR}}\) ବାହୁଦ୍ୱୟର ମଧ୍ୟବିନ୍ଦୁ ଯଥାକ୍ରମେ M ଓ N । \(\overline{\mathbf{PR}}\) ଉପରିସ୍ଥ S ଯେକୌଣସି ଏକ ବିନ୍ଦୁ ହେଲେ, ପ୍ରମାଣ କର ଯେ \(\overline{\mathbf{MN}}\), \(\overline{\mathbf{QS}}\) କୁ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରିବ ।
Solution:
ଦତ : △PQR 6ର \(\overline{\mathbf{PQ}}\) ଓ \(\overline{\mathbf{QR}}\) ର ମଧ୍ୟବିଦୁ ଯଥାଦୃ6ମ M ଓ N | \(\overline{\mathbf{PR}}\) ଭପରିସ୍ଥ ‘S’ ଏକ ବିଦୁ | \(\overline{\mathbf{QS}}\) ଓ \(\overline{\mathbf{MN}}\) ର 6ଛଦଦିଦୁ O |
ସ୍ତାମାଶ୍ୟ : OQ = OS

ପ୍ରମାଣ : \(\frac { QM }{ MP }\) = 1 (∵ QM = MP (ଦର) )
\(\frac { QN }{ NR }\) = 1 (∵ QN = NR (ଦର) )
⇒ \(\frac { QM }{ MP }\) = \(\frac { QN }{ NR }\) ⇒ \(\overline{\mathrm{MN}} \| \overline{\mathrm{PR}}\)
\(\overline{\mathrm{MO}} \| \overline{\mathrm{PS}}\) (∵ \(\overline{\mathrm{MN}} \| \overline{\mathrm{PR}}\) )
⇒ \(\frac { QM }{ MP }\) = \(\frac { QO }{ OS }\) ⇒ 1 = \(\frac { QO }{ OS }\) (∵ \(\frac { QM }{ MP }\) = 1)
⇒ OQ = OS (ପ୍ତମାଣିତ)

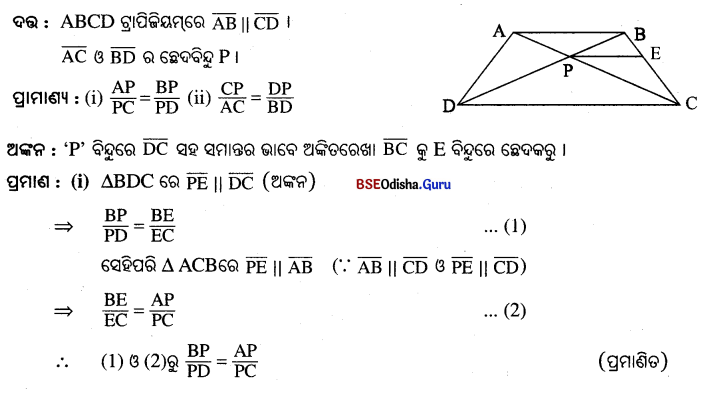
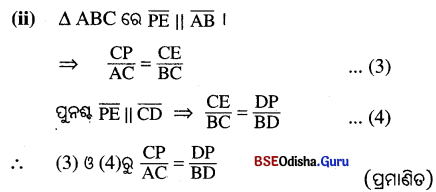
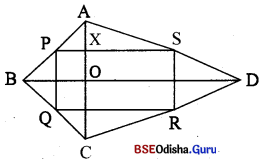
Question 8.
ABCD ଣ୍ଠାପିଲିଷ୍ଟମ6ର \(\overline{\mathbf{AB}} \| \overline{\mathbf{CD}}\) | ଲଣ \(\overline{\mathbf{AC}}\) ଓ \(\overline{\mathbf{BD}}\) ର 6ବ୍ଳଦଦିନ୍ଦି P 6ଦୃ6କ , ପ୍ତମାଶା କର 6ମ
(i) AP : PC = BP : PD
(ii) CP : AC = DP : BD |
Solution:

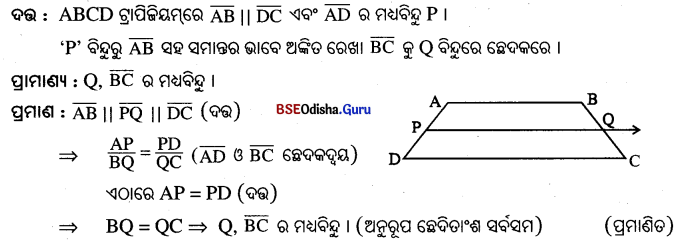
Question 9.
ABCD ଗ୍ରାପିଦିକ୍ଷ୍ମମ6ର \(\overline{\mathbf{AB}}\) || \(\overline{\mathbf{DC}}\) ଏର \(\overline{\mathbf{AD}}\) ର ମଧ୍ୟତିଦୁ P | \(\overline{\mathbf{AB}}\) ସଦୃ ସାପବ୍ଦର ଉ6ର ଅବିର \(\overleftrightarrow{\mathbf{P Q}}\) \(\overline{\mathbf{BC}}\) କ Q ଦିହି6ର 6ଛଦନ6କ , ପ୍ରମାଣ ଦ୍ଦର 6ଯ Q 6ଦୃରଚି \(\overline{\mathbf{BC}}\) ର ମଧ୍ୟନିନ୍ଦୁ |
Solution:

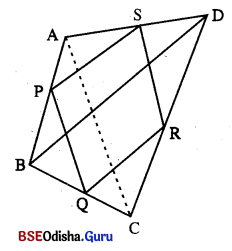
Question 10.
ABCD ଉପରୋକ୍ତ \(\overline{\mathrm{AB}}\) , \(\overline{\mathrm{BC}}\) , \(\overline{\mathrm{CD}}\) ,ଓ \(\overline{\mathrm{DA}}\) ର ମଧ୍ୟବିନ୍ଦୁ ସର୍ବସମ P, Q, R ଓ S |
(a) ପ୍ରମାଣ କର ଯେ PORS ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
(b) ଉପରୋକ୍ତ ଚତୁର୍ଭୁଜ ABCD ର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ହେଲେ, ପ୍ରମାଣକର ଯେ PORS ଏକ ଆୟତ ଚିତ୍ର ।
Solution:
(a) ଦତ୍ତ : ABCD ଉପରୋକ୍ତ \(\overline{\mathrm{AB}}\) , \(\overline{\mathrm{BC}}\) , \(\overline{\mathrm{CD}}\) , ଓ \(\overline{\mathrm{DA}}\) ର ମଧ୍ୟବିନ୍ଦୁ ସର୍ବସମ P, Q, R ଓ S |
ପ୍ରାମାଣ୍ୟ : PORS ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ଅଙ୍କନ : \(\overline{\mathrm{BD}}\) ଅଙ୍କନ କରାଯାଉ ।
ପ୍ରମାଣ : △ABD ରେ \(\overline{\mathrm{AB}}\) ର ମଧ୍ୟବିନ୍ଦୁ P ଓ \(\overline{\mathrm{AD}}\) ର ମଧ୍ୟବିନ୍ଦୁ S ।
\(\frac { AP }{ BP }\) = 1 (∵ AP = BP (ଦତ୍ତ))
ସେହିପରି ଧୂ) \(\frac { AS }{ SD }\) = 1 (∵ AS = SD (ଦତ୍ତ))

∴\(\frac { AP }{ BP }\) = \(\frac { AS }{ SD }\) ⇒ \(\overline{\mathrm{PS}}\) || \(\overline{\mathrm{BD}}\)
ସେହିପରି ପ୍ରମାଣ କରାଯାଇ ପାରିବ \(\overline{\mathrm{QR}}\) || \(\overline{\mathrm{BD}}\) |
\(\overline{\mathrm{PS}}\) || \(\overline{\mathrm{BD}}\) ଓ \(\overline{\mathrm{QR}}\) || \(\overline{\mathrm{BD}}\)
\(\overline{\mathrm{PS}}\) || \(\overline{\mathrm{QR}}\)
\(\overline{\mathrm{AC}}\) ଅଙ୍କନ କରି ସେହିପରି ପ୍ରମାଣ କରାଯାଇ ପାରେ ଯେ \(\overline{\mathrm{PQ}}\) || \(\overline{\mathrm{SR}}\) |
∴ PORS ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର |

(b) ଦତ୍ତ : ABCD ଚତୁର୍ଭୁଜରେ \(\overline{\mathrm{AC}}\) ⊥ \(\overline{\mathrm{BD}}\) | \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\), \(\overline{\mathrm{CD}}\) ଓ \(\overline{\mathrm{DA}}\) ର ମଧ୍ୟବିନ୍ଦୁ ଯଥାକ୍ରମେ P, Q, R, S |
ପ୍ରାମାଣ୍ୟ : PORS ଏକ ଆୟତଚିତ୍ର ।
ପ୍ରମାଣ : ମନେକର \(\overline{\mathrm{AC}}\) ଓ \(\overline{\mathrm{BD}}\) ଛେଦବିନ୍ଦୁ ( ଏବଂ \(\overline{\mathrm{PS}}\) ଓ \(\overline{\mathrm{AC}}\) ର ଛେଦବିନ୍ଦୁ X ।

(a) ର ଅନୁରୂପ ପ୍ରମାଣ ଦ୍ଵାରା PORS ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର 6ଚିତ୍ର ।
m∠AOB = 90° ⇒ m∠PXO = 90°
(∵ \(\overline{\mathrm{PS}}\) || \(\overline{\mathrm{BD}}\))
m∠XPXQ = 90° (∵ \(\overline{\mathrm{PQ}}\) || \(\overline{\mathrm{AC}}\))
∴ PQRS ଏକ ସାମାନ୍ତରିକ |

Question 11.
ନିମ୍ନ ଚିତ୍ରରେ △ABC ର \(\overline{\mathrm{BA}}\) ବାହୁ ସହ \(\overline{\mathrm{CM}}\) ସମାନ୍ତର, \(\overline{\mathrm{AB}}\) ର ପ୍ରାମାବିନ୍ଦୁ P | \(\overline{\mathrm{PQ}}\) || \(\overline{\mathrm{AC}}\), \(\overline{\mathrm{QR}}\) || \(\overline{\mathrm{CM}}\); ସାମାନ୍ତରିକ ମେ
\(\overline{\mathrm{PR}}\) || \(\overline{\mathrm{AM}}\) |
Solution:
ଦତ୍ତ : △ABC ରେ \(\overline{\mathrm{BA}}\) || \(\overline{\mathrm{CM}}\), AP = BP,
\(\overline{\mathrm{PQ}}\) || \(\overline{\mathrm{AC}}\) ଓ \(\overline{\mathrm{QR}}\) || \(\overline{\mathrm{CM}}\)
ପ୍ରାମାଣ୍ୟ : \(\overline{\mathrm{PR}}\)||\(\overline{\mathrm{AM}}\)
ପ୍ରମାଣ : △ABC ରେ \(\overline{\mathrm{PQ}}\) ||\(\overline{\mathrm{AC}}\) (ଦତ୍ତ) ।

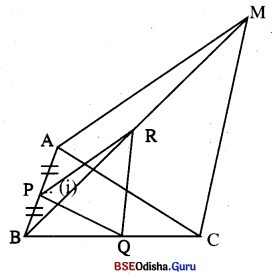
⇒ \(\frac { BP }{ AP }\) = \(\frac { BQ }{ QC }\)
△BCM ରେ \(\overline{\mathrm{QR}}\) ||\(\overline{\mathrm{CM}}\) (ଦତ୍ତ) ।
⇒ \(\frac { BQ }{ QC }\) = \(\frac { BR }{ RM }\) ……(i)
∴ (i) ଓ (ii)ରୁ \(\frac { BP }{ AP }\) = \(\frac { BR }{ RM }\)
△BCM ରେ \(\frac { BP }{ AP }\) = \(\frac { BR }{ RM }\) ⇒ \(\overline{\mathrm{PR}}\) ||\(\overline{\mathrm{AM}}\) (ପ୍ରମାଣିତ)
ତ୍ରିଭୁଜର କୋଣର ସମଦ୍ବିଖଣ୍ଡକ ସମ୍ବନ୍ଧୀୟ ଆଲୋଚନା