BSE Odisha 10th Class Maths Solutions Geometry Chapter 2 ବୃତ୍ତ Ex 2(b)

Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 2 ବୃତ୍ତ Ex 2(b) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Geometry Chapter 2 ବୃତ୍ତ Ex 2(b)

Question 1.
ନିମ୍ନ ଉକ୍ତିଗୁଡ଼ିକରେ ଠିକ୍ ଉକ୍ତି ପାଇଁ T ଓ ଭୁଲ ଉକ୍ତି ପାଇଁ F ଲେଖ ।
(i) ବୃତ୍ତର ଏକ ଉପସେଟ୍‌କୁ ଚାପ କହନ୍ତି ।
(ii) ଚାପର ଏକ ଅନ୍ତ୍ରମ୍ମ ଦିନ୍ଦୁ ସମ୍ରକ୍ର ଦୃଭର ଅନ୍ତ୍ରମ ବନ୍ଧୁ ନ୍ମ6ଦୃ |
(iii) ଗୋଟିଏ ବୃତ୍ତରେ P ଓ Q ଦୁଇଟି ଚାପର ସାଧାରଣ ପ୍ରାନ୍ତବିନ୍ଦୁ ହେଲେ ଚାପଦ୍ଵୟ ପରସ୍ପରର ପରିପୂରକ ଚାପ
(iv) ପ୍ରତ୍ୟେକ ଚାପର ପ୍ରାନ୍ତବିନ୍ଦୁକୁ କେନ୍ଦ୍ର ସହିତ ଯୋଗ କଲେ ଯେଉଁ କୋଣ ଉତ୍ପନ୍ନ ହୁଏ ତାହା ଉକ୍ତ ଚାପର କେନ୍ଦ୍ରସ୍ଥ କୋଣ ଅଟେ ।
(v) ଦୁଇଟି ଚାପର ଡିଗ୍ରୀ ପରିମାପର ସମଷ୍ଟି 360°ରୁ ଅଧ‌ିକ ହୋଇ ପାରିବ ନାହିଁ ।
(vi) ବୃତ୍ତ ଏକ ଉତ୍ତଳ ସେଟ୍ ନୁହେଁ ।
(vii) ଗୋଟିଏ ବୃତ୍ତରେ ଦୁଇଟି ଚାପର ଗୋଟିଏ ସାଧାରଣ ପ୍ରାନ୍ତ ବିନ୍ଦୁ ଥିଲେ ଚାପ ଦୁଇଟି ସନ୍ନିହିତ ଚାପ ହେବେ ।
(viii) ଦୁଇଟି ସର୍ବସମ ଜ୍ୟା ସହ ସମ୍ପୃକ୍ତ ଚାପଦ୍ଵୟ ସନ୍ନିହିତ ଚାପ ହେଲେ ଚାପଦ୍ଵୟର ସଂଯୋଗରେ ସର୍ବଦା ବୃହତ୍ ଚାପ ଗଠିତ ହେବ ।
(ix) ଦୁଇଟି ସର୍ବସମ ଜ୍ୟା ପରସ୍ପରକୁ ଲମ୍ବ ଭାବରେ ବୃତ୍ତର ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ P ରେ ଛେଦ କରନ୍ତି । ବୃତ୍ତର କେନ୍ଦ୍ର O ଠାରୁ ସେମାନଙ୍କ ପ୍ରତି \(\overline{\mathrm{OQ}}\), \(\overline{\mathrm{OR}}\) ଲମ୍ବ ଗଠନ କରାଯାଇଛି । ତେବେ ଠ, Q, P ଓ R ଏକ ବର୍ଗଚିତ୍ରର ଶୀର୍ଷବିନ୍ଦୁ ହେବେ ।
(x) \(\overparen{B P C}\) ର ଡିଗ୍ରୀ ପରିମାପ 30° । A ବୃତ୍ତ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ ହେଲେ △ABC ରେ ∠Aର ପରିମାଣ ସର୍ବଦା 15° 6ଦ୍ଵଦା
(xi) ଗୋଟିଏ ଚାପ ଅସଂଖ୍ୟ ବିନ୍ଦୁର ସମାହାର ଅଟେ ।
(xii) ବୃତ୍ତାନ୍ତର୍ଲିଖ ରମ୍ବସ୍ ଏକ ବର୍ଗଚିତ୍ର ।
Solution:
(i) T
(ii) T
(iii) T
(iv) F
(v) F
(vi) T
(vii) T
(viii) F
(ix) F
(x) F
(xi) T
(xii) T

Question 2.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(i) ଏକ ବୃହତ୍ ଚାପର ଡିଗ୍ରୀ ପରିମାପ …………….. ରୁ ବେଶୀ ।
(ii) ଗୋଟିଏ ସୁଷମ୍ ଷଡ଼ଭୁଜର ପ୍ରତ୍ୟେକ ବାହୁ ଏହାର ପରିବୃତ୍ତର କେନ୍ଦ୍ରଠାରେ ଉତ୍ପନ୍ନ କରୁଥିବା କେନ୍ଦ୍ରସ୍ଥ କୋଣର ପରିମାଣ ……………….. |
(iii)
(iv) ଗୋଟିଏ ବୃତ୍ତରେ ଦୁଇଟି ସର୍ବସମ ଜ୍ଯା \(\overline{\mathrm{AB}}\) ଓ \(\overline{\mathrm{CD}}\) ପରସ୍ପରକୁ ବୃତ୍ତର ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ Pରେ ଛେଦ କରନ୍ତି । O ବୃତ୍ତର କେନ୍ଦ୍ର ଏବଂ B ଓ C \(\overline{\mathrm{OP}}\)ର ଏକ ପାର୍ଶ୍ଵରେ ଥିଲେ \(\overparen{A D}\) ଓ ……………….. ଦୁହେଁ ସର୍ବସମ ।
(v) ଗୋଟିଏ ବୃତ୍ତରେ ଏକ ଜ୍ୟାର ଦୈର୍ଘ୍ୟ ବ୍ୟାସାର୍ଦ୍ଧ ସହ ସମାନ ହେଲେ ଉକ୍ତ ଜ୍ୟା ଦ୍ଵାରା ଛେଦିତ କ୍ଷୁଦ୍ର ଚାପର ତିଗ୍ରା ପରିମାପ ………….. |
(vi) \(\overline{\mathrm{AB}}\) ର ଏକ ପାଣ୍ଡରେ C ଓ D ଦୁଇଟି ଦିନ୍ଦୁ | m∠ACB = m∠ADB = 20° △ACD ର ପରିଦର୍ଭର 6କହ O 6ଦୃବେ m∠AOB ……………. |
(vii) m∠ABC = 90° ଚତୁର୍ଭୁକ △ABC ର ପରିଦଉଭେ AC ଏକ ………………… |
(viii) ABCD ଏକ ଦ୍ଵରାନ୍ତକଖର ଚତୁର୍ଭୁକ m∠BAD ………………. ଚାପର ଡିଗ୍ରୀ ପରିମାପର ଅର୍ଦ୍ଧେକ ।
(ix) ଏକ ଅର୍ଥବୃତ୍ତର ଡିଗ୍ରୀ ପରିମାପ ………….. |
(x) ଗୋଟିଏ ବୃତ୍ତରେ ଏକ ଚାପର ଡିଗ୍ରୀ ପରିମାପ 90° ହେଲେ, ସଂପୃକ୍ତ ଜ୍ୟା ଓ ବ୍ୟାସାର୍ଦ୍ଧର ଅନୁ ପାତ …………….. |
Solution:
(i) 180°
(ii) 60° \(\left(\frac{360^{\circ}}{6}=60^{\circ}\right)\)
(iii) 70° m∠D = 180° – 120° = 60°
m∠C = 180° – 50° = 130°
∴ m∠C – m∠D = 130° – 60° = 70°

(iv) \(\overparen{B C}\) \(\overparen{A C B}\) ≅ \(\overparen{C A D}\) ( ∵ AB ≅ CD (ଦତ୍ତ))
⇒ BC ≅ AD

(v) 60° ଜ୍ୟାର ପ୍ରାନ୍ତବିନ୍ଦୁଦ୍ଵୟ ଓ କେନ୍ଦ୍ରବିନ୍ଦୁ ଏକ ସମବାହୁ ତ୍ରିଭୁଜର ଶୀର୍ଷବିନ୍ଦୁ ହେବେ |
(vi) 40° O ବିଦୁଟି ବୃତ୍ତର କେନ୍ଦ୍ର ହେବ ।
(vii) ବ୍ୟାସ (ଅର୍ଦ୍ଧବୃତ୍ତଖଣ୍ଡସ୍ଥ କୋଣ ସମକୋଣ ।)
(viii) \(\overparen{B C D}\)
(ix) 90°
(x) √ 2 : 1 (ସଂପୃକ୍ତ ଜ୍ୟାଟି ବୃତ୍ତର ବ୍ୟାସ)

Question 3.
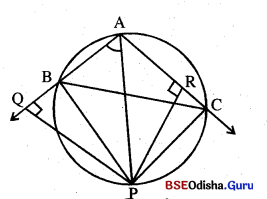
ଚିତ୍ରରେ △ABC ବୃତ୍ତାନ୍ତର୍ଲିଖ ଏବଂ ସୂକ୍ଷ୍ମକୋଣୀ । D, E, F ବୃତ୍ତ ଉପରିସ୍ଥ ତିନୋଟି ବିନ୍ଦୁ ହେଲେ ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।

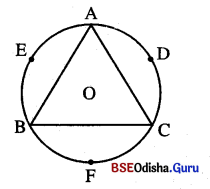
(i) ∠B କେଉଁ ଚାପର ଅନ୍ତର୍ଲିଖ୍ ?
(ii) ∠B ଦ୍ବାରା କେଉଁ ଚାପ ଛେଦିତ ?
(iii) \(\overline{\mathrm{AB}}\) ଜ୍ୟା ଦ୍ବାରା ଛେଦିତ କ୍ଷୁଦ୍ରଚାପ ଓ ବୃହତ୍ ଚାପ କିଏ ?
(iv) ∠A ର ପରିମାଣ କେଉଁ କେନ୍ଦ୍ରସ୍ଥ କୋଣ ପରିମାଣର ଅର୍ଦ୍ଧେକ ?
(v) △ABC ରେ ଯଦି AB = BC ହୁଏ ତେବେ କେଉଁ ଚାପ ଦ୍ଵୟ ସର୍ବସମ ହେବେ ?
(vi) ଦୁଇଟି ସନ୍ନିହିତ ଚାପର ନାମ ଲେଖ ଯେପରିକି ସେମାନଙ୍କ ସଂଯୋଗରେ \(\overparen{B A D}\) ଗଠିତ ହେବ ।
(vii) \(\overparen{B F C}\) ଉପରେ ଏପରି ଏକ ବିନ୍ଦୁ P ନିଅ ଯେପରିକି m∠BPA = m∠C । ଏପରି କେତୋଟି ବିନ୍ଦୁ ଅଛି ? ADC ଉପରେ ଏପରି କୌଣସି ବିନ୍ଦୁ ଅଛି କି ? \(\overparen{B E A}\) ଉପରେ ଏପରି କୌଣସି ବିନ୍ଦୁ ଅଛି କି ?
Solution::
(i) ∠B, \(\overparen{E B F}\) ର୍ଥିଥଚା \(\overparen{A B C}\) ର ଅନ୍ତ୍ର କିଣତ |
(ii) ∠Bଦ୍ଵାରା \(\overparen{A D C}\) ଛେଦିତ ।
(iii) \(\overline{\mathrm{BC}}\) ଖ୍ୟା ଦ୍ଵାରା ଛେଦିତ ସୁଦୃତାପ \(\overparen{B F C}\) ଦ୍ଦଦ୍ର ତ୍ତାପ \(\overparen{B A C}\) |
(iv) m∠A = \(\frac { 1 }{ 2 }\) m∠BOC
(v) △ABC ରେ \(\overparen{A E B}\) ≅ \(\overparen{B F C}\)
(vi) \(\overparen{B E A}\) ∪ \(\overparen{A D}\) = \(\overparen{B A D}\), \(\overparen{B E}\) ∪ \(\overparen{E A D}\) = \(\overparen{B A D}\)
(vii) ଏପରି ଅସଂଖ୍ୟ ବିନ୍ଦୁ ଅଛି । \(\overparen{A D C}\) ଉପରେ ମଧ୍ୟ ଅସଂଖ୍ୟ ବିନ୍ଦୁ ଅଛି । \(\overparen{B E A}\) ଚାପ ଉପରେ ଏପରି ବିନ୍ଦୁ ରହିବା ସମ୍ଭବ ନୁହେଁ ।

Question 4.
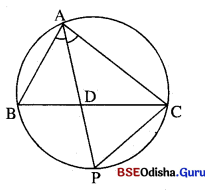
ଚିତ୍ରରେ ABCD ଏକ ବୃତ୍ତାନ୍ତର୍ଲିଖ୍ ଚତୁର୍ଭୁଜ ଯାହର କର୍ଣ୍ଣଦ୍ଵୟ ବୃତ୍ତର କେନ୍ଦ୍ରଠାରେ ଛେଦ କରନ୍ତି ।
m\(\overparen{A E B}\) = 100° 6 ଦ୍ଵ6କ |

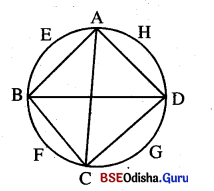
(i) ଚତୁର୍ଭୁଜର ସମସ୍ତ କୋଣ ପରିମାଣ ନିର୍ଣ୍ଣୟ କର ।
(ii) \(\overparen{A H D}\) ଓ \(\overparen{B F C}\) ମଧ୍ୟରେ କି ସମ୍ପର୍କ ଦେଖୁଛ ?
(iii) ABCD କି ପ୍ରକାର ଚତୁର୍ଭୁଜ ?
Solution:

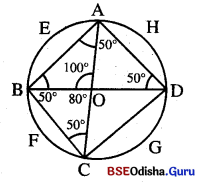
m \(\overparen{A E B}\) : 100°
⇒ m∠ADB = m∠ACB = 50°
m∠COD = 100° (ତ୍ପତାପ 6କାଶ)
⇒ m∠CBD = m∠CAD = 50°
m∠BOC = 180° – 100° = 80°
⇒ m∠BAC = m∠BDC = 40°
⇒ m∠AOD = 80°
⇒ m∠ACD = m∠ABC = 40°

(i) m∠A = m∠BAC + m∠CAD = 40° + 50° = 90°
6ସ ଦ୍ଵିପରି m∠С = 90°, m∠B = 90° ଓ m∠D = 90° |
(ii) \(\overparen{A H D}\) ≅ △\(\overparen{B F C}\)
(ii) ABCD ଏକ ଆୟତଚିତ୍ର ।

Question 5.
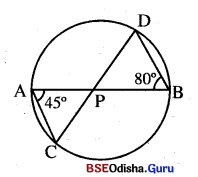
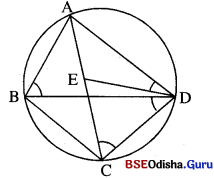
ଚିତ୍ରରେ \(\overline{\mathrm{AB}}\) ଓ \(\overline{\mathrm{CD}}\) ଜ୍ୟା ଦ୍ଵୟ ପରସ୍ପରକୁ ବୃତ୍ତର ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ P ଠାରେ ଛେଦ କରନ୍ତି । m∠PBD = 80°, m∠CAP = 45° 6ଦ୍ଵଲେ :
(i) △BPDର କୋଣ ପରିମାଣଗୁଡ଼ିକ ନିର୍ଣ୍ଣୟ କର ।
(ii) △APCର କୋଣ ପରିମାଣଗୁଡ଼ିକ ନିର୍ଣ୍ଣୟ କର ।
(iii) △APC ଓ △BPD ମଧ୍ୟରେ କି ସମ୍ପର୍କ ଦେଖୁଛ ?

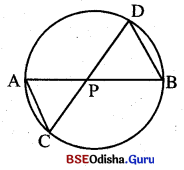
Solution:
m∠PBD = 80°, m∠CAP = 45°

(i) \(\overparen{B C}\) ଉପରିସ୍ଥ m∠CDB = m∠CAP = 45°
∴ m∠BPD = 180° – 80° – 45° = 55°
∴ △BPDର m∠BPD = 55°
m∠PDB = 45°, m∠PBD = 80°

(ii)
△APCର m∠CAP = 45° (ଦଉ)
m∠APC = m∠BPD = 55° (ପ୍ରତାପ 6କାଣ)
∴ m∠ACP = m∠PBD = 80° (\(\overparen{A D}\) ଉପରିସ୍ଥ ପରିଧ୍ଵସ୍ଥ ଏକ କୋଣ)

(iii) △APC ~ △BPD (କୋ . କୋ . କୋ . ପାଦଣ୍ୟ)

Question 6.
△ABCରେ ∠Aର ସମଦ୍ବିଖଣ୍ଡକ ତ୍ରିଭୁଜର ପରିବୃତ୍ତକୁ D ବିନ୍ଦୁରେ ଛେଦ କଲେ ପ୍ରମାଣ କର ଯେ, △BDC ସମଦ୍ବିବାହୁ ।
Solution:

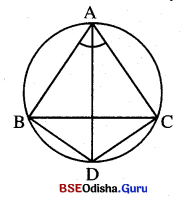
ଦତ୍ତ : △ABCର ∠Aର ସମଦ୍ଵିଖଣ୍ଡକ ତ୍ରିଭୁଜର ପରିବୃତ୍ତକୁ D ବିନ୍ଦୁରେ ଛେଦକରେ ।
ପ୍ରାମାଣ୍ୟ : △BDC ସମଦ୍ବିବାହୁ ।
ପ୍ରମାଣ : ∠BAD ≅ ∠CAD (ଦଉ)
⇒ \(\overparen{B D}\) ≅ \(\overparen{D C}\) ⇒ \(\overline{\mathrm{BD}}\) ≅ \(\overline{\mathrm{DC}}\) (ଚାପ ସର୍ବସମ ହେତୁ ଜ୍ୟାଦ୍ଵୟ ସର୍ବସମ)
=> △BDC ସମଦିବାହୁ ।

Question 7.
ଚିତ୍ରରେ ଗୋଟିଏ ବୃତ୍ତର ଏକ ବହିଃସ୍ଥ ବିନ୍ଦୁ A ଠାରୁ \(\overrightarrow{\mathbf{AP}}\) ଓ \(\overrightarrow{\mathbf{AR}}\) ରଶ୍ମିଦ୍ଵୟ ବୃତ୍ତକୁ ଯଥାକ୍ରମେ P, Q ଏବଂ R, S ଠାରେ ଛେଦ କରନ୍ତି ଯେପରି A-P-Q ଏବଂ A-R-S |
(a) ପ୍ରମାଣ କର ଯେ △APR ~ △AQS
(b) ପ୍ରମାଣ କର ଯେ △APS ~ △ARQ

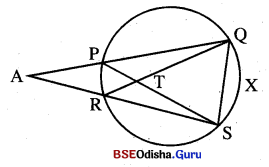
(C) ଯଦି \(\overline{\mathrm{PS}}\) ଓ \(\overline{\mathrm{QR}}\) ର ଛେନ୍ଦ୍ରବିନ୍ଦୁ T ହୁଏ, ତେଦେ
(i) ପ୍ରମାଣ କର ଯେ TP • TS = TR • TQ
(ii) ପ୍ତମାଣ କାର 6ପ m∠PTR = \(\frac { 1 }{ 2 }\) (m\(\overparen{Q S}\) + m\(\overparen{P R C}\))

(d) m∠PAR = 15° ଏବଂ m\(\overparen{Q X S}\) = 50° ହେଲେ m∠PTR ନିର୍ଣ୍ଣୟ କର ।
Solution:

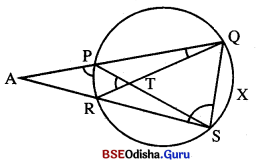
(a) ପ୍ରମାଣ : PRSQ ଏକ ଦ୍ଵରାନୁଲଖତ ଚତୁରୁଜ |
⇒ m∠RSQ + m∠RPQ = 180°
କିନ୍ନ m∠RPQ + m∠APR = 180°
⇒ m∠RSQ + m∠RPQ = m∠RPQ + m∠APR
m∠RSQ = m∠APR
△APR ଓ △AQS ମଧ୍ୟ6ର m∠RAP = m∠QAS
ଓ m∠RSQ = m∠APR |
⇒ △APR ~ △AQS (6କା-6କା ସାଦ୍ୱଣ)

(b) △APS ଓ △ARQ ମଧ୍ୟ6ର
m∠PAS = m∠RAQ (ମଧ୍ୟ6ର 6କା)
m∠ASP = m∠AQR (ଏକ ଚାପ ଉପରିମ ପରିଧମ 6କାଣ)
⇒ △APS ~ △ARQ

(c) (i) △ TPQ ଓ △TRS ମଧ୍ୟ6ର
m∠TPQ = m∠TRS (ଏକ ଚାପ ଉପରିମ ପରିଧମ 6କାଣ)
m∠PTQ = m∠RTS (ପ୍ତତାପ 6କାଣ)
⇒ △TPQ ~ △TRS (6କା-6କା ସାଦ୍ୱଣ)
⇒ \(\frac { TP }{ TR }\) = \(\frac { TQ }{ TS }\) ⇒ TP • TS = TR • TQ
=m∠SPQ + m∠PQR = \(\frac { 1 }{ 2 }\)m\(\overparen{Q S}\) + \(\frac { 1 }{ 2 }\)m\(\overparen{P R}\) = \(\frac { 1 }{ 2 }\) (m\(\overparen{Q S}\) + m\(\overparen{P R}\)) (9flêe)

(d) m∠PAR = 15°
m\(\overparen{Q X S}\) = 50° ⇒ m∠QPS = \(\frac { 50° }{ 2 }\) = 25°
△APS 6ର 6କାଣ m∠QPS = m∠PAR + m∠PSR
⇒ 25° = 15° +m∠PSR ⇒ m∠PSR = 25° – 15° = 10°
m∠QRS = m∠QPS = 25°
∴ m∠PTR = m∠QRS + m∠TSR = 25° + 10° = 35°

Question 8.
ଚିତ୍ରରେ ABC ଦଉର \(\overparen{A X B}\) ଓ \(\overparen{B Y C}\) ହୁକରି ଚାପର ଗିଗାମାପ ଯଥାକୃମେ 80° ଓ 140° |

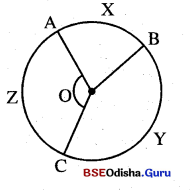
(i) m∠BAC କିଣ୍ଡଯ କର |
(ii) m\(\overparen{A B C}\) କିଣ୍ଡଯ କର |
(iii) m\(\overparen{A C B}\) କିଣ୍ଡଯ କର |
(iv) \(\overparen{A Z C}\) ଓ \(\overparen{B Y C}\) ମଧ୍ୟରେ କି ସମଳ ଅଛି ?
Solution:
m\(\overparen{A X B}\) + m\(\overparen{B Y C}\) + m\(\overparen{A Z C}\) = 360° ⇒ 80° + 140° + m\(\overparen{A Z C}\) = 360°
⇒ m\(\overparen{A Z C}\) = 360° – 80° – 140° = 140°
(i) M∠BAC = \(\frac { 1 }{ 2 }\) m\(\overparen{B Y C}\) = \(\frac { 1 }{ 2 }\) × 140° = 70°
(ii) \(\overparen{A B C}\) = 360° – 140° = 220°
(iii) \(\overparen{A C B}\) = M\(\overparen{A Z C}\) + m\(\overparen{B Y C}\) = 140° + 140° = 280°
(iv) \(\overparen{A Z C}\) ≅ \(\overparen{B Y C}\) (“: m∠AOC = m∠BOC)

Question 9.
ଏକ ବୃତ୍ତର କେନ୍ଦ୍ର O ଏବଂ \(\overline{\mathrm{AB}}\) ଏକ ବ୍ୟାସ । ବୃତ୍ତ ଉପରିସ୍ଥ P ଓ ଠୁ ବିଦୁ୍ୟଦ୍ୱୟ \(\overline{\mathrm{AB}}\) ର ଏକ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ । ଯଦି A ଓ P ପ୍ରାନ୍ତ ବିନ୍ଦୁ ବିଶିଷ୍ଟ ଚାପର ଡିଗ୍ରୀ ପରିମାପ 60° ଏବଂ B ଓ ( ପ୍ରାନ୍ତବିନ୍ଦୁ ବିଶିଷ୍ଟ ଚାପର ଡିଗ୍ରୀ ପରିମାପ 50° ହୁଏ ତେବେ–
(i) A ଓ Q ପ୍ରାନ୍ତବିନ୍ଦୁ ବିଶିଷ୍ଟ କ୍ଷୁଦ୍ରଚାପର ଡିଗ୍ରୀ
(ii) P ଓ B ପ୍ରାନ୍ତବିନ୍ଦୁ ବିଶିଷ୍ଟ ବୃହତ୍ ଚାପର ଡିଗ୍ରୀ
(iii) P ଓ Q ପ୍ରାନ୍ତବିନ୍ଦୁ ବିଶିଷ୍ଟ ବୃହତ୍ ଚାପର ଡିଗ୍ରୀ ପରିମାପ ନିର୍ଣ୍ଣୟ କର ।

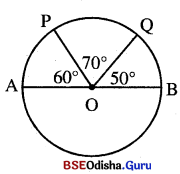
Solution:
m∠AOP = 60°
m∠BOQ = 50°
⇒ m⇒POQ = 180° – (60° + 50°) = 70°
(i) m\(\overparen{A Q}\) = 60° + 70° = 130°
(ii) m\(\overparen{P B}\) = 70° + 50° = 120°
(iii) m\(\overparen{P Q}\) = 70°

Question 10.
\(\overline{\mathrm{AB}}\) ଓ \(\overline{\mathrm{CD}}\) ଦୁଇଟି ସମାନ୍ତର ଜ୍ୟା । ପ୍ରମାଣ କର ଯେ,
(i) M\(\overparen{A X C}\) = m\(\overparen{B Y D}\), (ii) AC = BD |

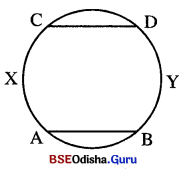
Solution:
ଦତ୍ତ : ABCD 96 \(\overline{\mathrm{CD}}\) || \(\overline{\mathrm{AB}}\) |
ପ୍ରାମାଣ୍ୟ :
(i) M\(\overparen{A X C}\) = m\(\overparen{B Y D}\)
(ii) AC = BD
ଅଙ୍କନ : \(\overline{\mathrm{BC}}\) ଅଙ୍କନ କର ।
ତ୍ପମାଣ : \(\overline{\mathrm{CD}}\) || \(\overline{\mathrm{AB}}\) (ଦଉ)

⇒ m∠ABC = m∠BCD
⇒ \(\frac { 1 }{ 2 }\) m\(\overparen{A X C}\) = \(\frac { 1 }{ 2 }\) m\(\overparen{B Y D}\)
⇒ m\(\overparen{A X C}\) = m\(\overparen{B Y D}\)

(ii) \(\overparen{A X C}\) = \(\overparen{B Y D}\) ⇒ AC = BD (ଚାପ ସବସମ ହେତ୍ ଲ୍ୟା ସଦସ୍ୟ)

Question 11.
ABCD ଏକ ଦ୍ଵରୀନ୍ତ୍ର କିଖବ ତତ୍କଲକ |
(i) AC = BD ଏବଂ \(\overline{\mathbf{AB}}\)||\(\overline{\mathbf{CD}}\) 6ଦ୍ର6କ ପ୍ରମାଣ କର ସେ, AD = BC |
(ii) AD = BC 6ଦ୍ର6କ ପ୍ରମାଣ କର ସେ, AC = BD ଏବଂ \(\overline{\mathbf{AB}}\)||\(\overline{\mathbf{CD}}\) |
Solution:
(i) ଦର : ABCD ଦୃଭାନ୍ତ୍ରରଖତ ଚତୁରୁକରେ
AC = BD ଏବଂ \(\overline{\mathbf{AB}}\)||\(\overline{\mathbf{CD}}\) |
ପ୍ରାମଣ୍ୟ: AD = BC
ପ୍ରମାଣ : AC = BD (ଦତ୍ତ)

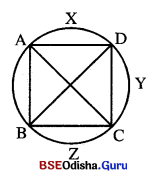
⇒ \(\overparen{A D C}\) ≅ \(\overparen{B C D}\)
⇒ l \(\overparen{A X D}\) + l \(\overparen{D Y C}\) = l \(\overparen{D Y C}\) + l \(\overparen{B Z C}\)
⇒ l \(\overparen{A X D}\) = l \(\overparen{B Z C}\) ⇒ \(\overparen{A X D}\) ≅ \(\overparen{B Z C}\)
⇒ AD = BC

(ii) ଦଉ : ABCD ଏକ ତ୍ରଭାନ୍ତକଖତ ତଡୁରୁକ | AD = BC
ପ୍ତମାଣ୍ୟ: (i) AC = BD (ii) \(\overline{\mathbf{AB}}\)||\(\overline{\mathbf{CD}}\)
ପ୍ରମଣ : AD = BC ⇒ \(\overparen{A X D}\) ≅ \(\overparen{B Z C}\)

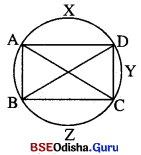
⇒ l \(\overparen{A X D}\) = l \(\overparen{B Z C}\)
⇒ l \(\overparen{A X D}\) + l \(\overparen{D Y C}\) = l \(\overparen{D Y C}\) + l \(\overparen{B Z C}\)
⇒ l \(\overparen{A D C}\) = l \(\overparen{B C D}\) ⇒ \(\overparen{A D C}\) ≅ \(\overparen{B C D}\) ⇒ AC = BD (i)
ପୁକଣ୍ଠ ∵ \(\overparen{A X D}\) ≅ \(\overparen{B Z C}\)
⇒ m \(\overparen{A X D}\) + m \(\overparen{B Z C}\) ⇒ \(\frac { 1 }{ 2 }\) m \(\overparen{A X D}\) = \(\frac { 1 }{ 2 }\) m \(\overparen{B Z C}\)
⇒ m∠ABD = m∠BDC (ଏକାନ୍ତ୍ରର) ⇒ \(\overline{\mathbf{AB}}\)||\(\overline{\mathbf{CD}}\) …(ii)

Question 12.
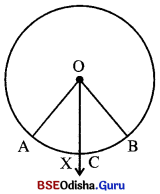
(i) ଗୋଟିଏ ବୃତ୍ତରେ \(\overparen{A X B}\) ଏକ ଚାପ । ପ୍ରମାଣ କର ଯେ \(\overparen{A X B}\)ର ଅନ୍ତଃସ୍ଥ ଗୋଟିଏ ଏବଂ କେବଳ ଗୋଟିଏ ବିନ୍ଦୁ C ଅଛି ଯେପରି \(\overparen{A C}\) ଓ \(\overparen{B C}\) ଚାପଦ୍ଵୟ ସର୍ବସମ ହେବେ । (C ବିନ୍ଦୁକୁ \(\overparen{A X B}\) ର ମଧ୍ୟବିନ୍ଦୁ କୁହାଯାଏ ।)
(ii) ଚାପର ମଧ୍ୟବିନ୍ଦୁ ଧାରଣାକୁ ବ୍ୟବହାର କରି ପ୍ରମାଣ କର ଯେ, AXBରେ ଅସଂଖ୍ୟ ବିନ୍ଦୁ ଅଛି ।

Solution:
(i) ଦତ୍ତ : O ବୃତ୍ତର କେନ୍ଦ୍ର । \(\overparen{A X B}\) ଏକ ଚାପ ।
ପ୍ରାମାଣ୍ୟ : (i) \(\overparen{A X B}\) ର ଅନ୍ତଃସ୍ଥ ଗୋଟିଏ
ଏବଂ କେବଳ ଗୋଟିଏ ବିନ୍ଦୁ C ଅଛି,
ଯେପରି \(\overparen{A C}\) = \(\overparen{C B}\)ହେବ ।
(ii) \(\overparen{A X B}\) ରେ ଅସଂଖ୍ୟ ବିନ୍ଦୁ ରହିଅଛି ।
∠AOB ର ସମଦ୍ଵିଖଣ୍ଡକ \(\overrightarrow{\mathrm{OC}}\) ଅଙ୍କନ କର ।
ଅଙ୍କନ :
ପ୍ରମାଣ :
(i) \(\overparen{A X B}\) ଚାପ ଉପରେ ଅବସ୍ଥିତ ଆବଶ୍ୟକ C ବିନ୍ଦୁଟି ଅନନ୍ୟ ଅର୍ଥାତ୍ ଗୋଟିଏ ଓ କେବଳ ଗୋଟିଏ ବିନ୍ଦୁ ହେବ ଯାହା m∠AOB ର ସମଦ୍ବିଖଣ୍ଡକ ରଶ୍ମି \(\overrightarrow{\mathrm{OC}}\) ଉପରେ ଅବସ୍ଥିତ ହେବ । ପୁନଶ୍ଚ ଚାପର ସର୍ବସମତା ଅନୁସାରେ ଦୁଇଟି ଚାପର ଡିଗ୍ରୀ ପରିମାପ ସମାନ ହେଲେ ଚାପଦ୍ଵୟ ସର୍ବସମ ହେବେ ।
ଦର ଚିତ୍ର6ର m∠AOC = m∠BOC 6ଦ୍ରଦ \(\overparen{A C}\) = \(\overparen{C B}\) 6ଦ୍ରଦ | (ପ୍ରମାଣିତ)

(ii) ଦତ୍ତ ଚିତ୍ରରେ A ଓ B ବିନ୍ଦୁ ସମେତ ‘A’ ଠାରୁ ‘B’ ପର୍ଯ୍ୟନ୍ତ ବୃତ୍ତ ଉପରିସ୍ଥ ସମସ୍ତ ବିନ୍ଦୁ ମାନଙ୍କର ସେଟ୍‌କୁ ଏକ ଚାପ କୁହାଯାଏ । A ଓ B ଏହି ଚାପର ଦୁଇଟି ପ୍ରାନ୍ତବିନ୍ଦୁ ଅଟନ୍ତି । ପ୍ରାନ୍ତବିନ୍ଦୁ ଭିନ୍ନ ଚାପ ଉପରିସ୍ଥ ଅନ୍ୟ ସମସ୍ତ ବିନ୍ଦୁମାନଙ୍କୁ ଚାପର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ କୁହାଯାଏ; ଯାହା ଅସଂଖ୍ୟ ବିନ୍ଦୁମାନଙ୍କର ସେଟ୍ ।(ପ୍ରମାଣିତ)

Question 13.
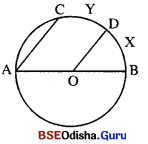
ଚିତ୍ରରେ AB ବୃତ୍ତର ଏକ ବ୍ୟାସ ଏବଂ O କେନ୍ଦ୍ର । OD ଯେକୌଣସି ଏକ ବ୍ୟାସାର୍ଦ୍ଧ | \(\overline{\mathbf{AC}}\)||\(\overline{\mathbf{OD}}\) ହେଲେ, ପ୍ରମାଣ କର ଯେ, \(\overparen{B X D}\) ଓ \(\overparen{D Y C}\) ସର୍ବସମ ଅର୍ଥାତ୍ D, \(\overparen{B D C}\)ର ମଧ୍ୟବିନ୍ଦୁ । (ସୂଚନା : \(\overline{\mathbf{OC}}\) ଅଙ୍କନ କରି ଦର୍ଶାଅ ଯେ, m∠BOD = m∠DOC)

Solution:
ଦତ୍ତ : ବୃତ୍ତର କେନ୍ଦ୍ର O | \(\overline{\mathbf{AB}}\) ବୃତ୍ତର ବ୍ୟାସ । \(\overline{\mathbf{AC}}\)||\(\overline{\mathbf{OD}}\) |
ପ୍ରାମାଣ୍ୟ : \(\overparen{B X D}\) ≅ \(\overparen{D Y C}\) ଅର୍ଥାତ୍ D, \(\overparen{B D C}\) ର ମଧ୍ୟବିନ୍ଦୁ ।
ଅଙ୍କନ : \(\overline{\mathbf{CO}}\) ଅଙ୍କନ କର ।

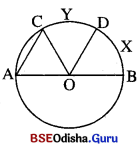
ପ୍ରମାଣ : △AOC ରେ OA = OC ⇒ m∠OAC = m∠OCA
କିନ୍ତୁ m∠OAC – m∠BOD (ଅନୁରୁପ)
∴ m∠OAC = m∠BOD (i)
ପୁନଶ୍ଚ m∠OCA=m∠COD …(ii)
(i) ଓ (ii) ରୁ m∠BOD = m∠COD ⇒ \(\overparen{B X D}\) ≅ \(\overparen{D Y C}\)
⇒ D, \(\overparen{B D C}\) ର ମଧ୍ୟବିନ୍ଦୁ ।

Question 14.
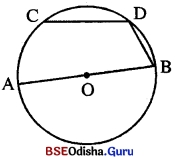
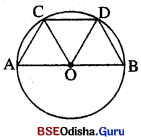
ଚିତ୍ରରେ \(\overline{\mathbf{CD}}\) ଜ୍ୟା \(\overline{\mathbf{AB}}\) ବ୍ୟାସ ସହ ସମାନ୍ତର ଏବଂ CD = OB |
ପ୍ରମାଣ୍ୟ କର ଯେ m∠BDC = 2m∠OBD |

Solution:
ଦତ୍ତ : ବୃତ୍ତର \(\overline{\mathbf{AB}}\) ବ୍ୟାସ । \(\overline{\mathbf{CD}}\) ଜ୍ୟା । CD = OB \(\overline{\mathbf{CD}}\) ର ଦୈର୍ଘ୍ୟ, ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ସହ ସମାନ ।
ପ୍ରାମାଣ୍ୟ : m∠BDC = 2m∠OBD
ଅଙ୍କନ : \(\overline{\mathbf{OC}}\) ଏବଂ \(\overline{\mathbf{OD}}\) ଅଙ୍କନ କର ।
ସ୍ତମାଣ : CD = OB = OC = OD ∴ △OCD ସମବାହୁ ।

⇒ m∠OCD = 60°
ପୁନଶ୍ଚ, COBD ଏକ ରମଣ (∵ CD = OB, \(\overline{\mathbf{CD}}\)||\(\overline{\mathbf{OB}}\) ଏବଂ OB = OC = CD)
∴ m∠OBD =m∠OCD = 60° ଏବଂ m∠BDC = 120°
∴ m∠BDC = 2m∠OBD (ପ୍ରମାଣିତ)

Question 15.
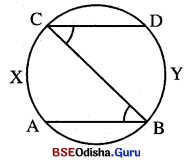
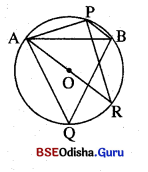
ABCD ବୃତ୍ତାନ୍ତର୍ଲିଖୂତ ଚତୁର୍ଭୁଜର \(\overline{\mathbf{AC}}\) ଓ \(\overline{\mathbf{BD}}\) କର୍ଣ୍ଣଦ୍ୱୟ ପରସ୍ପରକୁ P ଠାରେ ଛେଦ କରନ୍ତି । O ବୃତ୍ତର କେନ୍ଦ୍ର ଏବଂ B ଓ C, \(\overleftrightarrow{O P}\) ର ବିପରୀତ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ । ଯଦି AC = BD ହୁଏ, ତେବେ ପ୍ରମାଣ କର ଯେ,
(i) AB = CD, (ii) PA = PD 1° (iii) \(\overline{\mathbf{BC}}\) || \(\overline{\mathbf{AD}}\) |
Solution:
ଦତ୍ତ : ABCD ଏକ ବୃତ୍ତାନ୍ତର୍ଲିଖ୍ ଚତୁର୍ଭୁଜ । \(\overline{\mathbf{AC}}\) ଓ \(\overline{\mathbf{BD}}\) କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ P ଠାରେ ଛେଦ କରନ୍ତି ।
AC = BD |

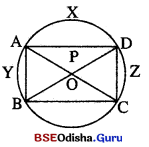
ପ୍ରାମାଣ୍ୟ : (i) AB = CD (ii) PA = PD (iii) \(\overline{\mathbf{BC}}\) || \(\overline{\mathbf{AD}}\)
ପ୍ତମାଣ: (i) AC = BD ⇒ \(\overparen{A D C}\) ≅ \(\overparen{B A D}\)
⇒ \(\overparen{A Y B}\) ≅ \(\overparen{C Z D}\)
(∵ \(\overparen{A X D}\) ଭରଯ \(\overparen{A D C}\) ଓ \(\overparen{B A D}\) ର ପାଧାରଣ ଚାପ )
⇒ AB = CD ….(i)

(ii) △ABD ଏବଂ △ADC ଦଯ6ର \(\overline{\mathbf{AD}}\) ପାଧାରଣ, AB = CD [(i) ରେ ପ୍ତମାଣିତ]
ଏବଂ AC = BD (ଦର)
∴ m∠ADB = m∠CAD ⇒ m∠ADP = m∠PAD
⇒ PA = PD …(ii)

(iii) m∠DAC = m∠DBC (ଏକ ଦ୍ଵରଖଣ୍ଡମ 6କାଣ)
କିନ୍ତୁ m∠DAC = m∠ADB
∴ m∠ADB = m∠PBC
କିନ୍ତୁ ଏମା6ନ ଏକାନ୍ତ୍ରର |
∴ \(\overline{\mathbf{BC}}\) || \(\overline{\mathbf{AD}}\)

Question 16.
(i) ପ୍ରମାଣ କର ଯେ ପ୍ରମାଣ କରଯେ ର ଥନ୍ତ୍ର କିଣିତ 6କାଶ ଏକ ପୁର6କାଣ |
(ii) ପ୍ରମାଣ କର ଯେ ଏକ ବୃହତ୍ ଚାପର ଅନ୍ତର୍ଲିଖ କୋଣ ଏକ ସୂକ୍ଷ୍ମକୋଣ ।
(ସୂଚନା : \(\overparen{A P B}\) ଏକ କ୍ଷୁଦ୍ର ଚାପ ଓ \(\overparen{A Q B}\) ଏକ ବୃହତ୍ ଚାପ ହେଉ ।
\(\overline{\mathbf{AD}}\) ଦ୍ୟାସ ଅକନ କର | m∠APD = 90° m∠APB)

Solution:
ଏବଂ m∠AQB < 90°
ଅଙ୍କନ : \(\overline{\mathbf{AR}}\) ବ୍ୟାସ ଅଙ୍କନ କରି । \(\overline{\mathbf{PR}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : (i) \(\overline{\mathbf{AR}}\) ବ୍ୟାସ । m∠APR ଅର୍ଥବୃତ୍ତଖଣ୍ଡସ୍ଥ କୋଣ । ∴ m∠APR = 90°
କିନ୍ତ୍ର R, ∠APB ର ଅନ୍ତ୍ ମ ହୋଇଥିବାରୁ m∠APR + m∠RPB = m∠APB
m∠APR = 90° ହେତୁ m∠APB > 90° ….. (i)
ଅର୍ଥାତ୍ ∠APB ଏକ ସ୍ଥୂଳକୋଣ ।

(iii) \(\overparen{A P B}\) କ୍ଷୁଦ୍ର ଚାପର ବିପରୀତ ଚାପ \(\overparen{A Q B}\) ଏକ ବୃହତ୍ ଚାପ ।
m∠APB+m∠AQB = 180° (·.· AQBP ଏକ ବୃହତ୍ ଚାପ ହେଉ )
(i) ରେ ପ୍ରମାଣିତ m∠APB > 90°
∴ m∠AQB < 90° ଅର୍ଥାତ୍ m∠AQB ଏକ ସୂକ୍ଷ୍ମକୋଣ । (ପ୍ରମାଣିତ)

Question 17.
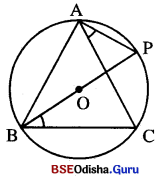
(i) △ABCର ପରିବୃତ୍ତର କେନ୍ଦ୍ର ( ତ୍ରିଭୁଜଟିର ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ହେଲେ ପ୍ରମାଣ କର ଯେ,
m∠BAC + m∠OBC = 90° |
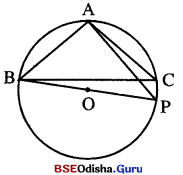
(ii) △ABCର ପରିବୃତ୍ତର କେନ୍ଦ୍ର O ତ୍ରିଭୁଜଟିର ଏକ ବହିଃସ୍ଥ ବିନ୍ଦୁ । O ଏବଂ A, \(\overline{\mathbf{BC}}\) ର ବିପରୀତ ପାଣମ 6ଦୃକେ, ଦେଲେ ପ୍ରମାଣ କର ଯେ, m∠BAC – m∠OBC = 90° |
Solution:
(i) ଦତ୍ତ : △ABCର ପରିବୃତ୍ତର କେନ୍ଦ୍ର ଠ, ତ୍ରିଭୁଜର ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ।
ପ୍ତାମାଣ୍ୟ: m∠BAC + m∠OBC = 90°
ଅଙ୍କନ : \(\overrightarrow{\mathrm{BO}}\) ବୃତ୍ତର ପରିଧ‌ିକୁ P ବିନ୍ଦୁରେ ଛେଦ କରୁ । \(\overline{\mathbf{PA}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : ABC ବୃତ୍ତର ବ୍ୟାସ \(\overline{\mathbf{BP}}\) |

⇒ m∠BAP = 90° (ଅଦି ଦ୍ଵରଖଣ୍ଡମ କୋଣ)
⇒m∠BAC+m∠CAP = 90°
ମାତ୍ର m∠CAP = m∠PBC (ଏକ ବୃତ୍ତଖଣ୍ଡସ୍ଥ କୋଣ)
⇒ m∠PBC=m∠OBC
⇒ m∠BAC+m∠OBC = 90°

(ii) ଦତ୍ତ : △ABCର ପରିବୃତ୍ତର କେନ୍ଦ୍ର ଠ ତ୍ରିଭୁଜଟିର ଏକ ବହିଃସ୍ଥ ବିନ୍ଦୁ ।
ପ୍ତାମାଣ୍ୟ: m∠BAC – m∠OBC = 90°
ଅଙ୍କନ : \(\overrightarrow{\mathrm{BO}}\) ବୃତ୍ତର P ବିନ୍ଦୁରେ ଛେଦକରୁ । \(\overline{\mathbf{PA}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ: ABC ଦ୍ଦଭର ବ୍ୟାସ \(\overline{\mathbf{BP}}\) |

⇒ m∠BAP = 90° (ଅଦି ଦ୍ଵରଖଣ୍ଡମ କୋଣ)
⇒ m∠BAC – m∠CAP = 90°
⇒ m∠BAC – m∠CBP = 90°
(∵ m∠CAP – m∠CBP ଏକ ବୃତ୍ତଖଣ୍ଡସ୍ଥ କୋଣ)
⇒ m∠BAC – m∠OBC = 90°

Question 18.
ପ୍ରମାଣ କର ଯେ ଏକ ଟ୍ରାପିଜିୟମ୍‌ର ଅସମାନ୍ତର ବାହୁଦ୍ୱୟ ସର୍ବସମ ହେଲେ ଟ୍ରାପିଜିୟମ୍ ବୃତ୍ତାନ୍ତର୍ଲିଖୁତ ହେବ ।
Solution:
ଦତ୍ତ : ABCD ଏକ ଟ୍ରାପିଜିୟମ୍ । \(\overline{\mathrm{AD}}\) || \(\overline{\mathrm{BC}}\) ଏବଂ \(\overline{\mathrm{AB}}\) ≅ \(\overline{\mathrm{CD}}\) |
ପ୍ରାମାଣ୍ୟ : ABCD ଏକ ବୃତ୍ତାନ୍ତର୍ଲିଖ୍ ଚତୁର୍ଭୁଜ ।

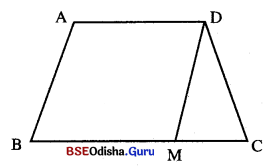
ଅଙ୍କନ : \(\overline{\mathrm{DM}}\) || \(\overline{\mathrm{AB}}\) ଅଙ୍କନ କର ।.
\(\overline{\mathrm{DM}}\) , \(\overline{\mathrm{BC}}\) କୁ M ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
ପ୍ରମାଣ : ADBM ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
(: \(\overline{\mathrm{AD}}\) || \(\overline{\mathrm{BM}}\) ଏବଂ \(\overline{\mathrm{DM}}\) || \(\overline{\mathrm{AB}}\) )
⇒ \(\overline{\mathrm{AB}}\) ≅ \(\overline{\mathrm{DM}}\)
କିନ୍ତୁ ଦକ \(\overline{\mathrm{AB}}\) ≅ \(\overline{\mathrm{DC}}\)
∴ \(\overline{\mathrm{DM}}\) ≅ \(\overline{\mathrm{DC}}\) ⇒ m∠DMC = m∠DCM
କିନ୍ତୁ \(\overline{\mathrm{AB}}\) || \(\overline{\mathrm{DM}}\), \(\overline{\mathrm{BC}}\) ଛେଦକ । ⇒ m∠ABM = m∠DMC (ଅନୁରୂପ)
m∠ABM = m∠DCM ⇒ m∠ABC = m∠DCB
\(\overline{\mathrm{AD}}\) || \(\overline{\mathrm{BC}}\) ହେତ୍ର m∠DAB + m∠ABC = 180°
⇒ m∠DAB + m∠DCB = 180° (∵ m∠ABC = m∠DCB)
⇒ ABCD ଏକ ବୃତ୍ତାନ୍ତର୍ଲିଖ୍ ଚତୁର୍ଭୁଜ । (ପ୍ରମାଣିତ)

Question 19.
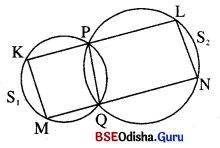
ଦୁଇଟି ବୃତ୍ତ ପରସ୍ପରକୁ P ଓ () ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । P ବିନ୍ଦୁ ମଧ୍ୟଦେଇ ଏକ ସରଳରେଖା ବୃତ୍ତଦ୍ଵୟକୁ K ଓ L ବିନ୍ଦୁରେ ଛେଦ କରେ । ସେହିପରି Q ମଧ୍ୟଦେଇ ଏକ ସରଳରେଖା ବୃତ୍ତଦ୍ଵୟକୁ M ଓ N ବିନ୍ଦୁରେ ଛେଦ କରେ । K ଓ M \(\overline{\mathrm{PQ}}\) ର ଏକ ପାର୍ଶ୍ବରେ ଥିଲେ ପ୍ରମାଣ କର ଯେ, \(\overline{\mathrm{KM}}\) || \(\overline{\mathrm{LN}}\) |

Solution:
ଦତ୍ତ : S₁ ଓ S₂ ବୃତ୍ତଦ୍ଵୟ ପରସ୍ପରକୁ P ଓ Q ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।
P ଓ Q ବିନ୍ଦୁ ମଧ୍ୟଦେଇ ଅଙ୍କିତ ସରଳରେଖା ବୃତ୍ତଦ୍ଵୟକୁ ଯଥାକ୍ରମେ
K, L ଏବଂ M, N ବିନ୍ଦୁରେ ଛେଦ କରୁଛନ୍ତି ।
ପ୍ରାମାଣ୍ୟ : \(\overline{\mathrm{KM}}\) || \(\overline{\mathrm{LN}}\)
ଅଙ୍କନ : \(\overline{\mathrm{PQ}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : m∠KMQ = m∠QPL (∵ ବୃତ୍ତାନ୍ତର୍ଲିଖୂତ ଚତୁର୍ଭୁଜର ବହିଃସ୍ଥ କୋଣର ପରିମାଣ, ଏହାର ବିପରୀତ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ ସହ ସମାନ ।)
କିନ୍ତୁ m∠QPL + m∠QNL = 180° (ଦୃଭାନ୍ତ୍ରକଖତ ଚତୁରୁକର ବିପର।ତ କୋଣ)
∴ m∠KMQ + m∠QNL = 180°; ମାତ୍ର ଏହି କୋଣଦ୍ଵୟ ଏକ ପାର୍ଶ୍ୱସ୍ଥ ଅନ୍ତଃସ୍ଥ କୋଣ ।
⇒ \(\overline{\mathrm{KM}}\) || \(\overline{\mathrm{LN}}\) (ପ୍ରମାଣିତ)

Question 20.
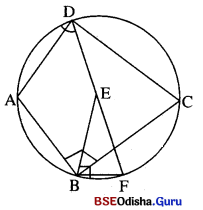
ABCD ଏକ ବୃତ୍ତାନ୍ତର୍ଲିଖ୍ ଚତୁର୍ଭୁଜରେ ∠B ଓ ∠Dର ସମତ୍ତିଖଣ୍ଡକ ଦ୍ଵୟ ପରସ୍ପରକୁ E ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । \(\stackrel{\longleftrightarrow}{\mathbf{D} E}\) ବୃତ୍ତକୁ F ବିନ୍ଦୁରେ ଛେଦ କଲେ ପ୍ରମାଣ କର ଯେ, \(\overline{\mathrm{BE}}\) ⊥ \(\overline{\mathrm{BF}}\) |

Solution:
ଦତ୍ତ : ABCD ଏକ ବୃତ୍ତାନ୍ତର୍ଲିଖତ ଚତୁର୍ଭୁଜ । ∠B ଓ ∠D ର
ସମଦ୍ୱିଖଣ୍ଡକଦ୍ୱୟ ପରସ୍ପରକୁ E ବିନ୍ଦୁରେ ଛେଦ କରୁଛନ୍ତି ।
\(\overrightarrow{\mathrm{DE}}\) ବୃତ୍ତକୁ F ବିନ୍ଦୁରେ ଛେଦ କରୁଛି ।
ପ୍ରାମାଣ୍ୟ : \(\overline{\mathrm{BE}}\) ⊥ \(\overline{\mathrm{BF}}\)
ପ୍ରମାଣ : m∠ADC + m∠ABC = 180° (ABCD ବୃତ୍ତାନ୍ତର୍ଲିଖ ଚତୁର୍ଭୁଜ)
\(\frac { 1 }{ 2 }\) m∠ADC + \(\frac { 1 }{ 2 }\) m∠ABC = 90°
⇒ m∠CDF + m∠EBC = 90°
କିନ୍ତୁ m∠CDF = m∠CBF (ଏକ ବୃତ୍ତଖଣ୍ଡସ୍ଥ କୋଣ)
m∠CBF + m∠EBC = 90° ⇒ m∠ERF = 90°
⇒ \(\overline{\mathrm{BE}}\) ⊥ \(\overline{\mathrm{BF}}\) (ପ୍ରମାଣିତ)

Question 21.
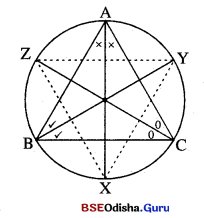
△ABCର କୋଣମାନଙ୍କର ସମଦ୍ବିଖଣ୍ଡକମାନେ ତ୍ରିଭୁଜର ପରିବୃତ୍ତକୁ X, Y ଓ Z ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । ପ୍ରମାଣ କର ଯେ, △XYZର କୋଣମାନଙ୍କର ପରିମାଣ ଯଥାକ୍ରମେ 90° – \(\frac { 1 }{ 2 }\) m∠A, 90° – \(\frac { 1 }{ 2 }\) m∠B ଓ 90° – \(\frac { 1 }{ 2 }\) m∠C |
Solution:
ଦତ୍ତ : △ABC ଦୁଲାନ୍ତ୍ରଖତ ∠A, ∠B ଓ ∠C ର ସମଦ୍ଵିଖଣ୍ଡକ ବୃତ୍ତକୁ ଯଥାକ୍ରମେ X, Y ଏବଂ Z ବିନ୍ଦୁରେ ଛେଦ କରେ ।
ପ୍ରାମାଣ୍ୟ : m∠X = 90° \(\frac { 1 }{ 2 }\)m∠A, \(\frac { 1 }{ 2 }\) m∠B ଏଦ m∠Z = 90° – \(\frac { 1 }{ 2 }\) m∠C

ପ୍ରମାଣ : \(\overparen{A Z}\) ର ଦିପରାତ ଗାପାନୁଇଖତ m∠AXZ = m∠ACZ
ଏବଂ \(\overparen{A Y}\) ଚାପର ବିପରୀତ ଚାପାନ୍ତର୍ଲିଖ କୋଣ m∠AXY = m∠ABY
∴ m∠AXZ + m∠AXY = m∠ACZ = m∠ABY
⇒ m∠X = \(\frac { m∠C }{ 2 }\) + \(\frac { m∠B }{ 2 }\)
⇒ m∠X = 90° – \(\frac { m∠A }{ 2 }\) (∵ \(\frac { m∠A }{ 2 }\) + \(\frac { m∠B }{ 2 }\) + \(\frac { m∠C }{ 2 }\) = 90°)
ସେହିପରି ପ୍ରମାଣ କରାଯାଇ ପାରେ ଯେ,
m∠Y = 90° – \(\frac { m∠B }{ 2 }\) ଏବଂ m∠Z = 90° – \(\frac { m∠C }{ 2 }\) ହେବ ।

Question 22.
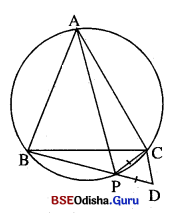
△ABC ଏକ ବୃତ୍ତାନ୍ତର୍ଲିଖ ସମବାହୁ ତ୍ରିଭୁଜ । \(\overline{\mathbf{BC}}\) ଜ୍ୟା ସହ ସମ୍ପୃକ୍ତ କ୍ଷୁଦ୍ର ଚାପ ଉପରେ P ଏକ ବିନ୍ଦୁ । ପ୍ରମାଣ କର ଯେ PA = PB + PC । (ସୂଚନା : \(\overrightarrow{\mathbf{B P}}\) ଉପରେ D ନିଅ ଯେପରି PC = PD ହେବ । △BCD ଓ △ACP ର ତୁଳନା କର ।)
Solution:
ଦତ୍ତ : △ABC ଏକ ବୃତ୍ତାନ୍ତର୍ଲିଖ ସମବାହୁ ତ୍ରିଭୁଜ । \(\overline{\mathbf{BC}}\) ଜ୍ୟା ସହ ସଂପୃକ୍ତ କ୍ଷୁଦ୍ରଚାପ ଉପରେ P ଏକ ବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : PA = PB + PC
ଅଙ୍କନ : \(\overrightarrow{\mathbf{B P}}\) ଉପରେ D ଏକ ବିନ୍ଦୁ ନିଅ ଯେପରିକି PC = PD ହେବ । \(\overline{\mathbf{CD}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : △ABC ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ।
m∠BAC = m∠CPD (ବୃତ୍ତାନ୍ତର୍ଲିଖ୍ ଚତୁର୍ଭୁଜର ବହିଃସ୍ଥ କୋଣ)
∴ m∠CPD = 60°
ସୁନଶ୍ଚ, △PCD ରେ PC = PD |

∴ △PCD ଏକ ସମବାହୁ ତ୍ରିଭୁଜ । ⇒ PC = CD = PD
ବର୍ତ୍ତମାନ m ∠ACB = m∠PCD = 60°
⇒ m∠ACB+m∠BCP=m∠PCD+m∠BCP
⇒ m∠ACP=m∠BCD
△APC ଓ △BCD ଦୟରେ AC = BC, PC = CD
ଏକ m∠ACP=m∠BCD
∴ △ACP ≅ △BCD
⇒ AP = BD ⇒ AP = BP + PD ⇒ AP = BP + PC

Question 23.
△ABCରେ ∠Aର ସମଦ୍ବିଖଣ୍ଡକ △ABCର ପରିବୃତ୍ତକୁ P ବିନ୍ଦୁରେ ଛେଦ କରେ । P ବିନ୍ଦୁରୁ \(\overrightarrow{\mathbf{AB}}\) ଓ \(\overline{\mathbf{AC}}\) ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ ଦ୍ବୟର ପାଦବିନ୍ଦୁ ଯଥାକ୍ରମେ Q ଏବଂ R । ପ୍ରମାଣ କର ଯେ, AQ = AR = \(\frac { AB+AC }{ 2 }\) | (ସ୍ମତନା : ଦଶାଥ ଯେ △PBQ ≅ △PCR ⇒ BQ = CR )
Solution:
ଦତ୍ତ : △ABC ର ∠A ର ସମଦ୍ବିଖଣ୍ଡକ ତ୍ରିଭୁଜର ପରିବୃତ୍ତକୁ P ବିନ୍ଦୁରେ ଛେଦ କରୁଛି । P ବିନ୍ଦୁରୁ \(\overrightarrow{\mathbf{AB}}\) ଓ \(\overrightarrow{\mathbf{AC}}\) ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ପାଦବିନ୍ଦୁ ଯଥାକ୍ରମେ Q ଏବଂ R । (ଏଠାରେ △ABCର AC > AB)
ପ୍ରାମାଣ୍ୟ : AQ = \(\frac { AB+AC }{ 2 }\) = AR
ଅଙ୍କନ : \(\overline{\mathbf{PB}}\) ଓ \(\overline{\mathbf{PC}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : ∠A ର ସମଦ୍ବିଖଣ୍ଡକ ପରିବୃତ୍ତକୁ P ବିନ୍ଦୁରେ ଛେଦକରେ ।
⇒ \(\overparen{B P}\) = \(\overparen{P C}\) ⇒ BP = PC
△BPQ ଏକ △CPR ଦଯରେ
BP = PC, m∠BQP = m∠CRP (= 90°)
ଏବଂ PQ = PR

(∵ କୋଣର ବାହୁମାନଙ୍କଠାରୁ ସମଦୂରବର୍ତ୍ତୀ ବିନ୍ଦୁମାନ, କୋଣ ସମଦ୍ବିଖଣ୍ଡକ ଉପରେ ଅବସ୍ଥାନ କରିବେ ।)
∴ △BPQ ≅ △CPR ⇒ BQ = CR
ପୁନଶ୍ଚ, △AQP ଓ △APR ଦ୍ବୟରେ
PQ = PR, \(\overline{\mathbf{AP}}\) ସାଧାରଣ ଏବଂ M∠AQP = m∠ARP
∴ △AQP ⇒ △APR ⇒ AQ = AR

ଚଇଂଲାନ 2AQ = AQ + AQ = AQ + AR = AB + BQ + AC – CR
= AB + AC (∵ BQ = CR)
∴ AQ = \(\frac { AB + AC }{ 2 }\) ⇒ AR = \(\frac { AB + AC }{ 2 }\)
⇒ AQ = \(\frac { AB + AC }{ 2 }\) = AR

Question 24.
△ABCରେ ∠Aର ସମଦ୍ବିଖଣ୍ଡକ △ABCର ପରିବୃତ୍ତକୁ P ବିନ୍ଦୁରେ ଛେଦ କରେ । \(\overline{\mathbf{AP}}\) ଓ \(\overline{\mathbf{BC}}\)ର ଛେଦ ବିନ୍ଦୁ D ହେଲେ ପ୍ରମାଣ କର ଯେ △ABD ଓ △APC ସଦୃଶ ଅଟନ୍ତି । ସୁତରାଂ ଦର୍ଶାଅ ଯେ, AB • AC = BD • DC + AD² |
(ପୁଚନା : △ABD ଓ △APC ପଦଣ ⇒ AB.AC = AD.AP, AD² = AD (AP – PD))
Solution:
ଦତ୍ତ : △ABC ର ∠A ର ସମଦ୍ବିଖଣ୍ଡକ, ଏହାର ପରିବୃତ୍ତକୁ P ବିନ୍ଦୁରେ ଛେଦ କରେ । \(\overline{\mathbf{BC}}\) ଓ \(\overline{\mathbf{AP}}\) ର ଛେଦବିନ୍ଦୁ D |
ପ୍ରାମାଣ୍ୟ : (i) △ABD ~ △APC
(ii) AB AC = BD · DC + AD²
ପ୍ରମାଣ : △ABD ଓ △APC ଦ୍ବୟରେ
m∠ABD = m∠APC (ଏକ ବୃତ୍ତଖଣ୍ଡସ୍ଥ କୋଣ)
m∠BAD=m∠PAC ଅବଶିଷ m∠ADB = m∠ACP

∴ △ABD ~ △APC
⇒ \(\frac { AB }{ AP }\) = \(\frac { AD }{ AC }\) ⇒ AB . AC = AD . AP
⇒ AB . AC = AD (AD + DP)
= AD² + AD . DP …..(i)
ପୁନଣ୍ଡ △ABD ~ △PDC
(∵m∠BAD = m∠DCP, m∠ADB = m∠PDC)
⇒ \(\frac { BD }{ DP }\) = \(\frac { AD }{ DC }\) ⇒ BD . DC = AD . DP
(i) ରେ ପ୍ତ6ଯାଗ କଲେ AB . AC = AD² + BD . DC

Question 25.
(ଟଲେମୀଙ୍କ ଉପପାଦ୍ୟ) ABCD ଏକ ବୃତ୍ତାନ୍ତଲିଖତ ଚତୁର୍ଭୁଜ ହେଲେ ପ୍ରମାଣ କର ଯେ,AC · BD = AB · CD + BC · AD | ଗୁଣଫଳ, ଚତୁର୍ଭୁଜର ସମ୍ମୁଖୀନ ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳର ସମଷ୍ଟି ସଙ୍ଗେ ସମାନ ।)
(ସୂଚନା : ମନେକର m∠ADB > m∠BDC | E, AC ଉପରେ ଏପରି ଏକ ବିନ୍ଦୁ ହେଉ ଯେପରି m∠BDC = m∠ADE | ବର୍ତ୍ତମାନ △ADE ଏବଂ △BDC ସଦୃଶ ⇒ \(\frac { AE }{ BC }\) = \(\frac { AD }{ BD }\) ପୁନଶ୍ଚ △ADB ଏବଂ △EDC ସଦୃଶ ⇒ \(\frac { CD }{ BD }\) = \(\frac { EC }{ AB }\) | )
Solution:
ଦଭ : ABCD ଏକ ବୃତ୍ତାନ୍ତଲିଖତ ଚତୁର୍ଭୁଜ ହେଲେ |
ପ୍ରାମାଣ୍ୟ : AC . BD = AB . CD + BC . AD
ଅକନ : ମନେକର m∠ADB > m∠BDC |
\(\overline{\mathbf{AC}}\) ଉପରିସ୍ଥ E ଏପରି ଏକ ବିନ୍ଦୁ ନିଅ ।
ଯେପରିକି m∠ADE = m∠BDC ହେବ ।
ପ୍ରମାଣ : ବର୍ତ୍ତମାନ △ADE ଏବଂ △BDC ଦ୍ଵୟରେ
m∠ADE = m∠BDC ଏବଂ m∠DAE = m∠DBC
ଥଗଣିପୁ m∠AED = m∠BCD

∴ △ADE ~ △BDC
⇒\(\frac { AE }{ BC }\) = \(\frac { AD }{ BD }\) ⇒ AE . BD = AD . BC
ପୁନ୍ଦଣ, △ADB ଏବଂ △EDC ଦ୍ଵପ୍ରେଭେ
m∠ABD + m∠ECD = m∠ADB + m∠EDC)
(∵m∠ADE = m∠BDC ⇒ m∠ADE + m∠EDB = m∠BDC + m∠EDB)
∴ △ADB ~ △EDC
⇒\(\frac { BD }{ CD }\) = \(\frac { AB }{ EC }\) ⇒ EC . BD = AB . CD
(i) ଓ (ii) ରୁ AE . BD + EC. BD = AD. BC + AB. CD
⇒ BD (AE + EC) = AB. CD + BC. AD
⇒ BD. AC = AB. CD + BC. AD