BSE Odisha 10th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(a)

Odisha State Board BSE Odisha 10th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(a)

Question 1.
(a) ହଉଇ ବ୍ୟାସାଦ
(i) 10 ସେ.ମି.
(ii) 2.8 ସେ.ମି.
(iii) 14 ସେ.ମି.
(iv) 4.2 ସେ.ମି. ହେଲେ ପରିଧ୍ କେତେ ? (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r ଏକକ ହେଲେ, ବୃତ୍ତର ପରିଧ୍ = 2πr ଏକକ

(i) ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ (r) = 10 ସେ.ମି.
∴ ବୃତ୍ତର ପରିଧୂ = 2πr = 2 × \(\frac { 22 }{ 7 }\) × 10 = \(\frac { 440 }{ 7 }\) ସେ.ମି. = 62 \(\frac { 6 }{ 7 }\) ସେ.ମି |

(ii) ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ (r) = 2.8 ସେ.ମି.
∴ ବୃତ୍ତର ପରିଧୂ = 2πr = 2 × \(\frac { 22 }{ 7 }\) × 2.8 = 17.6 ସେ.ମି

(iii) ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ (r) = 14 ସେ.ମି.
∴ ବୃତ୍ତର ପରିଧୂ = 2πr = 2 × \(\frac { 22 }{ 7 }\) × 14 = 88 ସେ.ମି

(iv) ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ (r) = 4.2 ସେ.ମି.
∴ ବୃତ୍ତର ପରିଧୂ = 2πr = 2 × \(\frac { 22 }{ 7 }\) × 4.2 = 26.4 ସେ.ମି

(b) ବୃତ୍ତର ପରିଧ୍ (i) 34.9 ସେ.ମି
(ii) 1047 ସେ.ମି
(iii) 25.128 ସେ.ମି
(iv) 15.705 ସେ.ମି ହେଲେ ପରିଧ୍ କେତେ ? (π ≃ 3.141)
Solution:
ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = ପରିଧ୍ / 2π

(i) ମନେକର ବ୍ୟାସାର୍ଦ୍ଧ = r ସେ.ମି., ତେବେ ପରିଧୂ = 2πr ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, 2πr = 34.9 ⇒ 2 × 3.141 × r = 34.9
⇒ r = \(\frac{34.9}{2 \times 3.141}\) = \(\frac { 349 }{ 10 }\) × \(\frac { 500 }{ 3141 }\) = \(\frac { 17450 }{ 3141 }\) = \(\frac { 50 }{ 9 }\) ବା 5\(\frac { 5 }{ 9 }\) ସେ.ମି
∴ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ 166\(\frac { 2 }{ 3 }\) ସେ.ମି |

(ii) ମନେକର ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r ସେ.ମି. ∴ ହେଲେ ପରିଧ୍ = 2πr ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, 2πr = 1047 ⇒ 2 × 3.141 × r = 1047 ⇒ r = \(\frac{1047}{2 \times 3.141}\)
⇒ r = \(\frac{1047 \times 500}{3141}\) = \(\frac { 500 }{ 3 }\) = 166\(\frac { 2 }{ 3 }\) ସେ.ମି
∴ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ 166\(\frac { 2 }{ 3 }\) ସେ.ମି |

(iii) ମନେକର ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r ସେ.ମି. .. ବୃତ୍ତର ପରିସ୍ = 2πr ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, 2лr = 25.128 ⇒ 2 × 3.141 × r = 25.128 ⇒ r = \(\frac{25.128}{2 \times 3.141}\) = 4 ସେ.ମି.
∴ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ 4 ସେ.ମି. ।

(iv) ମନେକର ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, 2лr = 15.705
∴ ହେଲେ ପରିଧ୍ = 2πr ସେ.ମି.
⇒ 2 × 3.141 × r = 15.705 ⇒ r = \(\frac{15.705}{2 \times 3.141}\) = 2.5 ସେ.ମି.

Question 2.
ଏକ ବୃତ୍ତର ଚାପର ଦୈର୍ଘ୍ୟ L, ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ r, ଚାପର ଡିଗ୍ରୀ ପରିମାପ θ ଦ୍ଵାରା ସୂଚିତ ହେଲେ ନିମ୍ନଲିଖ ପ୍ରଶ୍ନମାନଙ୍କର ସମାଧାନ କର । (л ≃ \(\frac { 22 }{ 7 }\))
(a) r = 56 ସେ.ମି. , θ = 45° ହେଲେ L କେତେ ?
(b) L = 110 ମି. θ = 75° ହେଲେ r କେତେ ?
(c) 2r=9 ସେ.ମି. L = 22 ସେ.ମି. ହେଲେ θ କେତେ ?
Solution:
(a) r=56 ସେ.ମି. θ = 45°
ଚାପର ଦୈର୍ଘ୍ୟ (L) = \(\frac { θ }{ 180 }\) × лr = \(\frac { 45 }{ 180 }\) × \(\frac { 22 }{ 7 }\) × 56 = 44 ସେ.ମି.

(b) L = 110, θ = 75°
ଆମେ ଜାଣିଛେ, L = \(\frac { θ }{ 180 }\) × лr
⇒ 110 = \(\frac { 75 }{ 180 }\) × \(\frac { 22 }{ 7 }\) × r ⇒ r = \(\frac{110 \times 180 \times 7}{75 \times 22}\) ⇒ r = 84 ମି.

(c) 2r = 9 ସେ.ମି. L = 22 ସେ.ମି. ⇒ r = \(\frac { 9 }{ 2 }\) ଡେ.ମି.
ଆମେ ଜାଣିଛେ, L = \(\frac { θ }{ 180 }\) × лr ⇒ 22 = \(\frac { θ }{ 180 }\) × \(\frac { 27 }{ 7 }\) × \(\frac { 9 }{ 2 }\)
⇒ θ = \(\frac{22 \times 180 \times 7 \times 2}{22 \times 9}\) = 280°

Question 3.
ନିମ୍ନଲିଖତ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ । (л ≃ \(\frac { 22 }{ 7 }\))
(a) କୌଣସି ଏକ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ 10.5 ସେ.ମି. ହେଲେ ସେହି ବୃତ୍ତର 11 ସେ.ମି. ପରିମିତ ଚାପର ଡିଗ୍ରୀ
Solution:
ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ (r) = 10.5 ସେ.ମି.
ଚାପର ଦୈର୍ଘ୍ୟ (L) = 11 ସେ.ମି.
ମନେକର ଚାପର ଡିଗ୍ରୀ ପରିମାପ = θ°
ଆମେ ଜାଣିଛେ, L = \(\frac { θ }{ 180° }\) × лr
⇒ 11 = \(\frac { θ }{ 180 }\) × \(\frac { 22 }{ 7 }\) × 10.5 ⇒ θ = \(\frac{11 \times 180 \times 7}{22 \times 10.5}\) = 60°

(b) 21 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଚାପର ଡିଗ୍ରୀ ପରିମାପ 72° ହେଲେ ଚାପଟିର ଦୈର୍ଘ୍ୟ କେତେ ହେବ ?
Solution:
ବୃତ୍ତର ବ୍ୟାସାର୍ଷ (r) = 21 ସେ.ମି., ଚାପର ଡିଗ୍ରୀ ପରିମାପ (θ) = 72°
∴ ଚାପର ଦୈର୍ଘ୍ୟ (L) = \(\frac { θ }{ 180 }\) × лr = \(\frac { 72 }{ 180 }\) × \(\frac { 22 }{ 7 }\) × 21 = 26.4 ସେ.ମି.

(C) ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ କେତେ ହେଲେ ସେହି ବୃତ୍ତର 11 ସେ.ମି. ପରିମିତ ଚାପର ଡିଗ୍ରୀ ପରିମାପ 10° ହେବ ?
Solution:
ମନେକର ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r ସେ.ମି., ବୃତ୍ତର ଚାପର ଡିଗ୍ରୀ ପରିମାପ = (θ) = 10°
ଚାପର ଦୈର୍ଘ୍ୟ (L) = 11 ସେ.ମି.
ଆମେ ଜାଣିଛେ, L = \(\frac { θ }{ 180° }\) × лr
⇒ 11 = \(\frac { 10 }{ 180 }\) × \(\frac { 22 }{ 7 }\) × r ⇒ r = \(\) = 63 ସେ.ମି.
∴ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧର ଦୈର୍ଘ୍ୟ 63 ସେ.ମି. ।

(d) ଏକ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧର ଦୈର୍ଘ୍ୟ x ଏକକ, ଚାପର ଦୈର୍ଘ୍ୟ y ଏକକ, ଚାପର ଡିଗ୍ରୀ ପରିମାପ Z ଡିଗ୍ରୀ ହେଲେ ବ୍ୟାସାର୍ଦ୍ଧର ଦୈର୍ଘ୍ୟ л ମାଧ୍ୟମରେ ନିର୍ଣ୍ଣୟ କର ।
Solution:
L = \(\frac { θ }{ 180° }\) × лr
(ଏଠାରେ L = y ଏକକ, θ = z°, r = x ଏକକ)
⇒ y = \(\frac { z }{ 180 }\) × лr ⇒ x = \(\frac { 180y }{ лz }\)
∴ ବ୍ୟାସାର୍ଦ୍ଧର ଦୈର୍ଘ୍ୟ \(\frac { 180y }{ лz }\) |

(e) r ଏକକ ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତରେ a ଏକକ ଦୀର୍ଘ ବାହୁ ବିଶିଷ୍ଟ ଏକ ବର୍ଗଚିତ୍ର ଅନ୍ତର୍ଲିଖ୍ ହେଲେ a ଏବଂ r ମଧ୍ଯରେ ସମ୍ପର୍କ ନିଶ୍ଚୟ କର ।
Solution:
ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r ଏକକ ଓ ବର୍ଗଚିତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = a ଏକକ ।
ଏକ ବୃତ୍ତ ମଧ୍ଯରେ ଗୋଟିଏ ବର୍ଗାକାର କ୍ଷେତ୍ର ABCD ଅନ୍ତର୍ଲିଖ୍ ହେଲେ, ବର୍ଗକ୍ଷେତ୍ରର କର୍ପୂର ଦୈର୍ଘ୍ୟ AC = ବୃତ୍ତର ବ୍ୟାସ ହେବ ।

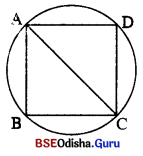
ବୃତ୍ତର ବ୍ୟାସ = 2r ଏକକ
ବର୍ଗକ୍ଷେତ୍ରର କଣ୍ଠ = √2 × ବାହୁର ଦୈର୍ଘ୍ୟ = √2a ଏକକ
∴ √2a = 2r ⇒ a = √2.r

Question 4.
ବିଷୁବରେଖାଠାରେ ପୃଥ‌ିବୀର ବ୍ୟାସ 12530 କି.ମି. ହେଲେ ବିଷୁବ ବୃତ୍ତର ପରିସ୍ କେତେ ? (л ≃ \(\frac { 22 }{ 7 }\))
Solution:
ପୃଥ‌ିବୀର ବ୍ୟାସ (d) = 12530 ସେ.ମି.
∴ ବିଷୁବ ବୃତ୍ତର ପରିଧ୍ = x × d = \(\frac { 22 }{ 7 }\) × 12530 = 22 × 1790 = 39380 ସେ.ମି.
∴ ବିଷୁବ ବୃତ୍ତର ପରିଧ୍ 39,380 ସେ.ମି. |

Question 5.
44 ମି. ଦୀର୍ଘ ତାରରୁ 5 ସେ.ମି. ବ୍ୟାସାର୍କ ବିଶିଷ୍ଟ କେତୋଟି ବୃତ୍ତ ତିଆରି କରାଯାଇ ପାରିବ ?(л ≃ \(\frac { 22 }{ 7 }\))
Solution:
ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ (r) = 5 ସେ.ମି., ତାରର ଦୈର୍ଘ୍ୟ = 44 ମି. = 4400 ସେ.ମି.
ଦ୍ରଭର ପରିଧ୍ = 2лr = 2 × \(\frac { 22 }{ 7 }\) × 5 = \(\frac { 220 }{ 7 }\) ସେ.ମି.
∴ ଦୃଭ ସଖ୍ୟା = ପାଇର ଦୈଶ୍ୟ / ଦରକ ପରିସ୍ = \(\frac{\frac{4400}{220}}{7}\) = 4400 × \(\frac {7 }{ 220 }\) = 140ଟି

Question 6.
ଗୋଟିଏ ବୃତ୍ତାକାର ରାସ୍ତାର ବାହାର ଓ ଭିତର ପରିଧୂ ଯଥାକ୍ରମେ 396 ଓ 352 ମିଟର ହେଲେ ରାସ୍ତାର ପ୍ରସ୍ଥ ନିର୍ଣ୍ଣୟ କର । (л ≃ \(\frac { 22 }{ 7 }\))
Solution:
ମନେକର ବହିଃବୃତ୍ତ ଏବଂ ଅନ୍ତଃବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ଯଥାକ୍ରମେ R ମି. ଏବଂ r ମି. ।

Question 7.
ଦୁଇଟି ବୃତ୍ତର ପରିତ୍ରର ଅନ୍ତର 44 ମିଟର ଏବଂ ସେମାନଙ୍କର ବ୍ୟାସାର୍ଦ୍ଧ ଦ୍ଵୟର ସମଷ୍ଟି 77 ମିଟର ହେଲେ ପରିଧ୍ 22 ଦ୍ଵୟ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ମନେକର ବହିଃବୃତ୍ତ ଏବଂ ଅନ୍ତଃବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ଯଥାକ୍ରମେ R ମି. ଓ r ମି. ।
ବହିଃବୃତ୍ତର ପରିସ୍ = 2πR ମି. ଓ ଅନ୍ତଃବୃତ୍ତର ପରିଧ୍ = 2πr ମି.
ପ୍ରଣାଳୁମାରେ, 2лR – 2лг = 44 ମି.
⇒ 2 × \(\frac { 22 }{ 7 }\) (R – r) = 44 ⇒ R – r = 44 × \(\frac { 7 }{ 44 }\) = 7 ମି.
⇒ R – r = 1 ….(i)
ପୁନଶ୍ଚ R + r = 77 ….(2)
ସମୀକରଣ (1) ଓ (2) କୁ ଯୋଗକଲେ , 2R = 84 ⇒ R = 42 ମି.
ସମୀକରଣ (2) R = 42 ମି. ବସାଇଲେ , r = 77 – 42 = 35 ମି.
∴ ବହିଃବୃତ୍ତର ପରିସ୍ = 2πR = 2 × \(\frac { 22 }{ 7 }\) × 42 = 264 ମି.
ଓ ଅନ୍ତଃବୃତ୍ତର ପରିସ୍ = 2πr = 2 × \(\frac { 22 }{ 7 }\) × 35 = 220 ମି.

Question 8.
ଦୁଇଟି ଏକକେନ୍ଦ୍ରିକ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ଦ୍ବୟର ଅନୁପାତ 3 : 4 । ସେମାନଙ୍କର ପରିଧ୍ ଦ୍ଵୟର ସମଷ୍ଟି 308 ସେ.ମି. ହେଲେ ବଳୟର ପ୍ରସ୍ଥ କେତେ ହେବ ? (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ମନେକର ଅନ୍ତଃବୃତ୍ତ ଏବଂ ବହିଃବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ଯଥାକ୍ରମେ 3x ସେ.ମି. ଓ 4x ସେ.ମି. ।
ଅନ୍ତଃବୃତ୍ତର ପରିଧୂ = 2π × 3x = 6πx ସେ.ମି. ଓ ବହିଃବୃତ୍ତର ପରିଧୂ = 2π × 4x = 8πx ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, 6πx + 8πx = 308
⇒ 14лx = 308 ⇒ 14 × \(\frac { 22 }{ 7 }\) × x = 308 ⇒ x = \(\frac { 308 }{ 44 }\) = 7 ସେ.ମି.
∴ ଦଳାଯାଇ ପ୍ରସ୍ଥ = (R – r) = (4x – 3x) = x = 7 ସେ.ମି.

Question 9.
ଗୋଟିଏ ବଳୟ ଆକାରର ରାସ୍ତାର ବାହାର ଓ ଭିତର ବୃତ୍ତର ପରିଧୂ ଯଥାକ୍ରମେ 300 ମିଟର ଓ 200 ମିଟର ହେଲେ, ରାସ୍ତାର ପ୍ରସ୍ଥ କେତେ ? (π ≃ √10)
Solution:
ମନେକର ବହିଃବୃତ୍ତ ଓ ଅନ୍ତଃବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ ଯଥାକ୍ରମେ R ମି. ଓ r ମି. |
ବହିଃବୃତ୍ତର ପରିଧ୍ = 2лR ମି. ଓ ଅନ୍ତଃବୃତ୍ତର ପରିଧ୍ = 2лr ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, 2лR = 300 ମି.
⇒ 2 × √10 × R = 300 ⇒ R = \(\frac{300}{2 \times \sqrt{10}}\) = 15√10 ମି.
ପୁନଶ୍ଚ, 2лR = 200 ମି.
⇒ 2 × √10 × r = 200 ⇒ r = \(\frac{200}{2 \times \sqrt{10}}\) = 10√10 ମି.
∴ ଦଳାଯାଇ ପ୍ରସ୍ଥ = R – r = (15√10 – 10√10) ମି. = 5√10 ମି.

Question 10.
7 ମି. ବ୍ୟାସାର୍କବିଶିଷ୍ଟ ବୃତ୍ତ ଉପରେ କେତେଥର ଘୂରିଲେ 11 କି.ମି. ଦୂରତା ଅତିକ୍ରମ କରିହେବ ? (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ (r) = 7 ମି.
ବୃତ୍ତର ପରିସ୍ = 2лr = 2 × \(\frac { 22 }{ 7 }\) × 7 = 44 ମି.
ବୃତ୍ତ ଉପରେ ଥରେ ଘୂରିଲେ 44 ମି. ବାଟ ଅତିକ୍ରମ କରିବ ।
11 କି.ମି. ଅର୍ଥାତ୍ (11 × 1000) ମି. ବାଟ ଅତିକ୍ରମ କଲେ ଘୂର୍ଣ୍ଣନ ସଂଖ୍ୟା = \(\frac{11 \times 1000}{44}\) = 250 ଥର
∴ 7ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବୃତ୍ତ ଉପରେ 250 ଥର ଘୂରିଲେ 11 କି.ମି. ଦୂରତା ଅତିକ୍ରମ କରିହେବ ।

Question 11.
ଗୋଟିଏ ସାଇକେଲ୍‌ର ପ୍ରତ୍ୟେକ ଚକ ମିନିଟ୍‌ରେ 80 ଥର ଘୂରନ୍ତି । ଚକର ବହିଃ ବ୍ୟାସ 42 ସେ.ମି. ହେଲେ ସାଇକେଲ୍‌ର ଘଣ୍ଟାପ୍ରତି ବେଗ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ସାଇକେଲ ଚକର ବହିଃ ବ୍ୟାସ = 42 ସେ.ମି.
ସାଇକେଲ ଚକର ପରିସ୍ = л × ବ୍ୟାସ = \(\frac { 22 }{ 7 }\) × 42 = 132 ସେ.ମି.
ସାଇକେଲ ଚକ ଥରେ ଘୂରିଲେ 132 ସେ.ମି. ଯାଏ ।
ସାଇକେଲ ଚକ.80 ଥର ଘୂରିଲେ ଯାଏ = 132 × 80 ସେ.ମି. = 10560 ସେ.ମି. ବାଟ ଅତିକ୍ରମ କରିବ ।
ସାଇକେଲ୍‌ର ମିନିଟ୍ ପ୍ରତି ବେଗ = 10560 ସେ.ମି.
∴ ସାଇକେଲ୍‌ର ମିନିଟ୍ ପ୍ରତି ବେଗ = 10560 × 60 ସେ.ମି. = 633600 ସେ.ମି. = 6336 ମି. 6.366 ମି.

Question 12.
ଗୋଟିଏ ଗାଡ଼ିର ବଡ଼ ଚକ ଓ ସାନ ଚକର ପରିଧର ଅନୁପାତ 4 : 1 | 440 ମିଟର ରାସ୍ତା ଅତିକ୍ରମ କରିବାରେ ସାନ ଚକ ବଡ଼ ଚକ ଅପେକ୍ଷା 15 ଥର ଅବ୍ଲକ ଘୂରେ । ପ୍ରତ୍ୟେକ ଚକର ପରିସ୍ ନିର୍ଣ୍ଣୟ କର | (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ମନେକର ଗାଡ଼ିର ବଡ଼ ଚକର ପରିଧୂ = 4x ମି. ଓ ସାନ ଚକର ପରିଧ୍ = x ମି. |
ଥରେ ଘୂରିଲେ ବଡ଼ ଚକ ଓ ସାନ ଚକ ଦ୍ଵୟ ଯଥାକ୍ରମେ 4x ମି. ଓ x ମି. ରାସ୍ତା ଅତିକ୍ରମ କରିବ ।
440 ମି. ରାସ୍ତା ଅତିକ୍ରମ କରିବାରେ ବଡ଼ ଚକ ଏବଂ ସାନ ଚକ ଯଥାକ୍ରମେ \(\frac { 440 }{ 4x }\) ଏବଂ \(\frac { 440 }{ x }\)
ସାନ ଚକ ଯଥାକ୍ରମେ , \(\frac { 440 }{ x }\) ଏବଂ \(\frac { 440 }{ 4x }\) = 15
⇒ \(\frac { 440 }{ x }\) – \(\frac { 440 }{ 4x }\) = 15 ⇒ \(\frac { 440 }{ x }\) (1 – \(\frac { 1 }{ 4 }\)) = 15
⇒ \(\frac { 440 }{ x }\) – \(\frac { 3 }{ 4 }\) = 15 ⇒ x = \(\frac{440 \times 3}{4 \times 15}\) = 22 ମି.
∴ ଦତ ଚଳଉ ପରିଧ = 4x ମି. = 4 × 22 ମି. = 88 ମି. ଓ ଦତ ଚଳଉ ପରିଧ = x ମି. = 22 ମି. |

Question 13.
ଗୋଟିଏ ଅଦ୍ଧବୃତ୍ତାକାର ଜମିର ଚାରିପାଖରେ ବାଡ଼ ଦେବା ଖର୍ଚ୍ଚ ମିଟରକୁ 75 ପଇସା ହିସାବରେ 216 ଟଙ୍କା ଖର୍ଚ୍ଚ ହେଲେ ଅର୍ଥବୃତ୍ତାକାର ଜମିର ବ୍ୟାସ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ଅର୍ଥବୃତ୍ତାକାର ଜମିର ପରିସୀମା = \(\frac { 21600 }{ 75 }\) = 288 ମି.
ଯଦି ଅର୍ଥବୃତ୍ତାକାର ଜମିର ବ୍ୟାସାର୍ଦ୍ଧ r ମି. ହୁଏ ତେବେ ପରିସୀମା = (лr + 2r) ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, лr + 2r = 288
⇒ r(\(\frac { 22 }{ 7 }\) + 2) = 288 ⇒ r(\(\frac{22+14}{7}\)) = 288 ⇒ r × \(\frac { 36 }{ 7 }\) = 288 ⇒ r = \(\frac{288 × 7}{36}\) = 56
∴ ଅର୍ଥବୃତ୍ତାକାର ଜମିର ବ୍ୟାପ = 56 × 2 = 112 ମି.

Question 14.
ଗୋଟିଏ ଘୋଡ଼ା ବୃତ୍ତ ଉପରେ ଥରେ ଘୂରିଆସି ସିଧା ଯାଇ କେନ୍ଦ୍ରରେ ପହଞ୍ଚିବା ପାଇଁ ତାକୁ 10 ମିନିଟ୍ 12 ସେକେଣ୍ଡ ସମୟ ଲାଗିଲା । ସେ କେବଳ ବୃତ୍ତ ଉପରେ ଘୂରିଥଲେ ତାକୁ କେତେ ସମୟ ଲାଗିଥାନ୍ତା ? (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ମନେକର ଘୋଡ଼ାଟିକୁ ବ୍ୟାସାର୍ଷ ଉପରେ ଯିବାକୁ r ମିନିଟ୍ ସମୟ ଲାଗିଥା’ନ୍ତା ।
ତେବେ ପରିଧ୍ ଉପରେ ଯିବାକୁ 2лr ମିନିଟ୍ ସମୟ ଲାଗିବ ।
ବୃତ୍ତାକାର ପଥରେ ଥରେ ଘୂରି ସିଧା କେନ୍ଦ୍ରରେ ପହଞ୍ଚିବା ପାଇଁ (2πr + r) ମିନିଟ୍ ସମୟ ଲାଗିବ ।
ପ୍ରଶ୍ନନୁସାରେ, (2πr + r) = 10\(\frac { 12 }{ 60 }\) ⇒ r(2 × \(\frac { 22 }{ 7 }\) + 1) = \(\frac { 51 }{ 5 }\)
⇒ r(\(\frac{44+7}{7}\)) = \(\frac { 51 }{ 5 }\) ⇒ r = \(\frac { 51 }{ 5 }\) × \(\frac { 7 }{ 51 }\) ⇒ r = \(\frac { 7 }{ 5 }\) ମିନିଟ୍
ବୃତ୍ତ ଉପରେ ଘୂରିବାପାଇଁ ଅର୍ଥାତ୍ 2πr = 2 × \(\frac { 22 }{ 7 }\) × \(\frac { 7 }{ 5 }\) = \(\frac { 44 }{ 5 }\) = ମିନିଟ୍ = 8\(\frac { 4 }{ 5 }\) ମିନିଟ୍
= 8 ମିନିଟ୍ 48 ସେକେଣ୍ଡ ସମୟ ଲାଗିବ ।
∴ ଘୋଡ଼ାଟି କେବଳ ବୃତ୍ତ ଉପରେ ଘୂରିଥଲେ ତାକୁ 8 ମିନିଟ୍ 48 ସେକେଣ୍ଡ ସମୟ ଲାଗିଥା’ନ୍ତା ।

Question 15.
ଗୋଟିଏ ବୃତ୍ତ ଉପରେ ଥରେ ଭ୍ରମଣ କରିବାକୁ ଯେତେ ସମୟ ଲାଗେ ବୃତ୍ତଟିର ବ୍ୟାସ ପରିମିତ ପଥ ଅତିକ୍ରମ କରିବାକୁ 45 ସେକେଣ୍ଡ କମ୍ ଲାଗେ । ଯଦି ଲୋକଟିର ବେଗ ଏକ ମିନିଟ୍‌ରେ 80 ମିଟର ହୁଏ ତେବେ ବୃତ୍ତର ବ୍ୟାସ କେତେ ହେବ ? (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ଲୋକଟି 1 ମିନିଟ୍‌ରେ 80 ମିଟର ପଥ ଅତିକ୍ରମ କଲେ 45 ସେକେଣ୍ଡରେ ଯିବ
=(80 × \(\frac { 45 }{ 60 }\)) ମିଟର = 60 ମି. ।
ମନେକର ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ r ମି., ବୃତ୍ତର ପରିଧୂ = 2πr ମି. ଓ ବ୍ୟାସ = 2r ମି. |
ପ୍ରଶ୍ନନୁସାରେ, 2πr – 2r = 60
⇒ 2r (\(\frac { 22 }{ 7 }\) – 1) = 60 ⇒ 2r (\(\frac{22-7}{7}\)) = 60
⇒ 2r = \(\frac{60 × 7}{15}\) ⇒ r = \(\frac { 28 }{ 2 }\) = 14 ମି.
∴ ଦୁଇର ବ୍ୟାସ = 2r = 2 × 14 ମି. = 28 ମିଟର |

Question 16.
ଖଣ୍ଡେ ତାରକୁ ସମବାହୁ ତ୍ରିଭୁଜାକୃତି କଲେ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ 1936√3 ବର୍ଗମିଟର ହୁଏ । ଉକ୍ତ ତ୍ରିଭୁଜର ପରିସୀମା ସହ ସମାନ ପରିଧ୍ ଥ‌ିବା ବୃତ୍ତଟିର ବ୍ୟାସ କେତେ ହେବ ? (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ସମବାହୁ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ = 1936√3 ବର୍ଗ ମି.
⇒ \(\frac{\sqrt{3}}{4}\) × (ବାହୁର ଦୈର୍ଘ୍ୟ)² = 1936√3
⇒ (ବାହୁର ଦୈର୍ଘ୍ୟ)² = \(\frac{1936 \sqrt{3} \times 4}{\sqrt{3}}\)
⇒ (ବାହୁର ଦୈର୍ଘ୍ୟ) = \(\sqrt{1936 \times 4}\) = 88 ମି.
∴ ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ 88 ମି. ।
ସମବାହୁ ତ୍ରିଭୁଜର ପରିସୀମା = 3 × 88 ମି. = 264 ମି. = ବୃତ୍ତର ପରିସ୍
ଯଦି ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ r ମି. ହୁଏ ତେବେ ପରିଧ୍ 2πr ମି. ହେବ ।
ପ୍ରଶ୍ନନୁସାରେ, 2πr = 264
⇒ 2 × \(\frac { 22 }{ 7 }\) × r = 264 ⇒ r = 264 × \(\frac{7}{2 \times 22}\) = 42 ମି.
∴ ଦୁଇର ବ୍ୟାସ = 2r = 2 × 42 = 84 ମି. |

Question 17.
20 ସେ.ମି. ଦୀର୍ଘ ବାହୁ ବିଶିଷ୍ଟ ଏକ ବର୍ଗଚିତ୍ର ମଧ୍ୟରେ ଏକ ବୃତ୍ତ ଅନ୍ତର୍ଲିଖ୍ତ ହେଲେ ବୃତ୍ତର ପରିସ୍ କେତେ ହେବ ? (n ≃ 3.14)
Solution:

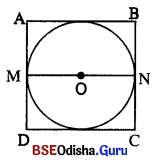
ABCD ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = 20 ସେ.ମି. ।
ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ର ମଧ୍ୟରେ ବୃତ୍ତଟିଏ ଅନ୍ତର୍ଲିଖ୍ତ ହେଲେ ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = ବୃତ୍ତର ବ୍ୟାସ ।
ବୃତ୍ତର ବ୍ୟାସ = MN = 20 ସେ.ମି.
∴ ଚଉର ପରିଧି = π × ବ୍ୟାସ = 3.14 × 20 ସେ.ମି. = 62.8 ସେ.ମି. |

Question 18.
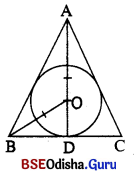
42 ସେ.ମି. ଦୀର୍ଘ ବାହୁ ବିଶିଷ୍ଟ ଏକ ସମବାହୁ ତ୍ରିଭୁଜର ପରିଲିଖ ଓ ଅନ୍ତର୍ଲିଖ୍ତ ବୃତ୍ତର ପରିସ୍ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ : ସମବାହୁ ତ୍ରିଭୁଜର ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ = 42 ସେ.ମି. |
ବୃତ୍ତରେ ABC ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ଅନ୍ତର୍ଲିଖ୍ ।
ପରିବୃତ୍ତ ଓ ଅନ୍ତଃବୃତ୍ତର କେନ୍ଦ୍ର ୦ ଏବଂ AD ⊥ BC|
ABC ଇଉତା (AD) = \(\frac{\sqrt{3}}{2}\) × ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac{\sqrt{3}}{2}\) × 42 ସେ.ମି.= 21, √3 ସେ.ମି.
O, △ABC ର ଭରକେନ୍ଦ୍ର ହେତୁ, AD = 3 OD
⇒ 3 OD = 21 √3
⇒ OD = \(\frac{21 \sqrt{3}}{3}\) = 7√3 ସେ.ମି. |

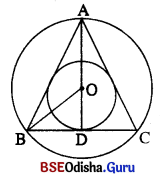
∴ ଅନ୍ତର୍ଲିଖ ବୃତ୍ତର ପରିସ୍ = 2 × \(\frac { 22 }{ 7 }\) × 7√3 ସେ.ମି. = 44√3 ସେ.ମି.
ପରିହରର ବ୍ୟାସାଦ = OA = 2 × OD = 2 × 7√3 = 14√3 ସେ.ମି.
∴ ଅନ୍ତର୍ଲିଖ ଚଉର ପରିଧି = 2 × \(\frac { 22 }{ 7 }\) × 14√3 ସେ.ମି. = 88√3 ସେ.ମି.

Question 19.
(a) 21 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ବୃତ୍ତକଳାର ପରିସୀମା 64 ସେ.ମି. ହେଲେ, ବୃତ୍ତକଳାର ଚାପର ଡିଗ୍ରୀ ପରିମାପ ସ୍ଥିର କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ବୃତ୍ତକଳାର ବ୍ୟାସାର୍ଦ୍ଧ (r) = 21 ସେ.ମି. ।
ମନେକର ବୃତ୍ତକଳାର ଚାପର ଦୈର୍ଘ୍ୟ = L ସେ.ମି. ଓ ଚାପର ଡିଗ୍ରୀ ପରିମାପ = m\(\widehat{\mathrm{ACB}}\) θ° |
ବୃତ୍ତକଳାର ପରିସୀମା = (L + 2r) ସେ.ମି.
= (L+ 2 × 21) ସେ.ମି.. = (L + 42) ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, L + 42 = 66 ସେ.ମି.

⇒ L = 64 – 42 = 22 ସେ.ମି.
ଆମେ ଜାଣିଛେ, L= \(\frac{\theta}{180^{\circ}}\) × πr
⇒ 22 = \(\frac { θ }{ 180 }\) × \(\frac { 22 }{ 7 }\) × 21
⇒ θ = \(\frac{22 \times 180 \times 7}{22 \times 21}\) = 60° ⇒ m\(\widehat{\mathrm{ACB}}\) 60°
∴ ବୃତ୍ତକଳାର ଚାପର ଡିଗ୍ରୀ ପରିମାପ 60° |

(b) ଏକ ବୃତ୍ତରେ ଯେଉଁ ବୃତ୍ତକଳାର ଚାପର ଡିଗ୍ରୀ ପରିମାପ 40°, ସେହି ବୃତ୍ତକଳାର ପରିସୀମା 26.98 ସେ.ମି. ହେଲେ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ କେତେ ? (π ≃ 3.14)
Solution:
ମନେକର ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ = r ସେ.ମି. ଓ ବୃତ୍ତକଳାର ଚାପର ଦୈର୍ଘ୍ୟ = L ସେ.ମି.
ବୃତ୍ତକଳାର ଚାପର ଡିଗ୍ରୀ ପରିମାପ (θ) = 40°
∴ ବୃତ୍ତକଳାର ପରିସୀମା = (L + 2r) ସେ.ମି.
କିନ୍ତୁ L = \(\frac { θ }{ 180 }\) × πr = \(\frac { 40 }{ 180 }\) × 3.14 × r = \(\frac { 2 }{ 9 }\) × 3.14r ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, L + 2r = 26.98 ⇒ r(\(\frac{6.28+18}{9}\)) = 26.98
⇒ r = 26.98 × \(\frac { 9 }{ 24.28 }\) = \(\frac { 24282 }{ 2428 }\) = 10 ସେ.ମି.
∴ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ 10 ସେ.ମି. ।

Question 20.
କୌଣସି ଏକ ବୃତ୍ତକଳାର କେନ୍ଦ୍ରସ୍ଥ କୋଣର ପରିମାଣ 90° । ଏହାର ବ୍ୟାସାର୍ଦ୍ଧର ଦୈର୍ଘ୍ୟ 5 ସେ.ମି. ହେଲେ ବୃତ୍ତକଳାର ପରିସୀମା ନିର୍ଣ୍ଣୟ କର । (π ≃ 3.1416)
Solution:
ବୃତ୍ତକଳାର କେନ୍ଦ୍ରସ୍ଥ କୋଣର ପରିମାଣ (θ) = 90°
ବ୍ୟାସାର୍ଦ୍ଧର ଦୈର୍ଘ୍ୟ (r) = 5 ସେ.ମି.
ବୃତ୍ତକଳାର ଚାପର ଦୈର୍ଘ୍ୟ (L) = \(\frac { θ }{ 180 }\) × πr
= \(\frac { 90 }{ 180 }\) × 3.1416 × 5 = 7.854 ସେ.ମି.
∴ ବୃତ୍ତକଳାର ପରିବାପା = L + 2r = (7.854 + 2 × 5) ସେ.ମି. = 17.854 ସେ.ମି.

Question 21.
କୌଣସି ଏକ ବୃତ୍ତର ଏକ ଚାପର ଡିଗ୍ରୀ ପରିମାପ 40 ଏବଂ ଅନ୍ୟ ଏକ ବୃତ୍ତର ସମଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ଚାପର ଡିଗ୍ରୀ ପରିମାପ 60° ହେଲେ ଉଭୟ ବୃତ୍ତର ବ୍ୟାସାର୍ଷର ଅନୁପାତ ନିର୍ଣ୍ଣୟ କର ।
Solution:
ମନେକର ପ୍ରଥମ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧର ଦୈର୍ଘ୍ୟ r₁ ସେ.ମି. ଓ ଦ୍ୱିତୀୟ
ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧର ଦୈର୍ଘ୍ୟ r₂ ସେ.ମି.
ପ୍ରଥମ ବୃତ୍ତର ଚାପର ଡିଗ୍ରୀ
ପରିମାପ (θ₁) = 40°
ଦିତାଯ ହଇର ଚାପର କିସ୍ଥା
ପରିମାପ (θ₂) = 60°

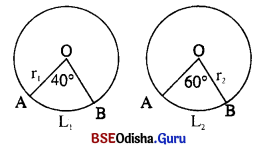
ପ୍ରଥମ ବୃତ୍ତର ଚାପର ଦୈର୍ଘ୍ୟ (L₁) = \(\frac{\theta_1}{180}\) × πr₁ = (\(\frac { 40 }{ 180 }\) × πr₁) ସେ.ମି.
ପ୍ରଥମ ବୃତ୍ତର ଚାପର ଦୈର୍ଘ୍ୟ (L₂) = \(\frac{\theta_2}{180}\) × πr₂ = (\(\frac { 60 }{ 180 }\) × πr₂) ସେ.ମି.
ମନେକର ପ୍ରଥମ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧର ଦୈର୍ଘ୍ୟ L₁ = L₂
⇒ \(\frac { 40 }{ 180 }\) × πr₁ = \(\frac { 60 }{ 180 }\) × πr₂ ⇒ \(\frac{r_1}{r_2}\) = \(\frac { 60 }{ 180 }\) × \(\frac { 180 }{ 40 }\) = \(\frac { 3 }{ 2 }\)
∴ r₁ : r₂ = 3:2

Question 22.
ଗୋଟିଏ ଘଣ୍ଟାର ମିନିଟ୍ କଣ୍ଟାର ଅଗ୍ରଭାଗ 5 ମିନିଟ୍‌ରେ 7\(\frac { 1 }{ 3 }\) ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ଏକ ଚାପ ଅଙ୍କନ କରେ । ମିନିଟ୍ କଣ୍ଟାର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
60 ମିନିଟ୍‌ରେ ମିନିଟ୍ କଣ୍ଟାଟି 360° କୋଣ ସୃଷ୍ଟି କରେ ।
5 ମିନିଟ୍‌ରେ ମିନିଟ୍‌ରେ କଣ୍ଟାଟି କେନ୍ଦ୍ରରେ ଉତ୍ପନ୍ନ କରୁଥିବା କୋଣର ପରିମାଣ = \(\frac { 360 }{ 60 }\) × 5 = 30°
ମିନିଟ୍ କଣ୍ଟାର ଅଗ୍ରଭାଗ ଦ୍ବାରା ଅତିକ୍ରାନ୍ତ ପଥ (L) = 7\(\frac { 1 }{ 3 }\) ସେ.ମି. = \(\frac { 22 }{ 3 }\) ସେ.ମି. |
ମନେକର ମିନିଟ୍ କଣ୍ଟାର ଦୈର୍ଘ୍ୟ = r ସେ.ମି.
ଆମେ ଜାଣିଛେ, L = \(\frac { θ }{ 180 }\) × πr ⇒ \(\frac { 22 }{ 3 }\) = \(\frac { 30 }{ 180 }\) × \(\frac { 22 }{ 7 }\) × r = \(\frac{22 \times 180 \times 7}{3 \times 30 \times 22}\) = 14 ସେ.ମି.
∴ ମିନିଟ୍ କଣ୍ଟାର ଦୈର୍ଘ୍ୟ 14 ସେ.ମି. |
ମିନିଟ୍ କଣ୍ଟାର ଅଗ୍ରଭାଗ 5 ମିନିଟ୍‌ରେ 7\(\frac { 1 }{ 3 }\) ସେ.ମି. = \(\frac { 22 }{ 3 }\) ସେ.ମି. ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ ଚାପ ଅଙ୍କନ କରେ ।
60 ମିନିଟ୍‌ରେ କଣ୍ଟାଟି ଦୈର୍ଘ୍ୟ ଅତିକ୍ରମ କରିବ = \(\frac { 22 }{ 3 }\) × 12 = 88 ସେ.ମି.
ଏହି ଦୈର୍ଘ୍ୟଟି ସମ୍ପୂର୍ଣ ଚାପ ଅର୍ଥାତ୍ ବୃତ୍ତର ପରିସ୍ ଅଟେ ।
∴ 2лr = 88
⇒ 2 × \(\frac { 22 }{ 7 }\)r = 88 ⇒ r = 88 × \(\frac { 7 }{ 44 }\) = 14 ସେ.ମି. |
∴ ମିନିଟ୍ କଣ୍ଟାର ଦୈର୍ଘ୍ୟ 14 ସେ.ମି. ।

Question 23.
ଗୋଟିଏ ବୃତ୍ତର ପରିସ୍ ଅନ୍ୟ ଏକ ବୃତ୍ତର ପରିଧୂର ତିନିଗୁଣ । ପ୍ରଥମ ବୃତ୍ତର 10 ସେ.ମି. ପରିମିତ ଚାପର ଡିଗ୍ରୀ ପରିମାପ 30° ହେଲେ ଦ୍ବିତୀୟ ବୃତ୍ତର ପରିସ୍ କେତେ ହେବ ନିର୍ଣ୍ଣୟ କର । (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
ପ୍ରଥମ ବୃତ୍ତର ଚାପର ଦୈର୍ଘ୍ୟ (L) = 10 ସେ.ମି. ଓ ଚାପର ଡିଗ୍ରୀ ପରିମାପ (θ) = 30°
L = \(\frac { θ }{ 180 }\) × πr ⇒ 10 = \(\frac { 30 }{ 180 }\) × πr ⇒ r = \(\frac{180 \times 10}{30 \times \pi}\) = \(\frac { 60 }{ π }\) ସେ.ମି.
ପ୍ରଥମ ବୃତ୍ତର ପରିସ୍ = 2πr = 2 π × \(\frac { 60 }{ π }\) = 120 ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, ପ୍ରଥମ ବୃତ୍ତର ପରିଧ ଦ୍ବିତୀୟ ବୃତ୍ତର ପରିଧର 3 ଗୁଣ ।
∴ ଦ୍ୱିତୀୟ ବୃତ୍ତର ପରିସ୍ = \(\frac { 120 }{ 3 }\) = 40 ସେ.ମି. |

Question 24.
ଗୋଟିଏ ବୃତ୍ତର ପରିଧ୍ 6.282 ସେ.ମି. ହେଲେ ଓ ଏହା ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ମଧ୍ୟରେ ଅନ୍ତର୍ଲିଖ୍ତ ହେଲେ, ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ କେତେ ? (π ≃ 3.141)
Solution:
ମନେକର ଅନ୍ତର୍ଲିଖ୍ତ ବୃତ୍ତର ବ୍ୟାସାର୍କର ଦୈର୍ଘ୍ୟ = r ସେ.ମି.
ତେବେ ପରିସ୍ଥି = 2πr ସେ.ମି. = 2 × 3.141 × r = 6.282 r ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ, 6.282 r = 6.282 ⇒ r = 1 ସେ.ମି.
ସମବାହୁ ତ୍ରିଭୁଜର ଅନ୍ତଃକେନ୍ଦ୍ର, ଭରକେନ୍ଦ୍ର ଓ ଲମ୍ବବିନ୍ଦୁ O ଅଭିନ୍ନ ଅଟେ ।

\(\overline{\mathrm{AD}}\) ଲମ୍ବ ଉପରିସ୍ଥ ‘O’ ଭରକେନ୍ଦ୍ର ହେତୁ OD = \(\frac { 1 }{ 3 }\) AD
ଆଥାତ୍ (AD) = 3 × OD = 3 × r = 3 × 1 = 3 ସେ.ମି.
ସମବାହୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ = ଉଚ୍ଚତା × \(\frac{2}{\sqrt{3}}\) = 3 × \(\frac{2}{\sqrt{3}}\) ସେ.ମି. = 2√3 ସେ.ମି.
∴ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ 2√3 ସେ.ମି. |

Question 25.
ଗୋଟିଏ ବୃତ୍ତକଳାର ଚାପର ଡିଗ୍ରୀ ପରିମାପ 60° । ଏହାର ଦୁଇ ବ୍ୟାସାର୍ଦ୍ଧ ଓ ଚାପକୁ ସ୍ପର୍ଶକରି ଏକ ବୃତ୍ତ ଅନ୍ତର୍ଲିଖ୍ । ପ୍ରମାଣ କର ଯେ, ଏହି ବୃତ୍ତର ପରିସ୍ ଓ ବୃତ୍ତକଳାର ପରିସୀମାର ଅନୁପାତ 11 : 16 | (π ≃ \(\frac { 22 }{ 7 }\))
Solution:
OACB ବୃତ୍ତକଳାର ଡିଗ୍ରୀ ପରିମାପ 60°
ଅର୍ଥାତ୍ m∠AOB = 60°
ବୃତ୍ତକଳାର ଅନ୍ତର୍ଲିଖ୍ତ ବୃତ୍ତର କେନ୍ଦ୍ର M ଓ D ସ୍ପର୍ଶବିନ୍ଦୁ ।
\(\overline{\mathrm{OC}}\) ବୃତ୍ତକୁ E ବିନ୍ଦୁରେ ଛେଦ କରୁଛି ।
\(\overline{\mathrm{DE}}\) ଅଙ୍କନ କରାଯାଉ ।
ବର୍ତ୍ତମାନ △OMDରେ ∠MOD = \(\frac{60^{\circ}}{2}\) = 30°
ମନେକର ବୃତ୍ତକଳାର ବ୍ୟାସାର୍ଦ୍ଧ R ଏକକ ଏବଂ ଅନ୍ତର୍ଲିଖ ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ r ଏକକ ।
ବୃତ୍ତକଳାର ବ୍ୟାସାର୍ଦ୍ଧ (R) = OC = OM + MC = 2r + r = 3r

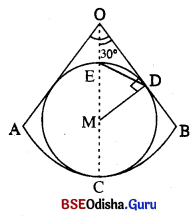
[∵ △OMDରେ sin 30° = \(\frac { MD }{ OM }\) ⇒ \(\frac { 1 }{ 2 }\) = \(\frac { r }{ OM }\) ⇒ OM = 2r]
\(\overparen{A C B}\) ର ଦୈର୍ଘ୍ୟ = \(\frac { 60 }{ 180 }\) × π × 3r = πr ଏକକ
ବୃତ୍ତକଳାର ପରିସୀମା = OA + OB + l \(\overparen{A C B}\)
= 2 × 3r + лr = 6r + πr = r (6 + \(\frac { 22 }{ 7 }\)) = r (\(\frac{42+22}{7}\)) = \(\frac { 64 }{ 7 }\) r ଏକକ
ଅନ୍ତର୍ଲିଖ ବୃତ୍ତର ପରିଧୂ = 2лr = 2 × \(\frac { 22 }{ 7 }\) × r = \(\frac { 44r }{ 7 }\) ଏକକ ।
∴ ବୃତ୍ତର ପରିଧୂ / ଦରଜକାର ପରିମାମା = \(\frac{\frac{44 \mathrm{r}}{7}}{\frac{64 \mathrm{r}}{7}}\) = \(\frac { 44 }{ 64 }\) = \(\frac { 11 }{ 16 }\) = 11 : 16
∴ ବୃତ୍ତର ପରିଧୂ : ଦରଜକାର ପରିମାମା = 11 : 16 |