BSE Odisha 10th Class Physical Science Solutions Chapter 8 ବିଦ୍ୟୁତ୍

Odisha State Board BSE Odisha 10th Class Physical Science Solutions Chapter 8 ବିଦ୍ୟୁତ୍ Textbook Exercise Questions and Answers.

BSE Odisha Class 10 Physical Science Solutions Chapter 8 ବିଦ୍ୟୁତ୍

ପ୍ରଶ୍ନ 1 ରୁ 4 ମଧ୍ୟରେ ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନ ପାଇଁ ଦିଆଯାଇଥ‌ିବା ଚାରୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛ ।

Question 1.
ଖଣ୍ଡିଏ ତାରର ପ୍ରତିରୋଧ ହେଉଛି R । ଏହି ତାରକୁ ପାଞ୍ଚଟି ସମାନ ଭାଗରେ ବିଭକ୍ତ କରାଗଲା ଏବଂ ଏଗୁଡ଼ିକୁ ସମାନ୍ତରାଳ ସଂଯୋଗ କରାଗଲା । ଏହି ସଂଯୋଗର ସମତୁଲ୍ୟ ପ୍ରତିରୋଧ R’ ହେଲେ, R/R’ ହେଲେ
(a) 1/25
(b) 1/5
(c) 5
(d) 25
Answer:
(d) 25

Question 2.
ନିମ୍ନୋକ୍ତ ପଦମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁଟି ବିଦ୍ୟୁତ୍ ପାଓ୍ବାର ସୂଚାଉ ନାହିଁ ?
(a) I²R
(b) IR²
(c) VT
(d) V²/R

Question 3.
220 V ଓ 100 W ଲେଖାଥ‌ିବା ଗୋଟିଏ ବଲ୍‌ବକୁ 110 V ଲାଇନ୍‌ରେ ଲଗାଇଲେ ପାୱାର ହେବ
(a) 100W
(b) 75 W
(c) 50 W
(d) 25 W
Answer:
(d) 25 W

Question 4.
ଏକା ବସ୍ତୁରୁ ତିଆରି ସମାନ ଦୈର୍ଘ୍ୟ ଓ ସମାନ ବ୍ୟାସ ବିଶିଷ୍ଟ ଦୁଇଟି ପରିବାହୀ ତାରକୁ ଯଥାକ୍ରମେ ପଙ୍‌କ୍ତି ସଂଯୋଗ ଓ ସମାନ୍ତରାଳ ସଂଯୋଗ କରାଗଲା । ଉଭୟ କ୍ଷେତ୍ରରେ ବିଭବାନ୍ତର ସମାନ ହେଲେ ପଙ୍‌କ୍ତି ସଂଯୋଗ ଓ ସମାନ୍ତରାଳ ସଂଯୋଗରେ ଉତ୍ପନ୍ନ ହେଉଥ‌ିବା ତାପର ଅନୁପାତ
(a) 1:2
(b) 2:1
(c) 1 : 4
(d) 4:1
Answer:
(c) 1 : 4

Question 5.
ପରିପଥର ଦୁଇଟି ବିନ୍ଦୁ ମଧ୍ୟରେ ବିଭବାନ୍ତର ମାପିବା ପାଇଁ ଭୋଲ୍‌ଟମିଟର କେମିତି ସଂଯୋଗ କରାଯାଏ ?
Answer:
ପରିପଥ ସହ ସମାନ୍ତରଭାବେ ଦୁଇଟି ବିନ୍ଦୁ ମଧ୍ୟରୁ + ପାର୍ଶ୍ଵ ବିନ୍ଦୁକୁ ଭୋଲଟମିଟର + ଅଗ୍ରସହ ଏବଂ ପରିପଥର ଅନ୍ୟ ଏକ ବିଯୁକ୍ତ (–) ଅଗ୍ରଥ‌ିବା ବିନ୍ଦୁକୁ ଭୋଲ୍‌ମିରର ବିଯୁକ୍ତ ଅଗ୍ରସହ ସମାନ୍ତରଭାବେ ସଂଯୁକ୍ତ କରାଯାଏ ।

Question 6.
ଖଣ୍ଡିଏ ତମ୍ବା ତାରର ବ୍ୟାସ 0.5 mm ଓ ପ୍ରତିରୋଧ 1.6 × 10^-8Ω m । 10 Ω ପ୍ରତିରୋଧ ବିଶିଷ୍ଟ ଏଭଳି ତାରର ଦୈର୍ଘ୍ୟ କେତେ ? ବ୍ୟାସ ଦୁଇଗୁଣ ହେଲେ ପ୍ରତିରୋଧ କେତେ ହେବ ?
Answer:
ଏଠାରେ R = 10 Ω,
d = 0.5 mm,
ପ୍ରତିରୋଧତା (ρ) = 1.6 x 10^-8Ω m
r = \(\frac { d }{ 2 }\) = \(\frac { 0.5 }{ 2 }\) = 0.25 mm = 0.25 x 10^-3 ମିଟର
A = πr² = 3.14 x (0.25 x 10^-3)²ମି². = 1962.50 x 10^-10 m² = 1962 x 10^-8 m²
ଆମେ ଜାଣୁ L = \(\frac { R.A }{ ρ }\) = \(\frac{10 \times 19.625 \times 10^{-8}}{1.6 \times 10^{-8}}\) m = 122.65
R = ρ \(\frac { L }{ A }\) = ρ \(\frac{\mathrm{L}}{\pi r^2}\)Ω, ବ୍ୟାସ = 2 x 2r = 4r ⇒ ବ୍ୟାସାର୍ଦ୍ଧ = \(\frac { 4r }{ 2 }\) = 2r
R = ρ \(\frac{\mathrm{L}}{\pi π(2r)^2}\) = ρ \(\frac{\mathrm{L}}{\pi π4r^2}\) = \(\frac { 1 }{ 4 }\) (ρ \(\frac{\mathrm{L}}{\pi πr^2}\))
ଅର୍ଥାତ୍ ବ୍ୟାସ 2 ଗୁଣ ହେଲେ ପ୍ରତିରୋଧ \(\frac { 1 }{ 4 }\) ଗୁଣ ହେବ।
∴ ପ୍ରତିରୋଧ = \(\frac { 10 }{ 4 }\) = 2 – 5 Ω

Question 7.
ଗୋଟିଏ ପ୍ରତିରୋଧୀର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟରେ ବିଭବାନ୍ତର ହିଁ ଓ ତହିଁରେ ପ୍ରବାହିତ ହେଉଥ‌ିବା ବିଦ୍ୟୁତ୍ ସ୍ରୋତ Iର ପରିମାଣ ନିମ୍ନରେ ଦିଆଯାଇଛି ।

V ଓ I ମଧ୍ଯରେ ଗ୍ରାଫ୍‌ଟିଏ ଅଙ୍କନ କରି ପ୍ରତିରୋଧୀର ପ୍ରତିରୋଧ ନିର୍ଣ୍ଣୟ କର ।
Answer:
CF = 6.7 – 3.4 = 3.3 ଅର୍ଥାତ୍ ବିଭବାନ୍ତର ପରିବର୍ତ୍ତନ = 3.3 V
BF = 2 – 1 = 1 ଅର୍ଥାତ୍ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ପରିବର୍ତ୍ତନ = 1A

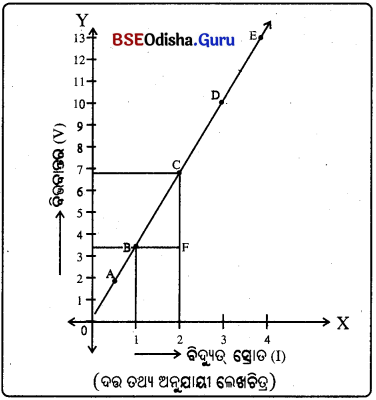
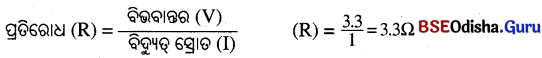
Question 8.
ଗୋଟିଏ ପ୍ରତିରୋଧୀର ଦୁଇ ପ୍ରାନ୍ତ ସହ ଏକ 12V ବ୍ୟାଟେରୀ ସଂଯୁକ୍ତ ହୋଇଛି । ପରିପଥରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହର ପରିମାଣ 2.5 m ହେଲେ ପ୍ରତିରୋଧୀର ପ୍ରତିରୋଧ ନିର୍ଣ୍ଣୟ କର ।
Answer:
ଏଠାରେ V = 12 V, I= 2.5 mA = 2.5 x 10^-3 A (∵ 1mA = 10^-3 A)
ଓମ୍‌ଙ୍କ ନିୟମ ଅନୁସାରେ R = \(\frac { V }{ I }\) = \(\frac{12 \mathrm{~V}}{2.5 \times 10^{-3} \mathrm{~A}}\) = 4800 Ω
∴ ପ୍ରତିରୋଧୀର ପ୍ରତିରୋଧ = 4800 Ω |

Question 9.
ଏକ 9V ବ୍ୟାଟେରୀ ଗୋଟିଏ 12 Ω ପ୍ରତିରୋଧୀ ସହ ସଂଯୁକ୍ତ । ପ୍ରତିରୋଧୀରେ କେଉଁ ପରିମାଣର ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେଉଛି ?
Answer:
ଏଠାରେ R = 12 Ω, V = 9 V, ଓମ୍ବକ ନିପ୍ନମ ଅନୁପାରେ V = IR
⇒ I = \(\frac { V }{ R }\) = \(\frac { 9V }{ 12Ω }\) = 0.75 A

Question 10.
କେତୋଟି 176 Ω ପ୍ରତିରୋଧୀର ସମାନ୍ତରାଳ ସଂଯୋଗ 220V ଲାଇନ୍‌ରୁ 5A ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ନେବ ?
Answer:
ଏଠାରେ I = 5A, V = 220 V, R = 176 Ω
ମନେକର xଟି 176 Ω ପ୍ରତିରୋଧୀର ସମାନ୍ତରାଳ ସଂଯୋଗ 220 V ଲାଇନ୍‌ରୁ 5A ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେବ ।
∴ \(\frac { 1 }{ R }\) = \(\frac { 1 }{ 176 }\) + \(\frac { 1 }{ 176 }\) + …………..x ଟି = \(\frac { x }{ 176 }\) ⇒ R = \(\frac { 176 }{ x }\) Ω
I = \(\frac { V }{ R }\) ⇒ 5 = \(\frac{220}{\frac{176}{x}}\)
⇒ \(\frac { x }{ 176 }\) = \(\frac { 220 }{ 5 }\) ⇒ x = \(\frac { 176×5 }{ 220 }\) = 4
∴ 4 ଟି 176 Ω ପ୍ରତିରୋଧୀ ଅ|ରଣ୍ୟକ |

Question 11.
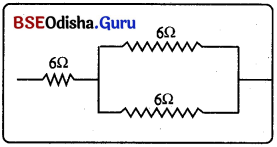
ତିନୋଟି ପ୍ରତିରୋଧୀ ମଧ୍ୟରୁ ପ୍ରତ୍ୟେକର ପ୍ରତିରୋଧ 6Ω । ଏଗୁଡ଼ିକୁ କିଭଳି ଭାବେ ସଂଯୋଗ କଲେ ସମତ୍ରଳ୍ୟ ପ୍ରତିରୋଧ ତ୍ରେ (i) 9Ω (ii) 4Ω ?
(i) R₁ = R₂ = R₃ = 6Ω
ଏଠାରେ ଦୁଇଟିକୁ ସମାନ୍ତର ସଂଯୋଗକରି ସେମାନଙ୍କର ମିଳିତ ପ୍ରତିରୋଧ ସହିତ ଗୋଟିଏ ପକ୍ତିରେ ସଂଯୋଗ କରାଯିବ ।
ସମାନ୍ତର ସଂଯୋଗ \(\frac { 1 }{ R }\) = \(\frac{1}{\mathrm{R}_1}\) + \(\frac{1}{\mathrm{R}_2}\)
= \(\frac { 1 }{ 6 }\) + \(\frac { 1 }{ 6 }\) = \(\frac { 2 }{ 6 }\) = \(\frac { 1 }{ 3 }\)Ω
⇒ R = 3Ω
ପଭକ୍ତି ସଂଯୋଗ = 3Ω + 6Ω = 9Ω

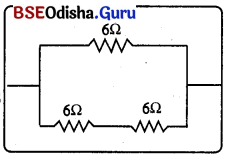
(ii) ଦୁଇଟିକୁ ପଙ୍‌କ୍ତିରେ ସଂଯୋଗକରି ପଙ୍‌କ୍ତି ସଂଯୋଗର ମିଳିତ ପ୍ରତିରୋଧ ସହିତ ଅନ୍ୟ ଏକ ସମାନ୍ତର ସଂଯୋଗ କରାଯାଡ |
R₁ = 6 + 6 = 12 Ω, R₂ = 6Ω
ସମାନ୍ତରାଳ ସଂଯୋଗ
(\(\frac { 1 }{ R }\)) = \(\frac{1}{\mathrm{R}_1}\) + \(\frac{1}{\mathrm{R}_2}\) = \(\frac { 1 }{ 12 }\) + \(\frac { 1 }{ 6 }\) = \(\frac { 1+2 }{ 12 }\) = \(\frac { 1 }{ 4 }\)
⇒ R = 3Ω

Question 12.
220 V ଲାଇନ୍‌ରେ ଲାଗିପାରୁଥିବା କେତେଗୁଡ଼ିଏ ବଲ୍‌ବର ପାଓ୍ବାର ହେଉଛି 10 W । ଯଦି ସର୍ବୋଚ୍ଚ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ 5 A ହୁଏ ତେବେ କେତୋଟି ବଲ୍‌ବକୁ ସେହି ଲାଇନ୍‌ରେ ସମାନ୍ତରାଳ ଭାବେ ସଂଯୋଗ କରାଯାଇପାରିବ ?
Answer:
ଏଠାରେ V = 220 V, P = 10 W, I = 5A
ପ୍ରତ୍ୟେକ ବଲ୍‌ବର ପ୍ରତିରୋଧ (R) = \(\frac{\mathrm{V}^2}{\mathrm{P}}\) = \(\frac{\mathrm{(220)}^2}{\mathrm{10}}\) = 4840 Ω
ମନେକର xଟି ବଲ୍‌ବ ସମାନ୍ତର ସଂଯୋଗରେ ସମତୁଲ୍ୟ ପ୍ରତିରୋଧ R_eq ।
\(\frac{1}{\mathrm{R}_eq}\) = \(\frac { 1 }{ 4840 }\) + \(\frac { 1 }{ 4840 }\) + ………. ଟି ସଂଖ୍ୟକ = \(\frac { x }{ 4840 }\) ⇒ \(\frac{1}{\mathrm{R}_eq}\) = \(\frac { 4840 }{ x }\) Ω
ଓମ୍‌ଙ୍କ ନିୟମ ଅନୁଯାୟୀ, \(\frac{1}{\mathrm{R}_eq}\) = \(\frac { V }{ I }\)
⇒\(\frac { 4840 }{ x }\) = \(\frac { 220 }{ 5 }\) ⇒ x = \(\frac { 4840×5 }{ 220 }\) = 110
∴ 110 ଟି 10 W ବଲ୍‌ବ 220 V ଲାଇନ୍‌ରେ ଲାଗିଲେ 5A ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହୁଏ ।

Question 13.
220 V ଲାଇନ୍‌ରେ ଲଗାଯାଇଥିବା ଗୋଟିଏ ବିଦ୍ୟୁତ୍ ଚୁଲାରେ ଦୁଇଟି 24 Ω ପ୍ରତିରୋଧ ବିଶିଷ୍ଟ ତାର କୁଣ୍ଡଳୀ ଅଛି । କୁଣ୍ଡଳୀ ଦୁଇଟିକୁ ଅଲଗା ଅଲଗା, ପଙ୍‌କ୍ତିରେ ଓ ସମାନ୍ତର ଭାବେ ବ୍ୟବହାର କଲେ ପ୍ରତି କ୍ଷେତ୍ରରେ କେତେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେବ ?
Answer:
(i) ଦୁଇଟି କୁଣ୍ଡଳୀକୁ ଅଲଗା ଅଲଗା ଲଗାଇଲେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ I = \(\frac { V }{ R }\) = \(\frac { 220V }{ 24Ω }\) = 9.2 Ω

(ii) ଦୁଇଟି କୁଣ୍ଡଳୀକୁ ପଙକ୍ତିରେ ସଂଯୋଗ କଲେ
ମୋଟ ପ୍ରତିରୋଧ (R) = 24 + 24 = 48 Ω, ବିଦ୍ୟୁତ୍ ସ୍ରୋତ (I) = \(\frac { V }{ R }\) = \(\frac { 220 }{ 48 }\) = 4.58 A

(iii) ଦୁଇଟି କୁଣ୍ଡଳୀକୁ ସମାନ୍ତରାଳ ସଂଯୋଗ କଲେ \(\frac { 1 }{ R }\) = \(\frac { 1 }{ 24 }\) + \(\frac { 1 }{ 24 }\) = \(\frac { 1+1 }{ 24 }\) = \(\frac { 2 }{ 24 }\) = \(\frac { 1 }{ 12 }\) ⇒ R = 12
ବିଦ୍ୟୁତ୍ ସ୍ରୋତ (I) = \(\frac { V }{ R }\) = \(\frac { 220 }{ 12 }\) = 18.33 A

Question 14.
ନିମ୍ନୋକ୍ତ ପରିପଥଗୁଡ଼ିକରେ 2 Q ପ୍ରତିରୋଧୀରେ ବ୍ୟବହାର ହେଉଥ‌ିବା ପାୱାରର ତୁଳନା କର ।
(i) 1Ω ଓ 2Ω ପ୍ରତିରୋଧୀ ସହ ଗୋଟିଏ 6V ବ୍ୟାଟେରୀର ପଙ୍‌କ୍ତି ସଂଯୋଗ ଏବଂ
(ii) 12 Ω ଓ 2 Ω ପ୍ରତିରୋଧୀ ସହ ଗୋଟିଏ 4 V ବ୍ୟାଟେରୀର ସମାନ୍ତରାଳ ସଂଯୋଗ ।
Answer:
(i) ପଙ୍‌କ୍ତି ସଂଯୋଗ ହୋଇଥିବାରୁ ମୋଟ ପ୍ରତିରୋଧ R = 1 + 2 = 3Ω
V = 6V, I = \(\frac { V }{ R }\) = \(\frac { 6 }{ 3 }\) = 2A
2 Ω ପ୍ରତିରୋଧୀଦ୍ଵାରା ବ୍ୟବହୃତ ପାଓ୍ବାର (P) = I²R = 2² x 2 = 8 ୱାଟ୍

(ii) 12 Ω2 ଓ 2 Ω ପ୍ରତିରୋଧୀଗୁଡ଼ିକ ସମାନ୍ତରାଳ ସଂଯୋଗ ହୋଇଥିବାରୁ 2Ω ପ୍ରତିରୋଧୀ ପାଇଁ ବିଭବାନ୍ତର 4V |
2 Ω ପ୍ରତିରୋଧୀଦ୍ଵାରା ବ୍ୟବହୃତ ପାୱାର = \(\frac{\mathrm{V}^2}{\mathrm{R}}\) = \(\frac{\mathrm{4}^2}{\mathrm{2}}\) = 8 ୱାଟ୍

Question 15.
ଗୋଟିଏ 100 W – 220 V ଓ ଗୋଟିଏ 60 W – 220 V ବିଦ୍ୟୁତ୍ଵବତୀ ଏକ 220 V ଲାଇନ୍‌ରେ ସମାନ୍ତର ଭାବେ ସଂଯୁକ୍ତ ହୋଇଛି । ଏହା ଲାଇନ୍‌ରୁ କେତେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ନେଉଛି ?
Answer:
ଦ୍ତଇଟି ଚଢା ବ୍ୟତତ୍ବାବ କରୁଥିବା ପାୱାର = 100 W + 60 W = 160 W V = 220 V
ଭୋଲ୍ଟେଜ୍ V = 220 V
P = VI ⇒ 1 = \(\frac { P }{ V }\) = \(\frac { 160 }{ 220 }\) = 0.727 A
∴ ଲାଇନରୁ 0.727 ଏମ୍ପିୟର ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ହେଉଛି ।

Question 16.
କେଉଁଟି ବେଶି ଶକ୍ତି ବ୍ୟବହାର କରେ ? 1 ଘଣ୍ଟା ଚାଲୁଥ‌ିବା ଗୋଟିଏ 250 W ଟିଭି ସେଟ୍ ନା 10 ମିନିଟ୍ ଚାଲୁଥ‌ିବା ଗୋଟିଏ 1200 W ଟୋଷ୍ଟର ?
Answer:
1 ଘଣ୍ଟା ଚାଲୁଥିବା ଗୋଟିଏ 250 W ଟିଭିସେଟ୍ ଖର୍ଚ୍ଚକରୁଥିବା ଶକ୍ତି (W) = Pt
= 250 W x 1h = 250 Wh
10 ମିନିଟ୍ ଚାଲୁଥ‌ିବା ଗୋଟିଏ 1200 W ଟୋଷ୍ଟର = 1200 W x 10 ମିନିଟ୍
= 1200 W x \(\frac { 10 }{ 60 }\)h = 1200 W
∴ ଟିଭି ସେଟ୍‌ଟି ଅଧ୍ଯକ ଶକ୍ତି ବିନିଯୋଗ କରୁଛି ।

Question 17.
ଗୋଟିଏ 8 Ω ହିଟର 2 ଘଣ୍ଟା ଧରି ଲାଇରୁ 15 A ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ନିଏ । ହିଟର୍‌ରେ ଉତ୍ପନ୍ନ ହେଉଥ‌ିବା ତାପର ହାର ନିର୍ଣ୍ଣୟ କର ।
Answer:
R = 8Ω, t = 2h, I = 15 A
ଉତ୍ପନ୍ନ ହେଉଥ‌ିବା ତାପର ହାର = ପାୱାର (ଶକ୍ତି)
H = \(\frac{\mathrm{I}^2 \mathrm{Rt}}{\mathrm{t}}\) = I²R
H = I²R= 15² × 8 = 225 x 8 = 1800 ୱାଗ୍ 31 = 1800 J/sec.
∴ ହିଟର୍‌ରେ ଉତ୍ପନ୍ନ ହେଉଥିବା ତାପର ହାର 1800 J/s |

Question 18.
ବୁଝାଅ :
(a) ବିଦ୍ୟୁତ୍ ବତୀର ଫିଲାମେଣ୍ଟ ପାଇଁ ଟଙ୍ଗଷ୍ଟନ୍ ଧାତୁ କାହିଁକି ବ୍ୟବହାର କରାଯାଏ ?
ଉ :
ଟଙ୍ଗ୍‌ଷ୍ଟନର ତାରର ପ୍ରତିରୋଧ’ବହୁତ ଅର୍ଧ ଏବଂ ଗଳନାଙ୍କ ଉଚ୍ଚ (3410°C) ହେତୁ, ‘ ଏହାକୁ ବିଦ୍ୟୁତ୍ ବତୀର ଫିଲାମେଣ୍ଟ୍‌ ପାଇଁ ବ୍ୟବହାର କରାଯାଏ ।

(b) ପାଉଁରୁଟି ଟୋଷ୍ଟର ଓ ଇସ୍ତ୍ରୀ ଭଳି ବିଦ୍ୟୁତ୍ ତାପନ ସାମଗ୍ରୀରେ କାହିଁକି ଶୁଦ୍ଧ ଧାତୁ ପରିବର୍ତ୍ତେ ମିଶ୍ରଧାତୁ ବ୍ୟବହାର କରାଯାଏ ?
ଉ :
ମିଶ୍ରଧାତୁର ପ୍ରତିରୋଧ ମୂଳ ଧାତୁଗୁଡ଼ିକର ପ୍ରତିରୋଧଠାରୁ ଅଧ‌ିକ ଏବଂ ମିଶ୍ରଧାତୁଗୁଡ଼ିକ ଉଚ୍ଚ ତାପମାତ୍ରାରେ ସହଜରେ ଜାରିତ ହୁଏ ନାହିଁ । ତେଣୁ ପାଉଁରୁଟି ଟୋଷ୍ଟର ଓ ଇସ୍ତ୍ରୀଭଳି ବିଦ୍ୟୁତ୍ ତାପନ ସାମଗ୍ରୀରେ ମିଶ୍ରଧାତୁ ବ୍ୟବହାର କରାଯାଏ ।

(c) ଗୃହ ବିଦ୍ୟୁତ୍ ପରିପଥରେ କାହିଁକି ପଙ୍‌ ସଂଯୋଗ ବ୍ୟବହାର କରାଯାଏ ନାହିଁ ?
ଉ :
ନିମ୍ନଲିଖତ କାରଣଗୁଡ଼ିକ ଯୋଗୁ ଗୃହ ବିଦ୍ୟୁତ୍ ପରିପଥରେ ପଙ୍‌କ୍ତି ସଂଯୋଗ ବ୍ୟବହାର କରାଯାଏ ନାହିଁ ।

• ପଙ୍‌କ୍ତି ସଂଯୋଗ କଲେ ଗୋଟିଏ ଉପକରଣ ଅଚଳ ହୋଇଗଲେ ସମୁଦାୟ ପରିପଥଟି ବିଚ୍ଛିନ୍ନ ହୋଇଯାଏ । ଅନ୍ୟ ଉପକରଣ ଗୁଡ଼ିକ କାର୍ଯ୍ୟ କରେ ନାହିଁ।
• ସମୂହ ପ୍ରତିରୋଧ ଅଧ୍ଯକ ହୋଇଯାଏ ଫଳରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ବହୁ ପରିମାଣରେ ହ୍ରାସପାଏ ।
• ପଙ୍‌କ୍ତିରେ ସଂଯୋଗ ଉପକରଣଗୁଡ଼ିକୁ ଏକ ସମୟରେ ବ୍ୟବହାର କରିବାକୁ ପଡ଼ିବ ।
• ଆବଶ୍ୟକ ଅନୁଯାୟୀ ସ୍ଵିଚ୍ ଗୁଡ଼ିକ ମୁଦିତ କିମ୍ବା ମୁକ୍ତ କରିପାରିବା ନାହିଁ ।

(d) ତାରର ପ୍ରତିରୋଧ କିଭଳି ଭାବେ ତା’ର ପ୍ରସ୍ଥଚ୍ଛେଦ କ୍ଷେତ୍ରଫଳ ଉପରେ ନିର୍ଭର କରେ ?
ଉ :
ଆମେ ଜାଣୁ R ∝ \(\frac { 1 }{ A }\)
⇒ R ∝ \(\frac{1}{\pi r^2}\) ⇒R ∝ \(\frac{1}{\mathrm{r}^2}\)
ତାରର ପ୍ରସ୍ଥଚ୍ଛେଦ କ୍ଷେତ୍ରଫଳ କମିଲେ ପ୍ରତିରୋଧ ବଢ଼େ, ପ୍ରସ୍ଥଚ୍ଛେଦ କ୍ଷେତ୍ରଫଳ ବଢ଼ିଲେ ପ୍ରତିରୋଧ ହ୍ରାସପାଏ ।

(e) ବିଦ୍ୟୁତ୍ ପରିବହନ ପାଇଁ ସାଧାରଣତଃ ତମ୍ବା ଓ ଏଲୁମିନିୟମ୍ ତାର କାହିଁକି ବ୍ୟବହାର କରାଯାଏ ?
ଉ :
ତମ୍ବା ଓ ଏଲୁମିନିୟମ୍ ଧାତୁର ପ୍ରତିରୋଧ କମ୍ ହେତୁ ସେଗୁଡ଼ିକୁ ବିଦ୍ୟୁତ୍ ପରିବହନ ପାଇଁ ବ୍ୟବହାର କରାଯାଏ ।

ପ୍ରଶ୍ନବଳୀ ଓ ଉତ୍ତର:

Question 1.
ବିଦ୍ୟୁତ୍ ପରିପଥ କହିଲେ କ’ଣ ତ୍ରଝ୍ ?
Answer:
ଏକ ଅବିଚ୍ଛିନ୍ନ ଓ ମୁଦିତ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ପଥକୁ ବିଦ୍ୟୁତ୍ ପରିପଥ କୁହାଯାଏ ।

Question 2.
ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ଏକକର ସଂଜ୍ଞା ଦିଅ ।
Answer:
ବିଦ୍ୟୁତ୍ ସ୍ରୋତର SI ଏକକ ହେଉଛି ଏମିୟର (A) । ଗୋଟିଏ ପରିବାହୀରେ ପ୍ରତି ସେକେଣ୍ଡରେ l କୁଲମ୍ ଚାର୍ଜ ପ୍ରବାହିତ ହେଉଥିଲେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ପରିମାଣ ହେବ । ଏମ୍ପିୟର ହେବ ।

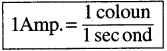
Question 3.
କେତୋଟି ଇଲେକ୍‌ଟ୍ରନର ଚାର୍ଜ ସମଷ୍ଟି ଏକ କୁଲମ୍ ହିସାବ କରି ଦେଖାଅ ।
Answer:
ଗୋଟିଏ ଇଲେକ୍‌ଟ୍ରନର ଚାର୍ଜର ପରିମାଣ = 1.6 x 10^-19 C
ମନେକର n ଟି ଇଲେକ୍‌ଟ୍ରନର ଚାର୍ଜ = 1 କୁଲମ୍
⇒ n x 1.6 x 10^-19 C = 1 C
⇒ n = \(\frac{1}{1.6 \times 10^{-19}}\) = \(\frac{10^{19}}{1 \cdot 6}\) = \(\frac{10 \times 10^{18}}{1.6}\) = 6.25 x 10¹⁸ ଇଲେକଟ୍ରନ (6 x 10¹⁸ ପ୍ରାୟ )
∴ 6 x 10⁸ ସଂଖ୍ୟକ ଇଲେକଟ୍ରନ ଚାର୍ଜର ସମଷ୍ଟି 1 କୁଲମ ।

Question 4.
କେଉଁ ଉପାୟରେ ପରିବାହୀର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟରେ ବିଭବାନ୍ତର ସ୍ଥିର ରଖାଯାଇପାରେ ?
Answer:
ବିଦ୍ୟୁତ୍ ସେଲ୍ ବା ବ୍ୟାଟେରୀ ସଂଯୋଗ କଲେ ପରିବାହୀର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟରେ ବିଭବାନ୍ତର ସ୍ଥିର ରଖାଯାଇପାରେ ।

Question 5.
ଦୁଇଟି ବିନ୍ଦୁ ମଧ୍ୟରେ ବିଭବାନ୍ତର 1V କହିଲେ କ’ଣ ବୁଝ ?
Answer:
ପରିବାହୀର ଦୁଇ ପ୍ରାନ୍ତ ମଧ୍ୟରେ 1 କୁଲମ୍ ଚାର୍ଜ ସ୍ଥାନାନ୍ତରଣ ହୋଇ ସମ୍ପାଦିତ କାର୍ଯ୍ୟ 1 ଜୁଲ ହେଲେ ପ୍ରାନ୍ତଦ୍ଵୟ ମଧ୍ଯରେ ବିଭବାନ୍ତର 1 ଭୋଲ୍ଡ ହେବ ।

Question 6.
ଗୋଟିଏ 12V ବ୍ୟାଟେରୀ ମଧ୍ୟଦେଇ 1C ଚାର୍ଜ ପ୍ରବାହିତ ହେବାରେ କେତେ ଶକ୍ତି ଆବଶ୍ୟକ ହୁଏ ?
Answer:
ଏଠାରେ V = 12 V, Q = 1 C
ଶକ୍ତି (W) = V.Q = 12V × 1C = 12 J = 12 ଜୁଲ୍ |

Question 7.
ଗୋଟିଏ ପରିବାହୀର ପ୍ରତିରୋଧ କେଉଁ କେଉଁ କାରକ ଉପରେ ନିର୍ଭର କରେ ?
Answer:
ଗୋଟିଏ ପରିବାହୀର ପ୍ରତିରୋଧ ନିମ୍ନଲିଖୁ କାରକ ଉପରେ ନିର୍ଭର କରେ –

• ପରିବାହୀର ଦୈର୍ଘ୍ୟ (l)
• ପରିବାହୀର ପ୍ରସ୍ଥଚ୍ଛେଦର କ୍ଷେତ୍ରଫଳ (A)
• ପରିବାହୀ ନିର୍ମିତ ପଦାର୍ଥର ପ୍ରତିରୋଧ (p)

Question 8.
ଗୋଟିଏ ବସ୍ତୁରୁ ତିଆରି ଖଣ୍ଡିଏ ମୋଟା ତାର ଓ ଖଣ୍ଡିଏ ସରୁ ତାର ଅଲଗା ଅଲଗା ଭାବେ ଗୋଟିଏ ବିଦ୍ୟୁତ୍ ଲାଇନ୍‌ରେ ସଂଯୁକ୍ତ ହେଲେ କେଉଁଥ‌ିରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ବେଶି ସହଜ ହେବ ? କାହିଁକି ?
Answer:
(i) ଗୋଟିଏ ବସ୍ତୁରୁ ତିଆରି ଖଣ୍ଡିଏ ମୋଟା ତାର ଓ ଖଣ୍ଡିଏ ସରୁ ତାର ଅଲଗା ଭାବେ ଗୋଟିଏ ବିଦ୍ୟୁତ୍ ଲାଇନ୍‌ରେ ସଂଯୁକ୍ତ ହେଲେ ମୋଟା ତାରରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ବେଶି ସହଜ ହେବ ।

(ii) କାରଣ ମୋଟା ତାରର ପ୍ରସ୍ଥଚ୍ଛେଦର କ୍ଷେତ୍ରଫଳ ଅଧ‌ିକ ହୋଇଥିବାରୁ ପ୍ରତିରୋଧ କମ୍ । ତେଣୁ ଇଲେକ୍‌ଟ୍ରନ୍‌ ଅଧ୍ଵ ସହଜରେ ଗତି କରିପାରିବ । କିନ୍ତୁ ସରୁ ତାରର ପ୍ରସ୍ଥଚ୍ଛେଦର କ୍ଷେତ୍ରଫଳ କମ୍ ଓ ପ୍ରତିରୋଧ ଅଧ୍ଵ । ତେଣୁ ଇଲେକ୍‌ଟ୍ରନ୍ ତା’ର ପରମାଣୁ ସହ ଧକ୍‌କା ଖାଇ କମ୍ ବେଗରେ ଗତି କରିବ ।

Question 9.
ଗୋଟିଏ ବିଦ୍ୟୁତ୍ ଉପାଂଶର ପ୍ରତିରୋଧକୁ ସ୍ଥିର ରଖ୍ ତା’ର ଦୁଇ ପ୍ରାନ୍ତ ମଧ୍ୟରେ ଥ‌ିବା ବିଭବାନ୍ତରକୁ ଅଧା କରି ଦିଆଗଲା । ତା’ ଭିତରେ ପ୍ରବାହିତ ହେଉଥ‌ିବା ବିଦ୍ୟୁତ୍ ସ୍ରୋତ କିଭଳି ପରିବର୍ତ୍ତିତ ହେବ ?
Answer:
ଓମ୍‌ଙ୍କ ନିୟମ ଅନୁଯାୟୀ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ତାପମାତ୍ରା ଓ ପ୍ରତିରୋଧରେ V ∝ I
ତେଣୁ ବିଭବାନ୍ତର ଅଧା ହେଲେ ତା’ ଭିତରେ ପ୍ରବାହିତ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ମଧ୍ଯ ଅଧା ହେବ ।

Question 10.
ବିଦ୍ୟୁତ୍ ଟୋଷ୍ଟର ଓ ବିଦ୍ୟୁତ୍ ଇସ୍ତ୍ରୀର କୁଣ୍ଡଳୀଗୁଡ଼ିକୁ କାହିଁକି ବିଶୁଦ୍ଧ ଧାତୁ ବଦଳରେ ମିଶ୍ରଧାତୁରୁ ତିଆରି କରାଯାକଥାଏ ?
Answer:

• ମିଶ୍ରଧାତୁର ପ୍ରତିରୋଧ ମୂଳ ଧାତୁଗୁଡ଼ିକଠାରୁ ଅଧିକ ।
• ମିଶ୍ରଧାତୁ ଉଚ୍ଚ ତାପମାତ୍ରାରେ ସହଜରେ ଜାରିତ ହୁଏ ନାହିଁ ।
• ମିଶ୍ରଧାତୁର ଗଳନାଙ୍କ ଉଚ୍ଚ ହୋଇଥାଏ । ତେଣୁ ବିଦ୍ୟୁତ୍ ଟୋଷ୍ଟର ଓ ବିଦ୍ୟୁତ୍ ଇସ୍ତ୍ରୀରେ କୁଣ୍ଡଳୀଗୁଡ଼ିକ ବିଶୁଦ୍ଧ ଧାତୁ ବଦଳରେ ମିଶ୍ରଧାତୁରେ ତିଆରି କରାଯାଏ ।

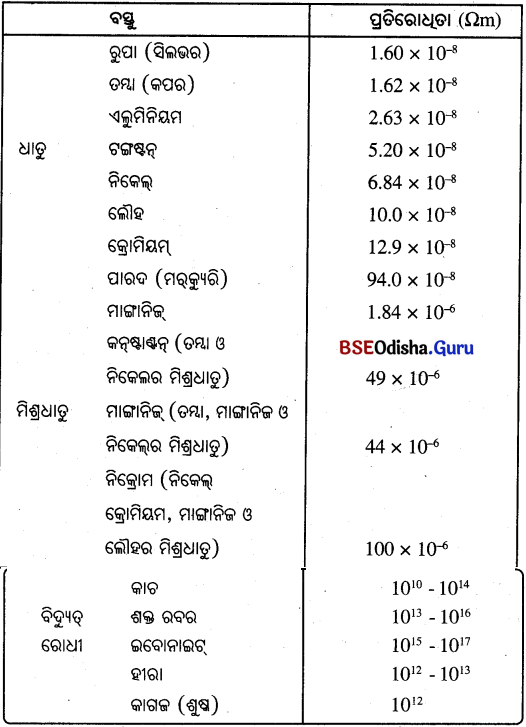
Question 11.
ସାରଣୀ ମଧ୍ଯରେ ଦିଆଯାଇଥ‌ିବା ତଥ୍ୟ ବ୍ୟବହାର କରି ଉତ୍ତର ଦିଅ ।
Answer:
(a) ଲୌହ ଓ ପାରଦ ମଧ୍ୟରୁ କେଉଁଟି ଉତ୍ତମ ପରିବାହୀ ?
ଉ :
ଲୌହତ ପ୍ରତିରୋଧୁତା = 10.0 × 10^-8 Ω m
ପାରଦର ପ୍ରତିରୋଧୁତା = 94.0 × 10^-8 Ω m
ଲୌହର ପ୍ରତିରୋଧ ପାରଦର ପ୍ରତିରୋଧ ଠାରୁ କମ୍ । ତେଣୁ ଲୌହ ପାରଦ ଅପେକ୍ଷା ଉତ୍ତମ ପରିବାହୀ ।

(b) କେଉଁ ପଦାର୍ଥଟି ସର୍ବୋତ୍କୃଷ୍ଟ ପରିବାହୀ ?
ଉ :
ରୁପାର ପ୍ରତିରୋଧ ସର୍ବନିମ୍ନ (1-60 x 10^-8 Ωm) । ତେଣୁ ରୁପା ସର୍ବୋତ୍କୃଷ୍ଟ ପରିବାହୀ ।

Question 12.
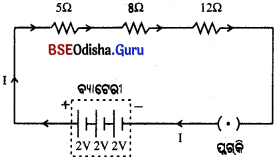
ଏକ ପରିପଥରେ ଗୋଟିଏ ବ୍ୟାଟେରୀ, 5Ω ପ୍ରତିରୋଧ, 8Ω ପ୍ରତିରୋଧ, 12Ω ପ୍ରତିରୋଧ ଓ ଗୋଟିଏ ପ୍ଲଗ୍ କି ର ପଙ୍‌କ୍ତି ସଂଯୋଗ ହୋଇଛି । ବ୍ୟାଟେରୀରେ ତିନୋଟି 2V ସେଲ୍ ଅଛି । ପରିପଥର ଚିତ୍ର କର ।
Answer:
ଦତ୍ତ ଅନ୍ମପାୟ1 ବିଦ୍ୟୁତପରିପଥ

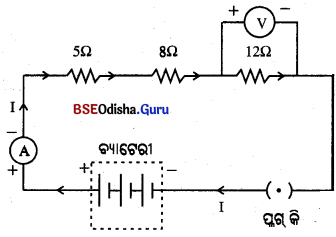
Question 13.
ପୂର୍ବ ପ୍ରଶ୍ନରେ ଦିଆଯାଇଥିବା ପରିପଥରେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ମାପିବା ପାଇଁ ଗୋଟିଏ ଏମିଟର୍ ଏବଂ 12Ω ପ୍ରତିରୋଧର ଦୁଇ ପ୍ରାନ୍ତ ମଧ୍ୟରେ ବିଭବାନ୍ତର ମାପିବା ପାଇଁ ଗୋଟିଏ ଭୋମିଟର ଲଗାଯାଇଛି । ଚିତ୍ରଟି କର । ଏମିଟର୍ ଓ ଭୋଲ୍ଟ ମିଟର୍‌ର ପାଠ୍ୟଙ୍କ କେତେ ହେବ ?
Answer:
R₁ = 5Ω, R₂ = 8Ω, R₃ = 12Ω
ମୋଟ ଭୋଲ୍ଟେଜ (V) = 3 x 2 = 6 V
ସମସ୍ର ପଥ ପଡକ୍ରି ସଂଯୋଗ ହୋଚ୍ଚଥିବାରୁ
ମୋଟ୍ ପ୍ରତିରୋଧ (R)
= R₁ + R₂ + R₃
= (5 + 8 + 12) Ω = 25 Ω
ଏମିଟରର ପାଠ୍ୟଙ୍କ (I) = \(\frac { V }{ R }\) = \(\frac { 6 }{ 25 }\) = 0 . 24 A
ଭୋଲ୍ଲମିଟର ପାଠ୍ୟଙ୍କ (V) = IR = 0·24 × 12 = 2.88 V

Question 14.
ନିମ୍ନୋକ୍ତ ପ୍ରତିରୋଧଗୁଡ଼ିକର ସମାନ୍ତରାଳ ସଂଯୋଗ ହୋଇଛି । ପ୍ରତି କ୍ଷେତ୍ରରେ ସମୂହ ପ୍ରତିରୋଧ କେତେ ହେବ ବିଚାର କର ।
(a) 1Ω ଓ 10⁶Ω

(b) 1Ω, 10³ Ω & 10⁶Ω
R₁ = 1Ω, R₂ = 10⁶ Ω ସମୂହ ପ୍ରତିରୋଧ R |
ସୂତ୍ର ଅନୁଯାୟୀ \(\frac { 1 }{ R }\) = \(\frac{1}{\mathrm{R}_1}\) + \(\frac{1}{\mathrm{R}_2}\)
\(\frac { 1 }{ R }\) = \(\frac { 1 }{ 1 }\) + \(\frac{1}{\mathrm{R}_6}\) = \(\frac{10^6+1}{10^6}\) = \(\frac { 1000000+1 }{ 1000000 }\) = \(\frac { 100000 }{ 1000000 }\)
⇒ R = \(\frac { 100000 }{ 1000001 }\) = 0.9 Ω
ସମୂହ ପ୍ରତିରୋଧ < 10

(b) R₁ = 1Ω, R₂ = 10³Ω, R₃ = 10⁶Ω
ସମାନ୍ତରାଳ ସଂଯୋଗରେ ସମୂହ ପ୍ରତିରୋଧ = R
ସୂତ୍ର ଅନୁଯାୟୀ ତୁ ତୂ \(\frac { 1 }{ R }\) = \(\frac{1}{\mathrm{R}_1}\) + \(\frac{1}{\mathrm{R}_2}\) + \(\frac{1}{\mathrm{R}_3}\) = \(\frac { 1 }{ 1 }\) + \(\frac{1}{10^3}\) + \(\frac{1}{10^6}\) Ω

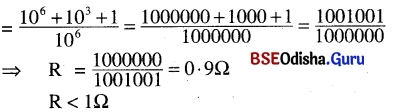
Question 15.
ଗୋଟିଏ 220V ବିଦ୍ୟୁତ୍ ଲାଇନ୍ ସହ ଗୋଟିଏ 100 Ω ବଲ୍‌ବ, ଗୋଟିଏ 50 Ω ଟୋଷ୍ଟର ଓ 500 Ω ଘର ପାଣି ଫିଲ୍ଟର’ ସମାନ୍ତରାଳ ଭାବେ ସଂଯୁକ୍ତ ହୋଇଛି । ସେହି ବିଦ୍ୟୁତ୍ ଲାଇନ୍ ସହ ଗୋଟିଏ ଇସ୍ତ୍ରୀ ମଧ୍ୟ ଲଗାଯାଇଛି । ଇସ୍ତ୍ରୀ ଆବଶ୍ୟକ କରୁଥ‌ିବା ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ବଲ୍‌ବ, ଟୋଷ୍ଟର ଓ ଫିଲ୍‌ଟରରେ ପ୍ରବାହିତ ହେଉଥ‌ିବା ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ସମଷ୍ଟିସହ ସମାନ । ଏହି ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ପରିମାଣ କେତେ ଏବଂ ଇସ୍ତ୍ରୀର ପ୍ରତିରୋଧ କେତେ ?
Answer:
ଗୋଟିଏ ବଲ୍‌ବର ପ୍ରତିରୋଧ R₁ 100 Ω
ଗୋଟିଏ ଟୋଷ୍ଟରର ପ୍ରତିରୋଧ R₂ = 50 Ω
ଗୋଟିଏ ପାଣି ଫିଲ୍ଟଟରର ପ୍ରତିରୋଧR₃ = 500 N
ସମୂହ ପ୍ରତିରୋଧ = R
ସୂତ୍ର ଅନୁଯାୟୀ \(\frac { 1 }{ R }\) = \(\frac{1}{\mathrm{R}_1}\) + \(\frac{1}{\mathrm{R}_2}\) + \(\frac{1}{\mathrm{R}_3}\)
⇒ \(\frac { 1 }{ R }\) = \(\frac { 1 }{ 100 }\) + \(\frac { 1 }{ 50 }\) + \(\frac { 1 }{ 500 }\) = \(\frac { 5+10+1 }{ 500 }\) = \(\frac { 16 }{ 500 }\)
⇒ R = \(\frac { 500 }{ 16 }\) = 31 – 25Ω
ଇସ୍ତ୍ର1ର ପ୍ରତିରୋଧ = 31 – 25Ω , V = 220 V
ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ପରିମାଣ I = \(\frac { V }{ R }\) = \(\frac { 220V }{ 31 – 25Ω }\) = 7.04A

Question 16.
ବିଦ୍ୟୁତ୍ ଉପକରଣଗୁଡ଼ିକୁ ବ୍ୟାଟେରୀ ସହ ସମାନ୍ତର ଭାବେ ସଂଯୋଗ କଲେ ପଙ୍‌କ୍ତି ସଂଯୋଗ ତୁଳନାରେ କ’ଣ ସୁବିଧା ହୁଏ ?
Answer:
ଉପକରଣଗୁଡ଼ିକୁ ସମାନ୍ତରାଳ ଭାବେ ସଂଯୁକ୍ତ କଲେ ପରିପଥର ସମୁଦାୟ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ବିଭିନ୍ନ ଉପକରଣ ଆବଶ୍ୟକତା ଅନୁସାରେ ପାଇଥାଏ । କିନ୍ତୁ ପଙ୍‌କ୍ତି ସଂଯୋଗରେ ପ୍ରତିରୋଧ ଗୁଡ଼ିକ ସମାନ ପରିମାଣର ବିତ୍ର୍ୟତ ପ୍ରୋତ ପାଇଥାନ୍ତି |

ଠିକ୍ ଠିକ୍ କାର୍ଯ୍ୟ କରିପାରିବ । କିନ୍ତୁ ପଙ୍‌କ୍ତି ସଂଯୋଗରେ ଗୋଟିଏ ଉପକରଣ ଅଚଳ ହୋଇଗଲେ ସମୁଦାୟ

Question 17.
ତିନୋଟି ପ୍ରତିରୋଧର ପରିମାଣ 2Ω, 3Ω ଓ 6Ω । ଏଗୁଡ଼ିକର କେମିତି ସଂଯୋଗ କରିବ ଯାହାଫଳରେ ସମୂହ ପ୍ରତିରୋଧ ହେବ (a) 4Ω (b) 1Ω ?
Answer:
ସମୂହ ପ୍ରତିରୋଧ 4Ω ପାଇବା ପାଇଁ 3Ω ଓ 6Ω ଥ‌ିବା ପ୍ରତିରୋଧକୁ ସମାନ୍ତର ସଂଯୋଗ ଏବଂ 2Ωକୁ ପଲ୍ଲିରେ ସଂଯୋଗ କରାଯିବ ।

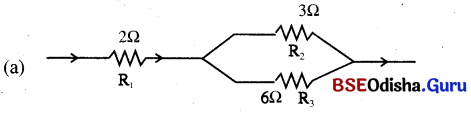
R₁ = 2Ω, R₂ = 3Ω, R₃ = 6Ω
3Ω ଓ 6Ω ପ୍ରତିରୋଧ ଦ୍ଵୟର ସମୂହ ପ୍ରତିରୋଧ R₄
\(\frac{1}{\mathrm{R}_4}\) = \(\frac{1}{\mathrm{R}_2}\) + \(\frac{1}{\mathrm{R}_3}\) = \(\frac { 1 }{ 3 }\) + \(\frac { 1 }{ 6 }\) = \(\frac { 2+1 }{ 6 }\) = \(\frac { 1 }{ 2 }[/latex ] ⇒ R₄ = 2Ω
ତିନୋଟି ପ୍ରତିରୋଧର ସମ୍ବହ ପ୍ରତିରୋଧ (R) = R₁ + R₄ = 2Ω + 2Ω = 4Ω

(b) ପ୍ରତିରୋଧ ତିନୋଟିକୁ ସମାନ୍ତରାଳ ସଂଯୋଗ କଲେ ସମୂହ ପ୍ରତିରୋଧ = R

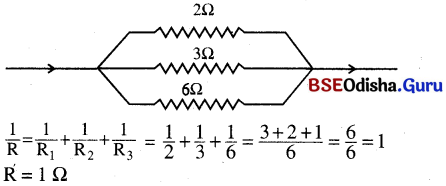
Question 18.
ଗୋଟିଏ ଲେଖାଏଁ 4Ω, 8Ω, 12Ω ଓ 24Ω ପ୍ରତିରୋଧ ଦିଆଯାଇଛି । ଏଗୁଡ଼ିକର ସଂଯୋଗରୁ ମିଳୁଥିବା
(a) ସର୍ବୋଚ୍ଚ ପ୍ରତିରୋଧ କେତେ ?
(b) ସର୍ବନିମ୍ନ ପ୍ରତିରୋଧ କେତେ ?
Answer:
R₁ = 4Ω,
R₂ = 8Ω,
R₃ = 12Ω,
R₄ = 24Ω

(a) ସମସ୍ତ ପ୍ରତିରୋଧଗୁଡ଼ିକୁ ପଂକ୍ତିରେ ସଂଯୋଗ କଲେ
ସର୍ବୋଚ୍ଚ ପ୍ରତିରୋଧ R = R₁ + R₂ + R₃ + R₄
= 4 + 8 + 12 + 24 = 48Ω

(b) ସମସ୍ତ ପ୍ରତିରୋଧଗୁଡ଼ିକୁ ପଂକ୍ତିରେ ସଂଯୋଗ କଲେ
[latex]\frac { 1 }{ R }\) = \(\frac { 1 }{ 4 }\) + \(\frac { 1 }{ 8 }\) + \(\frac { 1 }{ 12 }\) + \(\frac { 1 }{ 24 }\) = \(\frac { 6+3+2+1 }{ 24 }\) = \(\frac { 12 }{ 24 }\) = \(\frac { 1 }{ 2 }\)
∴ ସର୍ବନିମ୍ନ ପ୍ରତିରୋଧ, R = 2Ω

Question 19.
ବୈଦ୍ୟୁତିକ ହିଟର୍‌ର ତାର କୁଣ୍ଡଳୀ ଉତ୍ତପ୍ତ ହେଉଥିଲାବେଳେ ସଂଯୋଗୀ ତାର କାହିଁକି ଉତ୍ତପ୍ତ ହୁଏ ନାହିଁ ?
Answer:
ଆମେ ଜାଣୁ H = I²Rt
ଅର୍ଥାତ୍ H ∝ R
ବୈଦ୍ୟୁତିକ ହିଟର୍ ତାର କୁଣ୍ଡଳୀର ପ୍ରତିରୋଧ ଅଧ୍ବକ । ତେଣୁ ଅଧିକ ବିଦ୍ୟୁତ୍ ଶକ୍ତି ତାପଶକ୍ତିରେ ରୂପାନ୍ତରିତ ହୋଇ ଅଧ‌ିକ ତାପ ଓ ଆଲୋକ ଦିଏ । କିନ୍ତୁ ସଂଯୋଗୀ ତାରର ପ୍ରତିରୋଧ ତାର କୁଣ୍ଡଳୀର ପ୍ରତିରୋଧ ତୁଳନାରେ ବହୁତ କମ୍ । ତେଣୁ ତାହା ଉତ୍ତପ୍ତ ହୁଏନାହି ।

Question 20.
ଗୋଟିଏ 20 Ω ପ୍ରତିରୋଧ ବିଶିଷ୍ଟ ବୈଦ୍ୟୁତିକ ଇସ୍ତ୍ରୀରେ 5A ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ପ୍ରବାହିତ ହେଉଛି । 30 s ରେ କେତେ ତାପ ଉତ୍ପନ୍ନ ହେବ ?
Answer:
ଏଠାରେ R = 20Ω, I = 5A, t = 30 s
H = I²Rt = 5² × 20 × 30 = 15000 ଜ୍ତଲ୍ = 15 କିଲୋଜ୍ତଲ୍

Question 21.
ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଦ୍ଵାରା ପ୍ରଦତ୍ତ ଶକ୍ତିର ହାର କେଉଁ କାରକ ଉପରେ ନିର୍ଭର କରେ ?
Answer:
ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଦ୍ଵାରା ପ୍ରଦତ୍ତ ଶକ୍ତିର ହାର ବିଦ୍ୟୁତ୍ ପାଓ୍ବାର ଉପରେ ନିର୍ଭର କରେ ।

Question 22.
ଗୋଟିଏ ବିଦ୍ୟୁତ୍ ମୋଟର୍ 220 V ବିଦ୍ୟୁତ୍ ଲାଇନ୍‌ରୁ 5A ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ନିଏ । ମୋଟର୍‌ର ପାୱାର୍‌ କେତେ ? 2 ଘଣ୍ଟାରେ ଏହା କେତେ ଶକ୍ତି ବ୍ୟୟ କରିବ ?
Answer:
ଏଠାରେ I = 5A, V = 220V, t = 2 ଘଣ୍ଟା = 7200 ସେକେଣ୍ଡ
P = VI = 220 x 5 = 1100 W
ବ୍ୟୟିତ ଶକ୍ତି = ପାୱାର × ସମୟ = P x t
= 1100 W × 2 × 7200 ସେ = 7920000 ଜ୍ତଲ୍ = 7.92 × 10⁶ J

କାର୍ଯ୍ୟାବଳୀ (Activity)

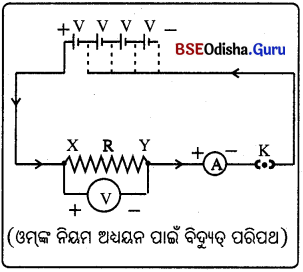
କାର୍ଯ୍ୟାବଳୀ- 1 (Activity-1)

ଆବଶ୍ୟକୀୟ ଉପକରଣ :
ଗୋଟିଏ 0.5 m ଦୈର୍ଘ୍ୟର ନିକ୍ରୋମ ତାର XY, ଏକ ଏମିଟର (A), ପ୍ଲଗ୍‌ବି, ପରିବାହୀ ତାର, 1.5 V ବିଶିଷ୍ଟ 4ଟି ସେଲ୍, ଗୋଟିଏ ଭୋଲଟ୍‌ଟର । ନିକ୍ରୋମ – (ନିକେଲ + କ୍ରୋମିୟମ୍ + ମାଙ୍ଗାନିଜ + ଲୌହ) ଏଲୟ ।

ପରୀକ୍ଷଣ :
ଚିତ୍ରରେ ଦର୍ଶାଇଲା ଭଳି ପରିପଥଟିଏ ତିଆରି କର, ଯେଉଁଥ୍ରେ 0.5 ମି ଦୈର୍ଘ୍ୟର ନିକ୍ରୋମ ତାର XY ଏମିଟରକୁ ପଙ୍‌କ୍ତିରେ ଏବଂ ଭୋଲ୍‌ଟମିଟରକୁ ସମାନ୍ତର ସଂଯୋଗ କରାଯାଏ ।

ପ୍ରଥମେ ଗୋଟିଏ ସେଲ୍ ନେଇ ଏମିଟରକୁ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ମୂଲ୍ୟାଙ୍କ ଏବଂ ଭୋଲ୍ସମିଟରରୁ ନିକ୍ରୋମ ତାରର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟରେ ଥିବା ବିଭବାନ୍ତର Vର ମୂଲ୍ୟ ପଢ଼ି ସାରଣୀରେ ଲେଖ ।

ସେହିଭଳି ଦୁଇଟି ସେଲ୍, ତିନୋଟି ସେଲ୍, ଚାରୋଟି ସେଲ୍‌ ସଂଯୋଗକରି ପ୍ରତ୍ୟେକ ଥର ବିଦ୍ୟୁତ୍ ସ୍ରୋତ I ଓ ବିଭବାନ୍ତର \(\frac { V }{ I }\) ର ମୂଲ୍ୟାଙ୍କ ଲେଖୁରଖ ଏବଂ ମୁଁ ବାହାର କର ।

ପଯ୍ୟରେକ୍ଷଣ :

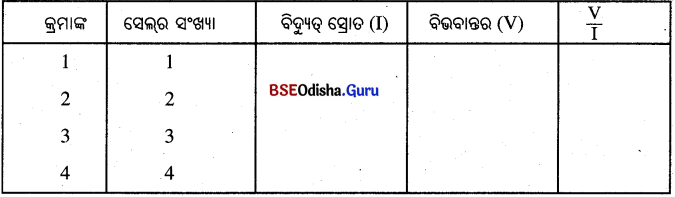
ବିଦ୍ୟୁତ୍ ସ୍ରୋତକୁ X ଅକ୍ଷରେ ଓ ବିଭବାନ୍ତରକୁ Y ଅକ୍ଷରେ ସୂଚାଇ ଲେଖଚିତ୍ର ଅଙ୍କନ କଲେ ଗ୍ରାଫ୍‌ଟି ଏକ ସରଳରେଖା ହୁଏ ।
V ଓ I ଗ୍ରାଫ୍‌ଟି ଏକ ସରଳରେଖା ହେବ ଓ ଏହା ଆଦ୍ୟବିନ୍ଦୁ ଠକୁ ଭେଦ କରିବ ।

ସିଦ୍ଧାନ୍ତ :
(i) V ଓ I ର ଗ୍ରାଫ୍ ସରଳରେଖାରୁ ଜଣାଯାଏ ଯେ, ଦୁଇ ପ୍ରାନ୍ତ ମଧ୍ୟରେ ଥ‌ିବା ବିଦ୍ୟୁତ୍‌ବିଭବ ପାର୍ଥକ୍ୟ ବଢ଼ିଲେ ବିଦ୍ଯୁସ୍ରୋତ ସେହି ଅନୁସାରେ ବଢ଼େ । V ଓ I ସମାନୁପାତୀ ।

(ii) V ଓ I ର ଅନୁପାତ ସ୍ଥିରାଙ୍କ ଅର୍ଥାତ୍ \(\frac { V }{ I }\) = R

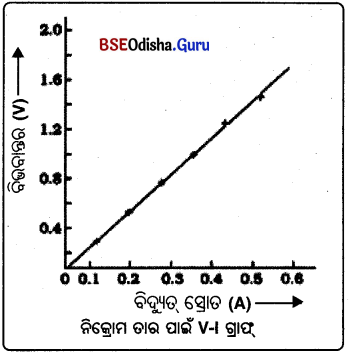
ପ୍ରତିରୋଧ :
ତାରର ବିଦ୍ୟୁତ୍ ବିଭବ ପାର୍ଥକ୍ୟ ଓ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ I ର ଭାଗଫଳକୁ ନିର୍ଦ୍ଦିଷ୍ଟ ତାରଟିର ପ୍ରତିରୋଧ R କୁହାଯାଏ ।

ଓମ୍‌ଙ୍କ ନିୟମ :
‘‘ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ତାପମାତ୍ରାରେ ଥିବା କୌଣସି ଏକ ପରିବାହୀର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟରେ ଥିବା ବିଭବାନ୍ତର ପରିବାହୀରେ ପ୍ରବାହିତ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ସହ ସମାନୁପାତୀ’’ ।

• ସାଙ୍କେତିକ ଭାଷାରେ ଓମ୍‌ଙ୍କ ନିୟମ ଅନୁସାରେ V ∝ I କିମ୍ବା \(\frac { V }{ I }\) = R = ସ୍ଥିରାଙ୍କ
  V = IR, R = \(\frac { V }{ I }\) ବା I = \(\frac { V }{ R }\)
• ଖଣ୍ଡିଏ ନିର୍ଦ୍ଦିଷ୍ଟ ଧାତବ ତାର ଓ ନିର୍ଦ୍ଦିଷ୍ଟ ତାପମାତ୍ରା ପାଇଁ R ଏକ ସ୍ଥିରାଙ୍କ । ଏହାକୁ ତାରର ପ୍ରତିରୋଧ (resistance) କୁହାଯାଏ |
• ପ୍ରତିରୋଧ ପରିବାହୀର ଏକ ଗୁଣ । ଏହା ଯୋଗୁଁ ଚାର୍ଜର ପ୍ରବାହ କମିଯାଏ ।
• ପ୍ରତିରୋଧର SI ଏକକ ହେଉଛି ଓମ୍ (Ω) ।
• ଯଦି କୌଣସି ପରିବାହୀର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟରେ ଥ‌ିବା ବିଦ୍ୟୁତ୍ ବିଭବାନ୍ତର IV ହୁଏ ଏବଂ ସେଥ‌ିରେ IA ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ପ୍ରବାହିତ ହେଉଥାଏ, ତେବେ ପ୍ରତିରୋଧ (R) ହେବ 1Ω ।

I = \(\frac { V }{ R }\) ରୁ ଜଣାଯାଏ ଯେ, ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବିଭବାନ୍ତର V ପାଇଁ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ I ପରିବାହୀର ପ୍ରତିରୋଧ R ସହ ପ୍ରତିଲୋମାନ୍ତପାତ1 (inversely proportional) |
(vi) ବିଭବାନ୍ତରକୁ ସ୍ଥିରରଖ୍ ପ୍ରତିରୋଧକୁ ଦୁଇଗୁଣ କଲେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଅଧା ହେବ ।
(vii) ବିଦ୍ୟୁତ୍ ପ୍ରବାହକୁ କମ୍ ବେଶୀ କରିବା ପାଇଁ ପରିବର୍ତ୍ତୀ ପ୍ରତିରୋଧ ବା ରିଓଷ୍ଟାଟ୍ ନାମକ ଉପକରଣ ବ୍ୟବହାର କରାଯାଏ ।

କାର୍ଯ୍ୟାବଳୀ – 2 (Activity – 2)
ଆବଶ୍ୟକ ଉପକରଣ: ଖଣ୍ଡିଏ ନିକ୍ରୋମ ତାର, ଗୋଟିଏ ଟର୍ଚ୍ଚ ବଲ୍‌ବ, ଗୋଟିଏ 10W ବଲ୍‌ବ, 0-5A ବିସ୍ତାର ଥ‌ିବା ଗୋଟିଏ ଏମିଟର, ଗୋଟିଏ ପ୍ଲଗ୍ କି, କିଛି ସଂଯୋଜୀତାର ଓ 4ଟି 1.5 volt ଶୁଷ୍କ ସେଲ୍ ।

ପରୀକ୍ଷଣ :

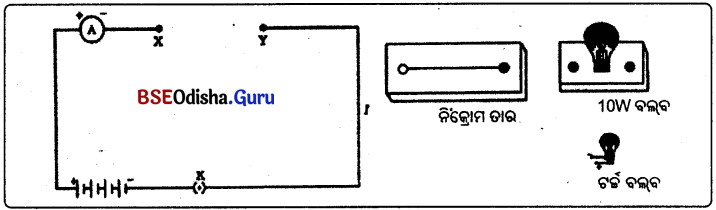
• ଉପରୋକ୍ତ ଉପକରଣଗୁଡ଼ିକୁ ନେଇ ଚିତ୍ରରେ ଦର୍ଶାଯାଇଥ‌ିବା ଭଳି ପରିପଥଟିଏ ତିଆରି କର । XY ହେଉଛି ପରିପଥର ଏକ ଶୂନ୍ୟସ୍ଥାନ |
• ପ୍ରଥମେ ନିକ୍ରୋମ ତାରକୁ XY ମଧ୍ୟରେ ଥ‌ିବା ଶୂନ୍ୟସ୍ଥାନ ମଧ୍ୟରେ ରଖ୍ ପ୍ଲଗ୍ ଚାବିକୁ ବନ୍ଦକରି ପରିପଥ ମୁଦିତ କର ।
• ଏହି ସମୟରେ ଏମିଟର ପାଠ୍ୟଙ୍କ ଟିପିରଖ
• ସେହିପରି 10W ବଲ୍‌ବ ଏବଂ ଏକ ଟର୍ଚ୍ଚ ବଲ୍‌ବ ଲଗାଇ ପୂର୍ବପରି ପରିପଥକୁ ମୁଦିତ କରି ଏମିଟରର ପାଠ୍ୟଙ୍କ ଟିପିରଖ ।

ପଯ୍ୟରେକ୍ଷଣ :

• ତିନୋଟି ଉପାଂଶ କ୍ଷେତ୍ରରେ ଏମିଟର ପାଠ୍ୟଙ୍କ ପରସ୍ପରଠାରୁ ଭିନ୍ନ ।
• ବିଭିନ୍ନ ଉପାଂଶ ବିଦ୍ୟୁତ୍ ପ୍ରବାହକୁ ଭିନ୍ନ ଭିନ୍ନ ମାତ୍ରାରେ ପ୍ରତିରୋଧ କରେ ।
• ପରିବାହୀରେ ଇଲେକ୍‌ଟ୍ରନ ଗତିରୁ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ସୃଷ୍ଟି ହୁଏ । ମାତ୍ର ପରିବାହୀରେ ରହିଥ‌ିବା ବହୁ ସଂଖ୍ୟକ ପରମାଣୁ ଯୋଗୁଁ ଇଲେକ୍‌ଟ୍ରନ ଗୁଡ଼ିକ ଅବାଧ ଭାବେ ଗତି କରିପାରନ୍ତି ନାହିଁ । ଇଲେକ୍‌ଟ୍ରନ୍‌ର ଗତି ପରମାଣୁଦ୍ୱାରା ପ୍ରତିରୋଧର ସମ୍ମୁଖୀନ ହୁଏ ।

ସିଦ୍ଧାନ୍ତ :

• ଯେଉଁ ପଦାର୍ଥ ଖୁବ୍ କମ୍ ପରିମାଣର ପ୍ରତିରୋଧ ଦିଏ ତାକୁ ସୁପରିବାହୀ (Good conductor) କୁହାଯାଏ ।
• ଯେଉଁ ପଦାର୍ଥ କିଛି ପରିମାଣର ପ୍ରତିରୋଧ ଦେଖାଏ ତାକୁ ପ୍ରତିରୋଧୀ ବା ରେଜିଷ୍ଟର (Resistor) କହନ୍ତି ।
• ଅଧ‌ିକ ପ୍ରତିରୋଧ ଦେଖାଉଥ‌ିବା ପଦାର୍ଥକୁ କୁପରିବାହୀ (Poor conductor) କହନ୍ତି ।
• ପ୍ରତିରୋଧ ବହୁତ ବେଶୀହେଲେ ପଦାର୍ଥକୁ ବିଦ୍ୟୁତ୍‌ରୋଧୀ (Insulator) କୁହାଯାଏ ।

କାର୍ଯ୍ୟାବଳୀ – 3 (Activity – 3)
ଆବଶ୍ୟକ ଉପକରଣ : ଗୋଟିଏ ସ୍କେଲ, ଗୋଟିଏ ଏମିଟର, ଖଣ୍ଡିଏ ନିକ୍ରୋମ ତାର ଓ ଗୋଟିଏ ପ୍ଲଗ୍ କି ।
ଦ୍ତରଖଣ୍ଡ ନିକ୍ରୋମ ଭାଇ ନିଥ ଯାହାର ଦୈର୍ଘ୍ୟ (l) ସମାନ; କିନ୍ତୁ ମୋଟେଇ ଭିନ୍ନ ଭିନ୍ନ । ଅନ୍ୟ ଏକ ନିକ୍ରୋମ ତାର ନିଅ ଯାହାର ଦୈର୍ଘ୍ୟ ପ୍ରଥମର 2ଗୁଣ (2I) ଏବଂ ଟଣ୍ଡେ ତମ୍ବାତାର ନିଅ

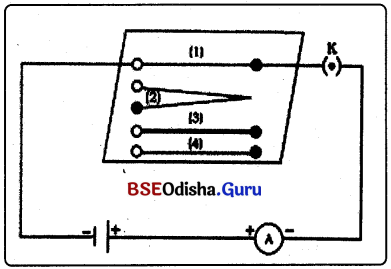
ପରୀକ୍ଷଣ :
ଚିତ୍ର ଅନୁସାରେ ପରିପଥଟିଏ ପ୍ରସ୍ତୁତ କର ।

• I ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ (1) ଚିହ୍ନିତ ନିକ୍ରୋମ ତାର ନେଇ ପରିପଥ ମୁଦିତ କରି ଏମିଟର ପାଠ୍ୟଙ୍କ ଟିପିରଖ ।
• ପ୍ରଥମ ନିକ୍ରୋମ ତାରର ମୋଟେଇ ସହ ସମାନ କିନ୍ତୁ ଦୈର୍ଘ୍ୟ ଦୁଇଗୁଣ (21) ନିକ୍ରୋମ ତାର ନେଇ ଏମିଟର ପାଠ୍ୟଙ୍କ ଟିପିରଖ ।
• ପ୍ରଥମ ନିକ୍ରୋମ ତାରର ଦୈର୍ଘ୍ୟ ସହ ସମାନ (l) ମାତ୍ର ମୋଟେଇ ଅଧିକ (ପ୍ରସ୍ଥଚ୍ଛେଦ ଅଧ୍ବକ) ନେଇ ଏମିଟର୍‌ର
• ନିକ୍ରୋମ ତାରର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥଚ୍ଛେଦ ସହ ସମାନ ଏକ ତମ୍ବାତାର ଚିତ୍ରରେ ଚିହ୍ନିତ (4) ନେଇ ଏମିଟର୍ ପାଠ୍ୟଙ୍କ ଟିପିରଖ ।
• ବିଭିନ୍ନ ତାପମାତ୍ରାରେ ପରୀକ୍ଷାଟି କରାଯାଉ ।

ପଯ୍ୟରେକ୍ଷଣ :

• ଏକା ପ୍ରକାରର ତାରର ଦୈର୍ଘ୍ୟ ଦୁଇଗୁଣ ହେଲେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ଅଧା ହୁଏ ।
• ତାରର ପ୍ରକାର ଓ ଦୈର୍ଘ୍ୟ ସମାନ ଥାଇ ପ୍ରସ୍ଥଚ୍ଛେଦ ବଢ଼ିଲେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ବଢ଼େ ।
• ତାରର ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥଛେଦ ସମାନଥାଇ ( ତମ୍ବା ଓ ନିକ୍ରୋମ) ବସ୍ତୁ ବଦଳିଲେ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ବଦଳେ ।

ସିଦ୍ଧାନ୍ତ :
ଗୋଟିଏ ସେଲ୍ ନିଆଯାଇଥ‌ିବା ଯୋଗୁଁ ବିଭବାନ୍ତର ସମାନ ରହିଛି । ପରିବାହୀର ପ୍ରତିରୋଧ ବିଦ୍ୟୁତ୍ ପ୍ରବାହ ସହ ପ୍ରତିଲୋମାନୁପାତୀ । ପ୍ରତିରୋଧ ନିମ୍ନ କାରଣଗୁଡ଼ିକ ଉପରେ ନିର୍ଭର କରେ ।

• ପରିବାହୀର ଦୈର୍ଘ୍ୟ
• ପରିବାହୀର ପ୍ରସ୍ଥଛେତ
• ପରିବାହୀ ଯେଉଁ ପଦାର୍ଥରୁ ତିଆରି ତା’ର ପ୍ରକୃତି
• ପରିବାହୀର ତାପମାତ୍ରା

ପ୍ରତିରୋଧ ସଂଜ୍ଞା ଓ ପ୍ରତିରୋଧତାର ଗାଣିତିକ ବ୍ୟାଖ୍ୟା :
ଅଧିକ ଉନ୍ନତ ପରୀକ୍ଷା ଓ ପର୍ଯ୍ୟବେକ୍ଷଣରୁ ଜଣାପଡ଼ିଛି ଯେ,
(i) ପରିବାହୀ ତାରର ପ୍ରତିରୋଧ ତାରର ଦୈର୍ଘ୍ୟ ସହ ସମାନୁପାତୀ ଓ

(ii) ପ୍ରସ୍ଥଚ୍ଛେଦର କ୍ଷେତ୍ରଫଳ ସହ ପ୍ରତିଲୋମାନୁପାତୀ ଅଟେ
ପ୍ରତିରୋଧର ସଙ୍କେତ R, ତାରର ଦୈର୍ଘ୍ୟର ସଙ୍କେତ | ଓ ପ୍ରସ୍ଥଛେଦର କ୍ଷେତ୍ରଫଳର ସଙ୍କେତ A ହୁଏ ତେବେ
R ∝l (A ସ୍ଥିର ଥିଲେ ) ……………….(i)

ଏବଂ R ∝ \(\frac { 1 }{ A }\) (/ ସ୍ଥିର ଥିଲେ) …(ii)
(i) ଓ (ii) ରୁ ଲେଖୁପାରିବା R ∝ l x \(\frac { 1 }{ A }\) (l ଓ A ବଦଳିଲେ)
⇒ R ∝ \(\frac { 1 }{ A }\) କିମ୍ବା R = p \(\frac { 1 }{ A }\)
ଏଠାରେ p (ଗ୍ରୀକ୍ ଅକ୍ଷର ରୋ (rho)) ହେଉଛି ସମାନୁପାତ ସ୍ଥିରାଙ୍କ ।
(iv) ଏହାକୁ ପରିବାହୀ ବସ୍ତୁର ବିଶିଷ୍ଟ ପ୍ରତିରୋଧ (Specific resistance) ବା ପ୍ରତିରୋଧତା (Resistivity) କୁହାଯାଏ ।

(v) ପ୍ରତିରୋଧତାର SI ଏକକ ହେଉଛି ଓମ୍-ମି. (Ωm) ।

(vi) ଏହା ବସ୍ତୁର ଗୁଣ ଉପରେ ନିର୍ଭର କରେ । ଧାତୁ ଓ ମିଶ୍ରଧାତୁମାନଙ୍କର ପ୍ରତିରୋଧ ଅପେକ୍ଷାକୃତ କମ୍ (10^-8 Ωm ରୁ 10^-6 Ωm )

(vii) ବସ୍ତୁର ପ୍ରତିରୋଧ ଓ ପ୍ରତିରୋଧ ଉଭୟ ତାପମାତ୍ରା ଉପରେ ନିର୍ଭର କରେ ।

20°C ତାପମାତ୍ରାରେ ବସ୍ତୁର ପ୍ରତିରୋଧ

କାର୍ଯ୍ୟାବଳୀ – 4 (Activity – 4)
ଆବଶ୍ୟକ ଉପକରଣ :
ତିନୋଟି ଭିନ୍ନ ଭିନ୍ନ ପ୍ରତିରୋଧ 1Ω, 2Ω, 3Ω,ଗୋଟିଏ 6V ବ୍ୟାଟେରୀ, ଗୋଟିଏ ଏମିଟର, ଗୋଟିଏ ପ୍ଲଗ୍ କି ।

ପରୀକ୍ଷଣ :

• 1Ω, 2Ω ଓ 3Ω ପ୍ରତିରୋଧଗୁଡ଼ିକୁ ପଙକ୍ତିରେ ସଂଯୋଗ କର । ପ୍ଲଗ୍ କିକୁ ବନ୍ଦ କରି ପରିପଥକୁ ମୁଦିତ କର ।
• ଏମିଟର ପାଠ୍ୟଙ୍କ ଲେଖ । ଏମିଟର ସ୍ଥାନ ପରିବର୍ତ୍ତନ କରି ପରିପଥର ପାଠ୍ୟଙ୍କ ଲେଖ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :
ଯେକୌଣସି ସ୍ଥାନରେ ଏମିଟର ରଖିଲେ ମଧ୍ୟ ଏମିଟର ମଧ୍ୟରେ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ସମାନ ରହୁଛି ।

ସିଦ୍ଧାନ୍ତ :
ପ୍ରତିରୋଧ ମାନଙ୍କ ପକ୍ତି ସଂଯୋଗରେ ପ୍ରତି ପ୍ରତିରୋଧ ଭିତରେ ସମାନ ପରିମାଣର ବିଦ୍ୟୁତ୍ ସ୍ରୋତ ପ୍ରବାହିତ ହୁଏ ।

କାର୍ଯ୍ୟାବଳୀ -5 (Activity-5)
ଆବଶ୍ୟକ ଉପକରଣ : 3ଟି ପ୍ରତିରୋଧ (R₁, R₂, R₃) ଏକ ଏମିଟର, ଏକ ଭୋଲ୍‌ଟର ପ୍ଲଗ୍ କି ବ୍ୟାଟେରୀ, ପ୍ଲଟଚାବି , ସପୋଖ1 ପରିବାବା

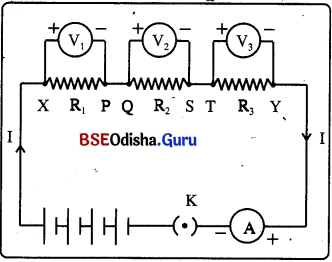
ପରୀକ୍ଷଣ :

• ଚିତ୍ରରେ ଦର୍ଶାଇଲା ଭଳି ଉପକରଣଗୁଡ଼ିକୁ ସଜାଅ ।
• ପ୍ଲଗ୍ କିକୁ ବନ୍ଦକରି ପରିପଥ ମୁଦିତ କର ଏବଂ ଭୋଲଟ୍ମିଟରର ପାଠ୍ୟାକ ଟିପିବଟ |
• ମନେକର V ହେଉଛି ପ୍ରତିରୋଧର ପଙ୍‌କ୍ତି ସଂଯୋଗର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟସ୍ଥ ବିଭବାନ୍ତର ।
• ଭୋଲ୍ସମିଟରକୁ ଖୋଲି ବ୍ୟାଟେରୀର ଦୁଇମୁଣ୍ଡ ସହ ସଂଯୋଗ କରି ବିଭବାନ୍ତର ମାପ ଓ ବିଭବାନ୍ତର ତୁଳନା କର ।
• ଭୋଲ୍ସମିଟରକୁ ପ୍ରତିରୋଧ R₁ ର ଦୁଇପ୍ରାନ୍ତ X ଓ P ସହ ସଂଯୋଗ କରି R₁ ର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟରେ ବିଭବାନ୍ତର ମାପ । ମନେକର ଏହା ହେଉଛି V₁
• ସେହିପରି ପ୍ରତିରୋଧ R₂, ଓ R₃ ର ଦୁଇପ୍ରାନ୍ତ ମଧ୍ୟରେ ରହିଥ‌ିବା ବିଭବାନ୍ତର ମାପ । ସେଗୁଡ଼ିକ ଯଥାକ୍ରମେ V₂ ଓ V₃ ହେଉ ।

ପର୍ଯ୍ୟବେକ୍ଷଣ :
ପ୍ରତିରୋଧମାନଙ୍କର ଶେଷାଗ୍ରରେ ଉତ୍ପନ୍ନ ବିଭବାନ୍ତରର ସମଷ୍ଟି V ହେବ ।

ସିଦ୍ଧାନ୍ତ :
(i)
V = V₁ + V₂ + V₃
ଅର୍ଥାତ୍ ପ୍ରତିରୋଧଗୁଡ଼ିକର ପଙ୍‌କ୍ତି ସଂଯୋଗ ଜନିତ ବିଭବାନ୍ତର ସେଗୁଡ଼ିକ ପୃଥକ୍ ପୃଥକ୍ ପ୍ରତିରୋଧ ଜନିତ ବିଭବାନ୍ତରର ସମଷ୍ଟି ସହ ସମାନ ।
ଏକାଧ୍ଵ ପ୍ରତିରୋଧର ପଙ୍‌କ୍ତି ସଂଯୋଗ ପରିବର୍ତ୍ତେ ଆମେ କେବଳ ଗୋଟିଏ ସମତୁଲ୍ୟ ପ୍ରତିରୋଧ R ନେଇପାରିବା ଯାହା ମଧ୍ୟଦେଇ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ I ପ୍ରବାହିତ ହେଉଥ‌ିବ ।
ଓମ୍‌ଙ୍କ ନିୟମ ଅନୁସାରେ V = IR
ଟି ଯାକ ପ୍ରତିରୋଧ ପାଇଁ V₁ = IR₁, V₂ = IR₂, V₃ = IR₃
∴ V = V₁ + V₂ + V₃
⇒ IR = IR₁ + IR₂ + IR₃
ଅର୍ଥାତ୍‌ R = R₁ + R₂ + R₃

ପ୍ରତିରୋଧଗୁଡ଼ିକର ପଙ୍‌କ୍ତି ସଂଯୋଗର ସମତୁଲ୍ୟ ପ୍ରତିରୋଧ ବା ସମୂହ ପ୍ରତିରୋଧ ସମ୍ପୃକ୍ତ ପ୍ରତିରୋଧଗୁଡ଼ିକର ସମଷ୍ଟି ସହ ସମାନ ।
ସମତୁଲ୍ୟ ପ୍ରତିରୋଧ ସମ୍ପୃକ୍ତ ଯେକୌଣସି ପ୍ରତିରୋଧଠାରୁ ଅଧ୍ଵ ।
ଏହାହିଁ ପକ୍ତି ସଂଯୋଗର ନିୟମ ।
ପଙ୍‌କ୍ତି ସଂଯୋଗର ଅସୁବିଧା :
ପରିପଥରେ କୌଣସି ଏକ ଉପକରଣ କିମ୍ବା ପ୍ରତିରୋଧଶୀଳ ହେଲେ ସମୁଦାୟ ପରିପଥରେ ବିଦ୍ୟୁତ ପ୍ରବାହ ବନ୍ଦ ହୋଇଯାଏ ।

କାର୍ଯ୍ୟାବଳୀ – 6 (Activity – 6)

ଆବଶ୍ୟକ ଉପକରଣ : ତିନୋଟି ପ୍ରତିରୋଧ
(R₁, R₂ ଓ R₃ ), ଏକ ଏମିଟର, ଭୋଲ୍ସମିଟର, ପ୍ଲଗ୍ କି, ପରିବାହୀ ତାର ।
ପରୀକ୍ଷଣ :

• ଚିତ୍ରରେ ଦର୍ଶାଯାଇଥିବା ଭଳି X ଓ Y ବିନ୍ଦୁ ତି ନୋଟି ପ୍ରତି ରୋଧର ସମାନ୍ତରାଳ ସଂଯୋଗ କର !
• X ଓ Y ମଧ୍ୟରେ ଗୋଟିଏ ଭୋଲ୍ସମିଟର ସଂଯୁକ୍ତ କର । ଏହି ସଂଯୋଗ ସହ ଗୋଟିଏ ବ୍ୟାଟେରୀ, ଗୋଟିଏ ପ୍ଲଗ୍ କି ଓ ଗୋଟିଏ ଏମିଟର ଲଗାଅ ।
• ପ୍ଲଗ୍ କି କୁ ବନ୍ଦ କରି ପରିପଥକୁ ମୁଦିତ କର । ଏମିଟର୍‌ର ପାଠ୍ୟଙ୍କ ଲେଖଖ । ପାଠ୍ୟଙ୍କ I ହେଉ ।
• ଭୋଲ୍ସମିଟରର ପାଠ୍ୟଙ୍କ V ହେଉ ।
• ପ୍ରତିରୋଧ R₁ ସହିତ ଏମିଟର ଲଗାଅ ମନେକର ପାଠ୍ୟଙ୍କ I₁ । ସେହିଭଳି R₂ ଓ R₃ ରେ ପ୍ରବାହିତ ହେଉଥ‌ିବା ବିଦ୍ୟୁତ୍ ସ୍ରୋତ I₂ ଓ I₃ ।

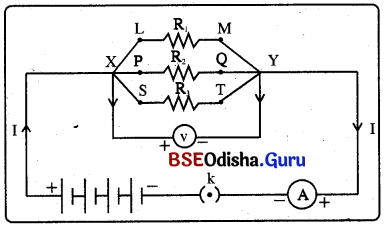
ପର୍ଯ୍ୟବେକ୍ଷଣ : I = I₁ + I₂ + I₃

ସିଦ୍ଧାନ୍ତ :
ପରିପଥର ସମୁଦାୟ ବିଦ୍ୟୁତ୍ ସ୍ରୋତ I ତିନୋଟି ପ୍ରତିରୋଧରେ ପ୍ରବାହିତ ହେଉଥ‌ିବା ପୃଥକ୍ ପୃଥକ୍ ବିଦ୍ୟୁତ୍ ସ୍ରୋତର ସମଷ୍ଟି ସହ ସମାନ ।
ଓମ୍‌ଙ୍କ ନିୟମ ଅନୁସାରେ I = \(\frac { V }{ R }\)
ତିନୋଟିଯାକ ପ୍ରତିରୋଧ ପାଇଁ I₁ = \(\frac{\mathrm{V}}{\mathrm{R}_1}\), I₂ = \(\frac{\mathrm{V}}{\mathrm{R}_2}\) , I₃ = \(\frac{\mathrm{V}}{\mathrm{R}_3}\)
\(\frac { V }{ R }\) = \(\frac{\mathrm{V}}{\mathrm{R}_1}\) + \(\frac{\mathrm{V}}{\mathrm{R}_2}\) + \(\frac{\mathrm{V}}{\mathrm{R}_3}\) କିମ୍ବା
\(\frac { 1 }{ R }\) = \(\frac{\mathrm{1}}{\mathrm{R}_1}\) + \(\frac{\mathrm{1}}{\mathrm{R}_2}\) + \(\frac{\mathrm{1}}{\mathrm{R}_3}\)
ପ୍ରତିରୋଧର ସମାନ୍ତରାଳ ସଂଯୋଗର ସମୂହ ପ୍ରତିରୋଧ ବା ସମତୁଲ୍ୟ ପ୍ରତିରୋଧର ବିଲୋମୀ (reciprocal)
ସମ୍ପୃକ୍ତ ପ୍ରତିରୋଧଗୁଡ଼ିକର ବିଲୋମୀର ସମଷ୍ଟି ସହ ସମାନ ।
ସମାନ୍ତରାଳ ସଂଯୋଗରେ ସମୂହ ପ୍ରତିରୋଧର ମୂଲ୍ୟ ସମ୍ପୃକ୍ତ ଯେକୌଣସି ପ୍ରତିରୋଧର ମୂଲ୍ୟଠାରୁ କମ୍ ।