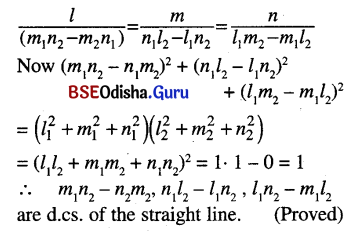CHSE Odisha Class 12 Math Solutions Chapter 13 Three Dimensional Geometry Ex 13(a)

Odisha State Board Elements of Mathematics Class 12 CHSE Odisha Solutions Chapter 13 Three Dimensional Geometry Ex 13(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 13 Three Dimensional Geometry Exercise 13(a)

Question 1.
Fill in the blanks in each of the following questions by choosing the appropriate answer from the given ones.
(a) The number of lines making equal angles with coordinate axes is _______. [1, 2, 4, 8]
Solution:
8

(b) The length of the projection of the line segment joining (1, 3, -1) and (3, 2, 4) on z-axis is _______. [1, 3, 4, 5]
Solution:
5

(c) If a line is perpendicular to z-axis and makes an angle measuring 60° with x-axis, then the angle it makes with y-axis measures _______. [30°, 60°, 90°, 120°]
Solution:
30°

(d) If the distance between the points (-1, -1, z) and (1, -1, 1) is 2 then z = _______. [1, √2, 2, 0]
Solution:
1

Question 2.
Which of the following statements are true (T) or false (F):
(a) The line through (1, -1, 2) and (-2, -1, 2) is always perpendicular to z-axis.
Solution:
True

(b) The line passing through (0, 0, 0) and (1, 2, 3) has direction cosines (-1, -2, -3)
Solution:
False

(c) if l, m, n be three real numbers proportional to the direction cosines of a line L, then l² + m² + n² = 1.
Solution:
False

(d) If α, β, γ be any three arbitrary angles then cos α, cos β, cos γ can always be considered as the direction cosines of a line.
Solution:
False

(e) If two lines are perpendicular to a third line, then the direction ratios of the two lines are proportional.
Solution:
False

Question 3.
(a) Show that the points (3, -2, 4), (1, 1, 1) and (-1, 4, -1) are collinear.
Solution:
Let A = (3, -2, 4), B = (1, 1, 1) and C = (-1, 4, -2)
D. rs of AB are < -2, 3, -3 >
D. rs of BC are < -2, 3, -3 >
As D.rs of AB are same as d.rs of BC it follows that A, B, C lie on the same straight line.
So the points are collinear. (Proved)

(b) Show that points (0, 1, 2), (2, 5, 8), (5, 6, 6) and (3, 2, 0) form a parallelogram.
Solution:
Let A = (0, 1, 2), B = (2, 5, 8), C = (5, 6, 6), D = (3, 2, 0)

∴ BC = AD
Thus the opposite sides of the quadrilateral ABCD are equal, hence it is a parallelogram.

Question 4.
(a) Find the co-ordinates of the foot of the perpendicular from the point (1, 1, 1) on the line joining (1, 4, 6) and (5, 4, 4).
Solution:

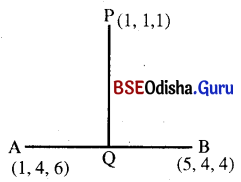
Let P = (1, 1, 1), A = (1, 4, 6) and B = (5, 4, 4)
Let Q be the foot of the perpendicular drawn from P on AB. Suppose that Q divides AB into the ratio m:n.

⇒ 4 (4m) – 2 (3m + 5n) = 0
16m – 6m – 10n = 0
⇒ 10m 10n = 0
⇒ m = n
∴ Q = (3, 4, 5)

(b) Find the co-ordinates of the point where the perpendicular from the origin meets the line joining the points (-9, 4, 5) and (11, 0, -1).
Solution:
Let A = (-9, 4, 5) and B = (11, 0, -1)

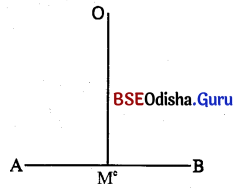
Let OM be the perpendicular drawn onto the line segment AB. Suppose that M divides AB into the ratio m:n.
Then co-ordinates of

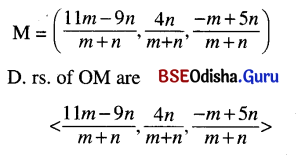
D.rs. of AB are < 20, -4, -6 >
As OM is perpendicular on to AB, then
20 (11m – 9n) – 4 (4n) – 6 (-m + 5n) = 0
⇒ 220m – 180n – 16n + 6m – 30n = 0
⇒ 226m – 226n = 0
⇒ m = n
∴ The ratio is \(\frac{m}{n}=\frac{1}{1}\)
∴ Co-ordinates of M are (1, 2, 2).

(c) Prove that the points P(3, 2, -4), Q (5, 4, -6) and R (9, 8, -10) are collinear.
Solution:
Given that P = (3, 2, -4), Q = (5, 4, -6), R = (9, 8, -10)
D. rs. of PQ are < 2, 2, -2 >
D. rs. of QR are < 4, 4, -4 >
i.e., < 2, 2, -2 >
Thus D.rs. of PQ and QR are same. So P, Q, R lie on the same straight line.
Hence P, Q, R are collinear. (Proved)

(d) If P (1, y, z) lies on the line through (3, 2, -1) and (-4, 6, 3) find y & z.
Solution:
Let A = (3, 2, -1), B = (-4, 6, 3)
Suppose that P (1, y, z) divides AB into the ratio m:n.

Question 5.
(a) If A, B, C, D are the points (6, 3, 2), (3, 5, 7), (2, 3, -1) and (3, 5, -3) respectively, then find the projection of \(\overline{A B} \text { on } \overleftrightarrow{CD}\).
Solution:
Given that
A = (6, 3, 2), B = (3, 5, 7), C = (2, 3, -1), D = (3, 5, -3)

(b) The projections of a line segment \(\overline{OP}\), through origin O, on the coordinate axes are 6, 2, 3. Find the length of the line segment \(\overline{OP}\) and its direction cosines.
Solution:

(c) The projections of a line segment of x, y and z-axis respectively are 12, 4, 3. Find the length and the direction cosines of the line segment.
Solution:
Let the length of the line segment be ‘r’ and suppose that it makes angles α, β, γ with the axes.
Then r cos α = 12, r cos β = 4 and r cos γ = 3

Question 6.
(a) If A, B, C are the points (1, 4, 2), (-2, 1, 2) and (2, -3, 4) respectively then find the angles of the triangle ABC.
Solution:

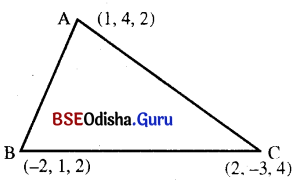
Given that A = (1, 4, 2), B = (-2, 1, 2) and C = (2, -3, 4)
D.r.s. of AB are < -3, -3, 0 >
D.r.s. of BC are < 4, -4, 2 >
D.r.s. of AC are < 1, -7, 2 >

(b) Find the acute angle between the lines passing through (-3, -1, 0), (2, -3, 1) and (1, 2, 3), (-1, 4, -2) respectively.
Solution:
Let A = (-3, -1, 0), B = (2, -3, 1), C = (1, 2, 3), D = (-1, 4, -2)
D.rs. of AB are < 5, -2, 1 >
D.rs. of CD are < -2, 2, -5 >

(c) Prove that measure of the angle between two main diagonals of a cube is cos^-1\(\frac{1}{3}\).
Solution:

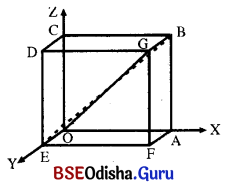
Let OABCDEFG be a cube of side ‘a’. Choose the vertex ‘O’ as origin, the line OA as x-axis, OE as y-axis and OC as z-axis.
Then
A = (a, 0, 0), B = (a, 0, a), C = (0, 0, a), D = (0, a, a), E = (0, a, 0), F = (a, a, 0) and G = (a, a, a)
The main diagonals are OG and BE
D.rs. of OG are < a, a, a >.

(d) Prove that measure of the angle between the diagonal of a face and the diagonal of a cube, drawn from a vertex is cos^-1\(\sqrt{\frac{2}{3}}\).
Solution:
See the figure of (c)
Consider the face OABC.
Let us find the angle between AC and AD.
D.rs. of AC are < -a, 0, a >

(e) Find the angle which a diagonal of a cube makes with one of its edges.
Solution:
See the figure of (c).
Let us find the angle between the edge AB and diagonal AD.

(f) Find the angle between the lines whose dcs. l, m, n are connected by the relation, 3l + m + 5n = 0 and 6mn – 2nl + 5lm = 0
Solution:
Given that 3l + m + 5n = 0 … (1)
6mn – 2nl + 5lm = 0 … (2)
From (1) we get
n = –\(\frac{3 l+m}{5}\)
Putting it in (2) we get
(6m – 2l) . (-\(\frac{3 l+m}{5}\)) + 5lm = 0
⇒ -18lm + 6l² – 6m² + 2lm + 25lm = 0
⇒ 6l² – 6m² + 9lm = 0
⇒ 2l² – 2m² + 3lm = 0
⇒ 2l² + 4lm – lm – 2m² = 0
⇒ 2l (l + 2m) – m (1 + 2m)
⇒ (l + 2m) (2l – m) = 0
⇒ l + 2m = 0 or, 2l – m = 0

Case (i) Let l + 2m = 0

Case (ii) Let 2l – m = 0

Question 7.
Show that measures of the angles between the four diagonals, of a rectangular paralle-lopiped whose edges are a, b, c are cos^-1\(\left(\frac{a^2 \pm b^2 \pm c^2}{a^2+b^2+c^2}\right)\).
Solution:

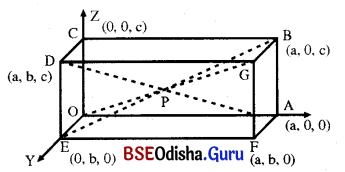
Let OABCDEFG be a rectangular parallelopiped whose edges are a, b, c.
Choose O as origin, OA as x-axis, OE as y-axis and OC as z-axis.
Then A = (a, 0, 0), B = (a, 0, c), C = (0, 0, c), D = (0, b, c), E = (0, b, 0), F = (a, b, 0), G = (a, b, c)
The four diagonals are OG, EB, AD and CF.
D. rs. of OG are < a, b, c >
D. rs. of EB are < a, -b, c >
D. rs. of AD are < -a, b, c >
D. rs. of CF are < a, b, -c >
Angle between OG and EB.

Similarly find the angles between the other diagonals. Thus the angles between the four diagonals are cos^-1\(\left(\frac{a^2 \pm b^2 \pm c^2}{a^2+b^2+c^2}\right)\).

Question 8.
If l₁, m₁, n₁ and l₂, m₂, n₂ are the direction cosines of two mutually perpendicular lines show that the d.cs. of the line perpendicular to both of them are m₁n₂ – n₁m₂, n₁l₂ – l₁n₂, l₁m₂ – m₁l₂
Solution:
Let < l₁, m₁, n₁ > and < l₂, m₂, n₂ > be the d.cs. of two mutually perpendicular straight lines.
Then l₁l₂ + m₁m₂ + n₁n₂ = 0 … (1)
Let < l, m, n > be the d.cs. of the straight line perpendicular to the above lines.
Then ll₁ + mm₁ + nn₁ = 0 … (2)
ll₂ + mm₂ + nn₂ = 0 … (3)
Solving (2) and (3) for l, m, n we get