Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 11 ପରିମିତି Ex 11.3 Textbook Exercise Questions and Answers.
BSE Odisha Class 6 Maths Solutions Chapter 11 ପରିମିତି Ex 11.3
ନିମ୍ନରେ କେତେକ ପ୍ରଶ୍ନ ଦିଆଯାଇଛି। ସେହି ପ୍ରଶ୍ନଗୁଡ଼ିକୁ କେତେକ ପିଲା ଯେପରି ସମାଧାନ କରିଛନ୍ତି, ତାହା ଲେଖାଯାଇଛି । ସେହି ସମାଧାନରେ କ’ଣ ଭୁଲ ଅଛି ଚିହ୍ନାଅ । ଏପରି ଭୁଲ କରିବାର କାରଣ କ’ଣ ଲେଖ।
Question 1.
ଗୋଟିଏ ଆୟତାକୃତି ବିଶିଷ୍ଟ ବଗିଟର ଚିତ୍ର ଆଙ୍କି ତାହାର ପରିସୀମାକୁ ଚିହ୍ନାଅ ।
ରଂଜିତା ଚିତ୍ରରେ କିପରି ରଙ୍ଗ ଦେଇ ପରିସୀମାକୁ ଚିହ୍ନାଇଲା ତାହା ତଳେ ଦେଖାଇ ଦିଆଯାଇଛି ।
ସମାଧାନ:
ଏଠାରେ ରଂଜିତା ପରିସୀମା ନ ଚିହ୍ନାଇ କ୍ଷେତ୍ରଫଳରେ ରଙ୍ଗ ଦେଇଛି ।
ରଂଜିତାର ପରିସୀମାର ଧାରଣା ନାହିଁ ।
Question 2.
ଗୋଟିଏ ଆୟତାକୃତି ବିଶିଷ୍ଟ ରୁମାଲର ଦୈର୍ଘ୍ୟ 24 ସେ.ମି. ଓ ପ୍ରସ୍ଥ 18 ସେ.ମି । ଏହାର ପରିସୀମା କେତେ ?
ଏହାର ପରିସୀମା = 24 ସେ.ମି. + 18 ସେ.ମି. = 42 ସେ.ମି.
ସମାଧାନ:
ଏଠାରେ ସମାଧାନରେ ଭୁଲ୍ ଅଛି । କେବଳ ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥର ମିଶାଣ ହୋଇଛି କିନ୍ତୁ 2 ଗୁଣନ କରାଯାଇନାହିଁ ।
ଆମେ ଜାଣିଛୁ, ପରିସୀମା = 2 × (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ)
Question 3.
ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ 3 ମିଟର । ଏହାର କ୍ଷେତ୍ରଫଳ କେତେ ହେବ ?
ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ବାହୁ × ବାହୁ
= 3 ମିଟର × 3 ମିଟର
= 9 ମିଟର
ସମାଧାନ:
3 ମି. × 3 ମି. = 9 ମିଟର । ଏହା ଭୁଲ୍ । କାରଣ ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କଲାବେଳେ ଏକକ ଓ ଏକକ ଗୁଣିଲେ ବର୍ଗ ଏକକ ହୁଏ ।
![]()
Question 4.
ପାର୍ଶ୍ଵରେ ଦିଆଯାଇଥିବା ଚିତ୍ରର ପରିସୀମା କେତେ ହେବ ?
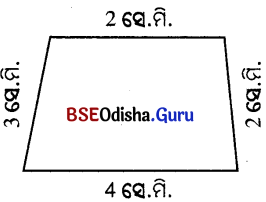
ଏହାର ଦୈର୍ଘ୍ୟ = 2 ସେ.ମି., ଏହାର ପ୍ରସ୍ତୁ = 3 ସେ.ମି.
ପରିସୀମା = ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ତୁର ଯୋଗଫଳର ଦୁଇ ଗୁଣ
= (2 ସେ.ମି. + 3 ସେ.ମି.) × 2 = 5 ସେ.ମି. × 2 = 10 ସେ.ମି.
ସମାଧାନ:
ଏହି ଚିତ୍ରଟି ଏକ ଚତୁର୍ଭୁଜ । ଏହା ଆୟତକ୍ଷେତ୍ର କିମ୍ବା ବର୍ଗକ୍ଷେତ୍ର ନୁହେଁ ।
ତେଣୁ ଏହାର ପରିସୀମା ସୂତ୍ର ନିର୍ଣ୍ଣୟ କରିବା ଠିକ୍ ହୋଇନାହିଁ ।
Question 5.
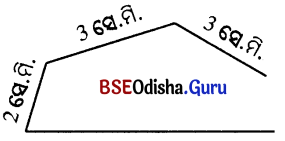
ଥରେ ମଧୁମିତା କହିଲା – ମୁଁ ମୋ ଖାତାରେ ଗୋଟିଏ ଚିତ୍ର ଆଙ୍କିଛି ଓ ତା’ର ପରିସୀମା ନିର୍ଣ୍ଣୟ କରିଛି ।
ପରିସୀମା = 2 ସେ.ମି. + 3 ସେ.ମି. + 3 ସେ.ମି. + 4 ସେ.ମି. = 12 ସେ.ମି.
ସମାଧାନ:
ଏହି ଚିତ୍ରଟି ଏକ ଆବଦ୍ଧ କ୍ଷେତ୍ର ନୁହେଁ । ତେଣୁ ଏହାର ପରିସୀମା ନିର୍ଣ୍ଣୟ କରିହେବ ନାହିଁ ।
Question 6.
ଗୋଟିଏ ଆୟତାକୃତି ବିଶିଷ୍ଟ କାଗଜର ଦୈର୍ଘ୍ୟ l ମିଟର ଓ ପ୍ରସ୍ଥ 80 ସେ.ମି. । ଏହାର ପରିସୀମା କେତେ ହେବ ? ରାଧ୍କା ପ୍ରଶ୍ନଟିର ସମାଧାନ ନିମ୍ନମତେ କଲା ।
ଦୈର୍ଘ୍ୟ = 1 ମିଟର, ପ୍ରସ୍ଥ = 80 ସେ.ମି.
ପରିସୀମା = 2 × (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ )
= 2 × (1 ମିଟର + 80 ସେ.ମି.)
= 2 × 81 ମିଟର
= 162 ମିଟର ।
ସମାଧାନ:
ଏହି ସମାଧାନରେ ଦୈର୍ଘ୍ୟ 1 ମିଟର = 100 ସେ.ମି. ଓ ପ୍ରସ୍ଥ 80 ସେ.ମି. ସହ ମିଶାଇ 2 ଗୁଣିଥିଲେ ଠିକ୍ ହୋଇଥାନ୍ତା ।
ଏଠାରେ 1 ମିଟର + 80 ସେ.ମି. = 81 ମିଟର ଲେଖାଯାଇଛି, ଏହା ସଂପୂର୍ଣ୍ଣ ଭୁଲ ।
Question 7.
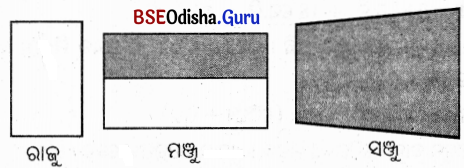
ଗୋଟିଏ ଆୟତକ୍ଷେତ୍ର ଚିତ୍ର ଆଙ୍କି ତାହାର କ୍ଷେତ୍ରଫଳକୁ ଲାଲ ରଙ୍ଗରେ ସୂଚାଇବାପାଇଁ ତିନିଜଣ ପିଲାଙ୍କୁ କୁହାଗଲା । ସେମାନେ କିପରି ଦେଖାଇଛନ୍ତି ଆସ ଦେଖିବା ।
ସମାଧାନ:
ଏହି ୩ଟି ଚିତ୍ର ମଧ୍ୟରୁ ୧ମ ଚିତ୍ରଟି ରଙ୍ଗ ଦିଆଯାଇନାହିଁ । ୨ ୟରେ ଅଧା ଓ ୩ୟଟି ଆୟତକ୍ଷେତ୍ର ନୁହେଁ । ତେଣୁ ପ୍ରଶ୍ନ ଅନୁସାରେ ଉତ୍ତର ଠିକ୍ ହୋଇନାହିଁ । କାରଣ ଆୟତଚିତ୍ରକୁ ଠିକ୍ ଚିହ୍ନିପାରିନାହାନ୍ତି ।
Question 8.
ଗୋଟିଏ ଆୟତାକୃତି ବିଶିଷ୍ଟ ଚିତ୍ର ଆଙ୍କି ତା’ର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ରମେଶ କିପରି ଚିତ୍ର ଆଙ୍କି ତା’ର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କରିଥିଲା ଦେଖ ।
ଦୈର୍ଘ୍ୟ = 4 ସେ.ମି., ପ୍ରସ୍ଥ = 2 ସେ.ମି.
କ୍ଷେତ୍ରଫଳ = 4 ସେ.ମି. × 2 ସେ.ମି. = 8 ବର୍ଗ ସେ.ମି. ।
ସମାଧାନ:

ରମେଶ ଆଙ୍କିଥିବା ଚିତ୍ର ଏକ ଆବଦ୍ଧ ଚିତ୍ର ନୁହେଁ ।
ତେଣୁ ଏହାର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କରିବା ସମ୍ଭବ ନୁହେଁ ।
Question 9.
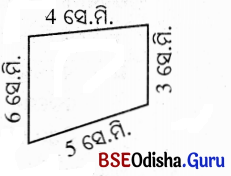
ତଳେ ଗୋଟିଏ ଆବଦ୍ଧ ଚିତ୍ର ଦେଖାଯାଇଛି । ଏହାର ପରିସୀମା କେତେ ?
ଏହି କ୍ଷେତ୍ରର ପରିସୀମା = 4 × 3 × 6 × 5 ବର୍ଗ ସେ.ମି. = 360 ବର୍ଗ ସେ.ମି. ।
ସମାଧାନ:
ଏହାର ପରିସୀମା ନିର୍ଣ୍ଣୟ କଲାବେଳେ ଦୈର୍ଘ୍ୟଗୁଡ଼ିକ ମିଶାଯିବ ମାତ୍ର ଗୁଣନ କରାଯାଇଛି ।
Question 10.
ଗୋଟିଏ ଆୟତାକୃତି ବିଶିଷ୍ଟ କ୍ଷେତ୍ରର ଦୈର୍ଘ୍ୟ 1 ମିଟର ଓ ପ୍ରସ୍ଥ 40 ସେ.ମି. । ଏହାର କ୍ଷେତ୍ରଫଳ କେତେ ?
ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = ଦୈର୍ଘ୍ୟ × ପ୍ରସ୍ଥ = 1 ମିଟର × 40 ସେ.ମି. = 40 ବର୍ଗ ମିଟର
ସମାଧାନ:
ଏଠାରେ 1 ମି. × 40 ସେ.ମି. = 1 ମିଟର × \(\frac{40}{100}\) ମିଟର = \(\frac{40}{100}\) ବର୍ଗ ମିଟର = 0.4 ବର୍ଗ ମିଟର ହୋଇଥାନ୍ତା ।
କିନ୍ତୁ 1 ମିଟର × 40 ସେ.ମି. = 40 ବର୍ଗ ମିଟର ହୋଇଛି । ଏହା ଭୁଲ୍ ଅଟେ ।
![]()
Question 11.
12 ସେ.ମି. ଦୀର୍ଘ ଓ 8 ସେ.ମି. ପ୍ରସ୍ଥ ଗୋଟିଏ ଆୟତଚିତ୍ର ABCD ଅଙ୍କନ କରାଯାଇଥିଲା (ଚିତ୍ର -କ) । ତା’ ସହିତ ଲଗାଇ 6 ସେ.ମି. ଦୀର୍ଘ ଓ 3 ସେ.ମି. ପ୍ରସ୍ଥ ଅନ୍ୟ ଏକ ଆୟତଚିତ୍ର ଅଙ୍କନ କରାଗଲା (ଚିତ୍ର – ଖ) (ଚିତ୍ର-ଖ) ରେ ଥିବା କ୍ଷେତ୍ରର ପରିସୀମା କେତେ ? ଭାବନା ନିମ୍ନମତେ ଏହି ପ୍ରଶ୍ନର ସମାଧାନ କଲା ।
(କ)

(ଖ)
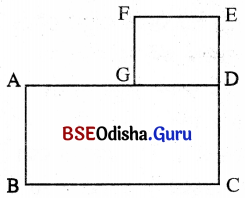
ABCD ର ପରିସୀମା = 2 (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ ) = 2 (12 + 8) = 2 × 20 ସେ.ମି. = 40 ସେ.ମି.
DEFG ର ପରିସୀମା = 2 (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ) = 2 (6 + 3) = 2 × 9 = 18 ସେ.ମି.
ସମଗ୍ର କ୍ଷେତ୍ରର ପରିସୀମା = ABCD ର ପରିସୀମା + DEFG ର ପରିସୀମା
= 40 ସେ.ମି. + 18 ସେ.ମି. = 58 ସେ.ମି. ।
ସମାଧାନ:
ଏଠାରେ ABCD କ୍ଷେତ୍ରର ପରିସୀମା ସହିତ DEFG ର ପରିସୀମା ମିଶାଇଲେ ଠିକ୍ ହେବ ନାହିଁ ।
କାରଣ ABCD କ୍ଷେତ୍ରର ପରିସୀମା ସହିତ FG + ED ର ଦୈର୍ଘ୍ୟ ମିଶିଲେ ସମଗ୍ରକ୍ଷେତ୍ରର ପରିସୀମା ନିର୍ଣ୍ଣୟ ଠିକ୍ ହେବ ।
କାରଣ GD ଦୁଇଥର ଯୋଗ କରାଯାଉଛି ।
ABCD କ୍ଷେତ୍ରର ପରିସୀମା = 2 (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ) = 2 (12 + 8) ସେ.ମି.
= (2 × 20) ସେ.ମି. = 40 ସେ.ମି.
ଚିତ୍ର (ଖ) ରେ କ୍ଷେତ୍ରର ପରିସୀମା = (40 + 3 + 3) ସେ.ମି. = 46 ସେ.ମି.
