Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 13 ଜ୍ୟାମିତିକ ଅଙ୍କନ InText Questions Textbook Exercise Questions and Answers.
BSE Odisha Class 6 Maths Solutions Chapter 13 ଜ୍ୟାମିତିକ ଅଙ୍କନ InText Questions
କହିଲ ଦେଖ୍:
ଡିଭାଇଡ଼ରକୁ କେଉଁ କେଉଁ କାମରେ ବ୍ୟବହାର କରାଯାଏ ?
ସମାଧାନ:
ସରଳରେଖାର ଦୈର୍ଘ୍ୟକୁ ମାପିବାରେ ଡିଭାଇଡ଼ର୍କୁ ବ୍ୟବହାର କରାଯାଏ ।
ତୁମ ନିକଟ ପରିବେଶରେ କେଉଁ କେଉଁଠାରେ ଲମ୍ବ ସୃଷ୍ଟି ହେଉଥିବାର ଲକ୍ଷ୍ୟ କରୁଛ ଲେଖ ।
ସମାଧାନ:
ରାସ୍ତାର ଚାରିଛକ, କାନ୍ଥର ଦୁଇଧାର ଯେଉଁଠି ମିଶିଥାଏ ଓ ଟେବୁଲ ଦୁଇଧାର ମିଶିଥିବା ସ୍ଥାନରେ ଲମ୍ବ ସୃଷ୍ଟି ହୋଇଥାଏ ।
ଚତୁର୍ଥ ସୋପାନ:
M͞N ଅଙ୍କନ କର । A͞B ଓ M͞N ଯେଉଁ ବିନ୍ଦୁରେ ପରସ୍ପରକୁ ଛେଦ କରୁଛନ୍ତି ତାର ନାମ ‘P’ ଦିଅ । P ବିନ୍ଦୁଠାରେ ସୃଷ୍ଟି ହେଉଥିବା ଚାରୋଟିଯାକ କୋଣର ପରିମାଣ ସ୍ଥିର କର । A͞P ଓ B͞P ର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର । କ’ଣ ପାଇଲ ?
ସମାଧାନ:
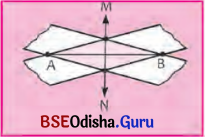
ଚାରୋଟି କୋଣର ପରିମାଣ ପ୍ରତ୍ୟେକ 90° ।
A͞P = B͞P = \(\frac{\mathrm{AB}}{2}\) ହେବ ।
![]()
ଚତୁର୍ଥ ସୋପାନ:
C͞D ଅଙ୍କନ କର । ଏହା A͞B କୁ ଠ ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
O ବିନ୍ଦୁ A͞B କୁ ଦୁଇ ସମାନ ଭାଗରେ ବିଭକ୍ତ କରୁଛି କି ନାହିଁ ପରୀକ୍ଷା କରି ଦେଖ ।
O ବିନ୍ଦୁଠାରେ ସୃଷ୍ଟି ହୋଇଥିବା କୋଣମାନଙ୍କର ପରିମାଣ ସ୍ଥିର କର ।
C͞D କୁ A͞B ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ କହିବା କି ? କାହିଁକି ?
ସମାଧାନ:
ଠ ବିନ୍ଦୁଠାରେ ସୃଷ୍ଟି ହୋଇଥିବା କୋଣର ପରିମାଣ ପ୍ରତ୍ୟେକ 90° ।
∠AOD = 90° ଓ ∠BOD = 90°
ହୋଇଥିବାରୁ C͞D କୁ A͞B ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ କହିବା ।
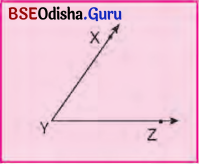
ପାର୍ଶ୍ଵର ଚିତ୍ରରେ ∠Y କୁ ଦର୍ଶାଯାଇଛି । ଏବେ କହ, ∠Y ର ଶୀର୍ଷବିନ୍ଦୁ ଓ ସନ୍ନିହିତ ବାହୁଦ୍ୱୟର ନାମ କ’ଣ ?
ସମାଧାନ:
∠Y ର ଶୀର୍ଷବିନ୍ଦୁ Y ଓ ସନ୍ନିହିତ ବାହୁଦ୍ୱୟର ନାମ YX ଓ YZ ।
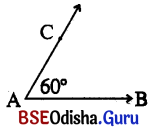
ପ୍ରୋଟ୍ରାକ୍ଟର ବ୍ୟବହାର କରି 60 ପରିମାଣର କୋଣ ଅଙ୍କନ କରିବାର ସୋପାନ ଗୁଡ଼ିକୁ ଲେଖ ।
ସମାଧାନ:
ସୋପାନ:
(i) ଯେ କୌଣସି ଗୋଟିଏ ରେଖାଖଣ୍ଡ AB ନିଅ ।
(ii) ରେଖାଖଣ୍ଡ ଉପରେ ପ୍ରୋଟ୍ରାକ୍ଟର ରଖ୍ 60 କୋଣ ପାଖରେ C ବିନ୍ଦୁ ଦିଅ ।
(iii) A ଓ C କୁ ଯୋଗ କର ।
(iv) ∠BAC = 60°
![]()
150 ପରିମାଣର କୋଣ କିପରି ଅଙ୍କନ କରିବ ?
ସମାଧାନ:
150 = 60° + 60° + \(\frac{60°}{2}\)
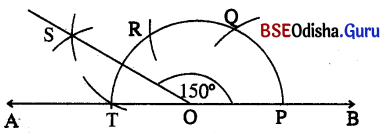
ଏଠାରେ ∠SOP ର ପରିମାଣ = 150° ।
