Odisha State Board BSE Odisha 6th Class Maths Solutions Chapter 2 ସଂଖ୍ୟା ସମ୍ବନ୍ଧୀୟ ଅଧ୍ବକ ଆଲୋଚନା Ex 2.5 Textbook Exercise Questions and Answers.
BSE Odisha Class 6 Maths Solutions Chapter 2 ସଂଖ୍ୟା ସମ୍ବନ୍ଧୀୟ ଅଧ୍ବକ ଆଲୋଚନା Ex 2.5
Question 1.
ଯଦି ଦୁଇଟି ସଂଖ୍ୟାର ଲ.ସା.ଗୁ. 16 ଓ ସେ ଦ୍ଵୟର ଗୁଣଫଳ 64 ହୁଏ ତେବେ ତା’ର ଗ.ସା.ଗୁ. ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ସଂଖ୍ୟା ଦ୍ବୟର ଲ.ସା.ଗୁ = 16 ଏବଂ ସଂଖ୍ୟା ଦ୍ଵୟର ଗୁଣଫଳ = 64 ।
ଗ.ସା.ଗୁ. = ସଂଖ୍ୟାଦ୍ଵୟର ଗୁଣଫଳ + ଲ.ସା.ଗୁ. = 64 + 16 = 4
Question 2.
ତିନୋଟି ସଂଖ୍ୟାର ଗୁଣଫଳ ସର୍ବଦା ତା’ର ଗ.ସା.ଗୁ. ଓ ଲ.ସା.ଗୁ.ର ଗୁଣଫଳ ସହିତ ସମାନ ଅଟେ କି?
ସମାଧାନ:
ତିନୋଟି ସଂଖ୍ୟାର ଗୁଣଫଳ ସର୍ବଦା ତା’ର ଗ.ସା.ଗୁ. ଓ ଲ.ସା.ଗୁର ଗୁଣଫଳ ସହିତ ସମାନ ନୁହେଁ ।
ଉଦାହରଣ – 4,6 ଓ 8 ର ଲ ସା.ଗୁ = 24 ଓ ଗ.ସା.ଗୁ = 2
ଲ.ସା.ଗୁ. × ଗ.ସା.ଗୁ = 24 × 2 = 48
ସଂଖ୍ୟାତ୍ରୟର ଗୁଣଫଳ = 4 × 6 × 8 = 192
![]()
Question 3.
ଦୁଇଟି ସଂଖ୍ୟାର ଗ.ସା.ଗୁ. ଓ ଲ.ସା.ଗୁ. ଯଥାକ୍ରମେ 13 ଓ 1989 ଅଟେ । ଯଦି ସେଥ୍ମଧ୍ୟରୁ ଗୋଟିଏ ସଂଖ୍ୟା 117 ହୁଏ, ତେବେ ଅନ୍ୟ ସଂଖ୍ୟାଟି କେତେ?
ସମାଧାନ:
ଦୁଇଟି ସଂଖ୍ୟାର ଗ.ସା.ଗୁ = 13, ଲ.ସା.ଗୁ. = 1989 ଓ ଗୋଟିଏ ସଂଖ୍ୟା = 117
ଲ.ସା.ଗୁ. × ଗ.ସା.ଗୁ. = 1989 × 13 = 25857
ପ୍ରଥମ ସଂଖ୍ୟା × ଦ୍ବିତୀୟ ସଂଖ୍ୟା = 25857
ପ୍ରଥମ ସଂଖ୍ୟା = 117 ହେଲେ ଦ୍ବିତୀୟ ସଂଖ୍ୟା = 25857 + 117 = 221
∴ ଅନ୍ୟ ସଂଖ୍ୟାଟି 221
Question 4.
ଦୁଇଟି ସଂଖ୍ୟାର ଗ.ସା.ଗୁ. 14 ଓ ଲ.ସା.ଗୁ. 204 ହୋଇପାରିବ କି ? କାରଣ ସହିତ ଉତ୍ତର ଦିଅ ।
ସମାଧାନ:
ସଂଖ୍ୟାଦୟର ଗ.ସା.ଗୁ. ସେମାନଙ୍କର ଲ.ସା.ଗୁର ଏକ ଗୁଣନୀୟକ ହେବ । ତେଣୁ ଗ.ସା.ଗୁ. ଦ୍ବାରା ଲ.ସା.ଗୁ ବିଭାଜ୍ୟ ହେବ ।
204 ÷ 14 = 14 ଭାଗଫଳ ଓ ଭାଗଶେଷ 8 ।
204, 14 ଦ୍ବାରା ବିଭାଜ୍ୟ ନୁହେଁ ।
∴ ଯେଉଁ ସଂଖ୍ୟା ଦୁଇଟିର ଗ.ସା.ଗୁ 14, ସେମାନଙ୍କର ଲ.ସା.ଗୁ. 204 ହୋଇପାରିବ ନାହିଁ ।
Question 5.
ଗୋଟିଏ ବିଦ୍ୟାଳୟର ଷଷ୍ଠ ଶ୍ରେଣୀରେ ଦୁଇଟି ବିଭାଗ ଅଛି । ସେ ଦୁଇଟି ହେଲେ A ଓ B A ବିଭାଗରେ ଛାତ୍ରଛାତ୍ରୀ ପ୍ରତି 32 ଦିନର ବ୍ୟବଧାନରେ ପ୍ରତିଯୋଗିତା ଆୟୋଜନ କରନ୍ତି । B ବିଭାଗର ଛାତ୍ର-ଛାତ୍ରୀମାନେ ଏହି ପ୍ରତିଯୋଗିତା 36 ଦିନର ବ୍ୟବଧାନରେ ଆୟୋଜନ କରନ୍ତି । ଦୁଇଟି ବିଭାଗ ବର୍ଷ ଆରମ୍ଭର ପ୍ରଥମ ଦିନ ପ୍ରତିଯୋଗିତା ଆୟୋଜନ କରନ୍ତି । ଏଠାରେ କ୍ଷୁଦ୍ରତମ ଦିନ ସଂଖ୍ୟା ନିର୍ଣ୍ଣୟ କର, ଯେତେଦିନ ପରେ ଉଭୟ ବିଭାଗର ପ୍ରତିଯୋଗିତା ଏକା ଦିନରେ ହେବ ।
ସମାଧାନ:
ଷଷ୍ଠ ଶ୍ରେଣୀର A ବିଭାଗର ଛାତ୍ରଛାତ୍ରୀ 32 ଦିନ ବ୍ୟବଧାନରେ ଓ B ବିଭାଗର ଛାତ୍ରଛାତ୍ରୀ 36 ଦିନ ବ୍ୟବଧାନରେ ପ୍ରତିଯୋଗିତା ଆୟୋଜନ କରନ୍ତି ।
ଏଠାରେ 32 ଓ 36 ର ଲ.ସା.ଗୁ. ନିର୍ଣ୍ଣୟ କରିବାକୁ ହେବ ।
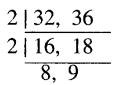
∴ ଲ.ସା.ଗୁ. = 2 × 2 × 8 × 9 = 288
288 ଦିନ ପରେ ଉଭୟ ବିଭାଗର ପ୍ରତିଯୋଗିତା ଆରମ୍ଭ ଏକା ଦିନରେ ହେବ ।
![]()
Question 6.
10,000 ର ନିକଟତମ ଦୁଇଟି ସଂଖ୍ୟା ନିର୍ଣ୍ଣୟ କର ଯାହା 2, 3, 4, 5, 6 ଓ 7 ପ୍ରତ୍ୟେକ ଦ୍ୱାରା ସମ୍ପୂର୍ଣ୍ଣଭାବେ ବିଭାଜ୍ୟ ହେବ ।
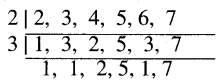
∴ ଲ.ସା.ଗୁ. = 2 × 3 × 2 × 5 × 7 = 420
10,000 ÷ 420 = 23 ଭାଗଫଳ ଓ ଭାଗଶେଷ 340
420 – 340 = 80
∴ ଗୋଟିଏ ସଂଖ୍ୟା = 10000 + 80 = 10080
ଅନ୍ୟ ସଂଖ୍ୟାଟି = 10000 – 340 = 9660
