Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 10 ପରିମିତି Ex 10.2 Textbook Exercise Questions and Answers.
BSE Odisha Class 7 Maths Solutions Chapter 10 ପରିମିତି Ex 10.2
Question 1.
ଗୋଟିଏ ବୃତ୍ତର ବ୍ୟାସ 0.42 ମି. ହେଲେ, ଏହାର ପରିଧ୍ କେତେ ହେବ ? (π = \(\frac{22}{7}\) ନିଅ)
ସମାଧାନ :
ଏଠ।ରେ ବୃତ୍ତର ବ୍ୟାସ (d) = 0.42 ମି. ।
ପରିଧ୍ = πd = \(\frac{22}{7}\) × 0.42 ମି. = 22 × 0.06 ମି. = 1.32 ମି.
ବୃତ୍ତର ପରିଧ୍ 1.32 ମିଟର ।
Question 2.
ଗୋଟିଏ ବୃତ୍ତାକୃତିର ତାରକୁ ସିଧା କରିଦିଆଗଲା । ତା’ପରେ ତାରଟିକୁ ବୃହତ୍ତମ ବର୍ଗ ଆକୃତିରେ ପରିଣତ କରିବାରୁ ତା’ର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ 22 ସେ.ମି. ହେଲା । ପୂର୍ବରୁ ଥିବା ବୃତ୍ତ ଆକୃତିର ବ୍ୟାସାର୍ଦ୍ଧ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
ବର୍ଗାକାର ଆକୃତିର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ 22 ସେ.ମି. ।
ଏହାର ପରିସୀମା = 4 × 22 = 88 ସେ.ମି.
ବୃତ୍ତାକୃତି ତାରର ଦୈର୍ଘ୍ୟ = 88 ସେ.ମି.
ବୃତ୍ତର ପରିଧ୍ଵ = 88 ସେ.ମି.
⇒ 2 × π × ବ୍ୟାସାର୍ଦ୍ଧ = 88 ସେ.ମି. ।
⇒ 2 × \(\frac{22}{7}\) × ବ୍ୟାସାର୍ଦ୍ଧ = 88 ସେ.ମି. ।
⇒ ବ୍ୟାସାର୍ଦ୍ଧ = \(\frac{88}{2 \times \frac{22}{7}}\) = \(\frac{88 \times 7}{44}\) ସେ.ମି. = 14 ସେ.ମି.
∴ ବୃତ୍ତ ଆକୃତିର ବ୍ୟାସାର୍ଦ୍ଧ 14 ସେ.ମି. ।
![]()
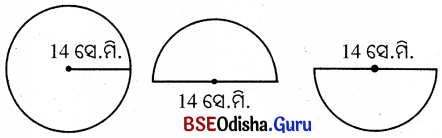
Question 3.
ଗୋଟିଏ 14 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ବୃତ୍ତାକୃତି ବିଶିଷ୍ଟ କାର୍ଡ଼ ବୋର୍ଡ଼କୁ କାଟି ଦୁଇଟି ଅଦ୍ଧବୃତ୍ତରେ ପରିଣତ କରାଗଲା । ଦୁଇଟି ଅଦ୍ଧବୃତ୍ତ ଧାରରେ ଲେସ୍ ଲଗାଇବା ପାଇଁ କେତେ ଲେସ୍ ଆବଶ୍ୟକ ?
ସମାଧାନ :
ଅର୍ଦ୍ଧବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ (r) = 14 ସେ.ମି.
ପ୍ରତି ଅଦ୍ଧବୃତ୍ତର ପରିସୀମା = r(π + 2)
= 14(\(\frac{22}{7}\) + 2) ସେ.ମି.
= 14(\(\frac{22+14}{7}\)) ସେ.ମି.
= 2 × 36 ସେ.ମି. = 72 ସେ.ମି.
ପ୍ରତି ଧାରରେ ଲେସ୍ ଲଗାଇବାକୁ 72 ସେ.ମି. ଲେସ୍ ଆବଶ୍ୟକ ।
∴ ଦୁଇଟି ଅର୍ବବୃତ୍ତର ଧାରରେ ଲେସ୍ ଲଗାଇବାକୁ 2 × 72 ସେ.ମି. = 144 ସେ.ମି. ଲେସ୍ ଆବଶ୍ୟକ ।