Odisha State Board BSE Odisha 7th Class Maths Solutions Chapter 5 ପରିମେୟ ସଂଖ୍ୟା Ex 5.6 Textbook Exercise Questions and Answers.
BSE Odisha Class 7 Maths Solutions Chapter 5 ପରିମେୟ ସଂଖ୍ୟା Ex 5.6
Question 1.
ନିମ୍ନଲିଖତ ପରିମେୟ ସଂଖ୍ୟାଗୁଡ଼ିକର ହରକୁ 10 ର ଘାତରାଶିରେ ପ୍ରକାଶ କରି ଦଶମିକ ସଂଖ୍ୟାରେ ପରିଣତ କର
(କ) \(\frac{2}{5}\)
ସମାଧାନ:
= \(\frac{2 \times 2}{5 \times 2}=\frac{4}{10}\) = 0.4
(ଖ) \(\frac{21}{20}\)
ସମାଧାନ:
= \(\frac{21 \times 2}{20 \times 5}=\frac{4}{10}\) = 1.05
(ଗ) \(\frac{-5}{4}\)
ସମାଧାନ:
= \(\frac{-5 \times 25}{4 \times 25}=\frac{-125}{100}\) = -1.25
![]()
(ଘ) \(\frac{-16}{25}\)
ସମାଧାନ:
= \(\frac{-16 \times 4}{25 \times 4}=\frac{-64}{100}\) = -0.64
Question 2.
ନିମ୍ନଲିଖୂତ ପରିମେୟ ସଂଖ୍ୟାଗୁଡ଼ିକୁ ଭାଗକ୍ରିୟା ପ୍ରଣାଳୀରେ ଦଶମିକ ସଂଖ୍ୟାରେ ପ୍ରକାଶ କର ।
(କ) \(\frac{3}{5}\)
ସମାଧାନ:
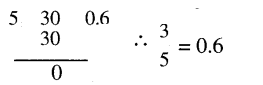
(ଖ) \(\frac{7}{8}\)
ସମାଧାନ:

(ଗ) \(\frac{9}{16}\)
ସମାଧାନ:

(ଘ) \(\frac{10}{3}\)
ସମାଧାନ:

(ଙ) \(\frac{-11}{5}\)
ସମାଧାନ:
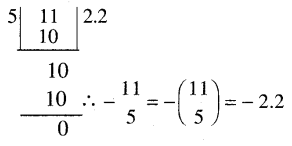
(ଚ) \(\frac{5}{11}\)
ସମାଧାନ:

(ଛ) \(\frac{2}{15}\)
ସମାଧାନ:

(ଜ) \(\frac{-2}{15}\)
ସମାଧାନ:
= -(\(\frac{2}{15}\)) = -0.13
![]()
Question 3.
ଭାଗକ୍ରିୟା ନ କରି ନିମ୍ନ ପରିମେୟ ସଂଖ୍ୟାମାନଙ୍କ ମଧ୍ୟରୁ କେଉଁଗୁଡ଼ିକ ସସୀମ ଦଶମିକ ସଂଖ୍ୟା ଓ କେଉଁଗୁଡ଼ିକ ଅସୀମ ଦଶମିକ ସଂଖ୍ୟା ହେବ ଲେଖ । ତୁମର ଉତ୍ତର ସପକ୍ଷରେ କାରଣ ଲେଖ ।
(କ) \(\frac{9}{4}\) (ଖ) \(\frac{17}{40}\) (ଗ) \(\frac{15}{11}\) (ଘ) \(\frac{22}{7}\) (ଙ) \(\frac{29}{250}\) (ଚ) \(\frac{37}{21}\) (ଛ) \(\frac{49}{14}\) (ଜ) \(\frac{126}{45}\)
ସମାଧାନ:
{କୌଣସି ପରିମେୟ ସଂଖ୍ୟା ହରର ମୌଳିକ ଗୁଣନୀୟକମାନଙ୍କ ମଧ୍ୟରେ 2 ବା 5 ଭିନ୍ନ ଅନ୍ୟ କୌଣସି ଗୁଣନୀୟକ ନଥିଲେ, ଉକ୍ତ ପରିମେୟ ସଂଖ୍ୟାଟି ସସୀମ ଦଶମିକ ସଂଖ୍ୟା ହୁଏ ।}
\(\frac{3}{5}, \frac{17}{40}, \frac{29}{250}\) ଆଦି ପରିମେୟ ସଂଖ୍ୟାର ହର ଯଥାକ୍ରମେ 4, 40, 250 ର ଗୁଣନୀୟକ କେବଳ 2 ବା 5 ଅଟେ । ତେଣୁ \(\frac{3}{5}, \frac{17}{40}, \frac{29}{250}\) – ସସୀମ ଦଶମିକ ସଂଖ୍ୟା ।
\(\frac{15}{11}, \frac{22}{7}, \frac{37}{21}\) ଆଦି ପରିମେୟ ସଂଖ୍ୟାର ହର ଯଥାକ୍ରମେ 11, 7, 21 ର ଗୁଣନୀୟକ 11, 7, 3 । ତେଣୁ \(\frac{15}{11}, \frac{22}{7}, \frac{37}{21}\) – ଅସୀମ ଦଶମିକ ସଂଖ୍ୟା ।
\(\frac{49}{14}, \frac{7}{2}\) ଓ \(\frac{126}{45}, \frac{14}{4}\) ପରିମେୟ ସଂଖ୍ୟାୟର ହର ଯଥାକ୍ରମେ 2, ଓ 5 । ତେଣୁ \(\frac{49}{14}, \frac{126}{45}\) – ସସୀମ ଦଶମିକ ସଂଖ୍ୟା ।
Question 4.
\(\frac{1}{2}+\frac{1}{3}+\frac{1}{5}\) କୁ ଦଶମିକ ପରିପ୍ରକାଶ କରି ତାହା ସସୀମ କି ଅସୀମ ଲେଖ ।
ସମାଧାନ:

Question 5.
\(\frac{11}{135}\) ପରିମେୟ ସଂଖ୍ୟାର ଦଶମିକ ରୂପ ସସୀମ ବା ଅସୀମ ହେବ ଭାଗକ୍ରିୟା ନକରି କିପରି ନିର୍ଣ୍ଣୟ କରିବ ଲେଖ ।
ସମାଧାନ:
ପରିମେୟ ସଂଖ୍ୟା \(\frac{11}{135}\) ର ହର 135 । 135 = 3 × 3 × 3 × 5
ଏଠାରେ 135ର ମୌଳିକ ଗୁଣନୀୟକ ମାନ 3 ଓ 5
ଦତ୍ତ ପରିମେୟ ସଂଖ୍ୟାର ହର 5 ବ୍ୟତୀତ 3 ମଧ୍ୟ ଏକ ମୌଳିକ ଗୁଣନୀୟକ ହେତୁ ପରିମେୟ ସଂଖ୍ୟାଟି ଏକ ଅସୀମ ଦଶମିକ ସଂଖ୍ୟା
