Odisha State Board BSE Odisha 8th Class Maths Notes Algebra Chapter 6 ବର୍ଗ-ବର୍ଗମୂଳ ଏବଂ ଘନ-ଘନମୂଳ will enable students to study smartly.
BSE Odisha Class 8 Maths Notes Algebra Chapter 6 ବର୍ଗ-ବର୍ଗମୂଳ ଏବଂ ଘନ-ଘନମୂଳ
→ ଉପକ୍ରମଣିକା (Introduction) :
(i) ଯଦି ଆଧାର ‘a’ ଏବଂ ଘାତ 2 ହୁଏ; ତେବେ ଘାତରାଶିଟି ହେବ a² । ଦୁଇଟି aର ଗୁଣଫଳକୁ a² ଭାବେ ପ୍ରକାଶ କରାଯାଏ । a²କୁ ଥର ବର୍ଗ (square) ବା ଦ୍ଵିତୀୟ ଘାତ କୁହାଯାଏ ।
a × a = a²
(ii) ସେହିପରି a × a × a = a³ ଅର୍ଥାତ୍ ତିନୋଟି ‘a’ର ଗୁଣଫଳକୁ ‘a’ର ଘନ ବା ‘a’ର ତୃତୀୟ ଘାତ ଭାବେ ପ୍ରକାଶ କରାଯାଏ ।
(iii) କୌଣସି ସଂଖ୍ୟାକୁ ସେହି ସଂଖ୍ୟାଦ୍ଵାରା ଗୁଣିଲେ ଗୁଣଫଳକୁ ସେହି ସଂଖ୍ୟାର ବର୍ଗ କୁହାଯାଏ ଏବଂ ବର୍ଗସଂଖ୍ୟାର ବର୍ଗମୂଳ (Square root) କୁହାଯାଏ ।
→ ସଂଖ୍ୟାର ବର୍ଗ ଏବଂ ପୂର୍ଣ୍ଣ ବର୍ଗସଂଖ୍ୟା (Square of a Number and Perfect Square) :
ଯଦି m ଗୋଟିଏ ପୂର୍ଣ୍ଣ ସଂଖ୍ୟା ଓ n ଏକ ଗଣନ ସଂଖ୍ୟା ଏବଂ n = m² ହୁଏ; ତେବେ n ଏକ ପୂର୍ଣ୍ଣ ବର୍ଗ ସଂଖ୍ୟା (Perfect Square Number) ରହିବ ।
ଯଥା – 3 × 3 = 3², 3² = 9, ତେଣୁ 3ର ବର୍ଗ 9 |
ସେହିପରି (-3) × (-3) = (-3)² = 9, ତେଣୁ (−3)ର ବର୍ଗ 9 |
9ର ବର୍ଗମୂଳକୁ ± 3 ରୂପେ ଲେଖାଯାଏ ।
![]()
0 ଓ + 1 ଠାରୁ ± 10 ପର୍ଯ୍ୟନ୍ତ ପୂର୍ବସଂଖ୍ୟାର ବର୍ଗର ସାରଣୀ :

ଗଣନ ସଂଖ୍ୟାମାନଙ୍କ ମଧ୍ୟରୁ 1, 4, 9, 16, 25….. ଆଦି ସଂଖ୍ୟାକୁ ପୂର୍ବବର୍ଗ ସଂଖ୍ୟା (Perfect square number କୁହାଯାଏ ।
- ପ୍ରତ୍ୟେକ ଗଣନ ସଂଖ୍ୟା ବର୍ଗ ସଂଖ୍ୟା ନୁହନ୍ତି ।
→ ପୂର୍ଣବର୍ଗ ସଂଖ୍ୟା ସମ୍ବନ୍ଧୀୟ ଧର୍ମ (Some Properties of perfect square numbers):
(i) ପ୍ରତ୍ୟେକ ପୂର୍ଣବର୍ଗ ସଂଖ୍ୟାର ଏକକ ସ୍ଥାନୀୟ ଅଙ୍କଟି 0, 1, 4, 5, 6 କିମ୍ବା 9 ହେବ । କିନ୍ତୁ 2, 3, 7, 8 କୌଣସି ପୂର୍ଣବର୍ଗ ସଂଖ୍ୟାର ଏକକ ସ୍ଥାନୀୟ ଅଙ୍କ ହେବ ନାହିଁ ।
- କୌଣସି ସଂଖ୍ୟାର ଶେଷରେ ଅଯୁଗ୍ମ ସଂଖ୍ୟକ ଶୂନ ଥିଲେ ସେହି ସଂଖ୍ୟାଟି ପୂର୍ଣବର୍ଗ ସଂଖ୍ୟା ହେବ ନାହିଁ ।
(ii) ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ବର୍ଗ ଏକ ଅଯୁଗ୍ମ ସଂଖ୍ୟା ଓ ଯୁଗ୍ମ ସଂଖ୍ୟାର ବର୍ଗ ଏକ ଯୁଗ୍ମ ସଂଖ୍ୟା ହେବ ।
(iii) ରୁ ବଡ଼ ଯେ କୌଣସି ପୂର୍ଣବର୍ଗ ସଂଖ୍ୟାକୁ 3 ଦ୍ଵାରା ଭାଗକଲେ ଭାଗଶେଷ 0 ବା 1 ହେବ ।
2² = 4 = 3 × 1 + 1, 3² = 3 × 3, 4² = 16 = 3 × 5 + 1
(iv) ରୁ ବଡ଼ ଯେ କୌଣସି ପୂଣ୍ଡବର୍ଗ ସଂଖ୍ୟାକୁ 4 ଦ୍ବାରା ଭାଗକଲେ ଭାଗଶେଷ 0 କିମ୍ବା 1 ରହିବ ।
2² = 4 = 4 × 1, 3² = 9 = 4 × 2 + 1, 4² = 16 = 4 × 4
(v) କୌଣସି ପୂର୍ଣ ବର୍ଗସଂଖ୍ୟା nକୁ ଯଦି କୌଣସି ଏକ ମୌଳିକ ସଂଖ୍ୟା p ଦ୍ଵାରା ଗୁଣନ କରାଯାଏ; ତେବେ ଗୁଣଫଳ ‘pn’ ଏକ ପୂର୍ଣବର୍ଗ ସଂଖ୍ୟା ହେବ ନାହିଁ ।
ଉଦାହରଣସ୍ୱରୂପ, 9 ଏକ ପୂର୍ବବର୍ଗ ସଂଖ୍ୟା ହେଲେ, ଏହାର 2 ଗୁଣ ବା 3 ଗୁଣ; ଅଥବା ଯେ କୌଣସି ମୌଳିକ ସଂଖ୍ୟାଦ୍ଵାରା ଗୁଣନ ଗୋଟିଏ ଗୋଟିଏ ପୂର୍ଣବର୍ଗ ସଂଖ୍ୟା ହେବ ନାହିଁ ।
(vi) ପିଥାଗୋରୀୟ ତ୍ରୟୀ (Pythagorean triplets):
ଏକ ସଂଖ୍ୟାତ୍ରୟୀ (Triplet) m, n, p ଗଣନ ସଂଖ୍ୟା ଓ m, n, p ମଧ୍ଯରେ p ବୃହତ୍ତମ ସଂଖ୍ୟା ଥାଇ ଯଦି m² + n² = p² ହୁଏ; ତେବେ (m, n, p) କୁ ପିଥାଗୋରୀୟ ତ୍ରୟୀ (Pythagorean triplet) କୁହାଯାଏ । ଉଦାହରଣସ୍ୱରୂପ, (3, 4, 5) ଏବଂ (5, 12, 13) ଗୋଟିଏ ଗୋଟିଏ ପିଥାଗୋରୀୟ ତ୍ରୟୀ ।
ଯେ କୌଣସି ସଂଖ୍ୟା m(m > 1) ପାଇଁ (2m, m² – 1, m² + 1) ଏକ ପିଥାଗୋରୀୟ ତ୍ରୟୀ ହେବେ ।
![]()
ମନେରଖ :
- ଯଦି m(m > 1) ଏକ ଅଯୁଗ୍ମ ସଂଖ୍ୟା ହୁଏ; ତେବେ \(\left(m, \frac{m^2-1}{2} \text { ଓ } \frac{m^2+1}{2}\right)\) ତ୍ରୟୀ ହେବ ।
- ଯଦି m (m > 2) ଏକ ଯୁଗ୍ମ ସଂଖ୍ୟା ହୁଏ; ତେବେ \(\left(m,\left(\frac{m}{2}\right)^2-1 \text { ଓ } \left(\frac{m}{2}\right)^2+1\right)\) ତ୍ରୟୀ ହେବ ।
(vii) ଦୁଇଟି କ୍ରମିକ ପୂର୍ଣ୍ଣବର୍ଗ ସଂଖ୍ୟାର ଅନ୍ତର, ସଂଖ୍ୟାଦ୍ଵୟର ସମଷ୍ଟି ସହ ସମାନ ହେବ ।
3² – 2² = 5 = 3 + 2
ବିପରୀତ କ୍ରମେ କୌଣସି ଏକ ଅଯୁଗ୍ମ ସଂଖ୍ୟା ଦୁଇଟି କ୍ରମିକ ସଂଖ୍ୟାର ବର୍ଗର ଅନ୍ତର ରୂପେ ପ୍ରକାଶିତ ହୋଇପାରିବ ।
9 = 9.1 = \(\left(\frac{9+1}{2}\right)^2-\left(\frac{9-1}{2}\right)^2=5^2-4^2\)
(viii) କୌଣସି ସଂଖ୍ୟାର ବର୍ଗ, ସେହି ସଂଖ୍ୟା ବିଶିଷ୍ଟ ପ୍ରଥମ ଅଯୁଗ୍ମ ଗଣନ ସଂଖ୍ୟାର ସମଷ୍ଟି ସହ ସମାନ । ଉଦାହରଣସ୍ୱରୂପ, ପ୍ରଥମ 10ଟି ଅଯୁଗ୍ମ ଗଣନ ସଂଖ୍ୟାର ସମଷ୍ଟି 10² = 100
1+ 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 = 10² = 100 ।
![]()
→ ସଂକ୍ଷିପ୍ତ ବର୍ଗ ନିରୂପଣ ପ୍ରଣାଳୀ (Short cut method to find square numbers) :
(i) ଏକକ ସ୍ଥାନରେ 5 ଥିବା ସଂଖ୍ୟାର ବର୍ଗ ନିର୍ଣ୍ଣୟ
ଆମେ ଜାଣୁ 15² = 225, 25² = 625, 35² = 1225
ଏଠାରେ ସଂଖ୍ୟାଟିର ଏକକ ସ୍ଥାନରେ 5 ରହିଲେ ବର୍ଗ ସଂଖ୍ୟାର ଏକକ ଓ ଦଶକ ସ୍ଥାନରେ ଅଙ୍କ ଯଥାକ୍ରମେ 5 ଏବଂ 2 ରହୁଛି । ଶତକ ସ୍ଥାନରେ, ସଂଖ୍ୟାଟିର ଦଶକ ସ୍ଥାନର ଅଙ୍କ ଏବଂ ତା’ର ପରବର୍ତ୍ତୀ ସଂଖ୍ୟାର ଗୁଣଫଳ ରହୁଛି ।
(ii) ଆମେ ଜାଣୁ a² – b² = (a + b) (a – b) ⇒ a² = (a + b) (a – b) + b²
ଉଦାହରଣ :
19ର ବର୍ଗ ନିରୂପଣ କର ।
19 ର ନିକଟବର୍ତୀ (10ର ଗୁଣିତକ) ସଂଖ୍ୟାଟି 20 1
a = 19 ହେଲେ, b = 20 – 19 = 1 ହେବ ।
19² = (19 + 1) (19 – 1) + 1² [∵ a² = (a + b) (a – b) + b²]
= 20 × 18+ 1 = 360 + 1 = 361
ସେହିପରି 372 = (37 + 3) (37 – 3) + 3² = 40 × 34 +9 = 1360 + 9 = 1369
(iii) (x + a)(x + b) = x² + x(a + b) + ab = x(x + a + b) + ab
172 = 17 × 17 = (10 + 7)(10 + 7) [ଏଠାରେ a = b = 7 ଏବଂ ଆଧାର 10 ]
= 10 (10 + 7 + 7) + 7 × 7 = 10 × 24 + 49 = 289
ସେହିପରି 36² = 36 x 36 = (40 – 4) (40 – 4)
= 40 {40 + (-4) + (-4)} + (-4) × (-4) (ଏଠାରେ a = b = -4 ଏବଂ ଆଧାର 40)
=40 × 32 + 16 = 1280 + 16 = 1296
(iv) (a + b)² = a² + 2ab + b² ସୂତ୍ରରେ ମଧ୍ୟ ବର୍ଗ ନିରୂପଣ କରାଯାଇପାରିବ ।
31² = (30 + 1)² = 30² + 2 × 30 × 1 + 1² = 900 + 60 + 1 = 961
ସେହିପରି 53² = (50 + 3)² = 50² + 2 × 50 × 3 + 3² = 2500 + 300 + 9 = 2809
(a – b)² = a² – 2ab + b² ସୂତ୍ରରେ ମଧ୍ୟ ବର୍ଗ ନିରୂପଣ କରାଯାଇପାରିବ ।
49² = (50 -1)² = 50² – 2 × 50 × 1 + 1² = 2500 – 100 + 1 = 2401
![]()
→ ପରିମେୟ ସଂଖ୍ୟା ବର୍ଗ (Square of rational numbers) :
-m, n ∈ Z 3 n ≠ 0 ହେଲେ, \(\frac{m}{n}\) ∈ Q; ଅର୍ଥାତ୍ \(\frac{m}{n}\) ଏକ ପରିମେୟ ସଂଖ୍ୟା ।
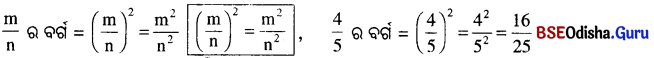
ଆମେ ଜାଣିଲେ ଯେ ମୂଳ ସଂଖ୍ୟାରେ ଦଶମିକ ପରେ ଗୋଟିଏ ଅଙ୍କ ଥିଲେ ବର୍ଗସଂଖ୍ୟାରେ ଦଶମିକ ପରେ ତା’ର ଦୁଇଗୁଣ ସଂଖ୍ୟା ଅଙ୍କ ରହିବ ।
→ ପୂର୍ଷବର୍ଗ ସଂଖ୍ୟାର ବର୍ଗମୂଳ :
m ଏକ ପରିମେୟ ସଂଖ୍ୟା ଏବଂ m² = n ହେଲେ, nର ବର୍ଗମୂଳ m ।
ଆମେ ଜାଣିଛେ 32 = 9 ଓ (-3)² = 9; ତେଣୁ 9 ର ବର୍ଗମୂଳ ± 3 ରୂପ ଲେଖାଯାଏ ।
√ ଚିହ୍ନିତ ଧନାତ୍ମକ ବର୍ଗମୂଳ ସୂଚକ ।
√9 , 9ର ଧନାତ୍ମକ ବର୍ଗମୂଳ = 3, -√9 , 9ର ଋଣାତ୍ମକ ବର୍ଗମୂଳ = -3
ତେଣୁ 9ର ବର୍ଗମୂଳ = ±√9 = ±3
ପ୍ରଥମ ଦଶଗୋଟି ପୂର୍ବବର୍ଗ ସଂଖ୍ୟାର ବର୍ଗମୂଳ ସାରଣୀରେ ଦିଆଯାଇଛି ।

→ ପୂର୍ଷବର୍ଗ ସଂଖ୍ୟାର ବର୍ଗମୂଳ ନିର୍ଣ୍ଣୟ ପ୍ରଣାଳୀ :
(a) ଉତ୍ପାଦକ ନିର୍ଣ୍ଣୟ ମାଧ୍ୟମରେ ବର୍ଗମୂଳ ନିର୍ଣ୍ଣୟ :
ଉଦାହରଣ :
484 ର ବର୍ଗମୂଳ ନିରୂପଣ କର ।
ସମାଧାନ :
484 = 2 × 2 × 11 × 11
√484 = √2 × 2 × 11 × 11 = 2 × 11 = 22
484 ର ବର୍ଗମୂଳ ±22
![]()
(b) ଭାଗକ୍ରିୟା ମାଧ୍ଯମରେ ବର୍ଗମୂଳ ନିରୂପଣ :
ସମାଧାନ :
ଭାଗକ୍ରିୟାଦ୍ଵାରା 60025 ର ବର୍ଗମୂଳ ନିରୂପଣ କର ।
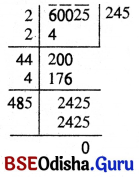
(i) ବର୍ଗସଂଖ୍ୟାଟି ପାଞ୍ଚଅଙ୍କ ବିଶିଷ୍ଟ । ଏହାର ଡାହାଣପାର୍ଶ୍ବରୁ ଯୋଡ଼ି ଯୋଡ଼ି କରି ଅଙ୍କ ନେଲେ ତିନିଯୋଡ଼ା ହେବ ଓ ଶେଷ ଯୋଡ଼ାଟି ଏକଅଙ୍କ ବିଶିଷ୍ଟ ହେବ ।
(ii) ତୃତୀୟ ଯୋଡ଼ିରେ \(\bar{6}\) ଦ୍ଵିତୀୟ ଯୋଡ଼ିରେ \(\bar{0 0}\) ଓ ପ୍ରଥମ ଯୋଡ଼ିରେ \(\bar{2 5}\) ରହିବ ।
(iii) ତୃତୀୟ ଯୋଡ଼ି ସଂଖ୍ୟା 6 ରୁ ସାନ ବୃହତ୍ତମ ପୂର୍ଣବର୍ଗ ସଂଖ୍ୟା 4 ବାଦଦେଇ ବର୍ଗମୂଳ ପାଇଁ ଭାଗଫଳ ସ୍ଥାନରେ 6 – 4 = 2 ଲେଖୁ ତାହାର ଡାହାଣପାଖରେ ଦ୍ଵିତୀୟ ଯୋଡ଼ି ସଂଖ୍ୟା 00 ଲେଖ ଓ ବର୍ଗମୂଳର ଏକକ ସ୍ଥାନବିଶିଷ୍ଟ ସ୍ଥାନରେ 4 ର ବର୍ଗମୂଳ 2 ଲେଖ ।
(iv) ପ୍ରଥମ ଭାଜକ 2 ତଳେ ଆଉ ଏକ 2 ଲେଖୁ ଯୋଗଫଳ4 ଦ୍ବିତୀୟ ଭାଜକର ପ୍ରଥମ ଅଙ୍କ ରୂପେ ଲେଖି ।
(v) ବର୍ତ୍ତମାନ ଦ୍ଵିତୀୟ ଭାଜକ 4 ର ଏକକ ଅଙ୍କ ଏପରି ଏକ ଅଙ୍କ ଲେଖ, ଯାହାଫଳରେ ଦ୍ଵିତୀୟ ଭାଜକଟି ଗୁଣଫଳ 200 ରୁ ଠିକ୍ କମ୍ ହେବ 44 x 4 = 176 ।
(vi) ବର୍ତ୍ତମାନ 4 କୁ ବର୍ଗମୂଳ ସ୍ଥାନରେ 2ର ପରବର୍ତ୍ତୀ ସଂଖ୍ୟାରୂପେ ଲେଖ ଏବଂ 200 ତଳେ 176 ଲେଖ୍ ବିୟୋଗକରି ବିୟୋଗ ଫଳ 24 ଲେଖ । 24 ର ପରେ ତୃତୀୟ ଯୋଡ଼ି ସଂଖ୍ୟା 25 ଲେଖ, ଫଳରେ ଭାଜ୍ୟ 2425 ହେବ ।
(vii) ଦ୍ବିତୀୟ ଭାଜକ 44 ର ଏକକ ଅଙ୍କ 4 ତଳେ 4 ଲେଖୁ ଯୋଗଫଳ 48 କୁ ତୃତୀୟ ଭାଜକର ପ୍ରଥମ ଦୁଇଟି ଅଙ୍କ ରୂପେ ନିଅ ।
(viii) 48 ପରେ 5 ବସାଇଲେ 485 ହେବ ଏବଂ 485 × 5 = 2425 କୁ ଭାଜ୍ୟ 2425 ତଳେ ଲେଖ୍ ବିୟୋଗଫଳ 0 ଲେଖ ଓ ବର୍ଗମୂଳର 24 ପରେ 5 ଅଙ୍କ ବସାଇ ବର୍ଗମୂଳ 245 ନିରୂପଣ କର ।
∴ 60025 ର ବର୍ଗମୂଳ ± 245 ।
→ ଭାଗକ୍ରିୟା ଦ୍ବାରା ବର୍ଗମୂଳ ସଂପର୍କରେ କିଛି ଜାଣିବା କଥା :
- ଦତ୍ତ ସଂଖ୍ୟାର (ଯାହାର ବର୍ଗମୂଳ ସ୍ଥିର କରାଯିବ) ଅଙ୍କଗୁଡ଼ିକୁ ଯୋଡ଼ି ଯୋଡ଼ି କଲାପରେ ଯଦି କୌଣସି ବଳକା ଅଙ୍କ ଥାଏ;ତେବେ ସଂଖ୍ୟାର ବାମ ପାଖରେ 0 ବସାଇ ବଳକା ଅଙ୍କ ସହ ଗୋଟିଏ ଅଙ୍କ-ଯୋଡ଼ି କରାଯିବ ।
- ଦତ୍ତ ସଂଖ୍ୟାରେ ଯେତୋଟି ଅଙ୍କ ଯୋଡ଼ି ଥାଏ, ଭାଗକ୍ରିୟା ସେତିକିଟି ପର୍ଯ୍ୟାୟରେ ସଂପାଦିତ ହୁଏ ।
- ଦତ୍ତ ସଂଖ୍ୟାର ପ୍ରତ୍ୟେକ ଯୋଡ଼ି ଅଙ୍କଲାଗି ବର୍ଗମୂଳରେ ଗୋଟିଏ ଅଙ୍କ ମିଳିବ ।
- ଏଣୁ ସଂଖ୍ୟାଟିକୁ ଦେଖିଲେ ଏହାର ବର୍ଗମୂଳ କେତେ ଅଙ୍କବିଶିଷ୍ଟ ତାହା ଜାଣିହେବ ।
→ ଦଶମିକ ବର୍ଗ ସଂଖ୍ୟାର ବର୍ଗମୂଳ ନିର୍ଣ୍ଣୟ :
a, b ∈ N ହେଲେ, \(\sqrt{\frac{\mathbf{a}}{\mathbf{b}}}=\frac{\sqrt{\mathbf{a}}}{\sqrt{\mathbf{b}}}\)
(i) ଭଗ୍ନାଂଶ (ଯାହାର ଲବ ଓ ହର ଉଭୟେ ପୂର୍ବବର୍ଗ ସଂଖ୍ୟା)ର ବର୍ଗମୂଳ ନିର୍ଣ୍ଣୟ :
ଉଦାହରଣ :
\(\frac{25}{841}\)ର ବର୍ଗମୂଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ :
\(\frac{25}{841}\)ର ବର୍ଗମୂଳ = ± \(\sqrt{\frac{25}{841}}=± \frac{\sqrt{25}}{\sqrt{841}\) = ± \(\frac{5}{29}\)
→ ଆସନ୍ନ ବର୍ଗମୂଳ ନିରୂପଣ :
ଉଦାହରଣ :
5ରେ ବର୍ଗମୂଳ ନିରୂପଣ କର ।
ସମାଧାନ :

ଦଶମିକ ଏକସ୍ଥାନ ପର୍ଯ୍ୟନ୍ତ 5 ର ଆସନ୍ନ ବର୍ଗମୂଳ = + 2.2
ଦଶମିକ ଦୁଇସ୍ଥାନ ପର୍ଯ୍ୟନ୍ତ 5 ର ଆସନ୍ନ ବର୍ଗମୂଳ = ± 2.24
ଦଶମିକ ତିନିସ୍ଥାନ ପର୍ଯ୍ୟନ୍ତ 5 ର ଆସନ୍ନ ବର୍ଗମୂଳ = ± 2.236
2.2.ର ବର୍ଗ = 4.84 ଯାହା 5 ଠାରୁ ସାମାନ୍ୟ ସାନ (0.16 ସାନ)
2.24 ର ବର୍ଗ = 5.0176 ଯାହା 5 ଠାରୁ 0.0176 ଅଧିକ
2.236 ର ବର୍ଗ = 4.999696 ଯାହା 5 ଠାରୁ 0.000304 ମାନ ।
![]()
→ ବର୍ଗମୂଳ ସମ୍ବନ୍ଧୀୟ ବିବିଧ ପ୍ରଶ୍ନ :
ଉଦାହରଣ :
8192 କୁ କେଉଁ କ୍ଷୁଦ୍ରତମ ସଂଖ୍ୟାଦ୍ଵାରା ଭାଗକଲେ ଭାଗଫଳ ଏକ ପୂର୍ଣ୍ଣସଂଖ୍ୟା ହେବ ?
ସମାଧାନ :

∴ 8192କୁ 2 ଦ୍ଵାରା ଭାଗକଲେ ଭାଗଫଳ ଏକ ପୂର୍ଣବର୍ଗ ସଂଖ୍ୟା ହେବ ।
ଉଦାହରଣ :
କେଉଁ ସଂଖ୍ୟାର \(\frac{1}{5}\) ଓ \(\frac{1}{6}\)ର ଗୁଣଫଳ 120 ହେବ ।
ସମାଧାନ :
ମନେକର ସଂଖ୍ୟାଟି x ।
∴ଏହାର \(\frac{1}{5}=\frac{x}{5}\) ଓ’ ଏହାର \(\frac{1}{6}=\frac{x}{6}\)
\(\frac{x}{5} \times \frac{x}{6}=120 \Rightarrow \frac{x^2}{30}=120 \Rightarrow x^2=30 \times 120=3600=60^2\)
⇒ x = ± 60
∴ସଂଖ୍ୟାଟି – 60 ବା 60 ।
→ ସଂଖ୍ୟାର ଘନ ଓ ପୂର୍ଣ୍ଣ ଘନ ସଂଖ୍ୟା (Cube of a number and a perfect cube number) :
5 × 5 × 5 = 125, ଏହାକୁ 5ର ଘନ = 125 ବୋଲି କୁହାଯାଏ ।
6 × 6 × 6 = 216, ଏହାକୁ 6ର ଘନ = 216 ବୋଲି କୁହାଯାଏ ।
ନିମ୍ନରେ ପ୍ରଦତ୍ତ ସାରଣୀରେ ପ୍ରଥମ ଦଶଟି ଗଣନ ସଂଖ୍ୟାର ଘନ ଦିଆଯାଇଛି ।

1, 8, 27, 64, ….. ଇତ୍ୟାଦି ପ୍ରତ୍ୟେକ ଗୋଟିଏ ଗୋଟିଏ ଘନ ସଂଖ୍ୟା ।
- n ଏକ ଗଣନ ସଂଖ୍ୟା ହେଲେ, n³ ଏକ ଘନ ସଂଖ୍ୟା (Cube number) ହୁଏ ଯୁଗ୍ମସଂଖ୍ୟାର ଘନ ଯୁଗ୍ମ ସଂଖ୍ୟା ଓ ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ଘନ ଅଯୁଗ୍ମ ସଂଖ୍ୟା ।
1 = 1 = 1³
3 + 5 = 8 = 2³
7 + 9 + 11 = 27 = 3³
13 + 15 + 17 + 19 = 64 = 4³
21 + 23 + 25 + 27 + 29 = 125 = 5³
10³ ପାଇବାପାଇଁ 10ଟି ଅଯୁଗ୍ମ ସଂଖ୍ୟାର ସମଷ୍ଟି ନେବାକୁ ପଡ଼ିବ ।
କୌଣସି ଏକ ସଂଖ୍ୟା ଘନସଂଖ୍ୟା କି ନୁହେଁ, ତାହା ଉତ୍ପାଦକୀକରଣରୁ ଜାଣିହୁଏ ।
![]()
ଉଦାହରଣ :
216 ଏକ ଘନ ସଂଖ୍ୟା କି ?
ସମାଧାନ :
216 = 2 × 2 × 2 × 3 × 3 × 3 = 2³ × 3³
∴ 216 ଏକ ଘନସଂଖ୍ୟା
ଉଦାହରଣ :
576 ଏକ ଘନ ସଂଖ୍ୟାକି ?
ସମାଧାନ :
576 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 = 2³ × 2³ × 3²
ଏହା ଏକ ଘନସଂଖ୍ୟା ନୁହେଁ ।
→ ଘନ ସଂଖ୍ୟା ସମ୍ବନ୍ଧୀୟ ସୂତ୍ର :
ଉଦାହରଣ :
(a × b)n = an × bn ଯେଉଁଠି a, b ∈ Q ଓ n ∈ N
ଏଠାରେ n = 3 696m, (a × b)3 = a3 × b3 a, b ∈ N ।
ଉଦାହରଣ :
3456 ରେ କେଉଁ ସର୍ବନିମ୍ନ ସଂଖ୍ୟା ହରିଲେ ଭାଗଫଳ ଏକ ଘନସଂଖ୍ୟା ହେବ ?
3456 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3
= 2³ × 2³ × 2 × 3³
3456ରେ ଉତ୍ପାଦକୀକରଣରେ 2ର ସଂଖ୍ୟା 7 ଓ ଗୁଣନୀୟକ 3ର ସଂଖ୍ୟା 3 ।
∴ 3456 କୁ ଅନ୍ୟୁନ 2 ଦ୍ବାରା ଭାଗକଲେ ଭାଗଫଳ ଏକ ଘନସଂଖ୍ୟା ହେବ ।
→ ମେଟ୍ରିକ୍ ମାପ ତାଲିକା :
ଘନଫଳ ମାପର ମେଟ୍ରିକ୍ ଏକକ ତାଲିକା ତଳେ ଦେଖ :
10 ମି. ମି. = 1 ସେ. ମି. ହେତୁ, 1000 ଘ. ମି. ମି. = 1 ଘ. ସେ. ମି.
10 ସେ. ମି. = 1 ଡେସି. ମି. ହେତୁ, 1000 ଘ. ସେ. ମି. = 1 ଘ. ଡେସି. ମି.
10 ଡେସି. ମି. = 1 ମି. ହେତୁ, 1000 ଘ. ଡେସି. ମି. = 1 ଘ. ମି.
ମନେରଖ :
- (କ) ଗୋଟିଏ ପାତ୍ରର ଆୟତନ ଯେତେ ଘନ ଡେସି ମିଟର, ସେଥିରେ ଧରୁଥିବା ଜଳର ପରିମାଣ ସେତିକି ଲିଟର ଅର୍ଥାତ୍ 1 ଘ. ଡେସି ମି. = 1000 ଘ. ସେ.ମି. = 1 ଲିଟର
(ଲିଟର ହେଉଛି ତରଳ ପଦାର୍ଥ ଲାଗି ମାପ ଏକକ) - (ଖ) ଗୋଟିଏ ପାତ୍ରର ଆୟତନ ଯେତେ ଘନ ମିଟର, ସେଥୁରେ ଧରୁଥିବା ଜଳର ପରିମାଣ ସେତିକି କିଲୋଲିଟ (ବା 1000 ଲିଟର) ।
- 1729 ଏକ ସଂଖ୍ୟା, ଯାହା ଦୁଇଟି ଉପାୟରେ ଦୁଇଟି ଘନ ସଂଖ୍ୟାର ସମଷ୍ଟି ରୂପେ ପ୍ରକାଶିତ ହୋଇପାରିବ;
ଯଥା – 1729 = 123 + 1 = 10 + 9 ଏହାକୁ Hardy-Ramanujan ସଂଖ୍ୟା କୁହାଯାଏ ।
ସେହିପରି 4104 = 2³ + 16³ = 9³ + 15³ ଏବଂ 13832 = 18³ + 20³ = 2³+ 24³ ଅସଂଖ୍ୟ ସଂଖ୍ୟା ପାଇବା । ଏଥିମଧ୍ୟରୁ 1729 କ୍ଷୁଦ୍ରତମ ।
- 1729 ଏକ ସଂଖ୍ୟା, ଯାହା ଦୁଇଟି ଉପାୟରେ ଦୁଇଟି ଘନ ସଂଖ୍ୟାର ସମଷ୍ଟି ରୂପେ ପ୍ରକାଶିତ ହୋଇପାରିବ;
→ ଘନମୂଳ (Cube root) :
m ଓ 1 ଗଣନସଂଖ୍ୟା ଏବଂ n = mè ହେଲେ, m କୁ n ର ଘନମୂଳ ବୋଲି କୁହାଯାଏ ।
ଏହାକୁ m = \(\sqrt[3]{n}\) ରୂପେ ଲେଖାଯାଏ । n = m³ ହେଲେ, m = \(\sqrt[3]{n}\) ; m,n ∈ N

→ ଘନମୂଳ ନିଶ୍ଚୟ ପ୍ରଣାଳୀ :
(a) ଉତ୍ପାଦକ ପ୍ରଣାଳୀ :
9261 ର ଘନମୂଳ ନିଶ୍ଚୟ କର ।
9261 = 3 × 3 × 3 × 7 × 7 × 7 = 3³ × 7³ = (3 × 7)³
∴ \(\sqrt[3]{9261}\) = 3 × 7 = 21
(b) ପୂର୍ବଘନ ସଂଖ୍ୟାର ଘନମୂଳ ନିର୍ଣ୍ଣୟର ଏକ ସଂକ୍ଷିପ୍ତ ପ୍ରଣାଳୀ :
ଭାସ୍କରଙ୍କ ଘନମୂଳ ଆନୟନ ସୂତ୍ର :
ସୋପାନ – 1 :
ସଂଖ୍ୟାର ଡାହାଣପଟୁ ତିନୋଟି ଲେଖାଏଁ ସଂଖ୍ୟାନେଇ ଗୋଟିଏ ଗୋଟିଏ ସଂଖ୍ଯାଗ୍ରୁପ୍ ଗଠନ କର ।
ସୋପାନ – 2 : ପ୍ରଥମ ଗ୍ରୁପରୁ ଘନମୂଳର ଏକକ ଅଙ୍କଟି ସ୍ଥିର କର ।

ସୋପାନ – 3 : ଦ୍ବିତୀୟ ଗ୍ରୁପରୁ ଘନମୂଳର ଦଶକ ଅଙ୍କ ମିଳିବ ।
ଉଦାହରଣ :
ତାହା ଯେଉଁ ଦୁଇଟି ସଂଖ୍ୟାର ଘନ ମଧ୍ୟରେ ଥବ, କ୍ଷୁଦ୍ରତମ ସଂଖ୍ୟାଟି ଦଶକସ୍ଥାନୀୟ ଅଙ୍କ ହେବ । ଏହି ପ୍ରଣାଳୀରେ ସାଧାରଣତଃ ଛଅଅଙ୍କ ବିଶିଷ୍ଟ ଘନ ସଂଖ୍ୟା ମଧ୍ୟରେ ଘନମୂଳ ନିରୂପଣ କରାଯାଇପାରିବ ।
![]()
ଉଦାହରଣ :
110592 ର ଘନମୂଳ ନିରୂପଣ କର ।
ପ୍ରଥମ ସୋପାନ – ଡାହାଣପଟ ଅଙ୍କଆଡ଼ୁ ତିନି ତିନିଟି ଅଙ୍କ ନେଇ ସଂଖ୍ୟା ଗ୍ରୁପ୍ ଗଠନକଲେ ପ୍ରଥମ ଗ୍ରୁପ୍ରେ ରହିବ \(\overline{592}\) ଓ ଦ୍ବିତୀୟ ଗ୍ରୁପ୍ରେ ରହିବ 110 ।
ଦ୍ବିତୀୟ ସୋପାନ – 592ର ଶେଷ ଅଙ୍କ 2 ହେତୁ ଘନମୂଳର ଏକକ ଅଙ୍କ 8 ହେବ ।
ତୃତୀୟ ସୋପାନ – ଦ୍ବିତୀୟ ଗ୍ରୁପ୍ 110 ସଂଖ୍ୟାଟି 4³ (64) ଓ 5³ (125)ର ମଧ୍ୟବର୍ତ୍ତୀ ଅର୍ଥାତ୍ 64 < 110 < 125 ।
∴ ଘନମୂଳ ସଂଖ୍ୟାଟିର ଦଶକ ଅଙ୍କ 4 । ∴ ସଂଖ୍ୟାଟି 48 ।
ପୂର୍ଣ୍ଣ ଘନ ସଂଖ୍ୟା ହେଉନଥିଲେ ଏହି ପ୍ରଣାଳୀରେ ଘନମୂଳ ନିର୍ଣ୍ଣୟ କରାଯାଇ ପାରିବ ନାହିଁ ।
ନିଜେ କର :
ନିମ୍ନ ସଂଖ୍ୟାଗୁଡ଼ିକର ଘନମୂଳ ନିର୍ଣ୍ଣୟ କର ।
(i) 17576, (ii) 12167, (iii) 32768, (iv) 4913
ଉ –
(i) \(\overline{17}\) \(\overline{576}\)
(a) ପ୍ରଥମ ଗ୍ରୁପ୍ରେ 576 ର ଶେଷ ଅଙ୍କ 6 ହେତୁ ଘନମୂଳର ଏକକ ଅଙ୍କ 6 ।
(b) ଦ୍ଵିତୀୟ ଗ୍ରୁପ୍ 17, 2³ ଓ 3³ ମଧ୍ୟବର୍ତ୍ତୀ ହେତୁ ଘନମୂଳର ଦଶକ ସ୍ଥାନୀୟ ଅଙ୍କଟି 2
(c) ସଂଖ୍ୟାଟିର ଘନମୂଳ 23 ।
(ii) \(\overline{12}\) \(\overline{167}\)
(a) ପ୍ରଥମ ଗ୍ରୁପ୍ର ଶେଷଅଙ୍କ 7 ତେଣୁ ଘନମୂଳର ଏକକ ଅଙ୍କ 3 ।
(b) ଦ୍ଵିତୀୟ ଗ୍ରୁପ୍ 12, 2³ ଓ 3³ ର ମଧ୍ୟବର୍ତ୍ତୀ ହେତୁ ଘନମୂଳର ଦଶକ ଅଙ୍କ 2 ।
(c) ତେଣୁ ନିର୍ଦେୟ ଘନମୂଳ 23 ।
(iii) \(\overline{32}\) \(\overline{768}\)
ପ୍ରଥମ ଗ୍ରୁପ୍ର ଶେଷ ଅଙ୍କ 8 ହେତୁ ଘନମୂଳର ଏକକ ଅଙ୍କ 2।
ଦ୍ବିତୀୟ ଗ୍ରୁପ୍ 32 ସଂଖ୍ୟାଟି ହେତୁ 3³ ଓ 4³ର ମଧ୍ୟବର୍ତ୍ତୀ । ଘନମୂଳର ଦଶକ ଅଙ୍କଟି 3 ।
ତେଣୁ ନିର୍ଦେୟ ଘନମୂଳ 32 ।
(iv) \(4 \overline{913}\)
(a) ପ୍ରଥମ ଗ୍ରୁପ୍ର ଶେଷଅଙ୍କ ଓ ହେତୁ ଘନମୂଳର ଏକକ ଅଙ୍କ 7 ।
(b) ଦ୍ବିତୀୟ ଗ୍ରୁପ୍ର 4 ଅଙ୍କଟି 1³ ଓ 2³ ମଧ୍ଯରେ ଅବସ୍ଥିତ ହେତୁ ଘନମୂଳର ଦଶକ ଅଙ୍କଟି 1 ।
(c) ତେଣୁ ନିର୍ଦେୟ ଘନମୂଳ 17 ।
→ ଋଣାତ୍ମକ ପୂର୍ବସଂଖ୍ୟାର ଘନ ଓ ଘନମୂଳ :
m ଓ n ପୂର୍ବସଂଖ୍ୟାର ଓ n = m³ ହେଲେ, m କୁ nର ଘନମୂଳ ବୋଲି କୁହାଯାଏ ।
\(\sqrt[3]{-27}=\sqrt[3]{-3 \times-3 \times-3}=-3\)
\(\sqrt[3]{-8}=\sqrt[3]{-2 \times-2 \times-2}=-2\)
\(\sqrt[3]{-1}=\sqrt[3]{-1 \times-1 \times-1}=-1\)
![]()
→ ମନେରଖ :
ପ୍ରତ୍ୟେକ ଘନସଂଖ୍ୟାର ସର୍ବମୋଟ ତିନୋଟି ଘନମୂଳ ଥାଏ । ସେଥୁମଧ୍ୟରୁ ଗୋଟିଏକୁ ଆମେ ସହଜରେ ଜାଣିପାରୁ, ଅନ୍ୟ ଦୁଇଟି ଆମେ ଜାଣିଥୁବା ସଂଖ୍ୟାସମୂହର ଅନ୍ତର୍ଭୁକ୍ତ ନୁହେଁ ।
ଉଦାହରଣ :
-19 ର ଘନ ନିରୂପଣ କର ।
ସମାଧାନ :
– 196 = (-19)×(-19)×(-19) = 361 × (-19) = -6859
ଉଦାହରଣ :
-10648 ର ଘନମୂଳ ସ୍ଥିର କର ।
ସମାଧାନ :
\(\sqrt[3]{-10648}=\sqrt[3]{-2 \times 2 \times 2 \times 11 \times 11 \times 11}\) = -2 × 11 = -22 ।
ଯଦି a ଓ h ଉଭୟେ ଘନସଂଖ୍ୟା ହୁଅନ୍ତି; ତେବେ \(\sqrt[3]{-1}=\sqrt[3]{-1 \times-1 \times-1}=-1\) ।
ଯଦି a, b, c ପୂର୍ବସଂଖ୍ୟା ଏବଂ ab = c³ ହୁଏ; ତେବେ \(\sqrt[3]{ab}\) = c ।
ଉଦାହରଣ :
ମାନ ନିର୍ଣ୍ଣୟ କର : \(\sqrt[3]{-54×32}\) ।
ସମାଧାନ :
\(\sqrt[3]{-54×32}\) = \(\sqrt[3]{-(3 \times 3 \times 3 \times 2) \times 2 \times 2 \times 2 \times 2 \times 2}=\sqrt[3]{-3^3 \times 2^3 \times 2^3}\)
= -(3 × 2 × 2) = -12
ପରିମେୟ ସଂଖ୍ୟାର ଘନ ନିଶ୍ଚୟ :
p, q ∈ Z ଓ q ≠ 0 ହେଲେ, \(\frac{p}{q}\) ଏକ ପରିମେୟ ସଂଖ୍ୟା ହେବ ।
- p, q ∈ Z ଏବଂ q ≠ 0 ହେଲେ, \((\frac{p}{q})^3=\frac{p^3}{q^3}\)
ଉଦାହରଣସ୍ୱରୂପ, \(\frac{3}{4}\)ର ଘନ = \(\frac{3^3}{4^3}=\frac{27}{64}\)
- \(– \frac{5}{7}\) ର ଘନ = \(\left(\frac{-5}{7}\right)^3=\frac{-125}{343}\)
(i) ଏକ ପରିମେୟ ସଂଖ୍ୟାର ଘନମୂଳ ନିଶ୍ଚୟ କଲାବେଳେ ଲବର ଘନମୂଳକୁ ଲବ ରୂପେ ଓ ହରର ଘନମୂଳକୁ ହର ରୂପେ ନେଇ ଦତ୍ତ ପରିମେୟ ସଂଖ୍ୟ ାର ଘନମୂଳ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
(ii) ପରିମେୟ ସଂଖ୍ୟାଟି ଋଣାତ୍ମକ ହେଲେ, ଘନମୂଳଟି ଋଣାତ୍ମକ ହେବ ।
(iii) ଯେଉଁ ପରିମେୟ ସଂଖ୍ୟାର ଲବ ଓ ହର ପ୍ରତ୍ୟେକ ଘନସଂଖ୍ୟା, ସେହି ପରିମେୟ ସଂଖ୍ୟାର ହିଁ ଘନମୂଳ ନିର୍ଣ୍ଣୟ କରାଯାଇପାରିବ ।
p, q ∈ Z ଓ q ≠ 0 ହେଲେ, \(\left(\frac{p}{q}\right)^3=\frac{p^3}{q^3}\)
- ସୂତ୍ର : p, q ∈ Z ଓ q ≠ 0 କ୍ଷେତ୍ରରେ p = m³, y = n³ ତେବେ \(– \frac{5}{7}\)
