Odisha State Board BSE Odisha 8th Class Maths Notes Geometry Chapter 3 ଚତୁର୍ଭୁଜ will enable students to study smartly.
BSE Odisha Class 8 Maths Notes Geometry Chapter 3 ଚତୁର୍ଭୁଜ
→ ଚତୁର୍ଭୁଜର ପରିଚୟ :
- ଗୋଟିଏ ସମତଳରେ ଚାରୋଟି ପୃଥକ୍ ବିନ୍ଦୁ ଗୋଟିଏ ସମତଳରେ ତିନି ପ୍ରକାର ଅବସ୍ଥାରେ ରହିପାରନ୍ତି; ଯଥା – (i) ସମସ୍ତ ବିନ୍ଦୁ ଏକରେଖୀ, (ii) ଯେ କୌଣସି ତିନୋଟି ବିନ୍ଦୁ ଏକରେଖୀ, (iii) ଯେ କୌଣସି ତିନିଗୋଟି
- ଏକ ସମତଳରେ ଅବସ୍ଥିତ ଚାରିଟି ପୃଥକ୍ ବିନ୍ଦୁ A, B, C ଓ D ମଧ୍ୟରୁ ଯଦି କୌଣସି ତିନୋଟି ବିନ୍ଦୁ ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ନ ହୁଅନ୍ତି ଏବଂ \(\overline{\mathrm{AB}})\), \(\overline{\mathrm{BC}})\),\(\overline{\mathrm{CD}})\) ଓ DA ପ୍ରାନ୍ତବିନ୍ଦୁ ଭିନ୍ନ ଅନ୍ୟ କୌଣସି ବିନ୍ଦୁରେ ପରସ୍ପରକୁ ଛେଦ କରନ୍ତି ନାହିଁ, ତେବେ AB, BC, CD ଓ DA ର ସଂଯୋଗକୁ ଏକ ଚତୁର୍ଭୁଜ କୁହାଯାଏ । ଏହି ଚତୁର୍ଭୁଜକୁ ‘ABCD ଚତୁର୍ଭୁଜ’ କୁହାଯାଏ ।
- ABCD ଚତୁର୍ଭୁଜକୁ ‘BCDA, CDAB ବା DABC ଚତୁର୍ଭୁଜ’ ମଧ୍ୟ କୁହାଯାଏ ।
- ABCD ଚତୁର୍ଭୁଜ ଏକ ସମତଳରେ ଅଙ୍କିତ ଏକ ସମତଳୀୟ ଚିତ୍ର ।
- AB, BC,CD ଓ DA – ରେଖାଖଣ୍ଡଗୁଡ଼ିକ ବିନ୍ଦୁ ମାନଙ୍କର ଗୋଟିଏ ଗୋଟିଏ ସେଟ୍ ଅଟନ୍ତି | ତେଣ୍ଡ ଏମାନକ ସଯୋଗରେ ଗଠିତ ABCD ଚତୁର୍ଭୁଜ ମଧ୍ୟ ବିନ୍ଦୁମାନଙ୍କର ସେଟ୍ ଅଟେ ।
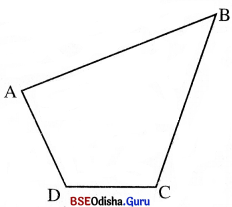
- ABCD ଚତୁର୍ଭୁଜ= AB ∪ BC ∪ CD ∪ DA |
![]()
→ ଚତୁର୍ଭୁଜ ସମ୍ବନ୍ଧୀୟ ଜାଣିବା କଥା :
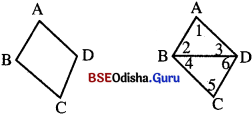
- A, B, C, D ବିନ୍ଦୁମାନଙ୍କୁ ABCD ଚତୁର୍ଭୁଜର ଶୀର୍ଷବିନ୍ଦୁ (Vertex) କୁହାଯାଏ ।
- AB, BC, CD, DA ରେଖାଖଣ୍ଡମାନକୁ ABCD ତତୁରୁକର ବାହୁ (side) କ୍ମଦାଯାଏ |
- ଗୋଟିଏ ବାହୁର ଦୁଇ ପ୍ରାନ୍ତବିନ୍ଦୁକୁ ଚତୁର୍ଭୁଜର କ୍ରମିକ ଶୀର୍ଷ କୁହାଯାଏ ଏବଂ କ୍ରମିକ ଶୀର୍ଷ ହୋଇ ନ ଥିବା ଶାପଦ୍ଵଯକୁ ଦିପରାତ ଶାପ କୁଦ୍ଦାଯାଏ |
- ABCD ଚତୁର୍ଭୁଜର A ଓ B, B ଓ C, C ଓ D, D ଓ A ମାନ କ୍ରମିକ ଶୀର୍ଷ ଏବଂ A ଓ C, B ଓ D ବିପରୀତ ଶୀର୍ଷ ଅଟନ୍ତି ।
- ∠ABC, ∠BCD, ∠CDA, ∠DAB କୁ ତଡୁରୁକ ABCDର ଗୋଟିଏ ଗୋଟିଏ କୋଣ କୁହାଯାଏ |
- ଦୁଇଟି କ୍ରମିକ ଶୀର୍ଷରେ ଥିବା କୋଣଦ୍ଵୟକୁ କ୍ରମିକ କୋଣ (ଯଥା – ∠A ଓ ∠B) ଏବଂ ବିପରୀତ ଶୀର୍ଷରେ ଥିବା କୋଣଦ୍ଵୟକୁ ଚତୁର୍ଭୁଜର ବିପରୀତ କୋଣ (ଯଥା -∠A ଓ ∠C) କୁହାଯାଏ ।
- ଚତୁର୍ଭୁଜର ପରସ୍ପରଛେଦୀ ବାହୁଦ୍ୱୟକୁ ସନ୍ନିହିତ ବାହୁ (ଯଥା – AB, BC ) ଏବଂ ପରସ୍ପରଛେଦୀ ହୋଇ ନ ଥିବା ପ୍ରତ୍ୟେକ ଯୋଡ଼ା ବାହୁକୁ (ଯଥା – AB, CD ଏବଂ AD, BC) ବିପରୀତ ବାହୁ କୁହାଯାଏ ।
- ଚତୁର୍ଭୁଜର ବିପରୀତ ଶୀର୍ଷର ସଂଯୋଜକ ରେଖାଖଣ୍ଡକୁ ଏହାର କର୍ୟ କୁହାଯାଏ । ABCD ଚତୁର୍ଭୁଜରେ AC ଓ BD ଦୁଇଟି କଣ୍ଠ ଅଟନ୍ତି ।
→ ଉତ୍ତଳ ଚତୁର୍ଭୁଜ (Convex quadrilateral) :
- ଯେଉଁ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ଛେଦକରନ୍ତି, ତାହାକୁ ଉତ୍ତଳ ଚତୁର୍ଭୁଜ କୁହାଯାଏ ।
→ ତତୁଭୁଲଭ ଥନ୍ତଲେକଣ ଦହାଦେଶ (Interior and Exterior of a Quadrilateral) :
- ଯେ କୌଣସି ଦୁଇ ବିପରୀତ କୋଣର ଅନ୍ତର୍ଦେଶର ସାଧାରଣ ଅଂଶ ଅର୍ଥାତ୍ ଅନ୍ତର୍ଦେଶର ଛେଦକୁ ଉତ୍ତଳ ଚତୁର୍ଭୁଜର ଅନ୍ତର୍ଦେଶ କୁହାଯାଏ ।
- ଅନ୍ତର୍ଦେଶରେ ଅବସ୍ଥିତ ବିନ୍ଦୁକୁ ଚତୁର୍ଭୁଜର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ କୁହାଯାଏ ।
- ବାହୁ ଉପରେ ନ ଥାଏ ଏବଂ ଚତୁର୍ଭୁଜର ଅନ୍ତର୍ଦେଶରେ ମଧ୍ୟ ନ ଥାଏ, ତେବେ ତାହାକୁ ଚତୁର୍ଭୁଜର ବହିଃସ୍ଥ ବିନ୍ଦୁ କୁହାଯାଏ ।
- ବହିଃସ୍ଥ ବିନ୍ଦୁମାନେ ଗଠନ କରୁଥିବା ସେଟ୍କୁ ଚତୁର୍ଭୁଜର ବହିର୍ଦେଶ କୁହାଯାଏ ।
ଗୋଟିଏ ଉତ୍ତଳ ଚତୁର୍ଭୁଜର ଅନ୍ତର୍ଦେଶ ଏକ ଉତ୍ତଳ ସେଟ୍ ।
ଚତୁର୍ଭୁଜାକାର କ୍ଷେତ୍ର (Quadrilateral Region) :
- ଗୋଟିଏ ଚତୁର୍ଭୁଜ ଓ ଏହାର ଅନ୍ତର୍ଦେଶର ସଂଯୋଗରେ ଗଠିତ ସେଟ୍କୁ ଏକ ଚତୁର୍ଭୁଜ ଆକୃତିବିଶିଷ୍ଟ କ୍ଷେତ୍ର ବା ଚତୁର୍ଭୁଜାକାର କ୍ଷେତ୍ର କୁହାଯାଏ ।
- ଚତୁର୍ଭୁଜର ଶୀର୍ଷବିନ୍ଦୁ, କୋଣ ଓ ବାହୁମାନଙ୍କୁ ଯଥାକ୍ରମେ ଏହି ଚତୁର୍ଭୁଜାକାର କ୍ଷେତ୍ରର ଶୀର୍ଷବିନ୍ଦୁ, କୋଣ ଓ ବାହୁ କୁହାଯାଏ ।
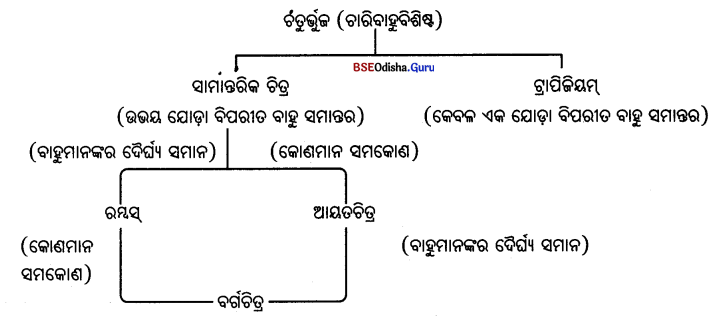
→ ବିଭିନ୍ନ ପ୍ରକାର ଚତୁର୍ଭୁଜ :
- ବିଭକ୍ତ; ଯଥା – (1) ଟ୍ରାପିଜିୟମ୍, (2) ସାମାନ୍ତରି, ଚିତ୍ର ।
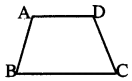
→ ଟ୍ରାପିଜିୟମ୍ :
ଯେଉଁ ଚତୁର୍ଭୁଜର କେବଳ ଏକ ଯୋଡ଼ା ବିପରୀତ ବାହୁ ସମାନ୍ତର, ତାହାକୁ ଟ୍ରାପିଜିୟମ୍
ABCD ଟ୍ରାପିଜିୟମ୍ର AD || BC |
→ ସାମାନ୍ତରିକ ଚିତ୍ର :
ଯେଉଁ ଚତୁର୍ଭୁଜର ଦୁଇଯୋଡ଼ା ବିପରୀତ ବାହୁ ସମାନ୍ତର, ତାହା ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ABCD ସାମାନ୍ତରିକ ଚିତ୍ରର AD || BC ଓ AB || CD |

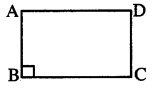
(i) ଆୟତଚିତ୍ର :
ଯେଉଁ ଚତୁର୍ଭୁଜର ପ୍ରତ୍ୟେକ କୋଣ ସମକୋଣ, ତାହା ଏକ ଆୟତ ଚିତ୍ର । ABCD ଏକ ଆୟତଚିତ୍ର ।
[ବି.ଦ୍ର. : ଆୟତଚିତ୍ର ଏକ ସ୍ଵତନ୍ତ୍ର ପ୍ରକାରର ସାମାନ୍ତରିକ ଚିତ୍ର, ଯାହାର ପ୍ରତ୍ୟେକ କୋଣ 90° ।]
(ii) ରମ୍ବସ୍ :
ଯେଉଁ ଚତୁର୍ଭୁଜର ବାହୁମାନଙ୍କ ଦୈର୍ଘ୍ୟ ସମାନ ତାହା ଏକ ରମ୍ବସ୍ । ABCD ଏକ କୋଣ |
[ବି.ଦ୍ର. : ରମ୍ବସ୍ ଏକ ସ୍ବତନ୍ତ୍ର ପ୍ରକାରର ସାମାନ୍ତରିକ ଚିତ୍ର ଯାହାର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ ସମାନ ।]
(iii) ବର୍ଗଚିତ୍ର :
ଯେଉଁ ଚତୁର୍ଭୁଜର ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ସମାନ ଓ ପ୍ରତ୍ୟେକ କୋଣର ପରିମାଣ 90° ତାହା ଏକ ବର୍ଗଚିତ୍ର ।
[ବି.ଦ୍ର. : ବର୍ଗଚିତ୍ର ଏକ ସମକୋଣବିଶିଷ୍ଟ ରମ୍ବସ୍ ।]
![]()
→ ଚତୁର୍ଭୁଜ ସମ୍ବନ୍ଧୀୟ କେତେକ ପରୀକ୍ଷା ଓ ସିଦ୍ଧାନ୍ତ :
ଚତୁର୍ଭୁଜର କୋଣମାନଙ୍କ ମଧ୍ୟରେ ସମ୍ବନ୍ଧ :
- ସିଦ୍ଧାନ୍ତ – 1 :
ଏକ ଚତୁର୍ଭୁଜର ଚାରି କୋଣର ପରିମାଣର ସମଷ୍ଟି 360° । - ତୁମପାଇ କାପ :
1. ଗୋଟିଏ କାର୍ଡ଼ବୋର୍ଡ଼ ଆଣି ସେଥରେ ଗୋଟିଏ ଚତୁର୍ଭୁଜ ଅଙ୍କନ କର ।
2. ତତୁରୁକାର ଗୋଟିଏ କଣ୍ଡ ଅଳନ କରି ତତୁରୁକକୁ ଦ୍ରରୁକରେ ପରିଣତ କର ।
3. ‘‘ତ୍ରିଭୁଜର ତିନିକୋଣର ପରିମାଣର ସମଷ୍ଟି 180°” ତଥ୍ୟକୁ ପ୍ରୟୋଗ କରି ଦର୍ଶାଅ ଯେ, ଚତୁର୍ଭୁଜର ଚାରିକୋଣର ପରିମାଣର ସମଷ୍ଟି 360° |
ନକେ କାର :
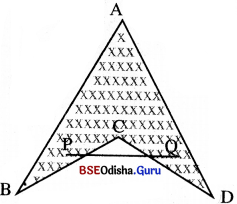
1. ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ p, q, r ଓ s ଚିହ୍ନିତ କୋଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି ସ୍ଥିର କର ।
ଉ – ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ p, q, r ଓ s ଚିହ୍ନିତ କୋଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି = 360°
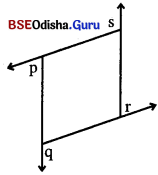
2. ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ r କୋଣର ପରିମାଣ 70 ଏବଂ p କୋଣର ପରିମାଣ 50° ହେଲେ q ଓ s କୋଣର ପରିମାଣର ସମଷ୍ଟି କେତେ ?
ଭ – ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ I କୋଣର ପରିମାଣ 70° ଓ p କୋଣର ପରିମାଣ = 50° ହେଲେ, q କୋଣର ପରିମାଣ = 130° ଓ s କୋଣର ପରିମାଣ = 110° ଦେଦ |
- ସାମାନ୍ତରିକ ଚିତ୍ରର ବିପରୀତ ବାହୁମାନଙ୍କର ପରସ୍ପର ସମାନ :
ସିଦ୍ଧାନ୍ତ – 2 : ସାମାନ୍ତରିକ ଚିତ୍ରର ବିପରୀତ ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ପରସ୍ପର ସମାନ ।
ଅନୁସିଦ୍ଧାନ୍ତ – 1 : ସାମାନ୍ତରିକ ଚିତ୍ରରେ ବିପରୀତ ବାହୁମାନ ସମାନ୍ତର ଓ ସମଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ।
ଅନୁସିଦ୍ଧାନ୍ତ – 2 : ଏକ ଚତୁର୍ଭୁଜର ଏକ ଯୋଡ଼ା ବିପରୀତ ବାହୁ ସମାନ୍ତର ଏବଂ ସମଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ହେଲେ, ଚତୁର୍ଭୁଜଟି ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ହେବ ।
![]()
ସାମାନ୍ତରିକ ଚିତ୍ରର ବିପରୀତ ବାହୁମାନଙ୍କର ପରସ୍ପର ସମାନ :
ସିଦ୍ଧାନ୍ତ – 3 : ସାମାନ୍ତରିକ ଚିତ୍ରର ବିପରୀତ ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ପରସ୍ପର ସମାନ ।
ଆମେ ଜାଣିଲେ – ସାମାନ୍ତରିକ ଚିତ୍ରର କ୍ରମିକ କୋଣଦ୍ଵୟ ପରସ୍ପର ପରିପୂରକ ।
ସାମାନ୍ତରିକ ଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ମଧ୍ଯରେ ସମ୍ବନ୍ଧ :
ସିଦ୍ଧାନ୍ତ – 4 : ସାମାନ୍ତରିକ ଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି ।
ରନ୍ପ୍ରଭ କର୍ଣ୍ଣଦ୍ଵୟ ମଧ୍ଯରେ ସମ୍ବନ୍ଧ :
ସିଦ୍ଧାନ୍ତ – 5 : ଏକ ରମ୍ବସ୍ର କଣ୍ଠଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି ।
ଆୟତଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ମଧ୍ଯରେ ସମ୍ବନ୍ଧ :
ସିଦ୍ଧାନ୍ତ – 6 :
ଏକ ଆୟତଚିତ୍ରର କଣ୍ଠଦ୍ଵୟର ଦୈର୍ଘ୍ୟ ସମାନ ଏବଂ ସେଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି ।
ରନ୍ପ୍ରଭ କର୍ଣ୍ଣଦ୍ଵୟ ମଧ୍ଯରେ ସମ୍ବନ୍ଧ :
ସିଦ୍ଧାନ୍ତ – 7 :
ଏକ ଆୟତଚିତ୍ରର କଣ୍ଠଦ୍ଵୟର ଦୈର୍ଘ୍ୟ ସମଦେଶ୍ୟଦିଶିପ୍ପ ଓ ସେଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି ।
→ ବିଭିନ୍ନ ସ୍ଵତନ୍ତ୍ର ଚତୁର୍ଭୁଜମାନଙ୍କର କର୍ଷ ମଧ୍ୟରେ ଥିବା ସମ୍ବନ୍ଧର ବିଶ୍ଳେଷଣ :
- ସାମାନ୍ତରିକ ଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି ।
- ରମକର କଣୃଦ୍ଵୟ ପରମଣକୁ ସମକୋଣରେ ସମଦ୍ୱଖସ୍ତ କରନ୍ତି |
- ଆୟତଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ସମଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ ଓ ପରସ୍ପରକୁ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି ।
- ବର୍ଗଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପର ସମଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ, ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ଓ ପରସ୍ପରକୁ ସମଦ୍ଵିଖଣ୍ଡ କରନ୍ତି ।
