Odisha State Board BSE Odisha 8th Class Maths Notes Geometry Chapter 4 ଅଙ୍କନ will enable students to study smartly.
BSE Odisha Class 8 Maths Notes Geometry Chapter 4 ଅଙ୍କନ
→ କେତେକ ମୌଳିକ ଅଙ୍କନ (ଭୁଲର୍ ସାହାଯ୍ୟରେ ଅଙ୍କନ) :
- ଦର ଦିନ୍ଦୁଦ୍ଵୟ ମଧ୍ୟରଦକ ଏକ ସରଳରେଖା ଅନେ
- ଦର ଦିନ୍ଦୁଦ୍ଵୟସଯୋକକ ସରଳରେଖା ଅନେ
- ଦତ୍ତ ରେଖାଖଣ୍ଡର ସମଦ୍ବିଖଣ୍ଡୀକରଣ
- ଏକ ଦତ୍ତ କୋଣର ସମଦ୍ଵିଖଣ୍ଡୀକରଣ
- ଏକ ଦତ୍ତ କୋଣର ସମପରିମାଣ ବିଶିଷ୍ଟ ଅନ୍ୟ ଏକ କୋଣ ଅଙ୍କନ
- ଏକ ଦତ୍ତ ରେଖା ସହ ସମାନ୍ତର କରି ତାହାର ବହିଃସ୍ଥ ଏକ ହିନ୍ଦୁ ଦେଇ ଏକ ରେଖା ଅଙ୍କନ
- ଏକ ଦତ୍ତ ସରଳରେଖା ବହିଃସ୍ଥ ଏକ ହିନ୍ଦୁ ସମପରିମାଣ ସହ ଅଙ୍କନ
→ ତ୍ରିଭୁଜ ଅଙ୍କନ :
ସୂଚନା :
- ତ୍ରିଭୁଜ ଅଙ୍କନ କରିବା ପୂର୍ବରୁ ପ୍ରଥମେ ଏକ ରଫ୍ ଚିତ୍ର ଅଙ୍କନ କରି ତାହାର ନାମକରଣ କରାଯାଏ ।
- ଦତ୍ତ ଥିବା ଅଂଶଗୁଡ଼ିକର ମାପକୁ ସମ୍ପୃକ୍ତ ଚିତ୍ରର ପାର୍ଶ୍ଵରେ ଦର୍ଶାଇଲେ ତାହାକୁ ‘ବିଶ୍ଳେଷଣ ଚିତ୍ର’ କୁହାଯାଏ ।
- ବିଶ୍ଳେଷଣ ଚିତ୍ରଦ୍ଵାରା ପ୍ରଥମେ କେଉଁ ଅଂଶ ଅଙ୍କନ କରିବାକୁ ହେବ ତାହା ଜାଣିହୁଏ ।
- ରଫ୍ ଚିତ୍ର ସାହାଯ୍ୟରେ ଅଙ୍କନର ବିଭିନ୍ନ ସୋପାନ ସହଜରେ ସ୍ଥିର କରିହୁଏ ।
ମନେରଖ:
△ABC ରେ ∠A, ∠B ଓ ∠C ର ସମ୍ମୁଖୀନ ବାହୁର ଦୈର୍ଘ୍ୟକୁ ଯଥାକ୍ରମେ a, b ଓ c ସଙ୍କେତଦ୍ୱାରା ପ୍ରକାଶ କରାଯାଏ ।
ତ୍ରିଭୁଜ ଅଙ୍କନ 1 : ତିନି ବାହୁର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଥିଲେ ତ୍ରିଭୁଜ ଅଙ୍କନ (ବାହୁ – ବାହୁ – ବାହୁ)
△ABC ଅଙ୍କନ କର, ଯାହାର a = 7 ସେ.ମି., b = 6 ସେ.ମି. ଓ c = · 5 ସେ.ମି. |
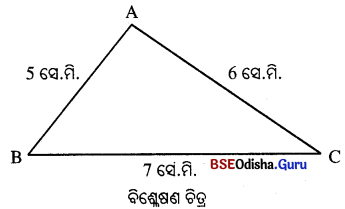
ଅଙ୍କନ ପ୍ରଣାଳୀ :
(i) 7 ସେ.ମି. ଦୈର୍ଘ୍ୟନେଇ \(\overline{\mathrm{BC}})\) ଅଙ୍କନ କର ।
![]()
(ii) Bକୁ କେନ୍ଦ୍ର ନେଇ 5 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧବିଶିଷ୍ଟ ଏକ ଚାପ ଅଙ୍କନ କର ।
(iii) C କୁ କେନ୍ଦ୍ର ନେଇ 6 ସେ.ମି. ବ୍ୟାସାର୍ଷବିଶିଷ୍ଟ ଏକ ଚାପ ଅଙ୍କନ କର, ଯେପରି B କୁ କେନ୍ଦ୍ରକରି ଅଙ୍କିତ ହୋଇଥିବା ଚାପକୁ ଏହା ଛେଦକରିବ । ଛେଦବିନ୍ଦୁର ନାମ A ଦିଅ ।
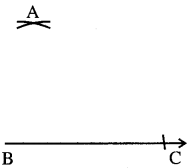
(iv) AB ଓ AC ଅଙ୍କନ କର । ବର୍ତ୍ତମାନ ABC ଆବଶ୍ୟକୀୟ ତ୍ରିଭୁଜ ।
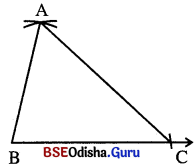
ଟୀକା : B ଓ C ବିନ୍ଦୁକୁ କେନ୍ଦ୍ର ନେଇ ଅଙ୍କନ କରାଯାଇଥିବା ଚାପଦ୍ଵୟ BC ର ଉଭୟ ପାର୍ଶ୍ଵରେ ପରସ୍ପରକୁ ଛେଦ କରି A ବିନ୍ଦୁର ଦୁଇଗୋଟି ଅବସ୍ଥିତି ମିଳିବ । ମାତ୍ର A ର ଯେ କୌଣସି ଗୋଟିଏ ଅବସ୍ଥିତିକୁ ନେଇ AABC ଅଙ୍କନ କରିବାକୁ ହେବ ।
![]()
ନିଜେ କର:
ନିମ୍ନରେ ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନରେ ତିନୋଟି ଲେଖାଏଁ ଦୈର୍ଘ୍ୟ ମାପ ଦିଆଯାଇଛି । କେଉଁ ତିନୋଟିକୁ ତ୍ରିଭୁଜର ବାହୁର ଦୈର୍ଘ୍ୟ ରୂପେ ନେଇ ତ୍ରିଭୁଜ ଅଙ୍କନ ସମ୍ଭବ ନୁହେଁ ଦର୍ଶାଅ ।
- 7 ସେ.ମି. , 5 ସେ.ମି. , 6.3 ସେ.ମି.
- 7 ସେ.ମି. , 4.5 ସେ.ମି. , 12 ସେ.ମି.
- 6.2 ସେ.ମି. , 9.5 ସେ.ମି. , 9.5 ସେ.ମି.
ଉତ୍ତର : 7 ସେ.ମି., 4.5 ସେ.ମି., 12 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ବାହୁତ୍ରୟକୁ ନେଇ ତ୍ରିଭୁଜ ଅଙ୍କନ ସମ୍ଭବ ନୁହେଁ ।
ବି.ଦ୍ର. : ତ୍ରିଭୁଜର ଯେ କୌଣସି ଦୁଇବାହୁର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି ଏହାର ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟଠାରୁ ବୃହତ୍ତର
→ ଚତୁର୍ଭୁଜ ଅଙ୍କନ
ଚତୁର୍ଭୁଜ ଅଙ୍କନ ସମ୍ବନ୍ଧୀୟ ବିଶ୍ଳେଷଣ :
- ଦତ୍ତ ମାପ ବ୍ୟବହାର କରି ଚତୁର୍ଭୁଜଟିଏ ଅଙ୍କନ ପୂର୍ବରୁ ଏକ ଚତୁର୍ଭୁଜର ରଫ୍ ଚିତ୍ର (ବିଶ୍ଳେଷଣ ଚିତ୍ର) ଅଙ୍କନ କର ।
- ଏହି ଚିତ୍ର ସଦ୍ୱାଯ୍ୟରେ ତତୁରୁଲଭ କେଉଁ ଅଣଟିକ୍ସ ଅଲମ କାରାଯାଉ ବା କେଉଁ ବାଦ୍ଵିଟିରୁ ଅଲମ କରାଯିବ ତାହା ସ୍ଥିର କରି ଅଙ୍କନ କରିବାକୁ ହେବ ।
ଚତୁର୍ଭୁଜ ଅଙ୍କନ – 1 : ଚାରିବାହୁ ଓ ଏକ କଣ୍ଠର ଦୈର୍ଘ୍ୟ ଦତ୍ତ ଥିଲେ, ଚତୁର୍ଭୁଜ ଅଙ୍କନ :
ABCD ଚତୁର୍ଭୁଜ ଅଙ୍କନ କର, ଯହିଁରେ AB = 4 ସେ.ମି., BC = 6 ସେ.ମି., CD = 5 ସେ.ମି., AD = 5.5 ସେ.ମି. 3 d AC = 8 ସେ.ମି. |
ବିଶ୍ଳେଷଣ : (i) ABCD ଚତୁର୍ଭୁଜର ରଫ୍ ଚିତ୍ରଟିଏ ଅଙ୍କନ କରି ତହିଁରେ \(\overline{\mathrm{AB}})\), BC, CD, AD ଓ ACର ମାପଗୁଡ଼ିକ ସୂଚାଯାଉ ।
(ii) △ABC ଓ △ACD ପ୍ରତ୍ୟେକର ତିନିବାହୁ ଦତ୍ତ ଥିବାରୁ ଆମେ କଣ୍ଠ ACର ଉଭୟ ପାର୍ଶ୍ଵରେ ABC ଓ ACD ତ୍ରିଭୁଜଦ୍ଵୟକୁ ଅଙ୍କନ କରିପାରିବା ଓ ଏହାଦ୍ଵାରା ABCD ଚତୁର୍ଭୁଜଟି ମିଳିଯିବ ।
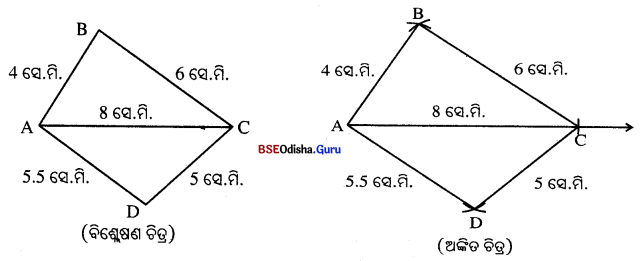
→ ଅଙ୍କନ ପ୍ରଣାଳୀ :
- 8 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ AC ଅଙ୍କନ କର ।
- A କୁ କେନ୍ଦ୍ର କରି 4 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ଏକ ଚାପ ଅଙ୍କନ କର ।
- C କୁ କେନ୍ଦ୍ର କରି 6 ସେ.ମି. ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଏକ ଚାପ ଅଙ୍କନ କର, ଯେପରି ତାହା A କୁ କେନ୍ଦ୍ର କରି ଅଙ୍କିତ ଚାପକୁ ଛେଦ କରିବ । ଛେଦବିଦୁର ନାମ B ଦିଅ ।
- ପୁନଶ୍ଚ A କୁ କେନ୍ଦ୍ର କରି 5.5 ସେ.ମି. ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ଅନ୍ୟ ଏକ ଚାପ, ACର ଯେଉଁ ପାର୍ଶ୍ଵରେ B ଅଛି, ତାହାର ବିପରୀତ ପାର୍ଶ୍ଵରେ ଅଙ୍କନ କର ।
- C କୁ କେନ୍ଦ୍ର କରି 5 ସେ.ମି. ବ୍ୟାସାର୍କ ବିଶିଷ୍ଟ ଅନ୍ୟ ଏକ ଚାପ ଅଙ୍କନ କର । ତାହା A କୁ କେନ୍ଦ୍ର କରି ଅଙ୍କିତ 5.5 ସେ.ମି. ବ୍ୟାସାର୍କ ବିଶିଷ୍ଟ ଚାପକୁ ଛେଦକରୁ । ଛେଦବିଦୁର ନାମ D ଦିଅ ।
- AB, BC, CD ଓ AD ଅଙ୍କନ କର । ବର୍ତ୍ତମାନ ଉଦ୍ଦିଷ୍ଟ ଚତୁର୍ଭୁଜ ABCD ମିଳିଲା ।
ସୂଚନା : ରଫ୍ ଚିତ୍ରରୁ ଆମେ ଜାଣିଲୁ ଯେ AB + BC > AC (କାରଣ 4 ସେ.ମି. + 6 ସେ.ମି. > 8 ସେ.ମି.) ଓ AD + DC > AC (କାରଣ 5.5 ସେ.ମି. + 5 ସେ.ମି. > 8 ସେ.ମି.) । ତେଣୁ ଚତୁର୍ଭୁଜଟି ଅଙ୍କନ କରିବା ସମ୍ଭବ ।
→ ବୃତ୍ତ ମଧ୍ୟରେ ସୁଷମ ଷଡ଼ଭୁଜ, ସମବାହୁ ତ୍ରିଭୁଜ ଓ ବର୍ଗଚିତ୍ରର ଅନ୍ତର୍ଲିଖନ :
-
- ବୃତ୍ତ ମଧ୍ଯରେ ସୁଷମ ଷଡ଼ଭୁଜର ଅନ୍ତର୍ଲିଖନ :
(i) ଯେଉଁ ଚତୁର୍ଭୁଜର ବାହୁଗୁଡ଼ିକ ସମଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ଓ କୋଣଗୁଡ଼ିକ ସମପରିମାଣ ବିଶିଷ୍ଟ, ତାହାକୁ ସୁଷମ ବହୁଭୁଜ କୁହାଯାଏ । ଛଅଟି ବାହୁ ବିଶିଷ୍ଟ ସୁଷମ ବହୁଭୁଜକୁ ସୁଷମ ଷଡ଼ଭୁଜ କହନ୍ତି ।
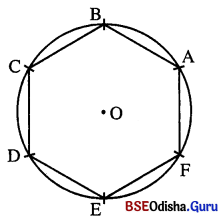
ମନେଇଖ :
ଗୋଟିଏ ଦଦୁରୁଲଭ ଶାଯଦିନ୍ଦୁଗୁଣିକ ଏକ ଦ୍ଵଭରେ ଅଦମିତ ହେଲେ ତାହାକୁ ବୃତ୍ତାନ୍ତର୍ଲିଖ୍ତ ବହୁଭୁଜ କୁହାଯାଏ । ଗୋଟିଏ ବୃତ୍ତରେ ଏକ ସୁଷମ ଷଡ଼ଭୁଜର ଅନ୍ତର୍ଲିଖନ କରିବାକୁ ହେଲେ ଆମକୁ ବୃତ୍ତ ଉପରେ ଛଅଟି ବିନ୍ଦୁ – A, B, C, D, E, F – ଏଭଳି ଭାବରେ ନିର୍ଣ୍ଣୟ କରିବାକୁ ହେବ, ଯେପରି ABCDEF ଏକ ସୁଷମ ବହୁଭୁଜ ହେବ।
- ବୃତ୍ତ ମଧ୍ଯରେ ସୁଷମ ଷଡ଼ଭୁଜର ଅନ୍ତର୍ଲିଖନ :
→ ଅଙ୍କନ ପ୍ରଣାଳୀ :
- ମନେକର ବୃତ୍ତର ବ୍ୟାସାର୍ଦ୍ଧ r ଅଟେ ।
- ବୃତ୍ତ ଉପରେ ଯେ କୌଣସି ଗୋଟିଏ ବିନ୍ଦୁ ନେଇ ତାହାର ନାମ A ଦିଅ ।
- A କୁ କେନ୍ଦ୍ର କରି R ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଗୋଟିଏ ଚାପ ଅଙ୍କନ କର । ଏହି ଚାପ ବୃତ୍ତକୁ ଛେଦକରୁଥିବା ଗୋଟିଏ ବିନ୍ଦୁର ନାମ B ଦିଅ । ପୁଣି B କୁ କେନ୍ଦ୍ର କରି ପୂର୍ବ ବ୍ୟାସାର୍ଷ ବିଶିଷ୍ଟ ଚାପ ଅଙ୍କନ କର । ତାହା ବୃତ୍ତକୁ ଯେଉଁ ବିନ୍ଦୁରେ ଛେଦ କରେ (A ଭିନ୍ନ ଅନ୍ୟ ଏକ ବିନ୍ଦୁ) ତାହାର ନାମ C ଦିଅ । ଏହି କ୍ରମରେ ବୃତ୍ତ ଉପରେ D, E, F ବିନ୍ଦୁ ନିର୍ଣ୍ଣୟ କର ।
- AB, BC, CD, DE, EF, \(\overline{\mathrm{FA}})\) ରେଖାଖଣ୍ଡମାନ ଅକ୍ କର | ABCDEF ରବିଯୁ ଦ୍ଵରାନ୍ତଲିଖଦ ସୁଷମ ଷଡ଼ଭୁଜ ।
କେତୋଟି ଜାଣିବା କଥା :
(a) F କୁ କେନ୍ଦ୍ରକରି I ବ୍ୟାସାର୍ଦ୍ଧ ନେଇ ଚାପ ଅଙ୍କନକଲେ ତାହା ବୃତ୍ତକୁ ଦୁଇଟି ବିନ୍ଦୁରେ ଛେଦ କରି ପାରିବ । ସେଥୁରୁ ଗୋଟିଏ ବିନ୍ଦୁ E ଓ ଅନ୍ୟଟି A ଅଟେ । ତେଣୁ ଷଡ଼ଭୁଜର ବାହୁ ଛଅଟି, ସମଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ।
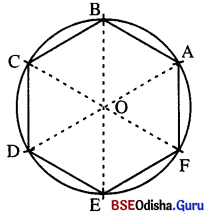
(b) ଚିତ୍ରରେ OA = OB = OC = OD = OE = OF = r (ବୃତ୍ତର ବ୍ୟାସାର୍କ) ସେହିପରି AB = BC = CD = DE = EF = FA = 1 (ଅଙ୍କନବେଳେ ଚାପଗୁଡ଼ିକର ବ୍ୟାସାର୍ଦ୍ଧ r ନିଆଯାଇଛି ।) ତେଣୁ ଷଡ଼ଭୁଜର ଶୀର୍ଷବିନ୍ଦୁ ଓ ବୃତ୍ତର କେନ୍ଦ୍ର ଠ ର ସଂଯୋଗକାରୀ ରେଖାଖଣ୍ଡମାନ ଅଙ୍କନକଲେ ଆମେ ବୃତ୍ତର ଅନ୍ତର୍ଦେଶରେ ଛଅଟି ସମବାହୁ ତ୍ରିଭୁଜ ପାଇବା ।
ସମବାହୁ ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ କୋଣର ପରିମାଣ 60° ହୋଇଥିବାରୁ ଅଙ୍କିତ ବହୁଭୁଜର ପ୍ରତ୍ୟେକ କୋଣର ପରିମାଣ 120° ଅଟେ ।
![]()
2. ବୃତ୍ତ ମଧ୍ୟରେ ସମବାହୁ ତ୍ରିଭୁଜର ଅନ୍ତର୍ଲିଖନ :
(i) ସୁଷମ ଷଡ଼ଭୁଜ ଅଙ୍କନ ପ୍ରଣାଳୀର ବୃତ୍ତ ଉପରେ A, B, C, D, E, F ବିନ୍ଦୁ କ୍ରମିକ ଭାବରେ ଅଙ୍କନ କର ।
(ii) ବିନ୍ଦୁଗୁଡ଼ିକୁ ଗୋଟିଏ ଛଡ଼ା ଗୋଟିକୁ (ଯେପରି A, C, E) ନେଇ ରେଖାଖଣ୍ଡ ଅଙ୍କନ କର, ଯେପରି \(\overline{\mathrm{AC}})\), \(\overline{\mathrm{CE}})\), \(\overline{\mathrm{EA}})\) |
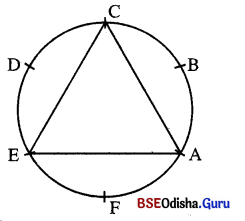
ଏ କ୍ଷେତ୍ରରେ △ACE ଆବଶ୍ୟକ ବୃତ୍ତାନ୍ତର୍ଲିଖ ସମବାହୁ ତ୍ରିଭୁଜ ।
ଦ୍ରଷ୍ଟବ୍ୟ : ଚିତ୍ରରେ ଆମେ ଅନ୍ୟ △BDF ସମବାହୁ ତ୍ରିଭୁଜ ଅନ୍ତର୍ଲିଖନ କରିପାରିବା |
3. ବୃତ୍ତ ମଧ୍ଯରେ ବର୍ଗଚିତ୍ର ଅନ୍ତର୍ଲିଖନ :
ବୃତ୍ତ ମଧ୍ୟରେ ପରସ୍ପରପ୍ରତି ଲମ୍ବ ଦୁଇଟି ବ୍ୟାସ ଅଙ୍କନ କରି ବର୍ଗଚିତ୍ର ଅଙ୍କନ କରାଯାଏ ।
→ ଅଙ୍କନ ପ୍ରଣାଳୀ :
- ମନେକର ବୃତ୍ତର କେନ୍ଦ୍ର O ଅଟେ । ବୃତ୍ତ ଉପରେ ଯେ କୌଣସି ଏକ ବିନ୍ଦୁ A ନେଇ \(\overrightarrow{\mathrm{AO}}\) ଅଙ୍କନ କର । ତାହା ବୃତ୍ତକୁ ଛେଦ– କରୁଥିବା ବିନ୍ଦୁର ନାମ C ଦିଅ । ବୃତ୍ତର AC ଗୋଟିଏ ବ୍ୟାସ ।
- \(\overrightarrow{\mathrm{OX}}\) ଅଙ୍କନ କର, ଯେପରି ∠AOX ଏକ ସମକୋଣ ହେବ ।
\(\overrightarrow{\mathrm{OX}}\) ଓ ବୃତ୍ତର ଛେଦବିନ୍ଦୁର ନାମ B ଦିଅ ।
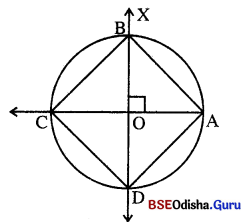
- \(\overrightarrow{\mathrm{BO}}\) ଅଙ୍କନ କର । ତାହା ବୃତ୍ତିକୁ ଛେଦକରୁଥିବା ବିନ୍ଦୁର ନାମ D ଦିଅ । BD ବୃତ୍ତର ଆଉ ଗୋଟିଏ ବ୍ୟାସ, ଯେପରି AC ⊥ BD |
- AB, BC, CD ଓ DA ଅଙ୍କନ କର । ABCD ଆବଶ୍ୟକ ବୃତ୍ତାନ୍ତର୍ଲିଖ ବର୍ଗଚିତ୍ର ।
