Odisha State Board BSE Odisha 8th Class Maths Solutions Algebra Chapter 8 ବ୍ୟାବସାୟିକ ଗଣିତ Ex 8(e) Textbook Exercise Questions and Answers.
BSE Odisha Class 8 Maths Solutions Algebra Chapter 8 ବ୍ୟାବସାୟିକ ଗଣିତ Ex 8(e)
Question 1.
ସର୍ବନିମ୍ନ କେତେ ଟଙ୍କା ଦେଇ ବ୍ୟାଙ୍କ୍ରେ ଏକ ଆକାଉଣ୍ଟ ଖୋଲାଯାଇ ପାରିବ ?
ସମାଧାନ :
ବର୍ତ୍ତମାନ କେତେକ ବ୍ୟାଙ୍କରେ 100 ଟଙ୍କାରେ ଆକାଉଣ୍ଟ ଖୋଲାଯାଇ ପାରୁଛି । କେତେକ ବ୍ୟାଙ୍ଗ୍ରେ ସର୍ବନିମ୍ନ 500 ଟଙ୍କା ରଖାଯାଉଛି ।
Question 2.
ଚେକ୍ ଦେଇ ବ୍ୟାଙ୍କ୍ସରୁ ଟଙ୍କା ଉଠାଇବା ପରେ ଆକାଉଣ୍ଟରେ ଅତି କମ୍ରେ କେତେ ଟଙ୍କା ରହିବା ଦରକାର ?
ସମାଧାନ :
ଚେକ୍ ଦେଇ ବ୍ୟାଙ୍କରୁ ଟଙ୍କା ଉଠାଇବା ପରେ ଷ୍ଟେଟ୍ ବ୍ୟାଙ୍କ୍ ଆକାଉଣ୍ଟଧାରୀଙ୍କ ଆକାଉଣ୍ଟରେ ଅତି କମ୍ରେ 1000 ଟଙ୍କା ଓ ଅନ୍ୟ ବ୍ୟାଙ୍କର ଆକାଉଣ୍ଟଧାରୀଙ୍କ ଆକାଉଣ୍ଟରେ ଅତି କମ୍ରେ 500 ଟଙ୍କା ରହିବା ଦରକାର ।
Question 3.
3. ବର୍ଷକୁ କେତେ ଥର ସଞ୍ଚୟ ବ୍ୟାଙ୍କ ଆକାଉଣ୍ଟ ପାଇଁ ବ୍ୟାଙ୍କ୍ ସୁଧ ହିସାବ କରେ ?
ସମାଧାନ :
ବର୍ଷକୁ ଦୁଇଥର ସଞ୍ଚୟ ବ୍ୟାଙ୍କ୍ ଆକାଉଣ୍ଟ ପାଇଁ ବ୍ୟାଙ୍କ୍ ସୁଧ ହିସାବ କରେ ।
![]()
Question 4.
(a) ଜଣେ ବ୍ୟକ୍ତି 500 ଟଙ୍କା ଦେଇ ଅପ୍ରେଲ 11 ତାରିଖରେ ଏକ ଆକାଉଣ୍ଟ ଖୋଲିଲେ । ଯଦି ଜୁନ୍ ମାସ ଶେଷ ସୁଦ୍ଧା ସେ ବ୍ୟାଙ୍କରୁ ଟଙ୍କା ଉଠାଇ ନ ଥାନ୍ତି ବା ଟଙ୍କା ଜମା ରଖ୍ ନଥାନ୍ତି; ତେବେ 6% ସୁଧ ହିସାବରେ ଜୁନ୍ ମାସ ଶେଷରେ କେତେ ସୁଧ ପାଇବେ ?
(b) ଅରୁଣର ସଂଚୟ ବ୍ୟାଙ୍କ୍ ଆକାଉଣ୍ଟରେ ଅଗଷ୍ଟ ମାସ ପାଇଁ ସର୍ବନିମ୍ନ ଅବଶେଷ 5010 ଟଙ୍କା ଥିଲା; ମାତ୍ର ଅରୁଣ ଅଗଷ୍ଟ ମାସ 30 ତାରିଖ ଦିନ ଆକାଉଣ୍ଟ ବନ୍ଦ ପାଇଁ ଦରଖାସ୍ତ କଲା; ତେବେ ଅରୁଣ ଅଗଷ୍ଟ ମାସ ପାଇଁ କେତେ ଟଙ୍କା ଉପରେ ସୁଧ ପାଇବ ?
ସମାଧାନ :
(a) ଅପ୍ରେଲ ମାସ 11 ତାରିଖରେ ଡିପୋଜିଟ୍ ପରିମାଣ ଉପରେ ସୁଧ ହିସାବ ହେବ ନାହିଁ ।
ମଇ ମାସରେ ସର୍ବନିମ୍ନ ଅବଶେଷ ଟଙ୍କା 500 ଟଙ୍କା ।
ଜୁନ୍ ମାସରେ ସର୍ବନିମ୍ନ ଅବଶେଷ ଟଙ୍କା 500 ଟଙ୍କା ।
ଜୁନ୍ ମାସ ଶେଷ ସୁଦ୍ଧା 500 ଟ. + 500 ଟ. = 1000 ଟଙ୍କା ଉପରେ ସୁଧ ହିସାବ କରାଯିବ ।
ଏଠାରେ ମୂଳଧନ (P) = 1000 ଟଙ୍କା, ସୁଧର ହାର (R) = 6% ଓ ସମୟ (T) = 1 ମାସ = \(\frac{1}{12}\) ବର୍ଷ |
ନିଶ୍ଚେୟ ସୁଧ (I) = \(\frac{1}{12}\) ଟଙ୍କା = 5
ସେ ଜୁନ୍ ମାସ ଶେଷରେ 5 ଟଙ୍କା ସୁଧ ପାଇବେ ।
(b) ଅଗଷ୍ଟ 30ରେ ଆକାଉଣ୍ଟ ବନ୍ଦ କରିବା ହେତୁ ଅଗଷ୍ଟ ମାସରେ ସର୍ବନିମ୍ନ ଅବଶେଷ 00 ଟଙ୍କା ହେବ । ତେଣୁ ସେ ଆଦୌ ସୁଧ ପାଇବ ନାହିଁ ।
![]()
Question 5.
ନମ୍ରତାର ବ୍ୟାଙ୍କ୍ରେ ଏକ ସଞ୍ଚୟ ଆକାଉଣ୍ଟ ଅଛି । ଆକାଉଣ୍ଟ ବହିରେ ଥିବା ହିସାବର ବିଶଦ ବିବରଣୀ ଏହିପରି –
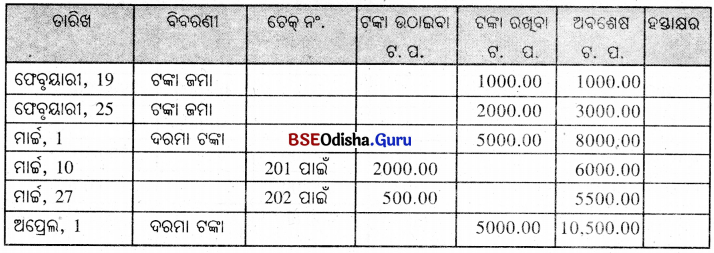
ଉପରୋକ୍ତ ଜମା ପାଇଁ ବାର୍ଷିକ ସୁଧର ହାର 5% ହେଲେ,
(i) ଫେବୃୟାରୀ ମାସ ପାଇଁ ନମ୍ରତା କେତେ ସୁଧ ପାଇବେ ?
(ii) ମାର୍ଚ୍ଚ ମାସ ପାଇଁ କେତେ ସୁଧ ପାଇବେ ?
(iii) ଅପ୍ରେଲ 21 ତାରିଖରେ ଆକାଉଣ୍ଟ ବନ୍ଦ କରିବାକୁ ନମ୍ରତା ଦରଖାସ୍ତ କଲେ, ସମୁଦାୟ ଜମା ଟଙ୍କା ପାଇଁ ସେ କେତେ ସୁଧ ପାଇବେ ?
ସମାଧାନ :
(i) ଫେବୃୟାରୀ ମାସର 19 ଏବଂ 25 ତାରିଖରେ ଜମାଥିବା ଟଙ୍କା ଉପରେ ନମ୍ରତା କୌଣସି ସୁଧ ପାଇବେ ନାହିଁ ।
(ii) ମାର୍ଚ୍ଚ ମାସରେ ସର୍ବନିମ୍ନ ଅବଶେଷର ପରିମାଣ 5500 ଟଙ୍କା ।
ମୂଳଧନ (P) = 5500 ଟଙ୍କା, ସମୟ (T) = \(\frac{1}{12}\) ବର୍ଷ, ହାର (R) = 5%
ସୁଧର ପରିମାଣ = \(\frac{\mathrm{PRT}}{100}=\frac{5500 \times 5 \times \frac{1}{12}}{100}=6 \cdot \frac{275}{12}\) = ଟ. 22.92
(iii) ଆମେ ଜାଣିଛୁ, ପ୍ରତି ମାସର 10 ତାରିଖରୁ ସେହି ମାସର ଶେଷ ତାରିଖ ପର୍ଯ୍ୟନ୍ତ ଆକାଉଣ୍ଟରେ ଥିବା ଟଙ୍କା ଉପରେ ସୁଧ ହିସାବ କରାଯାଏ ।
ନମ୍ରତା ଅପ୍ରେଲ 21 ତାରିଖରେ ଆକାଉଣ୍ଟ୍ ବନ୍ଦ କରିଥିବାରୁ ଅପ୍ରେଲ୍ ମାସର ସୁଧ ହିସାବ କରାଯିବ ନାହିଁ । ଅର୍ଥାତ୍ ଆକାଉଣ୍ଟ୍ ବନ୍ଦକଲେ ମାର୍ଚ୍ଚ ମାସର ସୁଧ = ଟ. 22.92
Question 6.
ହରିର ଏକ ସଞ୍ଚୟ ବ୍ୟାଙ୍କ୍ ଆକାଉଣ୍ଟ ଅଛି । 1998 ମସିହା ପାଇଁ ପାସ୍ବୁକ୍ରେ ଥିବା ଟଙ୍କାର ବିଶଦ ବିବରଣୀ ନିମ୍ନରେ ଦିଆଯାଇଛି । ଯଦି ଡିସେମ୍ବର ମାସ ଶେଷରେ ବର୍ଷକୁ ଥରେମାତ୍ର 5% ସୁଧରେ ସୁଧ ହିସାବ କରାଯାଏ ; ତେବେ ହରି 1998 ମସିହା ପାଇଁ କେତେ ସୁଧ ପାଇଲେ, ହିସାବ କର ।
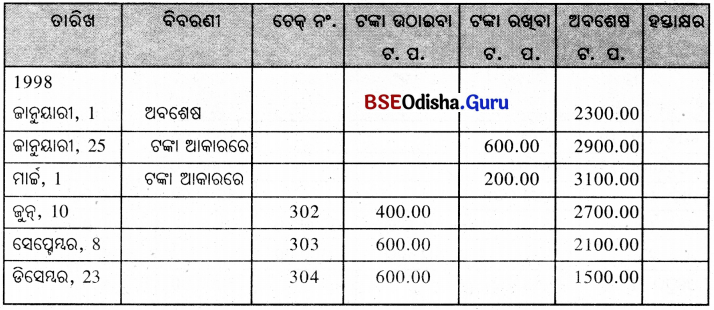
ସମାଧାନ :
ଜାନୁୟାରୀ ମାସରୁ ଡିସେମ୍ବର ମାସ ପାଇଁ ସର୍ବନିମ୍ନ ଅବଶେଷ ଏହିପରି ।
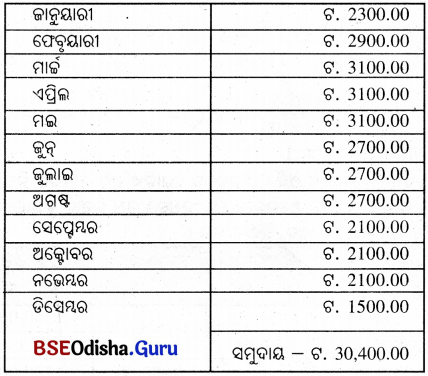
ଏଠାରେ ମୂଳଧନ (P) = 30,400 ଟଙ୍କା, ସୁଧର ହାର (R) = 5%, ସମୟ (T) = 1 ମାସ = \(\frac{1}{12}\) ବର୍ଷ |
ନିଶ୍ଚେୟ ସୁଧ (I) = \(\frac{PRT}{100}=\frac{30,400 × 5 × 1}{100 × 12}\) = ଟ. 126.67
ହରି 1998 ମସିହା ପାଇଁ ଟ. 126.67 ସୁଧ ପାଇଲେ ।
![]()
Question 7.
ତୁମେ ଭାରତୀୟ ଷ୍ଟେଟ୍ ବ୍ୟାଙ୍କରେ 500 ଟଙ୍କା ଦେଇ ଜାନୁୟାରୀ 5 ତାରିଖରେ ଏକ ସଞ୍ଚୟ ଆକାଉଣ୍ଟ ଖୋଲିଲ । ଜାନୁୟାରୀ 12 ତାରିଖରେ ଆଉ 1000 ଟଙ୍କା ଜମାଦେଲ । ଜାନୁଆରୀ 27 ତାରିଖରେ ଚେକ୍ଟିଏ ଦେଇ 300 ଟଙ୍କା ଉଠାଇଲ । ଫେବୃୟାରୀ 10 ତାରିଖରେ 700 ଟଙ୍କା ଜମାଦେଲ । ମାର୍ଚ୍ଚ 5 ତାରିଖରେ 200 ଟଙ୍କା ଉଠାଇବା ଫର୍ମ ଦେଇ ଟଙ୍କା ଉଠାଇଲ ।
(i) ଉପରୋକ୍ତ ବିଶଦ ବିବରଣୀ କିପରି ପାସ୍ବୁକ୍ରେ ଲେଖାଯିବ,
(ii) ଯଦି ବାର୍ଷିକ ସୁଧର ହାର 5% ହୋଇଥାଏ; ତେବେ ମାର୍ଚ୍ଚ ମାସ ଶେଷରେ ତୁମେ କେତେ ଟଙ୍କା ସୁଧ ପାଇବ ?
ସମାଧାନ :
(i)
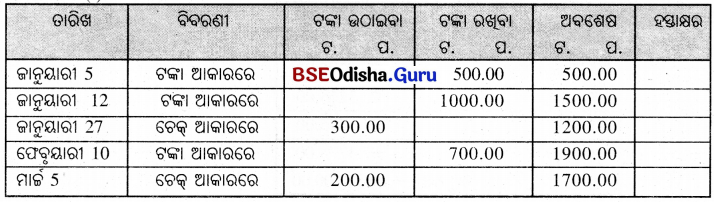
ସମୁଦାୟ ଟଙ୍କାର ପରିମାଣ, (ଯାହା ଉପରେ ସୁଧ ହିସାର ହେବ)
= 500+ 1900 + 1700 = 4100 ଟଙ୍କା
ମୂଳଧନ (P) = 4100 ଟଙ୍କା, ସମୟ (T)= 1 ମାସ = \(\frac{1}{12}\) ବର୍ଷ
ଏବଂ ସୁଧର ହାର (R) = 5%
ସୁଧ = \(\frac{PRT}{100}=\frac{4100×5×1}{12 × 100}\) = ଟ. 17.08
ସୁଧ ପରିମାଣ ଟ 17.08 ।
Question 8.
ସଲିମ୍ବର ଏକ ସଞ୍ଚୟ ବ୍ୟାଙ୍କ୍ ଆକାଉଣ୍ଟ ଅଛି । ପାସ୍ବୁକ୍ର ଗୋଟିଏ ପୃଷ୍ଠାର ନକଲ ନିମ୍ନରେ ଦିଆଯାଇଛି । ଯଦି ଡିସେମ୍ବର ମାସ ଶେଷରେ ବର୍ଷକୁ ଥରେମାତ୍ର 5% ସୁଧରେ ସୁଧ ହିସାବ କରାଯାଏ; ତେବେ ସଲିମ୍ 2001 ମସିହା ପାଇଁ କେତେ ସୁଧ ପାଇଥବ, ହିସାବ କର ।
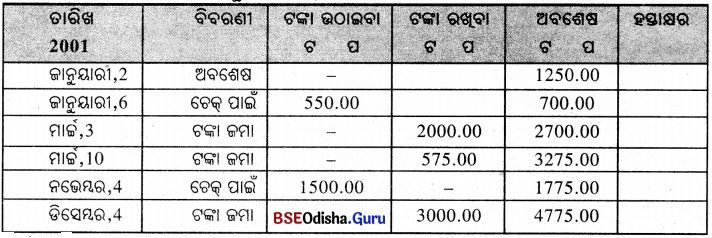
ସମାଧାନ :
ଜାନୁୟାରୀ ମାସଠାରୁ ଡିସେମ୍ବର ମାସପାଇଁ ସର୍ବନିମ୍ନ ଅବଶେଷ ଟଙ୍କା ଏହିପରି :
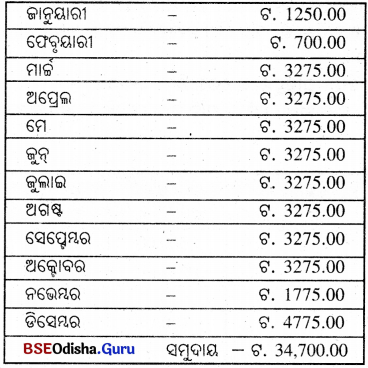
ମୂଳଧନ (P) = ଟ. 34,700.00
ସୁଧର ହାର (R) = 5%, ସମୟ (T) = 1 ମାସ = \(\frac{1}{12}\) ବର୍ଷ;
ନିର୍ଦେୟ ସୁଧ = \(\frac{PRT}{100}=\frac{34700×5×1}{12 × 100}\) = ଟ. 144.58
![]()
Question 9.
ଗୋଟିଏ ସଞ୍ଚୟ ପାସ୍ବୁକ୍ର ଏକ ପୃଷ୍ଠାର ନକଲ ଦିଆଯାଇଛି । ଯଦି ଫେବୃୟାରୀ ମାସଠାରୁ ଜୁଲାଇ ମାସ ମଧ୍ୟରେ ବ୍ୟକ୍ତିଜଣକ 111.45 ଟଙ୍କା ସୁଧ ପାଇଥା’ନ୍ତି; ତେବେ ଶତକଡ଼ା ସୁଧର ହାର ନିର୍ଣ୍ଣୟ କର ।
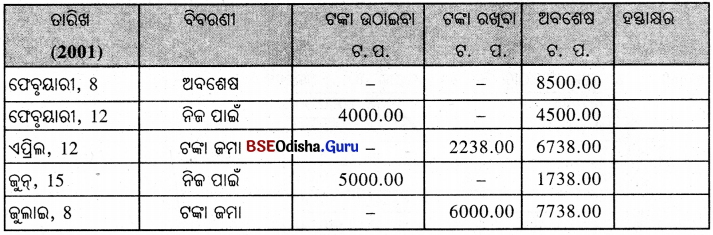
ସମାଧାନ :
ଫେବୃୟାରୀ ମାସରୁ ଜୁଲାଇ ମାସ ପର୍ଯ୍ୟନ୍ତ ସର୍ବନିମ୍ନ ଅବଶେଷ ଟଙ୍କା ଏହିପରି :
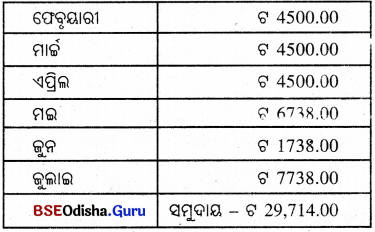
ଏଠାରେ ମୂଳଧନ (P) = ଟ. 29,714.00, ସମୟ (T) = 1 ମାସ = \(\frac{1}{12}\) ବର୍ଷ;
ମନେକର ସୁଧର ହାର = R%
ସୁଧ = \(\frac{PRT}{100}\) ⇒ 111.45 = \(\frac{29714×R×1}{12×100}\)
⇒ R = \(\frac{111.45×100×12}{29714}\) = 4.5%
ନିର୍ମେୟ ସୁଧର ହାର 4.5% ।
Question 10.
କୁଦୀପ୍ଙ୍କର ସଞ୍ଚୟ ପାସବୁକ୍ର ଏକ ପୃଷ୍ଠାର ନକଲ ନିମ୍ନରେ ଦିଆଯାଇଛି । 6% ହାରରେ ଜାନୁୟାରୀରୁ ଡିସେମ୍ବର 2000 ପର୍ଯ୍ୟନ୍ତ ସୁଧ ହିସାବ କର ।
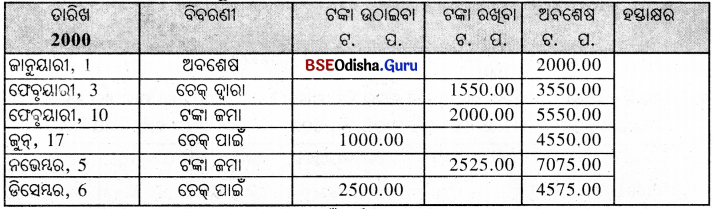
ସମାଧାନ :
ଜାନୁୟାରୀ ମାସଠାରୁ ଡିସେମ୍ବର ମାସପାଇଁ ସର୍ବନିମ୍ନ ଅବଶେଷ ଟଙ୍କା ଏହିପରି :
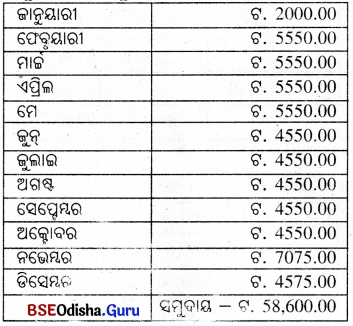
ମୂଳଧନ (P) = ଟ. 58,600.00, ସୁଧର ହାର(R) = 6%, ସମୟ (T) = 1 ମାସ = \(\frac{1}{12}\) ବର୍ଷ;
∴ ନିଶ୍ଚେୟ ସୁଧ = \(\frac{PRT}{100}=\frac{58600×6×1}{12×100}\) = ଟ. 293.00 ।
![]()
Question 11.
ମାନସର ସଂଚୟ ପାସ୍ବୁକ୍ର ନକଲ ନିମ୍ନରେ ଦିଆଯାଇଛି । 2007 ମସିହା ଜାନୁୟାରୀ ମାସଠାରୁ 2007 ଜୁନ୍ ମାସ ପର୍ଯ୍ୟନ୍ତ 4% ସୁଧ ହାରରେ ସୁଧ ହିସାବ କର ।
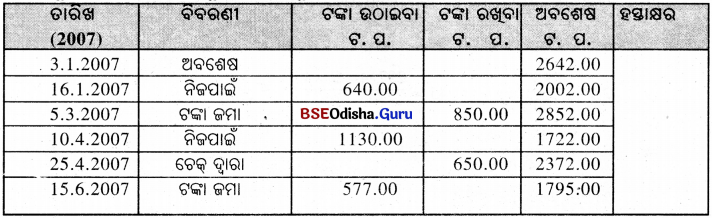
ସମାଧାନ :
ମାନସର 2007 ଜାନୁୟାରୀରୁ 2007 ଜୁନ ପର୍ଯ୍ୟନ୍ତ ସର୍ବନିମ୍ନ ଅବଶେଷ ଟଙ୍କା ଏହିପରି :
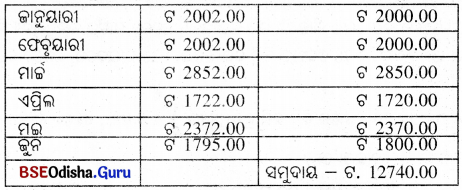
ଏଠାରେ ମୂଳଧନ (P) = 12740.00, ସୁଧର ହାର (R) = 4% ଓ ସମୟ = (T) = 1 ମାସ = \(\frac{1}{12}\) ବର୍ଷ
ସୁଧ (I) = \(\frac{PRT}{100}=\frac{12740×4×1}{12×100}\) = ଟ. 42.47 ।
2007 ମସିହା ଜୁନ୍ ମାସ ପର୍ଯ୍ୟନ୍ତ 4% ସୁଧ ହାରରେ ଟ. 42.47 ସୁଧ ମିଳିବ ।
Question 12.
ସୌମ୍ୟରଂଜନର ସଂଚୟ ପାସ୍ବୁକ୍ର ଏକ ପୃଷ୍ଠାର ନକଲ ନିମ୍ନରେ ଦିଆଯାଇଛି । 25.7.2004 ରେ ଆକାଉଣ୍ଟ ରଦ୍ଦ କରି ଟ.6042.45 ପାଇଥିଲା; ତେବେ ଶତକଡ଼ା ସୁଧର ହାର କେତେ ଥିଲା ସ୍ଥିର କର ।
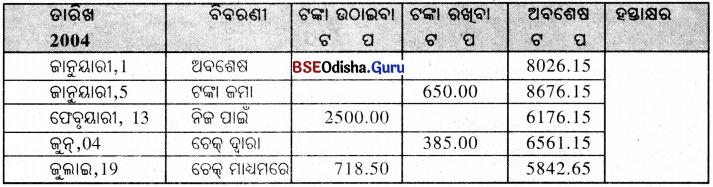
ସମାଧାନ :
ସୌମ୍ୟରଞ୍ଜନ 2004 ଜାନୁୟାରୀଠାରୁ ଜୁଲାଇ ପର୍ଯ୍ୟନ୍ତ ସର୍ବନିମ୍ନ ଅବଶେଷ ଏହିପରି :
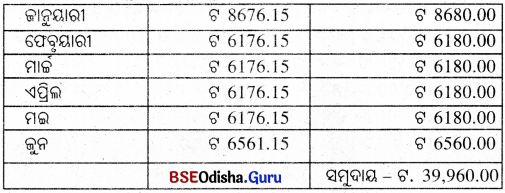
ସୁଧ (I) = ଟ. 6042.45 – ଟ. 5842.65 = ଟ. 199.80
ମୂଳଧନ (P) = ଟ. 39,960.00, ସମୟ (T) = 1 ମାସ = \(\frac{1}{12}\) ବର୍ଷ |
ମନେକର ସୁଧର ହାର R%
I = \(\frac{PRT}{100}=\frac{39,960×R×1}{1200}\) ⇒ R = \(\frac{199.80×1200}{39,960}\) = 6%
∴ ଶତକଡ଼ା ସୁଧର ହାର 6% ଥିଲା ।
