BSE Odisha 9th Class Physical Science Important Questions Chapter 5 ଗତି

Odisha State Board BSE Odisha 9th Class Physical Science Important Questions Chapter 5 ଗତି Important Questions and Answers.

BSE Odisha 9th Class Physical Science Important Questions Chapter 5 ଗତି

Subjective Type Questions With Answers

1. ବସ୍ତୁର ପ୍ରଥମ ଗତି ସମୀକରଣ ନିଗମନ କର ।
ଉ-
(i) ମନେ କ ର ଗୋଟିଏ ବ ସ୍ତୁ ଏ କ ସରକରେଖାରେ ସମତ୍ୱରଶ aରେଗତି କରୁଛି । t = 0 ସମୟରେ ଏହାର ପରିବେଗ = u ଓ t ସମୟ ପରେ ଏହାର ଅନ୍ତି ମ ପରିବେଗ = v ।
(ii) X ଅକ୍ଷରେଖାରେ ସମୟ ଓ Y ଅକ୍ଷରେଖାରେ ପରି ବେଗ ନେଲେ ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁ A ର ସ୍ଥାନାଙ୍କ (0. u) ଓ Bର ସ୍ଥାନାଙ୍କ (t, v) ।

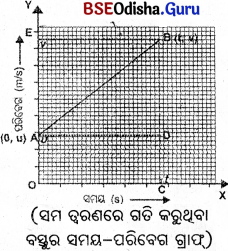
(ସମ ତ୍ଵରଣରେ ଗତି କରୁଥିବା
(iii) B ବିନ୍ଦୁରୁ X-ଅକ୍ଷରେଖା ପ୍ରତି BC ଲମ୍ବ ଅଙ୍କନ କରାଯାଉ, ଯାହା ବିନ୍ଦୁରୁ X- ଅକ୍ଷରେଖା ପ୍ରତି ଅଙ୍କିତ AD ସମାନ୍ତର ରେଖା, BC କୁ D ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
(iv) ଚିତ୍ର ଅନୁ ସାରେ OA = DC = u, BC = v, AD = t, BD = BC-DC = v – u
(v) ସଂଜ୍ଞାନୁସାରେ ତ୍ଵରଣ

⇒ at = v – u ⇒ v = u + at
ଏହା ଗତିର ପ୍ରଥମ ସମୀକରଣ ।

2. ଗତିର ଦ୍ଵିତୀୟ ସମୀକରଣ ସମୟ-ପରି ବେଗ ଲେଖଚିତ୍ରରୁ ନିଗମନ କର ।
ଉ –
(i) ମନେ କ ର ଗୋଟିଏ ବସ୍ତୁ ଏ କ ସରକରେ ଖ। ରେସମତ୍ୱରଣ aରେ ଗତି କରୁଛି । t = 0 ସମୟରେ ଏହାର ପରିବେଗ = u ଓ t ସମୟ ପରେ ଏହାର ଅନ୍ତଃ ମ ପରିବେଗ = v ।
(ii) X ଅକ୍ଷରେଖାରେ ସମୟ ଓ Y ଅକ୍ଷରେଖାରେ ପରି ବେଗ ନେଲେ ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁ Aର ସ୍ଥାନାଙ୍କ (0, u) ଓ Bର ସ୍ଥାନାଙ୍କ (t, v) ।
(iii) B ବିନ୍ଦୁରୁ X-ଅକ୍ଷରେଖା ପ୍ରତି BC ଲମ୍ବ À ବିନ୍ଦୁରୁ X- ଅଙ୍କନ କରାଯାଉ, ଯାହା ଅକ୍ଷରେଖା ପ୍ରତି ଅଙ୍କିତ AD ସମାନ୍ତର ରେଖା, BC କୁ D ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
(iv) ଚିତ୍ର ଅନୁ ସାରେ OA = DC = u, BC = v, AD = t, BD = BC – DC = v – u

ବସ୍ତୁର ସମୟ-ପରିବେଗ ଗ୍ରାଫ୍)
(v) ମନେକର ବସ୍ତୁଟି ମୂଳବିନ୍ଦୁରୁ ଯାତ୍ରା ଆରମ୍ଭ କରି ଏକ ସରଳରେଖାରେ ତ୍ଵରଣ ରେ ଗତିକରି । ସମୟ ମଧ୍ୟରେ s ଦୂରତା ଅତିକ୍ରମ କରିଛି ।
(vi) କୋଖ AB ଓ X-ଅକ୍ଷରେଖା ମଧ୍ୟର t କ୍ଷେତ୍ର (ABCର କ୍ଷେତ୍ର ଫଳ । ସମୟ ମଧ୍ୟରେ ବସ୍ତୁଦ୍ୱାରା ଅତିକ୍ରାନ୍ତ ଦୂରତା sର ପରିମାଣ ସହ ସମାନ ।
s = OABC କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ = OADC ଆୟକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ + AABDର କ୍ଷେତ୍ରଫଳ
= (OA x OC) + \(\frac {1}{2}\)(AD x BD)
= u x t + \(\frac {1}{2}\) t x at (∵BD = v – u = at)
= u t + \(\frac {1}{2}\) at²
∴ s = u t + \(\frac {1}{2}\) at²
ଏହା ଗତିର ଦ୍ଵିତୀୟ ସମୀକରଣ ଅଟେ ।

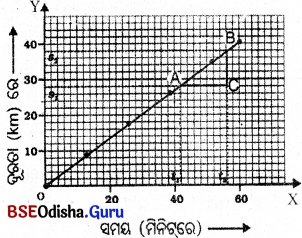
3. ସମବେଗରେ ଗତିଶୀଳ ବସ୍ତୁର ସମୟ-ଦୂରତା ଗ୍ରାଫ୍ ରୁ ବେଗ ନିର୍ଣ୍ଣୟ କି ପରି କରାଯାଏ ଦର୍ଶାଅ ।
ଉ –
(i) ମନେକର ଗୋଟିଏ ବସ୍ତୁ ସରଳରେଖାରେ ସମ ବେଗରେ ଗତି କରୁଛି । ଏହି ଗତିରେ ଅନ୍ତ ର। ଳ ରେ ସମାନ ପରି ମାଣ ରେ ବୃଦ୍ଧିପାଏ ।
(ii) ସମବେଗରେ ଗତିଶୀଳ ବସ୍ତୁର ସମୟ- ତ୍ରର ତାଗ୍ର।ଫ୍ତାର୍ଯଧକ ସରଳରେଖା ହୁଏ ଓ ଏଥ‌ିରୁ ଜଣାଯାଏ ଦୂରତା ସମ ହାରରେ ବୃଦ୍ଧି ପାଉଛି ।
(iii) ସମୟ-ଦୂରତା ଗ୍ରାଫ୍‌ରେ ଦୁଇଟି ବିନ୍ଦୁ A ଓ B ନି ଆଯାଉ । A ସ୍ଥାନରେ ସମୟର ପଠ୍ୟାଙ୍କ t₁ ଏବଂ B ଯୁ। ନରେ ସମୟର ପଠ୍ୟାଙ୍କ t₂ ଦ୍ରେଡ I A ବିଯୁର ହରତାର ପଠ୍ୟାଙ୍କ s₁ ଏବଂ B ବିଯୁର ହରତାର ପଠ୍ୟାଙ୍କ s₂ ବ୍ରେଡ ।

(ସମବେଗରେ ଗତିଶୀଳ ବସ୍ତୁର ସମୟ-ଦୂରତା ଗ୍ରାଫ୍)
(iv) A ବିନ୍ଦୁରୁ x-ଅକ୍ଷରେଖା ସହ ସମାନ୍ତର କରି ଏକ ରେଖା ଏବଂ B ବିନ୍ଦୁରୁ y-ଅକ୍ଷରେଖା ସହ ସମାନ୍ତର କରି ଅନ୍ୟ ଏକ ରେଖା ଟାଣ । ରେ ଖାଦ୍ଵୟ ପରି ସ୍ପରକୁ ୯ ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତୁ ।
(v) ∆ ABC ରେ AC = ସମୟ ବବଧାନ
= t₁ – t₂ ଓ BC
= ଦୂରତାର ବ୍ୟବଧାନ = S₂ – S₁

4. ସମୟ-ପରିବେଟ ଲେଖଚିତ୍ର ମାଧ୍ୟମରେ v² = u² + 2as ଗତି ସମୀକରଣର ସୂତ୍ର ନିଗମନ କର ।
ଉ-
ମନେ କ ର ସମ ତ୍ଵରଣରେ ଓ ଏ କ t ସମୟ ମଧ୍ୟରେ s ଦୂରତା ବିସ୍ଥାପିତ ହେଲା । ଏହି ଗତିର ସମୟ-ପରିବେଗ ଲେଖଚିତ୍ର ଏଠାରେ ପ୍ରଦର୍ଶିତ ହୋଇଛି ।

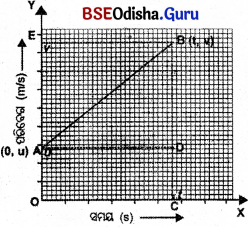
X-ଅକ୍ଷରେଖାରେ ସମୟକୁ ଏବଂ Y-ଅକ୍ଷରେଖାରେ ପରିବେଗକୁ ଦର୍ଶାଯାଇଛି ।
u = ବସ୍ତୁର ପ୍ରାରମ୍ଭିକ ପରିବେଗ (t = 0 ସମୟରେ )
v = ବସ୍ତୁର ଅନ୍ତିମ ପରିବେଗ (t = t ସମୟରେ)
t= ଗତି କରୁଥିବା ସମୟ ଅବଧୂ
a = ବସ୍ତୁର ତ୍ଵରଣ
s = t ସମୟ ମଧ୍ୟରେ ବସ୍ତୁଦ୍ଵାରା ଅତିକ୍ରାନ୍ତ ଦୂରତା ଏହି ସମୟ ପରିବର୍ତ୍ତନ ଓ ପରିବେଗର ପରିବର୍ତ୍ତନ ଲେଖଚିତ୍ରରେ ପ୍ରଦର୍ଶିତ ହୋଇଛି ।
t = 0 ସମୟରେ ପ୍ରାରମ୍ଭିକ ଅବସ୍ଥାନ A ର ନିର୍ଦ୍ଦେଶାଙ୍କଦ୍ଵୟ (0, u) । t ସମୟ ପରେ ଅବସ୍ଥାନ B ର ନିର୍ଦ୍ଦେଶାଙ୍କଦ୍ଵୟ (t, v) । B ବିନ୍ଦୁରୁ ଅକ୍ଷରେଖା ପ୍ରତି BC ଲମ୍ବ ଅଙ୍କିତ ଯାହା A ବିନ୍ଦୁରୁ X-ଅକ୍ଷରେଖା ପ୍ରତି ଅଙ୍କିତ AD ସମାନ୍ତର ରେଖା, BC କୁ D ବିନ୍ଦୁରେ ଛେଦ କରିବ ।
∴ ଚିତ୍ର ଅନୁ ସାରେ OA = CD = u,
OC = AD = t
BC = v, BD = BC – CD = v – u
t ସମୟ ମଧ୍ୟରେ ଆବଦ୍ଧ କ୍ଷେତ୍ର 0ABC ର କ୍ଷେତ୍ର ଫଳ ବସ୍ତ୍ର ଦ୍ୱାରା ଅତିକ୍ରାନ୍ତ ଦୂରତା ବିସ୍ଥାପନକୁ ସୂଚାଇଥାଏ ।
s = OABC ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ

OA = u, BC = v, OC = t ହେଲେ

⇒ at = v – u
∴ t = \(\frac {v – u}{a}\)
t ର ଏହି ମୂଲ୍ୟ ସଂସ୍ଥାପନ କଲେ

⇒ 2as = v² – u²
⇒ v² = u² + 2as

5. ଦୂରତା ଓ ବିସ୍ଥାପନ କହିଲେ କ’ଣ ବୁଝ ଉଦାହରଣ ସହ ବୁଝାଅ । ?
ଉ-
ଦୂରତା :
(i) ଗୋଟିଏ ବସ୍ତୁ ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁରୁ ବାହାରି କୌଣସି ଏକ ପଥରେ ଗତିକରି ଅଛି ମ ବିନ୍ଦୁରେ ପହଞ୍ଚିଲେ ବସ୍ତୁଟି ଅତିକ୍ରମ କରିଥିବା ପଥର ପ୍ରକୃତ ଦୈର୍ଘ୍ୟ (Length) କୁ ଦୂରତା କୁହାଯାଏ ।
(ii) ଦୂରତା ଏକ ଅଦିଶ ରାଶି କାରଣ ଏହାର ଦିଗ ନଥାଏ ।
(iii) ଏହି ଭୌତିକ ରାଶିର ପରିମାଣକୁ କେବଳ ସଂଖ୍ୟାଦ୍ଵାରା ପ୍ରକାଶ କରାଯାଏ ।
ଏକକ : S.I. ପଦ୍ଧତିରେ ଦୂରତାର ଏକକ କି.ମି. ବା ମି. । CGS ପଦ୍ଧତିରେ ଦୂରତାର ଏକକ ସେ.ମି. ।

ଉଦାତ୍ରରଣ:

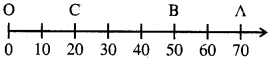
ମନେକର ଗୋଟିଏ ବସ୍ତୁ ଏକ ସରଳରେଖାରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବିନ୍ଦୁ ୦ ଠାରୁ ତାହାର ଗତି ଆରମ୍ଭ କଲା । ଭିନ୍ନ ଭିନ୍ନ ସମୟରେ A, B ଓ C ବସ୍ତୁର ବିଭିନ୍ନ ଅବସ୍ଥାନର ତିନୋଟି ବିନ୍ଦୁ । ବସ୍ତୁଟି C ଓ B ବିନ୍ଦୁ ଦେଇ A ଆଡ଼କୁ ଯାଇଛି । ସେଠାରୁ ପୁନଶ୍ଚ ସେ B ବିନ୍ଦୁ ଦେଇ ୯ ବିନ୍ଦୁକୁ ଫେରିଆସିଛି । ବସ୍ତୁଟି ଅତିକ୍ରାନ୍ତ କରିଥିବା ମୋଟ ଦୂରତା
= OA + AC
= 70 କି.ମି. + 50 କି.ମି. 120 କି.ମି.

ବିସ୍ଥାପନ :
(i) ଗୋଟିଏ ବସ୍ତୁ ଏକ ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁରୁ ତା’ର ଗତି ଆରମ୍ଭ କରି ଏକ ଅନ୍ତିମ ବିନ୍ଦୁରେ ପହଞ୍ଚିଲା ପରେ ସେହି ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ଯରେ ଥ‌ିବା ସର୍ବନିମ୍ନ ଦୂର ତ।କୁ ବସ୍ତୁର ବି ସ୍ଥାପନ କୁହାଯାଏ ।
(ii) ବିସ୍ଥାପନ ଏକ ସଦିଶ ରାଶି କାରଣ ଏହାର ଉଭୟ ପରିମାଣ ଓ ଦିଗ ରହିଥାଏ ।
(iii) ବିସ୍ଥାପନର ଦିଗ ସର୍ବଦା ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁରୁ ଅନ୍ତିମ ବିନ୍ଦୁ ଆଡ଼କୁ ହୋଇଥାଏ ।

ଉଦାତ୍ରରଣ:
(i) ଉପରିସ୍ଥ ଚିତ୍ରରେ ବସ୍ତୁଟି ( ଠାରୁ A ପର୍ଯ୍ୟନ୍ତ ଏକ ସରଳରେଖାରେ 70 କି.ମି. ଦୂରତା ଯାଇଛି । ଏଠାରେ ବିସ୍ଥାପନର ପରିମାଣ = ତ୍ରରତା = 70 କି.ମି.
(ii) ବସ୍ତୁଟି ୦ ଠାରୁ A ପର୍ଯ୍ୟନ୍ତ ଯାଇ ପୁନଶ୍ଚ B କୁ ଫେରି ଆସିଲେ ଅତିକ୍ରାନ୍ତ ଦୂରତା = OA + AB = 70 କି.ମି. + 20 କି.ମି. = ୨୦ କି.ମି. ମାତ୍ର B ସ୍ଥାନରେ ମୂଳବିନ୍ଦୁ ୦ ଠାରୁ ବସ୍ତୁର ବିସ୍ଥାପନ 50 କି.ମି. । ତେଣୁ ବିସ୍ଥାପନର ପରିମାଣ (50 କି.ମି.) ଅତିକ୍ରାନ୍ତ ଦୂରତାର ପରିମାଣ (୨୦ କି.ମି.) ସହ ସମାନ ନୁହେଁ ।
(iii) ଯଦି ବସ୍ତୁଟି ମୂଳବିନ୍ଦୁ ୦ ଠାରୁ ବାହାରି A ପର୍ଯ୍ୟନ୍ତ ଯାଇ ପୁଣି ଠ କୁ ଫେରି ଆସିଲେ, ଅତିକ୍ରାନ୍ତ୍ର ତୂରତା = 70 କି.ମି + 70 କି.ମି = 140 କି.ମି. । କିନ୍ତୁ ବସ୍ତୁର ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁ ଓ ଅନ୍ତିମ ବିନ୍ଦୁ ସମାନ ହୋଇଯିବାରୁ ବସ୍ତୁର ବିସ୍ଥାପନ ଶୂନ ହେବ ।

ଗୋଟିଏ ବିନ୍ଦୁରେ ବସ୍ତୁର ବିସ୍ଥାପନ ଶୂନ ହୋଇପାରେ, ମାତ୍ର ଅତିକ୍ରାନ୍ତ ଦୂରତା ଶୂନ ହେବ ନାହିଁ ।
ଦୂରତାର ଏକକ ବିସ୍ଥାପନର ଏକକ ସହ ସମାନ । ସମାନ ।
ମୋଟରଯାନ ଗତି କରୁଥିବାବେଳେ ଅତିକ୍ରମ କରୁଥିବା ଦୂରତା ମାପିବା ପାଇଁ ସେଣ୍ଟ୍ରେ ଓଡ଼ୋମିଟର (Odometer) ଲାଗିଥାଏ ।

1. ସମବୃତ୍ତୀୟ ଗତି କ’ଣ ? ସମବୃତ୍ତୀୟ ଗତିର ଏକ ଉଦାହରଣ ଦିଅ । ଏହା କାହିଁକି ଏକ ତ୍ବରାନ୍ବିତ ଗତି ବୁଝାଅ ।
ଉ-
(i) ଯେତେବେଳେ କୌଣସି ବସ୍ତୁ ବୃତ୍ତାକାର ପଥରେ ସାମ ବେଗରେ ଗତି କରେ ଗତି କୁହାଯାଏ ।
(ii) ଗୋଟିଏ ସୂତା ଅଗ୍ରରେ ଏକ ଲୌହ ବଲ୍‌କୁ ବାନ୍ଧି ଏହାର ଗୋଟିଏ ମୁଣ୍ଡକୁ ଆଙ୍ଗୁଠିରେ ଚାପିରଖ୍ ଲୌହବଲ୍‌ କୁ ବୃତ୍ତାକାର ପଥରେ ଘୂରାଇଲେ ଲୌହବଲ୍‌ର ଗତି ସମବୃତ୍ତୀୟ ଗତି ହେବ ।
(iii) ଏ ପ୍ରକାର ଗତିରେ ବସ୍ତୁଟି ପ୍ରତି ମୁହୂର୍ତ୍ତରେ ଦିଗ ବଦଳାଏ । ତେଣୁ ବସ୍ତୁର ପରିବେଗର ପରି ମାଣ ସମାନ ଥିଲେ ମଧ୍ୟ ଦି ଗ ବଦଳୁଥ‌ିବାରୁ ଏହାର ତ୍ଵରଣ ଥାଏ । ତେଣୁ ଏହା ଏକ ତ୍ଵରାନ୍ଵିତ ଗତି ।

2. ଜଣେ ବ୍ୟକ୍ତି 120 m ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ଏକ ପୋଖରୀର ଦୈର୍ଘ୍ୟ ଦିଗରେ ଗୋଟିଏ ପ୍ରାନ୍ତରୁ ପହଁରି ଅପରପ୍ରାନ୍ତକୁ ଯାଇ ସେହି ସ୍ଥାନକୁ ସିଧା ରିଆସିଲା ଏବଂ ଏଥିପାଇଁ ତାକୁ 6 ମିନିଟ୍ ସମୟ ଲାଗିଲା, ତେବେ ବ୍ୟକ୍ତିର ହାରାହାରି ବେଗ ଓ ହାରାହାରି ପରିବେଗ ନିରୂପଣ କର ।
ଉ-
ମୋଟ ଅତିକ୍ରାନ୍ତ ଦୂରତା = 120 m + 120 m = 240 m ଓ ସମୟ = 6 ମିନିଟ୍ = 360 ସେକେଣ୍ଡ ।

3. 80 m ଉଚ୍ଚ ଟାୱାର ଉପରୁ ଏକ ବଲ୍‌ ତଳକୁ ପକାଇ ଦି ଆଗଲା। ବଲ୍ ଟି ଭୂମିକୁ ଭୂମି କୁ ସ୍ପର୍ଶ କଲାବେଳେ ତା’ର ପରିବେଗ କେତେ ଥିଲା ? (g = 10m/s²)
ଉ-
ଏଠାରେ ପ୍ରାରମ୍ଭିକ ପରିବେଗ (u) = 0
ଅତିକ୍ରାନ୍ତ୍ର ତୂରତା (s) = 80 m ଓ g = 10 m/s²
∴ v² = u² + 2as
= v² = 0² + 2 x 10 m/s² × 80 m = 1600 m²/s²
v = 40 m/s
∴ ବଲ୍ଟି ଭୂମିକୁ ସ୍ପର୍ଶକଲାବେଳେ ତା’ର ପରିବେଗ 40 m/s ଥିଲା ।

4. ଗୋଟିଏ ବସ୍ତୁକୁ ଭୂଲମ୍ବ ଦିଗରେ ଭୂମିଠାରୁ ଉପରକୁ ନିକ୍ଷେପ କରାଗଲା । ଏହା 4 ସେକେଣ୍ଡ ପରେ ପ୍ରାରମ୍ଭିକ ସ୍ଥାନକୁ (ଯେଉଁ ସ୍ଥାନରୁ ଯାଇଥୁଲା ସେହି ସ୍ଥାନକୁ) ଫେରି ଆସିଲା । ତାହାହେଲେ ଏହାର ପ୍ରାରମ୍ଭିକ ବେଗ କେତେ ଥିଲା ? ଏହା କେତେ ଉପରକୁ ଉଠିଥିଲା ? (g = 10 m/s²)
ଉ-
ମୋଟ ସମୟ ଲାଗିଛି = 4 sec
କେବଳ ଉପରକୁ ଉଠିବାକୁ ସମୟ ଲାଗିଛି = \(\frac {4 sec}{2}\) = 2 sec.
(ଉପରକୁ ଉଠିବାକୁ ଯେତିକି ସମୟ ଲାଗିବ ତଳକୁ ଖସିବାକୁ ସେତିକି ସମୟ ଲାଗିବ ।) ଉପରକୁ ଉଠିବାପାଇଁ v = 0, t = 2 sec, g = – 10 m/s²
v = u + at ⇒ 0 = u + at
⇒ u = -at = -(-10m/s²) x 2s = 20 m/s
v² = u² + 2gs ⇒ 0 = u² + 2 gs
⇒ s = \(\frac{-\mathrm{u}^2}{2 \mathrm{~g}}=\frac{-(20 \mathrm{~m} / \mathrm{s})^2}{2 \times\left(-10 \mathrm{~m} / \mathrm{s}^2\right)}=\frac{-400 \mathrm{~m}^2 / \mathrm{s}^2}{-20 \mathrm{~m} / \mathrm{s}^2}\)
= 2o m
∴ ବସ୍ତୁଟି 20m ଉପରକୁ ଉଠିଥିଲା ଓ ତାହାର ପ୍ରାରମ୍ଭିକ ବେଗ 20 m/s ଥିଲା ।

5. ଗୋଟିଏ ବସ୍ତୁ ଭୂମିଠାରୁ 20 m ଉପରୁ ସ୍ଥିରାବସ୍ଥାରୁ ମୁକ୍ତ ଭାବରେ ପଡ଼ିଲା । ଭୂପୃରେ ପଡ଼ିବାକୁ ଏହାକୁ କେତେ ସମୟ ଲାଗିବ ? ଠିକ୍ ଭୂମିକୁ ଛୁଇଁବା ବେଳେ ଏହାର ପରିବେଗ କେତେ ହେବ? (g = 10 m/s²)
ଉ-
ଏଠାରେ ପ୍ରାରମ୍ଭିକ ପରିବେଗ (u) = 0
ଅତିକ୍ରାନ୍ତ ଦୂରତା (s) = 20 m
ଓ ମାଧ୍ୟାକର୍ଷଣ ଜନିତ ତ୍ଵରଣ (g) = 10 m/s²
v² = u² + 2gs = 2gs (∵ u = 0)
⇒ v = \(\sqrt{2 \mathrm{gs}}=\sqrt{2 \times 10 \mathrm{~m} / \mathrm{s}^2 \times 20 \mathrm{~m}}=\sqrt{400 \mathrm{~m}^2 / \mathrm{s}^2}\)
= 20 m/s
v = u + gt
⇒ t = \(\frac{\mathrm{v}-\mathrm{u}}{\mathrm{g}}=\frac{20 \mathrm{~m} / \mathrm{s}}{10 \mathrm{~m} / \mathrm{s}^2}\)
∴ ଭୂପୃଷ୍ଠରେ ପଡ଼ିବାକୁ 2 ସେକେଣ୍ଡ ସମୟ ଲାଗିବ ଓ ଠିକ୍ ଭୂମିରେ ଛୁଇଁବା ବେଳେ ଏହାର ପରିବେଟ। 20 m/s ହେବ।

6. ସ୍ଥିରାବସ୍ଥାରୁ ଗୋଟିଏ କାର୍ ଗତି ଆରମ୍ଭ କରି ଏକ ସିଧା ରାସ୍ତାରେ 4 m/s² ସମ ତ୍ଵରଣରେ ଗତି କଲା । 10 ସେକେଣ୍ଡ ପରେ ଏହାର ପରିବେଗ କେତେ ହେବ ? ଏହି ସମୟ ମଧ୍ୟରେ କାର୍‌ଟି କେତେ ଦୂର ଯାଇଥିବ ?
ଉ-
ଏଠାରେ ପ୍ରାରମ୍ଭିକ ପରି ବେଗ (u) = 0,
ତ୍ଵରଶ (a) = 4 m/s²
ସମୟ (t) = 10s
ଆନ୍ତିମ ପରିବେଗ = v ହେଲେ
v = u + at = 0 + 4 m/s² x 10s = 40 m/s
ଅତିକ୍ରାନ୍ତ ହରତା (s) = ut + \(\frac {1}{2}\) at²
= 0 x t + \(\frac {1}{2}\) × 4 m/s² × (100 s)²
= \(\frac {1}{2}\) x 4 m/s² × (100 s)² = 200 m
∴10 ସେକେଣ୍ଡ ପରେ କାର୍‌ର ପରିବେଗ ହେବ 40 m/s । ଏହି ସମୟ ମଧ୍ୟରେ କାର୍‌ଟି 200 m

7. ଗୋଟିଏ ଟ୍ରେନ୍ 9୦ km/h ବେଗରେ ଗତି କରୁ ଥିଲା । ହଠାତ୍‌ ଟ୍ରେନ୍ ର ବ୍ରେକ୍ ଦେଇ ଟ୍ରେନ୍ ଟିର ତ୍ଵରଣ – 0.5 m/s² କରାଗଲା । ଟ୍ରେନ୍ ଟି ସ୍ଥିର ହେବ। ପୂର୍ବରୁ କେତେ ଦୂର ଯାଇପାରିବ ?
ଉ-
ଟ୍ରେନ୍ ର ପ୍ରାରମ୍ଭିକ ବେଗ (u) = 90 କି.ମି./ ଘଣ୍ଟା
= \(\begin{aligned}90000 \\3600\end{aligned}\) ମିଟର / ସେକେଣ୍ଡ = 25 ମି/ସେକେଣ୍ଡ
ତ୍ଵରଣ (a) = -0.5 ମିଟର / ସେକେଣ୍ଡ²
ଅନ୍ତିମ ବେଗ (v) = 0
v² = u² + 2as ⇒ 0 = u² + 2as

∴ ଟ୍ରେନ୍‌ ଟି ସ୍ଥିର ହେବ। ପୂର୍ବରୁ 625 ମିଟର ଦୂରଯାଇପାରିବ ।

8. ଗୋଟିଏ ଗମ୍ବୁଜ ଉପରୁ ହାତରେ ଧରି ଖୁବ। ପଥରଟିକୁ ଛାଡ଼ିଦେଲା ପରେ 4 ସେକେଣ୍ଡ ପରେ ତାହା ଭୂଇଁରେ ପଡ଼ିଲା । ଗମ୍ବୁଜର ଉଚ୍ଚ ତ କେତେ ? (g = 10 m/s²)
ଉ-
ଗମ୍ବୁଜ ଉପରୁ ପଥରଟିକୁ ଛଡ଼ାଗଲା । ତେଣୁ ପ୍ରାରମ୍ଭିକ ପରିବେଗ (u) = 0,
ସମୟ (t) = 4 ସେକେଣ୍ଡ
ଗମ୍ବୁଜର ଉଚ୍ଚତା (s) = ut + \(\frac {1}{2}\) gt² (a = g = 10 ମିଟର / ସେକେଣ୍ଡ²)
\(\frac {1}{2}\) gt² = \(\frac {1}{2}\) x 4 x 4 = 80 ମିଟର ।
∴ ଗମ୍ବୁଜର ଉଚ୍ଚତା 80 ମିଟର ।

9. ଦୂରତା ଓ ବିସ୍ଥାପନ ମଧ୍ୟରେ ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।
ଉ-
ଦୂରତା:
(i) ଗୋଟିଏ ବସ୍ତୁ ଏକ ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁରୁ ତା’ର ଗତି ଆରମ୍ଭ କରି ଏକ ଅନ୍ତିମ ବିନ୍ଦୁରେ ପହଞ୍ଚିଲେ ସେ ଯେତିକି ପଥ ଅତିକ୍ରମ କରେ ତାହାକୁ ଦୂରତା କୁହାଯାଏ ।
(ii) ଦୂରତା ଏକ ଅଦିଶ ରାଶି ।
(iii) ବସ୍ତୁର ଗତି ଥିଲେ ଦୂରତା ଆଦୌ ଶୂନ ହୁଏ ନାହିଁ ।

ବିସ୍ଥାପନ:
(i) ଗୋଟିଏ ବସ୍ତୁ ଏକ ପ୍ରାରମ୍ଭିକ ବିନ୍ଦୁରୁ ତା’ର ଗତି ଆରମ୍ଭ କରି ଏକ ଅନ୍ତିମ ବିନ୍ଦୁରେ ପହଞ୍ଚିବା ପରେ ସେହି ବିନ୍ଦୁଦ୍ଵୟ ମଧ୍ୟରେ ଥ‌ିବା ସର୍ବନିମ୍ନ ଦୂରତାକୁ ବସ୍ତୁର ବିସ୍ଥାପନ କୁହାଯାଏ ।
(ii) ବିସ୍ଥାପନ ଏକ ସଦିଶ ରାଶି ।
(iii) ବସ୍ତୁର ଗତି ଥିଲେ ମଧ୍ୟ ବିସ୍ଥାପନ ଶୂନ ହୋଇପାରେ ।

10. ବେଗ ଓ ପରିବେଗ
ଉ-
ବେଗ:
(i) ଏକକ ସମୟରେ ଏକ ବସ୍ତୁ ଅତିକ୍ରମ କରୁଥିବା ଦୂରତାକୁ ବେଗ କୁହାଯାଏ ।
(ii) ଗୋଟିଏ ଗତିଶୀଳ ବସ୍ତୁ t ସମୟରେ ୫ ଦୂରତା ଅତିକ୍ରମ କଲେ ବେଗ \(\mathbf{S}\mathbf{t}\) |
(iii) ବେଗ ଏକ ଅଦିଶ ରାଶି ।

ପରିବେଗ:
(i) ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦିଗରେ ଗତିଶୀଳ ବସ୍ତୁର ବେଗକୁ ପରିବେଗ କୁହାଯାଏ ।
(ii) ଗୋଟିଏ ବସ୍ତୁ t ସମୟରେ ସମବେଗରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦିଗରେ \(\overrightarrow{\mathrm{S}}\) ଦୂରତା ଅତିକ୍ରମ କଲେ, ପରିବେଗ
\((\vec{v})\) = \(\begin{aligned}\overrightarrow{\mathrm{s}} \\\mathrm{t}\end{aligned}\)
(iii) ପରିବେଗ ଏକ ସଦିଶ ରାଶି ।

11. ତ୍ଵରଣ ଓ ମନ୍ଦନ
ଉ-
ତ୍ଵରଣ:
(i) ପରିବେଗର ବୃଦ୍ଧିର ହାରକୁ ତ୍ଵରଣ କୁହାଯାଏ ।
(ii) ପରିବେଗର ବୃଦ୍ଧି ଘଟିଲେ ତ୍ଵରଣର ବୃଦ୍ଧି ଘଟେ ।
(iii) ଏହା ଯୁକ୍ତାତ୍ମକ ରାଶିଦ୍ଵାରା ପ୍ରକାଶିତ ହୁଏ ।

ମନ୍ଦନ:
(i) ପରିବେଗର ହ୍ରାସର ହାରକୁ ମନ୍ଦନ କୁହାଯାଏ।
(ii) ପରିବେଗର ବୃଦ୍ଧି ଘଟିଲେ ମନ୍ଦନ ହ୍ରାସପାଏ ।
(iii) ଏହା ବିଯୁକ୍ତାତ୍ମକ ରାଶିଦ୍ଵାରା ପ୍ରକାଶିତ ହୁଏ ।

12. ସମ ଗତି ଓ ଅସମ ଗତି
ଉ-
ସମ ଗତି:
(i) କୌଣସି ଏକ ବସ୍ତୁ ସମାନ ସମୟ ବ୍ୟବଧାନରେ ସମାନ ଦୂରତା ଅତିକ୍ରମ କରୁଥିଲେ ତାହା ସମ ଗତିରେ ଯାଉଛି ବୋଲି କୁହାଯାଏ ।
(ii) ଦୈନନ୍ଦିନ ଜୀବନରେ ସମ ଗତି ସଂପର୍କିତ ଦୃଷ୍ଟାନ୍ତ କ୍ଵଚିତ୍ର ଦେଖିବାକୁ ମିଳେ ।
(iii) ସଳଖ ଫାଙ୍କା ରାସ୍ତାରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବେଗରେ ଯାଉଥୁବା ଗାଡ଼ି, ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବେଗରେ ଘୁରୁଥୁବା ବିଦ୍ୟୁତ୍ ପଙ୍ଖା, ପୃଥ‌ିବୀର ପୂର୍ଶନ ଆଦି ସମ ଗତିର ଉଦାହରଣ ।

ଅସମ ଗତି:
(i) କୌଣସି ଏକ ବସ୍ତୁ ସମାନ ସମୟ ବ୍ୟବଧାନରେ ଅସମାନ ଦୂରତା ଅତିକ୍ରମ କରୁଥିଲେ ତାହା ଅସମ ଗତିରେ ଯାଉଛି ବୋଲି କୁହାଯାଏ ।
(ii) ଦୈନନ୍ଦିନ ଜୀବନରେ ପରିଲକ୍ଷିତ ହେଉଥିବା
(iii) ଉଠାଣି ବା ଗଡ଼ାଣି ରାସ୍ତାରେ ଯାନବାହନର ଗତି, ଘାସ ପଡ଼ିଆ ବା ପିଚ୍ଛିଳ ପୃଷ୍ଠରେ ଗୋଟିଏ ପେଣ୍ଡୁର ଗତି, ଗହଳିଆ ରାସ୍ତାରେ ଚାଲିବାର ଗତି ଆଦି ଅସମ ଗତିର ଉଦାହରଣ ।

1. ସମ ଗତି ଓ ଅସମ ଗତି କ’ଣ ପ୍ରତ୍ୟେକରୁ ଗୋଟିଏ ଲେଖା ଉଦାହରଣ ଦିଅ ।
ଉ-
ସମଗତି : ସମଗତି-ସମାନ ସମୟରେ ବସ୍ତୁ ସମାନ ଦୂରତା ଅତିକ୍ରମ କରୁଥିବା ଗତିକୁ ସମଗତି କହନ୍ତି ।
ଉଦାହରଣ:
ଗୋଟିଏ ବସ୍ତୁ ପ୍ରଥମ l ଘଣ୍ଟାରେ 5 କି.ମି., 2ୟ ଘଣ୍ଟାରେ 5 କି.ମି., ତୃତୀୟ ଘଣ୍ଟାରେ 5 କି.ମି. ପଥ ଅତିକ୍ରମ କଲେ ଏପ୍ରକାର ଗତିକୁ ସମଗତି କହନ୍ତି ।
ଅସମ ଗତି – ସମାନ ସମୟରେ ବସ୍ତୁ ଅସମାନ ଦୂରତା ଅତିକ୍ରମ କରୁଥିବା ଗତିକୁ ଅସମ ଗତି କହନ୍ତି ।
ଉଦାହରଣ – ଗୋଟିଏ ବସ୍ତୁ ପ୍ରଥମ 1 ଘଣ୍ଟାରେ 5 କି.ମି., ଦ୍ଵିତୀୟ ଘଣ୍ଟାରେ 8 କି.ମି., ତୃତୀୟ ଘଣ୍ଟାରେ 6 କି.ମି ଦୂରତା ଅତିକ୍ରମ କଲେ ଏ ପ୍ରକାର ଗତିକୁ ଅସମ ଗତି କହନ୍ତି ।

2. ଗୋଟିଏ କାର୍‌ର ଓଡ଼ୋମିଟର ପାଠ୍ୟଙ୍କ 12350 km ଥିଲା । 5 ଘଣ୍ଟାର ଯାତ୍ରାପରେ ଏହାର ଅନ୍ତ ମ ପାଠ୍ୟଙ୍କ 12605 km ହେଲା । ତେବେ କାରର ହାରାହାରି ବେଗ କେତେ ?
ଉ-
ଅତିକ୍ରାନ୍ତ ଦୂରତା (s)
=(12605 – 12350) km = 255 km,
ସମୟ (t) = 5h
∴ହାରାହାରି ବେଗ (v_av)
= \(\frac{s}{t}=\begin{gathered}255 \mathrm{~km} \\5 \mathrm{~h}\end{gathered}\) = 51 km/h
∴କାର୍‌ର ହାରାହାରି ବେଗ୍ 51 km/h ।

3. ଗୋଟିଏ ନଡ଼ିଆ ଗଛରୁ ଏକ ନଡ଼ିଆ ଝଡ଼ିଯାଇ 1.5 ସେକେଣ୍ଡ ପରେ ଭୂମିକୁ ସ୍ପର୍ଶକଲା । ତେବେ ନଡ଼ିଆଗଛର ଉଚ୍ଚତା କେତେ ? (g = 10m/s²)
ଏ0।ରେ u = 0, g = 10 m/s², t = 1.5 s
∴s = ut + \(\frac {1}{2}\) gt² = \(\frac {1}{2}\)gt² (∵u = 0)
\(\frac {1}{2}\) x 10 m/s² x (1.5s)²
= 5 m/s² x 2.25 s² = 11.25 m
∴ନଡ଼ିଆ ଗଛର ଉଚ୍ଚତା 11.25 m

4. ହାରାହାରି ବେଗ କ’ଣ ବୁଝାଇ ଲେଖ ।
ଉ-
(i) ଗୋଟିଏ ଗତିଶୀଳ ବସ୍ତୁ ସମାନ ସମୟ କରୁଥିଲେ, ଅସମ ବେଗରେ ଗତି କରୁଛି ବୋଲି କୁହାଯାଏ । ଅସମ ବେଗରେ ଗତିଶୀଳ ବସ୍ତୁ ପାଇଁ ହାରାହାରି ବେଗ (Average Speed) ନିର୍ଦ୍ଦେଶ କରାଯାଏ ।
(ii) ମନେକର ଗୋଟିଏ ବସ୍ତୁ t₁ ସମୟରେ s₁ ଦୂରତା, t₂ ସମୟରେ s₂ ଦୂରତା ଓ t₃ ସମୟରେ s₃ ଦୂରତା ଅତିକ୍ରମ କରୁଅଛି । ତେଣୁ ତାହାର
ହାରାହାରି ପରିବେଗ = \(\begin{aligned}\mathrm{s}_1+\mathrm{s}_2+\mathrm{s}_3 \\
\mathrm{t}_1+\mathrm{t}_2+\mathrm{t}_3\end{aligned}\)

5. ଗୋଟିଏ ଦେଉଳ ଉପରୁ ଖଣ୍ଡିଏ ପଥର ଖସିଲାପରେ 4 ସେକେଣ୍ଡରେ ଭୂମିକୁ ଛୁଇଁଲା । ଦେଉଳର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।(g = 10 m/s²)
ଉ-
ସମୟ t = 4 ସେକେଣ୍ଡ
ଖସିବା ପୂର୍ବରୁ ପଥର ସ୍ଥିରାବସ୍ଥାରେ ଥ‌ିବାରୁ ପ୍ରାରମ୍ଭିକ
ବେଗ u = 0
ମାଧ୍ୟାକର୍ଷଣ ଜନିତ ତ୍ଵରଣ a = g = 10 ମି/ସେ²
ପଥରଟି ଖସିଥିବା ଦୂରତା = s = ut + \(\frac {1}{2}\)at²
= 0 × 4 + \(\frac {1}{2}\) × 10 × 4² = 80 ମି.
∴ ଦେଉଳର ଉଚ୍ଚତା 80 ମିଟର ।

6. ଏକ ମୋଟର ବୋଟ୍ ସ୍ଥିରାବସ୍ଥାରୁ ଗୋଟିଏ ହ୍ରଦରେ ଏକ ସରଳରେଖାରେ ଗତି କଲା । 8 ସେକେଣ୍ଡ ସମୟରେ ତାହାର ତ୍ଵରଣ 3 ମି. । ସେ² ହେଲା । ଏହି ସମୟ ମଧ୍ୟରେ ବୋଟ୍‌ କେତେ ଦୂରତା ଅତିକ୍ରମ ଦୂରତା ଅତିକ୍ରମ କରିଥିଲା ?
ଉ-
ପ୍ରାରମ୍ଭିକ ବେଗ u = 0,
ତ୍ଵରଣ ଥ = 3 ମି./ ସେ² ଓ ସମୟ t = 8 ସେକେଣ୍ଡ ଅତିକ୍ରାନ୍ତ ଦୂରତା s = ut + \(\frac {1}{2}\) at²
= 0 × 3 + \(\frac {1}{2}\) × 3 × 8 × 8 = 96 ମୋଟର ।
∴ବୋଟ୍‌ଟି 96 ମିଟର ଦୂରତା ଅତିକ୍ରମ କରିଥିଲା ।

7. ବସ୍ତୁର ବେଗ କାହାକୁ କୁହାଯାଏ ଓ ଏହାର ଏକକ ଲେଖ ।
ଉ-
(i) ଏକ ବସ୍ତୁ ଏକକ ସମୟ ଅନ୍ତରାଳରେ ଅତିକ୍ରାନ୍ତ କରିଥୁବା ଦୂରତାକୁ ସେହି ବସ୍ତୁର ବେଗ କୁହାଯାଏ ।
ଏକକ : S.I. ପଦ୍ଧତିରେ ବେଗର ଏକକ m/s ବା ms^-1। CGS ପଦ୍ଧତିରେ ବେଗର ଏକକ cm/s ବା cm . s^-1। ବେଗର ଅନ୍ୟ ଏକକ ମଧ୍ୟ km/h ବା kmh^-1।

8. ନିଉଟନଙ୍କ ଗତି ସମ୍ବନ୍ଧୀୟ ସମୀକରଣ ଲେଖ ।
ଭ –
ନିଉଟନ୍‌ଙ୍କ ଗତି ସମ୍ବନ୍ଧୀୟ ସମୀକରଣ :
ପ୍ରଥମ ସମୀକରଣ : v = ut + at²
ଦ୍ଵିତୀୟ ସମୀକରଣ : s = ut + \(\frac {1}{2}\)at²
ତୃତୀୟ ସମୀକରଣ : 2as = v² – u²

9. ବସ୍ତୁର ତ୍ଵରଣ ବେଳେବେଳେ ଯୁକ୍ତାତ୍ମକ ଓ ବେଳେବେଳେ ବିଯୁକ୍ତାତ୍ମକ ହେବ ଲେଖ ।
ଉ-
ପରିବେଗ ଦିଗରେ ତ୍ଵରଣ ହେଲେ ତାହାକୁ ଯୁକ୍ତାତ୍ମକ ତ୍ଵରଣ ଏବଂ ପରିବେଗର ବିପରୀତ ଦିଗରେ ତୁ” ହେଲେ ତାହାକୁ ବିଯୁକ୍ତାତ୍ମକ ତ୍ଵରଣ ବା ମନ୍ଦନ କୁହାଯାଏ।

Objective Type Questions With Answers

A ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।

1. ହାରାହାରି ବେଗ କହିଲେ କ’ଣ ବୁଝ ?
ଉ-
ଗୋଟିଏ ବସ୍ତୁଦ୍ଵାରା ମୋଟ ଅତିକ୍ରାନ୍ତ ଦୂରତା ଓ କୁହାଯାଏ ।

2. ଅଦିଶ ରାଶି କାହାକୁ କୁହାଯାଏ ?
ଉ-
ଯେଉଁ ଭୌତିକ ରାଶି କେବଳ ପରି ମାଣଦ୍ଵାରା ପ୍ରକାଶିତ ହୁଏ, ତାହାକୁ ଅଦିଶ ରାଶି କୁହାଯାଏ ।

3. ସଦିଶ ରାଶି କାହାକୁ କୁହାଯାଏ ?
ଉ-
ଯେଉଁ ଭୌତିକ ରାଶି ଉଭୟ ପରିମାଣ ଓ ଦିଗଦ୍ଵାରା ପ୍ରକାଶିତ ହୁଏ, ତାହାକୁ ସଦିଶ ରାଶି କୁହାଯାଏ ।

4. ବିଯୁକ୍ତ ତ୍ଵରଣ କହିଲେ କ’ଣ ବୁଝ ?
ଉ-
ଦିଗର ପରିବର୍ତ୍ତନ ନ ଘଟି ଗୋଟିଏ ବସ୍ତୁର ପରିବେଗ ହ୍ରାସ ପାଇବାକୁ ବିଯୁକ୍ତ ତ୍ଵରଣ ବା ମନ୍ଦ ନ କୁହାଯାଏ ।

5. ଆପେକ୍ଷିକ ଗତି କ’ଣ ?
ଉ-
ଦୁଇଟି ବସ୍ତୁ ମଧ୍ୟରେ ଦୂରତା ବୃଦ୍ଧି ପାଇଲେ କିମ୍ବା ହ୍ରାସ ପାଇଲେ ସେମାନଙ୍କ ଗତିକୁ ଆପେକ୍ଷିକ ଗତି କୁହାଯାଏ ।

6. ଗୋଟିଏ ଉଦାହରଣ ଦିଅ ଯେଉଁ ଗତିରେ ହାରାହାରି ପରିବେଗ ଶୂନ, କିନ୍ତୁ ହାରାହାରି ବେଗ ଶୂନ ହୁଏ ନାହିଁ ?
ଉ-

ଶୂନ ହୋଇଥାଏ, କିନ୍ତୁ ହାରାହାରି ବେଗ ଶୂନ ଶୂନ ହୋଇଥାଏ, କିନ୍ତୁ ହାରାହାରି ବେଗ ଶୂନ ହୋଇନଥାଏ ।

7. ବେଗ କାହାକୁ କୁହାଯାଏ ?
ଉ-
ଏକ ବସ୍ତୁ ଏକକ ସମୟ ଅନ୍ତରାଳରେ ଅତିକ୍ରାନ୍ତ କରିଥିବା ଦୂରତାକୁ ସେହି ବସ୍ତୁର ବେଗ କୁହାଯାଏ

8. ସମ ଗତି କହିଲେ କ’ଣ ବୁଝ ?
ଉ-
ଏକ ବସ୍ତୁ ସମାନ ସମୟ ଅନ୍ତରାଳରେ ସମାନ ଦୂରତା ଅତିକ୍ରମ କଲେ ତାହାର ଗତିକୁ ସମଗତି କୁହାଯାଏ ।

9. ଅସମ ଗତି କହିଲେ କ’ଣ ବୁଝ ?
ଉ-
ହରତା ଅତିକ୍ରମ କଲେ ତାହା ର ଗତିକୁ ଅସମ ଗତି ଏକ ବସ୍ତୁ ସମାନ ସମୟ ଅନ୍ତରାଳରେ ଅସମାନ କୁହାଯାଏ ।

10. ପରିବେଗ କାହାକୁ କୁହାଯାଏ ?
ଉ-
ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଦିଗରେ ଗତିଶୀଳ ବସ୍ତୁର ବେଗକୁ ପରିବେଗ କୁହାଯାଏ ।

11. ତ୍ଵରଣ କାହାକୁ କହନ୍ତି ?
ଉ-
ପରିବେଗର ପରିବର୍ତ୍ତନ ହାରକୁ ତ୍ଵରଣ କୁହାଯାଏ ।

12. କେଉଁ ପରିସ୍ଥିତିରେ ହାରାହାରି ପରି ବେଗର ପରିମାଣ ହାରାହାରି ବେଗ ସହ ସମାନ ?
ଉ-
ବ ସ୍ତୁ ଟି ଏକ ସରଳରେ ଖାରେ ଏବଂ ସମପରି ବେଗ ରେ ଗତି କରୁଥିଲେ ଏହିର ହ।ରାହରି ହେବ ।

13. ଏକ କଣିକା ସମତ୍ଵରଣରେ ଗତିକଲେ ଏହାର ସମୟ-ପରିବେଗ ଲେଖ କ’ଣ ହୁଏ ?
ଉ-
ଏକ କଣିକା ସମତ୍ଵରଣରେ ଗତିକଲେ ଏହାର ସମୟ – ପରି ବେ ଗ ଲେଖି ସମୟ ଅକ୍ଷ ସହ ସୂକ୍ଷ୍ମକୋଣ କରୁଥିବା ଆନତ ରେଖା ହୁଏ ।

14. ସମବୃତ୍ତୀୟ ଗତି କ’ଣ ?
ଉ-
କୌଣସି ବସ୍ତୁ ବୃତ୍ତାକାର ପଥରେ ସମ ପରିବେଗରେ ଗତିକଲେ ତାହାର ଗତିକୁ ସମବୃତ୍ତୀୟ ଗତି କୁହାଯାଏ ।

15. ଗତି କ’ଣ ?
ଉ-
ସମୟ ଅନୁସାରେ ବସ୍ତର ଅବସ୍ଥାନ ପରିବର୍ତ୍ତନକୁ ବସ୍ତର ଗତି କୁହାଯାଏ ।

16. ମନ୍ଦନ କ’ଣ?
ଉ-
ପରି ବେଗର ବିପରୀତ ଦିଗରେ ତ୍ଵରଣ ହେଲେ ତାହାକୁ ମନ୍ଦନ କୁହାଯାଏ ।

B ଗୋଟିଏ ପଦରେ ଉତ୍ତର ଦିଅ ।

1. ଗତିର ତୃତୀୟ ସମୀକରଣଟି କ’ଣ ?
2. ବିସ୍ଥାପନ କେଉଁ ରାଶି ?
3. ଏକ ଘଣ୍ଟାରେ ମିନିଟ୍ କଣ୍ଟାର ବିସ୍ଥାପନ କେତେ ସମୟ ପରେ ଶୂନ ହେବ ?
4. ସଳଖ ରାସ୍ତାରେ ଗୋଟିଏ ଗତିଶୀଳ ଯାନ x ଦୂରତା v ସମ ପରିବେଗରେ ଓ ପରବର୍ତ୍ତୀ x ଦୂରତ୍ଵ y, ସମ କେତେ ହେବ ?
5. ପରିବେଗ-ସମୟ ଆଲେଖ ଓ ସମୟ ଅକ୍ଷ ମଧ୍ୟରେ ଆବଦ୍ଧ କ୍ଷେତ୍ରଫଳ କ’ଣ ସୂଚାଇବ ?
6. କଟକରୁ ପୁରୀକୁ ଗୋଟିଏ ଗାଡ଼ି ଘଣ୍ଟା ପ୍ରତି 40 କି.ମି ବେଗରେ ଯାଇ ଘଣ୍ଟା ପ୍ରତି 60 କି.ମି. ବେଗରେ ଫେରିଲା । ତାହାର ହାରାହାରି ବେଗ ଘଣ୍ଟା ପ୍ରତି କେତେ କି.ମି. ?
7. ଗୋଟିଏ ଘଣ୍ଟାର ସେକେଣ୍ଡ କଣ୍ଟାର ବିସ୍ଥାପନ କେତେ ସମୟ ପରେ ଶୂନ ହେବ ?
8. ସିଲେଇ ମେସିନ୍‌ରେ ସିଲେଇ କଲାବେଳେ ଛୁଞ୍ଚୁର ଗତି କେଉଁ ପ୍ରକାରର ହୋଇଥାଏ ?
9. ସମ ତ୍ବରାନ୍ବିତ ଗତି କ୍ଷେତ୍ରରେ କ’ଣ ଶୂନ ହୋଇଥାଏ ?
10. ଗୋଟିଏ ବସ୍ତୁ Aରୁ Bକୁ ଯାଇ Bରୁ Aକୁ ଫେରିଲା, ତେବେ ତା’ର ଅତିକ୍ରାନ୍ତ ଦୂରତା କେତେ ? ଯଦି AB = 125 F. I
11. ଗୋଟିଏ ବସ୍ତର ପରିବେଗ ଅତିକ୍ରାନ୍ତ ସମୟ ସହ ସମାନୁପାତୀ ହେଲେ, ବସ୍ତଟିର କ’ଣ ରହିବ ?
12. ସମୟ-ବେଗ ଗ୍ରାଫ୍‌ ଆନତି କ’ଣ ସୂଚାଏ ?
13. ଯେତେବେଳେ ଏକ ବସ୍ତର ଅତିକ୍ରାନ୍ତ ଦୂରତା ସମୟ ସହ ସମାନୁପାତୀ ହୁଏ, ଏହା କିପରି ଗତି କରି ଥାଏ ?
14. ସମୟ-ପରିବେଗ ଗ୍ରାଫ୍‌ର ଆନତି କ’ଣ ସୂଚାଏ ?
15. ଘଣ୍ଟାର ମିନିଟ୍ କଣ୍ଟାରେ କେଉଁ ଗତି ଦେଖାଯାଏ ?
16. ସମୟ-ଦୂରତା ଗ୍ରାଫ୍‌ ଆନତିରୁ କ’ଣ ସୂଚନା ମିଳେ ?
17. ସମୟ-ପରି ବେଗ ଗ୍ରାଫ୍‌ ଆନତି କ’ଣ ସୂଚିତ କରେ ?
18. ସମୟ-ପରିବେଗ ଗ୍ରାଫ୍ ମଧ୍ୟରେ ଆବଦ୍ଧ କ୍ଷେତ୍ରଫଳ ଏକ ଭୌତିକ ରାଶି ଉପସ୍ଥାପିତ କରେ, ଯାହାର ଏକକ କେତେ ?
19. ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ବୃତ୍ତାକାର ପଥରେ କଣିକାଟିଏ ଘୂରୁଛି । ଅର୍ଥବୃତ୍ତ ଘୂର୍ଣ୍ଣନପରେ ଏହାର ବିସ୍ଥାପନ କେତେ ହେବ ?
20. ଗୋଟିଏ ବସ୍ତୁକୁ ଭୂଲମ୍ବ ଦିଗରେ ଊର୍ଦ୍ଧ୍ଵ କୁ u ପରିବେଗରେ ନିକ୍ଷେପ କରାଗଲେ, ଏହା ସର୍ବାଧ୍ଵକ କେତେ ଉଚ୍ଚ ଉଠିବ ?

Answer:
1. v² = u² + 2as
2. ସଦିଶ
3. 1 ଘଣ୍ଟା
4. \(\frac{2}{\left(\frac{1}{v_1}+\frac{1}{v_2}\right)}\)
5. ଦୂରତା
6. 48
7. 1 ମିନିଟ୍
8. କମ୍ପନ,
9. ତ୍ଵରଣ
10. 250 ମି.
11. ସମ ତ୍ଵରଣ
12. ତ୍ଵରଣ
13. ସ୍ଥିର ବେଗରେ
17. ତରଣ
14. ତ୍ଵରଣ
15. ବୃତ୍ତୀୟ
16. ବେଗ
18. m
19. 2r
20. u²/2g

C ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

1. ଏକ ବସ୍ତୁ 20 ସେକେଣ୍ଡରେ 500 ମିଟର ଗତିକଲେ ଏହାର ହାରାହାରି ବେଗ ……………….।
2. ଏକ ବସ୍ତୁ Aରୁ Bକୁ ଯାଇ Bରୁ Aକୁ ସେହି ବେଗରେ ଫେରି ଆସିଲା । ତା’ର ହାରାହାରି ପରି ବେ ଗ ……………….।
3. Aରୁ Bର ଦୂରତା 8 ମିଟର । ଜଣେ ବ୍ୟକ୍ତି Aରୁ B ଗତିକରି Bରୁ Aକୁ ଫେରି ଆସିଲେ । ତାର ମୋଟ ବିସ୍ଥାପନ ……………….ହେବ ।
4. ନିର୍ଦ୍ଦିଷ୍ଟ ………………. ରେ,ବେଗକୁ ପରିବେଗ କୁହାଯାଏ ।
5. ଗୋଟିଏ ଘଣ୍ଟାର ଘଣ୍ଟାକଣ୍ଟାର ବିସ୍ଥାପନ ………………. ସମୟ ପରେ ଶୂନ ହେବ ।
6. ଉପରକୁ ଗୋଟିଏ ଟେକା ଭୂଲମ୍ବ ଦିଗରେ ପଡ଼ା ହେଲେ ଏହାର ଅନ୍ତିମ ପରିବେଗ ……………….. ବେଳେ ତାହା ସର୍ବାଧ‌ିକ ଉଚ୍ଚତାକୁ ଉଠିବ ।
7. ଏକ ଟେକା ଉପରକୁ ଫୋପଡ଼ା ହେଲେ ତାହା ଉଠିଲାବେଳର ତ୍ଵରଣ ଓ ରିଲାବେଳର ତ୍ଵରଣର ସମଷ୍ମି …………………।
8. ସମବୃଭୟ ଗତି ଏକ ……………….. ଗତି।
9. ………………… ଯନ୍ତ୍ର ସାହାଯ୍ୟରେ ଦୂରତା ମପାଯାଏ ।ଗତି ।
10 ପରି ବେଗର ପରିବର୍ତ୍ତନର ହାର କୁ ……………….. କୁହାଯାଏ ।
11. v² = u² + 2as ଗତି ସମାକରଣରେ s ………………. ସୂଚାଏ ।
12. ଯଦି ବସ୍ତାର ଅତିକ୍ରାନ୍ତ ଦୂରତା ସମୟ ସହ ସମାନୁପାତୀ ହୁଏ, ତେବେ ଏହା ……………….. ଗତି କରେ ।
13. ସଦିଶ ରାଶିର ………………. ରହିଥାଏ ।
14. ବିସ୍ଥାପନର ପରିବର୍ତ୍ତନ ହାରକୁ ……………….. କୁହାଯାଏ ।
15. ପରି ବେଗ-ସମୟ ଲେଖରୁ ବସ୍ତଦ୍ୱାରା ଅତିକ୍ରାନ୍ତ ତ୍ରରତା ………………….. ହେବ ।
16. ସମୟ ଅନୁସାରେ ବସ୍ତର ଅବସ୍ଥାନ ପରିବର୍ତ୍ତନକୁ …………………. କୁହାଯାଏ ।
17. ଆରମ୍ଭ ବିନ୍ଦୁ ଓ ଅନ୍ତିମ ବିନ୍ଦୁ ମଧ୍ୟରେ ଥିବା ସର୍ବନିମ୍ନ ଦୂରତାକୁ ……………….. କୁହାଯାଏ ।
18. ସମୟ – ପରି ବେଗ ଗ୍ରାଫ୍ରେ ସମୟ ଅକ୍ଷ ସହ ସମାନ୍ତର ସରଳରେଖା ହେଲେ, ଏଥୁରୁ ବସ୍ତର ………………. ଚ୍ଚଶ।ପଡ ।
19. ସମୟ-ବେଗ ଗ୍ରାଫ୍‌ ଆନତି ……………….. ସୂଚାଏ ।
20. ଅଦିଶ ରାତିଣ କେବଳ ………………….. ଥାଏ ।

Answer:
1. 25 m/s
2. 0
3. 0
4. ଦିଗ
5. 12 ଘଣ୍ଟା
6. 0
7. 0
8. ତ୍ବରାନ୍ବିତ
9. ଓଡ଼ୋମିଟର
10. ତ୍ଵରଣ
11. ବିସ୍ଥ।ପିନ
12. ସ୍ଥିର ବେଗରେ
13. ପରିମାଣ ଓ ଦିଗ
14. ପରିବେଗ
15. ଲେଖଦ୍ଵାରା ଆବଦ୍ଧ କ୍ଷେତ୍ରଫଳ
16. ଗତି
17. ବିସ୍ଥାପନ
18. ସମପରିବେଗରେ ଗତି
19. ତ୍ଵରଣ
20. ପରିମାଣ

D ଠିକ୍ ଉକ୍ତି ପାଇଁ (✗) ଓ ଭୁଲ ଉକ୍ତି ପାଇଁ (✓) ଚିହ୍ନ ଦିଅ

1. ଜଳ ବିଦ୍ୟୁତ୍ କେନ୍ଦ୍ରରେ ଜଳର ନିୟନ୍ତ୍ରିତ ଗତି ଯୋଗୁଁ ବିଦ୍ୟୁତ୍ ଶକ୍ତି ଉତ୍ପନ୍ନ ହୁଏ ।
2. ଜଣେ ବ୍ୟକ୍ତି A ଠାରୁ B କୁ ଯାଇ ପୁନଶ୍ଚ B ରୁ A କୁ ଫେରିଲା ତେବେ ତାର ମୋଟ ବିସ୍ଥାପନ ସର୍ବଦା 0 ହେବ ।
3. ଦୂରତା ଏକ ସଦିଶ ରାଶି ।
4. ଅତିକ୍ରାନ୍ତ ଦୂରତା କେବେ ହେଲେ 0 ହେବ ନାହିଁ ଯଦି ବସ୍ତୁଟି ଗତି କରୁଥାଏ ।
5. ବିସ୍ଥାପନ ଓ ଦୂରତାର ଏକକ ସମାନ ନୁହେଁ ।
6. ପ୍ରକୃତିରେ ଅଧିକାଂଶ ଗତି ଅସମ ଗତି ।
7. ବେଗ ଏକ ଅଦଶ ରାଶ ମାତ୍ର ପରବେଗ ଏକ ସଦଶ ରାଶି ।
8. ଗତିଶକ ବଯ୍ତୁ ରହି। ରହ। ରି ପରିବଗ ନ ଓ ହିରହରି ବେଗ ସର୍ବଦା ସମାନ ।
9. କୌଣସି ବସ୍ତୁରେ ପରିବେଗର ପରିବର୍ତ୍ତନ କୌଣସି ସମୟ ଅନ୍ତରାଳରେ ଶୂନ୍ୟ ହେବ ନାହିଁ ।
10. ସମୟ ଦୂରତା ଗ୍ରାଫ୍‌ ବେଗ ନିର୍ଣ୍ଣୟ କରାଯାଏ ।
11. v² = u² + 2as ଗତିର ଦ୍ଵିତୀୟ ସମୀକରଣର ଏକ ବ୍ୟଞ୍ଜକ ।
12. ବସ୍ତୁଟିର ଏକକ ସମୟ ଅନ୍ତରାଳରେ ଅତିକ୍ରାନ୍ତ କରିଥ‌ିବା ଦୂରତାକୁ ସେହି ବସ୍ତୁର ପରି ବେ ଗ କୁହାଯାଏ ।
13. SI ପଦ୍ଧତିରେ ବେଗର ଏକକ m x s^-1।
14. ପରିବେଗ-ସମୟ ଆଲେଖ ଓ ସମୟ ଅକ୍ଷ ମଧ୍ୟରେ ଆବଦ୍ଧ କ୍ଷେତ୍ରଫଳ ବେଗ ସୂଚାଇବ ।
15. ଏକ ଘଣ୍ଟାରେ ମିନିଟ୍ କଣ୍ଟାର ବିସ୍ଥାପନ 1 ଘଣ୍ଟା ସମୟ ପରେ ଶୂନ ହେବ ।
16. କଟକରୁ ପୁରୀକୁ ଗୋଟିଏ ଗାଡ଼ି ଘଣ୍ଟା ପ୍ରତି 40 କି.ମି. ବେଗରେ ଯାଇ ଘଣ୍ଟା ପ୍ରତି 60 କି.ମି. ବେଗରେ ଫେରିଲା । ତାହାର ହାରାହାରି ବେଗ ଘଣ୍ଟା ପ୍ରତି 48 କି.ମି. ।
17. ସିଲେଇ ମେସିନ୍‌ରେ ସିଲେଇ କଲାବେଳେ ଛଞ୍ଚାର ଗତି ଚଳନ ଗତି ହୋଇଥାଏ ।
18. ନିର୍ଦ୍ଦିଷ୍ଟ ଦିଗରେ ଗତିଶୀଳ ବସ୍ତୁର ବେଗକୁ ପରିବେଗ କହିନ୍ତି ।
19, ମନ୍ଦନର SI ଏକକ m x s^-1।
20. ଏକ ଟ୍ରେନ୍‌ର ପରିବେଗ 8 ସେକେଣ୍ଡରେ ସ୍ଥିରାବସ୍ଥାରୁ 40 m/s କୁ ବୃଦ୍ଧି ପାଇଲା । ଟ୍ରେନ୍‌ର ତ୍ଵରଣ 5 m/s²
21. ସ୍ଥିର ଥ‌ିବା ବସ୍ତୁର ସମୟ-ଦୂରତା ଆଲେଖ ସମୟ ଅକ୍ଷ ସହ ସମାନ୍ତର ହେବ ।
22. ଗୋଟିଏ ରେଳଗାଡ଼ିର ଘଣ୍ଟାପ୍ରତି ବେଗ 60 km ହେଲେ ଏହାର ବେଗ ସେକେଣ୍ଡ ପ୍ରତି \(\begin{aligned}50\\3\end{aligned}\) ମିଟର ।

Answer:
1. (✓)
2. (✓)
3. (✗)
4. (✓)
5. (✗)
6. (✓)
7. (✓)
8. (✗)
9. (✓)
10. (✓)
11. (✓)
12. (✗)
13. (✓)
14. (✗)
15. (✓)
16. (✓)
17. (✗)
18. (✓)
19. (✓)
20. (✓)
21. (✓)
22. (✓)

E. ‘କ’ ସ୍ତମ୍ଭର ଶବ୍ଦକୁ ‘ଖ’ ସ୍ତମ୍ଭ ର ଶବ୍ଦ ସହ ମିଳନ କରି ଲେଖ ।

1. କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
ସମ ତ୍ଵରାନ୍ଵିତ ଗତି	ସ୍ରୋତର ଗତି
ଅସମ ତ୍ୱରାନ୍ଵିତ ଗତି	ପୃଥ‌ବୀ ଚାରିପଟେ  ଚନ୍ଦ୍ରର ଗତି
ସମତୁଭ। ୟଗତି	ମୁକ୍ତ ପତନଶ।ଳବସ୍ତୁ
ସରଳ ରୈଖ୍ୟକ ଗତି	ସଳଖରାସ୍ତା ରେ ଗଢିଶଳ ଏକ କାର
ନିୟନ୍ତି ଗତି	ଗରବି। ଚ୍ଚନ୍ ର ଘୂର୍ଣ୍ଣନ

ଉ-

କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
ସମ ତ୍ଵରାନ୍ଵିତ ଗତି	ମୁକ୍ତ ପତନଶ।ଳବସ୍ତୁ
ଅସମ ତ୍ୱରାନ୍ଵିତ ଗତି	ସଳଖରାସ୍ତା ରେ ଗଢିଶଳ ଏକ କାର
ସମତୁଭ। ୟଗତି	ପୃଥ‌ବୀ ଚାରିପଟେ  ଚନ୍ଦ୍ରର ଗତି
ସରଳ ରୈଖ୍ୟକ ଗତି	ସ୍ରୋତର ଗତି
ନିୟନ୍ତି ଗତି	ଗରବି। ଚ୍ଚନ୍ ର ଘୂର୍ଣ୍ଣନ

 

2. ‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
ଗତିର ପ୍ରଥମ ସମୀକରଣ	ତ୍ୱରାନ୍ୱିତି ଗତି
ଗତିର ତ୍ବିତୀୟ ସମୀକରଣ	ମନ୍ଦିତ ଗତି
ଗତିର ଢୃତୀୟ ସମୀକରଣ	v = u + at
ଗଛରୁ ଫଳ ପଡ଼ିବା	s = ut + \(\frac {1}{2}\) at2
ଉପରକୁ ଟେକା ଫିଙ୍ଗିବା	v2 = u2 + 2as

ଉ-

‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
ଗତିର ପ୍ରଥମ ସମୀକରଣ	v = u + at
ଗତିର ତ୍ବିତୀୟ ସମୀକରଣ	s = ut + \(\frac {1}{2}\) at2
ଗତିର ଢୃତୀୟ ସମୀକରଣ	v2 = u2 + 2as
ଗଛରୁ ଫଳ ପଡ଼ିବା	ତ୍ୱରାନ୍ୱିତି ଗତି
ଉପରକୁ ଟେକା ଫିଙ୍ଗିବା	ମନ୍ଦିତ ଗତି

 

3. ‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
ବେଗର ଏକକ	ବେଗ
ତ୍ଵରଣର ଏକକ	m ବା km
ସଦିଶ ରାଶି	m/s
ଅଦିଶ ରାଶି	m/s2
ଦୂରତାର ଏକକ	ପରିବେଟ

ଉ-

‘କ’ ସ୍ତମ୍ଭ	‘ଖ’ ସ୍ତମ୍ଭ
ବେଗର ଏକକ	m/s
ତ୍ଵରଣର ଏକକ	m/s2
ସଦିଶ ରାଶି	ପରିବେଟ
ଅଦିଶ ରାଶି	ବେଗ
ଦୂରତାର ଏକକ	m ବା km

 

F ପ୍ରଥମ ଯୋଡ଼ିର ସମ୍ପର୍କକୁ ଲକ୍ଷ୍ୟ କରି ଦ୍ଵିତୀୟ ଯୋଡ଼ିର ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

1. ବେଗ : ଅଦିଶ ରାଶି :: ଦୂରତା : ………………….।
2. ଯୁକ୍ତାତ୍ମକ : ତ୍ଵରଣ :: ବିଯୁକ୍ତାତ୍ମକ : ………………….।
3. ପରିବେଗ : ବେଗ :: ବିସ୍ଥାପନ : ………………….।
4. v : u + at :: v² : ………………….।
5. ଉପରକୁ ଟେକାଫୋପଡ଼ା g = – 10 m/s² :: ଟେକା ତଳକୁ ଖସିବା : ………………….।
6. v : m/s :: a : ………………….।
7. ଦୂରତା : ମିଟର :: ବିସ୍ଥାପନ : ………………….।
8. ବେଗ : m/s :: ପରିବେଗ : ………………….।
୨. ବେଗ-ସମୟ ଆଲେଖ : ଦୂରତା : : ଦୂରତା-ସମୟ ଆଲେଖ : ………………….।
10. ପରିବେଗର ବୃଦ୍ଧି : ତ୍ଵରଣ :: ପରିବେଗର ହ୍ରାସ : ………………….।

Answer:
1. ଅଦିଶ ରାଶି
2. ମନ୍ଦନ
3. ଦୂରତା
4. u² + 2as
5. g = 10 m/s²
6. m/s²
7. ମିଟର
8. m/s
9. ବେଗ
10. ମନ୍ଦନ

G ଚାରିଗୋଟି ସମ୍ଭାବ୍ୟ ଉତ୍ତର ମଧ୍ୟରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ ।

1. ସୁନାମିରେ ସ୍ରୋତର ଗତି କି ପ୍ରକାର ଗତି ?
(A) ନିୟନ୍ତ୍ରିତ
(B) ଅନିୟନ୍ତ୍ରିତ
(C) ଘୂର୍ଣ୍ଣନ
(D) ପୌନଃପୁନିକ
Answer:
(B) ଅନିୟନ୍ତ୍ରିତ

2. ଝୁଲଣି ଖେଳରେ ଦଉଡ଼ିର ଗତି କି ପ୍ରକାର ?
(A) ସ୍ଥାନାନ୍ତରଣ
(B) ଘୂର୍ଣ୍ଣନ
(C) ଦୋଳନ
(D) ଚଳନ
Answer:
(C) ଦୋଳନ

3. ମନ୍ଦନର S.I. ଏକକ କ’ଣ ହେବ ?
(A) m. s
(B) m.s²
(C) m.s^-2
(D) kmh²
Answer:
(C) m.s^-2

4. v² = u² + 2as ଗତି ସମୀକରଣରେ s କ’ଣ ସୂଚାଏ ?
(A) ପ୍ରାରମ୍ଭିକ ପରିବେଗ
(B) ଅନ୍ତିମ ପରିବେଗ
(C) ତ୍ଵରଣ
(D) ବିସ୍ଥାପନ
Answer:
(D) ବିସ୍ଥାପନ

5. ଏକ ସରଳରେଖାରେ ସମ ଗତିରେ ଗତି କରୁଥିବା ବସ୍ତୁର ସମୟ ଦୂରତା ଗ୍ରାଫ୍ କପରି ହେବ ?
(A) ଅବତଳ
(B) ଉତ୍ତଳ
(C) ସରଳରେଖା
(D) ଅଙ୍କାବଙ୍କା
Answer:
(C) ସରଳରେଖା

6. ଏକ ଘଣ୍ଟାରେ ମିନିଟ୍ କଣ୍ଟାର ବିସ୍ଥାପନ କେତେ ସମୟ ପରେ ଶୂନ ହେବ ?
(A) 1 ମିନିଟ୍
(B) 1 ଘଣ୍ଟା
(C) 12 ଘଣ୍ଟା
(D) 24 ଘଣ୍ଟା
Answer:
(B) 1 ଘଣ୍ଟା

7. ସମୟ ଦୂରତା ଗ୍ରାଫ୍‌ରୁ କେଉଁ ଭୌତିକ ରାଶିଟିକୁ ନିର୍ଣ୍ଣୟ କରାଯାଇ ପାରିବ ?
(A) ତ୍ଵରଣ
(B) ସଂବେଗ
(C) ବସ୍ତୁତ୍ଵ
(D) ବେଗ
Answer:
(D) ବେଗ

8. ପରିବେଗର ପରିବର୍ତ୍ତନର ହାରକୁ କ’ଣ କୁହାଯାଏ ?
(A) ସଂବେଗ
(C) ତ୍ଵରଣ
(B) ବିସ୍ଥାପନ
(D) ବେଗ
Answer:
(C) ତ୍ଵରଣ

9. ଜଣେ ବ୍ୟକ୍ତି 50 କି.ମି. ରାସ୍ତାକୁ 5 ଘଣ୍ଟାରେ ଅତିକ୍ରମ କଲେ, ତାଙ୍କର ବେଗ କେତେ ହେବ ?
(A) 100 km/h
(C) 80 km/h
(B) 5km/h
(D) 10 km/h
Answer:
(D) 10 km/h

10. କେଉଁ ଯନ୍ତ୍ର ସାହାଯ୍ୟରେ ଦୂରତା ମପାଯାଏ ?
(A) ଓଡ଼ୋମିଟର
(B) ସ୍ବିଡ଼ୋମିଟର
(C) ବାରୋମିଟର
(D) ଥର୍ମୋମିଟର
Answer:
(A) ଓଡ଼ୋମିଟର

11. ବସ୍ତୁର କ’ଣ ଏହାର ଜଡ଼ତ୍ଵର ମାପକ ଅଟେ ?
(A) ଓଜନ
(B) ବସ୍ତୁତ୍ଵ
(C) ବେଗ
(D) ତ୍ଵରଣ
Answer:
(B) ବସ୍ତୁତ୍ଵ

12. ନିର୍ଦ୍ଦିଷ୍ଟ ଦିଗରେ ବସ୍ତୁର ବେଗକୁ କ’ଣ କୁହାଯାଏ ?
(A) ପରିବେଗ
(B) ବିସ୍ଥାପନ
(C) ତ୍ଵରଣ
(D) ବଳ
Answer:
(A) ପରିବେଗ

13. କେଉଁଟି ଏକ ସଦିଶ ରାଶି ?
(A) ବେଗ
(B) ତ୍ଵରଣ
(C) ଦୂରତା
(D) ବସ୍ତୁତ୍ଵ
Answer:
(B) ତ୍ଵରଣ

14. ଗୋଟିଏ ଘଣ୍ଟାର ଘଣ୍ଟା କଣ୍ଟାର ବିସ୍ଥାପନ କେତେ ସମୟ ପରେ ଶୂନ ହେବ ?
(A) 12
(B) 24
(C) 1 ଘଣ୍ଟା
(D) 1 ମିନିଟ୍
Answer:
(A) 12

15. ବସ୍ତୁରେ ସୃଷ୍ଟି ହେଉଥ‌ିବା ତ୍ଵରଣ, କାହା ସହ
(A) ବସ୍ତୁତ୍ଵ
(B) ବଳ
(D) ସମୟ
(C) ବେଗ
Answer:
(A) ବସ୍ତୁତ୍ଵ

16. କେଉଁଟି ସର୍ବନିମ୍ନ ତ୍ଵରଣ ?
(A) 1 ସେ.ମି./ସେ²
(B) 1 ମି./ସେ²
(C) ମି. ମିନିଟ୍
(D) କି.ମି./ ଘଣ୍ଟା
Answer:
(D) କି.ମି./ ଘଣ୍ଟା

17. ଗୋଟିଏ ଗାଡ଼ିର ପରିବେଗ 10 m/s ହେଲେ ଏହା କି.ମି. ଘଣ୍ଟାରେ କେତେ ହେଁ ବି ?
(A) 36
(B) 72
(C) 18
(D) 24
Answer:
(A) 36

18. ସମବେଗରେ ବୃତ୍ତାକୃତି ପଥରେ ଘୂରୁଥୁବା ବସ୍ତୁ ପାଇଁ କେଉଁଟି ପ୍ରଯୁଜ୍ୟ ?
(A) ତ୍ଵରଣ ଅପରିବର୍ତ୍ତନୀୟ
(B) ତ୍ଵରଣ ପରିବର୍ତ୍ତନୀୟ
(C) ତ୍ଵରଣ ନାହିଁ
(D) ପରିବେଗ ନାହିଁ
Answer:
(A) ତ୍ଵରଣ ଅପରିବର୍ତ୍ତନୀୟ

19. ପରିବେଗ -ସମୟ ଆଲେଖ ଓ ସମୟ ଅକ୍ଷ ମଧ୍ୟରେ ଆବଦ୍ଧ କ୍ଷେତ୍ରଫଳ କ’ଣ ସୂଚାଇବ ?
(A) ଦୂରତା
(C) ପରିବେଗ
(B) ବେଗ
(D) ତ୍ଵରଣ
Answer:
(A) ଦୂରତା

20. R ବ୍ୟାସାର୍ଦ୍ଧ ବିଶିଷ୍ଟ ବୃତ୍ତାକାର ପଥରେ ଗୋଟିଏ ବସ୍ତୁ πR ଦୂରତା ଅତିକ୍ରମ କଲେ, ଏହାର ବିସ୍ଥାପନ କେତେ ହୋଇଥାଏ ?
(A) R
(B) 2R
(C) 2πr
(D) 0
Answer:
(B) 2R

21. ଗୋଟିଏ ବସ୍ତୁ ସମ ପରି ବେଗ ୨.୫ m/s ରେ ଗତିକଲେ, ଏହାର ତ୍ଵରଣ କେତେ ହୋଇଥାଏ ?
(A) 0
(B) 4.9 m/s²
(C) 9.8 m/s²
(D) 19.6 m/s²
Answer:
(C) 9.8 m/s²