Odisha State Board BSE Odisha 8th Class Maths Solutions Geometry Chapter 2 ତ୍ରିଭୁଜ Ex 2 Textbook Exercise Questions and Answers.
BSE Odisha Class 8 Maths Solutions Geometry Chapter 2 ତ୍ରିଭୁଜ Ex 2
Question 1.
ନିମ୍ନ ଉକ୍ତିଗୁଡ଼ିକ ଠିକ୍ ଥିଲେ କୋଠରି ମଧ୍ୟରେ ✓ ଚିହ୍ନ ଓ ଭୁଲ୍ ଥିଲେ × ଚିହ୍ନ ଦିଅ ।
(a) \(\overleftrightarrow{\mathrm{AB}}\), \(\overleftrightarrow{\mathrm{BC}}\), \(\overleftrightarrow{\mathrm{CA}}\) ପ୍ରତ୍ୟେକ ତ୍ରିଭୁଜ ABC ର ଗୋଟିଏ ଗୋଟିଏ ବାହୁ ।
(b) \(\overline{\mathrm{AB}})\), \(\overline{\mathrm{BC}})\) ଓ \(\overline{\mathrm{CA}})\) ରେଖାଖଣ୍ଡତ୍ରୟ ଦ୍ଵାରା △ABC ଗଠିତ ହୁଏ ।
(c) ତ୍ରିଭୁଜ ବିନ୍ଦୁମାନଙ୍କର ସେଟ୍ ।
(d) ଗୋଟିଏ ସ୍ଥୂଳକୋଣୀ ତ୍ରିଭୁଜରେ ଅତିବେଶୀରେ ଗୋଟିଏ ସ୍ଥୂଳକୋଣ ରହିବ ।
(e) △ABC ର ∠B ଓ ∠C କୁ A ଠାରେ ଥିବା ବହିଃସ୍ଥ କୋଣର ଅନ୍ତଃସ୍ଥ ଦୂରବର୍ତ୍ତୀ କୋଣ କୁହାଯାଏ |
(f) ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜରେ ଅତିବେଶୀରେ ଦୁଇଗୋଟି ସୂକ୍ଷ୍ମକୋଣ ରହିପାରିବ ।
(g) △ABC ରେ AB = AC ହେଲେ, ∠A ଓ ∠B ର ପରିମାଣଦ୍ଵୟ ସମାନ ହେବେ ।
(h) ତ୍ରିଭୁଜର ମଧ୍ଯମାତ୍ରୟର ଛେଦବିନ୍ଦୁ ସର୍ବଦା ତ୍ରିଭୁଜର ଅନ୍ତର୍ଦେଶରେ ଅବସ୍ଥାନ ନ କରିପାରନ୍ତି ।
(i) ତ୍ରିଭୁଜର ଦୁଇ କୋଣର ପରିମାଣର ସମଷ୍ଟି ସର୍ବଦା ତୃତୀୟ କୋଣର ପରିମାଣ ଠାରୁ ବୃହତ୍ତର ।
(j) ତ୍ରିଭୁଜର ଦୈର୍ଘ୍ୟର ବାହୁର ଦୈର୍ଘ୍ୟ ଅପେକ୍ଷା ବୃହତ୍ତର ।
(k) ତ୍ରିଭୁଜର ଦୁଇ ବାହୁର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟ ଅପେକ୍ଷା ବୃହତ୍ତର ।
(l) ଗୋଟିଏ ତ୍ରିଭୁଜର ଏକ ଶୀର୍ଷବିନ୍ଦୁରେ ଉତ୍ପନ୍ନ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ ସର୍ବଦା ଏହି ଶୀର୍ଷସ୍ଥ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣଠାରୁ ବୃହତ୍ତର ।
Solution:
(a) x
(b) x
(c) ✓
(d) ✓
(e) ✓
(f) ✓
(g) x
(h) x
(i) x
(j) x
(k) ✓
(1) x
![]()
Question 2.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(a) ଗୋଟିଏ ତ୍ରିଭୁଜର …….. ଗୋଟି ଶୀର୍ଷବିନ୍ଦୁ ଅଛି ।
(b) ଗୋଟିଏ ତ୍ରିଭୁଜର ମଧ୍ୟମା ସଂଖ୍ୟା ……………… |
(c) ଗୋଟିଏ ତ୍ରିଭୁଜର ବାହୁ ସଂଖ୍ୟା ……………… |
(d) ଗୋଟିଏ ସୂକ୍ଷ୍ମକୋଣୀ ତ୍ରିଭୁଜର କୌଣିକ ବିନ୍ଦୁରୁ ବିପରୀତ ବାହୁପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ ସଂଖ୍ୟା …………… |
(e) ଗୋଟିଏ ତ୍ରିଭୁଜର କୋଣ ସଂଖ୍ୟା ……………… |
Solution:
(a) 3
(b) 3
(c) 3
(d) 3
(e) 3
Question 3.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ର ଦେଖ୍ ସାରଣୀରେ ଥିବା ବିନ୍ଦୁର ଅବସ୍ଥାନ ଅନୁଯାୟୀ ଉପଯୁକ୍ତ କୋଠରିରେ ✓ ଚିହ୍ନ ଦିଅ ।
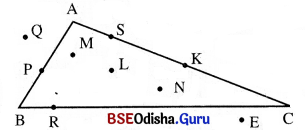
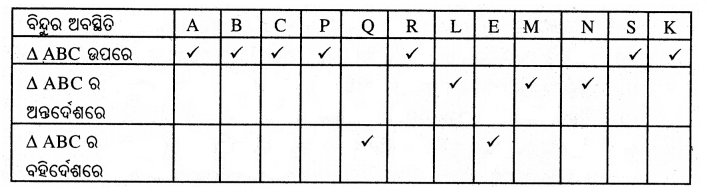
Question 4.
△ABC ର ବହିଃସ୍ଥ କୌଣମାନ ∠BAF, ∠CBD ଏବଂ ∠ACE | ଯଦି m∠BAF = 112° ଏବଂ m∠ABC = 53°; ତେବେ ଅନ୍ୟ ସମସ୍ତ କୋଣର ପରିମାଣ ସ୍ଥିର କର ।
Solution:
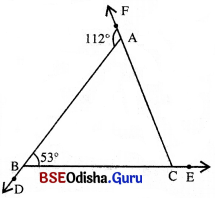
△ABC ର ବହିଃସ୍ଥ କୋଣମାନ ∠BAF, ∠CBD ଓ ∠ACE |
∴ m∠BAF = 112° ଓ m∠ABC = 53°
ବହିଃସ୍ଥ m∠BAF = m∠ABC + m∠ACB
⇒ 112° = 53° + m∠ACB ⇒ m∠ACB = 112° – 53° = 59°
m∠BAC = 180° – (m∠ABC + m∠ACB) = 180° – (53° + 59°) = 180° – 122° = 68°
ବହିଃସ୍ଥ m∠CBD = m∠BAC + m∠ACB = 68° + 59° = 127°
ବହିଃସ୍ଥ m∠ACE = m∠ABC + m∠BAC = 53° + 68° = 121°
Question 5.
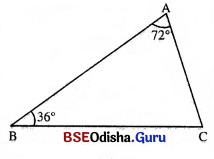
△ABC ର m∠A : = 72° ଓ m∠B = 36° ହେଲେ, ∠C ର ପରିମାଣ ସ୍ଥିର କର । △ABC କି ପ୍ରକାର ତ୍ରିଭୁଜ ? ଏହାର ଉତ୍ତର କାରଣ ସହ ଦର୍ଶାଅ ।
Solution:
△ABC ରେ m∠A = 72° ଓ m∠B = 36° (ଦତ୍ତ)
ଆମେ ଜାଣିଛୁ, ତ୍ରିଭୁଜର ତିନିକୋଣର ସମଷ୍ଟି 180° |
ଅର୍ଥାତ୍ m∠A + m∠B + m∠C = 180°
⇒ 72° + 36° + m∠C = 180° ⇒ 180° + m∠C = 180°
⇒ m∠C = 180° – 1o8° = 72°
m∠A = 72° ଓ m∠C = 72°
⇒ m∠A = m∠C ଅର୍ଥାତ୍ AB = BC
∴ △ABC ଏକ ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜ ।
କାରଣ, ସମଦ୍ବିବାହୁ ତ୍ରିଭୁଜର ଦୁଇଟି ବାହୁ ପରସ୍ପର ସମାନ ଓ ଏହାର ବିପରୀତ କୋଣ ଦ୍ଵୟ ସମାନ ।
Question 6.
△ABC ର ∠A ର ପରିମାଣ ∠B ର ପରିମାଣ ଅପେକ୍ଷା 10° ଅଧୂକ ଓ ∠B ର ପରିମାଣ ∠C ର ପରିମାଣ ଅପେକ୍ଷା 10° ଅଧିକ ହେଲେ, କୋଣତ୍ରୟର ପରିମାଣ ସ୍ଥିର କର ।
Solution:
ମନେକର △ABC ର ∠C ର ପରିମାଣ x° ।
∴ m∠B = x + 10°
ଓ m∠A = (x + 10°) + 10° = x + 20°
ଅଧୂକ ପରିମାଣ, m∠A + m∠B + m∠C = 180° (ନ୍ତିଜ୍ମକର ତିନିକୋଣର ସମୟି 180°)
⇒ x° + 20° + x° + 10° + x° = 180° ⇒ 3x° + 30° = 180°
⇒ 3x° = 180° – 30° = 150° ⇒ x° = \(\frac { 150° }{ 3 }\) = 50°
∠C ର ପରିମାଣ = 50°, ∠B ର ପରିମାଣ = x° + 10° = 50° + 10° = 60°
ଏବଂ ∠A ର ପରିମାଣ = x + 20° = 50° + 20° = 70°
![]()
Question 7.
△ABC ରେ m∠B = 90° ହେଲେ, ନସମ୍ ପ୍ରଣଗୁଡିକର ଉତ୍ତର ଦିଅ |
(i) m∠A + m∠C କେତେ ?
(ii) AB = BC ହେଲେ, m∠A କେତେ ?
(iii) m∠C = 30° ହେଲେ, m∠A କେତେ ?
(iv) B ବିନ୍ଦୁରେ △ABC ର ବହୁସ୍ଥ କୋଣର ପରିମାଣ କେତେ ?
(v) m∠A = 45° ହେଲେ, △ABC ର କେଉ ଭୁଲ ବାଦୁଇ ଦେଶ୍ୟ ସାମାନ ଦେବେ ?
Solution:
(i) m∠A + m∠C = (180° – m∠B)
(∵ ତ୍ରିଭୁକର ତିନିକୋଣର ସମଷ୍ଟି 180°)
⇒ m∠A + m∠C = 180° – 90° = 90°
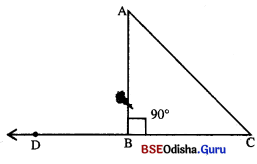
(ii) △ABC ରେ AB = AC ହେଲେ, m∠A = m∠C
(i) ରୁ କଣାଅଛି ଯେ, m∠A + m∠C = 90°
⇒ m∠A = m∠C = \(\frac { 90° }{ 2 }\) = 45°
∴ m∠A = 45°
∴ AB = AC ହେଲେ, m∠A = 45° |
(iii) m∠A + m∠C = 90°
⇒ m∠A + 30° = 90° [∵ m∠C = 30° (ଦୁଇ)
⇒ m∠A = 90° – 30° = 60°
∴ m∠C = 30° ହେଲେ, m∠A = 90° |
(iv) B ଦିନ୍ଦୁରେ △ABC ର ଦହିମ କୋଣର ପରିମାଣ = m∠ABD = m∠A + m∠C = 90°
(v) ଆପେ (ii) ରୁ କାଣିଛି ମେ m∠A = 45° ଓ m∠C = 45°
ଆଧ୍ୟାତ୍ m∠A = m∠C
⇒ BC = AB
∴ m∠A = 45° ହେଲେ, △ABC ରୁ AB ଓ BC ବାହୁର ଦେଶ୍ୟ ସମାନ ଦେବ |
Question 8.
ABC ସମକୋଣା ତ୍ରିଭୁଜରେ m∠B = 90°, ∠A ରୁ ପରିମାଣର 5 ଗୁଣ ହେଲେ, କୋଣଦ୍ୱୟର ପରିମାଣ ସ୍ଥିର କର ।
Solution:
ABC ସମକୋଣା ତ୍ରିଭୁଜରେ m∠B = 90° ହେଲେ,
m∠A +m∠C = 90° [∵ m∠A + m∠B + m∠C = 180°]
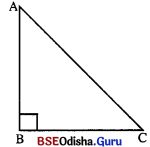
ମନେକର ∠C ର ପରିମାଣ x |
ତେବେ ∠A ର ପରିମାଣ 5x |
m∠A+m∠C = 90°
⇒ 5x + x = 90° ⇒ 6x = 90° ⇒ x = \(\frac { 90° }{ 6 }\) = 15° = 5x = 15° × 5 = 75°
∴ ABC ସମକୋଣୀ ତ୍ରିଭୁଜର ∠A ର ପରିମାଣ 75° ଓ ∠C ର ପରିମାଣ 15° |
Question 9.
△ABC ର m∠A = 48° ଓ m∠B = 110° ହେଲେ, ନିମ୍ନମ୍ ରକ୍ତଶ୍ନତିକରେ ଥିବା ଶୂନ୍ୟମାନ ପୂରଣ କର |
(a) ଶାପଦିନ୍ଦ ________ ରେ ଥିବା ବହିଃସ୍ଥ କୋଣ ଏକ ସୂକ୍ଷ୍ମକୋଣ ।
(b) ଶୀର୍ଷବିନ୍ଦୁ A ଠାରେ ଥିବା ବହିଃସ୍ଥ କୋଣର ପରିମାଣ ________ |
(c) Bଠାରେ ଥିବା ବହିଃସ୍ଥ କୋଣର ପରିମାଣ ________ |
(d) Cଠାରେ ଥିବା ବହିଃସ୍ଥ କୋଣର ପରିମାଣ ________ |
Solution:
(a) B
(b) 132°
(c) 70°
(d) 158°
[m∠C = 180° – (m∠A + m∠B) = 180° – (48° + 110°) = 22°
∴ A ଠାରେ ଥିବା ବହିଃସ୍ଥ କୋଣର ପରିମାଣ = m∠B + m∠C, ସେହିପରି B ଠାରେ ଥିବା ବହିଃସ୍ଥ କୋଣର ପରିମାଣ = m∠A + m∠C ଏବଂ C ଠାରେ ଥିବା ବହିଃସ୍ଥ କୋଣର ପରିମାଣ = m∠A + m∠B]
![]()
Question 10.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ \(\overline{\mathrm{AD}})\) ⊥ \(\overline{\mathrm{BC}})\), AD = BD ଓ m∠DAC ହେଲେ, 1, 2, 3 ଚିହ୍ନିତ କୋଣମାନଙ୍କର ପରିମାଣ ସ୍ଥିର କର ।
Solution:
△ABC ରେ AD ⊥BC ହେଲେ m∠ADC = 90° |
ବହିଃସ୍ଥ m∠ADC = m∠BAD + m∠ABD
⇒ 90° = m∠BAD + m∠ABD
ପୁନଶ୍ଚ, AD = BD (ଦତ୍ତ)
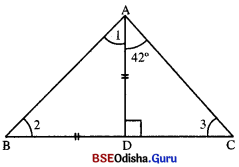
⇒ m∠BAD = m∠ABD
(∵ △ ର ଦୁଇଟି କୋଣର ପରିମାଣ ସମାନ ହେଲେ ଏହି କୋଣଦ୍ଵୟର ସମ୍ମୁଖୀନ ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ସମାନ)
କିନ୍ତୁ ∠1 + ∠2 = 90° ଏବଂ ∠1 = ∠2 ହେଲେ ∠1 = ∠2 = \(\frac { 90° }{ 2 }\) = 45°
ADC ସମକୋଣୀ △ ରେ m∠ADC = 90° ହେଲେ
m∠DAC + m∠ACD = 90°
⇒ 42° + ∠3 = 90° [∵ m∠DAC = 42° (ଦତ୍ତ)]
⇒ ∠3 = 90° – 42° = 48°
∴ ∠1 = 45°, ∠2 = 45° ଓ ∠3 = 48° |
Question 11.
△ABC ଚିତ୍ରରେ AB = AC ହେଲେ, ଦର୍ଶାଅ ଯେ, B ଓ C ବିନ୍ଦୁରେ ଉତ୍ପନ୍ନ ବହିଃସ୍ଥ କୌଣଦ୍ୱୟର ପରିମାଣ ସମାନ ।
Solution:
ଦତ୍ତ : △ABC ରେ AB = AC | △ABC ର B ଓ C ବିନ୍ଦୁରେ ଉତ୍ପନ୍ନ ବହିଃସ୍ଥ କୌଣଦ୍ଵୟ ଯଥାକ୍ରମେ ∠ABD ଓ ∠ACE |
ପ୍ରାମାଣ୍ୟ m∠ABD = m∠ACE
ପ୍ରମାଣ: AB = AC (ଦତ୍ତ)
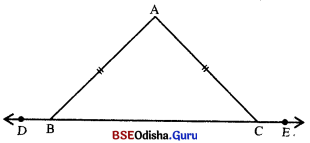
ଆମେ ଜାଣିଛେ, ଧ ର ଦୁଇଟି ବାହୁର ଦୈର୍ଘ୍ୟ ସମାନ ହେଲେ, ଏହି ବାହୁଦ୍ୱୟର ସମ୍ମୁଖୀନ କୋଣଦ୍ୱୟର ପରିମାଣ ସମାନ ।
ଆଥାତ୍, m∠ABC = m∠ACB
m∠ABD + m∠ABC = 180° (ସନ୍ନିହିତ ପରିପୂରକ କୋଣ)
ସେହିପରି m∠ACE + m∠ACB = 180° (ସନ୍ନିହିତ ପରିପୂରକ କୋଣ)
(1) ଓ (2) ରୁ m∠ABD + m∠ABC = m∠ACE + m∠ACB
ମାତ୍ର m∠ABC + m∠ACB
⇒ m∠ABD + m∠ACE
Question 12.
ଗୋଟିଏ ତ୍ରିଭୁଜର ଏକ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ 120° ଏବଂ ତାହାର ଅନ୍ତଃସ୍ଥ ଦୂରବର୍ତ୍ତୀ କୋଣଦ୍ଵୟ ମଧ୍ୟରୁ ଗୋଟିକର ପରିମାଣ 70° ହେଲେ, ଅନ୍ୟ ଅନ୍ତଃସ୍ଥ ଦୂରବର୍ତ୍ତୀ କୋଣଟିର ପରିମାଣ କେତେ ?
Solution:
ଗୋଟିଏ ତ୍ରିଭୁଜର ଏକ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ 120° |
ଅନ୍ତଃସ୍ଥ ଦୂରବର୍ତ୍ତୀ କୋଣଦ୍ଵୟ ମଧ୍ୟରୁ ଗୋଟିକର ପରିମାଣ 70° ହେଲେ ଅନ୍ୟ ଅନ୍ତଃସ୍ଥ ଦୂରବର୍ତ୍ତୀ କୋଣଟିର ପରିମାଣ = 120° – 70° = 50° |
Question 13.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ଦର୍ଶାଅ ଯେ,
AB+ BC + CD + AD > 2AC
Solution:
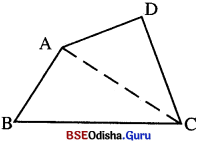
ଦତ୍ତ: ଦତ୍ତ ଚିତ୍ରରେ △ABC ଓ △ACD ଦୁଇଟି ତ୍ରିଭୁଜ ।
ପ୍ରାମାଣ୍ୟ: AB + BC + CD + AD > 2AC
ଅଙ୍କନ: AC ଯୋଗ କର ।
ପ୍ରମାଣ:ଆମେ ଜାଣିଛେ, ଏକ ତ୍ରିଭୁଜର ଯେ କୌଣସି ଦୁଇ ବାହୁର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି ଏହାର ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟଠାରୁ ଦୁଦ୍ରରର |
△ABC ରେ, AB + BC > AC …(i)
କୋଣଟିର △ACD ରେ, AD + CD > AC …(ii)
(i) ଓ (ii) କୁ ଯୋଗକଲେ,
AB + BC + AD + CD > AC + AC
AB + BC + CD + AD > 2AC (ପ୍ରମାଣିତ)
Question 14.
ଗୋଟିଏ ତ୍ରିଭୁଜର ତିନିକୋଣ ମଧ୍ୟରୁ ଗୋଟିକର ପରିମାଣ, କ୍ଷୁଦ୍ରତମ କୋଣର ପରିମାଣର ଦୁଇଗୁଣ ଏବଂ ଅନ୍ୟଟିର ପରିମାଣ, ପୁତ୍ରତମ କୋଣର ପରିମାଣର ତିନିଗୁଣ ହେଲେ, ବୃହତମ କୋଣର ପରିମାଣ କର ।
Solution:
ମନେକର △ABC ରେ ∠A କ୍ଷୁଦ୍ରତମ କୋଣ |
ପ୍ରଶ୍ନନୁସାରେ, m∠B = 2m∠A ଓ m∠C = 3m∠A
ଆମେ ଜାଣିଲେ ଯେ,
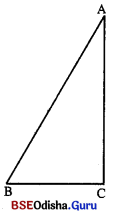
m∠A +m∠B + m∠C = 180°
(∵ △ର ତିନିକୋଣ ପରିମାଣର କୋଣ 180°)
⇒ m∠A + 2m∠A + 3m∠A = 180°
⇒ 6m∠A = 180° ⇒ m∠A = \(\frac { 180° }{ 6 }\) = 30°
∴ ବୃହତମ କୋଣର ପରିମାଣ = m∠C = 3m∠A = 3 × 30° = 90°
![]()
Question 15.
ଚିତ୍ର (i), (ii) (iii) ରେ ଥିବା ପାଣସ୍ଥ ଚିତ୍ରମାନକରେ x ଚିହ୍ନିତ କୋଣର ପରିମାଣ ମିଳ କର |
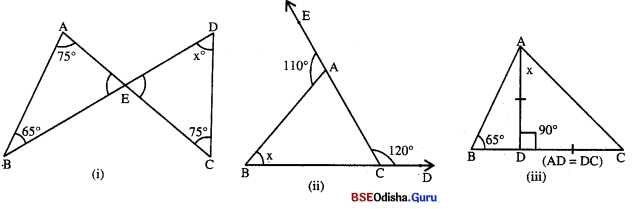
Solution:
ଚିତ୍ର (i) △ABE ରେ ପାଣସ୍ଥ m∠AED = m∠BAE + m∠ABE = 75° + 65° = 140°
△CED ରେ ପାଣସ୍ଥ m∠DEA = m∠EDC + m∠ECD = x° + 75°
⇒ 140° = x° + 75° ⇒ x = 140° – 75° = 65°
ଚିତ୍ର (ii) m∠ACB + m∠ACD = 180°
⇒ m∠ACB + 120° = 180°
⇒ m∠ACB = 180° – 120° = 60°
△ABC ରେ ପାଣସ୍ଥ m∠EAB = m∠ABC + m∠ACB
⇒ 110° = x + 60°
⇒ x = 110° – 60° = 50°
ଚିତ୍ର (iii) △ABC ରେ AD ⊥ BC | ଆଥାତ୍, m∠ADB = m∠ADC = 90°
△ABD ରେ, m∠ADB + m∠BAD = 90°
⇒ 65° + m∠BAD = 90°
⇒ m∠BAD = 90° – 65° = 25°
△ADC ରେ, AD = DC (ଦତ୍ତ)
⇒ m∠ACD = m∠CAD
△ADC ରେ, m∠ADC + m∠CAD + m∠ACD = 180°
⇒ 90° + m∠CAD + m∠ACD = 180°
⇒ m∠CAD + m∠ACD = 180° – 90° = 90°
∴ m∠CAD = m∠ACD = \(\frac { 90° }{ 2 }\) = 45°
⇒ m∠CAD = 45°
∴ x = m∠BAD + m∠DAC = 25° + 45° = 70°
Question 16.
ଗୋଟିଏ ତ୍ରିଭୁଜର କୋଣତ୍ରୟର ପରିମାଣର ଅନୁପାତ 2 : 3 : 4 ହେଲେ, ସେମାନଙ୍କର ପରିମାଣ ସ୍ଥିର କର ।
Solution:
ମନେକର ର କୋଣପ୍ରୟର ପରିମାଣ ଯଥାକ୍ରମେ 2x, 3x ଓ 4x |
ଆମେ ଜାଣିଛ, ତ୍ରିକୁକର କୋଣତ୍ରୟ ପରିମାଣର ଗମନ 180° |
⇒ 2x + 3x + 4x = 180°
⇒ 9x = 180° ⇒ x = \(\frac { 180° }{ 9 }\) = 20°
⇒ 2x = 2 × 20° = 40°, 3x = 3 × 20 = 60°
ଓ 4x = 4 × 20 = 80°
∴ ତ୍ରିକୁକର କୋଣତ୍ରୟ ପରିମାଣ ପରିମାଣର 40°, 60° ଓ 80° |
Question 17.
△ABC ରେ m∠A + m∠B = 125° ଏବଂ m∠A + m∠C = 113° ହେଲେ, ପ୍ତିକୁକାର କୋଣପ୍ରୟତ ପରିପାଣ ମିଳ କାର |
Solution:
△ABC ରେ ଦଇ ଅଛି ଯେ, m∠A + m∠B = 125° …(i)
ଏବଂ m∠A + m∠C = 113° …(ii)
(i) ଓ (ii) କ୍ମ ଯୋଗକଲେ, m∠A + m∠B + m∠A + m∠C = 125° + 113°
⇒ (m∠A + m∠B + m∠C) + m∠A = 238°
⇒ 180° + m∠A = 238° (∵ △ ର ତିନିକୋଣର ସମୟ 180°)
⇒m∠A = 238° – 180° = 58°
(i) ରୁ m∠A + m∠B = 125°
⇒ 58°+m∠B = 125° (∵ m∠A = 58°)
⇒ m∠B = 125° – 58° = 67°
(ii) ରୁ m∠A + m∠C = 113°
⇒ 58° + m∠C = 113° (∵ m∠A= 58°)
⇒m∠C 113° – 58° = 55°
∴△ABC ର m∠A = 58°, m∠B = 67° ଓ m∠C= 55° |
Question 18.
△ABC ରେ ଯଦି 2m∠A = 3m∠B = 6m∠C ହଏ, ତେବେ କୋଣତ୍ରୟର ପରିମାଣ ସ୍ଥିର କର |
Solution:
ବାର ଅଛି ଯେ, △ABC ରେ
2m∠A = 3m∠B = 6m∠C
2m∠A = 3m∠B
m∠A : m∠B = 3 : 2
ସେତ୍ତିପରି 3 m∠B = 6m∠C
⇒ m∠B : m∠C = 6 : 3 = 2 : 1
∴ m∠A : m∠B : m∠C = 3 : 2 : 1
ପରିମାଣ, m∠A = 3x°, m∠B = 2x° ଏବଂ m∠C = x°
ଆମେ ଜାଣିଲେ, m∠A + m∠B + m∠C = 180°
3x° + 2x° + 3x° = 180°
⇒ 6x = 180° ⇒ x = 30°
∴ m∠A = 3 × 30° = 90°, m∠B = 2x = 2 × 30° = 60°
ଏବଂ m∠C = x° = 30°
![]()
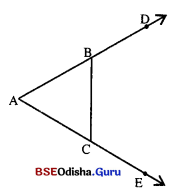
Question 19.
ପାଣଣ୍ଠ ଚିତ୍ରରେ ଦେଖାଅ ଯେ ,
m∠DBC + m∠BCE > 2m∠A
Solution:
ଦଇ: △ABC ରେ m∠DBC ଓ m∠BCE ଦୁଇଟି ବହୁମୁ କୋଣ |
ପ୍ରାମାଣ୍ୟ: m∠DBC + m∠BCE > 2m∠A
ପ୍ରମାଣ : △ABC ରେ ଦସ୍ତସ୍ଥ m∠DBC > m∠A …(i)
ସେହିପରି ବହୁଣ୍ଠ m∠DBC > m∠A …(ii)
(i) ଓ (ii) ରୁ ପାଇବା m∠DBC + m∠BCE > 2m∠A
(∵ ବହ୍ରୁମ କୋଣର ପରିମାଣ ପ୍ରତ୍ୟେକ ଅନ୍ତରମ କୋଣର ପରିମାଣଠାରୁ ବହୁତର |)
Question 20.
△ABC m∠A = m∠B + m∠C ଏବଂ m∠B = 2m∠C ହେଲେ, କୋଣତ୍ରୟର ପରିମାଣ ସ୍ଥିର କର ।
Solution:
ଦତ୍ତ ଅଛି ଯେ, △ABC ରେ m∠A = m∠B + m∠C
⇒ m∠A + m∠A = m∠A + m∠B + m∠C (ଉଭୟ ପାର୍ଶ୍ଵରେ m∠A ଯୋଗକଲେ) (∵ ଧର ତିନିକୋଣର ପରିମାଣର ସମଷ୍ଟି 180°)
⇒ 2m∠A = 180° (∵ △ର ତିନିକୋଣର ପରିମାଣର ସମଷ୍ଟି 180°)
m∠A = \(\frac { 180° }{ 2 }\) = 90°
∴ m∠B + m∠C = 180° – m∠A 180° – 90° = 90°
∴ m∠B + m∠C = 90°
⇒ 2m∠C + m∠C = 90°
⇒ 3m∠C = 90° ⇒ m∠C = \(\frac { 90° }{ 3 }\) = 30°
∴ m∠B = 2 × m∠C = 2 × 30° = 60°
