BSE Odisha 9th Class Maths Notes Algebra Chapter 5 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି

Odisha State Board BSE Odisha 9th Class Maths Notes Algebra Chapter 5 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି will enable students to study smartly.

BSE Odisha Class 9 Maths Notes Algebra Chapter 5 ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି

ବିଷୟବସ୍ତୁ ସମ୍ବନ୍ଧୀୟ ସୂଚନା ଓ ବିଶ୍ଳେଷଣ

ଉପକ୍ରମଣିକା (Introduction) :

1. ଏକ ସମତଳରେ ବା ଶୂନ୍ୟରେ ଏକ ବିନ୍ଦୁର ଚିହ୍ନଟିକରଣ ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି (Co-ordinate Geometry)ର ଉଦ୍ଭାବନ ପରେ ସମ୍ଭବ ହୋଇପାରିଛି ।
2. ପ୍ରାଚୀନ କାଳରେ ମିଶରର ସର୍ବେକ୍ଷକ ଓ ପରବର୍ତ୍ତୀ କାଳରେ ରୋମାନ୍ ସର୍ବେକ୍ଷକମାନେ ନଗର ଓ ଜମିର ଅବସ୍ଥିତି ସୂଚାଇବାକୁ ମୋଟାମୋଟି ଭାବେ ଆଜିକାଲିର ସ୍ଥାନଙ୍କ ପଦ୍ଧତି ଅବଲମ୍ବନ କରୁଥିଲେ । ନଗରମାନଙ୍କର ଅବସ୍ଥିତି ନିର୍ଣ୍ଣୟ ପାଇଁ ରୋମାନ୍‌ମାନେ ସମକୋଣରେ ଛେଦ କରୁଥ‌ିବା ଦୁଇଟି ଅକ୍ଷ ନେଇଥିଲେ ।
3. ପରବର୍ତ୍ତୀ କାଳରେ ଗ୍ରୀକ୍‌ମାନେ ମଧ୍ୟ ଠିକ୍ ଏହି ପଦ୍ଧତିରେ ସ୍ଥାନର ଅବସ୍ଥିତି ନିର୍ଣ୍ଣୟ କରୁଥିଲେ ।
4. ମଧ୍ୟଯୁଗରେ ନିକୋଲ ଓରେସମେ (1360 ଖ୍ରୀଷ୍ଟାବ୍ଦ) ପ୍ରଥମ କରି ଧନାତ୍ମକ ଭୁଜ ଓ କୋଟିର ଧାରଣା ଦେଇଥିଲେ । ପ୍ରକୃତପକ୍ଷେ ଏହି ସମୟରୁ ହିଁ ସର୍ବପ୍ରଥମେ ବିନ୍ଦୁର ସ୍ଥାନଙ୍କର ବ୍ୟବହାର ଦେଖିବାକୁ ମିଳେ ।
5. ପ୍ରାୟ 2500 ବର୍ଷ ତଳର Euclidean Geometry ଏବେ ଗଣିତ ଶିକ୍ଷାରେ ଏକ ପ୍ରଧାନ ଅଙ୍ଗ ଭାବେ ପରିଗଣିତ
6. Euclidean Geometry ଓ Algebra ସମ୍ପୂର୍ଣ ପୃଥକ୍ ବିଷୟ; ମାତ୍ର ସପ୍ତଦଶ ଶତାବ୍ଦୀରେ ଫରାସୀ ଗଣିତଜ୍ଞ Rene Descartes (1596-1650)ଙ୍କଦ୍ଵାରା ପ୍ରଦତ୍ତ ଏକ ନୂତନ ଧାରଣାକୁ ଆଧାର କରି ସ୍ଥାନଙ୍କ ଜ୍ୟାମିତି ବା ବିଶ୍ଳେଷଣାତ୍ମକ ଜ୍ୟାମିତି (Analytical Geometry) ଜନ୍ମ ଲାଭ କଲା ଓ ଏଥ‌ିରେ ଜ୍ୟାମିତିକ ଚର୍ଚ୍ଚାରେ ବୀଜଗଣିତ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ଭୂମିକା ଲାଭ କଲା ।
7. ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତି ଉପରେ Rene Descartesଙ୍କଦ୍ୱାରା ପ୍ରସ୍ତୁତ ପ୍ରଥମ ପୁସ୍ତକ 1637ରେ ପ୍ରକାଶ ଲାଭ କରିଥିଲା । 
8. ସ୍ଥାନାଙ୍କ ଜ୍ୟାମିତିର ମୁଖ୍ୟ ସୋପାନ ହେଲା, ସମତଳରେ ଦୁଇଟି ପରସ୍ପରଛେଦୀ ସରଳରେଖା (ସଂଖ୍ୟାରେଖା) ନେଇ ଗୋଟିଏ ବିନ୍ଦୁକୁ ଦୁଇଟି ସଂଖ୍ୟାର କ୍ରମିତ ଯୋଡ଼ି (Ordered pair)ରୂପେ ନେଇ ଚିହ୍ନିତ କରିବା ଏବଂ ସେହିପରି ଶୂନ୍ୟରେ ଥ‌ିବା କୌଣସି ବିନ୍ଦୁକୁ ଏକ ସଂଖ୍ଯାତ୍ରୟୀ (Ordered triad) ମାଧ୍ୟମରେ ଚିହ୍ନଟ କରିବା ।

ସମତଳରେ ବିନ୍ଦୁ (Points on a Plane) :
(i) ସରଳରେଖା ଏକ ମାତ୍ରା (Que Dimension) ବିଶିଷ୍ଟ । ସୁତରାଂ ଏହା ଉପରିସ୍ଥ ବିନ୍ଦୁକୁ ସୂଚାଇବା ପାଇଁ କେବଳ ଗୋଟିଏ ମାତ୍ର ବାସ୍ତବ ସଂଖ୍ୟା ଯଥେଷ୍ଟ । ସରଳରେଖା ଉପରିସ୍ଥ ଯେକୌଣସି ବିନ୍ଦୁକୁ ସୂଚାଉଥ‌ିବା ବାସ୍ତବ ସଂଖ୍ୟାଟିକୁ ଉକ୍ତ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (Coordinate) କୁହାଯାଏ ।
(ii)

(iii) ସମତଳ ଦୁଇ ମାତ୍ରା ବିଶିଷ୍ଠ । ସମତଳ ଉପରେ ଅବସ୍ଥିତ ବିନ୍ଦୁ Pର ଅବସ୍ଥିତିକୁ ଚିହ୍ନଟ କରିବା ପାଇଁ ପରସ୍ପର ଲମ୍ବ ଭାବେ ଥବା ଦୁଇଟି ସଂଖ୍ୟାରେଖା \(\overleftrightarrow{X^{\prime} \mathrm{X}}\) ଓ \(\overleftrightarrow{Y^{\prime} \mathrm{Y}}\) ନିଆଯାଏ । \(\overleftrightarrow{X^{\prime} \mathrm{X}}\) କୁ x- ଅକ୍ଷ ଓ \(\overleftrightarrow{Y^{\prime} \mathrm{Y}}\) କୁ y – ଅକ୍ଷ କୁହାଯାଏ ।
(iv) ଅକ୍ଷଦ୍ବୟ ପରସ୍ପରକୁ ୦ ବିନ୍ଦୁରେ ସମକୋଣରେ ଛେଦ କରନ୍ତୁ । \(\overrightarrow{\mathrm{OX}}\) ଓ \(\overrightarrow{\mathrm{ox}^{\prime}}\) ଯଥାକ୍ରମେ x-ଅକ୍ଷର ଧନଦିଗ ଓ ଋଣ ଦିଗ ଏବଂ \(\overrightarrow{\mathrm{OY}}\) ଓ \(\overrightarrow{\mathrm{oy}^{\prime}}\) ଯଥାକ୍ରମେ y-ଅକ୍ଷର ଧନ ଦିଗ ଓ ଋଣ ଦିଗ ଅଟନ୍ତି। O ବିନ୍ଦୁଟିକୁ ମୂଳବିନ୍ଦୁ (origin) କୁହାଯାଏ ।
(v) ସାଧାରଣତଃ x-ଅକ୍ଷ ଆନୁଭୂମିକ (Horizontal) ଓ y-ଅକ୍ଷ ଉଲ୍ଲମ୍ବ (Vertical) ଭାବେ ଅଙ୍କନ କରାଯାଏ । 
(vi) x – ଓ y – ଅକ୍ଷକୁ ଆୟତୀୟ ଅକ୍ଷ (Rectangular axes) ଏବଂ ସମତଳସ୍ଥ ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କକୁ ଆୟତୀୟ ସ୍ଥାନାଙ୍କ (Rectangular co-ordinate) କୁହାଯାଏ; କାରଣ ଅକ୍ଷଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ଛେଦ କରନ୍ତି । 
(vii) ମନେକର P ସମତଳ ଉପରିସ୍ଥ ଏକ ବିନ୍ଦୁ । P ବିନ୍ଦୁରୁ x – ଓ y- ଅକ୍ଷପ୍ରତି ଅଙ୍କିତ ଲମ୍ବ x – ଓ y ଅକ୍ଷକୁ ଯଥାକ୍ରମେ M ଓ N ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତୁ ।

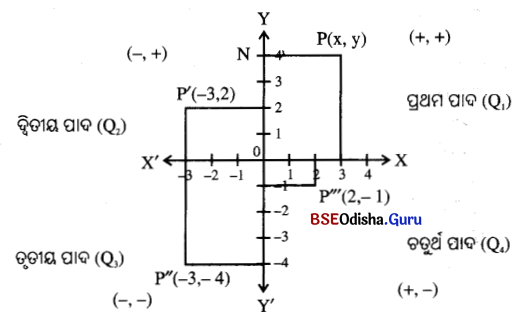
(viii) M ଓ N ବିନ୍ଦୁର x – ଓ y – ଅକ୍ଷ ଉପରେ ସୂଚକ ସଂଖ୍ୟା ଦ୍ଵୟ ଯଥାକ୍ରମେ x ଓ y ହେଲେ P ବିନ୍ଦୁକୁ ଚିହ୍ନଟ କରୁଥିବା ସଂଖ୍ୟା ଦ୍ଵୟକୁ କ୍ରମିତ ଯୋଡ଼ି (x, y) ଭାବେ ଲେଖାଯାଏ । (x, y) କ୍ରମିତ ଯୋଡ଼ିକୁ P ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (coordinates) କୁହାଯାଏ । x କୁ x- ସ୍ଥାନଙ୍କ ବା ଭୁଜ (abscissa) ଓ y କୁ y- ସ୍ଥାନଙ୍କ ବା କୋଟି (ordinate) କୁହାଯାଏ ।
(ix) P ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (x, y) କୁ ମଧ୍ଯ P(x, y) ରୂପେ ଲେଖାଯାଏ । ଚିତ୍ରରେ Pର ସ୍ଥାନାଙ୍କ (3, 4), P’ ବିନ୍ଦୁଟିର ସ୍ଥାନାଙ୍କ (-3, 2), P” ର ସ୍ଥାନାଙ୍କ (-3, -4) ଓ P”’ ର ସ୍ଥାନାଙ୍କ (2, -1) 
(x) x ଓ y – ଅକ୍ଷଦ୍ବୟ ଦ୍ୱାରା ସମତଳଟି ଚାରିଗୋଟି ପାଦ (Quadrant)ରେ ବିଭାଜିତ ହୁଏ । ଚାରିଗୋଟି ପାଦକୁ Q₁, Q₂, Q₃, ଓ Q₄ କୁହାଯାଏ ।

• {ପ୍ରଥମ ପାଦ (Q₁)ରେ x > 0, y > 0, ଦ୍ଵିତୀୟ ପାଦ (Q₂)ରେ x < 0, y > 0
  ତୃତୀୟ ପାଦ (Q₃)ରେ x < 0, y < 0, ଦ୍ଵିତୀୟ ପାଦ (Q₄)ରେ x > 0, y < 0}
• {Q₁ = {(x, y) : x > 0, y > 0}, Q₂ = {(x, y) : x < 0, y > 0 }
  Q₃ = {(x, y) : x < 0, y < 0 } ଓ Q₄ = {(x, y) : x > 0, y < 0}}

ଅକ୍ଷଉପରିସ୍ଥ ବିନ୍ଦୁର ସ୍ଥାନଙ୍କ (Coordinate of points on axes):
(i) x- ଅକ୍ଷ ଉପରିସ୍ଥ ଯେକୌଣସି ବିନ୍ଦୁର y- ସ୍ଥାନଙ୍କ ଶୂନ ଏବଂ x ∈ R 
ଏପରି ସମସ୍ତ ବିନ୍ଦୁମାନଙ୍କର ସେଟ୍ x-ଅକ୍ଷ ଅଟେ ।
∴ x ଅକ୍ଷ = {(x, y) | x ∈ R, y = 0} ଅଥବା x-ଅକ୍ଷ = {(x, 0); x ∈ R}
(ii) y-ଅକ୍ଷ ଉପରିସ୍ଥ ଯେକୌଣସି ବିନ୍ଦୁରେ x-ସ୍ଥାନାଙ୍କ ଶୂନ ଏବଂ y ∈ R 
ଏପରି ସମସ୍ତ ବିନ୍ଦୁମାନଙ୍କର ସେଟ୍ y- ଅକ୍ଷ ଅଟେ ।
∴ y ଅକ୍ଷ = {(x, y) | x = 0, y ∈ R} ଅଥବା y- ଅକ୍ଷ = {(0, y) | y ∈ R)}
(iii) ମୂଳବିଦୁର ସ୍ଥାନାଙ୍କ (0, 0) (ଅକ୍ଷଦ୍ବୟର ଛେଦବିନ୍ଦୁ) ।
⇒ {Q₁ ∪ Q₂ ∪ Q₃ ∪ Q₄ ∪ {(x, 0) : x ∈ R} ∪ {(0, y) : y ∈ R} = R² ଅଥବା R × R}

xy- ସମତଳ (xy – plane) :

• ଯେଉଁ ସମତଳରେ x-ଅକ୍ଷ ଓ y-ଅକ୍ଷ ଅଙ୍କନ କରି ବିନ୍ଦୁମାନଙ୍କୁ (x ଓ y) ସ୍ଥାନାଙ୍କଦ୍ୱାରା ସୂଚିତ କରାଯାଏ, ସେହି ସମତଳକୁ xy-ସମତଳ କୁହାଯାଏ । xy-ସମତଳର ସମସ୍ତ ବିନ୍ଦୁମାନଙ୍କ ସେଟ୍‌ଟି R × R = R² = {(x, y) | x, y ∈ R}, ଯେଉଁଠାରେ R × R କାର୍ଟେଜୀୟ ଗୁଣନ ସେଟ୍ । xy -ସମତଳଟିକୁ ମଧ୍ଯ କାର୍ଟେଜୀୟ ସମତଳ (Cartesian plane) ବା R²-ସମତଳ କୁହାଯାଏ ।
• x- ଅକ୍ଷ ଓ y- ଅକ୍ଷ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ନିଆଯାଇଥିବା ହେତୁ ସମତଳ ଉପରିସ୍ଥ ବିନ୍ଦୁର ସ୍ଥାନଙ୍କ (x, y) କୁ ମଧ୍ୟ ଆୟତୀୟ ସ୍ଥାନଙ୍କ (rectangular coordinates) କୁହାଯାଏ ।

ଅର୍ଥ ସମତଳ (Half plane) :
(i) x- ଅକ୍ଷ ଦ୍ଵାରା xy- ସମଚଳଟି ଦୁଇଟି ଅର୍ଥ ସମତଳ ଅର୍ଥାତ୍ Q₁ ∪ Q₂, (ଉର୍ଦ୍ଧ୍ଵ ଅର୍ଥ ସମତଳ) ଏବଂ Q₃ ∪ Q₂ (ଅଧଃ ଅର୍ଥ ସମତଳ)ରେ ବିଭକ୍ତ ହୋଇଥାଏ ।
⇒ x- ଅକ୍ଷ = {(x, 0) : x ∈ R}
⇒ y- ଅକ୍ଷ = {(0, y) : y ∈ R}
(ii) ସେହିପରି y – ଅକ୍ଷ, xy ସମତଳକୁ ଦୁଇଟି ଅର୍ଥ ସମତଳ ଯଥା : ଦକ୍ଷିଣ ଅର୍ଥ ସମତଳ = {(x, y) : x > 0, y ∈ R} ଅଥବା Q₁ ∪ Q₄, ଓ ବାମ ଅର୍ଷ ସମତଳ = {(x, y): x < 0,∈ R} ଅଥବା Q₂ ∪ Q₃ ରେ ବିଭାଜିତ କରିଥାଏ । 

ସରଳରେଖାର ସମୀକରଣ (Equation of a line):
(i) ax + by + c = 0 କୁ x ଓ y ରେ ଏକଘାତୀ ସମୀକରଣ କୁହାଯାଏ । ଏଠାରେ xର ସହଗ (coefficient) a, y ର ସହଗ b ଏବଂ c ଧ୍ରୁବକ ରାଶି (constant) ଅଟେ a, b ∈ R ଓ a ଓ b ≠ 0
(ii) ଚଳରାଶି x ଓ y ରୁ x କୁ ସ୍ବାଧୀନ ଚଳ ଓ yକୁ ସାପେକ୍ଷ ଚଳ ବା x ଉପରେ ନିର୍ଭରଶୀଳ ଚଳ କୁହାଯାଏ । ଆମେ ଗ୍ରାଫ୍ ଅଙ୍କନ କରିବା ସମୟରେ ସିର୍ବଦା xକୁ ସ୍ବାଧୀନ ଚଳ ରାଶି ରୂପେ ବିଚାର କରିବା ।
(iii) ax + by + c = 0) ସମୀକରଣରେ ଥ‌ିବା ସହଗ ଓ ଧ୍ରୁବକ ରାଶି a, b ଓ  c ର ଭିନ୍ନ ଭିନ୍ନ ମୂଲ୍ୟ ନେଇ ଲେଖଚିତ୍ର ଅଙ୍କନ କଲେ xy-ସମତଳରେ ବିଭିନ୍ନ ସରଳରେଖା ମିଳିବ ।

• a = 0 ଓ b ≠ 0 ହେଲେ ax + by +c = 0 ର ରୂପ y = k₁ ଯେଉଁଠାରେ k₁ = \(\left(-\frac{c}{b}\right)\)
• b = 0 ଓ a ≠ 0 ହେଲେ ax + by +c = 0 ର ରୂପ x = k₂ ଯେଉଁଠାରେ k₂ = \(\left(-\frac{c}{a}\right)\)
• a ≠ 0 ଓ b ≠ 0 ହେଲେ ax + by +c = 0 ର ରୂପ y = mx + c ଯେଉଁଠାରେ m = \(\left(-\frac{a}{b}\right)\) କାରଣ ax + by + c = 0 ⇒ y = \(\left(-\frac{a}{b}\right) x+\left(-\frac{c}{b}\right)\)

ପରିସ୍ଥିତି:  
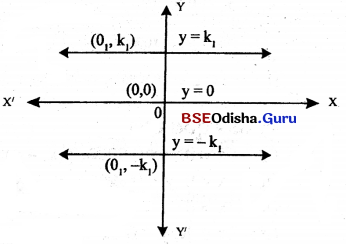
(i) y = k₁ ସମୀକରଣ xy – ସମତଳରେ x ଅକ୍ଷସହ ସମାନ୍ତର ଏକ ସରଳରେଖାକୁ ସୂଚାଏ ।
(a) ଯଦି k₁ = 0, ସରଳରେଖାଟି x ଅକ୍ଷ ହେବ ।
(b) ଯଦି k₁ > 0 ହେଲେ ସରଳରେଖାଟି x ଅକ୍ଷର ଊର୍ଦ୍ଧ୍ବ-ଅର୍ଥ ସମତଳରେ ରହିବ ।
(c) ଯଦି k₁ < 0 ହେଲେ ସରଳରେଖାଟି x ଅକ୍ଷର ଅଧଃ-ଅର୍ଥ ସମତଳରେ ଅବସ୍ଥିତ ରହିବ । 
y = k₁ ଏହା ଏକ ଆନୁଭୂମିକ ସରଳରେଖା (Horizontal lines)
y = 0 ସମୀକରଣଟି x- ଅକ୍ଷକୁ ସୂଚାଏ ।

ପରିସ୍ଥିତି:
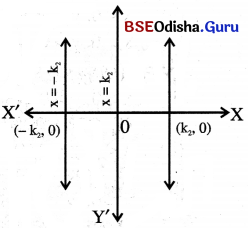
(ii) x = k₂, ସମୀକରଣ xy – ସମତଳରେ y ଅକ୍ଷସହ ସମାନ୍ତର ଏକ
ସରଳରେଖାକୁ ସୂଚାଏ ।
(a) ଯଦି k₂ = 0 ହୁଏ ତେବେ ସରଳରେଖାଟି y ଅକ୍ଷ ହେବ ।
(b) ଯଦି k₂ > 0 ହୁଏ ତେବେ ସରଳରେଖାଟି y ଅକ୍ଷର ଦକ୍ଷିଣ ପାର୍ଶ୍ବରେ ରହିବ ।
(c) ଯଦି k₂ < 0 ହୁଏ ତେବେ ସରଳରେଖାଟି y ଅକ୍ଷର ବାମ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ହେବ ।
x = k₂ ଏହା ଏକ ଉଲ୍ଲମ୍ବ ସରଳରେଖା (Vertical lines) । 
x = 0 ସମୀକରଣଟି y ଅକ୍ଷକୁ ସୂଚାଏ ।

ପରିସ୍ଥିତି:
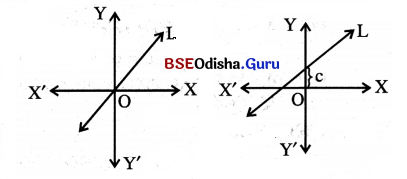
(iii) ଏଠାରେ xy – ସମତଳରେ ax + by + c = 0 ସମୀକରଣର ସମୀକରଣର ଲେଖଚିତ୍ରଟି ଏକ ତୀର୍ଯକ ସରଳରେଖା ହେବ ।
ଯାହାର ଅନ୍ୟ ଏକ ରୂପଟି ହେଉଛି y = mx + c 
ଏଠାରେ ସରଳରେଖାର Lର ସ୍ଲୋପ୍ (slope) ଓ y ଛେକାଂଶ 
(y-intercept) ଯଥାକ୍ରମେ m ଓ c ।
L ମୂଳବିନ୍ଦୁ O (0,0) ଦେଇ ଅଙ୍କିତ ହୋଇଥିଲେ ଏହାର 
ସମୀକରଣ y = mx + c, x = 0 ଓ y = 0 ଦ୍ଵାରା ସିଦ୍ଧ ହେବ ।
y = mx + c = c = 0
(y- ଅକ୍ଷକୁ ଛାଡ଼ି)ର ସମୀକରଣ y = mx ହେବ ।

{ଉଲ୍ଲମ୍ବ ସରଳରେଖାର ସ୍କୋପ୍ ନିରର୍ଥକ କାରଣ θ = 90° ହେଲେ ସ୍ଲୋପ୍ tan 8 ନିରର୍ଥକ ହେବ । L ସରଳରେଖାଟି ଆନୁଭୂମିକ ହୋଇଥିଲେ ଏହାର ଆନତି θ = 0° ଅର୍ଥାତ୍‌ କ୍ଲୋପ୍ tan θ = 0}

ସରଳରେଖା Lର କ୍ଲୋପ ନିଷ୍କ୍ରିୟ :
ସମୀକରଣ y = mx + c ଦ୍ବାରା ଅଙ୍କିତ ସରଳରେଖା L ଉପରେ P₁(x₁, y₁) ଓ P₂(x₂, y₂) ଦୁଇଗୋଟି ବିନ୍ଦୁ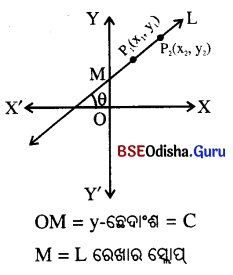
ହେଲେ \(\overleftrightarrow{\mathrm{P}_1 \mathrm{P}_2}\) = L 
ଏଠାରେ y = mx + c ସମୀକରଣଟି (x₁, y₁) ଓ (x₂, y₂) କ୍ରମିତ ଯୋଡ଼ି ଦ୍ବାରା ସିଦ୍ଧ ହେବ ।
y₁ = mx₁ + c  …. (i)
ଏବଂ y₂ = mx₂ + c ….. (ii)
(i) ଓ (ii) ରୁ c କୁ ଅପସାରଣ କଲେ ପାଇବା : m (x₁ – x₂) = y₁ – y₂
⇒ m = \(\frac{y_1-y_2}{x_1-x_2}\) ଅଥବା m = \(\frac{y_2-y_1}{x_2-x_1}\) ଅଥବା
L ରେଖାର ସ୍ଲୋପ୍ = \(\frac{y-ସ୍ଥାନାଙ୍କ ଦ୍ବୟର ଅନ୍ତର}{x-ସ୍ଥାନାଙ୍କ ଦ୍ବୟର ଅନ୍ତର}\)

ଦୁଇ ଅଜ୍ଞାତ ରାଶିବିଶିଷ୍ଟ ଏକଘାତୀ ସମୀକରଣର ଲେଖଚିତ୍ର (Graph of the Linear equation in two variables):

• ax + by + c = 0 ଓ y = mx + c ସମୀକରଣଗୁଡ଼ିକର ଲେଖଚିତ୍ର ସମତଳରେ ଗୋଟିଏ ଗୋଟିଏ ସରଳରେଖା । 
• ଲେଖ କାଗଜରେ x- ଓ y- ଆୟତୀୟ ଅକ୍ଷ ଅଙ୍କନ କରି ଦତ୍ତ ସମୀକରଣର ସହାୟତାରେ ଚାରି କିମ୍ବା ପାଞ୍ଚଗୋଟି ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ (କ୍ରମିତ ଯୋଡ଼ି) ନିରୂପଣ କରାଯାଏ ଓ ସେଗୁଡ଼ିକୁ ନେଇ ଲେଖ କାଗଜରେ ବିନ୍ଦୁମାନ ସ୍ଥାପନ କରାଯାଏ । ଏହି ବିନ୍ଦୁମାନଙ୍କୁ ସ୍କେଲ୍ ସାହାଯ୍ୟରେ ଯୋଗକଲେ ଦତ୍ତ ସମୀକରଣଟିର ଲେଖଚିତ୍ର ଏକ ସରଳରେଖା ହୁଏ ।