Odisha State Board BSE Odisha 9th Class Maths Notes Geometry Chapter 2 ତ୍ରିଭୁଜମାନଙ୍କ ସର୍ବସମତା will enable students to study smartly.
BSE Odisha Class 9 Maths Notes Geometry Chapter 2 ତ୍ରିଭୁଜମାନଙ୍କ ସର୍ବସମତା
ସର୍ବସମତା (Congruence):
ଦୁଇଟି ଏକପ୍ରକାର ଜ୍ୟାମିତିକ ଚିତ୍ର ମଧ୍ୟରୁ ଗୋଟିକର ଅବିକଳ ନକଲ (trace copy) କୁ ନେଇ ଅନ୍ୟ ଉପରେ ପକାଇଲେ ଯଦି ସେହି ଚିତ୍ରଦ୍ଵୟ ପରସ୍ପର ସହିତ ସଂପୂର୍ଣ୍ଣ ଭାବରେ ମିଳିଯାଆନ୍ତି, ତେବେ ଚିତ୍ରଦ୍ଵୟ ମଧ୍ୟରେ ପୂର୍ଣ୍ଣମେଳନ ସଂପର୍କ ଅଛି ବୋଲି କୁହାଯାଏ । ଏପରିସ୍ଥଳେ ଚିତ୍ରଦ୍ଵୟ ସର୍ବସମ (equal in all respects) ହୁଅନ୍ତି । ସର୍ବସମ ସଂପର୍କକୁ ‘=’ ଦ୍ଵାରା ସୂଚିତ କରାଯାଏ । ସର୍ବସମ କହିଲେ ଆକାର ଓ ଆକୃତିକୁ ବୁଝାଏ ।
(i) ଦୁଇଟି ରେଖାଖଣ୍ଡର ସର୍ବସମତା ( Congruence of two segments):
ରେଖାଖଣ୍ଡଦ୍ଵୟ ସର୍ବସମ ଅଟନ୍ତି ।
AB ଓ CD ଦୁଇଟି ରେଖାଖଣ୍ଡ ଯେପରି କି
AB = CD । ତେବେ AB ଓ CD ସର୍ବସମ ଅଟନ୍ତି ।
ଅର୍ଥାତ୍ AB = CD ⇔ AB ≅ CD
(ii) ଦୁଇଟି କୋଣର ସର୍ବସମତା (Congruence of two angles):
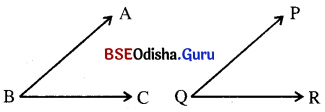ଦୁଇଟି କୋଣର ପରିମାଣ ସମାନ ହେଲେ ସେହି କୋଣଦ୍ୱୟ
ସର୍ବସମ ହୁଅନ୍ତି ।
∴ ∠ABC ଓ ∠PQR ଦୁଇଟି କୋଣ ଯେପରି m∠ABC = m∠PQR
∴ ∠ABC ଓ ∠PQR ସର୍ବସମ ଅଟନ୍ତି ।
∴ m∠ABC = m∠PQR ⇔ ∠ABC = ∠PQR
ଦୁଇଟି ତ୍ରିଭୁଜର ସର୍ବସମତା (Congruence of two triangle):
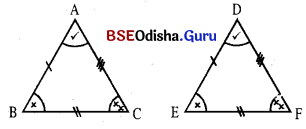(i) ଦୁଇଟି ତ୍ରିଭୁଜ ମଧ୍ୟରେ ଗୋଟିଏ ତ୍ରିଭୁଜର ତିନିବାହୁ ଅନ୍ୟଟିର ତିନିବାହୁ ସହ ସର୍ବସମ ହେଲେ ଏବଂ ସର୍ବସମ ବାହୁଗୁଡ଼ିକର ବିପରୀତ କୋଣମାନ ସର୍ବସମ ହେଲେ ତ୍ରିଭୁଜଦ୍ଵୟକୁ ସର୍ବସମ ତ୍ରିଭୁଜ କୁହାଯାଏ ।
AB ≅ DE, BC ≅ EF, AC ≅ DF
ଏବଂ ∠A ≅ ∠D, ∠B ≅ ∠E, ∠C ≅ ∠F 626 Δ ABC ≅ ΔDEF
(ii) ତ୍ରିଭୁଜ ଦ୍ବୟରେ AB, BC ଓ CA ବାହୁମାନଙ୍କର ଯଥାକ୍ରମେ DE, EF ଓ F͞D ଅନୁରୂପ ବାହୁ ଓ ∠A, ∠B, ∠Cର ଯଥାକ୍ରମେ ∠D, ∠E, ∠F ଅନୁରୂପ କୋଣ ଅଟନ୍ତି । ।
ଦୁଇଟି ତ୍ରିଭୁଜର ସର୍ବସମତା ପାଇଁ ନୂନତମ ସର୍ଭ :
ସ୍ଵୀକାର୍ଯ୍ଯ -10 : ବା-କୋ-ବା (ବାହୁ-କୋଣ-ବାହୁ) ସ୍ଵୀକାର୍ଯ୍ୟ :
ଦୁଇଟି ତ୍ରିଭୁଜ ମଧ୍ୟରେ ଗୋଟିକର ଦୁଇ ବାହୁ ଓ ଅନ୍ତର୍ଗତ କୋଣ ଯଥାକ୍ରମେ ଅନ୍ୟ ତ୍ରିଭୁଜର ଦୁଇବାହୁ ଓ ଅନ୍ତର୍ଗତ କୋଣ ସହ ସର୍ବସମ ହେଲେ ତ୍ରିଭୁଜଦ୍ବୟ ସର୍ବସମ ।
ଉଦାହରଣ ସ୍ୱରୂପ : Δ ABC ଓ Δ DEF ମଧ୍ୟରେ \(\overline{\mathrm{AB}} \cong \overline{\mathrm{DE}}, \overline{\mathrm{BC}} \cong \overline{\mathrm{EF}}\) ଏବଂ ∠B ≅ ∠E ହେଲେ Δ ABC = Δ DEF
ଏହାକୁ ବାହୁ-କୋଣ-ବାହୁ (ବା-କୋ-ବା) ସ୍ଵୀକାର୍ଯ୍ୟ (Side-Angle-Side or S-A-S axiom) କୁହାଯାଏ ।
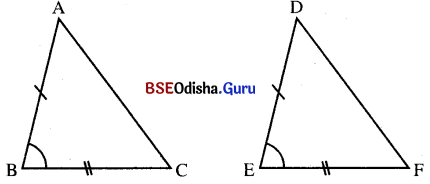
ଉପପାଦ୍ୟ – 11 : ଗୋଟିଏ ତ୍ରିଭୁଜର ଦୁଇଟି ବାହୁ ସର୍ବସମ ହେଲେ, ସେହି ବାହୁଦ୍ୱୟର ସମ୍ମୁଖୀନ କୋଣଦ୍ୱୟ ସର୍ବସମ ।
ଅନୁସିଦ୍ଧାନ୍ତ :
- ଏକ ସମବାହୁ ତ୍ରିଭୁଜର କୋଣ ତ୍ରୟର ପରିମାଣ ସମାନ ।
- Δ ABC ରେ AB = AC ହେଲେ ∠Aର ସମଦ୍ବିଖଣ୍ଡକ BC ର ସମଦ୍ବିଖଣ୍ଡକ ଲମ୍ବ ହେବ ।
ଉପପାଦ୍ୟ – 12 (କୋ-ବା-କୋ ଉପପାଦ୍ୟ) : ଗୋଟିଏ ତ୍ରିଭୁଜର ଦୁଇକୋଣ ଓ ଅନ୍ତର୍ଗତ ବାହୁ ଯଥାକ୍ରମେ ଅନ୍ୟ ଏକ ତ୍ରିଭୁଜର ଦୁଇ କୋଣ ଓ ଅନ୍ତର୍ଗତ ବାହୁ ସହ ସର୍ବସମ ହେଲେ, ତ୍ରିଭୁଜଦ୍ଵୟ ସର୍ବସମ ।
ଅନୁସିଦ୍ଧାନ୍ତ (କୋ-କୋ-ବା ସର୍ବସମତା) : ଗୋଟିଏ ତ୍ରିଭୁଜର ଦୁଇକୋଣ ଓ ଯେକୌଣସି ଗୋଟିଏ ବାହୁ ଯଥାକ୍ରମେ ଅନ୍ୟ ଏକ ତ୍ରିଭୁଜର ଦୁଇକୋଣ ଓ ଅନୁରୂପ ବାହୁ ସହ ସର୍ବସମ ହେଲେ ତ୍ରିଭୁଜଦ୍ଵୟ ସର୍ବସମ ।
ଉପପାଦ୍ୟ – 13 : ଗୋଟିଏ ତ୍ରିଭୁଜର ଦୁଇଟି କୋଣ ସର୍ବସମ ହେଲେ, ସେମାନଙ୍କର ସମ୍ମୁଖୀନ ବାହୁଦ୍ୱୟ ମଧ୍ୟ ସର୍ବସମ ।
ଉପପାଦ୍ୟ – 14 (ବା-ବା-ବା ସର୍ବସମତା) : ଗୋଟିଏ ତ୍ରିଭୁଜର ତିନି ବାହୁ ଅନ୍ୟ ଏକ ତ୍ରିଭୁଜର ତିନିବାହୁ ସହ ସର୍ବସମ ହେଲେ, ତ୍ରିଭୁଜଦ୍ଵୟ ସର୍ବସମ ।
ଉପପାଦ୍ୟ – 15 (ସ-କ-ବା ସର୍ବସମତା) : ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜର କଣ୍ଠ ଓ ଅନ୍ୟ ଏକ ବାହୁ ଯଥାକ୍ରମେ ଅନ୍ୟ ଏକ ସମକୋଣୀ ତ୍ରିଭୁଜର କର୍ଣ୍ଣ ଓ ଏକ ବାହୁ ସହ ସର୍ବସମ ହେଲେ, ତ୍ରିଭୁଜ ଦୁଇଟି ସର୍ବସମ ।
ତ୍ରିଭୁଜରେ କିଛି ଅସମାନତା ସମ୍ବନ୍ଧ (Some Inequality Relations in a triangle) :
ଉପପାଦ୍ୟ – 16 : ଗୋଟିଏ ତ୍ରିଭୁଜର ଏକ ବାହୁର ଦୈର୍ଘ୍ୟ ଏହାର ଅନ୍ୟ ଏକ ବାହୁର ଦୈର୍ଘ୍ୟଠାରୁ ବୃହତ୍ତର ହେଲେ, ବୃହତ୍ତର ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ ବାହୁର ସମ୍ମୁଖୀନ କୋଣର ପରିମାଣ କ୍ଷୁଦ୍ରତର ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ ବାହୁର ସମ୍ମୁଖୀନ କୋଣର ପରିମାଣଠାରୁ ବୃହତ୍ତର ।
ଅନୁସିଦ୍ଧାନ୍ତ ଗୋଟିଏ ତ୍ରିଭୁଜର ବୃହତ୍ତମ ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ ବାହୁର ସମ୍ମୁଖୀନ କୋଣ ବୃହତ୍ତମ ପରିମାଣ ବିଶିଷ୍ଟ ।
ଉପପାଦ୍ୟ – 17 : ଗୋଟିଏ ତ୍ରିଭୁଜର ଗୋଟିଏ କୋଣର ପରିମାଣ ଅନ୍ୟ ଏକ କୋଣର ପରିମାଣଠାରୁ ବୃହତ୍ତର ହେଲେ, ବୃହତ୍ତର ପରିମାଣବିଶିଷ୍ଟ କୋଣର ସମ୍ମୁଖୀନ ବାହୁର ଦୈର୍ଘ୍ୟ, କ୍ଷୁଦ୍ରତର ପରିମାଣବିଶିଷ୍ଟ କୋଣର ସମ୍ମୁଖୀନ ବାହୁର ଦୈର୍ଘ୍ୟଠାରୁ ବୃହତ୍ତର ।
ଅନୁସିଦ୍ଧାନ୍ତ: ଗୋଟିଏ ତ୍ରିଭୁଜର ବୃହତ୍ତମ ପରିମାଣବିଶିଷ୍ଟ କୋଣର ସମ୍ମୁଖୀନ ବାହୁ ବୃହତ୍ତମ ଦୈର୍ଘ୍ୟବିଶିଷ୍ଟ ।
ଉପପାଦ୍ୟ – 18 : ତ୍ରିଭୁଜର ଯେକୌଣସି ଦୁଇ ବାହୁର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି ତୃତୀୟ ବାହୁର ଦୈର୍ଘ୍ୟଠାରୁ ବୃହତ୍ତର ।
ଉପପାଦ୍ୟ – 19 : ଗୋଟିଏ ସରଳରେଖାର ବହିଃସ୍ଥ ଏକ ବିନ୍ଦୁକୁ ସରଳରେଖାଟିର ବିନ୍ଦୁମାନଙ୍କ ସହିତ ଯୋଗକରି ଯେତେଗୁଡ଼ିଏ ରେଖାଖଣ୍ଡ ଅଙ୍କନ କରାଯାଇପାରେ ସେମାନଙ୍କ ମଧ୍ୟରେ ଲମ୍ବ ହେଉଥିବା ରେଖାଖଣ୍ଡର ଦୈର୍ଘ୍ୟ କ୍ଷୁଦ୍ରତମ ।