Odisha State Board BSE Odisha 9th Class Maths Notes Geometry Chapter 3 ଚତୁର୍ଭୁଜ will enable students to study smartly.
BSE Odisha Class 9 Maths Notes Geometry Chapter 3 ଚତୁର୍ଭୁଜ
ଚତୁର୍ଭୁଜ ଓ ଉଉଳ ଚତୁର୍ଭୁଜ (Quadrilateral and convex quadrilateral) :
(1) ଚତୁର୍ଭୁଜ : ମନେକର A, B, C, D ଏକ ସମତଳରେ ଅବସ୍ଥିତ ଚାରୋଟି ବିନ୍ଦୁ ଏବଂ ଏମାନଙ୍କ ମଧ୍ୟରୁ ଯେକୌଣସି ତିନୋଟି ବିନ୍ଦୁ ଏକ ସରଳରେଖାରେ ଅବସ୍ଥିତ ନୁହଁନ୍ତି । A͞B , B͞C , C͞D ଓ DA ସେମାନଙ୍କ ପ୍ରାନ୍ତବିନ୍ଦୁ ବ୍ୟତୀତ ଅନ୍ୟ କୌଣସି ବିନ୍ଦୁରେ ଛେଦ କରୁ ନଥ୍ଲେ, ଏହି ଚାରି ଗୋଟି ରେଖାଖଣ୍ଡଦ୍ଵାରା ଗଠିତ ସେଟ୍ AB ∪ BC ∪ CD ∪ DA କୁ ABCD ଚତୁର୍ଭୁକର କୁହାଯାଏ ।
(2) AB, BC, CD ଓ DA କୁ ABCD ଚତୁର୍ଭୁକର ବାହୁ ଓ ∠BAD, ∠ABC, ∠CDA ଓ ∠BCD କୁ ଏହାର କୋଣ (Angle) କୁହାଯାଏ A, B, C, D କୁ ଚତୁର୍ଭୁର୍ଜର ଶୀର୍ଷବିନ୍ଦୁ (Vertex) କୁହାଯାଏ ।
(3) ଚତୁର୍ଭୁଜର ଯେଉଁ ଦୁଇଟି ବାହୁର ଏକ ସାଧାରଣ ପ୍ରାନ୍ତବିନ୍ଦୁ ଥାଏ ସେ ଦ୍ୱୟକୁ ସନ୍ନିହିତ (Adjacent) ବାହୁ ବା କୌଣସି ସାଧାରଣ ପ୍ରାନ୍ତ ବିନ୍ଦୁ ନଥିବା ବାହୁଦ୍ୱୟକୁ ବିପରୀତ (Opposite) ବାହୁ କୁହାଯାଏ । ଚତୁର୍ଭୁଜର ଗୋଟିଏ ବାହୁର ଦୁଇଟି ପ୍ରାନ୍ତ ବିନ୍ଦୁକୁ କ୍ରମିକ ଶୀର୍ଷ ଓ କ୍ରମିକ ଶୀର୍ଷରେ ଥିବା କୋଣଦ୍ଵୟକୁ କ୍ରମିକ କୋଣ କୁହାଯାଏ । ଯେଉଁ ନୁହଁନ୍ତି ସେ ଦ୍ଵୟକୁ ବିପରୀତ ଶୀର୍ଷ କୁହାଯାଏ । ବିପରୀତ ଶୀର୍ଷ ବିନ୍ଦୁରେ ଥିବା କୋଣଦ୍ଵୟକୁ ବିପରୀତ କୋଣ କୁହାଯାଏ ।
AB ଓ BC ସନ୍ନିହିତ ବାହୁ ଏବଂ AB ଓ CD ବିପରୀତ ବାହୁ;
∠A, ∠B କ୍ରମିକ କୋଣ ଓ ∠A, ∠C ବିପରୀତ କୋଣ; A ଓ B କ୍ରମିକ ଶୀର୍ଷ ଏବଂ A ଓ C ବିପରୀତ ଶୀର୍ଷ ଅଟେ ।
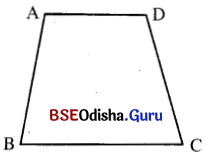
(4) ଉତ୍ତଳ ଚତୁର୍ଭୁଜ : ଯେଉଁ ଚତୁର୍ଭୁଜର ପ୍ରତ୍ୟେକ ବାହୁ ଏହାର ବିପରୀତ ବାହୁଦ୍ୱାରା ନିର୍ମିତ ସରଳରେଖାକୁ ଛେଦ ନକରେ, ତା’ହେଲେ ଏହାକୁ ଏକ ଉତ୍ତଳ ଚତୁର୍ଭୁଜ (Convex Quadrilateral) କୁହାଯାଏ ।
(5) ABCD ଏକ ଉତ୍ତର ଚତୁର୍ଭୁଜ ହେଲେ A ଓ B ବିଦୁ୍ୟଦ୍ୱୟ \(\stackrel{\leftrightarrow}{\mathrm{CD}}\) ର ଏକ ପାର୍ଶ୍ବରେ, B ଓ C ବିନ୍ଦୁଦ୍ଵୟ \(\stackrel{\leftrightarrow}{\mathrm{DA}}\) ର ଏକ ପାର୍ଶ୍ବରେ, C ଓ D ବିନ୍ଦୁଦ୍ଵୟ \(\stackrel{\leftrightarrow}{\mathrm{AB}}\) ର ଏକ ପାର୍ଶ୍ବରେ ଏବଂ D ଓ A ବିନ୍ଦୁଦ୍ଵୟ \(\stackrel{\leftrightarrow}{\mathrm{BC}}\) ର ଏକ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ହେବା ଆବଶ୍ୟକ ।
- ଉତ୍କଳ ଚତୁର୍ଭୁଜ ଉତ୍ତଳ ସେଟ୍ ନୁହେଁ ଏବଂ ଉତ୍ତଳ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ଚତୁର୍ଭୁଜର ଅନ୍ତର୍ଦେଶରେ ଛେଦକରନ୍ତି ।
- ଉତ୍ତଳ ଚତୁର୍ଭୁଜର ଅନ୍ତର୍ଦେଶ ଏକ ଉତ୍ତଳ ସେଟ୍ ।
ବହୁଭୂଜ(polygon):
ମନେକର P1, P2, ….. Pn ଏକ ସମତଳରେ ଅବସ୍ଥିତ କେତେକ ବିନ୍ଦୁ (n ≥ 3) ଏବଂ ଏମାନଙ୍କ ମଧ୍ୟରୁ କୌଣସି ତିନୋଟି ବିନ୍ଦୁ ଏକରେଖୀୟ ନୁହନ୍ତି । P1P2, P2P3, ….. Pn-1Pn, PnP1 ସେମାନଙ୍କ ପ୍ରାନ୍ତବିନ୍ଦୁ ବ୍ୟତୀତ ଅନ୍ୟ କୌଣସି ବିନ୍ଦୁରେ ଛେଦକରୁନଥୁଲେ ଏହି n ସଂଖ୍ୟକ ରେଖାଖଣ୍ଡଦ୍ୱାରା ଗଠିତ ସେଟ୍ P1P2, ∪ P2P3, ∪ ….. Pn-1Pn, ∪ PnP1 କୁ P1P2 ….. Pn ବହୁଭୁଜ କୁହାଯାଏ ।
P1P2, P2P3 ….. PnP1 ବହୁଭୁଜର ବାହୁ ଓ P1P2 ….. Pn ବହୁଭୁଜର ଶୀର୍ଷବିନ୍ଦୁ ଅଟନ୍ତି ।
{n ସଂଖ୍ୟକ ବାହୁବିଶିଷ୍ଟ ଏକ ବହୁଭୁଜର n ସଂଖ୍ୟକ ଅନ୍ତଃସ୍ଥ କୋଣ ଥାଏ ।}
![]()
ଉତ୍ତଳ ବହୁଭୁଜ (Convex Polygon) :
P1P2P3 ….. Pnବହୁଭୁଜର ପ୍ରତ୍ୟେକ ବାହୁଦ୍ୱାରା ନିର୍ମିତ ରେଖାର ଏକ ପାର୍ଶ୍ଵରେ ଯଦି ବହୁଭୁଜର ଅନ୍ୟ ସମସ୍ତ ଶୀର୍ଷ ଅବସ୍ଥାନ କରନ୍ତି, ତେବେ ବହୁଭୁଜକୁ ଉତ୍ତଳ ବହୁଭୁଜ କୁହାଯାଏ ।
ସୁଷମ ବହୁଭୁଜ (Regular Polygon) :
ଯେଉଁ ବହୁଭୁଜର ସମସ୍ତ ବାହୁର ଦୈର୍ଘ୍ୟ ସମାନ ଏବଂ ସମସ୍ତ କୋଣର ପରିମାଣ ସମାନ ସେପରି ବହୁଭୁଜକୁ ସୁଷମ ବହୁଭୁଜ କୁହାଯାଏ
ବହୁଭୁଜର ବାହୁ ସଂଖ୍ୟା ଉପରେ ବହୁଭୁଜର ନାମକରଣ ନିର୍ଭର କରେ ।
{ବହୁଭୁଜ ମଧ୍ୟରେ ସର୍ବାଧିକ ମୌଳିକ ହେଉଛି ତ୍ରିଭୁଜ ଯାହାର ବାହୁ ସଂଖ୍ୟା 3 ।}
| ବାହୁ ସଂଖ୍ୟା | ବହୁଭୁଜର ନାମ |
| 33 | ତ୍ରିଭୁଜ (Triangle) |
| 4 | ଚତୁର୍ଭୁଜ (Quadrilateral) |
| 5 | ପେଣ୍ଟାଗନ୍ (Pentagon) |
| 6 | ଷଡ଼ଭୁଜ (Hexagon) |
ବହୁଭୁଜର ବହିଃସ୍ଥ କୌଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି (Sum of the measures of the exterior angles of a polygon):
(i) ପ୍ରତ୍ୟେକ n ଭୁଜ (n ≥ 3) ବିଶିଷ୍ଟ ବହୁଭୁଜର ବହିଃସ୍ଥ କୋଣ ସଂଖ୍ୟା n l ପ୍ରତ୍ୟେକ ଶୀର୍ଷରେ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ + ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ = 180° = 2 ସମକୋଣ ଗୋଟିଏ n ଭୁଜବିଶିଷ୍ଟ ବହୁଭୁଜର ବହିଃସ୍ଥ କୋଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି
= n × 2 ସମକୋଣ୍ଡ – n ସଂଖ୍ୟକ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣର ସମଷ୍ଟି
= n × 2 ସମକୋଣ – (2n – 4) ସମକୋଣ 4 ସମକୋଣ = 360°
{ପ୍ରତ୍ୟେକ ବହୁଭୁଜର ବହିଃସ୍ଥ କୌଣମାନଙ୍କର ପରିମାଣ ସମଷ୍ଟି 360°}
(ii) ଯେଉଁ ବହୁଭୁଜର ସମସ୍ତ ବାହୁର ଦୈର୍ଘ୍ୟ ପରସ୍ପର ସମାନ ହେବା ସଙ୍ଗେ ସଙ୍ଗେ ସମସ୍ତ କୋଣର ପରିମାଣ ମଧ୍ୟ ପରସ୍ପର ସମାନ ତାହାକୁ ସମବହୁଭୁଜ ବା ସୁଷମ ବହୁଭୁଜ (Regular polygon) କୁହାଯାଏ ।
⇒ ଏଣୁ n ବାହୁ ବିଶିଷ୍ଟ ସୁଷମ ବହୁଭୁଜର ପ୍ରତ୍ୟେକ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ = \(\frac{2n-4}{n}\) ସମକୋଣ
⇒ ଏବଂ n ବାହୁ ବିଶିଷ୍ଟ ସୁଷମ ବହୁଭୁଜର ପ୍ରତ୍ୟେକ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ = \(\frac{360°}{n}\)
⇒ n ବାହୁ ବିଶିଷ୍ଟ ସୁଷମ ବହୁଭୁଜର ଏକ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ =\(\frac{2n-4}{n}\) ସମକୋଣ
⇒ ଏବଂ ଏକ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ = \(\frac{360°}{n}\)
ନିମ୍ନରେ ପ୍ରଦତ୍ତ ସାରଣୀରେ କେତେଗୋଟି ବହୁଭୁଜମାନଙ୍କ ଅନ୍ତଃସ୍ଥ ଓ ବହିଃସ୍ଥ କୌଣମାନଙ୍କ ପରିମାଣର ସମଷ୍ଟି ଓ ବହୁଭୁଜଟି ସୁଷମ ହୋଇଥିଲେ ପ୍ରତ୍ୟେକ କୋଣମାନଙ୍କ ପରିମାଣ ଦିଆଯାଇଛି ।
| ବହୁଭୁଜ | ଅନ୍ତଃସ୍ଥ କୋଣମାନଙ୍କ ପରିମାଣର ସମଷ୍ଟି | ବହିଃସ୍ଥ କୋଣମାନଙ୍କ ପରିମାଣର ସମଷ୍ଟି | ବହୁଭୁଜ ସୁଷମ ହୋଇଥିଲେ ପ୍ରତ୍ୟେକ ଅନ୍ତଃସ୍ଥ କୋଣର ପରିମାଣ |
| ତ୍ରିଭୁଜ | 2 ସମକୋଣ | 4 ସମକୋଣ | 60° |
| ବହୁର୍ଭୁଜ | 4 ସମକୋଣ | 4 ସମକୋଣ | 90° |
| ପେଣ୍ଟାଗନ୍ | 6 ସମକୋଣ | 4 ସମକୋଣ | 108° |
| ଷଡ଼ଭୁଜ | 8 ସମକୋଣ | 4 ସମକୋଣ | 120° |
![]()
କେତେକ ବିଶେଷ ଚତୁର୍ଭୁଜ :
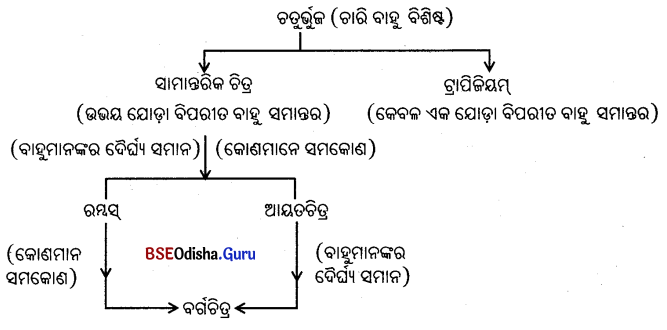
ଚତୁର୍ଭୁଜର ବିପରୀତ ବାହୁଯୋଡ଼ା ମଧ୍ଯରେ ଥିବା ସମାନ୍ତରଣର ସର୍ଭ ଅନୁଯାୟୀ ଚତୁର୍ଭୁଜ ମୁଖ୍ୟତଃ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ; ଯଥା-
(i) ଟ୍ରାପିଜିୟମ୍ ଓ (ii) ସାମାନ୍ତରିକ ଚିତ୍ର ।
ଟ୍ରାପିଜିୟମ୍ (Trapezium) : ଯେଉଁ ଚତୁର୍ଭୁଜର କେବଳ ଏକ ଯୋଡ଼ା ବିପରୀତ ବାହୁ ସମାନ୍ତର ତାହାକୁ ଟ୍ରାପିଜିୟମ୍ କୁହାଯାଏ । ABCD ଚତୁର୍ଭୁଜର AD||BC ହେତୁ ABCD ଚତୁର୍ଭୁଜର ଟ୍ରାପିଜିୟମ୍ର ଦୁଇ ସମାନ୍ତର ବାହୁ ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତାକୁ ଟ୍ରାପିଜିୟମ୍ର ଉଚ୍ଚତା ଟ୍ରାପିଜିୟମ୍ । ଏ କ୍ଷେତ୍ରରେ AB ଓ DC ଦ୍ଵୟ ଅସମାନ୍ତର । (Height) କୁହାଯାଏ ।
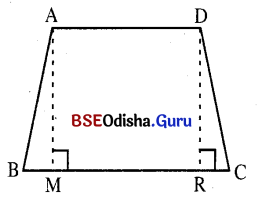
ସାମାନ୍ତରିକ ଚିତ୍ର (Parallelogram) : ଯେଉଁ ଚତୁର୍ଭୁଜର ବିପରୀତ
(i) ABCD ଚତୁ ଭୁଜର ବିପରୀତ ବାହୁ AB || CD ଏବଂ AD || BC । ଉକ୍ତ ଚତୁର୍ଭୁଜକୁ ସାମାନ୍ତରିକ ଚିତ୍ର କୁହାଯାଏ ।
(ii) ସାମାନ୍ତରିକ ଚିତ୍ରରେ ବିପରୀତ ବାହୁ AD ଓ BC ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା AM ଏବଂ AB ଓ CD ମଧ୍ୟବର୍ତ୍ତୀ ଦୂରତା CN । ABCD ସାମାନ୍ତରିକ ଚିତ୍ରର BC ଅଥବା AD ବାହୁକୁ ଭୂମି ନିଆଗଲେ AMକୁ ଉଚ୍ଚତାରୂପେ B ନିଆଯାଏ । ସେହିପରି AB ଅଥବା DC ଭୂମି ହେଲେ ସାମାନ୍ତରିକ ଚିତ୍ରର ଉଚ୍ଚତା CN ହୁଏ ।
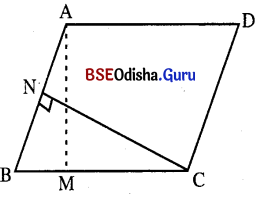
ଆୟତଚିତ୍ର (Rectangle) : ଯେଉଁ ଚତୁର୍ଭୁଜର ପ୍ରତ୍ୟେକ କୋଣ ସମକୋଣ ତାହା ଏକ ଆୟତଚିତ୍ର । ଆୟତଚିତ୍ର ଏକ ସ୍ଵତନ୍ତ୍ର ପ୍ରକାରର ସାମାନ୍ତରିକ ଚିତ୍ର, ଯାହାର ପ୍ରତ୍ୟେକ କୋଣର ପରିମାଣ 90° । ABCD ଏକ ଆୟତଚିତ୍ର ।
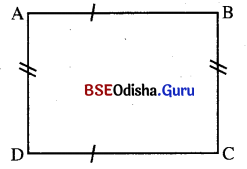
ରମ୍ବସ୍ (Rhombus) : ଯେଉଁ ଚତୁର୍ଭୁଜର ବାହୁମାନଙ୍କ ଦୈର୍ଘ୍ୟ ସମାନ ତାହା ଏକ ରମ୍ବସ୍ । ରମ୍ବସ ମଧ୍ୟ ଗୋଟିଏ ସ୍ବତନ୍ତ୍ର ପ୍ରକାରର ସାମାନ୍ତରିକ ଚିତ୍ର, ଯାହାର ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ସମାନ । ଦତ୍ତ ଚିତ୍ରରେ ABCD ଏକ ରମ୍ବସ ।
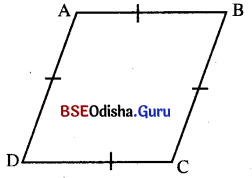
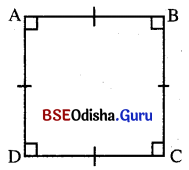
ବର୍ଗଚିତ୍ର (Square) : ଯେଉଁ ଚତୁର୍ଭୁଜର ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ ସମାନ । ଓ ପ୍ରତ୍ୟେକ କୋଣର ପରିମାଣ 90° ତାହା ଏକ ବର୍ଗଚିତ୍ର । ଏଣୁ ବର୍ଗଚିତ୍ର ଏକ ସମକୋଣ ବିଶିଷ୍ଟ ରମ୍ବସ୍ ଅଟେ । ଚିତ୍ରରେ ABCD ଏକ ବର୍ଗଚିତ୍ର ।
କେତେକ ଉପପାଦ୍ୟ :
ଉପପାଦ୍ୟ 20 : ଗୋଟିଏ ଚତୁର୍ଭୁଜର ଦୁଇଟି ବିପରୀତ ବାହୁ ସର୍ବସମ ଓ ସମାନ୍ତର ହେଲେ ଚତୁର୍ଭୁଜଟି ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ଉପପାଦ୍ୟ 21 : ସାମାନ୍ତରିକ ଚିତ୍ରର ବିପରୀତ ବାହୁମାନେ ସର୍ବସମ ।
ଉପପାଦ୍ୟ 22 : ଗୋଟିଏ ଚତୁର୍ଭୁଜର ବିପରୀତ ବାହୁମାନ ସର୍ବସମ ହେଲେ ଏହା ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ଉପପାଦ୍ୟ 23 : ସାମାନ୍ତରିକ ଚିତ୍ରର ବିପରୀତ କୋଣମାନେ ସର୍ବସମ ।
ଉପପାଦ୍ୟ 24 : ଗୋଟିଏ ଚତୁର୍ଭୁଜର ବିପରୀତ କୋଣମାନ ସର୍ବସମ ହେଲେ ଏହା ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ଉପପାଦ୍ୟ 25 : ଏକ ସାମାନ୍ତରିକ ଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି ।
ଉପପାଦ୍ୟ 26 : ଯେଉଁ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି ତାହା ଏକ ସାମାନ୍ତରିକ ଚିତ୍ର ।
ଉପପାଦ୍ୟ 27 : ଆୟତଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ସର୍ବସମ ।
ଉପପାଦ୍ୟ 28 : ଯେଉଁ ସାମାନ୍ତରିକ ଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ସର୍ବସମ ତାହା ଏକ ଆୟତଚିତ୍ର ।
ଉପପାଦ୍ୟ 29 : ଗୋଟିଏ ରମ୍ବସର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ।
ଅନୁସିଦ୍ଧାନ୍ତ – 1 : ଏକ ସାମାନ୍ତରିକ ଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ସର୍ବସମ ଓ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ହେଲେ ଏହା ଏକ ବର୍ଗଚିତ୍ର ।
ଅନୁସିଦ୍ଧାନ୍ତ – 2 : ଗୋଟିଏ ବର୍ଗଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ଓ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ।
ଅନୁସିଦ୍ଧାନ୍ତ – 3 : ଯେଉଁ ସାମାନ୍ତରିକ ଚିତ୍ରର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ, ତାହା ଏକ ରମ୍ବସ୍ ।
ସମାନ୍ତର ସରଳରେଖା ଏବଂ ତ୍ରିଭୁଜ (Parallel lines and Triangles) :
ଉପପାଦ୍ୟ 30 : ଗୋଟିଏ ତ୍ରିଭୁଜର ଏକ ବାହୁର ମଧ୍ୟବିନ୍ଦୁରୁ ଅନ୍ୟ ଏକ ବାହୁ ସହ ସମାନ୍ତର ଭାବେ ଅଙ୍କିତ ସରଳରେଖା ତୃତୀୟ ବାହୁକୁ ସମଦ୍ବିଖଣ୍ଡ କରେ ।
ଉପପାଦ୍ୟ31 : ଗୋଟିଏ ତ୍ରିଭୁଜର ଯେକୌଣସି ଦୁଇ ବାହୁର ମଧ୍ୟବିନ୍ଦୁକୁ ଯୋଗ କରୁଥିବା ରେଖାଖଣ୍ଡ ତୃତୀୟ ବାହୁ ସହ ସମାନ୍ତର ଓ ଏହାର ଅର୍ଥ-ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ।
![]()
ଛେଦାଶ (Intercepts) :
(i) ଏକ ସମତଳରେ ଅବସ୍ଥିତ l ଓ m ଦୁଇଟି ସରଳରେଖା । ଯଦି ଏକ ଛେଦକ n, ସରଳରେଖା ଦ୍ୱୟକୁ P ଓ Q ଦୁଇଟି ବିନ୍ଦୁରେ ଛେଦ କରେ, ତେବେ P͞Q କୁ ଛେଦକର ଏକ ଛେତାଂଶ ବା ଛେଦିତ ଅଂଶ କୁହାଯାଏ ।
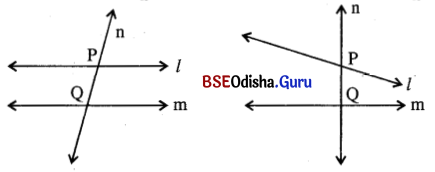
(ii) ଯଦି ଏକ ସମତଳରେ ଦୁଇ ବା ତତୋଽଧିକ ସରଳରେଖା (ପରସ୍ପର ସମାନ୍ତର କିମ୍ବା ସମାନ୍ତର ନହୋଇବି ପାରନ୍ତି)କୁ ଗୋଟିଏ ଛେଦକ ଦୁଇ ବା ତତୋଽଧ୍ଵକ ବିନ୍ଦୁରେ ଛେଦକରେ, ତେବେ ଛେଦକର ଛେଦିତାଂଶ (Intercepts) ମଧ୍ଯ ଥାଏ ।
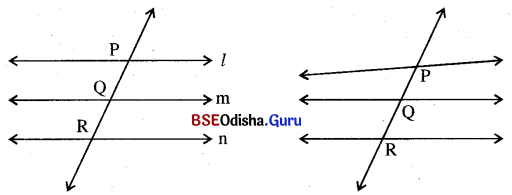
ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ PQ ଏବଂ Q͞R ଛେଦିତାଂଶ (Intercepts) ଅଟନ୍ତି ।
(iii) ପ୍ରତ୍ୟେକ କ୍ଷେତ୍ରରେ ଛେଦିତାଂଶ ବା ଛେଦଂଶର ଦୈର୍ଘ୍ୟ ସମାନ ବା ଅସମାନ ହୋଇପାରନ୍ତି ।
(iv) ଛେଦକର ଛେକାଂଶ ମାନ, ଛେଦିତ ସରଳରେଖାମାନଙ୍କଦ୍ୱାରା ଉତ୍ପନ୍ନ ହୋଇଥାଏ ।
ଉପପାଦ୍ୟ 32 : ତିନି ବା ତତୋଽଧ୍ଵକ ସମାନ୍ତର ସରଳରେଖାକୁ ଛେଦ କରୁଥିବା ଏକ ଛେଦକର ଛେଦିତ ଅଂଶଗୁଡ଼ିକ ସର୍ବସମ ହେଲେ, ଅନ୍ୟ ଯେକୌଣସି ଛେଦକର ଛେଦିତ ଅନୁରୂପ ଅଂଶଗୁଡ଼ିକ ମଧ୍ୟ ସର୍ବସମ ହେବ ।
