Odisha State Board BSE Odisha 9th Class Maths Notes Geometry Chapter 4 କ୍ଷେତ୍ରଫଳ will enable students to study smartly.
BSE Odisha Class 9 Maths Notes Geometry Chapter 4 କ୍ଷେତ୍ରଫଳ
ଉପକ୍ରମଣିକା :
(i) ପ୍ରତ୍ୟେକ ସରଳରେଖ୍ ଆବଦ୍ଧ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ଥାଏ । କ୍ଷେତ୍ରଫଳ (Area) ଏକ ଧନାତ୍ମକ ବାସ୍ତବ ସଂଖ୍ୟା ଯାହା କ୍ଷେତ୍ର (region) ସହ ଜଡ଼ିତ ।
(ii) ସରଳରୈଖ୍କ ଚିତ୍ର ଓ ଏହାର ଅନ୍ତର୍ଦେଶର ସଂଯୋଗରେ ସରଳରେଖକ କ୍ଷେତ୍ରର ସୃଷ୍ଟି ।
ତ୍ରିଭୁଜ ଏବଂ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଉଚ୍ଚତା (Height of a Triangle and a Parallelogram):
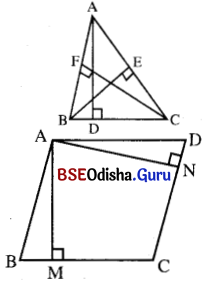
(a) ତ୍ରିଭୁଜର ଉଚ୍ଚତା : ଏକ ତ୍ରିଭୁଜର ଯେକୌଣସି ବାହୁକୁ ଭୂମିନେଇ ଏହାର ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଭୂମିପ୍ରତି ଲମ୍ବ ଅଙ୍କନ କଲେ, ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟକୁ ତ୍ରିଭୁଜର ଉଚ୍ଚତା କୁହାଯାଏ । ଲମ୍ବର ଦୈର୍ଘ୍ୟ, ଉଚ୍ଚତା ଅଟେ । ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ A ABCର ଉଚ୍ଚତାଶ୍ରୟ AD, BE ଓ CF
(b) ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଉଚ୍ଚତା : କୌଣସି ଏକ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଯେକୌଣସି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟକୁ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଉଚ୍ଚତା କୁହାଯାଏ । ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ABCD ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଉଚ୍ଚତାଦ୍ବୟ AM ଏବଂ AN
ସମାନ୍ତର ସରଳରେଖାଦ୍ଵୟ ମଧ୍ଯରେ ଅବସ୍ଥିତ କ୍ଷେତ୍ରମାନଙ୍କର ଉଚ୍ଚତା :
(i) ଦୁଇଟି ତ୍ରିଭୁଜ ସମାନ୍ତର ସରଳରେଖାଦ୍ଵୟ ମଧ୍ଯରେ ଅବସ୍ଥିତ ହେଲେ, ସେମାନଙ୍କର ଭୂମି ଏକ ସରଳରେଖା ଉପରେ ଅବସ୍ଥିତ ହେବା ସଙ୍ଗେ ସଙ୍ଗେ ଏମାନଙ୍କର ଶୀର୍ଷବିନ୍ଦୁ ଅପର ସରଳରେଖା ଉପରେ ଅବସ୍ଥିତ ହେବ ।
(ii) ସାମାନ୍ତରିକ କ୍ଷେତ୍ରମାନ ସମାନ୍ତର ସରଳରଖାଦ୍ଵୟ ମଧ୍ଯରେ ଅବସ୍ଥିତ ହେଲେ, ଗୋଟିଏ ସରଳରେଖା ଉପରେ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରଗୁଡ଼ିକର ଗୋଟିଏ ଲେଖାଏଁ ବାହୁ ଏବଂ ଅପର ସମାନ୍ତର ସରଳରେଖା ଉପରେ କ୍ଷେତ୍ରଗୁଡ଼ିକର ବିପରୀତ ବାହୁଗୁଡ଼ିକ ଅବସ୍ଥିତ ହେବ ।
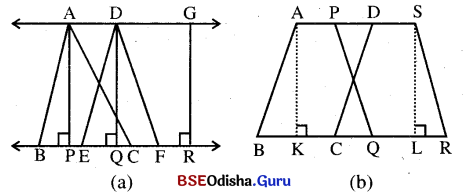
(iii) ଚିତ୍ର (a) ରେ \(\overleftrightarrow{\mathrm{AG}}\) ଓ \(\overleftrightarrow{\mathrm{BR}}\) ଦୁଇଟି ସମାନ୍ତର ସରଳରେଖା ମଧ୍ଯରେ Δ ABC ଓ Δ DEF ଦ୍ଵୟ ଅବସ୍ଥାନ କରୁଛି; କାରଣ ଏହାର ଭୂମି B͞C ଓ B͞F, \(\overleftrightarrow{\mathrm{BR}}\) ଉପରେ ଏବଂ ସେମାନଙ୍କର ଶୀର୍ଷବିନ୍ଦୁ A ଓ D \(\overleftrightarrow{\mathrm{AG}}\) ଉପରେ ଅବସ୍ଥିତ । AP ଓ DQ ଯଥାକ୍ରମେ D ABC ଓ DEFଦ୍ଵୟର ଉଚ୍ଚତା APDQ ଏକ ଆୟତକ୍ଷେତ୍ର ହେତୁ AP = DQ |
(iv) ଚିତ୍ର (b)ରେ \(\overleftrightarrow{\mathrm{AS}}\) ଓ \(\overleftrightarrow{\mathrm{BR}}\) ସମାନ୍ତର ସରଳରେଖା ଦ୍ଵୟ ମଧ୍ୟରେ ABCD ଓ PORS ସାମାନ୍ତରିକ କ୍ଷେତ୍ରଦ୍ଵୟ ଅବସ୍ଥିତ । AK ଓ SL ଯଥାକ୍ରମେ ABCD ଓ PORS ସାମାନ୍ତରିକ କ୍ଷେତ୍ରଦ୍ୱୟର ଉଚ୍ଚତା AKLS ଏକ ଆୟତକ୍ଷେତ୍ର ହେତୁ AK = SLI
{ସମାନ୍ତର ସରଳରେଖାଦ୍ଵୟ ମଧ୍ଯରେ ଅବସ୍ଥିତ କ୍ଷେତ୍ରମାନଙ୍କର ଉଚ୍ଚତା ପରସ୍ପର ସମାନ ।}
(v) ଯଦି ଦୁଇ ବା ତତୋଽଧ୍ୱକ ତ୍ରିଭୁଜ ବା ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର ଉଚ୍ଚତା ସମାନ ହୁଏ ଏବଂ ସେମାନେ ଏକ ସରଳରେଖା ଉପରେ ଓ ତାହାର ଏକ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ହୁଅନ୍ତି, ତେବେ ସେମାନେ ସମାନ୍ତର ସରଳରେଖାଦ୍ବୟ ମଧ୍ୟରେ ଅବସ୍ଥିତ ହେବେ ।
(vi) ABCD ସାମାନ୍ତରିକ କ୍ଷେତ୍ର ଏବଂ A POR ଏକ ସରଳରେଖା B͞R ଉପରେ ଓ ତାହାର ଏକ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ଏବଂ
DK = PL ହେବେ \(\overleftrightarrow{\mathrm{AP}} \| \overleftrightarrow{\mathrm{BR}}\) ହେବ
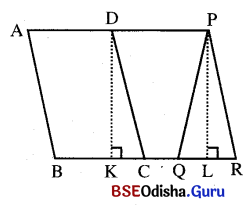
ସର୍ବସମ ସରଳରେଖକ କ୍ଷେତ୍ରମାନଙ୍କର କ୍ଷେତ୍ରଫଳ :
ଦୁଇଟି ସରଳରେଖକ କ୍ଷେତ୍ର ସର୍ବସମ ହେଲେ, ସେମାନଙ୍କର କ୍ଷେତ୍ରଫଳ ସମାନ,
କିନ୍ତୁ କ୍ଷେତ୍ରଫଳ ସମାନ ହେଲେ, ସେମାନେ ସର୍ବସମ ହୋଇନପାରିଛି ।
![]()
ଉପପାଦ୍ୟ ଏବଂ ଅନୁସିଦ୍ଧାନ୍ତ :
ଉପପାଦ୍ୟ 33 : ଏକା ଭୂମି ଉପରେ ଏବଂ ଏକା ସମାନ୍ତର ସରଳରେଖାଦ୍ବୟ ମଧ୍ୟରେ ଅବସ୍ଥିତ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରଗୁଡ଼ିକର କ୍ଷେତ୍ରଫଳ ସମାନ ।
ଅନୁସିଦ୍ଧାନ୍ତ 1 : ଏକା ଭୂମି ଭୁପରେ ଦଣ୍ଡାୟମାନ ଏବଂ ଏକା ଉଚ୍ଚତା ବିଶିଷ୍ଟ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରମାନଙ୍କର କ୍ଷେତ୍ରଫଳ ସମାନ ।
ଅନୁସିଦ୍ଧାନ୍ତ 2 : ଏକା ଭୂମି ଉପରେ ଏବଂ ଏକା ସମାନ୍ତର ସରଳରେଖାଦ୍ଵୟ ମଧ୍ଯରେ ଅବସ୍ଥିତ ସାମାନ୍ତରିକ କ୍ଷେତ୍ର ଓ ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ସମାନ ।
ଅନୁସିଦ୍ଧାନ୍ତ 3 : କୌଣସି ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ, ତାହାର ଭୂମିର ଦୈର୍ଘ୍ୟ ଓ ଉଚ୍ଚତାର ଗୁଣଫଳ ସଙ୍ଗେ ସମାନ ।
ଅନୁସିଦ୍ଧାନ୍ତ 4 : ସମାନ ସମାନ ଭୂମି ଏବଂ ଏକା ସମାନ୍ତର ସରଳରେଖାଦ୍ବୟ ମଧ୍ୟରେ ଅବସ୍ଥିତ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରଗୁଡ଼ିକର କ୍ଷେତ୍ରଫଳ ସମାନ ।
ଅନୁସିଦ୍ଧାନ୍ତ 5 : ଗୋଟିଏ ତ୍ରିଭୁଜ ଓ ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ର ଏକା ଭୂମି ଉପରେ ଏବଂ ଏକା ସମାନ୍ତର ସରଳରେଖାଦ୍ଵୟ ମଧ୍ଯରେ ଅବସ୍ଥିତ ହେଲେ, ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳର ଅର୍ଦ୍ଧେକ ହେବ ।
ଉପପାଦ୍ୟ 34 : ଏକା ଭୂମି ଉପରେ ଏବଂ ଏକା ସମାନ୍ତର ସରଳରେଖାଦ୍ଵୟ ମଧ୍ଯରେ ଅବସ୍ଥିତ ତ୍ରିଭୁଜଗୁଡ଼ିକର କ୍ଷେତ୍ରଫଳ ସମାନ ।
ଅନୁସିଦ୍ଧାନ୍ତ 6 : ସମାନ ସମାନ ଭୂମି ଉପରେ ଏବଂ ଏକା ସମାନ୍ତର ସରଳରେଖାଦ୍ଵୟ ମଧ୍ୟରେ ଅବସ୍ଥିତ ଅର୍ଥାତ୍ ସମାନ ଉଚ୍ଚତା ବିଶିଷ୍ଟ ତ୍ରିଭୁଜଗୁଡ଼ିକର କ୍ଷେତ୍ରଫଳ ସମାନ ।
ଉପପାଦ୍ୟ 35 : ସମାନ କ୍ଷେତ୍ରଫଳବିଶିଷ୍ଟ ତ୍ରିଭୁଜମାନଙ୍କର ଭୂମି ସମାନ ହେଲେ, ସେମାନଙ୍କର ଅନୁରୂପ ଉଚ୍ଚତା ସମାନ ।
ଅନୁସିଦ୍ଧାନ୍ତ 7 : ସମକ୍ଷେତ୍ରଫଳବିଶିଷ୍ଟ ତ୍ରିଭୁଜମାନଙ୍କର ଉଚ୍ଚତା ସମାନ ହେଲେ ସେମାନଙ୍କର ଭୂମିମାନ ସମାନ ହେବ ।
ଉପପାଦ୍ୟ 36 : ଏକା ଭୂମି ଉପରେ ଏବଂ ତାହାର ଏକ ପାର୍ଶ୍ଵରେ ଅବସ୍ଥିତ ସମାନ କ୍ଷେତ୍ରଫଳବିଶିଷ୍ଟ ତ୍ରିଭୁଜମାନ ଏକା ସମାନ୍ତର ସରଳରେଖାଦ୍ଵୟ ମଧ୍ୟରେ ଅବସ୍ଥିତ
କ୍ଷେତ୍ରଫଳ ସମ୍ବନ୍ଧୀୟ କେତେକ ସିଦ୍ଧାନ୍ତ :
- ତ୍ରିଭୁଜ ଓ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରମାନଙ୍କର କ୍ଷେତ୍ରଫଳ, ସେମାନଙ୍କର ଭୂମି ଏବଂ ଉଚ୍ଚତା ଉପରେ ନିର୍ଭର କରେ ।
- ଏହି କ୍ଷେତ୍ରମାନଙ୍କର ଭୂମିର ଦୈର୍ଘ୍ୟ, ଉଚ୍ଚତା ଓ କ୍ଷେତ୍ରଫଳ ମଧ୍ୟରୁ ଯେକୌଣସି ଦୁଇଟି ଏକା ବା ସମାନ ହେଲେ, ତୃତୀୟଟି ଏକା ବା ସମାନ ହେବେ ।
- ଦୁଇଟି ତ୍ରିଭୁଜ ବା ସାମାନ୍ତରିକ କ୍ଷେତ୍ର ଏକା ସମାନ୍ତର ସରଳରେଖାଦ୍ଵୟ ମଧ୍ଯରେ ଅବସ୍ଥିତ ହେଲେ ସେମାନଙ୍କର ଉଚ୍ଚତା ସମାନ ଏବଂ ବିପରୀତ କ୍ରମେ, ସେମାନଙ୍କର ଉଚ୍ଚତା ସମାନ ହେଲେ ଏବଂ ସେମାନେ ଏକ ଭୂମିର ଏକ ପାର୍ଶ୍ଵରେ ଥିଲେ ସେମାନେ ଏକା ସମାନ୍ତର ସରଳରେଖା ମଧ୍ଯରେ ଅବସ୍ଥିତ ହେବେ ।
- ଗୋଟିଏ ତ୍ରିଭୁଜ ଓ ଗୋଟିଏ ସାମାନ୍ତରିକ କ୍ଷେତ୍ର ଏକା ଭୂମି ଉପରେ ଅବସ୍ଥିତ ଏବଂ ଏକା ଉଚ୍ଚତା ବିଶିଷ୍ଟ ହେଲେ ତ୍ରିଭୁଜର କ୍ଷେତ୍ରଫଳ ସାମାନ୍ତରିକ କ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳର ଅର୍ଦ୍ଧେକ ହେବ ।
- ଏକା (ବା ସମାନ) ଭୂମି ଏବଂ ଏକା (ବା ସମାନ) ଉଚ୍ଚତା ବିଶିଷ୍ଟ ସାମାନ୍ତରିକ କ୍ଷେତ୍ର, ଆୟତକ୍ଷେତ୍ର, ରମ୍ବସ୍ ଓ ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ସମାନ ।
