BSE Odisha 9th Class Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(a)

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(a) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 3 ବୀଜଗାଣିତିକ ପରିପ୍ରକାଶ ଓ ଅଭେଦ Ex 3(a)

Question 1.
ନିମ୍ନଲିଖୂତ ମନୋମିଆଲଗୁଡ଼ିକୁ ସାନରୁ ବଡ଼ ଘାତାଙ୍କ କ୍ରମରେ ସଜାଇ ଲେଖ ।
1.4y³, √2y², -51, 7y⁸, -8y⁴, \(\frac{11}{13}\)y⁹, √3y
ସମାଧାନ:
ମନୋମିଆଲଗୁଡ଼ିକୁ ସାନରୁ ବଡ଼ ଘାତାଙ୍କ କ୍ରମରେ ସଜାଇ ଲେଖିଲେ ହେବ –
-51, √3y, √2y², 1.4y³, -8y⁴, 7y⁸, ଓ \(\frac{11}{13}\)y⁹ .

Question 2.
ନିମ୍ନରେ ପ୍ରଦତ୍ତ ମନୋମିଆଲ୍‌ଗୁଡ଼ିକ ମଧ୍ୟରୁ ସଦୃଶ ମନୋମିଆଲ୍‌ଗୁଡ଼ିକୁ ବାଛି ପୃଥକ୍ ଭାବେ ଲେଖ ।
12x², -3x, \(\frac{1}{\sqrt{2}}\) x³, -5x², \(\frac{x}{7}\), 15, √3x³, 10x⁴, \(\frac{8}{11}\)
ସମାଧାନ:
(12x², -5x²), (-3x, \(\frac{x}{7}\)), (\(\frac{1}{\sqrt{2}}\) x³, √3x³), (15, \(\frac{8}{11}\))
ସଦୃଶ ମନୋମିଆଲ୍‌ଗୁଡ଼ିକୁ ବନ୍ଧନୀ ମଧ୍ଯରେ ରଖାଯାଇଛି ।

Question 3.
ନିମ୍ନସ୍ଥ ପ୍ରତ୍ୟେକ ପ୍ରକାର ପଲିନୋମିଆଲ୍‌ରୁ ଦୁଇଟି ଲେଖାଏଁ ଉଦାହରଣ ଦିଅ ।

(i) ଣୂନଘାତା ପଲିନୋମିଆଲ୍
ସମାଧାନ:
2, –\(\frac{1}{4}\)

(ii) ଏକପଦ ବିଶିଷ୍ଟ ଦ୍ୱିଘାତୀ ପଲିନୋମିଆଲ୍
ସମାଧାନ:
5x², -3x²

(iii) ଦୁଇପଦ ବିଶିଷ୍ଟ ତ୍ରିଘାତୀ ପଲିନୋମିଆଲ୍
ସମାଧାନ:
2x³ – 3x², \(\frac{4}{5}\) x³ + 5x

(iv) ତିନିପଦ ବିଶିଷ୍ଟ ଦ୍ୱିଘାତୀ ପଲିନୋମିଆଲ୍
ସମାଧାନ:
x² – 3x + 2, 3x² – 4x – 5
(ଦତ୍ତ ଉଦାହରଣ ବ୍ୟତୀତ ଅନ୍ୟ ଉଦାହରଣ ଦିଆଯାଇପାରେ ।)

Question 4.
ଯାେଗ କର

(i) 2y³ – 3y – 4, 2 – y³ + 5y
ସମାଧାନ:
(2y³ – 3y –  4) + (2 – y³ + 5y)
= (2y² – 3y –  4) + (-y³ + 5y + 2) (ପ୍ରତ୍ୟେକ ପଲିନୋମିଆଲ୍‌କୁ ଘାତାଙ୍କ କ୍ରମରେ ସଜାଇବା)
= (2y³ –  y³) + (-3y + 5y) + (- 4 + 2) (ସଦୃଶ ପଦଗୁଡ଼ିକୁ ଏକାଠି କରି)
= y³ + 2y – 2
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = y³ + 2y – 2

(ii) 3x⁴ – 2x³ – 5 + x – 5x², 3x³ + 2x² – x⁴ – x + 1
ସମାଧାନ:
(3x⁴ – 2x³ – 5 + x – 5x²) + (3x³ + 2x² – x⁴ – x + 1)
= (3x⁴ – 2x³ – 5x² + x – 5) + (-x⁴ + 3x³ + 2x² – x + 1) (ଘାତାଙ୍କ କ୍ରମରେ ସଜାଇ)
= (3x⁴ – x⁴) + (-2x³ + 3x³) + (-5x² + 2x²) + (x – x) + (-5 + 1) (ସଦୃଶ ପଦଗୁଡ଼ିକୁ ଏକାଠି କରି)
= 2x⁴ + x³ – 3x² + 0 – 4 = 2x⁴ + x³ – 3x² – 4
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = 2x⁴ + x³ – 3x² – 4

(iii) \(\frac{3}{4}\) x² – \(\frac{4}{5}\) x – 3, \(\frac{1}{4}\) x² + \(\frac{4}{5}\) x + 2
ସମାଧାନ:
\(\left(\frac{3}{4} x^2-\frac{4}{5} x-3\right)+\left(\frac{1}{4} x^2+\frac{4}{5} x+2\right)\)
= \(\left(\frac{3}{4} x^2+\frac{1}{4} x^2\right)+\left(-\frac{4}{5} x+\frac{4}{5} x\right)\) + (-3 + 2) (ସଦୃଶ ପଦଗୁଡ଼ିକୁ ଏକାଠି କରି)
= \(\frac{4}{4}\) x² + 0.x – 1 = x² – 1
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = x² – 1

(iv) 2.1x³ + 3.2x² + 5 – 3x, 1.9x³ – 1.2x² + 2x – 1
ସମାଧାନ:
(2.1x³ + 3.2x² + 5 – 3x) + (1.9x³ – 1.2x² + 2x – 1)
= (2.1x³ + 3.2x² – 3x + 5) + (1.9x³ – 1.2x² + 2x – 1)
= (2.1x³ + 1.9x³) + (3.2x² – 1.2x²) + (-3x + 2x) + (5 – 1)
= 4x³ + 2x² – x + 4
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = 4x³ + 2x² – x + 4

(v) \(\frac{1}{2}\)z³ – \(\frac{3}{2}\) z² + 6z, \(\frac{1}{2}\) z² – \(\frac{1}{2}\) z³ – 3z – 1, z³ + 2z² + 3z – 4
ସମାଧାନ:

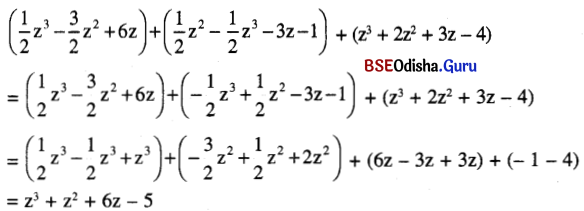
(vi) 8x – 3xy + 2xyz, 2xy – 5x + 3xyz, xy – 3x + 4xyz
ସମାଧାନ:
(8x – 3xy + 2xyz) + (2xy – 5x + 3xyz) + (xy – 3x + 4xyz)
= (2xyz – 3xy + 8x) + (3xyz + 2xy – 5x) + (4xyz + xy – 3x)
= (2xyz + 3xyz + 4xyz) + (- 3xy + 2xy + xy) + (8x- 5x – 3x)
= 9xyz + 0 + 0 = 9xyz
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = 9xyz

(vii) 5x² – 2xy + y², 4xy – 2y² – 3x², 4y² – xy – x²
ସମାଧାନ:
(5x² – 2xy + y²) + (4xy – 2y² – 3x²) + (4y² – xy + x²)
= (5x² – 2xy + y²) + (-3x² + 4xy – 2y²) + (-x² – xy + 4y²)
= (5x² – 3x² – x²) + (-2xy + 4xy – xy) + (y² – 2y² + 4y²)
= x² + xy + 3y²
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = x² + xy + 3y²

Question 5.
ବିୟୋଗ କର :

(i) 6x³ – 13x² + 14 ରୁ -x³ + 2x – 7x² + 11
ସମାଧାନ:
(6x³ – 13x² + 14) – (-x³ + 2x – 7x² + 11)
= (6x³ – 13x² + 14) – (-x³ – 7x² + 2x + 11) (ଘାତାଙ୍କ କ୍ରମରେ ଲେଖିଲେ)
= (6x³ – 13x² + 14) + {- (-x³ – 7x² + 2x + 11)} [∵ a – b = a + (- b)]
= (6x³ – 13x² + 14) + (x³ + 7x² – 2x – 11)
= 6x³ + x³ – 13x² + 7x² – 2x + 14 – 11 (ସଦୃଶ ପଦଗୁଡ଼ିକୁ ଏକାଠି କରି ସଜାଇ ଲେଖିଲେ)
= 7x³ – 6x² – 2x + 3
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = 7x³ – 6x² – 2x + 3

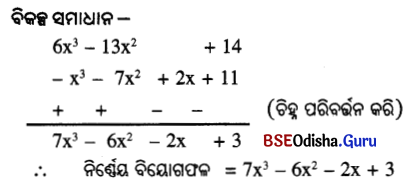
(ii) t⁴ – 11 + 2t² – t³ ରୁ 2t³ – 8t² – 10
ସମାଧାନ:
(t⁴ – 11 + 2t² – t³) – (2t³ – 8t² – 10)
= (t⁴ – t³ + 2t² – 11) – (2t³ – 8t² – 10)
= (t⁴ – t³ + 2t² – 11) + {-(2t³ – 8t² – 10)}
= (t⁴ – t³ + 2t² – 11) + (-2t³ + 8t² + 10)
= t⁴ – t³ – 2t³ + 2t² + 8t² – 11 + 10 = t⁴ – 3t³ + 10t² – 1
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = t⁴ – 3t³ + 10t² – 1

(iii) \(\frac{12}{13}\) y² – \(\frac{5}{13}\) y³ – 15 ରୁ – \(\frac{1}{13}\) y² + \(\frac{8}{13}\) y³ + 20
ସମାଧାନ:

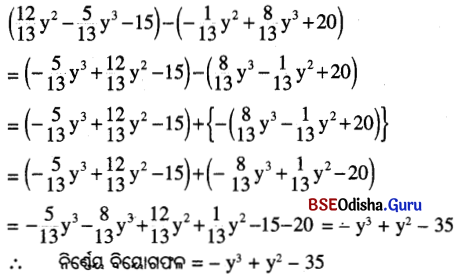
(iv) 2.5x³ – 7 – 3.5x² ରୁ 2.5x² + 1.5x³ + 8 – 2x
ସମାଧାନ:
(2.5x³ – 7 – 3.5x²) – (2.5x² + 1.5x³ + 8 – 2x)
= (2.5x³ – 3.5x² – 7) – (1.5x³ + 2.5x² – 2x + 8)
= (2.5x³ – 3.5x² – 7) + {-(1.5x³ + 2.5x² – 2x + 8)}
= (2.5x³ – 3.5x² – 7) + (-1.5x³ – 2.5x² + 2x – 8)
= 2.5x³ – 1.5x³ – 3.5x² – 2.5x² + 2x – 7 – 8
= x³ – 6x² + 2x – 15
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = x³ – 6x² + 2x – 15

(v) x² – 2xy + 3y² ରୁ 2x² – xy – 2y²
ସମାଧାନ:
(x² – 2xy + 3y²) – (2x² – xy – 2y²)
= (x² – 2xy + 3y²) + {-(2x² – xy – 2y²)}
= (x² – 2xy + 3y²) + (-2x² + xy + 2y²)
= x² – 2x² – 2xy + xy + 3y² + 2y² = -x² – xy + 5y²
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = -x² – xy + 5y²

(vi) 2x² – 3xy – 4xy² ରୁ x² – xy – 2xy²
ସମାଧାନ:
(2x² – 3xy- 4xy²) – (x² – xy – 2xy²)
= (2x² – 3xy – 4xy²) + {-(x² – xy – 2xy²)}
= (2x² – 3xy – 4xy²) + (-x² + xy + 2xy²)
= 2x² – x² – 3xy + xy – 4xy² + 2xy² = x² – 2xy – 2xy²
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = x² – 2xy – 2xy²

(vii) a – 3b + 2c ରୁ 3b – 7c + 2a
ସମାଧାନ:
(a – 3b + 2c) – (3b – 7c + 2a) = (a – 3b + 2c) – (2a + 3b – 7c)
= (a – 3b + 2c) + {-(2a + 3b – 7c)} = (a – 3b + 2c) + (-2a – 3b + 7c)
= a – 2a – 3b – 3b + 2c + 7c = -a – 6b + 9c
∴ ନିର୍ଣ୍ଣେୟ ଯୋଗଫଳ = -a – 6b + 9c

(viii) \(\frac{1}{2}\) a + \(\frac{2}{3}\) b – \(\frac{3}{2}\) c ରୁ a – \(\frac{1}{3}\) b + \(\frac{1}{2}\) c
ସମାଧାନ:

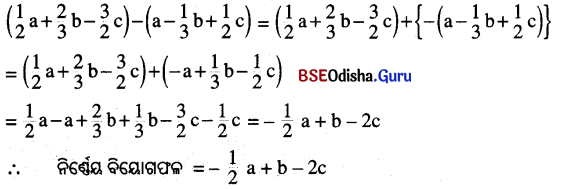
Question 6.
ନିମ୍ନରେ ଦତ୍ତ ପଲିନୋମିଆଲ୍‌ଗୁଡ଼ିକର ଗୁଣଫଳ ସ୍ଥିର କରି ଗୁଣଫଳର ଘାତ ନିରୂପଣ କର ।

(i) 2x² – 3x + 5 ଓ x² + 8x + 2
ସମାଧାନ:
(2x² – 3x + 5)(x² + 5x + 2)
= 2x²(x² + 5x + 2) -3x(x² + 5x + 2) + 5(x² + 5x + 2) ( ବଣ୍ଠନ ନିୟମ)
= 2x⁴ + 10x³ + 4x² – 3x³ – 15x² – 6x + 5x² + 25x + 10 (ପୁନଃବଣ୍ଟନ ନିୟମ)
= 2x⁴ + (10x³ – 3x³) + (4x² – 15x² + 5x²) + (-6x + 25x) + 10 (ସଦୃଶ ପଦଗୁଡ଼ିକୁ ଏକାଠି ରଖୁ)
= 2x⁴ + 7x³ – 6x² + 19x + 10
∴ ଗୁଣଫଳର ଘାତ = 4 ।
∴ ଯଦି p(x) ଓ q(x) ଦୁଇଟି ପଲିନୋମିଆଲ୍ ହୁଏ, ତେବେ {p(x) × g(x)} ର ଘାତ = p(x)ର ଘାତ + q(x)ର ଘାତ ।

(ii) y³ – 5y² + 11y ଓ y⁵ – 20y⁴ + 17
ସମାଧାନ:
(y³ – 5y² + 11y)(y⁵ – 20y⁴ + 17)
= y³(y⁵ – 20y⁴ + 17) – 5y²(y⁵ – 20y⁴ + 17) + 11y(y⁵ – 20y⁴ + 17)
=y⁸ – 20y⁷ + 17y³ – 5y⁷ + 100y⁶ – 85y² + 11y⁶ – 220y⁵ + 187y
=y⁸ + (-20y⁷ – 5y⁷) + (100y⁶ + 11y⁶) – 220y⁵ + 17y³ – 85y² + 187y
= y⁸ – 25y⁷ + 111y⁶ – 220y⁵ + 17y³ – 85y² + 187y
∴ ଗୁଣଫଳର ଘାତ = 8 ।

(iii) (2x + 3) ଓ 5x² – 7x + 8
ସମାଧାନ:
(2x + 3)(5x² – 7x + 8)
= 2x(5x² – 7x + 8) + 3(5x² – 7x + 8) = 10x³ – 14x² + 16x + 15x² – 21x + 24
= 10x³ + (-14x² + 15x²) + (16x – 21x) + 24 = 10x³ + x² – 5x + 24
∴ ଗୁଣଫଳର ଘାତ = 3 ।

(iv) (x – 1), (7x – 9) ଓ 3x³ – 14x² + 8
ସମାଧାନ:
(x – 1)(7x – 9)(3x³ – 14x² + 8)
= {(x – 1)(7x – 9)} (3x³ – 14x² + 8) = {x(7x – 9) – 1(7x – 9)} (3x³ – 14x² + 8)
= (7x² – 9x – 7x + 9)(3x³ – 14x² + 8) = (7x² – 16x + 9)(3x³ – 14x² + 8)
= 7x² (3x³ – 14x² + 8) – 16x(3x³ – 14x² + 8) + 9(3x³ – 14x² + 8)
= 21x⁵ – 98x⁴ + 56x² – 48x⁴ + 224x³ – 128x + 27x³ – 126x² + 72
= 21x⁵ + (- 98x⁴ – 48x⁴) + (224x³ + 27x³) + (56x² – 126x²) – 128x + 72
= 21x⁵ – 146x⁴ + 251x³ – 70x² – 128x + 72
∴ ଗୁଣଫଳର ଘାତ = 5 ।

(v) (x² + y²) ଓ (x⁴ – x²y² + y⁴)
ସମାଧାନ:
(x² + y²)(x⁴ – x²y² + y⁴)
= x² (x⁴ – x²y² + y⁴) + y² (x⁴ – x²y² + y⁴) = x⁶ – x⁴y² + x⁷y⁴ + x⁴y² – x²y⁴ + y⁶
= x⁶ + (-xy + x⁴y²) + (x²y⁴ – x²y⁴) + y⁶ = x⁶ + 0 + 0 + y⁶ = x⁶ + y⁶
∴ ଗୁଣଫଳର ଘାତ = 6 ।

(vi) (2x + 3y), (2x – 3y) ଓ (4x² + 9y²)
ସମାଧାନ:
(2x + 3y)(2x – 3y)(4x² + 9y²) = {(2x + 3y)(2x – 3y)} (4x² + 9y²)
= {2x(2x – 3y) + 3y(2x – 3y)} (4x² + 9y²)
= (4x² – 6xy + 6xy – 9y²)(4x² + 9y²) = (4x² – 9y²)(4x² + 9y²)
= 4x² (4x² + 9y²) – 9y² (4x² + 9y²) = 16x⁴ + 36x²y² – 36x²y² – 81y⁴
= 16x⁴ + 0 – 81y⁴ = 16x⁴ – 81y⁴
∴ ଗୁଣଫଳର ଘାତ = 4 ।

Question 7.
ଭାଗଫଳ ଓ ଭାଗଶେଷ ନିରୂପଣ କର ।

(i) (x³ – 1) + (x – 1)
ସମାଧାନ:

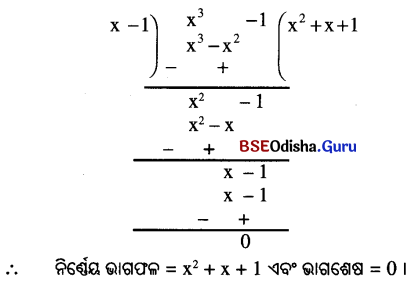
(ii) (-81y² + 64) + (8 – 9y)
ସମାଧାନ:

(iii) (2x³ – 7x² – x + 2) + (x² – 3x – 2)
ସମାଧାନ:

(iv) (x³ – 14x² + 37x – 26) + (x – 2)
ସମାଧାନ:

(v) (t³ – 6t² + 11t – 6) + (t² – 5t + 6)
ସମାଧାନ:

(vi) (8a² – 34ab + 21b²) + (4a + 3b)
ସମାଧାନ:

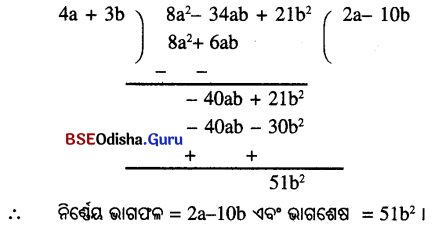
(vii) (16xy² – 21x²y + 9X³ – 4y3) + (x – y)
ସମାଧାନ:

(viii) (x⁴ + x²y² + y4) + (x² – xy + y²)
ସମାଧାନ:

ଭାଜ୍ୟ = ଭାଜକ x ଭାଗଫଳ + ଭାଗଶେଷ Euclidian Algorithmର ପ୍ରୟୋଗରେ ଭାରକ୍ରିୟାର ସତ୍ୟତା ନିରୂପଣ କରାଯାଇଥାଏ ।

Question 8.
ଯଦି p(x) = 3x³ – 6x² + 2 ଏବଂ q(x) = 2x² – 5x + 1 ତେବେ

(i) 2p(x) – 5q(x)
ସମାଧାନ:
ଯଦି p(x) = 3x³ – 6x² + 2 ଏବଂ q(x) = 2x² – 5x + 1
2p(x) – 5q(x) = 2(3x³ – 6x² + 2) – 5(2x² – 5x + 1)
= 6x³ – 12x² + 4 – 10x² + 25x – 5
= 6x³ – 12x² – 10x² + 25x + 4 – 5 = 6x³ – 22x² + 25x – 1

(ii) 4p(x) + 3q(x) ବମାନ ସ୍ଥିର କରା
ସମାଧାନ:
ଯଦି p(x) = 3x³ – 6x² + 2 ଏବଂ q(x) = 2x² – 5x + 1
4p(x) + 3q(x) = 4(3x³ – 6x² + 2) + 3(2x² – 5x + 1)
= 12x³ – 24x² + 8 + 6x² – 15x + 3
= 12x³ – 24x² + 6x² – 15x + 8 + 3 = 12x³ – 18x² – 15x + 11

Question 9.
ଯଦି p(x) = 2x³ + 3x + 5 ଏବଂ q(x) = x² + 4x + 1 ଓ r(x) = x – 1 ହୁଏ ତେବେ ଦର୍ଣ।ଅ ଯେ,

(i) p(x) × q(x) = q(x) × p(x)
ସମାଧାନ:
ଯଦି p(x) = 2x³ + 3x + 5 ଏବଂ q(x) = x² + 4x + 1 ଓ r(x) = x – 1
ବାମପାର୍ଶ୍ଵ = p(x) × q(x) = (2x³ + 3x + 5)(x² + 4x + 1)
= 2x³ (x² + 4x + 1) + 3x(x² + 4x + 1) + 5(x² + 4x + 1)
= 2x⁵ + 8x⁴ + 2x³ + 3x³ + 12x² + 3x + 5x² + 20x + 5
= 2x⁵ + 8x⁴ + 5x³ + 12x² + 5x² + 3x + 20x + 5
= 2x⁵ + 8x⁴ + 5x³ + 17x² + 23x + 5
ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ = q(x) × p(x) = (x² + 4x + 1)(2x³ + 3x + 5)
= x² (2x³ + 3x + 5) + 4x (2x³ + 3x + 5) + 1(2x³ + 3x + 5)
= 2x⁵ + 3x³ + 5x² + 8x⁴ + 12x² + 20x + 2x³ + 3x + 5
= 2x⁵ + 8x⁴ + 3x³ + 2x³ + 5x² + 12x² + 20x + 3x + 5
= 2x⁵ + 8x⁴ + 5x³ + 17x² + 23x + 5 (ପଲିନୋମିଆଲ୍ ଦ୍ଵୟର ଗୁଣନ କ୍ରମବିନିମୟୀ ।)
∴ ବାମପାର୍ଶ୍ଵ = ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ (ପ୍ରମାଣିତ)

(ii) p(x) × {(q(x) + r(x)} = p(x) . q(x) + p(x) . r(x)
ସମାଧାନ:
ବାମପାର୍ଶ୍ଵ = P(x) × {q(x) + r(x)}
= (2x³ + 3x + 5) x {(x² + 4x + 1) + (x – 1)} = (2x³ + 3x + 5) + (x² + 4x + 1 + x – 1)
= (2x³ + 3x + 5)(x² + 5x) = 2x³ (x² + 5x) + 3x(x² + 5x) + 5(x² + 5x)
= 2x⁵ + 10x⁴ + 3x³ + 15x² + 5x² + 25x = 2x⁵ + 10x⁴ + 3x³ + 20x² + 25x
ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ = P(x) . q(x) + p(x) . r(x)
= (2x³ + 3x + 5)(x² + 4x + 1) + (2x³ + 3x + 5)(x – 1)
= 2x³ (x2 + 4x + 1) + 3x(x² + 4x + 1) + 5(x² + 4x + 1)+ 2x³ (x – 1) + 3x(x – 1) + 5(x – 1)
= 2x⁵ + 8x⁴ + 2x³ + 3x³ + 12x² + 3x + 5x² + 20x + 5 + 2x⁴ – 2x³ + 3x² – 3x + 5x – 5
= 2x⁵ + 8x⁴ + 2x⁴ + 2x³ + 3x³ – 2x³ + 12x² + 5x² + 3x² + 3x + 20x – 3x + 5x + 5 – 5
= 2x⁵ + 10x⁴ + 3x³ + 20x² + 25x
∴ ବାମପାର୍ଶ୍ଵ = ଦକ୍ଷିଣ ପାର୍ଶ୍ଵ (ପ୍ରମାଣିତ)
(ପଲିନୋମିଆଲ୍ ଦ୍ଵୟର ଗୁଣନ କ୍ରମବିନିମୟୀ ।)

Question 10.
ସରଳ କର :

(i) (x² – 3x + 5) + (2x² – x – 2) – (3x² + 7x – 3)
ସମାଧାନ:
(x² – 3x + 5) + (2x² – x – 2) – (3x² + 7x – 3)
= x² – 3x + 5 + 2x² – x – 2 – 3x² – 7x + 3
= x² + 2x² – 3x² – 3x – x – 7x + 5 – 2 + 3
= 0 – 11x + 6 = -11x + 6

(ii) (x² – xy + 2y²) – (2x² + 4xy + 3y²) + (4x² – 2xy – y²)
ସମାଧାନ:
(x² – xy + 2y²) – (2x² + 4xy + 3y²) + (4x² – 2xy – y²)
= x² – xy + 2y² – 2x² – 4xy – 3y² + 4x² – 2xy – y²
= x² – 2x² + 4x² – xy – 4xy – 2xy + 2y² – 3y² – y²
= 3x² – 7xy – 2y²

(iii) (x + b + c) (a – b + c) – (a + b – c) (a – b – c)
ସମାଧାନ:
(a + b + c)(a – b + c) – (a + b – c)(a – b – c)
= [a(a – b + c) + b(a – b + c) + c(a – b + c)] – [a(a – b – c) + b(a – b – c) – c(a – b – c)]
= (a² – ab + ca + ab – b² + bc + ca –  bc + c²) – (a² – ab – ac + ab – b² – bc – ca + bc + c²)
= (a² – b² + c² – ab + ab + ca + ca + bc – bc) – (a² – b² + c² – ab + ab – ac – ac – bc + bc)
= (a² – b² + c² + 2ca) – (a² – b² + c² – 2ca) = a² – b² + c² + 2ca – a² + b² – c² + 2ca
= a² – a² – b² + b² + c² – c² + 2ca + 2ca = 4ca