BSE Odisha 9th Class Maths Solutions Algebra Chapter 6 ଅନୁପାତ ଓ ସମାନୁପାତ Ex 6

Odisha State Board BSE Odisha 9th Class Maths Solutions Algebra Chapter Chapter 6 ଅନୁପାତ ଓ ସମାନୁପାତ Ex 6 Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Algebra Chapter 6 ଅନୁପାତ ଓ ସମାନୁପାତ Ex 6

Question 1.
ବନ୍ଧନୀ ମଧ୍ଯରୁ ଠିକ୍ ଉତ୍ତରଟି ବାଛି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

(i) a : b = 3 : 4, b : c = 5 : 6, c : d = 11 : 9 ହେଲେ, a : d = _______ (65 : 84, 30 : 40, 55 : 72, 45 : 63)
ସମାଧାନ:
55 : 72

(ii) \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{2}{5}\) ହେଲେ, \(\frac{a}{d}\) = ______ (\(\frac{4}{25}, \frac{5}{2}, \frac{8}{125}, \frac{2}{25}\))
ସମାଧାନ:
\(\frac{8}{125}\)

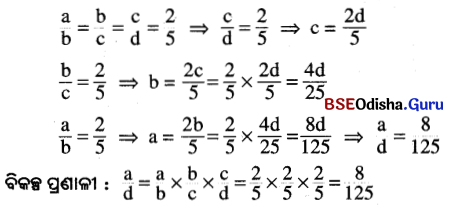
(iii) p : q :: r : s ହେଲେ, p : r = ______ (q : s, s : q, p : s, q : r)
ସମାଧାନ:
q : s
\(\frac{\mathrm{p}}{\mathrm{q}}=\frac{\mathrm{r}}{\mathrm{s}} \Rightarrow \frac{\mathrm{p}}{\mathrm{r}}=\frac{\mathrm{q}}{\mathrm{s}}\)

(iv) a : b = 2 : 3 ହେଲେ, (4a + b) : (2a + 3b) = _______ (3 : 5, 5 : 8, 7 : 9, 11 : 13)
ସମାଧାନ:
11 : 13
\(\frac{4 a+b}{2 a+3 b}=\frac{4\left(\frac{a}{b}\right)+1}{2\left(\frac{a}{b}\right)+3}=\frac{4 \times \frac{2}{3}+1}{2 \times \frac{2}{3}+3}=\frac{8+8}{4+9}=\frac{11}{13}\)
∴ (4a + b) : (2a + 3b) = 11 : 13

(v) 2x = 3y = 4z ହେଲେ, x : y : z = ______ (2 : 3 : 4, 6 : 4 : 3, 2 : 3 : 4, 4 : 3 : 2)
ସମାଧାନ:
6 : 4 : 3
2x = 3y = 4z = k (ମନେକର) x = \(\frac{k}{2}\), y = \(\frac{k}{3}\), z = \(\frac{k}{4}\)
(x : y : z = \(\frac{k}{2}\) : \(\frac{k}{3}\) : \(\frac{k}{4}\) = 6k : 4k : 3k = 6 : 4 : 3

(vi) x : y = 2 : 5, y : z = 3 : 4 ହେଲେ, x : y : z = _______ (20 : 15 : 6, 6 : 15 : 20, 2 : 5 : 3, 5 : 3 : 4)
ସମାଧାନ:
6 : 15 : 20
\(\frac{x}{y}=\frac{2}{5}=\frac{2 \times 3}{5 \times 3}=\frac{6}{15}, \frac{y}{z}=\frac{3}{4}=\frac{3 \times 5}{4 \times 5}=\frac{15}{20}\)
∴ x : y : z = 6 : 15 : 20

(vii) 3 : (k + 2) :: 5 : (k + 4) ହେଲେ, k = ________ (2, 4, 1, 6)
ସମାଧାନ:
1
\(\frac{3}{k+2}=\frac{5}{k+4}\) ⇒ 3 (k + 4) = 5(k + 2)
⇒ 3k + 12 = 5k + 10 ⇒ 2k = 2 ⇒ k = 1

Question 2.
ନିମ୍ନ ଉକ୍ତିଗୁଡ଼ିକ ଠିକ୍ ବା ଭୁଲ୍ ଦର୍ଶାଅ ।

(i) a, b, c, d ସମାନୁପାତୀ ହେଲେ, ସମସ୍ତ ରାଶି ଏକ ଜାତୀୟ ହେବା ଆବଶ୍ୟକ ।
ସମାଧାନ:
ଭୂଲ
a, b, c, d ସମାନୁପାତୀ ହେଲେ, ସମସ୍ତ ରାଶି ସମଜାତୀୟ ହେବା ଆବଶ୍ୟକ ।
ଉକ୍ତିଟି ଭୁଲ ଅଟେ ।
କାରଣ –2 ମିଟର ଓ 5 ମିଟର ଅନୁପାତ ଯାହା 2 kg ଓ 5 kg, 2 sec ଓ 5 sec, 2 ଟନ୍ ଓ 5 ଟନ୍‌ର ଅନୁପାତ ତାହା । ତେଣୁ ସମାନୁପାତ ପାଇଁ ରାଶିଗୁଡ଼ିକ ସମଜାତୀୟ ହେବାର ଆବଶ୍ୟକତା ନାହିଁ ।

(ii) a, b, c, d ସମାନୁପାତୀ ହେଲେ, ସେମାନେ କ୍ରମିକ ସମାନୁପାତୀ ହେବେ ।
ସମାଧାନ:
ଭୂଲ
ଉକ୍ତିଟି ଭୁଲ ଅଟେ ।
କାରଣ – 5, 10, 7, 14 ସମାନୁପାତୀ ହେଲେ ସେମାନେ କ୍ରମିକ ସମାନୁପାତୀ ନୁହଁନ୍ତି ।
ଅଥ।ତ୍ \(\frac{5}{10} \neq \frac{10}{7} \neq \frac{7}{14}\)

(iii) କ୍ରମିକ ସମାନୁପାତରେ ସମସ୍ତ ରାଶି ଏକ ଜାତୀୟ ହେବେ ।
ସମାଧାନ:
ଠିକ୍
ଉକ୍ତିଟି ଠିକ୍ ଅଟେ ।
କାରଣ – କ୍ରମିକ ସମାନୁପାତୀରେ ପ୍ରଥମ-ଦ୍ୱିତୀୟ, ଦ୍ୱିତୀୟ-ତୃତୀୟ ରାଶି ମଧ୍ୟରେ ପରସ୍ପର ସମ୍ପର୍କ ଥାଏ, ତେଣୁ ରାଶିଗୁଡ଼ିକ ସମଜାତୀୟ ହେବା ଆବଶ୍ୟକ ।

(iv) ଚାରୋଟି ରାଶି କ୍ରମିକ ସମାନୁପାତୀ ହେଲେ, ପ୍ରଥମ ଓ ଚତୁର୍ଥର ଅନୁପାତ, ଦ୍ୱିତୀୟ ଓ ତୃତୀୟର ଘନାନୁପାତ ସହିତ
ସମାଧାନ:
ଠିକ୍
ମନେକର a, b, c ଓ d କ୍ରମିକ ସମାନୁପାତୀ ।
⇒ \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}\) ⇒ ac = b², bd = c², ad = bc
ପ୍ରମାଣ କରିବା, \(\frac{a}{d}=\frac{b^3}{c^3}\)
ଦକ୍ଷିଣପାର୍ଶ୍ବ = \(\frac{b^3}{c^3}=\frac{b^2 \cdot b}{c^2 \cdot c}=\frac{a c b}{b d c}=\frac{a}{d}\) = L.H.S ∴ ଉକ୍ତିଟି ଠିକ୍ ଅଟେ ।
ବିକକ୍ପ ପ୍ରମାଳା \(\frac{a}{d}=\frac{a}{b} \times \frac{b}{c} \times \frac{c}{d}=\left(\frac{b}{c}\right)^3 \quad\left[∴ \frac{a}{b}=\frac{c}{d}=\frac{b}{c}\right]\)

(v) ତିନୋଟି ରାଶି କ୍ରମିକ ସମାନୁପାତୀ ହେଲେ ପ୍ରଥମ ଓ ତୃତୀୟର ଅନୁପାତ, ଦ୍ଵିତୀୟ ଓ ତୃତୀୟର ବର୍ଗାନୁପାତ ସହିତ ସମାନ ।
ସମାଧାନ:
ଠିକ୍
ମନେକର a, b ଓ c କ୍ରମିକ ସମାନୁପାତୀ । ପ୍ରମାଣ କରିବା \(\frac{a}{c}=\frac{b^2}{c^2}\)
a, b ଓ c କ୍ରମିକ ସମାନୁପାତୀ ⇒ \(\frac{a}{b}=\frac{b}{c}\) ⇒ b² = ac
ଦକ୍ଷିଣପାର୍ଶ୍ବ = \(\frac{b^2}{c^2}=\frac{a c}{c^2}=\frac{a}{c}\) = ବାମପାର୍ଶ୍ବ ∴ ଉକ୍ତିଟି ଠିକ୍ ଅଟେ ।

(vi) ଚାରୋଟି ରାଶି କ୍ରମିକ ସମାନୁପାତୀ ହେଲେ, ପ୍ରଥମ ଓ ଦ୍ଵିତୀୟର ଅନୁପାତ, ପ୍ରଥମ ଓ ତୃତୀୟର ଉପବର୍ଗାନୁପାତ ସହିତ ସମାନ ।
ସମାଧାନ:
ଠିକ୍
ମନେକର a, b, c, d କ୍ରମିକ ସମାନୁପାତୀ ⇒ \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d} \Rightarrow \frac{a}{b}=\frac{b}{c}\) ⇒ b² = ac
ପ୍ରମାଣ କରିବା \(\frac{a}{b}=\frac{\sqrt{a}}{\sqrt{c}}\)
ଦକ୍ଷିଣପାର୍ଶ୍ବ = \(\frac{\sqrt{a}}{\sqrt{c}}=\sqrt{\frac{a c}{c^2}}=\sqrt{\frac{b^2}{c^2}}=\frac{b}{c}=\frac{a}{b}\)
∴ ଉକ୍ତିଟି ଠିକ୍ ଅଟେ ।

(vii) a, b, c କ୍ରମିକ ସମାନୁପାତୀ ହେଲେ, a + 2, b + 2, c + 2 ମଧ୍ଯ କ୍ରମିକ ସମାନୁପାତୀ ହେବେ ।
ସମାଧାନ:
ଭୂଲ
a, b, c ରାଶିତ୍ରୟ କ୍ରମିକ ସମାନୁପାତୀ ହେଲେ \(\frac{a+2}{b+2}=\frac{b+2}{c+2}\) ଉକ୍ତିଟି ଭୁଲ୍ ।
କାରଣ 2, 4, 8 କ୍ରମିକ ସମାନୁପାତୀ କିନ୍ତୁ \(\frac{2+2}{4+2} \neq \frac{4+2}{8+2}\) ∴ ଉକ୍ତିଟି ଭୁଲ୍ ଅଟେ ।

(viii) ଚାରୋଟି ରାଶି କ୍ରମିକ ସମାନୁପାତୀ ହେଲେ, ସେମାନଙ୍କର ବ୍ୟସ୍ତାନୁପାତଗୁଡ଼ିକ ମଧ୍ୟ କ୍ରମିକ ସମାନୁପାତୀ ହେବେ ।
ସମାଧାନ:
ଠିକ୍
a, b, c, d କ୍ରମିକ ସମାନୁପାତୀ ହେଲେ \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d} \Rightarrow \frac{b}{a}=\frac{c}{b}=\frac{d}{c}\)
∴ ଉକ୍ତିଟି ଭୁଲ୍ ଅଟେ ।

Question 3.
ନିମ୍ନ ରାଶିମାନଙ୍କର ଚତୁର୍ଥ ସମାନୁପାତୀ ନିର୍ଣ୍ଣୟ କର ।

{\(\frac{a}{b}=\frac{c}{d}\) ରେ ‘d’ ରାଶି a, b, cର ଚତୁର୍ଥ ସମାନୁପାଢ।}

(i) 5, 7, 15
ସମାଧାନ:
ମନେକର ଚତୁର୍ଥ ସମାନୁପାତୀ x  ∴ 5, 7, 15 ଓ x ସମାନୁପାତୀ
⇒ \(\frac{5}{7}=\frac{15}{x}\) ⇒ 5x = 15 × 7 ⇒ x = \(\frac{15 \times 7}{5}\) = 21
∴ ନିର୍ଦେୟ ଚତୁର୍ଥ ସମାନୁପାତୀ 21 ।

(ii) 0.1, 0.01, 0.001
ସମାଧାନ:
ମନେକର ଚତୁର୍ଥ ସମାନୁପାତୀ x  ∴ 0.1, 0.01, 0.001 ଓ x ସମାନୁପାତୀ
⇒ \(\frac{0.1}{0.01}=\frac{0.001}{x} \Rightarrow \frac{10}{1}=\frac{1}{1000 x}\) ⇒ 10000x =1 ⇒ x = \(\frac{1}{10000}\) = 0.0001
∴ ନିର୍ଦେୟ ଚତୁର୍ଥ ସମାନୁପାତୀ 0.0001 ।

(iii) a, a²b, a²b²
ସମାଧାନ:
ମନେକର ଚତୁର୍ଥ ସମାନୁପାତୀ x  ∴ a, a²b, a²b² ଓ x ସମାନୁପାତୀ
⇒ \(\frac{a}{a^2 b}=\frac{a^2 b^2}{x}\) ⇒ ax = a⁴b³ ⇒ x = \(\frac{a^4 b^3}{a}\) = a³b³
∴ ନିର୍ଦେୟ ଚତୁର୍ଥ ସମାନୁପାତୀ a³b³ ।

(iv) a² – b², a + b, a – b
ସମାଧାନ:
ମନେକର ଚତୁର୍ଥ ସମାନୁପାତୀ x  ∴ a² – b², a + b, a – b ଓ x ସମାନୁପାତୀ
⇒ \(\frac{a^2-b^2}{a+b}=\frac{a-b}{x} \Rightarrow \frac{(a+b)(a-b)}{a+b}=\frac{a-b}{x}\) ⇒ x = 1
∴ ନିର୍ଦେୟ ଚତୁର୍ଥ ସମାନୁପାତୀ 1 ।

(v) a² + 5a + 6, 3a + 6, 4a + 12
ସମାଧାନ:
ମନେକର ଚତୁର୍ଥ ସମାନୁପାତୀ x  ∴ a² + 5a + 6, 3a + 6, 4a + 12 ଓ x ସମାନୁପାତୀ
⇒ \(\frac{a^2+5 a+6}{3 a+6}=\frac{4 a+12}{x} \Rightarrow \frac{(a+2)(a+3)}{3(a+2)}=\frac{4(a+3)}{x}\) ⇒ x = 12
∴ ନିର୍ଦେୟ ଚତୁର୍ଥ ସମାନୁପାତୀ 12 ।

(vi) a³ – b³, a⁴ + a²b² + b⁴, a – b
ସମାଧାନ:
ମନେକର ଚତୁର୍ଥ ସମାନୁପାତୀ x  ∴ a³ – b³, a⁴ + a²b² + b⁴, a – b ଓ x ସମାନୁପାତୀ
⇒ \(\frac{a^3-b^3}{a^4+a^2 b^2+b^4}=\frac{a-b}{x} \Rightarrow \frac{(a-b)\left(a^2+a b+b^2\right)}{\left(a^2+a b+b^2\right)\left(a^2-a b+b^2\right)}=\frac{a-b}{x}\)
⇒ x(a – b) = (a – b) (a² – ab + b²) ⇒ x = a² – ab + b²
∴ ନିର୍ଦେୟ ଚତୁର୍ଥ ସମାନୁପାତୀ (a² – ab + b²) ।

Question 4.
ଦତ୍ତ ରାଶିମାନଙ୍କର ତୃତୀୟ ସମାନୁପାତୀ ନିର୍ଣ୍ଣୟ କର ।

{\(\frac{a}{b}=\frac{c}{d}\) ହେଲେ a, bର ତୃତୀୟ ସମାନୁପାତୀ c ହେବ ।}

(i) 9, 15
ସମାଧାନ:
ମନେକର ତୃତୀୟ ସମାନୁପାତୀ x ∴ 9, 15 ଓ x କ୍ରମିକ ସମାନୁପାତୀ ।
⇒ \(\frac{9}{15}=\frac{15}{x}\) ⇒ 9x = 225 ⇒ x = \(\frac{225}{9}\) ⇒ x = 25
∴ ନିର୍ଦେୟ ତୃତୀୟ ସମାନୁପାତୀ 25 

(ii) a²b, ab²
ସମାଧାନ:
ମନେକର ତୃତୀୟ ସମାନୁପାତୀ x ∴ a²b, ab² ଓ x କ୍ରମିକ ସମାନୁପାତୀ ।
⇒ \(\frac{a^2 b}{a b^2}=\frac{a b^2}{x}\) ⇒ x = \(\frac{a b^2 \times a b^2}{a^2 b}\) = b³
∴ ନିର୍ଦେୟ ତୃତୀୟ ସମାନୁପାତୀ b³

(iii) x² – y², x + y
ସମାଧାନ:
ମନେକର ତୃତୀୟ ସମାନୁପାତୀ x ∴ x² – y², x + y ଓ x କ୍ରମିକ ସମାନୁପାତୀ ।
⇒ \(\frac{x^2-y^2}{x+y}=\frac{x+y}{a} \Rightarrow \frac{(x+y)(x-y)}{x+y}=\frac{x+y}{a} \Rightarrow a=\frac{x+y}{x-y}\)
∴ ନିର୍ଦେୟ ତୃତୀୟ ସମାନୁପାତୀ \(\frac{x+y}{x-y}\)

(iv) \(\frac{a}{b}+\frac{b}{a}, \sqrt{\mathbf{a}^2+b^2}\)
ସମାଧାନ:
ମନେକର ତୃତୀୟ ସମାନୁପାତୀ x ∴ \(\frac{a}{b}+\frac{b}{a}, \sqrt{\mathbf{a}^2+b^2}\) ଓ x କ୍ରମିକ ସମାନୁପାତୀ ।
⇒ \(\frac{\frac{a}{b}+\frac{b}{a}}{\sqrt{a^2+b^2}}=\frac{\sqrt{a^2+b^2}}{x} \Rightarrow\left(\frac{a^2+b^2}{a b}\right)\) x = a² + b² ⇒ x = ab
∴ ନିର୍ଦେୟ ତୃତୀୟ ସମାନୁପାତୀ ab

Question 5.
ନିମ୍ନ ରାଶିମାନଙ୍କର ମଧ୍ଯସମାନୁପାତୀ ନିର୍ଣ୍ଣୟ କର ।

{\(\frac{a}{b}=\frac{b}{c}\) ହେଲେ a ଓ c ର ମଧ୍ଯସମାନୁପାତୀ b }

(i) 9, 25
ସମାଧାନ:
ମନେକର ତୃତୀୟ ସମାନୁପାତୀ x ∴ 9, 25 ଓ x କ୍ରମିକ ସମାନୁପାତୀ ।
⇒ \(\frac{9}{x}=\frac{x}{25}\) ⇒ x² = 25 × 9 ⇒ x = ± 15
∴ ନିର୍ଦେୟ ତୃତୀୟ ସମାନୁପାତୀ ± 15

(ii) 4a²b, 9bc²
ସମାଧାନ:
ମନେକର ତୃତୀୟ ସମାନୁପାତୀ x ∴ 4a²b, 9bc² ଓ x କ୍ରମିକ ସମାନୁପାତୀ ।
⇒ \(\frac{4 a^2 b}{x}=\frac{x}{9 b c^2}\) ⇒ x² = 36a²b²c² ⇒ x = ± 6abc
∴ ନିର୍ଦେୟ ତୃତୀୟ ସମାନୁପାତୀ ± 6abc

(iii) (a – b)(a + b)³, (a + b)(a – b)³
ସମାଧାନ:
ମନେକର ତୃତୀୟ ସମାନୁପାତୀ x ∴ (a – b)(a + b)³, (a + b)(a – b)³ ଓ x କ୍ରମିକ ସମାନୁପାତୀ ।
⇒ \(\frac{(a-b)(a+b)^3}{x}=\frac{x}{(a+b)(a-b)^3}\) ⇒ x² = (a – b)⁴(a + b)⁴
⇒ x = ± (a – b)²(a + b)² ⇒ x = + [(a – b)(a + b)]² = ± (a² – b²)²
∴ ନିର୍ଦେୟ ତୃତୀୟ ସମାନୁପାତୀ ± (a² – b²)²

Question 6.

{a ଓ c ର ମଧ୍ଯସମାନୁପାତୀ b ହେଲେ \(\frac{a}{b}=\frac{b}{c}\) ହେବ ।}

(i) (2 + a) ଓ (5 + a) ର ମଧ୍ଯସମାନୁପାତୀ (3 + a) ହେଲେ, a ର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ:
(2 + a) ଓ (5 + a) ର ମଧ୍ଯସମାନୁପାତୀ (3 + a)
∴ (2 + a), (3 + a) ଓ (5 + a) କ୍ରମିକ ସମାନୁପାତୀ 
⇒ \(\frac{2+a}{3+a}=\frac{3+a}{5+a}\) ⇒ (2 + a)(5 + a) = (3 + a)²
⇒ 10 + a² + 7a = 9 + a² + 6a ⇒ a = -1 ∴ ର ମାନ -1

(ii) (23 – x), (28 – x) ଓ (19 – x) ର ମଧ୍ଯସମାନୁପାତୀ ହେଲେ, x ର ମାନ ସ୍ଥିର କର ।
ସମାଧାନ:
(23 – x), (28 – x) ଓ (19 – x) ର ମଧ୍ଯସମାନୁପାତୀ
∴ (28 – x), (23 – x) ଓ (19- x) କ୍ରମିକ ସମାନୁପାତୀ 
\(\frac{28-x}{23-x}=\frac{23-x}{19-x}\) ⇒ (28 – x)(19 – x) = (23 – x)²
⇒ 532 – 47x + x² = 529 + x² – 46x ⇒ -47x + 46x = 529 – 532 ⇒ x = 3
∴ x ର ମାନ 3

(iii) a ଓ c ର ମଧ୍ଯସମାନୁପାତୀ b ହେଲେ, ପ୍ରମାଣ କର ଯେ a² + b² ଓ b² + c² ର ମଧ୍ଯସମାନୁପାତୀ ab + bc ହେବ ।
ସମାଧାନ:
a ଓ c ର ମଧ୍ଯସମାନୁପାତୀ b [ପ୍ରାନ୍ତ ରାଶିଦ୍ଧୟର ଗୁଣଫଳ = ମଧ୍ଯରାଶିର ବର୍ଗ]
∴ a, b ଓ c କ୍ରମିକ ସମାନୁପାତୀ ⇒ \(\frac{a}{b}=\frac{b}{c}\) ⇒ b² = ac
ଆମକୁ ଦର୍ଶାଇବାକୁ ପଡ଼ିବ ଯେ, (a² + b²)(b² + c²) = (ab + bc)²
(a² + b²)(b² + c²) = (a² + ac)(ac + c²) [∵ b² = ac]
= a(a + c) c(a + c) = ac(a + c)² = b²(a + c)² = {b(a + c)}² = (ab + bc)²
∴ a² + b² ଓ b² + c² ମଧ୍ଯସମାନୁପାତୀ (ab + bc)

(iv) ଯଦି b, a ଓ c ର ମଧ୍ଯସମାନୁପାତୀ ହୁଏ, ତେବେ ପ୍ରମାଣ କର ଯେ (ab + bc + ca)³ = abc(a + b + c)³
ସମାଧାନ:
b, a ଓ c ର ମଧ୍ଯସମାନୁପାତୀ ⇒ \(\frac{a}{b}=\frac{b}{c}\) ⇒ b² = ac
ବାମପାର୍ଶ୍ବ = (ab + bc + ca)³ = (ab + bc + b²)³
= {b (a + b + c))³ = b³ (a + b + c)³
= b².b(a + b + c)³ = abc (a + b + c)³ = ଦକ୍ଷିଣପାର୍ଶ୍ବ

Question 7.
(i) 1, 7, 17 ପ୍ରତ୍ୟେକରେ କେଉଁ ସଂଖ୍ୟା ବିୟୋଗ କଲେ, ଯୋଗଫଳଗୁଡ଼ିକ ସମାନୁପାତୀ ହେବେ?
ସମାଧାନ:
ମନେକର 1, 7, 17 ପ୍ରତ୍ୟେକରେ x ଯୋଗକଲେ ଯୋଗଫଳଗୁଡ଼ିକ କ୍ରମିକ ସମାନୁପାତୀ ହେବେ ।
⇒ \(\frac{1+x}{7+x}=\frac{7+x}{17+x}\) ⇒ (7 + x)² = (1 + x)(17 + x)
⇒ 49 + 14x + x² ⇒ 14x – 18x = 17 – 49
⇒ -4x = -32 ⇒ 4x = 32 ⇒ x = 8
∴ 1, 7, 17 ପ୍ରତ୍ୟେକରେ 8 ଯୋଗକଲେ ଯୋଗଫଳ କ୍ରମିକ ସମାନୁପାତୀ ହେବେ ।

(ii) 6, 14, 18 ଓ 38 ପ୍ରତ୍ୟକରେ କେତେ ଯୋଗକଲେ ଯୋଗଫଳଗୁଡ଼ିକ ସମାନୁପାତୀ ହେବେ?
ସମାଧାନ:
ମନେକର 6, 14, 18 ଓ 38 ପ୍ରତ୍ୟେକରେ x ଯୋଗକଲେ ଯୋଗଫଳଗୁଡ଼ିକ କ୍ରମିକ ସମାନୁପାତୀ ହେବେ ।
⇒ \(\frac{6+x}{14+x}=\frac{18+x}{38+x}\) ⇒ (6+ x)(38 + x) = (18 + x)(14 + x)
⇒ 228 + 44x + x² ⇒ 44x – 32x = 252 – 228
⇒ 12x = 24 ⇒ x = 2
∴ 6, 14, 18 ଓ 38 ପ୍ରତ୍ୟେକରେ 2 ଯୋଗକଲେ ଯୋଗଫଳ କ୍ରମିକ ସମାନୁପାତୀ ହେବେ ।

(iii) 5, 9 ଓ 17 ପ୍ରତ୍ୟେକରୁ କେଉଁ ସଂଖ୍ୟା ବିୟୋଗ କଲେ, ବିୟୋଗଫଳଗୁଡ଼ିକ କ୍ରମିକ ସମାନୁପାତୀ ହେବେ?
ସମାଧାନ:
ମନେକର 5, 9 ଓ 17 ପ୍ରତ୍ୟେକରେ x ଯୋଗକଲେ ଯୋଗଫଳଗୁଡ଼ିକ କ୍ରମିକ ସମାନୁପାତୀ ହେବେ ।
⇒ \(\frac{5-x}{9-x}=\frac{9-x}{17-x}\) ⇒ (9 – x)² = (5 – x)(17 – x)
⇒ 85 – 22x + x² ⇒ 18x – 22x = 81 – 85
⇒ -4x = -4 ⇒ x = 1
∴ 5, 9 ଓ 17 ପ୍ରତ୍ୟେକରେ 1 ଯୋଗକଲେ ଯୋଗଫଳ କ୍ରମିକ ସମାନୁପାତୀ ହେବେ ।

(iv) 14, 17, 34 ଓ 42 ପ୍ରତ୍ୟେକରୁ କେଉଁ ସଂଖ୍ୟା ବିୟୋଗ କଲେ ବିୟୋଗଫଳଗୁଡ଼ିକ ସମାନୁପାତୀ ହେବେ?
ସମାଧାନ:
ମନେକର 14, 17, 34 ଓ 42 ପ୍ରତ୍ୟେକରେ x ଯୋଗକଲେ ଯୋଗଫଳଗୁଡ଼ିକ କ୍ରମିକ ସମାନୁପାତୀ ହେବେ ।
⇒ \(\frac{14-x}{17-x}=\frac{34-x}{42-x}\) ⇒ (14 – x)(42 – x) = (34 – x)(17 – x)
⇒ 588 – 56x + x² ⇒ 56x – 51x = 588 – 578
⇒ 5x = 10 ⇒ x = 2
∴ 14, 17, 34 ଓ 42 ପ୍ରତ୍ୟେକରେ 2 ଯୋଗକଲେ ଯୋଗଫଳ କ୍ରମିକ ସମାନୁପାତୀ ହେବେ ।

Question 8.
(i) a : b = 2 : 3 ହେଲେ, (3a + 4b) : (4a + 5b) ର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ:

(ii) a : b = 3 : 4 ହେଲେ, (6a + 5b): (5a + 4b) ର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ:

(iii) 581 କୁ a, b, c ତିନୋଟି ଅଂଶରେ ଭାଗ କର ଯେପରି 4a = 5b = 7c ହେବ
ସମାଧାନ:

(iv) 6x + 5y : 6x – 5y = 3 : 2 ହେଲେ, 2x + 3y : 2x – 3y ର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ:

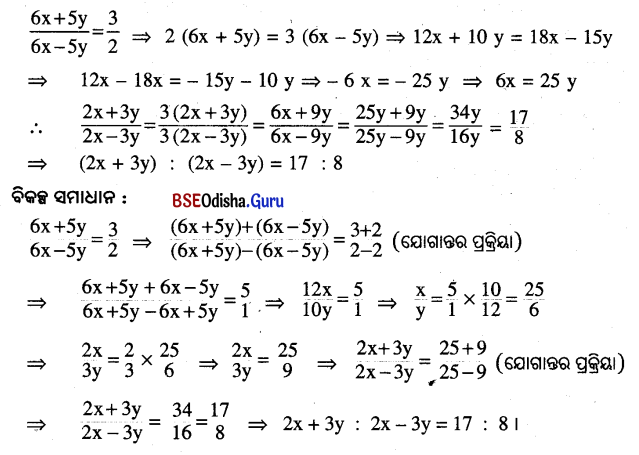
(v) (a – b) : (a + b) = 1 : 5 ହେଲେ, a² – b²: a² + b² ର ମୂଲ୍ୟ ନିରୂପଣ କର ।
ସମାଧାନ:

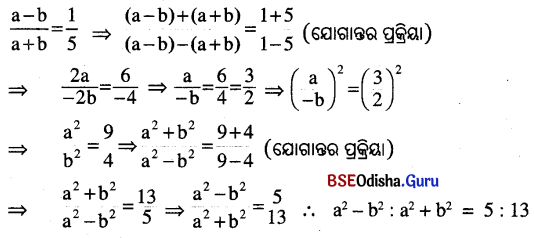
Question 9.
a, b, c, d ସମାନୁପାତୀ ହେଲେ, ପ୍ରମାଣ କର ଯେ

{ଦତ୍ତ a, b, c ଓ d ସମାନୁପାତୀ \(\frac{a}{b}=\frac{c}{d}\) =k (ମନେକର) ⇒ a = bk ଏବଂ c = dk

(i) pa + qc : pb + qd = ma + nc : mb + nd
ସମାଧାନ:

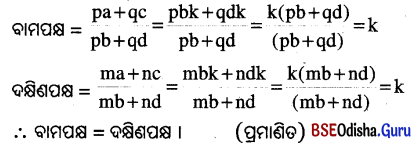
(ii) 3a + 4b : 3c + 4d = \(\sqrt{a^2+b^2}: \sqrt{c^2+d^2}\)
ସମାଧାନ:

(iii) b² : d² = a² + b² : c² + d²
ସମାଧାନ:
ଦକ୍ଷିଣପକ୍ଷ = \(\frac{a^2+b^2}{c^2+d^2}=\frac{(b k)^2+b^2}{(d k)^2+d^2}=\frac{b^2 k^2+b^2}{d^2 k^2+d^2}=\frac{b^2\left(k^2+1\right)}{d^2\left(k^2+1\right)}=\frac{b^2}{d^2}\)
∴ ବାମପକ୍ଷ = ଦକ୍ଷିଣପକ୍ଷ । (ପ୍ରମାଣିତ)

(iv) b² : a² = b² + d² : a² + c²
ସମାଧାନ:

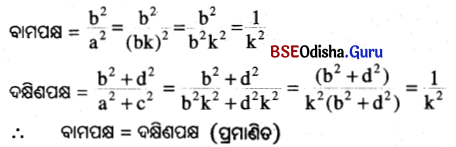
Question 10.
\(\frac{a}{b}=\frac{c}{d}=\frac{e}{f}\) ହେଲେ ପ୍ରମାଣ କର ଯେ,

(i) \(\frac{a c}{b d}=\frac{a^2-3 c^2+5 e^2}{b^2-3 d^2+5 f^2}\)
ସମାଧାନ:

(ii) \(\frac{\text { ace }}{b d f}=\frac{a^3+c^3+e^3}{b^3+d^3+f^3}\)
ସମାଧାନ:

(iii) \(\frac{(a+c+e)^3}{(b+d+f)^2}=\frac{a^3}{b^2}+\frac{c^3}{d^2}+\frac{e^3}{f^2}\)
ସମାଧାନ:

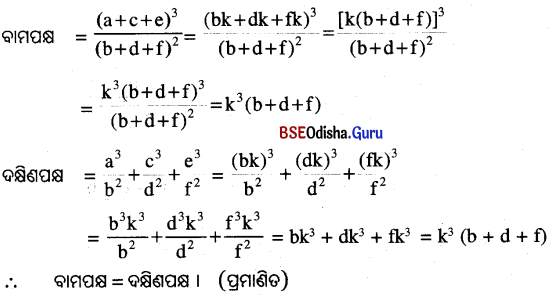
(iv) \(\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\frac{4 a-6 c-9 e}{4 b-6 d-9 f}\)
ସମାଧାନ:
ଦକ୍ଷିଣପକ୍ଷ = \(\frac{4 a-6 c-9 \mathrm{e}}{4 b-6 d-9 f}=\frac{4 b k-6 d k-9 f k}{4 b-6 d-9 f}=\frac{k(4 b-6 d-9 f)}{4 b-6 d-9 f}\)
= k = \(\frac{a}{b}=\frac{c}{d}=\frac{e}{f}\) ବାମପକ୍ଷ (ପ୍ରମାଣିତ)

(v) (a² + c² + e²)(b² + d² + f²) = (ab + cd + ef)²
ସମାଧାନ:
ବାମପକ୍ଷ = (a² + c² + e²)(b² + d² + f²) = {(bk)² + (dk)² + (fk)²} (b² + d² + f²)
= (b²k² + d²k² + fk²)(b² + d² + f²)
= k²(b² + d² + f²)(b² + d² + f²) = k²(b² + d² + f²)²
ଦକ୍ଷିଣପକ୍ଷ = (ab + cd + ef)² = (bk.b + dk.d + fk.f)² = (b²k + d²k + f²k)²
= [k(b² + d² + f²)]² = k²(b² + d² + f²)²
∴ ବାମପକ୍ଷ = ଦକ୍ଷିଣପକ୍ଷ (ପ୍ରମାଣିତ)

Question 11.
a, b, c କ୍ରମିକ ସମାନୁପାତୀ ହେଲେ ପ୍ରମାଣ କର ଯେ,

(i) a : c = a² : b²
ସମାଧାନ:
ଦକ୍ଷିଣପକ୍ଷ = \(\frac{a^2}{b^2}=\frac{a^2}{a c}=\frac{a}{c}\) = ବାମପକ୍ଷ (ପ୍ରମାଣିତ)

(ii) a : c = (a² + b²) : (b² + c²)
ସମାଧାନ:
ଦକ୍ଷିଣପକ୍ଷ = \(\frac{a^2+b^2}{b^2+c^2}=\frac{a^2+a c}{a c+c^2}=\frac{a(a+c)}{c(a+c)}=\frac{a}{c}\) = ବାମପକ୍ଷ (ପ୍ରମାଣିତ)

(iii) (a² + b²)(b² + c²) = (ab + bc)²
ସମାଧାନ:
ଦକ୍ଷିଣପକ୍ଷ = (a² + b²) (b² + c²) = (a² + ac) (ac + c²) [∵ b² = ac]
= a(a + c) . c(a + c) = ac(a + c)² = b² (a + c)² = {b(a + c)}²
= (ab + bc)² = ବାମପକ୍ଷ (ପ୍ରମାଣିତ)

(iv) 2a + 3b : 3a + 2b = 2b + 3c : 3b + 2c
ସମାଧାନ:
ବାମପକ୍ଷ = \(\frac{2 a+3 b}{3 a+2 b}=\frac{b(2 a+3 b)}{b(3 a+2 b)}=\frac{2 a b+3 b^2}{3 a b+2 b^2}=\frac{2 a b+3 a c}{3 a b+2 a c}\)[∵ b² = ac]
= \(\frac{a(2 b+3 c)}{a(3 b+2 c)}=\frac{2 b+3 c}{3 b+2 c}\) = ଦକ୍ଷିଣପକ୍ଷ (ପ୍ରମାଣିତ)

Question 12.
a, b, c, d କ୍ରମିକ ସମାନୁପାତ ହେଲେ ପ୍ରମାଣ କର ଯେ,

(i) (b + c)(b + d) = (c + a)(c + d)
ସମାଧାନ:
a, b, c, d କ୍ରମିକ ସମାନୁପାତ ⇒ \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}\) ⇒ b² = ac, c² = bd ଏବଂ ad = bc
ବାମପକ୍ଷ = (b + c)(b + d) = b² + bc + bd + cd = ac + bc + bd + cd [∵ b² = ac]
ଦକ୍ଷିଣପକ୍ଷ = (c + a)(c + d) = c² + ac + cd + ad = bd + ac + cd + bc (∵ c² = bd ଓ ad = bc)
∴ ବାମପକ୍ଷ = ଦକ୍ଷିଣପକ୍ଷ (ପ୍ରମାଣିତ)

(ii) \(\frac{a}{c}=\frac{a^2-b^2+c^2}{b^2-c^2+d^2}\)
ସମାଧାନ:

(iii) \(\frac{a b+c d}{a b-c d}=\frac{b^2+d^2}{b^2-d^2}\)
ସମାଧାନ:

(iv) a – b ଓ c – d ର ମଧ୍ଯସମାନୁପାତ b – c
ସମାଧାନ:
\(\frac{a}{b}=\frac{b}{c}-\frac{c}{d}\) ⇒ b² = ac, c² = bd ଏବଂ bc = ad
(a – b) ଓ (c – d) ର ମଧ୍ଯସମାନୁପାତ b – c ⇒ \(\frac{a-b}{b-c}=\frac{b-c}{c-d}\) ⇒ (b – c)² = (a – b)(c – d)
ଦକ୍ଷିଣପକ୍ଷ = (a – b) (c – d) = ac – bc – ad + bd
= b² – bc – bc + c² (∴ ac = b², ad = ac, bd = c²)
= b² – 2bc + c² = (b – c)² = ବାମପକ୍ଷ (ପ୍ରମାଣିତ)

(v) a² – b² ଓ c² – d² ର ମଧ୍ଯସମାନୁପାତ b² – c²
ସମାଧାନ:
\(\frac{a}{b}=\frac{b}{c}-\frac{c}{d}\) ⇒ b² = ac, c² = bd ଏବଂ bc = ad
a² – b² ଓ c² – d² ର ମଧ୍ଯସମାନୁପାତ b² – c² ⇒ \(\frac{a^2-b^2}{b^2-c^2}=\frac{b^2-c^2}{c^2-d^2}\) ⇒ (b² – c²)² = (a² – b²)(c² – d²)
ଦକ୍ଷିଣପକ୍ଷ = (a² – b²)(c² – d²) = a²c² – b²c² – a²d² + b²d²
= (ac)² – (ad)² – (bc)² + (bd)² = (b²)² – b²c² – b²c² + (c²)² [∴ ac = b², ad = bc ଏବଂ bd = c²]
= b⁴ – 2b²c² + c⁴ = (b² – c²)² = ବାମପକ୍ଷ (ପ୍ରମାଣିତ)
∴ a² – b² ଓ c² – d² ର ମଧ୍ଯସମାନୁପାତ b² – c²

(vi) (b – c)² + (c – a)² + (b – d)² = (a – d)²
ସମାଧାନ:
a, b, c, d କ୍ରମିକ ସମାନୁପାତ ଅର୍ଥାତ୍ \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}\) = k (ମନେକର)
c = dk, b = ck = dk . k = dk², a = bk = dk². k = dk³
ବାମପକ୍ଷ = (b – c)² + (c – a)² + (b – d)²
= (dk² – dk)² + (dk – dk³)² + (dk² – d)²
= {dk(k – 1)}² + {dk(1 – k²)² + {d(k² – 1)}²
= d²k²(k² + 1 – 2k) + d²k²(1 + k⁴ – 2k²) + d²(k⁴ +1 – 2k²)
= d²k⁴ + d²k² – 2d²k³ + d²k² + d²k⁶ – 2d²k⁴ + d²k⁴ + d² – 2d²k²
= d²k⁶ + d² – 2d²k³ = (dk³)² + (d)² – 2. 2 . dk³ . d
= (dk³ – d)² = (a – d)² ଦକ୍ଷିଣପକ୍ଷ (ପ୍ରମାଣିତ)
ବିକଳ୍ପ ସମାଧାନ : \(\frac{a}{b}=\frac{b}{c}-\frac{c}{d}\) ⇒ b² = ac, c² = bd ଏବଂ bc = ad
ବାମପକ୍ଷ = (b – c)² + (c – a)² + (b – d)² = b² + c² – 2bc + c² + a² – 2ca + b² + d² – 2bd
= 2b² – 2ac + 2c² – 2bd + a² + d² – 2bc
= 2ac – 2ac + 2bd – 2bd + a² + d² – 2ad = a² + d² – 2ad = (a – d)² = ଦକ୍ଷିଣପକ୍ଷ

Question 13.
(i) x = \(\frac{2 a b}{a+b}\) ହେଲେ, ପ୍ରମାଣ କର ଯେ \(\frac{x+a}{x-a}+\frac{x+b}{x-b}\) = 2
ସମାଧାନ:

(ii) x = \(\frac{6 a b}{a+b}\) ହେଲେ, ପ୍ରମାଣ କର ଯେ \(\frac{x+3 a}{x-3 a}+\frac{x+3 b}{x-3 b}\) = 2
ସମାଧାନ:

(iii) x = \(\frac{8 a b}{a+b}\) ହେଲେ, ପ୍ରମାଣ କର ଯେ \(\frac{x+4 a}{x-4 a}+\frac{x+4 b}{x-4 b}\) = 2
ସମାଧାନ:

Question 14.
(i) x + y, y + z, x – y, y – z ସମାନୁପାତୀ ହେଲେ, ପ୍ରମାଣ କର ଯେ x, y, z କ୍ରମିକ ସମାନୁପାତୀ ହେବେ ।
ସମାଧାନ:

(ii) \(\frac{x}{b+c}=\frac{y}{c+a}=\frac{z}{a+b}\) ହେଲେ, ପ୍ରମାଣ କର ଯେ (b – c) x + (c – a) y + (a – b) z = 0
ସମାଧାନ:
\(\frac{x}{b+c}=\frac{y}{c+a}=\frac{z}{a+b}\) = k (ମନେକର)
⇒ x = k(b + c), y = k(c + a) z = k(a + b)
ବାମପକ୍ଷ = (b – c) x + (c – a) y + (a – b) z
= (b – c) {k(b + c)} + (c – a) {k(c + a)} + (a – b) {k(a + b)}
= k(b + c)(b – c) + k(c + a)(c – a) + k(a + b)(a – b)
= k(b² – c²) + k(c² – a²) + k(a² – b²)
= k(b² – c² + c² – a² + a² – b²) = k . 0 = 0 = ଦକ୍ଷିଣପକ୍ଷ (ପ୍ରମାଣିତ)

(iii) \(\frac{x}{b^2+b c+c^2}=\frac{y}{c^2+c a+a^2}=\frac{z}{a^2+a b+b^2}\) ହେଲେ, ପ୍ରମାଣ କର ଯେ (b – c) x + (c – a) y + (a – b) z = 0
ସମାଧାନ:
\(\frac{x}{b^2+b c+c^2}=\frac{y}{c^2+c a+a^2}=\frac{z}{a^2+a b+b^2}\) = k(ମନେକର)
⇒ x = k(b² + bc + c²), y = k(c² + ca + a²) ଏବଂ z = k(a² + ab + b²)
∴ ବାମପକ୍ଷ = (b – c) x + (c – a) y + (a – b) z
= (b – c) {k(b² + bc + c²)} + (c – a) {k(c² + ca + a²) } + (a – b) {k(a² + ab + b²)}
= k(b – c)(b² + bc + c²) + k(c – a)(c² + ca + a²) + k(a – b)(a² + ab + b²)
= k(b³ – c³) + k(c³ – a³) + k(a³ – b³)
= k(b³ – c³ + c³ – a³ + a³ – b³) = k.0 = 0 = କ୍ଷିଣପକ୍ଷ (ପ୍ରମାଣିତ)

Question 15.
ସ୍ମୃତି, ସୃଷ୍ଟିଠାରୁ ଦୁଇବର୍ଷ ବଡ଼ । ଦଶ ବର୍ଷ ପୂର୍ବେ ସୃଷ୍ଟି ଓ ସ୍ଥିତିର ବୟସର ଅନୁପାତ 1 : 2 ଥିଲା । ବର୍ତ୍ତମାନ ସେମାନଙ୍କର ବୟସ କେତେ ?
ସମାଧାନ:
ମନେକର ସୃଷ୍ଟିର ବର୍ତ୍ତମାନ ବୟସ x ବର୍ଷ । ପ୍ରଶ୍ନନୁସାରେ, ସ୍ନିତିର ବର୍ତ୍ତମାନ ବୟସ (x + 2) ବର୍ଷ ।
ଦଶ ବର୍ଷ ପୂର୍ବେ ସୃଷ୍ଟିର ବୟସ ଥିଲା = (x – 10) ବର୍ଷ |
ଦଶ ବର୍ଷ ପୂର୍ବେ ସ୍ମୃତିର ବୟସ ଥିଲା = (x + 2) – 10 = (x – 8) ବର୍ଷ ।
ପ୍ରଶ୍ବାନୁସାରେ, \(\frac{x-10}{x-8}=\frac{1}{2}\) ⇒ 2(x – 10) = x – 8 ⇒ 2x – 20 = x – 8
⇒ 2x – x = 20 – 8 ⇒ x = 12
∴ ସୃଷ୍ଟିର ବର୍ତ୍ତମାନ ବୟସ = 12 ବର୍ଷ ଓ ସ୍ନିତିର ବର୍ତ୍ତମାନ ବୟସ = x + 2 = 12 + 2 = 14 ବର୍ଷ ।

Question 16.
ଚାରିବର୍ଷ ପୂର୍ବେ ଅନିଲ ଓ ସୁନିଲ୍‌ର ବୟସର ଅନୁପାତ 3 : 5 ଥିଲା । ଚାରିବର୍ଷ ପରେ ଏହି ଅନୁପାତ 5 : 7 ହେବ ।  ବର୍ତ୍ତମାନ କାହାର ବୟସ କେତେ ?
ସମାଧାନ:
ମନେକର ଚାରିବର୍ଷ ପୂର୍ବେ ଅନିଲ୍ ଓ ସୁନିଲ୍‌ର ବୟସ ଯଥାକ୍ରମେ 3x ଏବଂ 5x ବର୍ଷ ଥିଲା । 
ବର୍ତ୍ତମାନ ଅନିଲ୍ ଓ ସୁନିଲ୍‌ର ବୟସ ଯଥାକ୍ରମେ (3x + 4) ଓ (5x + 4) ବର୍ଷ ।
4 ବର୍ଷ ପରେ ଅନିଲ୍ସର ବୟସ ହେବ = (3x + 4 + 4) ବର୍ଷ = (3x + 8) ବର୍ଷ । 
4 ବର୍ଷ ପରେ ସୁନିଲ୍‌ର ବୟସ ହେବ = (5x + 4 + 4) ବର୍ଷ = (5x + 8) ବର୍ଷ ।
କିନୁ \(\frac{3 x+8}{5 x+8}=\frac{5}{7}\) ⇒ 5(5x + 8) = 7(3x + 8)
⇒ 25x + 40 = 21x + 56 ⇒ 25x – 21x = 56 – 40 ⇒ 4x = 16 ⇒ x = 4
∴ ଅନିଲ୍‌ର ବର୍ତ୍ତମାନ ବୟସ = 3x + 4 = 3 × 4 + 4 = 16 ବର୍ଷ
ସୁନିଲ୍‌ର ବର୍ତ୍ତମାନ ବୟସ = 5x + 4= = 5 × 4 + 4 = 24 ବର୍ଷ ।

Question 17.
1400 ଜଣ ଛାତ୍ର ଥ‌ିବା ଗୋଟିଏ ବିଦ୍ୟାଳୟରେ ଛାତ୍ର ଓ ଶିକ୍ଷକ ସଂଖ୍ୟାର ଅନୁପାତ 35 : 2 ଅଟେ । ଆଉ ଅଧିକ କେତେଜଣ ଶିକ୍ଷକ ବିଦ୍ୟାଳୟରେ ଯୋଗଦେଲେ ଏହି ଅନୁପାତ 25 : 2 ହେବ?
ସମାଧାନ:
ମନେକର ବର୍ତ୍ତମାନ ବିଦ୍ୟାଳୟରେ ଶିକ୍ଷକ ସଂଖ୍ୟା x
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{1400}{x}=\frac{35}{2}\) ⇒ 35x = 2800 x = \(\frac{2800}{35}\) = 80
ମନେକର ଆଉ y ଜଣ ଶିକ୍ଷକ ଯୋଗଦେଲେ ଛାତ୍ର ଓ ଶିକ୍ଷକ ସଂଖ୍ୟାର ଅନୁପାତ 25 : 2 ହେବ ।
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{1400}{80+y}=\frac{25}{2}\) ⇒ 25(80 + y) = 2800 ⇒ 2000 + 25y = 2800
⇒ 25y = 2800 – 2000 = 800 ⇒ y = \(\frac{800}{25}\) = 32
∴ ଅଧ୍ଵକ 32 ଜଣ ଶିକ୍ଷକ ଯୋଗଦେଲେ ଛାତ୍ର ଓ ଶିକ୍ଷକ ସଂଖ୍ୟାର ଅନୁପାତ 25 : 2 ହେବ ।

Question 18.
60 ଲିଟର ମିଶ୍ରଣରେ କ୍ଷୀର ଓ ଜଳର ଅନୁପାତ 2 :1 । ସେଥ‌ିରେ ଆଉ କେତେ ଲିଟର ଜଳ ମିଶାଇଲେ ମିଶ୍ରଣରେ କ୍ଷୀର ଓ ଜଳର ଅନୁପାତ 8: 5 ହେବ ?
ସମାଧାନ:
60 ଲିଟର ମିଶ୍ରଣରେ କ୍ଷୀର ଓ ଜଳର ଅନୁପାତ 2 : 1 ।
ମନେକର 60 ଲିଟର ମିଶ୍ରଣରେ କ୍ଷୀରର ପରିମାଣ 2x ଲିଟର ଓ ଜଳର ପରିମାଣ x ଲିଟର ।
ପ୍ରଶ୍ନନୁସାରେ, 2x + x = 60 ⇒ 3x = 60 = x ⇒ \(\frac{60}{3}\) = 20
ମିଶ୍ରଣରେ କ୍ଷୀରର ପରିମାଣ = 2 × 20 = 40 ଲିଟର ଓ ଜଳର ପରିମାଣ 20 ଲିଟର । 
ମନେକର ମିଶ୍ରଣରେ ଆଉ y ଲିଟର ଜଳ ମିଶାଇଲେ କ୍ଷୀର ଓ ଜଳର ଅନୁପାତ 8 : 5 ହେବ ।
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{40}{20+y}=\frac{8}{5}\) ⇒ 160 + 8y = 200 ⇒ 8y = 40 ⇒ y = 5
∴ 5 ଲିଟର ଜଳ ମିଶାଇଲେ ନୂତନ ମିଶ୍ରଣରେ କ୍ଷୀର ଏବଂ ଜଳର ଅନୁପାତ 8 : 5 ହେବ ।

Question 19.
A ଓ B ଆୟର ଅନୁପାତ 3 : 2 ଏବଂ ସେମାନଙ୍କର ବ୍ୟୟର ଅନୁପାତ 5 : 3 ଅଟେ । ଯଦି ପ୍ରତ୍ୟେକ 1500 ଟଙ୍କା ସଞ୍ଚୟ କରୁଥ‌ିବେ, ତେବେ B ର ଆୟ କେତେ?
ସମାଧାନ:
A ଓ B ର ଆୟର ଅନୁପାତ 3 : 2 । ମନେକର A ଓ B ର ଆୟ ଯଥାକ୍ରମେ 3x ଟଙ୍କା ଏବଂ 2x ଟଙ୍କା ।
A ର ସଞ୍ଚୟ = B ର ସଞ୍ଚୟ = 1500 ଟଙ୍କା
A ର ବ୍ୟୟ = (3x – 1500) ଟଙ୍କା ଓ B ର ବ୍ୟୟ = (2x – 1500) ଟଙ୍କା
ପ୍ରଶ୍ନନୁସାରେ, \(\frac{3 x-1500}{2 x-1500}=\frac{5}{3}\) ⇒ 5(2x – 1500) = 3(3x – 1500)
⇒ 10x – 7500 = 9x – 4500 ⇒ 10x – 9x = 7500 – 4500 ⇒ x = 3000
∴ B ର ଆୟ = 2x = 2 × 3000 = 6000 ଟଙ୍କା ।

Question 20.

{\(\frac{a}{b}\), \(\frac{c}{d}\), \(\frac{e}{f}\) ର ଯୌଗିକ ଅନୁପାତ = \(\frac{ace}{bdf}\)}

(i) ଦର୍ଶାଅ ଯେ, 3 : 4 ର ବର୍ଗାନୁପାତ, 15 : 17 ର ପ୍ରତିଲୋମୀ ଅନୁପାତ ଏବଂ 25 : 49 ର ବର୍ଗମୂଳାନୁପାତର ଯୌଗିକ ଅନୁପାତ 51 : 112 ହେବ ।
ସମାଧାନ:
3 : 4 ର ବର୍ଗାନୁପାତ = \(\left(\frac{3}{4}\right)^2=\frac{9}{16}\), 15 : 17 ର ପ୍ରତିଲୋମୀ ଅନୁପାତ = \(\frac{17}{15}\)
25 : 49 ର ବର୍ଗମୂଳାନୁପାତ = \(\sqrt{\frac{25}{49}}=\frac{5}{7}\)
∴ ଏମାନଙ୍କର ଯୌଗିକ ଅନୁପାତ = \(\frac{9}{16} \times \frac{17}{15} \times \frac{5}{7}=\frac{51}{112}\)

(ii) ଦର୍ଶାଅ ଯେ, 7 : 6 ର ବର୍ଗାନୁପାତ, 125 : 343 ର ଘନମୂଳାନୁପାତ ଏବଂ 35 :36 ର ପ୍ରତିଲୋମୀ ଅନୁପାତର ଯୌଗିକ ଅନୁପାତ 1:1 ହେବ ।
ସମାଧାନ:
7 : 6 ର ବର୍ଗାନୁପାତ =\(\left(\frac{7}{6}\right)^2=\frac{49}{36}\), 125 : 343 ର ପ୍ରତିଲୋମୀ ଅନୁପାତ = \(\sqrt[3]{\frac{125}{343}}=\frac{5}{7}\)
35 : 36 ର ବର୍ଗମୂଳାନୁପାତ = \(\frac{36}{35}\)
∴ ଏମାନଙ୍କର ଯୌଗିକ ଅନୁପାତ = \(\frac{49}{36} \times \frac{5}{7} \times \frac{36}{35}\) = 1 : 1

Question 21.
120 ଟଙ୍କାକୁ A, B ଓ C ମଧ୍ୟରେ ଏପରି ବାଣ୍ଟିଦିଅ ଯେପରି ସେମାନେ ପାଉଥ‌ିବା ଟଙ୍କାରୁ ଯଥାକ୍ରମେ 15 ଟଙ୍କା, 10 ଟଙ୍କା ଓ 5 ଟଙ୍କା କମାଇ ଦେଲେ ସେମାନଙ୍କର ଅବଶିଷ୍ଟ ଟଙ୍କା 2, 3, 4 ସହ ସମାନୁପାତୀ ହେବେ ।
ସମାଧାନ:
ମନେକର 120 ଟଙ୍କା ମଧ୍ୟରୁ A, B ଓ C ଯଥାକ୍ରମେ x ଟଙ୍କା, y ଟଙ୍କା ଏବଂ z ଟଙ୍କା ପାଇବେ । 
ପ୍ରଶ୍ନନୁସାରେ, x + y + z = 120    …..(i)
A ଟଙ୍କାରୁ 15 ଟଙ୍କା, B ଟଙ୍କାରୁ 10 ଟଙ୍କା ଓ C ଟଙ୍କାରୁ 5 ଟଙ୍କା କମାଇ ଦେଲେ ପରେ ଅବଶିଷ୍ଟ ଟଙ୍କାର ଅନୁପାତ
x – 15 ; y – 10 : z – 5
ପ୍ରଶ୍ନନୁସାରେ, x – 15 : y – 10 : z – 5 = 2 : 3 : 4

‘y’ ର ମାନ ସମୀକରଣ (ii) ରେ ପ୍ରୟୋଗ କଲେ 3x – 2 × 40 = 25 ⇒ 3x = 105 ⇒ x = \(\frac{105}{3}\)
∴ z = 120 – (35 + 40) = 45
∴ x, y, z ଯଥାକ୍ରମେ 35 ଟଙ୍କା, 40 ଟଙ୍କା ଏବଂ 45 ଟଙ୍କା ପାଇବେ ।
ବିକଳ୍ପ ସମାଧାନ:
ମନେକର A ଟଙ୍କାରୁ 15 ଟଙ୍କା, B ଟଙ୍କାରୁ 10 ଟଙ୍କା ଓ C ଟଙ୍କାରୁ 5 ଟଙ୍କା କମାଇ ଦେଲାପରେ ଅବଶିଷ୍ଟ ଟଙ୍କା ଯଥାକ୍ରମେ 2x, 3x ଏବଂ 4x 
∴ A ର ଭାଗ, B ର ଭାଗ ଏବଂ C ର ଭାଗ ଥୁବା ଟଙ୍କାର ପରିମାଣ ଯଥାକ୍ରମେ
2x+15, 3x + 10 ଏବଂ 4x+5 ଟଙ୍କା
ପ୍ରଶ୍ନନୁସାରେ,  2x+15+ 3x + 10 + 4x + 5 = 120
⇒ 9x + 30 = 120 ⇒ 9x = 90 ⇒ x = 10
∴ A ର ଭାଗ = 2x + 15 = 2 x 10 + 15 = 35 ଟଙ୍କା
B ର ଭାଗ = 3x + 10 = 3 × 10 + 10 = 40 ଟଙ୍କା
C ର ଭାଗ = 4x + 5 = 4 × 10 + 5 = 45 ଟଙ୍କା

Question 22.
ତିନିଶ୍ରେଣୀ ବିଶିଷ୍ଟ ଗୋଟିଏ ବିଦ୍ୟାଳୟରେ ଅଷ୍ଟମ, ନବମ ଓ ଦଶମ ଶ୍ରେଣୀର ଛାତ୍ର ଓ ଛାତ୍ରୀ ସଂଖ୍ୟାର ଅନୁପାତ ଯଥାକ୍ରମେ 2 : 3, 3 : 7 ଓ 7 : 8 । ପ୍ରତି ଶ୍ରେଣୀରେ ଯଦି ସମାନ ସଂଖ୍ୟକ ଛାତ୍ର, ଛାତ୍ରୀ ଥାଆନ୍ତି, ତେବେ ବିଦ୍ୟାଳୟରେ ଛାତ୍ର ଓ ଛାତ୍ରୀ ସଂଖ୍ୟାର ଅନୁପାତ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଅଷ୍ଟମ ଶ୍ରେଣୀର ଛାତ୍ରୀ ଓ ଛାତ୍ର ସଂଖ୍ୟା ଯଥାକ୍ରମେ 2x ଏବଂ 3x, ନବମ ଶ୍ରେଣୀର ଛାତ୍ରୀ ଓ ଛାତ୍ର ସଂଖ୍ୟା ଯଥାକ୍ରମେ 3y ଏବଂ 7y ଏବଂ ଦଶମ ଶ୍ରେଣୀର ଛାତ୍ରୀ ଓ ଛାତ୍ର ସଂଖ୍ୟା ଯଥାକ୍ରମେ 7z ଏବଂ 8z 

Question 23.
ସମାନୁପାତ ସମ୍ବନ୍ଧୀୟ ତଥ୍ୟଗୁଡ଼ିକର ପ୍ରୟୋଗରେ ସମାଧାନ କର ।

(i) \(\frac{\sqrt{3 x}+\sqrt{2 x+1}}{\sqrt{3 x}-\sqrt{2 x+1}}\) = 5
ସମାଧାନ:

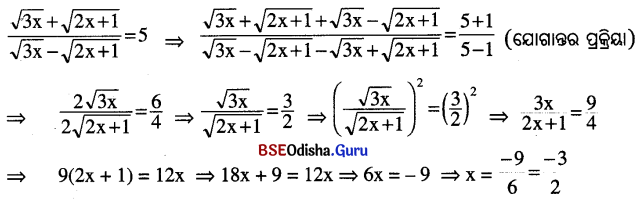
(ii) \(\frac{\sqrt{3 x+1}+\sqrt{x+1}}{\sqrt{3 x+1}-\sqrt{x+1}}\) = 4
ସମାଧାନ:

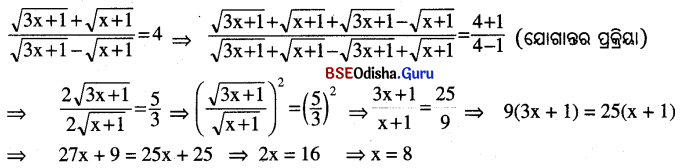
(iii) \(\frac{\sqrt{a+x}+\sqrt{a-x}}{\sqrt{a+x}-\sqrt{a-x}}\) = b
ସମାଧାନ: