Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 1 ରେଖା ଓ କୋଣ Ex 1(b) Textbook Exercise Questions and Answers.
BSE Odisha Class 9 Maths Solutions Geometry Chapter 1 ରେଖା ଓ କୋଣ Ex 1(b)
Question 1.
ନିମ୍ନଲିଖତ ପଦଗୁଡ଼ିକର ସଂଜ୍ଞା ଲେଖ ।
କୋଣର ଅନ୍ତର୍ଦେଶ, ସନ୍ନିହିତ କୋଣ, ପ୍ରତୀପ କୋଣ, ପରିପୂରକ କୋଣ, ଅନୁପୂରକ କୋଣ ।
ସମାଧାନ:
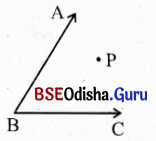
କୋଣର ଅନ୍ତର୍ଦେଶ:
∠ABC ର \(\overleftrightarrow{\mathrm{BC}}\) ର A – ପାର୍ଶ୍ବ \(\overleftrightarrow{\mathrm{AB}}\) ର C – ପାର୍ଶ୍ଵର ଛେଦକୁ ∠ABC ର ଅନ୍ତର୍ଦେଶ କୁହାଯାଏ । ∠ABC ର ଅନ୍ତର୍ଦେଶରେ ଥିବା ପ୍ରତ୍ୟେକ ବିନ୍ଦୁକୁ ∠ABC ର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ କୁହାଯାଏ । ଦତ୍ତ ଚିତ୍ରରେ P, ∠ABC ର ଗୋଟିଏ ଅନ୍ତସ୍ଥ ବିନ୍ଦୁ ଅଟେ । ଏହିପରି ଅସଂଖ୍ୟ ବିନ୍ଦୁକୁ ନେଇ କୋଣର ଅନ୍ତର୍ଦେଶ ଗଠିତ ।
ସନ୍ନିହିତ କୋଣ:
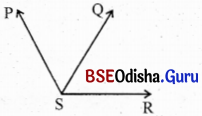
ଦୁଇଟି କୋଣର ଗୋଟିଏ ସାଧାରଣ ବାହୁ ଓ କୋଣଦ୍ୱୟର ଅନ୍ୟ ବାହୁ ଦୁଇଟି ସାଧାରଣ ବାହୁର ବିପରୀତ ପାର୍ଶ୍ବରେ ବିସ୍ତୃତ ହେଲେ, ସେମାନଙ୍କୁ ସନ୍ନିହିତ କୋଣ (Adjacent angles) କୁହାଯାଏ ।
ଦତ୍ତ ଚିତ୍ରରେ ∠PSQ ଓ ∠QSR ସନ୍ନିହିତ ଅଟନ୍ତି ।
ପ୍ରତୀପ କୋଣ:
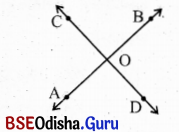
ଗୋଟିଏ କୋଣର ବାହୁଦ୍ୱୟର ବିପରୀତ ରଶ୍ମିମାନଙ୍କ ଦ୍ବାରା ଗଠିତ କୋଣକୁ ଉକ୍ତ କୋଣର ପ୍ରତୀପ କୋଣ (Vertically OppositeAngle) କୁହାଯାଏ । ଦତ୍ତ ଚିତ୍ରରେ ∠BOC ଓ ∠AOD ପରସ୍ପର ପ୍ରତୀପ ଏବଂ ∠AOC ଓ ∠BOD ପରସ୍ପର ପ୍ରତୀପ ଅଟନ୍ତି ।
ପରିପୂରକ କୋଣ:
ଗୋଟିଏ ରଶ୍ମିର ଶୀର୍ଷବିନ୍ଦୁ ଅନ୍ୟ ଏକ ରେଖାରେ ଅବସ୍ଥିତ ହେଲେ ଯେଉଁ ଦୁଇଟି ସନ୍ନିହିତ କୋଣ ଉତ୍ପନ୍ନ ହୁଅନ୍ତି, ସେମାନେ ପରସ୍ପର ପରି ପୂରକ (Supplementary angle); ଅର୍ଥାତ୍ ସେମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି 180° ଅଟେ ।
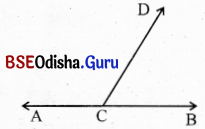
ଦତ୍ତ ଚିତ୍ରରେ m∠ACD + m∠BCD = 180° ଅର୍ଥାତ୍ ∠ACD ଓ ∠BCD ପରସ୍ପର ପରିପୂରକ ଅଟନ୍ତି ।
ଅନୁପୂରକ କୋଣ:
ଦୁଇଟି କୋଣର ପରିମାଣର ସମଷ୍ଟି 90° ହେଲେ ସେମାନଙ୍କୁ ପରସ୍ପର ଅନୁପୂରକ କୋଣ (Complementary angles) କୁହାଯାଏ ।
![]()
Question 2.
ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।
(i) ଗୋଟିଏ କୋଣର କେତୋଟି ବାହୁ ଥାଏ ?
ସମାଧାନ:
ଦୁଇଟି
(ii) ଗୋଟିଏ କୋଣର କେତୋଟି ଶୀର୍ଷବିନ୍ଦୁ ଥାଏ ?
ସମାଧାନ:
ଗୋଟିଏ
(ii) କୋଣର ଅନ୍ତର୍ଦେଶରେ କେତୋଟି ବିନ୍ଦୁ ଥାଏ ?
ସମାଧାନ:
ଅସଂଖ୍ୟ
(iv) କୋଣ ଓ ଏହାର ଅନ୍ତର୍ଦେଶର ଛେଦରେ କେତୋଟି ବିନ୍ଦୁ ଥାଏ ?
ସମାଧାନ:
କୌଣସି ବିନ୍ଦୁ ନଥାଏ
Question 3.
ନିମ୍ନରେ ଦିଆଯାଇଥିବା ତାଲିକାରୁ କେଉଁଗୁଡ଼ିକ ଉତ୍ତଳ ସେଟ୍ ଦର୍ଶାଅ ।
(i) ରେଖାଖଣ୍ଡ
(ii) ରଶ୍ମି
(iii) ରେଖା
(iv) କୋଣ
(v) କୋଣର ଅନ୍ତର୍ଦ୍ଦେଶ
(vi) ସମତଳ
(vii) କୋଣର ବହିର୍ଦେଶ
ସମାଧାନ:
(i) ରେଖାଖଣ୍ଡ
(ii) ରଶ୍ମି
(iii) ରେଖା
(v) କୋଣର ଅନ୍ତଦ୍ଦେଶ ଓ
(vi) ସମତଳ
Question 4.
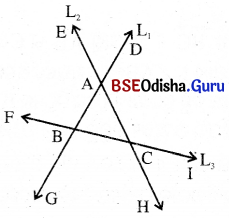
ତିନୋଟି ସରଳରେଖା ପରସ୍ପରକୁ ଛେଦକରୁଥିବାର ଏକ ଚିତ୍ର ଅଙ୍କନ କର । ତତ୍ପରେ ଚିତ୍ରକୁ ଦେଖ୍ ପ୍ରତୀପ କୋଣ ।
ସମାଧାନ:
ପ୍ରତୀପ କୋଣ ଯୋଡ଼ା:
(i) ∠EAD ଓ ∠BAC
(ii) ∠EAB ଓ ∠CAD
(iii) ∠FBG ଓ ∠ABC
(iv) ∠FBA ଓ ∠GBC
(v) ∠ICH ଓ ∠ACB
(vi) ∠ACI ଓ ∠BCH
Question 5.
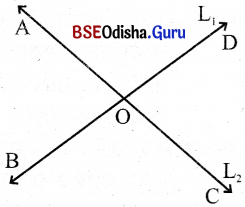
ଦୁଇଟି ସରଳରେଖା ପରସ୍ପରକୁ ଗୋଟିଏ ବିନ୍ଦୁରେ ଛେଦ କରୁଥିବାର ଚିତ୍ରଟିଏ ଅଙ୍କନ କର । ତତ୍ପରେ ଚିତ୍ରରୁ ସନ୍ନିହିତ ପରିପୂରକ କୋଣଯୋଡ଼ାଗୁଡ଼ିକୁ ଲେଖ ।
ସମାଧାନ:
(i) ∠AOBର ସନ୍ନିହିତ ପରିପୂରକ ∠AOD
(ii) ∠AOBର ସନ୍ନିହିତ ପରିପୂରକ ∠BOC
(ii) ∠BOCର ସନ୍ନିହିତ ପରିପୂରକ ∠COD
(iv) ∠CODର ସନ୍ନିହିତ ପରିପୂରକ ∠AOD
![]()
Question 6.
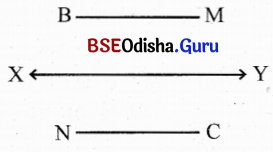
XY ସରଳରେଖାର ବିପରୀତ ପାର୍ଶ୍ବରେ M ଓ N ବିନ୍ଦୁକୁ ଚିହ୍ନଟ କର । ଅଙ୍କିତ ସରଳରେଖାର N-ପାର୍ଶ୍ଵରେ C ବିନ୍ଦୁ ଏବଂ M-ପାର୍ଶ୍ବରେ B ବିନ୍ଦୁ ଚିହ୍ନଟ କର । ଚିତ୍ର ମାଧ୍ୟମରେ ଦର୍ଶାଅ ଯେ, BM ଓ NC ରେଖାଖଣ୍ଡଦ୍ଵୟ ସରଳରେଖାର ବିପରୀତ ପାର୍ଶ୍ବରେ ରହିବେ ?
ସମାଧାନ:
(i) \(\overleftrightarrow{\mathrm{XY}}\) (ସରଳରେଖା)ର ବିପରୀତ ପାର୍ଶ୍ବରେ M ଓ N ବିନ୍ଦୁ ଚିହ୍ନଟ ହୋଇଛି ।
(ii) ଅଙ୍କିତ ସରଳରେଖାର N ପାର୍ଶ୍ଵରେ C ବିନ୍ଦୁ ଓ M ପାର୍ଶ୍ବରେ B ବିନ୍ଦୁ ଚିହ୍ନଟ ହୋଇଛି ।
(iii) ଚିତ୍ରରୁ ସୁସ୍ପଷ୍ଟ ଯେ, \(\overline{\mathrm{BM}}\) ଓ \(\overline{\mathrm{NC}}\) ରେଖାଖଣ୍ଡଦ୍ଵୟ \(\overleftrightarrow{\mathrm{XY}}\) ସରଳରେଖାର ବିପରୀତ ପାର୍ଶ୍ଵରେ ଅଛନ୍ତି ।
Question 7.
ନିମ୍ନ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ । ଆବଶ୍ୟକସ୍ଥଳେ ଚିତ୍ର ଅଙ୍କନ କର ।
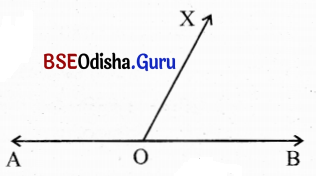
(i) X ବିନ୍ଦୁ \(\overleftrightarrow{\mathrm{AB}}\) ଉପରେ ଅବସ୍ଥିତ ନ ହେଲେ ଓ A – O – B ହେଲେ,
m∠XOA + m∠XOB କେତେ ?
ସମାଧାନ:
m∠XOA + m∠XOB = 180°
( ∵ ∠XOA ଏବଂ ∠XOB ସନ୍ନିହିତ ପରିପୂରକ)
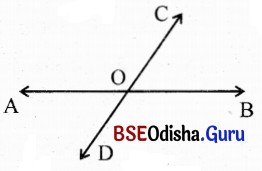
(ii) \(\overleftrightarrow{\mathrm{AB}}\) ଓ \(\overleftrightarrow{\mathrm{CD}}\) ର ଛେଦବିନ୍ଦୁ O ହେଲେ, ∠AOC ର ପ୍ରତୀପ କୋଣ
କେଉଁଟି ?
ସମାଧାନ:
\(\overleftrightarrow{\mathrm{AB}}\) ଓ \(\overleftrightarrow{\mathrm{CD}}\) ଦ୍ଵୟର ଛେଦବିନ୍ଦୁ O ।
∠AOC ର ପ୍ରତୀପ କୋଣ ∠BOD ।
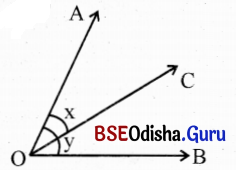
(iii) m∠AOB ର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ m∠AOC = x ଓ m∠AOB = y ହେଲେ, m∠BOC କେତେ ?
ସମାଧାନ:
m∠AOB ର ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ C NC
m∠AOC = x ଏବଂ m∠AOB = y
∴ m∠BOC = m∠AOB – m∠AOC = y – x
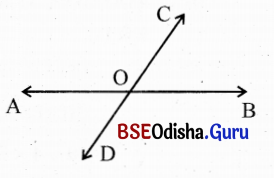
(iv) ଦୁଇଟି ସରଳରେଖା ପରସ୍ପରକୁ ଛେଦକଲେ ଉତ୍ପନ୍ନ ହେଉଥିବା କୋଣଗୁଡ଼ିକ ମଧ୍ୟରୁ ଯଦି ଗୋଟିଏ କୋଣର ପରିମାଣ 30° ହୁଏ, ତେବେ ଏହାର ପ୍ରତୀପ କୋଣର ପରିପୂରକ କୋଣର ପରିମାଣ କେତେ ହେବ ?
ସମାଧାନ:
\(\overleftrightarrow{\mathrm{AB}}\) ଓ \(\overleftrightarrow{\mathrm{CD}}\) ଦ୍ଵୟ ପରସ୍ପରକୁ O ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।
ମନେକର m∠BOC = 30°
m∠BOC = m∠AOD (∵ ପ୍ରତୀପ କୋଣ)
m∠AOD ର ପରିପୂରକ କୋଣର ପରିମାଣ = 180° – 30° = 150° (∵ ପରିପୂରକ କୋଣଦ୍ଵୟର ସମଷ୍ଟି 180° ।)
![]()
Question 8.
(i) m∠AOB = x ଓ∠AOB ର ଅନୁପୂରକ କୋଣର ପରିମାଣ 2x° ହେଲେ xର ମାନ ଡିଗ୍ରୀରେ ପ୍ରକାଶ କର ।
ସମାଧାନ:
m∠AOB = x
m∠AOB କୋଣର ଅନୁପୂରକ କୋଣର ପରିମାଣ = 2x
⇒ ପ୍ରଶ୍ନନୁସାରେ, 90°- x = 2x
⇒ 2x + x = 90°
⇒ 3x = 90°
⇒ x = \(\frac{90^{\circ}}{3}\) = 30°
(ii) ଗୋଟିଏ କୋଣର ପରିମାଣ, ଏହାର ପରିପୂରକ କୋଣର ପରିମାଣର ଦୁଇଗୁଣରୁ 18° ଅଧିକ ହେଲେ, କୋଣଟିର ପରିମାଣ କେତେ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର କୋଣ ଦ୍ଵୟର ପରିମାଣ ଯଥାକ୍ରମେ θ ଏବଂ 2θ + 18° ।
ପ୍ରଶ୍ନନୁସାରେ କୌଣଦ୍ଵୟ ପରସ୍ପର ପରିପୂରକ । ଅର୍ଥାତ୍ θ + 2θ + 18° = 180°
⇒ 3θ = 180° – 18° = 162°
⇒ θ = \(\frac{162}{3}\) = 54°
∴ ନିଶ୍ଚେୟ କୋଣର ପରିମାଣ = 2θ + 18° = 2 × 54 + 18 = 108 + 18 = 126°
ବିକଳ୍ପ ପ୍ରଣାଳୀ:
ମନେକର କୋଣଟିର ପରିମାଣ θ । ଏହାର ପରିପୂରକ କୋଣର ପରିମାଣ (180 – θ°) ।
ପ୍ରଶ୍ନନୁସାରେ θ = 2(180°- θ) + 18°
⇒ θ = 360° – 2θ + 18°
⇒ 3θ = 378°
⇒ θ = \(\frac{378}{3}\) = 126°
(iii) ଗୋଟିଏ କୋଣର ପରିମାଣ ତାହାର ପରିପୂରକ କୋଣର ପରିମାଣର ଏକପଞ୍ଚମାଂଶ ହେଲେ କୋଣଟିର ପରିମାଣ ସ୍ଥିର କର ।
ସମାଧାନ:
ମନେକର କୋଣଦ୍ଵୟର ପରିମାଣ θ ଏବଂ \(\frac{θ}{5}\) ।
ପ୍ରଶାନୁସାରେ, କୋଣଦ୍ଵୟ ପରସ୍ପର ପରିପୂରକ ।
⇒ θ + \(\frac{θ}{5}\) = 180°
⇒ \(\frac{5 \theta+\theta}{5}\) = 180°
⇒ 6θ = 180° × 5
⇒ \(\frac{180^{\circ} \times 5}{6}\) = 150°
∴ ନିଶ୍ଚେୟ କୋଣର ପରିମାଣ = \(\frac{θ}{5}\) = \(\frac{150^{\circ}}{5}\) = 30°
ବିକଳ୍ପ ପ୍ରଣାଳୀ:
ମନେକର କୋଣଟିର ପରିମାଣ θ । ଏହାର ପରିପୂରକ କୋଣର ପରିମାଣ (180 – θ°)
ପ୍ରଶ୍ନନୁସାରେ θ = \(\frac{180^{\circ}-\theta}{5}\)
⇒ 5θ = 180° – θ
⇒ 6θ = 180°
⇒ θ = 30°
(iv) ଦୁଇଟି ସନ୍ନିହିତ ପରିପୂରକ କୋଣର ପରିମାଣର ଅନୁପାତ 4 : 5 ହେଲେ, କୋଣଦ୍ୱୟର ପରିମାଣ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ସନ୍ନିହିତ ପରିପୂରକ କୋଣଦ୍ୱୟର ପରିମାଣ ଯଥାକ୍ରମେ 4θ ଓ 5θ ।
ପ୍ରଶ୍ନନୁସାରେ, 4θ + 5θ = 180°
9θ = 180°
θ = \(\frac{180}{9}\) = 20°
∴ 4θ = 4 × 20° = 80° ଓ 5θ = 5 × 20° = 100°
∴ ନିର୍ଦେୟ କୋଣଦ୍ଵୟର ପରିମାଣ ଯଥାକ୍ରମେ 80° ଓ 100° ।
(v) ଗୋଟିଏ କୋଣର ପରିମାଣ, ତାହାର ପରିପୂରକ କୋଣର ପରିମାଣଠାରୁ 20° କମ୍ ହେଲେ, କୋଣଟିର ପରିମାଣ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର କୋଣଦ୍ଵୟର ପରିମାଣ ଯଥାକ୍ରମେ θ ଓ θ – 20° ।
ପ୍ରଶ୍ନନୁସାରେ, କୋଣଦ୍ୱୟ ପରସ୍ପର ପରିପୂରକ ।
⇒ θ + θ – 20° = 180°
⇒ 20 = 180° + 20°
⇒ θ = \(\frac{200}{2}\) = 100°
∴ ନିଶ୍ଚେୟ କୋଣର ପରିମାଣ = θ – 20° = 100° – 20° = 80°
(vi) ଦୁଇଟି ସନ୍ନିହିତ ପରିପୂରକ କୋଣର ପରିମାଣର ଅନ୍ତର 30° ହେଲେ କୋଣଦ୍ୱୟର ପରିମାଣ ସ୍ଥିର କର ।
ସମାଧାନ:
ମନେକର କୋଣଦ୍ବୟର ପରିମାଣ ଯଥାକ୍ରମେ θ ଓ θ + 30° ।
θ + θ + 30° = 180°
⇒ 2θ + 30° = 180°
⇒ 2θ = 180° – 30°
⇒ θ = \(\frac{150}{2}\) = 75°
∴ ବୃହତ୍ତର ପରିମାଣ ବିଶିଷ୍ଟ କୋଣର ପରିମାଣ = θ + 30° = 75° + 30° = 105° ।
(vii) ଗୋଟିଏ କୋଣର ପରିମାଣ ତାହାର ଅନୁପୂରକ କୋଣ ପରିମାଣର ଏକ-ପଞ୍ଚମାଂଶ ହେଲେ, କୋଣଟିର ପରିମାଣ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର କୋଣଟିର ପରିମାଣ x° ।
ଏହାର ଅନୁପୂରକ କୋଣର ପରିମାଣ (90 – x°) ।
ପ୍ରଶ୍ନନୁସାରେ, x = \(\frac{90-x}{5}\)
⇒ 5x = 90 − x
6x = 90
⇒ x = \(\frac{90}{6}\) = 15°
∴ କୋଣଟିର ପରିମାଣ 15° ।
![]()
Question 9.
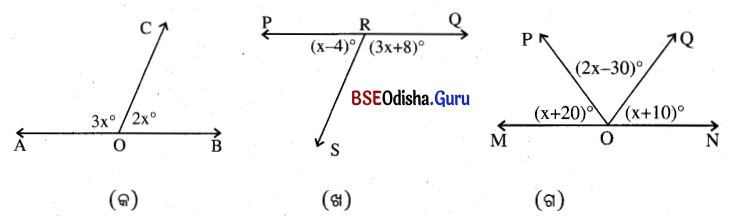
ନିମ୍ନସ୍ଥ ଚିତ୍ରଗୁଡ଼ିକ ଅନୁସାରେ x ର ମାନ କେତେ ହେବ ସ୍ଥିର କର ।
ସମାଧାନ:
(i) ଚିତ୍ର (କ) ରେ ∠AOC ଓ ∠BOC ଦ୍ବୟ ସନ୍ନିହିତ ପରିପୂରକ ହେତୁ m∠AOC + m∠BOC = 180°
⇒ 3x + 2x = 180
⇒ 5x = 180
⇒ x = \(\frac{180}{5}\) = 36
∴ x = 36°
(ii) ଚିତ୍ର (ଖ) ରେ ∠PRS ଓ ∠ORS ଦ୍ବୟ ସନ୍ନିହିତ ପରିପୂରକ ହେତୁ m∠PRS + m∠QRS = 180°
(x – 4) + (3x + 8) = 180
⇒ 4x + 4 = 180
⇒ 4x = 180 – 4
⇒ x = \(\frac{176}{4}\) = 44
∴ x = 44°
(iii) ଚିତ୍ର (ଗ) ରେ m∠MOP + m∠POQ + m∠QON = 180°
⇒ (x + 20) + (2x – 30) + (x + 10) = 180°
⇒ 4x = 180°
⇒ x = \(\frac{180}{4}\) = 45°
∴ x = 45°
Question 10.
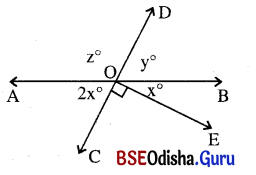
ଦତ୍ତ ଚିତ୍ରରେ \(\overleftrightarrow{\mathrm{AB}}\) ଓ \(\overleftrightarrow{\mathrm{CD}}\) ସରଳରେଖାଦ୍ଵୟ ପରସ୍ପରକୁ O ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।
m∠COE = 90° ହେଲେ x, Y ଓ z ର ମାନ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
m∠AOC = m∠BOD (ପ୍ରତୀପ) ⇒ 2x = y
ସେହିପରି m∠AOD = m∠BOC (ପ୍ରତୀପ)
⇒ z = 90° + x (∴ m∠COE = 90°)
![]() m∠AOC + m∠AOD = 180°
m∠AOC + m∠AOD = 180°
⇒ 2x + 90° + x = 180°
⇒ 3x = 90°
⇒ x = 30° (∵ m∠AOD = 90° + x)
y = 2x = 2 × 30° = 60°,
z = 90° + x = 90° + 30° = 120°
Question 11.
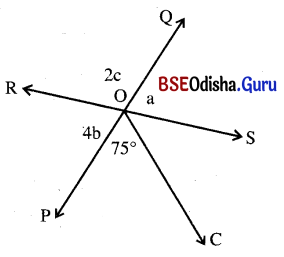
ଦତ୍ତ ଚିତ୍ରରେ \(\overleftrightarrow{\mathrm{PQ}}\) ଓ \(\overleftrightarrow{\mathrm{RS}}\) ଦ୍ବୟର ଛେଦବିନ୍ଦୁ O ଓ m∠POC = 75° ହେଲେ, a, b ଏବଂ c ର ମାନ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
∠ROP ଓ ∠POS ସନ୍ନିହିତ ପରିପୂରକ ହେତୁ,
m∠ROP + m∠POS = 180°
⇒ m∠ROP + m∠POC + m∠COS = 180°
⇒ 4b + 75° + b = 180°
⇒ 5b + 75° = 180°
⇒ 5b = 180° – 75° = 105°
⇒ b = \(\frac{105}{5}\) = 21°
m∠QOS = m∠ROP (ପ୍ରତୀପ କୋଣ)
⇒ a = 4b = b × 21 = 84°
∠ROQ ଓ ∠QOS ![]() m∠ROQ + m∠QOS = 180°
m∠ROQ + m∠QOS = 180°
⇒ 2c + a = 180°
⇒ 2c + 84° = 180°
⇒ 2c = 180° – 84° = 96°
∴ c = \(\frac{96°}{2}\) =48°
∴ a = 84°, b = 21°, c = 48°
![]()
Question 12.
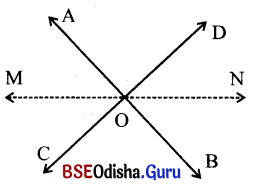
ପ୍ରମାଣ କର ଯେ, ଦୁଇଟି ପ୍ରତୀପ କୋଣର ସମଦ୍ବିଖଣ୍ଡକ ଏକ ସରଳରେଖା ଉପରିସ୍ଥ ଦୁଇଟି ବିପରୀତ ରଶ୍ମି ହେବେ ।
ସମାଧାନ:
ଦତ୍ତ : \(\overleftrightarrow{\mathrm{AB}}\) ଓ \(\overleftrightarrow{\mathrm{CD}}\) ରେଖାଦ୍ବୟର ଛେଦବିନ୍ଦୁ O ।
\(\overrightarrow{\mathrm{OM}}\) ଏବଂ \(\overrightarrow{\mathrm{ON}}\) ଯଥାକ୍ରମେ ∠AOC ଓ ∠BOD ର ସମଦ୍ବିଖଣ୍ଡକ ।
ପ୍ରାମାଣ୍ୟ : \(\overrightarrow{\mathrm{OM}}\) ଏବଂ \(\overrightarrow{\mathrm{ON}}\) ବିପରୀତ ରଶ୍ମି ଅଟନ୍ତି ।
ପ୍ରାମାଣ୍ : m∠AOC + m∠AOD = 180°
⇒ \(\frac{1}{2}\)m∠AOC + \(\frac{1}{2}\)m∠AOC + m∠AOD = 180°
(∵ m∠AOC = \(\frac{1}{2}\)m∠AOC + \(\frac{1}{2}\)m∠AOC)
\(\frac{1}{2}\)m∠AOC + \(\frac{1}{2}\)m∠BOD + m∠AOD = 180°
m∠AOM + m∠DON + m∠AOD = 180°
m∠AOM + m∠AON = 180°
\(\overrightarrow{\mathrm{OM}}\) ଓ \(\overrightarrow{\mathrm{ON}}\) ବିପରୀତ ରଶ୍ମି ଅଟନ୍ତି ।
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 13.
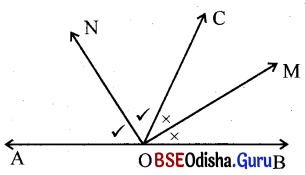
ପ୍ରମାଣ କର ଯେ, ଦୁଇଟି ସନ୍ନିହିତ ପରିପୂରକ କୋଣର ସମଦ୍ବିଖଣ୍ଡକ ରଶ୍ମିଦ୍ବୟ ପରସ୍ପର ପ୍ରତି ଲମ୍ବ ।
ସମାଧାନ:
ଦତ୍ତ : ∠AOC ଓ ∠BOC ସନ୍ନିହିତ ପରିପୂରକ ।
OM ଓ ON ଯଥାକ୍ରମେ ∠BOC ଏବଂ ∠AOC ର ସମଦ୍ବିଖଣ୍ଡକ ।
ପ୍ରାମାଣ୍ୟ : \(\overrightarrow{\mathrm{OM}} \perp \overrightarrow{\mathrm{ON}}\) ଅର୍ଥାତ୍ m∠MON = 90°
ପ୍ରମାଣ : ∠AOC ଓ ∠BOC ସନ୍ନିହିତ ପରିପୂରକ ।
⇒ m∠AOC +m∠BOC = 180°
⇒ \(\frac{1}{2}\)m∠AOC + \(\frac{1}{2}\)m∠BOC = \(\frac{1}{2}\) × 180°
⇒ m∠CON + m∠COM = 90° (∵ \(\overrightarrow{\mathrm{OM}}\), ∠BOC ର ଏବଂ \(\overrightarrow{\mathrm{ON}}\), ∠AOC ର ସମଦ୍ବିଖଣ୍ଡକ)
⇒ m∠MON = 90°
∴ \(\overrightarrow{\mathrm{OM}} \perp \overrightarrow{\mathrm{ON}}\)
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 14.
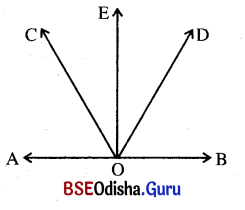
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ∠AOE ଏବଂ ∠EOB ଦୁଇଟି ସନ୍ନିହିତ ପରିପୂରକ କୋଣ ଓ \(\overrightarrow{\mathrm{OC}}\), ∠AOC କୁ ସମଦ୍ବିଖଣ୍ଡ କରେ ।
m∠COD = 90° ହେଲେ ଦର୍ଶାଅ ଯେ, \(\overrightarrow{\mathrm{OD}}\), ∠EOB ର ସମଦ୍ବିଖଣ୍ଡକ ହେବ ।
ସମାଧାନ:
ଦତ୍ତ : ∠AOE ଏବଂ ∠EOB ସନ୍ନିହିତ ପରିପୂରକ ।
\(\overrightarrow{\mathrm{OC}}\), ∠AOE କୁ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରେ ଏବଂ m∠COD = 90° ।
ପ୍ରାମାଣ୍ୟ : \(\overrightarrow{\mathrm{OD}}\), ∠EOB ର ସମଦ୍ବିଖଣ୍ଡକ ।
ପ୍ରମାଣ : ∠AOE ଏବଂ ∠EOB ସନ୍ନିହିତ ପରିପୂରକ ।
⇒ m∠AOE + m∠EOB = 180°
⇒ \(\frac{1}{2}\)m∠AOE + \(\frac{1}{2}\)∠EOB = 90°
⇒ m∠COE + \(\frac{1}{2}\)m∠EOB = 90° … (i)
କିନ୍ତୁ mZCOD = 90° (ଦତ୍ତ)
∴ m∠COE + m∠EOD = 90° … (ii)
⇒ (i) ଓ (ii) ରୁ m∠COE + \(\frac{1}{2}\)m∠EOB = m∠COE + m∠EOD
⇒ \(\frac{1}{2}\)m∠EOB = m∠EOD
⇒ \(\overrightarrow{\mathrm{OD}}\), ∠EOB ର ସମଦ୍ବିଖଣ୍ଡକ ।
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
![]()
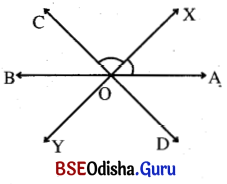
Question 15.
\(\overleftrightarrow{AB}\) ଓ \(\overleftrightarrow{CD}\) ପରସ୍ପରକୁ O ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି । m∠AOC ର ସମଦ୍ବିଖଣ୍ଡକ \(\overrightarrow{OX}\) । ପ୍ରମାଣ କର ଯେ, \(\overleftrightarrow{XO}\) କୋଣ BOD କୁ ସମର୍ଦ୍ଦିଖଣ୍ଡ କରେ ।
ସମାଧାନ:
ଦତ୍ତ : \(\overleftrightarrow{AB}\) ଓ \(\overleftrightarrow{CD}\) ପରସ୍ପରକୁ ଠ ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।
\(\overrightarrow{OX}\), ∠AOC ର ସମଦ୍ବିଖଣ୍ଡକ ।
\(\overrightarrow{OX}\) ର ବିପରୀତ ରଶ୍ମି \(\overrightarrow{OY}\) ।
ପ୍ରାମାଣ୍ୟ : \(\overrightarrow{OY}\), ZBOD ର ସମଦ୍ବିଖଣ୍ଡକ ।
ପ୍ରମାଣ : \(\overrightarrow{OX}\) ର ବିପରୀତ ରଶ୍ମି OY ହେତୁ ଏକ ସରଳରେଖା \(\overleftrightarrow{XY}\)
ଏବଂ \(\overleftrightarrow{AB}\) ପରସ୍ପରକୁ ଠ ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।
⇒ m∠AOX = m∠BOY (ପ୍ରତୀପ କୋଣ)
ପୁନଶ୍ଚ, \(\overleftrightarrow{XY}\) ଏବଂ \(\overleftrightarrow{CD}\) ପରସ୍ପରକୁ ଠ ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।
⇒ m∠XOC = m∠YOD (ପ୍ରତୀପ କୋଣ)
\(\overrightarrow{OX}\), ∠AOC ର ସମଦ୍ବିଖଣ୍ଡକ।
⇒ m∠A0X = m∠XOC
⇒ m∠BOY = m∠YOD (∵ ∠AOX = ∠BOY ଏବଂ ∠XOC = ∠YOD)
∴ \(\overrightarrow{OY}\), ∠BOD ର ସମଦ୍ବିଖଣ୍ଡକ ।
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
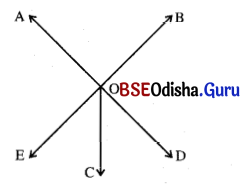
Question 16.
\(\overrightarrow{\mathrm{OA}}\), \(\overrightarrow{\mathrm{OB}}\), \(\overrightarrow{\mathrm{OC}}\) ଏକ ସମତଳରେ ଅବସ୍ଥିତ ରଶି । କୌଣସି ରଶି ଅନ୍ୟ ରଶି ଦଇଟି ଦାରା ଗଠିତ କୋଣର ଅନ୍ତର୍ଦେଶରେ ବିସ୍ତୃତ ନୁହେଁ । ପ୍ରମାଣ କର ଯେ, m∠AOB + m∠BOC + m∠COA =360°
ସମାଧାନ:
ଦତ୍ତ : \(\overrightarrow{\mathrm{OA}}\), \(\overrightarrow{\mathrm{OB}}\) ଓ \(\overrightarrow{\mathrm{OC}}\) , O ବିନ୍ଦୁଗାମୀ ତିନୋଟି ଭିନ୍ନ ଭିନ୍ନ ରଶ୍ମି ।
ପ୍ରାମାଣ୍ୟ : m∠AOB + m∠BOC + m∠AOC = 360°
ଅଙ୍କନ : \(\overrightarrow{\mathrm{OA}}\) ର ବିପରୀତ ରଶ୍ମି \(\overrightarrow{\mathrm{OD}}\) ଏବଂ \(\overrightarrow{\mathrm{OB}}\) ର ବିପରୀତ ରଶ୍ମି \(\overrightarrow{\mathrm{OE}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : m∠AOE +m∠EOD = 180° (ସନ୍ନିହିତ ପରିପୂରକ କୋଣ)
⇒ m∠AOE + m∠EOC + m∠COD = 180° … (i)
[∵ m∠EOD = m∠EOC + m∠COD]
ସେହିପରି m∠AOB + m∠BOD = 180° (ସନ୍ନିହିତ ପରିପୂରକ କୋଣ) … (ii)
ସମୀକରଣ (i) ଓ (ii)କୁ ଯୋଗକଲେ,
m∠AOE + m∠EOC + m∠COD + m∠AOB + m∠BOD = 180° + 180°
⇒ m∠AOB + (m∠BOD + m∠DOC) + (m∠AOE + m∠EOC) = 360°
⇒ m∠AOB + m∠BOC + m∠COA = 360°
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
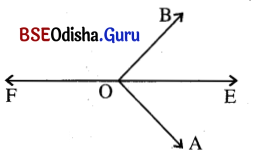
Question 17.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ \(\overrightarrow{\mathrm{OE}}\), ∠AOB ର ସମଦ୍ବିଖଣ୍ଡକ ରଶ୍ମି । \(\overrightarrow{\mathrm{OF}}\), \(\overrightarrow{\mathrm{OE}}\) ର ବିପରୀତ ରଶ୍ମି ହେଲେ, ଦର୍ଶାଅ ଯେ,
m∠BOF = m∠AOF l
ସମାଧାନ:
ଦତ୍ତ : \(\overrightarrow{\mathrm{OE}}\), ∠AOB ର ସମର୍ଦ୍ଦିଖଣ୍ଡକ । \(\overrightarrow{\mathrm{OF}}\) ର ବିପରୀତ ରଶ୍ମି \(\overrightarrow{\mathrm{OE}}\) l
ପ୍ରାମାଣ୍ୟ : m∠BOF=m∠AOF
ପ୍ରମାଣ : ∠BOF ଏବଂ ∠BOE ସନ୍ନିହିତ ପରିପୂରକ ।
⇒ m∠BOF + m∠BOE = 180° … (i)
ପୁନଶ୍ଚ, ∠AOF ଏବଂ ∠AOE ସନ୍ନିହିତ ପରିପୂରକ ।
⇒ m∠AOF + m∠AOE = 180° … (ii)
⇒ (i) ଓ (ii) ରୁ m∠BOF + m∠BOE = m∠AOF + m∠AOE
⇒ m∠BOF = m∠AOF (∵\(\overrightarrow{\mathrm{OE}}\), ∠AOB ର ସମଦ୍ବିଖଣ୍ଡକ)
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
