BSE Odisha 9th Class Maths Solutions Geometry Chapter 1 ରେଖା ଓ କୋଣ Ex 1(c)

Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 1 ରେଖା ଓ କୋଣ Ex 1(c) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Geometry Chapter 1 ରେଖା ଓ କୋଣ Ex 1(c)

Question 1.
ନିମ୍ନଲିଖ ଉକ୍ତିଗୁଡ଼ିକ ଠିକ୍ ବା ଭୁଲ ଲେଖ ।
(a) L₁ || L₂ ଓ L₂ || L₃ ହେଲେ L₁ || L₃
ସମାଧାନ:
ଠିକ୍

(b) L₁ ⊥ ଓ L₂ ⊥ L₃ ହେଲେ L₁ ⊥ L₃
ସମାଧାନ:
ଭୁଲ

(c)  L₁ = L₂ ହେଲେ L₁ || L₂
ସୂଚନା : L₁ = L₂ ର ଅର୍ଥ ହେଉଛି L₁ ଓ L₂ ରେଖା ଏକ ଅଭିନ୍ନ ।
ସମାନ୍ତର ସରଳରେଖା ସଂଜ୍ଞା ବ୍ୟବହାର କର ।
ସମାଧାନ:
ଠିକ୍

(d) ଦୁଇଟି ସମାନ୍ତର ସରଳରେଖା ଏକ ସମତଳରେ ଅବସ୍ଥିତ ।
ସମାଧାନ:
ଭୁଲ

(e) ∠ABC ଓ ∠DEF ମଧ୍ୟରେ \(\overleftrightarrow{\mathbf{AB}}\) || \(\overleftrightarrow{\mathbf{ED}}\) ଓ \(\overleftrightarrow{\mathbf{BC}}\) || \(\overleftrightarrow{\mathbf{EF}}\) ହେଲେ m∠ABC = m∠DEF ହେବ ।
ସମାଧାନ:
ଠିକ୍

Question 2.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ L₁ || L₂ ଓ L₃ ସେମାନଙ୍କର ଛେଦକ । ଛେଦବିନ୍ଦୁରେ ଉତ୍ପନ୍ନ କୋଣଗୁଡ଼ିକ 1, 2, 3 …. 8 ସଂଖ୍ୟା ଦ୍ଵାରା ଚିହ୍ନିତ । m∠3 = 65° ହେଲେ, ଅନ୍ୟ କୋଣଗୁଡ଼ିକର ପରିମାଣ ସ୍ଥିର କର ।
ସମାଧାନ:

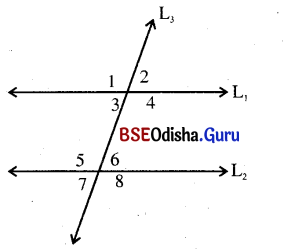
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ L₁ || L₂ ଓ L₃ ଛେଦକ ।
m∠3 = 65° (ଦତ୍ତ)
∴ m∠3 + m∠1 = 180° (ସନ୍ନିହିତ ପରିପୂରକ)
⇒ m∠1 = 180° – m∠3 = 180° – 65° = 115°
m∠1 = m∠4 (ପ୍ରତୀପ କୋଣ) ⇒ m∠4 = 115°
m∠3 = m∠2 (ପ୍ରତୀପ କୋଣ) ⇒ m∠2 = 65°
m∠4 = m∠5 (ଏକାନ୍ତର କୋଣ) ⇒ m∠5 = 115°
m∠5 = m∠8 (ପ୍ରତୀପ କୋଣ) ⇒ m∠8 = 115°
m∠4 = m∠7 (ଏକାନ୍ତର କୋଣ) ⇒ m∠7 = 1 15°
m∠7 = m∠6 (ପ୍ରତୀପ କୋଣ) ⇒ m∠6 = 65°
∴ m∠1 = m∠4 = m∠5 = m∠8 = 115° ଏବଂ m∠2 = m∠3 = m∠6 = m∠7 = 65° ।

Question 3.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ L₁ || L₂ ଏବଂ L₃ || L₄ ଚିତ୍ରରୁ ନିମ୍ନଲିଖ କୋଣଗୁଡ଼ିକର ପରିମାଣ ସ୍ଥିର କରି ଶୂନ୍ୟସ୍ଥାନଗୁଡ଼ିକୁ ପୂରଣ କର ।
m∠x = ________, m∠z = ________
m∠p = ________, m∠q = ________
m∠r = ________, m∠s = ________
ସମାଧାନ:

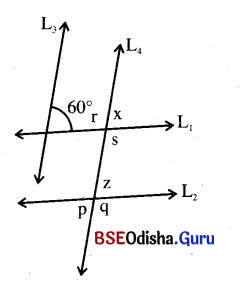
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ L₁ || L₂ ଓ L₃ || L₄
m∠x = 60°, m∠z = 60° (ଅନୁପୂରକ)
m∠p = 60° = m∠z, m∠z = m∠q = 120° (ପରସ୍ପର ପରିପୂରକ)
m∠r = 120° (ପ୍ରତୀପ), m∠s = 120° (∵ ∠x ଓ ∠r ପରସ୍ପର ପରିପୂରକ)

Question 4.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ L₁ || L₂ । ଚିତ୍ରକୁ ବ୍ୟବହାର କରି a, b, c, d ଦ୍ଵାରା ଚିହ୍ନିତ କୋଣଗୁଡ଼ିକର ପରିମାଣ ସ୍ଥିର କର ।
ସମାଧାନ:

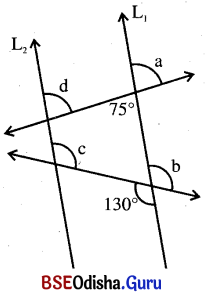
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ L₁ || L₂
m∠a = 75° (∵ ପ୍ରତୀପ କୋଣ)
m∠b = 130° (∵ ପ୍ରତୀପ କୋଣ)
m∠b = m∠c = 130° (∵ ଅନୁପୂରକ କୋଣ)
m∠a = m∠d = 75° (∵ ଅନୁପୂରକ କୋଣ)

Question 5.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ AB || CD ଏବଂ AD || BC । ଚିତ୍ରରୁ x, y, z ର ମାନ ସ୍ଥିର କର ।
ସମାଧାନ:

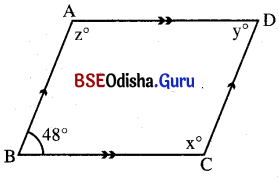
ଦତ୍ତ ଚିତ୍ରରେ AB || CD, AD || BC ଏବଂ m∠B = 48° ।
m∠B + m∠C = 180° (∵ AB || CD)
⇒ 48° + m∠x – 180° ⇒ x = 180° – 48° = 132°
ସେ୍ହିପରି m∠C + m∠D = 180° (∵ AD || BC)
⇒ x + y = 1 80°
⇒ 132 + y = 180° ⇒ y = 180° – 132° = 48°
ପୁନଣ୍ଚ m∠D + m∠A = 180° (∵ AB || CD)
⇒ y + z = 180°
⇒ 48 + z = 180°
⇒ z = 180° – 48° = 132°
x = 132°, y = 48°, z = 132° ।

Question 6.
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ PQ || RS । \(\overleftrightarrow{\mathbf{RS}}\) କୁ \(\overleftrightarrow{\mathbf{BN}}\) C ବିନ୍ଦୁରେ ଛେଦ କରେ । ଚିତ୍ରରୁ x ଓ y ର ମାନ ସ୍ଥିର କର ।
ସମାଧାନ:

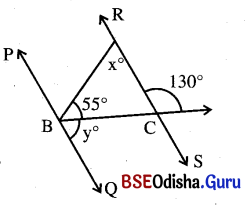
ଦତ୍ତ ଚିତ୍ରରେ m∠ACN + m∠ACB = 180° (ସନ୍ନିହିତ ପରିପୂରକ କୋଣ) 
m∠PBC = m∠ACN = 130° (ଅନୁଗୁପ)
∴ m∠ACB = 180° – 130° = 50°
\(\overleftrightarrow{\mathbf{PQ}}\) || \(\overleftrightarrow{\mathbf{RS}}\)
⇒ m∠ACB = m∠CBQ = 50° = y (ଏକାନ୍ତର କୋଣ)
m∠ABP = m∠PBC – m∠ABC = 130° – 55° = 75°
∴ m∠CAB = m∠ABP (ଏକାନ୍ତର)
∴ x = 75°
∴ x = 75° ଓ y = 50°

Question 7.
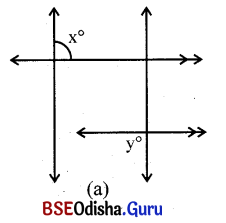
ଚିତ୍ରରେ ପ୍ରତ୍ୟେକ ଚିତ୍ର ଦୁଇଯୋଡ଼ା ସମାନ୍ତର ରେଖାଦ୍ଵାରା ଗଠିତ ଏବଂ ପ୍ରତ୍ୟେକ ଚିତ୍ରରେ ଦୁଇଟି କୋଣର ପରିମାଣ ସଂକେତରେ ଦର୍ଶାଯାଇଛି ।
(i) ଚିତ୍ର (a) ରୁ x ଓ y ମଧ୍ଯରେ ସମ୍ବନ୍ଧ ସ୍ଥିର କର ।

ସମାଧାନ:
ଦତ୍ତ ଚିତ୍ରରେ \(\overleftrightarrow{\mathbf{AB}}\) || \(\overleftrightarrow{\mathbf{CD}}\) ଓ \(\overleftrightarrow{\mathbf{PQ}}\) || \(\overleftrightarrow{\mathbf{ST}}\)
ଚିତ୍ର (a) ରୁ m∠x + m∠CQP = 180° (∵ \(\overleftrightarrow{\mathbf{AB}}\) || \(\overleftrightarrow{\mathbf{CD}}\))
ସେ୍ହିପରି m∠CQP = m∠QRS (ଅନୁଗୁପ କୋଣ) (∵ \(\overleftrightarrow{\mathbf{PQ}}\) || \(\overleftrightarrow{\mathbf{ST}}\))
m∠APQ = m∠PQR (ଏକାନ୍ତର କୋଣ) = x
∴ m∠x + m∠QRS = 180° (∵ \(\overleftrightarrow{\mathbf{PQ}}\) || \(\overleftrightarrow{\mathbf{ST}}\))
ମାତ୍ର m∠y + m∠QRS = 180°
∴ m∠x + m∠QRS = m∠y + m∠QRS
⇒ m∠x – m∠y

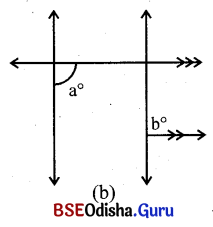
(ii) ଚିତ୍ର (b) ରୁ a ଓ b ମଧ୍ୟରେ ସମ୍ବନ୍ଧ ସ୍ଥିର କର ।

ସମାଧାନ:
ଦତ୍ତ ଚିତ୍ରରେ \(\overleftrightarrow{\mathbf{AB}}\) || \(\overleftrightarrow{\mathbf{CD}}\) ଓ \(\overleftrightarrow{\mathbf{PT}}\) || \(\overleftrightarrow{\mathbf{RS}}\)
⇒ m∠QPB = m∠TQR = a° (ଅନୁଗୁପ କୋଣ)
ଏବଂ ∠TQR + m∠SRQ = 180° (ସନ୍ନିହିତ ପରିପୂରକ)
⇒ m∠a + m∠b = 180°

Question 8.
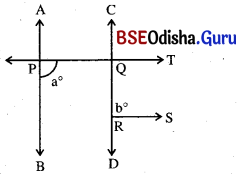
(i) ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ m∠ABC = 74°, m∠EDC = 38° ଓ m∠BCD = 36° । ପ୍ରମାଣ କର ଯେ, \(\overrightarrow{\mathrm{DE}}\) || \(\overrightarrow{\mathrm{BA}}\) ।
ସମାଧାନ:
ଦତ୍ତ : ଦତ୍ତ ଚିତ୍ରରେ m∠ABC = 74°, m∠EDC = 38° ଓ m∠BCD = 36° ।
ପ୍ରାମାଣ୍ୟ : \(\overrightarrow{\mathrm{DE}}\) || \(\overrightarrow{\mathrm{BA}}\)
ପ୍ରମାଣ : ΔCDF ରେ ବତ୍ହିଃସ୍ଥ m∠EFC = m∠FDC + m∠FCD = 38° + 36° = 74°
m∠ABF = 74°
∴ m∠ABF = m∠EFC = 74°
ତେଣୁ ଏମାନେ ଅନୁରୂପ । ⇒ \(\overleftrightarrow{\mathbf{DE}}\) || \(\overleftrightarrow{\mathbf{BA}}\) (ପ୍ରମାଣିତ)

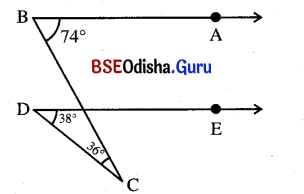
(ii) ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ m∠ABC = 60°, m∠EDC = 38° ଏବଂ \(\overrightarrow{\mathrm{DE}}\) || \(\overrightarrow{\mathrm{BA}}\) । ହେଲେ ଦର୍ଶାଅ ଯେ m∠BCD = 22° ।
ସମାଧାନ:
ଦତ୍ତ : ଦତ୍ତ ଚିତ୍ରରେ m∠ABC = 60°, m∠EDC = 38° ଓ \(\overrightarrow{\mathrm{DE}}\) || \(\overrightarrow{\mathrm{BA}}\) ।
ପ୍ରାମାଣ୍ୟ : m∠BCD = 22°
ପ୍ରମାଣ : \(\overrightarrow{\mathrm{DE}}\) || \(\overrightarrow{\mathrm{BA}}\)
m∠ABF = m∠EFC = 60° (ଅନୁଗୁପ କୋଣ)
ΔCDF ରେ ବତ୍ହିଃସ୍ଥ m∠EFC = 60°
m∠FCD = 60° – 38° = 22°
m∠BCD ର ପରିମାଣ 22° ।

Question 9.
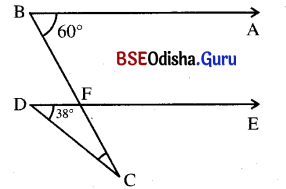
(i) ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ ∠ACD ର ସମଦ୍ବିଖଣ୍ଡକ \(\overrightarrow{\mathrm{CE}}\)
ଏବଂ AB ସହ ସମାନ୍ତର ହେଲେ, ପ୍ରମାଣ କର ଯେ, m∠A = m∠B ।
ସମାଧାନ:
ଦତ୍ତ : \(\overrightarrow{\mathrm{CE}}\) || AB ଓ \(\overrightarrow{\mathrm{CE}}\), ∠ACD ର ସମଦ୍ବିଖଣ୍ଡକ । 
ପ୍ରାମାଣ୍ୟ : m∠A = m∠B
ପ୍ରମାଣ : AB || \(\overrightarrow{\mathrm{CE}}\) ଏବଂ AC ଛେଦକ ।
⇒ m∠A = m∠ACE (ଏକାନ୍ତର କୋଣ)
ସେହିପରି AB || \(\overrightarrow{\mathrm{CE}}\) ଏବଂ BD ଛେଦକ ।
⇒ m∠ABC = m∠ECD (ଅନୁରୂପ କୋଣ)
ମାତ୍ର m∠ACE = m∠ECD (ଦତ୍ତ)
ସମୀକରଣ (i) ଓ ସମୀକରଣ (ii) ରୁ m∠A = m∠ABC
⇒ m∠A = m∠B
 (ପ୍ରମାଣିତ)

(ii) ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ \(\overrightarrow{\mathrm{CE}}\) || AB, m∠ECD = 70° ଏବଂ 
m∠A = 50° ହେଲେ ଦର୍ଶାଅ ଯେ, m∠ACB = 60° ।
ସମାଧାନ:
ଦତ୍ତ : ଦତ୍ତ ଚିତ୍ରରେ \(\overrightarrow{\mathrm{CE}}\) || AB, m∠ECD = 70° ଓ mZA = 50° ।
ପ୍ରାମାଣ୍ୟ : m∠ACB = 60°
ପ୍ରମାଣ : \(\overrightarrow{\mathrm{CE}}\) || AB, BD ଛେଦକ ।
⇒ m∠ECD = m∠ABC = 70° (ଅନୁରୂପ କୋଣ)
ପୁନଶ୍ଚ m∠A = m∠ACE = 50°
m∠ACD = m∠ACE + m∠ECD = 50° + 70° = 120°
କିନ୍ତୁ ∠ACB ଓ ∠ACD ସନ୍ନିହିତ ପରିପୂରକ
∴ m∠ACB = 180° – 120° = 60°
(ପ୍ରମାଣିତ)

Question 10.
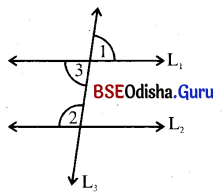
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ L₁ || L₂ ଓ L₁, L₂ ର ଛେଦକ L₃
(i) m∠2 = 2m∠1 ହେଲେ, ∠1 ଓ ∠2 ର ପରିମାଣ ସ୍ଥିର କର । 
ସମାଧାନ:
ଦତ୍ତ : L₁ || L₂ ଓ L₃ ଛେଦକ । m∠2 = 2m∠1
ନିଶ୍ଚେୟ : ∠1 ଓ ∠2 ର ପରିମାଣ ।
m∠1 = m∠3 (ପ୍ରତୀପ)
m∠2 + m∠3 = 180° (ଛେଦକର ଏକ ପାର୍ଶ୍ଵସ୍ଥ ଅନ୍ତରସ୍ଥ କୋଣ)
⇒ 2m∠1 + m∠1 = 180° (∵ m∠2 = 2m∠1)
⇒ 3m∠1 = 180°
⇒ ∠1 = \(\frac{180°}{3}\) = 60°
⇒ m∠2 = 2m∠1 = 2 × 60° = 120°
∴ m∠1 = 60° ଓ m∠2 = 120°

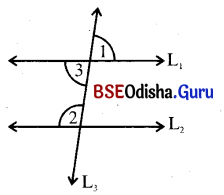
(ii) m∠2 = 3m∠1 ହେଲେ, ∠1 ଓ ∠2 ର ପରିମାଣ ସ୍ଥିର କର । 
ସମାଧାନ:
ଦତ୍ତ : ଦତ୍ତ ଚିତ୍ରରେ m∠2 = 3m∠1
ନିଶ୍ଚେୟ : ∠1 ଓ ∠2 ର ପରିମାଣ ।
m∠1 = m∠3 (ପ୍ରତୀପ)
m∠2 + m∠3 = 180° (ଛେଦକର ଏକ ପାର୍ଶ୍ଵସ୍ଥ ଅନ୍ତରସ୍ଥ କୋଣ)
⇒ 3∠1 + ∠1 = 180° (∵ m∠2 = 3m∠1)
⇒ 4∠1 = 180°
⇒ ∠1 = \(\frac{180°}{4}\) = 45°
⇒ ∠2 = 3m∠1 = 45° × 3 = 135°
∴ ∠1 = 45° ଓ ∠2 = 135°

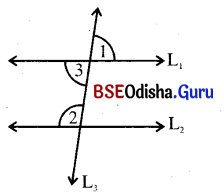
(iii) m∠1 : m∠2 = 2 : 3 ହେଲେ, ∠1 ଓ ∠2 ର ପରିମାଣ ସ୍ଥିର କର ।
ସମାଧାନ:
ଦତ୍ତ : m∠1 : m∠2 = 2 : 3
ନିଶ୍ଚେୟ : ∠1 ଓ ∠2 ର ପରିମାଣ ।
ମକେତେ m∠1 = 2x° ଓ m∠2 = 3x°
m∠1 = m∠3 (ପ୍ରତୀପ)
m∠2 + m∠3 = 180° (ଛେଦକର ଏକ ପାର୍ଶ୍ଵସ୍ଥ ଅନ୍ତରସ୍ଥ କୋଣ)
⇒ 3x + 2x = 180°
⇒ 5x = 180°
⇒ x = \(\frac{180°}{5}\) = 36°
∴ m∠1 = 2x = 2 × 36° = 72°
m∠2 = 3x = 3 × 36° = 108°

Question 11.
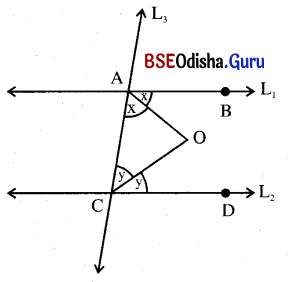
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ L₁ || L₂ | L₃ ଛେଦକ L₁ ଓ L₂ ସରଳ ରେ ଖାଦ୍ୟକୁ ଯଥାକ୍ରମେ A ଓ C ବିନ୍ଦୁରେ ଛେଦକରେ । ∠BACର ସମଦ୍ଵିଖଣ୍ଡକ ଓ ∠ACDର ସମଦ୍ବିଖଣ୍ଡକ ପରସ୍ପରକୁ O ବିନ୍ଦୁରେ ଛେଦକରନ୍ତି । ଦର୍ଶାଅ ଯେ, ∠AOC = 90° ।
ସମାଧାନ:
ଦତ୍ତ : L₁ || L₂ ଓ L₃ ଛେଦକ । 
AO, ∠Aର ସମଦ୍ବିଖଣ୍ଡକ ଓ CO, ∠Cର ସମଦ୍ବିଖଣ୍ଡକ ।
ପ୍ରାମାଣ୍ୟ : m∠AOC = 90° 
ପ୍ରମାଣ : m∠A + m∠C = 180° (ଛେଦକର ଏକ ପାର୍ଶ୍ଵସ୍ଥ ଅନ୍ତରସ୍ଥ କୋଣର ସମଷ୍ଟି 180°)
⇒ m∠OAC + 2m∠OCA = 180° (∵ AO, ∠BACର ସମଦ୍ବିଖଣ୍ଡକ ଓ CO, ∠ACD ର ସମଦ୍ବିଖଣ୍ଡକ)
⇒ m∠OAC + m∠OCA = \(\frac{180°}{2}\) = 90°
ΔAOC ରେ m∠OAC + m∠OCA + m∠AOC = 180°
⇒ 90° + m∠AOC = 180°
⇒ m∠AOC = 180° – 90° = 90°
(ପ୍ରମାଣିତ)

Question 12.
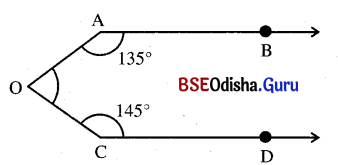
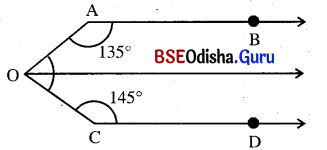
(i) ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ \(\overleftrightarrow{\mathbf{AB}}\) || \(\overleftrightarrow{\mathbf{CD}}\), m∠OAB = 135°, m∠OCD = 145° ହେଲେ ∠AOCର ପରିମାଣ ସ୍ଥିର କର ।

ସମାଧାନ:
ଦତ୍ତ : \(\overleftrightarrow{\mathbf{AB}}\) || \(\overleftrightarrow{\mathbf{CD}}\), m∠OAB = 35° ଓ m∠OCD = 145°
ନିର୍ଦେୟ : ∠AOCର ପରିମାଣ ।
ଅଙ୍କନ : O ବିନ୍ଦୁରେ \(\overrightarrow{\mathrm{OE}}\) || \(\overrightarrow{\mathrm{AB}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : \(\overrightarrow{\mathrm{AB}}\) || \(\overrightarrow{\mathrm{OE}}\)
⇒ m∠BAO + m∠AOE = 180°
⇒ m∠AOE = 180° – m∠BAO
= 180° – 105° = 45° (∵ m∠BAO = 135°)
ସେହିପରି \(\overrightarrow{\mathrm{OE}}\) || \(\overrightarrow{\mathrm{CD}}\) (∵ \(\overrightarrow{\mathrm{AB}}\)  || \(\overrightarrow{\mathrm{CD}}\))
⇒ m∠OCD + m∠EOC = 180°
⇒ m∠EOC = 180° – m∠OCD
⇒ m∠EOC = 180° – 145° = 35°
∴ m∠AOC = m∠AOE + m∠COE = 45° + 35° = 80°

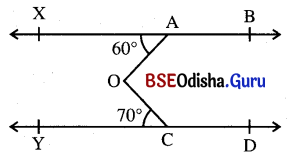
(ii) ପାର୍ଶ୍ୱ ସ୍ଥ ଚିତ୍ରରେ \(\overleftrightarrow{\mathbf{XB}}\) || \(\overleftrightarrow{\mathbf{YD}}\), m∠XAO = 60°, m∠YCO = 70° ହେଲେ ଦର୍ଶାଅ ଯେ m∠AOC = 130° ।

ସମାଧାନ:
ଦତ୍ତ : \(\overleftrightarrow{\mathbf{XB}}\) || \(\overleftrightarrow{\mathbf{YD}}\), m∠XAO = 60° ଓ m∠YCO = 70°
ପ୍ରାମାଣ୍ୟ : m∠AOC = 130°
ଅଙ୍କନ : \(\overrightarrow{\mathrm{AO}}\), YD କୁ E ବିନ୍ଦୁରେ ଛେଦ କରୁ ।
ପ୍ରମାଣ : \(\overleftrightarrow{\mathbf{XB}}\) || \(\overleftrightarrow{\mathbf{YD}}\) ଏବଂ AE ଛେଦକ ।
⇒ m∠XAE = m∠OEC = 60° (ଏକାନ୍ତର କୋଣ)
ΔOEC ରେ ବତ୍ହିଃସ୍ଥ m∠AOC = m∠OEC + m∠OCE = 60° + 70° = 130°

Question 13.
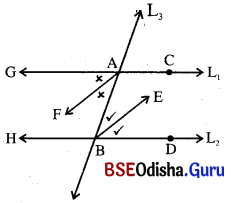
ଗୋଟିଏ ସରଳରେଖା ଅନ୍ୟ ଦୁଇଟି ସମାନ୍ତର ସରଳରେଖାକୁ ଛେଦକଲେ ପ୍ରମାଣ କର ଯେ,
(i) ଯେକୌଣସି ଏକାନ୍ତର କୋଣ ଦୁଇଟିର ଅନ୍ତଃସମଦ୍ୱିଖଣ୍ଡକଦ୍ବୟ ପରସ୍ପର ସମାନ୍ତର ।
ସମାଧାନ:
ଦତ୍ତ : L₁ || L₂ ଏବଂ L₃ ଛେଦକ । \(\overrightarrow{\mathrm{AF}}\), ∠Aର ସମଦ୍ୱିଖଣ୍ଡକ ଏବଂ \(\overrightarrow{\mathrm{BE}}\), ∠Bର ସମଦ୍ବିଖଣ୍ଡକୁ ।
ପ୍ରାମାଣ୍ୟ : \(\overrightarrow{\mathrm{AF}}\) || \(\overrightarrow{\mathrm{BE}}\)
ପ୍ରମାଣ : m∠GAB = m∠ABD (ଏକାନ୍ତର )
⇒ \(\frac{1}{2}\)m∠GAB = \(\frac{1}{2}\)m∠ABD
⇒ m∠FAB = m∠ABE
ମାତ୍ର ଏମାନେ ଏକାନ୍ତର ।
⇒ \(\overrightarrow{\mathrm{AF}}\) || \(\overrightarrow{\mathrm{BE}}\)
(ପ୍ରମାଣିତ)

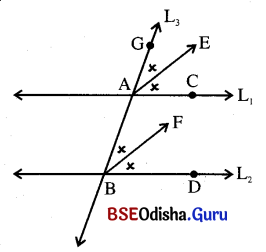
(ii) ଯେକୌଣସି ଅନୁରୂପ କୋଣ ଦୁଇଟିର ଅନ୍ତଃସମଦ୍ବିଖଣ୍ଡକଦ୍ବୟ ପରସ୍ପର ସମାନ୍ତର ।
ସମାଧାନ:
ଦତ୍ତ : L₁ || L₂ ଏବଂ L₃ ଛେଦକ l \(\overrightarrow{\mathrm{AE}}\), ∠Aର ସମଦ୍ୱିଖଣ୍ଡକ ଏବଂ \(\overrightarrow{\mathrm{BF}}\), ∠Bର ସମଦ୍ବିଖଣ୍ଡକ ।
ପ୍ରାମାଣ୍ୟ : \(\overrightarrow{\mathrm{AE}}\) || \(\overrightarrow{\mathrm{BF}}\)
ପ୍ରମାଣ : m∠GAC = m∠ABD (ଅନୁରୂପ)
⇒ \(\frac{1}{2}\)m∠GAC = \(\frac{1}{2}\)m∠ABD
⇒ m∠GAE = m∠ABF
(∵ \(\overrightarrow{\mathrm{AE}}\) m∠GACର ଏବଂ \(\overrightarrow{\mathrm{BF}}\), m∠ABD ର ସମଦ୍ବିଖଣ୍ଡକ)
 କିନ୍ତୁ ଏମାନେ ଅନୁରୂପ କୋଣ ।
⇒ \(\overrightarrow{\mathrm{AE}}\) || \(\overrightarrow{\mathrm{BF}}\)
(ପ୍ରମାଣିତ)

Question 14.
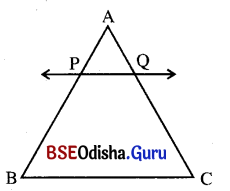
ΔABCର m∠B = m∠C, B͞C ସହ ସମାନ୍ତର କରି ଅଙ୍କିତ ସରଳରେଖା AB ଓ AC କୁ ଯଥାକ୍ରମେ P ଓ Q ବିନ୍ଦୁରେ ଛେଦକଲେ ଦର୍ଶାଅ ଯେ, m∠APQ = m∠AQP ।
ସମାଧାନ:
ଦତ୍ତ : ΔABC ରେ m∠B = m∠C ଓ BC || \(\overleftrightarrow{\mathbf{PQ}}\)
ପ୍ରାମାଣ୍ୟ : m∠APQ = m∠AQP
ପ୍ରମାଣ : BC || \(\overleftrightarrow{\mathbf{PQ}}\) ।
⇒ m∠APQ = m∠B ଏବଂ m∠AQP = m∠C (ଅନୁଗୁପ କୋଣ)
ମାତ୍ର ∠B = ∠C (ଦତ୍ତ)
⇒ m∠APQ = m∠AQP
(ପ୍ରମାଣିତ)

Question 15.
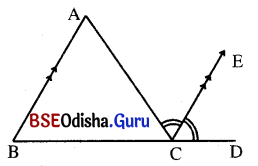
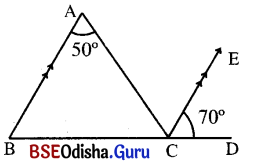
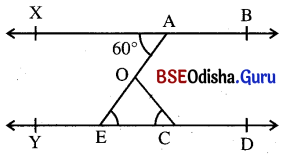
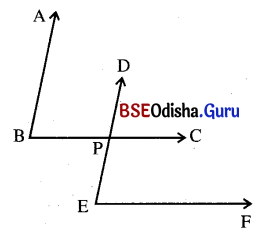
ଗୋଟିଏ କୋଣର ଦୁଇବାହୁ ଅନ୍ୟ ଏକ କୋଣର ଦୁଇବାହୁ ସହ ସମାନ୍ତର ହେଲେ ପ୍ରମାଣ କର ଯେ, କୋଣଦ୍ଵୟ ସମପରିମାଣ ବିଶିଷ୍ଟ ବା ପରିପୂରକ ହେବେ ।
ସମାଧାନ:
ଦତ୍ତ : ଦତ୍ତ ଚିତ୍ରରେ \(\overrightarrow{\mathrm{BA}}\) || \(\overrightarrow{\mathrm{ED}}\) ଏବଂ \(\overrightarrow{\mathrm{BC}}\) || \(\overrightarrow{\mathrm{EF}}\) ।
ପ୍ରାମାଣ୍ୟ : (i) m∠B = m∠E
(ii) m∠B + m∠E = 180°
ପ୍ରମାଣ : \(\overrightarrow{\mathrm{AB}}\) || \(\overrightarrow{\mathrm{DP}}\) ଏବଂ \(\overrightarrow{\mathrm{BC}}\)  ଛେଦକ ।
⇒ m∠ABC = m∠DPC (ଅନୁଗୁପ କୋଣ)
ପୁନଶ୍ଚ \(\overrightarrow{\mathrm{BC}}\) || \(\overrightarrow{\mathrm{EF}}\) ଏବଂ \(\overrightarrow{\mathrm{PE}}\) ଛେଦକ ।
⇒ m∠DPC = m∠PEF (ଅନୁଗୁପ କୋଣ)
ସମୀକରଣ (i) ଓ (ii) ରୁ m∠ABC = m∠PEF
⇒ m∠B = m∠E
(ପ୍ରମାଣିତ)

(ii) \(\overrightarrow{\mathrm{AB}}\) || \(\overrightarrow{\mathrm{ED}}\) ଏବଂ \(\overrightarrow{\mathrm{BC}}\) ଛେଦକ ।
⇒ m∠B = m∠CPE (ଅନୁଗୁପ କୋଣ)
ପୁନଶ୍ଚ \(\overrightarrow{\mathrm{PC}}\) || \(\overrightarrow{\mathrm{EF}}\) ଏବଂ \(\overrightarrow{\mathrm{PE}}\) ଛେଦକ ।
⇒ m∠CPE + m∠PEF = 180°
⇒ m∠B + m∠PEF = 180° (∵ m∠B = m∠CPE)
⇒ m∠B + m∠E = 180°
(ପ୍ରମାଣିତ)

Question 16.
ଗୋଟିଏ ସରଳରେଖା ଦୁଇଟି ସମାନ୍ତର ସରଳରେଖାକୁ ଛେଦକରି ସେଥୁମଧ୍ୟରୁ କୌଣସି ଗୋଟିଏ ପ୍ରତି ଲମ୍ବ ହେଲେ, ପ୍ରମାଣ କର ଯେ ତାହା ଅନ୍ୟଟି ପ୍ରତି ମଧ୍ୟ ଲମ୍ବ ହେବ ।
ସମାଧାନ:
ଦତ୍ତ : L₁ || L₂ ଏବଂ L₃ ଛେଦକ । L₃ ⊥ L₁
ପ୍ରାମାଣ୍ୟ : L₃ ⊥ L₂
ପ୍ରମାଣ :  L₁ || L₂ ଏବଂ L₃ ଛେଦକ ।
⇒ m∠PAC = m∠ABD (ଅନୁଗୁପ କୋଣ)
ମାତ୍ର m∠PAC = 90° (ଦତ୍ତ)
m∠ABD = 90° ⇒ L₁ ⊥ L₂
(ପ୍ରମାଣିତ)