Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 1 ରେଖା ଓ କୋଣ Ex 1(d) Textbook Exercise Questions and Answers.
BSE Odisha Class 9 Maths Solutions Geometry Chapter 1 ରେଖା ଓ କୋଣ Ex 1(d)
Question 1.
ନିମ୍ନ ଉକ୍ତିଗୁଡ଼ିକ ମଧ୍ୟରୁ ଭୁଲ ଉକ୍ତ ପାଖରେ ‘✗’ ଚିହ୍ନ ଏବଂ ଠିକ୍ ଉକ୍ତି ପାଖରେ ‘✓’ ଚିହ୍ନ ଦିଅ ।
(a)କୌଣସି ତ୍ରିଭୁଜର ଦୁଇଟି କୋଣର ପରିମାଣ ସମଷ୍ଟି ତୃତୀୟ କୋଣର ପରିମାଣ ସହ ସମାନ ହେଲେ ତ୍ରିଭୁଜଟି ସମକୋଣୀ ।
ସମାଧାନ:
✓
(b) କୌଣସି ତ୍ରିଭୁଜର ଦୁଇଟି କୋଣର ପରିମାଣ ସମଷ୍ଟି ତୃତୀୟ କୋଣର ପରିମାଣ ଠାରୁ ବୃହତ୍ତର ହେଲେ, ତ୍ରିଭୁଜଟି ସୂକ୍ଷ୍ମକୋଣ ।
ସମାଧାନ:
✓
(c) ତ୍ରିଭୁଜର ଗୋଟିଏ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ ଏହାର ଅନ୍ତଃସ୍ଥ ଦୂରବର୍ତ୍ତୀ କୋଣଦ୍ୱୟର ପରିମାଣର ସମଷ୍ଟି ସହ ସମାନ ।
ସମାଧାନ:
✓
(d) ଗୋଟିଏ ତ୍ରିଭୁଜରେ ଅତି ବେଶିରେ ଗୋଟିଏ ସ୍ଥୂଳକୋଣ ରହିପାରିବ ।
ସମାଧାନ:
✓
(e) ତ୍ରିଭୁଜର ତିନିକୋଣର ପରିମାଣର ସମଷ୍ଟି ସର୍ବଦା 180° ।
ସମାଧାନ:
✓
(f) ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜର ସୂକ୍ଷ୍ମକୋଣଦ୍ବୟ ପରସ୍ପରର ପରିପୂରକ ।
ସମାଧାନ:
✗
(g) ତ୍ରିଭୁଜର ବହିଃସ୍ଥକୋଣ ସର୍ବଦା ଏକ ସ୍ଥୂଳକୋଣ ।
ସମାଧାନ:
✗
(h) ତ୍ରିଭୁଜର ବହିଃସ୍ଥକୋଣର ପରିମାଣ ଏହାର ପ୍ରତ୍ୟେକ ଅନ୍ତସ୍ଥ ଦୂରବର୍ତ୍ତୀ କୋଣର ପରିମାଣ ଠାରୁ ବୃହତ୍ତର ।
ସମାଧାନ:
✓
![]()
Question 2.
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
(a) ଗୋଟିଏ ସମକୋଣୀ ତ୍ରିଭୁଜର ସୂକ୍ଷ୍ମକୋଣଦ୍ଵୟ ମଧ୍ୟରୁ ଗୋଟିକର ପରିମାଣ 30° ହେଲେ, ଅନ୍ୟଟିର ପରିମାଣ ________ ।
ସମାଧାନ:
60°
(b) ତ୍ରିଭୁଜର ଗୋଟିଏ ବହିଃସ୍ଥ କୋଣର ପରିମାଣ 130° । ଏହାର ଏକ ଅନ୍ତଃସ୍ଥ ଦୂରବର୍ତ୍ତୀ କୋଣର ପରିମାଣ 75° ହେଲେ, ଅନ୍ୟ ଅନ୍ତଃସ୍ଥ ଦୂରବର୍ତ୍ତୀ କୋଣର ପରିମାଣ ________ ।
ସମାଧାନ:
55°
(c ) ΔABC ରେ m∠A = 55° ଏବଂ m∠B = 75° ହେଲେ ∠C ର ପରିମାଣ ________ ।
ସମାଧାନ:
50°
(d) କୌଣସି ତ୍ରିଭୁଜର କୋଣମାନଙ୍କର ପରିମାଣର ସମଷ୍ଟି ________ ।
ସମାଧାନ:
180°
(e) ΔABC ରେ m∠A = 90°, m∠B = 2 m∠C ହେଲେ ∠Cର ପରିମାଣ ________ ।
ସମାଧାନ:
30°
(f) ΔABC ରେ AB = AC, m∠A = 60° ହେଲେ m∠B = ________ ।
ସମାଧାନ:
60°
(g) ଗୋଟିଏ ତ୍ରିଭୁଜର ଶୀର୍ଷକୋଣର ପରିମାଣ 120° ଏବଂ ଅନ୍ୟ ଦୁଇକୋଣର ପରିମାଣ ସମାନ ହେଲେ, ପ୍ରତ୍ୟେକ ସମାନ କୋଣର ପରିମାଣ ________ ।
ସମାଧାନ:
30°
(h) ΔABC ରେ AB = AC, m∠B = 30° ହେଲେ ∠A ର ପରିମାଣ ________ ।
ସମାଧାନ:
120°
Question 3.
ନିମ୍ନରେ ଦିଆଯାଇଥିବା ପ୍ରତ୍ୟେକ ଚିତ୍ରରେ ‘x’ ଚିହ୍ନିତ କୋଣର ପରିମାଣ ସ୍ଥିର କର ।
(i)
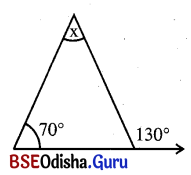
ସମାଧାନ:
ଦତ୍ତ ଚିତ୍ରରେ ବତ୍ହିଃସ୍ଥ m∠ACD = m∠ABC + m∠BAC
⇒ 130° = x + 70°
⇒ x = 130 – 70° = 60°
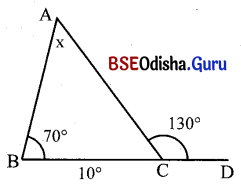
(ii)
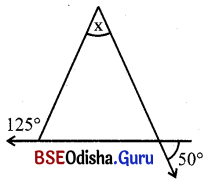
ସମାଧାନ:
ଦତ୍ତ ଚିତ୍ରରେ m∠DCE = m∠ACB = 50° (ପ୍ରତୀପ)
ΔABC ରେ ବତ୍ହିଃସ୍ଥ m∠ABF = m∠A + m∠ACB
⇒ 125° = x + 50°
⇒ x = 125° – 50° = 75°
![]()
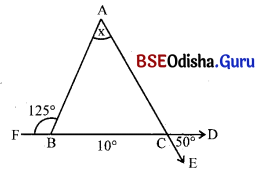
(iii)
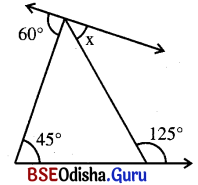
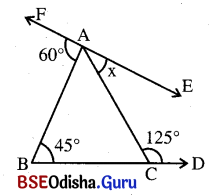
ସମାଧାନ:
ଦତ୍ତ ଚିତ୍ରରେ m∠ACD + m∠ACB = 180° (ସନ୍ନିହିତ ପରିପୂରକ କୋଣ)
⇒ 125° + m∠ACB = 180°
⇒ m∠ACB = 180° – 125° = 55°
ΔABC ରେ m∠BAC = 125° – 45° = 80°
⇒ ପୁନଣ୍ଚ m∠FAB + m∠BAC + m∠CAE = 180°
⇒ 60° + 80° + x = 180°
⇒ 140° + x = 180°
⇒ x = 180° – 140° = 40°
(iv)
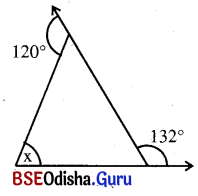
ସମାଧାନ:
ଦତ୍ତ ଚିତ୍ରରେ m∠ACD + m∠ACB = 180°
⇒ 132° + m∠ACB = 180°
⇒ m∠ACB = 180° – 132° = 48°
ΔABC ରେ ବତ୍ହିଃସ୍ଥ m∠EAB = m∠ABC + m∠ACB
⇒ 126° = x + 48°
⇒ x = 126° – 48° = 78°
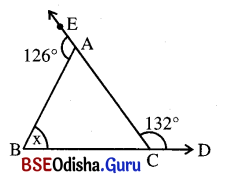
(v)
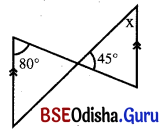
ସମାଧାନ:
ଦତ୍ତ ଚିତ୍ରରେ m∠DOC = m∠AOB = 45° (ପ୍ରତୀପ)
ΔAOB ରେ m∠ABO = 180° – (80° + 45°)
= 180° – 125° = 55°
AB || CD ଏବଂ BD ଛେଦକ ।
⇒ m∠ABO = m∠ODC = 50° (ଏକାନ୍ତର)
(vi)
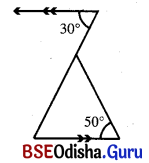
ସମାଧାନ:
\(\overrightarrow{\mathrm{DE}}\) || BC ଏବଂ BD ଛେଦକ ।
⇒ m∠EDB = m∠DBC = 30° (ଏକାନ୍ତର)
m∠DAC = m∠DBC + m∠ACB = 30° + 50° = 80
m∠BAC = 180° – m∠DAC = 180° – 80° = 100°
(vii)
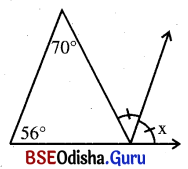
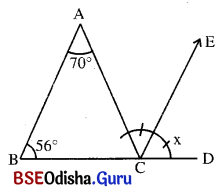
ସମାଧାନ:
ΔABC ରେ ବତ୍ହିଃସ୍ଥ m∠ACD = m∠A + m∠B = 70° + 56° = 126°
ମାତ୍ର m∠ACE = m∠ECD (ଦତ୍ତ)
⇒ m∠ACE + m∠ECD = m∠ACD
⇒ 2m∠ECD = 126° ⇒ 2x = 126°
⇒ x = \(\frac{126°}{2}\) = 63°
![]()
Question 4.
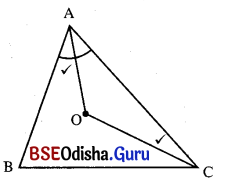
ΔABCର ଅନ୍ତଃସ୍ଥ ଏକ ବିନ୍ଦୁ O । ଦର୍ଶାଅ ଯେ, m∠BOC = m∠BAC + m∠ABO + m∠ACO ।
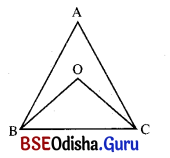
ସମାଧାନ:
ଦତ୍ତ : O, ΔABCର ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ।
ପ୍ରାମାଣ୍ୟ : m∠BOC = m∠BAC + m∠ABO + m∠ACO
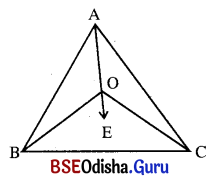
ଅଙ୍କନ : \(\overrightarrow{\mathrm{AO}}\) ଅଙ୍କନ କର ।
ପ୍ରମାଣ : ΔABO ରେ ବହିଃସ୍ଥ m∠BOE = m∠BAO + m∠ABO … (i)
ΔACO ରେ ବହିଃସ୍ଥ m∠COE = m∠OAC + m∠OCA … (ii)
ସମୀକରଣ (i) ଓ ସମୀକରଣ (ii)କୁ ଯୋଗକଲେ
⇒ m∠BOE + m∠COE = m∠BAO + m∠ABO + m∠OAC + m∠ACO
⇒ m∠BOC = (m∠BAO + m∠OAC) + (m∠ABO + m∠ACO)
⇒ m∠BOC = m∠BAC + m∠ABO + m∠ACO
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 5.
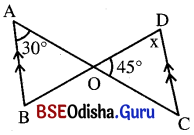
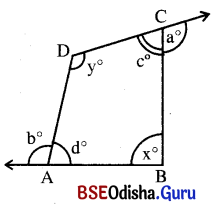
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରୁ ଦର୍ଶାଅ ଯେ, a° + b° = x° + y° ।
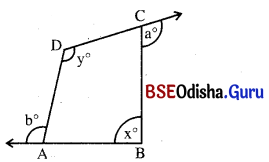
ସମାଧାନ:
ମନେକରାଯାଉ ∠BCD = c° ଓ ∠DAB = d°
a° + c° = 180° (ସନ୍ନିହିତ ପରିପୂରକ କୋଣ)
b° + d° = 180° (ସନ୍ନିହିତ ପରିପୂରକ କୋଣ)
ଯୋଗକକେ a° + b° + c° + d° = 180° + 180° = 360° … (i)
ABCD ଚତୁର୍ଭୁଜର x° + c° + y° + d° = 360° … (ii)
(ଚତୁର୍ଭୁଜର ଚାରି କୋଣର ସମଷ୍ଟି 360°)
ସମୀକରଣ (i) ଓ (ii) ରୁ
a° + b° + c° + d° = x° + c° +y° + d° ⇒ a° + b° = x° + y° (ପ୍ରମାଣିତ)
ବିକଳ୍ପ ପ୍ରଣାଳୀ : BD ଅଙ୍କନ କର ।
ΔADB ରେ ବହିଃସ୍ଥ b° = m∠ADB + m∠ABD
ΔCDB ରେ ବହିଃସ୍ଥ a° = m∠CDB + m∠CBD
∴ a° + b° = (m∠ADB + m∠CDB) + m∠ABD + m∠CBD
= m∠ADC + m∠ABC = y° + x°
∴ a° + b° = x° + y°
Question 6.
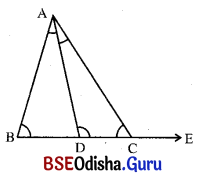
ΔABC ରେ ∠A ର ସମଦ୍ବିଖଣ୍ଡକ AD, BC କୁ D) ବିନ୍ଦୁରେ ଛେଦକରେ । ଦର୍ଶାଅ ଯେ, m∠ABC + m∠ACE = 2m∠ADC ।
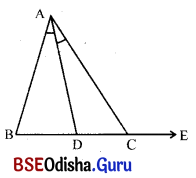
ସମାଧାନ:
ଦତ୍ତ : ΔABCରେ ∠A ର ସମଦ୍ବିଖଣ୍ଡକ AD, BC କୁ D ବିନ୍ଦୁରେ ଛେଦକରୁଛି ।
ΔABCର ଶୀର୍ଷବିନ୍ଦୁ Cରେ ∠ACE କୋଣ ଏକ ବହିଃସ୍ଥ କୋଣ ।
ପ୍ରାମାଣ୍ୟ : m∠ABC + m∠ACE = 2m∠ADC
ପ୍ରମାଣ : ΔABD ରେ ବତ୍ହିଃସ୍ଥ m∠ADC = m∠ABD + m∠BAD
⇒ m∠ADC = m∠ABD + m∠CAD
[∵ m∠BAD = m∠CAD ଦତ୍ତ]
⇒ m∠ABD = m∠ADC – m∠CAD … (i)
ΔACD ରେ ବତ୍ହିଃସ୍ଥ m∠ACE = m∠CAD + m∠ADC … (ii)
ସମୀକରଣ (i) ଓ (ii) କୁ ଯୋଗକଲେ,
m∠ABD + m∠ACE = m∠ADC – m∠CAD + m∠CAD + m∠ADC
⇒ m∠ABD + m∠ACE = m∠ADC + m∠ADC
⇒ m∠ABD + m∠ACE = 2m∠ADC
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
![]()
Question 7.
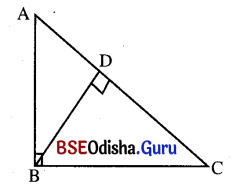
ΔABC ରେ m∠B = 90° । BD ⊥ AC । ପ୍ରମାଣ କର ଯେ, m∠ABD = m∠ACB ଏବଂ m∠BAD = m∠DBC ।
ସମାଧାନ:
ଦତ୍ତ : ΔABC ରେ ∠B ସମକୋଣ ଏବଂ BD ⊥ AC ।
ପ୍ରାମାଣ୍ୟ : (i) m∠ABD = m∠ACB
(ii) m∠BAD = m∠DBC
ପ୍ରମାଣ : (i) m∠ABC = 90° (ଦତ୍ତ)
⇒ m∠ABD + m∠DBC = 90° (କୋଣ ସମଷ୍ଟି ସ୍ୱାକା୍ଯ) … (i)
ΔBDC ରେ m∠BDC = 90° (ଦତ୍ତ)
m∠DBC + m∠DCB = 90° (∵ ତ୍ରିଭୁଜର ତିନିକୋଣର ପରିମାଣର ସମଷ୍ଟି 180°) … (ii)
ସମୀକରଣ (i) ଓ (ii)ରୁ
⇒ m∠ABD + m∠DBC = m∠DBC + m∠DCB
m∠ABD = m∠DCB
⇒ m∠ABD = m∠ACB
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
(ii) m∠ABC = 90° (ଦତ୍ତ)
⇒ m∠ABD + m∠DBC = 90° (କୋଣ ସମଷ୍ଟି ସ୍ୱାକା୍ଯ) … (i)
ΔABD ରେ m∠DBC = 90° (ଦତ୍ତ)
⇒ m∠BAD + m∠ABD = 90° (∵ ତ୍ରିଭୁଜର ତିନିକୋଣର ପରିମାଣର ସମଷ୍ଟି 180°) … (ii)
ସମୀକରଣ (i) ଓ (ii)ରୁ
m∠ABD + m∠DBC = m∠BAD + m∠ABD
⇒ m∠DBC = m∠BAD (ପ୍ରମାଣିତ)
Question 8.
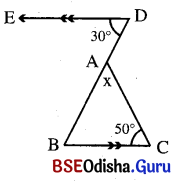
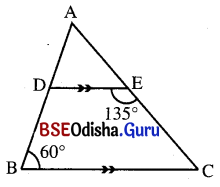
ΔABC ରେ D͞E || B͞C, m∠ABC = 60° ଏବଂ m∠DEC = 135° ହେଲେ, ∠Aର ପରିମାଣ ସ୍ଥିର କର ।
ସମାଧାନ:
ଦତ୍ତ : ΔABC ରେ DE || BC, m∠DEC = 135° ଓ m∠DBC = 60° ।
ପ୍ରାମାଣ୍ୟ : ∠A ର ପରିମାଣ ।
ପ୍ରମାଣ : DE || BC (ଦତ୍ତ) ଏବଂ E͞C ଛେଦକ ।
⇒ m∠DEC + m∠ECB = 180° (ଛେଦକର ଏକ ପାର୍ଶ୍ଵସ୍ଥ କୋଣ)
⇒ 135° + m∠ECB = 180°
⇒ m∠ECB = 180° – 135° = 45°
ΔABC ରେ m∠A + m∠B + m∠C = 180°
m∠A + 60° + 45° = 180°
⇒ m∠A + 105° = 180°
⇒ m∠A = 180° – 105° = 75°
∴ ∠A ର ପରିମାଣ 75° ।
Question 9.
ପ୍ରମାଣ କର ଯେ, କୌଣସି ତ୍ରିଭୁଜର ପ୍ରତ୍ୟେକ ଯୋଡ଼ା କୋଣର ପରିମାଣର ସମଷ୍ଟି, ତୃତୀୟ କୋଣର ପରିମାଣ ଠାରୁ ବୃହତ୍ତର ହେଲେ, ତ୍ରିଭୁଜଟି ସୂକ୍ଷ୍ମକୋଣୀ ।
ସମାଧାନ:
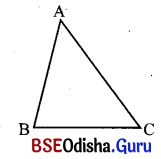
ଦତ୍ତ : ABC ଏକ ତ୍ରିଭୁଜ । m∠B + m∠C > m∠A, m∠A + m∠C > m∠B, m∠A + m∠B > m∠C
ପ୍ରାମାଣ୍ୟ : ΔABC ସୂକ୍ଷ୍ମକୋଣୀ ।
ପ୍ରମାଣ : ΔABC ରେ m∠B + m∠C > m∠A (ଦତ୍ତ)
⇒ m∠A + m∠B + m∠C > m∠A + m∠A (ଉଭୟ ପାର୍ଶ୍ଵରେ m∠A ଯୋଗକରାଗଲେ ।)
⇒ 180° > 2m∠A ⇒ \(\frac{180^{\circ}}{2}\) > \(\frac{2 \mathrm{~m} \angle \mathrm{A}}{2}\)
⇒ 90° > m∠A ⇒ m∠A < 90° … (i)
ସେହିପରି m∠A + m∠C > m∠B
⇒ m∠A + m∠B + m∠C > m∠B + m∠B (ଉଭୟ ପାର୍ଶ୍ଵରେ m∠B ଯୋଗକରାଗଲେ ।)
⇒ 180° > 2m∠B ⇒ \(\frac{180^{\circ}}{2}\) > \(\frac{2 \mathrm{~m} \angle \mathrm{B}}{2}\)
⇒ 90° > m∠B ⇒ m∠B < 90° … (ii)
ସେହିପରି ପ୍ରମାଣ କରାଯାଇପାରେ m∠C < 90° … (iii)
ସମୀକରଣ (i) ଓ (ii) ରୁ ∠A < 90°, ∠B < 90° ଓ ∠C < 90°
∴ ΔABC ସୂକ୍ଷ୍ମକୋଣୀ । (ପ୍ରମାଣିତ)
Question 10.
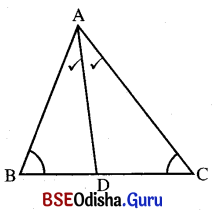
A ABCରେ m∠ABC = m∠ACB, ∠BACର ସମଦ୍ବିଖଣ୍ଡକ BC କୁ D ବିନ୍ଦୁରେ ଛେଦକରେ । ପ୍ରମାଣ କର ଯେ AD, BC ପ୍ରତି ଲମ୍ବ ।
ସମାଧାନ:
ଦତ୍ତ : ΔABC ରେ m∠ABC = m∠ACB ଏବଂ AD, m∠Aର ସମର୍ଦ୍ଦିଖଣ୍ଡକ ।
ପ୍ରାମାଣ୍ୟ : AD ⊥ BC
ପ୍ରମାଣ : ΔABCରେ m∠ABC + m∠BAC + m∠ACB = 180°
⇒ m∠ABC + m∠BAD + m∠CAD + m∠ACB = 180°
ମାତ୍ର m∠ABC = m∠ACB (ଦତ୍ତ)
ଏବଂ m∠BAD = m∠CAD (∠BACର ସମର୍ଦ୍ଦିଖଣ୍ଡକ AD)
⇒ 2m∠ABC + 2m∠BAD = 180°
⇒ 2(m∠ABC + m∠BAD) = 180°
⇒ m∠ABC + m∠BAD = \(\frac{180^{\circ}}{2}\) = 90°
⇒m∠ABD + m∠BAD = 90°
ΔABD ରେ m∠ABD + m∠BAD + m∠ADB = 180°
⇒ 90° + m∠ADB = 180° ⇒ m∠ADB = 180° – 90° = 90
⇒ A͞D ⊥ B͞C
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
![]()
Question 11.
ΔABCରେ ∠Bର ଅନ୍ତଃସମଖଣ୍ଡକ ଏବଂ C ବିନ୍ଦୁରେ ଉତ୍ପନ୍ନ ବହିଃସ୍ଥକୋଣର ସମଦ୍ବିଖଣ୍ଡକର ଛେଦବିନ୍ଦୁ E ହେଲେ ପ୍ରମାଣ କର ଯେ, m∠BEC = m∠A ।
ସମାଧାନ:
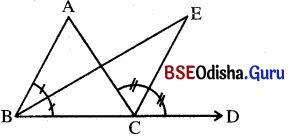
ଦତ୍ତ : ΔABC ରେ ∠Bର ଅନ୍ତଃସମଦ୍ବିଖଣ୍ଡକ BE ଓ ∠C ବହିଃସମଦ୍ଵିଖଣ୍ଡକ CE ପରସ୍ପରକୁ E ବିନ୍ଦୁରେ ଛେଦ କରନ୍ତି ।

Question 12.
ΔABCରେ ∠ABC ଓ ∠ACB ର ଅନ୍ତଃସମଦ୍ବିଖଣ୍ଡକଦ୍ୱୟ ପରସ୍ପରକୁ O ବିନ୍ଦୁରେ ଛେଦକଲେ, ପ୍ରମାଣ କର ଯେ
m∠BOC = 90° + \(\frac{1}{2}\)m∠A ।
ସମାଧାନ:
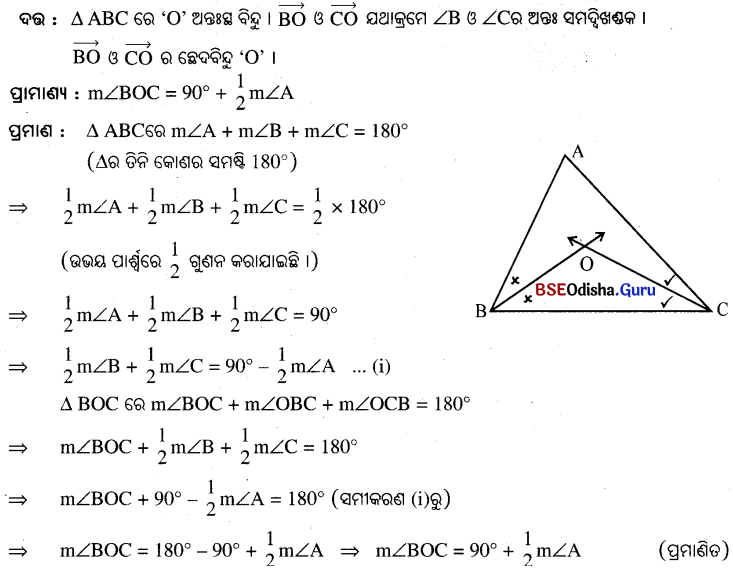
Question 13.
ΔABCରେ ∠B ଓ ∠Cର ବହିଃସମଦ୍ବିଖଣ୍ଡକଦ୍ବୟ ପରସ୍ପରକୁ ୦ ବିନ୍ଦୁରେ ଛେଦକଲେ, ପ୍ରମାଣ କର ଯେ,
m∠BOC = 90° – \(\frac{1}{2}\)m∠A ।
ସମାଧାନ:
ଦତ୍ତ : ΔABC ରେ ∠B ଓ ∠Cର ବହିଃ ସମଦ୍ବିଖଣ୍ଡ ଦ୍ବୟର ଛେଦବିନ୍ଦୁ O।


Question 14.
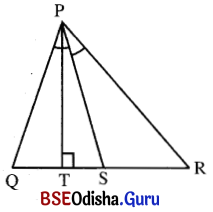
ପାର୍ଶ୍ୱସ୍ଥ ଚିତ୍ରରେ PS, ∠Pର ସମଦ୍ବିଖଣ୍ଡକ ଏବଂ PT ⊥ OR ।
ପ୍ରମାଣ କର ଯେ, m∠TPS = \(\frac{1}{2}\)(m∠Q – m∠R)
ସମାଧାନ:
ଦତ୍ତ : ΔPQR ରେ PS, ∠Pର ସମଦ୍ବିଖଣ୍ଡକ ଏବଂ PT ⊥ OR ।
ପ୍ରାମାଣ୍ୟ : m∠TPS = \(\frac{1}{2}\)(m∠Q – m∠R)
ପ୍ରମାଣ : PT ⊥ OR (ଦତ୍ତ)
⇒ m∠PTQ = m∠PTR = 90°
ΔPQT ରେ ବତ୍ହିଃସ୍ଥ m∠PTS = m∠Q + m∠QPT … (i)
ΔPTS ରେ ବତ୍ହିଃସ୍ଥ m∠PTQ = m∠TPS + m∠PST … (ii)
ମାତ୍ର m∠PTQ = m∠PTS = 90°
∴ (i) ଓ (ii) ରୁ m∠Q + m∠QPT = m∠TPS + m∠PST
⇒ m∠Q + m∠QPT + m∠TPS = m∠TPS + m∠PST + m∠TPS
(ଉଭୟ ପାର୍ଶ୍ଵରେ m∠TPS ଯୋଗ କରାଗଲେ ।)
⇒ m∠Q + m∠QPS = 2m∠TPS + m∠PST
⇒ 2m∠TPS = m∠Q – m∠PST + m∠QPS
⇒ 2m∠TPS = m∠Q – m∠PSQ + m∠SPR (∵ PS, ∠P ର ସମଦ୍ବିଖଣ୍ଡକ)
⇒ 2m∠TPS = m∠Q – m∠SPR – m∠R + m∠SPR
⇒ 2m∠TPS = m∠Q – m∠R (∵ ΔPSR ରେ ବତ୍ହିଃସ୍ଥ m∠PSQ = m∠SPR + m∠R)
⇒ m∠TPS = \(\frac{1}{2}\)(m∠Q – m∠R)
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
![]()
Question 15.
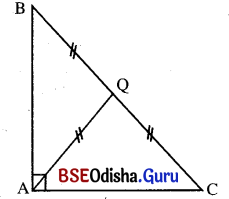
ΔABC ରେ BC ର ମଧ୍ୟବିନ୍ଦୁ O ଏବଂ BQ = AQ ହେଲେ, ପ୍ରମାଣ କର ଯେ ∠BAC ସମକୋଣ ।
ସମାଧାନ:
ଦତ୍ତ : ΔABC ରେ BC ର ମଧ୍ୟବିନ୍ଦୁ Q ଅର୍ଥାତ୍ BQ = AQ ।
ପ୍ରାମାଣ୍ୟ : m∠BAC = 90°
ପ୍ରମାଣ : BC ର ମଧ୍ୟବିନ୍ଦୁ Q । ⇒ BQ = CQ
BQ = AQ (ଦତ୍ତ) ⇒ AQ = BQ = CQ
⇒ m∠BAQ = m∠ABQ = m∠ACQ = m∠QAC
(Δର ଦୁଇଟି ବାହୁ ସମାନ ହେଲେ ସେମାନଙ୍କର ବିପରୀତ କୌଣମାନ ସମପରିମାଣ ବିଶିଷ୍ଟ ହେବେ ।)
ΔABCରେ m∠A + m∠B + m∠C = 180° (Δର ତିନିକୋଣର ସମଷ୍ଟି 180°)
⇒ m∠BAQ + m∠CAQ + m∠ABQ + m∠ACQ = 180°
⇒ 2m∠BAQ + 2m∠CAQ = 180°
⇒ 2(m∠BAQ + m∠CAQ) = 180°
⇒ m∠BAQ + m∠CAQ = \(\frac{180°}{2}\)
⇒ m∠BAC = 90°
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
Question 16.
ΔABCର O ଏକ ଅନ୍ତସ୍ଥ ବିନ୍ଦୁ । ଯଦି m∠OAB = m∠OCA ହୁଏ, ପ୍ରମାଣ କର ଯେ m∠A0C + m∠BAC = 180° ।
ସମାଧାନ:
ଦତ୍ତ : ΔABC ରେ ‘O’ ଏକ ଅନ୍ତଃସ୍ଥ ବିନ୍ଦୁ ଅର୍ଥାତ୍ m∠OAB = m∠OCA ।
ପ୍ରାମାଣ୍ୟ : mZAOC + m∠BAC = 180°
ପ୍ରମାଣ : ΔAOC ରେ m∠AOC + m∠OCA + m∠OAC = 180° (Δର ତିନିକୋଣର ସମଷ୍ଟି 180°)
⇒ m∠AOC + m∠BAO + m∠OAC = 180° [∵ m∠OAB = m∠OCA (ଦତ୍ତ)]
⇒ m∠AOC + m∠BAC = 180°
 (ପ୍ରମାଣିତ)
(ପ୍ରମାଣିତ)
