BSE Odisha 9th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(c)

Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(c) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(c)

Question 1.
ନିମ୍ନଲିଖ ପ୍ରଶ୍ନମାନଙ୍କ ଉତ୍ତର ଦିଅ ।
(i) ଗୋଟିଏ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ 288 ବର୍ଗ ମିଟର ଏବଂ ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ 18 ମିଟର ହେଲେ ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ ଓ = 288 ବର୍ଗ ମିଟର ଓ ବାହୁର ଦୈର୍ଘ୍ୟ = 18 ମିଟର ।

ରମ୍ବସ୍‌ର ଉଚ୍ଚତା 16 ମିଟର ।

(ii) ଗୋଟିଏ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ 16 ବର୍ଗ ସେ.ମି. ଏବଂ ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 28 ସେ.ମି. ହେଲେ, ଅନ୍ୟ କଣ୍ଠଟିର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ = 196 ବର୍ଗ ସେ.ମି. ଓ ଗୋଟିଏ କର୍ପୂର ଦୈର୍ଘ୍ୟ = 28 ସେ.ମି.

∴ କର୍ଣ୍ଣପ୍ରତି ଅଙ୍କିତ ଲମ୍ବର ଦୈର୍ଘ୍ୟ 14 ଏକକ ।

(iii) ଗୋଟିଏ ରମ୍ବସ୍‌ର ଦୁଇ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 24 ମିଟର ଓ 10 ମିଟର ହେଲେ, ବାହୁର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ରମ୍ବସ୍‌ର ଦୁଇ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ d₁ = 24 ମିଟର ଓ d₂ = 10 ମିଟର ।

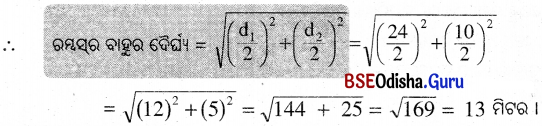
∴ ରମ୍ବସ୍‌ର ବାହୁର ଦୈର୍ଘ୍ୟ = 13 ମିଟର ।

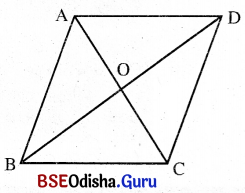
(iv) ABCD ରମ୍ବସ୍‌ର କର୍ଣ୍ଣଦ୍ୱୟର ଛେଦବିନ୍ଦୁ O ଏବଂ AO = 3 ସେ.ମି. ଓ OB = 4 ସେ.ମି. ହେଲେ ABCD ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ABCD ରମ୍ବସ୍‌ର କର୍ଣ୍ଣଦ୍ୱୟର ଛେଦବିନ୍ଦୁ ‘O’, AO = 3 ସେ.ମି. ଏବଂ OB = 4 ସେ.ମି. ।
AC = 2 × AO = 2 × 3 = 6 ସେ.ମି.
ଓ BD = 2 × OB = 2 × 4 = 8 ସେ.ମି. ।
ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × କର୍ଣ୍ଣଦ୍ଵୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳ 
= \(\frac{1}{2}\) × 6 ସେ.ମି. × 8 ସେ.ମି. = 24 ବର୍ଗ ସେ.ମି. ।
∴ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ 24 ବର୍ଗ ସେ.ମି. ।

(v) ABCD ରମ୍ବସ୍‌ର କଣ୍ଠଦ୍ଵୟର ଛେଦବିନ୍ଦୁ O ଓ AO = 6 ସେ.ମି. ଓ AB = 10 ସେ.ମି. ହେଲେ, ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ABCD ରମ୍ବସ୍‌ର କଣ୍ଠଦ୍ଵୟର ଛେଦବିନ୍ଦୁ ‘O’,
AO = 6 ସେ.ମି. ଓ AB = 10 ସେ.ମି. ।
∴ AC କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 2 × AO = 2 × 6 ସେ.ମି. = 12 ସେ.ମି. ।
ରମ୍ବସ୍‌ର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ସମଦ୍ବିଖଣ୍ଡ କରନ୍ତି ।

Question 2.
ଗୋଟିଏ ରମ୍ବସ୍‌ର ବାହୁର ଦୈର୍ଘ୍ୟ 10 ସେ.ମି. ଏବଂ ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 12 ସେ.ମି. ହେଲେ, ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ରମ୍ବସ୍‌ର ବାହୁର ଦୈର୍ଘ୍ୟ = 10 ସେ.ମି. ଓ ଗୋଟିଏ କର୍ପୂର ଦୈର୍ଘ୍ୟ (d₁)= 12 ସେ.ମି. । 
ମନେକର ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ (d₂)= x ସେ.ମି. ।

∴ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ 96 ବର୍ଗ ସେ.ମି. ।

Question 3.
ଗୋଟିଏ ରମ୍ବସ୍‌ର ପରିସୀମା 52 ମିଟର ଏବଂ ଏହାର ବୃହତ୍ତମ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 24 ମିଟର ହେଲେ, ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ରମ୍ବସ୍‌ ପରିସୀମା = 52 ମିଟର ।

ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 10 ମିଟର ।

Question 4.
ଗୋଟିଏ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ 144 ବର୍ଗ ସେ.ମି. ଏବଂ ଏହାର ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ ଅନ୍ୟଟିର 2 ଗୁଣ ହେଲେ, କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ରମ୍ବସର କ୍ଷେତ୍ରଫଳ = 144 ବର୍ଗ ସେ.ମି. ।
ମନେକର ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = x ସେ.ମି. ଓ ପ୍ରଶାନୁସାରେ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 2x ସେ.ମି. ।
ରମ୍ବସର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ସେ.ମି. ଓ ପ୍ରଶ୍ନନୁସାରେ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 2x ସେ.ମି. ।
⇒ 144 = \(\frac{1}{2}\) (x × 2x) ⇒ x² = 144 ⇒ x = 12 ସେ.ମି. ।
ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = x = 12 ସେ.ମି.
ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 2x = 2 × 12 = 24 ସେ.ମି.
∴ କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 12 ସେ.ମି. ଓ 24 ସେ.ମି. ।

Question 5.
ଗୋଟିଏ ରମ୍ବସ୍‌ର ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ 18 ସେ.ମି. ଏବଂ ବିପରୀତ ବାହୁଠାରୁ ଏହାର ଦୂରତା 14 ସେ.ମି. ହେଲେ, ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ରମ୍ବସ୍‌ର ବାହୁର ଦୈର୍ଘ୍ୟ = 18 ସେ.ମି. ।
ବିପରୀତ ବାହୁଠାରୁ ଏହାର ଦୂରତା = ରମ୍ବସ୍‌ର ଉଚ୍ଚତା = 14 ସେ.ମି. ।
∴ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ = ବାହୁର ଦୈର୍ଘ୍ୟ × ଉଚ୍ଚତା = 18 ସେ.ମି. × 14 ସେ.ମି. = 252 ବର୍ଗ ସେ.ମି. । 
∴ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ 252 ବର୍ଗ ସେ.ମି. ।

Question 6.
ଗୋଟିଏ ରମ୍ବସ୍‌ର ଏକ କର୍ଷର ଦୈର୍ଘ୍ୟ ଅନ୍ୟ କର୍ତ୍ତଟିର ଦୈର୍ଘ୍ୟର 80 ପ୍ରତିଶତ (ଶତକଡ଼ା 80 ଭାଗ) ହେଲେ, ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ ବୃହତ୍ତମ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟର ବର୍ଗର କେତେ ଗୁଣ ହେବ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ରମ୍ବସ୍‌ର ବୃହତ୍ତମ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = x ଏକକ

Question 7.
ଗୋଟିଏ ବର୍ଗକ୍ଷେତ୍ର ଓ ଗୋଟିଏ ରମ୍ବସ୍ ଏକା ଭୂମି ଉପରେ ଦଣ୍ଡାୟମାନ । ତେବେ ବର୍ଗକ୍ଷେତ୍ର ଓ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ କେତେ ହେବ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:

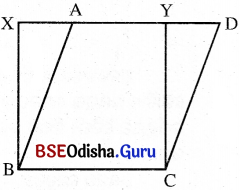
ABCD ରମ୍ବସ୍ ଓ XBCY ବର୍ଗକ୍ଷେତ୍ର ଏକା ଭୂମି BC ଉପରେ ଅବସ୍ଥିତ 
ମନେକର ରମ୍ବସ୍‌ର ବାହୁର ଦୈର୍ଘ୍ୟ = x ଏକକ
= ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ
∴ ରମ୍ବସ୍‌ର ଉଚ୍ଚତାର ଦୈର୍ଘ୍ୟ = ବର୍ଗକ୍ଷେତ୍ରର ବାହୁର ଦୈର୍ଘ୍ୟ = x ଏକକ

∴ ବର୍ଗକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ଓ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ 1 : 1 ।

Question 8.
ଗୋଟିଏ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ 560 ବର୍ଗ ମିଟର । ଏହାର ବାହୁର ଦୈର୍ଘ୍ୟ ଓ ଉଚ୍ଚତାର ଅନୁପାତ୍ର 7 : 5 ହେଲେ, ସେମାନଙ୍କର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ରମ୍ବସ୍‌ର ବାହୁର ଦୈର୍ଘ୍ୟ 7x ମିଟର ଓ ଉଚ୍ଚତାର ଦୈର୍ଘ୍ୟ 5x ମିଟର ।
ରମ୍ବସର କ୍ଷେତ୍ରଫଳ = ବାହୁର ଦୈର୍ଘ୍ୟ x ଉଚ୍ଚତା = 7x × 5x = 35x² ବର୍ଗ ମି.
ପ୍ରଶ୍ବାନୁସାରେ, 35x² = 560 ⇒ x² = \(\frac{560}{35}\) = 15
⇒ x = \(\sqrt{16}\) = 4 ମି.
∴ ରମ୍ବସର ବାହୁର ଦୈର୍ଘ୍ୟ = 7x = 7 × 4 = 28 ମି. ଓ ଉଚ୍ଚତାର ଦୈର୍ଘ୍ୟ = 5x = 5 × 4 = 20 ମି. ।

Question 9.
ଗୋଟିଏ ରମ୍ବସ୍‌ର କଣ୍ଠଦ୍ଵୟର ଦୈର୍ଘ୍ୟ 4 ଡେସିମିଟର 8 ସେଣ୍ଟିମିଟର ଓ 6 ଡେସିମିଟର 4 ସେଣ୍ଟିମିଟର ହେଲେ, ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ ଓ ପରିସୀମା ନିଶ୍ଚୟ କର ।
ସମାଧାନ:
ଗୋଟିଏ ରମ୍ବସ୍‌ର କଣ୍ଠଦ୍ଵୟର ଦୈର୍ଘ୍ୟ (d₁) = 4 ଡେ. ମି. 8 ସେ.ମି. = 48 ସେ.ମି. 
ଓ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ (d₂) = 6 ଡେ.ମି. 4 ସେ.ମି. = 64 ସେ.ମି.

ରମ୍ବସର ପରିସୀମା = 4 × 40 = 160 ସେ.ମି. ।

Question 10.
ଗୋଟିଏ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ 1320 ବର୍ଗ ମିଟର । ଏହାର ଗୋଟିଏ କର୍ପୂର ଦୈର୍ଘ୍ୟ 22 ମିଟର ହେଲେ, ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ ଓ ବାହୁର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ରମ୍ବସ୍‌ର ଗୋଟିଏ କର୍ପୂର ଦୈର୍ଘ୍ୟ (d₁) = 22 ମି. । 
ମନେକର ଏହାର ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ (d₂) = x ମି.

Question 11.
ଗୋଟିଏ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ 3456 ବର୍ଗ ସେ.ମି. ଓ ଏହାର କର୍ଣ୍ଣଦ୍ୱୟର ଅନୁପାତ 3 : 4 ହେଲେ, ରମ୍ବସ୍‌ର ପରିସୀମା ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ରମ୍ବସ୍‌ର ଗୋଟିଏ କର୍ପୂର ଦୈର୍ଘ୍ୟ = 3x ସେ.ମି. ଏବଂ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 4x ସେ.ମି.

ରମ୍ବସ୍‌ର ପରିସୀମା = 4 × ବାହୁର ଦୈର୍ଘ୍ୟ = 4 × 60 = 240 ସେ.ମି. ।

Question 12.
ଗୋଟିଏ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ 867 ବର୍ଗମିଟର ଏବଂ ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ ଅନ୍ୟଟିର \(\frac{2}{3}\) ହେଲେ କର୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର । 
ସମାଧାନ:

Question 13.
ଗୋଟିଏ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ 240 ବର୍ଗ ସେ.ମି. । ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟଠାରୁ 14 ସେ.ମି. ବେଶୀ ହେଲେ, ରମ୍ବସର ପରିସୀମା ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ରମ୍ବସ୍‌ର ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = x ସେ.ମି. । ପ୍ରଶ୍ନନୁସାରେ, ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = (x + 14) ସେ.ମି.

ରମ୍ବସ୍‌ର ପରିସୀମା = 4 × ବାହୁର ଦୈର୍ଘ୍ୟ = 4 × 17 = 68 ସେ.ମି. ।

Question 14.
ଗୋଟିଏ ରମ୍ବସ୍‌ର ବାହୁର ଦୈର୍ଘ୍ୟ 13 ମିଟର ଓ ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 24 ମିଟର । ଏହାର ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ ଓ ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ଗୋଟିଏ କଣ୍ଠର ଦୈର୍ଘ୍ୟ (d₁) = 24 ମି. । ମନେକର ରମ୍ବସ୍‌ର ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ (d₂) = 2x ମି. ।

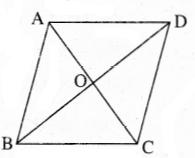
ବିକଳ୍ପ ସମାଧାନ:
ABCD ରମ୍ବସ୍‌ରେ AC = 24 ମି. ଓ BC = 13 ମି.

Question 15.
ଗୋଟିଏ ରମ୍ବସ୍‌ର ଗୋଟିଏ ବାହୁ 17 ସେ.ମି. ଏବଂ କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଅନୁପାତ 8 : 15 ହେଲେ, ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଗୋଟିଏ କଣ୍ଠର ଦୈର୍ଘ୍ୟ (d₁) = 8x ସେ.ମି. ଏବଂ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ (d₂) = 15x ସେ.ମି. ।

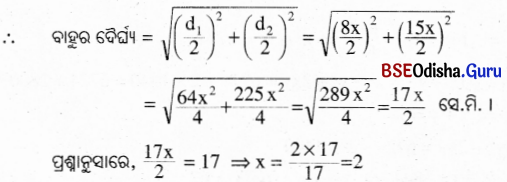
ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 8x = 8 x 2 = 16 ସେ.ମି. ଏବଂ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 15x = 15 × 2 = 30 ସେ.ମି.
∴ ରମ୍ବସର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳ = \(\frac{1}{2}\) × 16 × 30 = 240 ବର୍ଗ ସେ.ମି. ।

Question 16.
ଗୋଟିଏ ରମ୍ବସ୍‌ର ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ 15 ମିଟର ଏବଂ ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟଠାରୁ 6 ମିଟର ବେଶୀ । ରମ୍ବସ୍‌ର କ୍ଷେତ୍ରଫଳ ସ୍ଥିର କର ।
ସମାଧାନ:
ମନେକର ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ (d₁) = x ମି. । ପ୍ରଶାନୁସାରେ, ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ (d₂) = (x + 6) ମି. ।

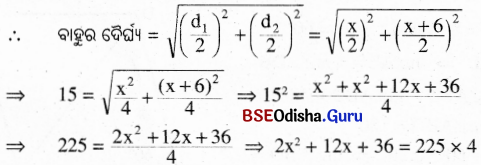
⇒ 2x² + 12x + 36 – 900 = 0
⇒ 2x² + 12x – 864 = 0
⇒ 2(x² + 6x – 432) = 0
⇒ x² + 6x – 432 = 0
⇒ x² + 24x – 18x – 432 = 0
⇒ x(x + 24) – 18 (x + 24) = 0
⇒ (x + 24) (x – 18) = 0
⇒ x + 24 = 0 କିମ୍ବା x – 18 = 0
ଯଦି x + 24 = 0 ⇒ x = -24 (ଏହା ଅସମ୍ଭବ )
ଏବଂ x – 18 = 0 ⇒ x = 18
ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 18 ମିଟର ଏବଂ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = x + 6 = 18 + 6 = 24 ମିଟର
∴ ରମ୍ବସର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳ = \(\frac{1}{2}\) × 18 × 24 = 216 ବର୍ଗ ମି. ।

Question 17.
720 ବର୍ଗମିଟର କ୍ଷେତ୍ରଫଳ ବିଶିଷ୍ଟ ଏକ ରମ୍ବସ୍‌ର ଗୋଟିଏ ବାହୁର ଦୈର୍ଘ୍ୟ 41 ମିଟର ହେଲେ, କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ରମ୍ବସ୍‌ କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ x ମି. ଓ Y ମି. ।

∴ y = 98 – 80 = 18 ମି. 
∴ ରମ୍ବସର କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 80 ମିଟର ଓ 18 ମିଟର ।

Question 19.
ଗୋଟିଏ ରମ୍ବସ୍‌ର ଗୋଟିଏ କୋଣର ପରିମାଣ 60° ଓ ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ 8 ମିଟର ହେଲେ, ଏହାର କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଓ କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ABCD ରମ୍ବସ୍‌ର AB = 8 ମି. ଓ m∠BAD = 60°
Δ ABD ରେ AB = AD ⇒ m∠ABD = m∠ADB
କିନ୍ତୁ m∠BAD + m∠ABD + m∠ADB = 180°
⇒ 60° + m∠ABD + m∠ABD = 180°
⇒ 2m∠ABD = 180° – 60° = 120° ⇒ m∠ABD = 60°
m∠ABD = m∠ADB = 60°

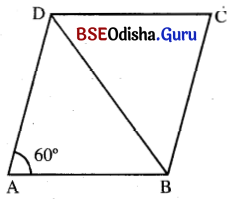
ତ୍ରିଭୁଜର କୋଣତ୍ରୟର ପରିମାଣ ସମାନ । ତେଣୁ ଏହା ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜ । BD = AB = 8 ମି. । 
ତେଣୁ ଗୋଟିଏ କର୍ଷ ଦୈର୍ଘ୍ୟ (d₁) = 8 ମିଟର । ମନେକର ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ (d₂) = x ମିଟର ।

ବିକଳ୍ପ ସମାଧାନ:

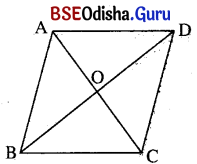
ABCD ରମ୍ବସ୍‌ରେ m∠B = 60°, AB = BC = CD = DA = 8 ସେ.ମି. ।
କଣ୍ଠ A͞C ଓ କଣ୍ଠ B͞D ର ଛେଦବିନ୍ଦୁ O ।
m∠B = 60°, AB = BC ହେତୁ m∠BAC = m∠BCA = 60°
∴ Δ ABC ଏକ ସମବାହୁ ତ୍ରିଭୁଜ । ∴ AC = 8 ମିଟର ।
ABC ସମବାହୁ ତ୍ରିଭୁଜର ଉଚ୍ଚତା OB = \(\frac{\sqrt{3}}{2}\) × ବାହୁର ଦୈର୍ଘ୍ୟ = \(\frac{\sqrt{3}}{2}\) × 8 ମି. = 4√3
∴ BD = 2 × OB = 2 × 4√3 = 8√3 ମି. ।
∴ ABCD ରମ୍ବସର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × AC × BD = \(\frac{1}{2}\) × 8 × 8√3 = 32√3 ବର୍ଗ ସେ.ମି. ।