BSE Odisha 9th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(e)

Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(e) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(e)

Question 1.
(ଆବଶ୍ୟକସ୍ଥଳେ 3 ର ମାନ 1.732 ନିଅ।)
(a) ଗୋଟିଏ ଚତୁର୍ଭୁଜର ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 25 ମିଟର ଏବଂ ଏହି କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିଦୁ୍ୟଦ୍ୱୟରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 13 ସେ.ମି. ଓ 11 ସେ.ମି. ହେଲେ ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 25 ମି. = 2500 ସେ.ମି.,
କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 13 ସେ.ମି. ଓ 11 ସେ.ମି. ।
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ଉଚ୍ଚତା × ସମାନ୍ତର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି
=  \(\frac{1}{2}\) × 2500 × (13 + 11) = 30000 ବର୍ଗ ସେ.ମି. ।

(b) ଗୋଟିଏ ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ 560 ବର୍ଗ ସେ.ମି. ଏବଂ କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ଵୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି 28 ସେ.ମି. ହେଲେ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ କେତେ ?
ସମାଧାନ:
ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = 560 ବର୍ଗ ସେ.ମି. ।
କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବାହୁରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ଵୟର ସମଷ୍ଟି = 28 ସେ.ମି. l

= \(\frac{2 \times 560}{28}\) = 40 ସେ.ମି. l
∴ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 40 ସେ.ମି. l

(c) ଗୋଟିଏ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 36 ମିଟର ଏବଂ କ୍ଷେତ୍ରଫଳ 270 ବର୍ଗ ମିଟର ହେଲେ, କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିଦୁ୍ୟଦ୍ୱୟରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି କେତେ ?
ସମାଧାନ:
ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 36 ମିଟର, କ୍ଷେତ୍ରଫଳ = 270 ବର୍ଗ ମିଟର । 
ମନେକର କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି = x ମିଟର
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ଉଚ୍ଚତା × ସମାନ୍ତର ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି
⇒ 270 = \(\frac{1}{2}\) × 36 × x ⇒ 18x = 270 ⇒ x = \(\frac{270}{18}\) = 15 ମିଟର ।
∴ କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି 15 ମିଟର ।

(d) ବହିଃସ୍ଥ କର୍ଣ୍ଣ ବିଶିଷ୍ଟ ଗୋଟିଏ ଚତୁର୍ଭୂଜର ବହିଃସ୍ଥ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 36 ସେ.ମି. ଏବଂ କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 24 ସେ.ମି. ଓ 16 ସେ.ମି. ହେଲେ ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ଚତୁର୍ଭୁଜରେ ବହିଃସ୍ଥ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 36 ସେ.ମି.,
କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ଵୟ 24 ସେ.ମି. ଓ 16 ସେ.ମି. ।
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ବହିଃସ୍ଥ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ × କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ଵୟର ଦୈର୍ଘ୍ୟର ଅନ୍ତର
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × 36 ସେ.ମି. × (24 – 16) ସେ.ମି.
= 18 ସେ.ମି. × 8 ସେ.ମି. = 144 ବର୍ଗ ମିଟର । 
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ 144 ବର୍ଗ ମିଟର । 

(e) ଗୋଟିଏ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ଛେଦ କରନ୍ତି । କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 24 ମିଟର ଓ 15 ମିଟର ହେଲେ, ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ଚତୁର୍ଭୁଜରେ କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ଛେଦକରନ୍ତି । କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ = 24 ମି. ଓ 15 ମି. ।
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳ
ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × 24 ମି. × 15 ମି. = 180 ବର୍ଗ ମିଟର । 
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ 180 ବର୍ଗ ମିଟର । 

(f) ଗୋଟିଏ ବହିଃସ୍ଥ କର୍ଣ୍ଣ ବିଶିଷ୍ଟ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିଦୁ୍ୟଦ୍ବୟରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ଵୟର ଅନ୍ତର 10 ସେ.ମି. ଓ କ୍ଷେତ୍ରଫଳ 180 ବର୍ଗ ସେ.ମି. ହେଲେ, ଉକ୍ତ ବହିଃସ୍ଥ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ କେତେ ?
ସମାଧାନ:
ଚତୁର୍ଭୁଜର ବହିଃସ୍ଥ କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିଦୁ୍ୟଦ୍ୱୟରୁ ଅଙ୍କିତ ଲମ୍ବନ୍ବୟର ଅନ୍ତର = 10 ସେ.ମି.
ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = 180 ବର୍ଗ ସେ.ମି. । ମନେକର ବହିଃସ୍ଥ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = x ସେ.ମି.
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × ବହିଃସ୍ଥ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ × କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିଦୁ୍ୟଦ୍ୱୟରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଅନ୍ତର
⇒ 180 ବର୍ଗ ସେ.ମି. = \(\frac{1}{2}\) × x × 10 ସେ.ମି.
⇒ 5x = 180 ⇒ x = \(\frac{180}{5}\) = 36 ସେ.ମି.
∴ ବହିଃସ୍ଥ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 36 ସେ.ମି.

(g) ଗୋଟିଏ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ୱୟ ପରସ୍ପରକୁ ସମକୋଣରେ ଛେଦ କରନ୍ତି । ଯଦି ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 32 ମିଟର ଏବଂ କ୍ଷେତ୍ରଫଳ 640 ବର୍ଗ ମିଟର ହୁଏ, ତେବେ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ କେତେ ?
ସମାଧାନ:
ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ଛେଦ କରନ୍ତି ।
ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 32 ମିଟର ଓ କ୍ଷେତ୍ରଫଳ = 640 ବର୍ଗ ମିଟର ।
ମନେକର ଚତୁର୍ଭୁଜର ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = x
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × କର୍ଣ୍ଣଦ୍ଵୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳ
⇒ 640 ବର୍ଗ ମି. = \(\frac{1}{2}\) × 32 ମି. × x ମିଟର ⇒ 16x = 640
⇒ x = \(\frac{640}{16}\) = 40 ମିଟର ।
∴ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 40 ମିଟର ।

Question 2.
ଗୋଟିଏ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 48 ମିଟର ଏବଂ ଏହାର କ୍ଷେତ୍ରଫଳ 1296 ବର୍ଗ ମିଟର । ଏହି କର୍ଣ୍ଣ ଉପରେ ବିପରୀତ କୌଣିକ ବିଦୁ୍ୟଦ୍ୱୟରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଅନୁପାତ 4 : 5 ହେଲେ, ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର କର୍ଣ୍ଣ ଉପରେ ବିପରୀତ କୌଣିକ ବିନ୍ଦୁଦ୍ଵୟରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 4x ମି. ଓ 5x ମି. ।
ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ × କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିଦୁ୍ୟଦ୍ୱୟର ଅଙ୍କିତ ଲମ୍ବଦ୍ବୟର ସମଷ୍ଟି
∴ ଟ୍ରାପିଜିୟମ୍‌ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × 48 × (4x + 5x) = 24 × 9x = 216 ବର୍ଗ ମି. ।
କିନ୍ତୁ ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = 1296 ବର୍ଗ ମି. ⇒ 216x = 1296 ⇒ x = \(\frac{1296}{216}\) = 6 ମିଟର
∴ ଗୋଟିଏ ଲମ୍ବର ଦୈର୍ଘ୍ୟ = 4x = 4 × 6 = 24 ମି. ଏବଂ ଅନ୍ୟ ଲମ୍ବର ଦୈର୍ଘ୍ୟ = 5x = 5 × 6 = 30 ମି. ।

Question 3.
ଗୋଟିଏ ଚତୁର୍ଭୁଜର ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 28 ମିଟର ଏବଂ ଏହାର କ୍ଷେତ୍ରଫଳ 336 ବର୍ଗ ମିଟର । ଏହି କର୍ଣ୍ଣ ପ୍ରତି ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ଵୟ ମଧ୍ୟରୁ ଗୋଟିଏ ଅନ୍ୟଠାରୁ 6 ମିଟର ଅଧିକ ହେଲେ, ଲମ୍ବନ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଗୋଟିଏ ଲମ୍ବର ଦୈର୍ଘ୍ୟ = x ମି. । ପ୍ରଶାନୁସାରେ, ଅନ୍ୟ ଲମ୍ବର ଦୈର୍ଘ୍ୟ = (x + 6) ମି. । 
ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ × କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ବୟର ସମଷ୍ଟି
∴ ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × 28 × (x + x + 6) = \(\frac{1}{2}\) × 28 × 2(x + 6) = 28(x + 3) ବର୍ଗ ମି. ।
ପ୍ରଶ୍ବାନୁସାରେ, 28(x + 3) = 336
⇒ x + 3 = \(\frac{336}{28}\) = 12
⇒ x + 3 = 12
⇒ x = 12 – 3 = 9 ମି.
∴ ଗୋଟିଏ ଲମ୍ବର ଦୈର୍ଘ୍ୟ 9 ମି. ଏବଂ ଅନ୍ୟ ଲମ୍ବର ଦୈର୍ଘ୍ୟ = 9 + 6 = 15 ମି. ।

Question 4.
କୌଣସି ଚତୁର୍ଭୁଜର ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 70 ସେ.ମି. । ଏହି କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି ଦତ୍ତ ଦୈର୍ଘ୍ୟର \(\frac{3}{5}\) ହେଲେ, ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ଚତୁର୍ଭୁଜର ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 70 ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି
= କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ × \(\frac{3}{5}\) = 70 × \(\frac{3}{5}\) = 42 ସେ.ମି.
ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ × କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବଦ୍ବୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି
∴ ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × 70 × 42 = 70 × 21 = 1470 ବର୍ଗ ସେ.ମି.

Question 5.
ଗୋଟିଏ ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ 192 ବର୍ଗ ମିଟର ଏବଂ ଏହାର ବହିଃସ୍ଥ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ 32 ମିଟର । ଏହି କର୍ଣ୍ଣ ଉପରେ ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଏହା ପ୍ରତି ଅଙ୍କିତ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ସମଷ୍ଟି 26 ମିଟର ହେଲେ, ସେମାନଙ୍କର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର କର୍ଣ୍ଣପ୍ରତି ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଅଙ୍କିତ ଲମ୍ବନ୍ବୟର ଦୈର୍ଘ୍ୟ x ମି. ଓ y ମି. ।
ପ୍ରଶାନୁସାରେ, x + y = 26 ମି. … (i)

y = 26 – x = 26 – 19 = 7 ମି.
∴ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣ ଉପରେ ବିପରୀତ କୌଣିକ ବିନ୍ଦୁରୁ ଏହାପ୍ରତି ଅଙ୍କିତ ଲମ୍ବଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 19 ମି. ଓ 7 ମି. ।

Question 6.
ଗୋଟିଏ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ଛେଦ କରନ୍ତି । ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ 864 ବର୍ଗ ମିଟର ଓ କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଅନୁପାତ 3 : 4 ହେଲେ, କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 3x ମି. ଓ 4x ମି. ।
ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳ
ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × 3x × 4x = 6x² ବର୍ଗ ମି. ।
∴ ପ୍ରଶ୍ବାନୁସାରେ, 6x² = 864 ⇒ x² = \(\frac{864}{6}\) = 144
⇒ x = √144 = 12 ମି.
ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 3 × 12 = 36 ମି ଏବଂ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 4 × 12 = 48 ସେ.ମି. ।
∴ କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 36 ମି. ଓ 48 ମି. ।

Question 7.
ଗୋଟିଏ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ଛେଦ କରନ୍ତି । ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ 400 ବର୍ଗ ମିଟର । ଯଦି ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ ଅନ୍ୟଟି ଅପେକ୍ଷା 7 ମିଟର ବେଶୀ ହୁଏ, ତେବେ କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଚତୁର୍ଭୁଜର ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = x ମି. । ପ୍ରଶ୍ନନୁସାରେ, ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = (x + 7) ମି.
ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳ
= \(\frac{1}{2}\) × x(x + 7) = \(\frac{x(x+7)}{2}\) ବର୍ଗ ମି. ।
ପ୍ରଶାନୁସାରେ, \(\frac{x(x+7)}{2}\) = 400
⇒ x² + 7x = 800
⇒ x² + 7x – 800 = 0
⇒ x² + 32x – 25x – 800 = 0
⇒ x(x + 32) – 25 (x + 32) = 0
⇒ (x + 32) (x – 25) = 0
⇒ x + 32 = 0  କିମ୍ବା x – 25 = 0
ଯଦି x + 32 = 0 ⇒ x = -32 (ଏହା ଅସମ୍ଭବ) ଏବଂ x – 25 = 0 ⇒ x = 25 
ଚତୁର୍ଭୁଜର ଗୋଟିଏ କର୍ଣ୍ଣ ଦୈର୍ଘ୍ୟ = 25 ମି. ଏବଂ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 25 + 7 = 32 ମି. ।
∴ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 25 ମି. ଓ 32 ମି. ।

Question 8.
ଗୋଟିଏ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ଛେଦ କରନ୍ତି ଏବଂ ଏହାର କ୍ଷେତ୍ରଫଳ 90 ବର୍ଗ ମିଟର । ଯଦି କର୍ଣ୍ଣଦ୍ୱୟର ସମଷ୍ଟି 28 ମିଟର ହୁଏ, ତେବେ କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଚତୁର୍ଭୁଜର ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = x ମି.. । ପ୍ରଶାନୁସାରେ, ଅନ୍ୟ ଲମ୍ବର ଦୈର୍ଘ୍ୟ = (28 – x) ମି. ।
ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳ
= \(\frac{1}{2}\) × x(28 – x) = \(\frac{x(28-x)}{2}\) ବର୍ଗ ମି. ।
ପ୍ରଶାନୁସାରେ, \(\frac{x(28-x)}{2}\) = 90
⇒ 28x – x² = 180
⇒ 28x – x² – 180 = 0
⇒ x² – 18x – 10x + 180 = 0
⇒ x(x – 18) – 10 (x – 18) = 0
⇒ (x – 18) (x – 10) = 0
⇒ x – 18 = 0  କିମ୍ବା x – 10 = 0
ଯଦି x – 18 = 0 ⇒ x = 18 ଏବଂ x – 10 = 0 ⇒ x = 10
x = 18 ହେଲେ 28 – x = 28 – 18 = 10; x = 10 ହେଲେ 28 – x = 28 – 10 = 18
∴ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 10 ମି. ଓ 18 ମି. ।

Question 9.
ଗୋଟିଏ ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ 396 ବର୍ଗ ମିଟର ଏବଂ ଏହାର କର୍ଣ୍ଣଦ୍ଵୟ ପରସ୍ପରକୁ ସମକୋଣରେ ଛେଦ କରନ୍ତି । ଏହାର ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟର 2 ଗୁଣରୁ 8 ମିଟର ବେଶୀ ହେଲେ, କରର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଚତୁର୍ଭୁଜର ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = x ମି. ଓ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 2x + 8 ମି. ।
ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଗୁଣଫଳ = \(\frac{1}{2}\) × x(2x + 8)
= \(\frac{1}{2}\) × x × 2(x + 4) = x(x + 4) ବ. ମି.
ପ୍ରଶାନୁସାରେ, x(x + 4) = 396 ⇒ x² + 4x = 396
⇒ x² + 4x – 396 = 0
⇒ x² + 22x – 18x – 396 = 0
⇒ x(x + 22) – 18(x + 22) = 0
⇒ (x + 22) (x – 18) = 0
⇒ x + 22 = 0 ବା x – 18 = 0
⇒ x = -22 (ଅସମ୍ଭବ) ବା x = 18
ଗୋଟିଏ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 18 ମି. ଓ ଅନ୍ୟ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 2x + 8 = 2 × 18 + 8 = 36 + 8 = 44 ମି.
∴ ଚତୁର୍ଭୁଜର କର୍ଣ୍ଣଦ୍ୱୟର ଦୈର୍ଘ୍ୟ 18 ମିଟର ଓ 44 ମିଟର ।

Question 10.
ABCD ଚତୁର୍ଭୁଜର AB, BC, CD, DA ଏବଂ AC କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 29 ସେ.ମି., 36 ସେ.ମି., 40 ସେ.ମି., 39 ସେ.ମି. ଏବଂ 25 ସେ.ମି. ହେଲେ, ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:

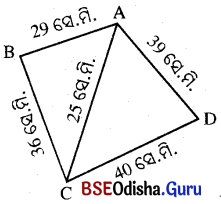
ABCD ଚତୁର୍ଭୁଜରେ AB = 29 ସେ.ମି.,
BC= 36 ସେ.ମି., CD = 40 ସେ.ମି.,
DA = 39 ସେ.ମି., & AC = 25 ସେ.ମି.।
ABCD ଚତୁର୍ଭୁଜ AC କର୍ଣ୍ଣଦ୍ୱ‍।ରା Δ ABC ଓ Δ ACD ରେ ବିଭକ୍ତ ହୋଇଛି ।

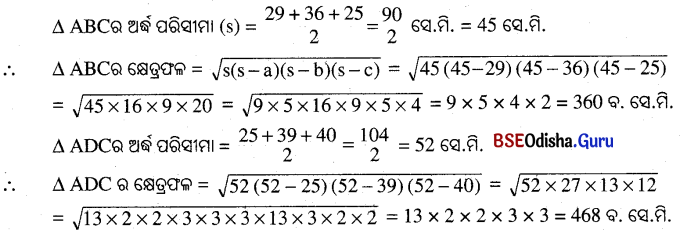
∴ ABCD ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = Δ ABC ର କ୍ଷେତ୍ରଫଳ + Δ ACD ର କ୍ଷେତ୍ରଫଳ
= 360 ବ. ସେ.ମି. + 468 ବ. ସେ.ମି. = 828 ବ. ସେ.ମି. ।

Question 11.
ଗୋଟିଏ ଚତୁର୍ଭୁଜର ଚାରିବାହୁର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 15 ସେ.ମି., 36 ସେ.ମି., 52 ସେ.ମି. ଓ 65 ସେ.ମି. ଏବଂ ପ୍ରଥମ ଦୁଇ ବାହୁର ଅନ୍ତର୍ଗତ କୋଣର ପରିମାଣ 90° ଅଟେ । ଏହାର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:

∴ ABCD ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = Δ ABC ର କ୍ଷେତ୍ରଫଳ + Δ ACD ର କ୍ଷେତ୍ରଫଳ
= (270 + 1014) ବର୍ଗ ସେ.ମି. = 1284 ବର୍ଗ ସେ.ମି.

Question 12.
ଗୋଟିଏ ଚତୁର୍ଭୁଜର ଦୁଇଟି ବାହୁର ଦୈର୍ଘ୍ୟ 8 ମିଟର ଓ 15 ମିଟର ଏବଂ ସେମାନଙ୍କର ଅନ୍ତର୍ଗତ କୋଣ ଗୋଟିଏ ସମକୋଣ । ଯଦି ଅନ୍ୟ ବାହୁ ଦୁଇଟିର ଦୈର୍ଘ୍ୟ ପ୍ରତ୍ୟେକ 17 ମିଟର ହୁଅନ୍ତି, ତେବେ ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:

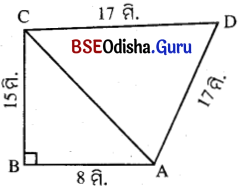
ABCD ଚତୁର୍ଭୁଜର AB = 8 ମି.,
BC = 15 ମି., AD = CD = 17 ମି., ଏବଂ m∠ABC = 90°।

∴ ABCD ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = Δ ABC ର କ୍ଷେତ୍ରଫଳ + Δ ACD ର କ୍ଷେତ୍ରଫଳ
= 60 ବ. ମି. + 125.13 ବ. ମି. = 185.13 ବ. ମି. ।

Question 13.
ଗୋଟିଏ ଚତୁର୍ଭୁଜର ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟ 20 ସେ.ମି., 20 ସେ.ମି., 16 ସେ.ମି. ଓ 12 ସେ.ମି. ଏବଂ ପ୍ରଥମ ବାହୁଦ୍ୱୟର ଅନ୍ତର୍ଗତ କୋଣର ପରିମାଣ 60° ହେଲେ କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:

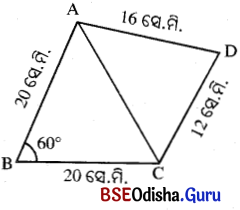
ABCD ଚତୁର୍ଭୁଜର AB = 20 ସେ.ମି., BC = 20 ସେ.ମି., DC = 12 ସେ.ମି. DA = 16 ସେ.ମି. ଏବଂ m∠ABC = 60° ।
Δ ABC ରେ AB = BC = 20 ସେ.ମି.
କିନ୍ତୁ m∠ABC = 60° (ଦତ୍ତ)
∴ m∠ACB = m∠BAC = 60°
∴ Δ ABC ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ।
∴ Δ ABC ର କ୍ଷେତ୍ରଫଳ = \(\frac{\sqrt{3}}{4}\) × (ବାହୁର ଦୈର୍ଘ୍ୟ)² = \(\frac{\sqrt{3}}{4}\) × 20 × 20
= 1.732 × 100 = 173.2  ବର୍ଗ ସେ.ମି.
∴ Δ ACD ରେ, 16² + 12² = 20²
⇒ AD² + CD² = AC²
∴ Δ ACD ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ।
∴ Δ ACD ର କ୍ଷେତ୍ରଫଳ = \(\frac{1}{2}\) × AD × CD = \(\frac{1}{2}\) 16 × 12 = 96 ବର୍ଗ ସେ.ମି.
∴ ABCD ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = Δ ABC ର କ୍ଷେତ୍ରଫଳ + Δ ACD ର କ୍ଷେତ୍ରଫଳ
= 173.2 + 96 = 269.2 ବର୍ଗ ସେ.ମି.

Question 14.
ABCD ଚତୁର୍ଭୁଜର AB = BC = 50 ସେ.ମି., ଏବଂ m∠ABC = 60°, AD = 30 ସେ.ମି. ଓ m∠ADC = 90° ହେଲେ ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:

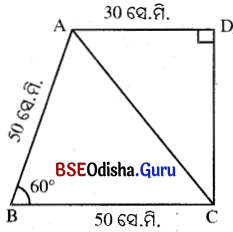
ABCD ଚତୁର୍ଭୁଜର AB = BC = 50 ସେ.ମି.,
AD = 30 ସେ.ମି., m∠ABC = 60° ସେ.ମି.,
ଏବଂ m∠ADC = 90° ।
Δ ABC ରେ AB = BC ⇒ m∠ACB = m∠BAC
Δ ABC ରେ m∠BAC + m∠ACB = 120°
(∵ m∠ABC = 60°)
⇒ m∠BAC = m∠ACB = 60° ।
∴ Δ ABC ଏକ ସମବାହୁ ତ୍ରିଭୁଜ ।
⇒ AB = BC = AC = 50 ସେ.ମି.

∴ ABCD ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = Δ ABC ର କ୍ଷେତ୍ରଫଳ + Δ ACD ର କ୍ଷେତ୍ରଫଳ
= (1082.5 + 600) ବର୍ଗ ସେ.ମି. = 1682.5 ବର୍ଗ ସେ.ମି.

Question 15.
 ABCD ଚତୁର୍ଭୁଜର AB = 36 ସେ.ମି., BC = 48 ସେ.ମି., CD = DA = 50 ସେ.ମି., ଏହାର m∠ABC = 90° ହେଲେ ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:

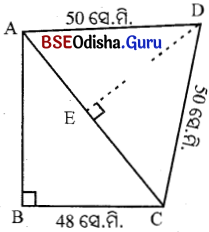
 ABCD ଚତୁର୍ଭୁଜର AB = 36 ସେ.ମି.,
BC = 48 ସେ.ମି., CD = DA = 50 ସେ.ମି.,
ଏବଂ m∠ABC = 90°

∴ ABCD ଚତୁର୍ଭୁଜର କ୍ଷେତ୍ରଫଳ = Δ ABC ର କ୍ଷେତ୍ରଫଳ + Δ ACD ର କ୍ଷେତ୍ରଫଳ
= (864 + 1200) ବର୍ଗ ସେ.ମି. = 2064 ବର୍ଗ ସେ.ମି.