BSE Odisha 9th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(f)

Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(f) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Geometry Chapter 5 ପରିମିତି Ex 5(f)

Question 1.
ନିମ୍ନଲିଖ ପ୍ରଶ୍ନଗୁଡ଼ିକର ଉତ୍ତର ଦିଅ ।
(a) ଗୋଟିଏ ଆୟତଘନାକାର ବସ୍ତୁର ଭୂମିର ଦୈର୍ଘ୍ୟକୁ ଉଚ୍ଚତା ଓ ଉଚ୍ଚତାକୁ ଭୂମିର ଦୈର୍ଘ୍ୟ କଲେ ଏହାର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳରେ କିଛି ପରିବର୍ତ୍ତନ ହେବ କି ?
ସମାଧାନ:
ଗୋଟିଏ ଆୟତଘନାକାର ବସ୍ତୁର ଭୂମିର ଦୈର୍ଘ୍ୟକୁ ଉଚ୍ଚତା ଓ ଉଚ୍ଚତାକୁ ଭୂମିର ଦୈର୍ଘ୍ୟ କଲେ ଏହାର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳରେ କିଛି ପରିବର୍ତ୍ତନ ହେବନାହିଁ ।

(b) କାର୍ଡବୋର୍ଡରେ ନିର୍ମିତ ଢାଙ୍କୁଣି ନଥ‌ିବା ଏକ ସମଘନାକୃତି ବାକ୍ସର ପ୍ରତ୍ୟେକ ବାହୁ 6 ସେ.ମି. ହେଲେ ବାକ୍ସରେ ବ୍ୟବହୃତ କାର୍ଡ଼ବୋର୍ଡ଼ର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
କାର୍ଡ଼ବୋର୍ଡ଼ରେ ନିର୍ମିତ ଢାଙ୍କୁଣି ନଥିବା ଏକ ସମଘନାକୃତି ବାକ୍ସର ପାର୍ଶ୍ଵ ସଂଖ୍ୟା = 5 ଏହାର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ = 6 ସେ.ମି. ।
କାର୍ଡ଼ବୋର୍ଡ଼ର କ୍ଷେତ୍ରଫଳ = 5a² = 5 × 6² = 5 × 36 = 180 ବ ସେ.ମି. ।

(c) ଗୋଟିଏ ଆୟତଘନର ଭୂମିର ପରିସୀମା 22 ସେ.ମି. ଓ ଉଚ୍ଚତା 15 ସେ.ମି. ହେଲେ, ଏହାର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ
କେତେ ?
ସମାଧାନ:
ଆୟତଘନର ଭୂମିର ପରିସୀମା = 22 ସେ.ମି. ଓ ଉଚ୍ଚତା = 15 ସେ.ମି. ।
ମନେକର ଆୟତଘନର ଦୈର୍ଘ୍ୟ = a ସେ.ମି., ପ୍ରସ୍ଥ = b ସେ.ମି. ଓ ଉଚ୍ଚତା (c) = 15 ସେ.ମି. ।
∴ ଆୟତଘନର ଭୂମିର ପରିସୀମା = 2 (ଦୈର୍ଘ୍ୟ + ପ୍ରସ୍ଥ) = 2 (a + b) ସେ.ମି. ।
ପ୍ରଶ୍ବାନୁସାରେ 2 (a + b) = 22 ସେ.ମି. ଓ c = 15 ସେ.ମି. ।
∴ ଆୟତଘନର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2c (a + b) = 2 (a + b) c = 22 × 1 5 = 330 ବର୍ଗ ସେ.ମି. ।
∴ ଆୟତଘନର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 330 ବର୍ଗ ସେ.ମି. ।

(d) ଗୋଟିଏ ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 216 ବର୍ଗ ମି. ହେଲେ, ବାହୁର ଦୈର୍ଘ୍ୟ କେତେ ?
ସମାଧାନ:
ମନେକର ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = a ମି.
ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 6a² ବର୍ଗ ମି.
ପ୍ରଶ୍ବାନୁସାରେ 6a² = 216 ବ. ମି.
⇒ a² = \(\frac{216}{6}\) ବ. ମି.
⇒ a² = 36 ବ. ମି. ⇒ a = √36 ବ. ମି. = 6 ମି. ।
∴ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ 6 ମିଟର ।

(e) ଗୋଟିଏ ଆୟତଘନର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 336 ବର୍ଗ ମି. ଏବଂ ଭୂମିର ପରିସୀମା 24 ମିଟର ହେଲେ ଉଚ୍ଚତା କେତେ ?
ସମାଧାନ:
ମନେକର ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = a ମି.,  ପ୍ରସ୍ଥ = b ମି. ଓ ଉଚ୍ଚତା = c ମି.
ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2c (a + b) ବର୍ଗ ମି. ଓ ଭୂମିର ପରିସୀମା = 2 (a + b) ମି.
ପ୍ରଶ୍ବାନୁସାରେ, 2c (a + b) = 336 ବର୍ଗ ମି. ଏବଂ 2 (a + b) = 24 ମି.
 c × 2 (a + b) = 336 ବର୍ଗ ମି. ⇒ c × 24 ମି. = 536 ବର୍ଗ ମି.
⇒ c = \(\frac{336}{24}\) ବର୍ଗ ମି. = 14 ମି.
∴ ଆୟତଘନର ଉଚ୍ଚତା 14 ମିଟର ।

(f) a ଏକକ ବାହୁ ବିଶିଷ୍ଟ ତିନିଗୋଟି ସମଘନକୁ ଏପରି ଭାବେ ସଜାଇ ପାଖାପାଖ ରଖାଗଲା ଯେ, ଉତ୍ପନ୍ନ ଘନବସ୍ତୁଟି ଏକ ଆୟତଘନ ହେଲା । ତେବେ ଆୟତଘନର ସମଗ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ତିନୋଟି ସମଘନକୁ ସଜାଇ ଏକ ଆୟତଘନ କଲେ,
ଆୟତଘନର ଦୈର୍ଘ୍ୟ = 3a ଏକକ, ପ୍ରସ୍ଥ = a ଏକକ ଓ ଉଚ୍ଚତା = a ଏକକ ହେବ ।
ଆୟତଘନର ସମଗ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2( 3a · a + a · a + a · 3a) 
= 2 (3a² + a² + 3a²) = 14a² ବର୍ଗ ଏକକ ।
∴ ଆୟତଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 14a² ବର୍ଗ ଏକକ ।

(g) ଦୁଇଟି ସମଘନର ଆୟତନର ଅନୁପାତ 8 : 1 ହେଲେ, ସେମାନଙ୍କର ବାହୁମାନଙ୍କର ଅନୁପାତ କେତେ ?
ସମାଧାନ:
ମନେକର ପ୍ରଥମ ସମଘନର ଆୟତନ = 8x³ ଘନ ଏକକ ଓ ଦ୍ବିତୀୟ ସମଘନର ଆୟତନ = x³ ଘନ ଏକକ ।
ପ୍ରଥମ ସମଘନର ବାହୁ =\(\sqrt[3]{8 x^3}\) = 2x ଏକକ ଓ ଦ୍ୱିତୀୟ ସମଘନର ବାହୁ = \(\sqrt{x^3}\) = x ଏକକ
∴ ସମଘନଦ୍ବୟର ବାହୁର ଅନୁପାତ = 2x : x = 2 : 1 ।

(h) ତିନୋଟି ଧାତବ ସମଘନର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 5 ସେ.ମି., 4 ସେ.ମି. ଓ 3 ସେ.ମି. । ଏହି ତିନୋଟି ଧାତବ ସମଘନକୁ ତରଳାଇ ଗୋଟିଏ ନୂତନ ସମଘନ ତିଆରି କଲେ ତାହାର ବାହୁର ଦୈର୍ଘ୍ୟ କେତେ ?
ସମାଧାନ:
ପ୍ରଥମ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = 5 ସେ.ମି., ପ୍ରଥମ ସମଘନର ଘନଫଳ = (5)³ = 125 ଘ. ସେ.ମି. 
ଦ୍ବିତୀୟ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = 4 ସେ.ମି., ଦ୍ୱିତୀୟ ସମଘନର ଘନଫଳ = (4)³ = 64 ଘନ ସେ.ମି. ।
ତୃତୀୟ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = 3 ସେ.ମି., ତୃତୀୟ ସମଘନର ଘନଫଳ = (3)³ = 27 ଘନ ସେ.ମି. ।
∴ ତିନୋଟି ସମଘନର ଘନଫଳର ସମଷ୍ଟି 
= 125 ଘ. ସେ.ମି. + 64 ଘନ ସେ.ମି. + 27 ଘନ ସେ.ମି. = 216 ଘନ ସେ.ମି. ।
ନୂତନ ସମଘନର ସଘନଫଳ = 216 ଘନ ସେ.ମି. ।
‍∴ ନୂତନ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = \(\sqrt[3]{216}\) = 6 ସେ.ମି. ।

(i) ଗୋଟିଏ ସମଘନର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ ଦୁଇଗୁଣ ବଢ଼ିଗଲେ ଏହାର ଆୟତନ ପୂର୍ବାପେକ୍ଷା କେତେ ଗୁଣ ବଢ଼ିବ ? 
ସମାଧାନ:
ମନେକର ପ୍ରଥମ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = a ଏକକ ଆୟତନ = a ଘନ ଏକକ
ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ ଦୁଇଗୁଣ ବଢ଼ିଗଲେ ଏହାର ବାହୁର ଦୈର୍ଘ୍ୟ ହେବ = 2x ଏକକ
ଆୟତନ = (2x)³ = 8x³ ଘନ ଏକକ ।
ନୂତନ ସମଘନର ଆୟତନ – ପ୍ରଥମ ସମଘନର ଆୟତନ = 8x³ – x³ = 7x³ ଘନ ଏକକ ।
ଏହା ପ୍ରଥମ ସମଘନଠାରୁ ବଢ଼ିବ = \(\frac{7 x^3}{x^3}\) = 7 ଗୁଣ ।

(j) ଦୁଇଟି ସମଘନର ଆୟତନର ଅନୁପାତ 1 : 27 ହେଲେ, ସେମାନଙ୍କର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ କେତେ ?
ସମାଧାନ:
ମନେକର ପ୍ରଥମ ସମଘନର ଆୟତନ = x³ ଘନ ଏକକ ଓ ଦ୍ବିତୀୟ ସମଘନର ଆୟତନ = 27x³ ଘନ ଏକକ । 
ପ୍ରଥମ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = \(\sqrt[3]{{x}^3}\) = x ଏକକ ଓ
ଦ୍ବିତୀୟ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = \(\sqrt[3]{27 x^3}\) = 3x ଏକକ ।
∴ ପ୍ରଥମ ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 6 × x² = 6x² ବର୍ଗ ଏକକ
ଦ୍ବିତୀୟ ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 6 · (3x)² = 6 · 9x² = 54x² ବର୍ଗ ଏକକ ।
∴ ସମଘନଦ୍ଵୟର ସମଗ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ = \(\frac{6 x^2}{54 x^2}\) = \(\frac{1}{9}\) = 1 : 9

(k) ଗୋଟିଏ ଆୟତାକାର ପୋଖରୀର ଆଧାରର କ୍ଷେତ୍ରଫଳ 6500 ବର୍ଗ ସେ.ମି. ଏବଂ ଏଥ‌ିରେ ଥ‌ିବା ପାଣିର ଆୟତନ 2.6 ଘନ ମିଟର ହେଲେ, ଜଳର ଗଭୀରତା କେତେ ?
ସମାଧାନ
ଆୟତାକାର ପୋଖରୀର ଆଧାରର କ୍ଷେତ୍ରଫଳ = 6500 ବର୍ଗ ସେ.ମି.
ପୋଖରୀର ଥ‌ିବା ପାଣିର ଆୟତନ = 2.6 ଘନ ମି. = 2.6 × (100)³ ଘନ ମି. (∵ 1 ଘନ ମି. = (100)³ ଘ. ସେ.ମି. 

∴ ପୋଖରୀର ଜଳର ଗଭୀରତା 4 ମିଟର ।

(l) 40 ମିଟର ଦୈର୍ଘ୍ୟ, 16 ମିଟର ପ୍ରସ୍ଥ ଓ 2 ମିଟର ଗଭୀରତା ବିଶିଷ୍ଟ ଗୋଟିଏ ଖାତ ଖୋଳିଲେ ଖୋଳାଯାଇଥିବା ମାଟିର ଆୟତନ କେତେ ?
ସମାଧାନ: 
ମାଟିର ଦୈର୍ଘ୍ୟ (a) = 40 ମି., ପ୍ରସ୍ଥ (b) = 16 ମି. ଓ ଗଭୀରତା (c) = 2 ମି.
∴ ଖୋଳାଯାଇଥିବା ମାଟିର ଆୟତନ = abc = 40 ମି. × 16 ମି. × 2 ମି. = 1280 ଘନ ମି.

(m) P ଓ Q, √3 ସେ.ମି. ବାହୁ ବିଶିଷ୍ଟ ଏକ ସମଘନ ଉପରିସ୍ଥ ଯେକୌଣସି ଦୁଇଟି ବିନ୍ଦୁ ହେଲେ, PQ ଦୂରତାର ସର୍ବାଧିକ ମାନ କେତେ ?
ସମାଧାନ:
ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = √3 ସେ.ମି.
PQ ଦୂରତା = ସମଘନର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = √3a = √3 × √3 ସେ.ମି. = 3 ସେ.ମି. । 
PQ ଦୂରତାର ସର୍ବାଧିକ ମାନ 3 ସେ.ମି. ।

Question 2.
(a) ଗୋଟିଏ ଇଟାର ଦୈର୍ଘ୍ୟ, ପ୍ରସ୍ଥ ଓ ଉଚ୍ଚତା ଯଥାକ୍ରମେ 21 ସେ.ମି., 12 ସେ.ମି. ଓ 8 ସେ.ମି. ଅଟେ । 9 ମିଟର ଦୈର୍ଘ୍ୟ, 1 ମିଟର ଉଚ୍ଚତା ଓ 7 ମିଟର ପ୍ରସ୍ଥ ବିଶିଷ୍ଟ କାନ୍ଥ ନିର୍ମାଣ କରିବା ପାଇଁ କେତୋଟି ଇଟା ଲାଗିବ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ଇଟାର ଦୈର୍ଘ୍ୟ = 21 ସେ.ମି., ପ୍ରସ୍ଥ = 12 ସେ.ମି. ଓ ଉଚ୍ଚତା = 8 ସେ.ମି. ।
∴ ଇଟାର ଆୟତନ = ଦୈର୍ଘ୍ୟ x ପ୍ରସ୍ଥ x ଉଚ୍ଚତା = 21 ସେ.ମି. × 12 ସେ.ମି. × 8 ସେ.ମି. = 2016 ଘନ ସେ.ମି. ।
କାନ୍ଥର ଦୈର୍ଘ୍ୟ = 9 ମି. = 900 ସେ.ମି.; ପ୍ରସ୍ଥ = 1 ମି. = 100 ସେ.ମି., ଉଚ୍ଚତା = 7 ମି. = 700 ସେ.ମି.
କାନ୍ତର ଆୟତନ = ଦୈର୍ଘ୍ୟ × ପ୍ରସ୍ଥ × ଉଚ୍ଚତା
= 900 ସେ.ମି. × 100 ସେ.ମି. × 700ସେ.ମି. = 63000000 ଘନ ସେ.ମି. ।

∴ କାନ୍ଥ ନିର୍ମାଣ କରିବାପାଇଁ 31250 ଟି ଇଟା ଲାଗିବ ।

(b) ଗୋଟିଏ ସମଘନର ପ୍ରତ୍ୟେକ ବାହୁକୁ 50 ପ୍ରତିଶତ ବଢ଼ାଇଲେ ଏହାର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ କେତେ ପ୍ରତିଶତ ବଢ଼ିବ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ସମଘନର ପ୍ରତ୍ୟେକ ସମାନ ବାହୁର ଦୈର୍ଘ୍ୟ = x ଏକକ
ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 6x² ବର୍ଗ ଏକକ

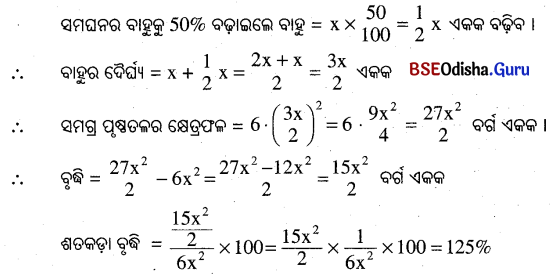
∴ ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 125% ବଢ଼ିବ ।

(c) 2 ମିଟର ଗଭୀର ଏବଂ 45 ମିଟର ପ୍ରସ୍ଥ ବିଶିଷ୍ଟ ନଦୀର ଜଳ ଘଣ୍ଟାକୁ 3 କି.ମି. ହିସାବରେ ପ୍ରବାହିତ ହେଉଛି । ପ୍ରତି ମିନିଟ୍‌ରେ ସମୁଦ୍ରକୁ ପ୍ରବାହିତ ହେଉଥ‌ିବା ଜଳର ପରିମାଣ ନିରୂପଣ କର । 
ସମାଧାନ: 
1 ଘଣ୍ଟାକୁ ପ୍ରବାହିତ ନଦୀଜଳର ଦୂରତା = 3 କି.ମି. = 3000 ମି.,
ମିନିଟ୍ ପ୍ରତି ନଦୀଜଳର ଦୂରତା = \(\frac{3000}{60}\) ମି. = 50 ମିଟର 
ନଦୀର ଲମ୍ବ = 50 ମି., ପ୍ରସ୍ଥ = 45 ମି. ଓ ଗଭୀରତା ବା ଉଚ୍ଚତା = 2 ମିଟର ।
ନଦୀରେ ଥ‌ିବା ଜଳର ଆୟତନ = ଦୈର୍ଘ୍ୟ × ପ୍ରସ୍ଥ × ଉଚ୍ଚତା = 50 ମି. × 45 ମି. × 2 ମି. = 4500 ମି.
ପ୍ରତି ମିନିଟ୍‌ରେ ସମୁଦ୍ରକୁ ପ୍ରବାହିତ ହେଉଥ‌ିବା ଜଳର ପରିମାଣ 4500 ଘନ ମିଟର ।

(d) 12 ମିଟର ଦୈର୍ଘ୍ୟ ଓ 8 ମିଟର ପ୍ରସ୍ଥ ବିଶିଷ୍ଟ ଗୋଟଏ ବେଦି ତିଆରି କରିବାକୁ ପ୍ରତି ଘନମିଟରକୁ 10 ଟଙ୍କା ହିସାବରେ 480 ଟଙ୍କା ଖର୍ଚ୍ଚ ହେଲା, ବେଦିର ଉଚ୍ଚତା ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ: 
ବେଦିର ଦୈର୍ଘ୍ୟ = 12 ମି. ଓ ପ୍ରସ୍ଥ = 8 ମି.

(e) (i) 1 ସେ.ମି. ବାହୁ ବିଶିଷ୍ଟ ସମଘନର କର୍ଣ୍ଣକୁ ବାହୁ ଭାବେ ନେଇ ଗଠିତ ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = l ସେ.ମି.
ସମଘନର କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = √3 × ବାହୁର ଦୈର୍ଘ୍ୟ = √3 × 1 ସେ.ମି. = √3 ସେ.ମି. । 
ଉତ୍ପନ୍ନ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = 3 ସେ.ମି. ।
∴ ଉତ୍ପନ୍ନ ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 6 × (ବାହୁ)² = 6 × (√3)² =18 ବର୍ଗ ସେ.ମି. ।

(ii) ଦତ୍ତ ସମଘନ ଓ ଉତ୍ପନ୍ନ ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ କେତେ ?
ସମାଧାନ:
ଦତ୍ତ ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 6 × (ବାହୁ)² = 6 × (1) = 6 ବର୍ଗ ସେ.ମି. । 
ଉତ୍ପନ୍ନ ସମଘନର ସମଗ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 18 ବର୍ଗ ସେ.ମି. ।
∴ ସେମାନଙ୍କର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳର ଅନୁପାତ = 6 : 18 = 1 : 3

Question 3.
ଗୋଟିଏ ଆୟତଘନର ଦୈର୍ଘ୍ୟ, ପ୍ରସ୍ଥ ଓ ଉଚ୍ଚତା ଯଥାକ୍ରମେ 12 ମିଟର, 8 ମିଟର ଓ 5 ମିଟର ହେଲେ
(i) ଏହାର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ
(ii) ଏହାର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ଏବଂ
(iii) ଆୟତନ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ଆୟତଘନର ଦୈର୍ଘ୍ୟ (a) = 12 ମିଟର, ପ୍ରସ୍ଥ (b) = 8 ମିଟର ଓ ଉଚ୍ଚତା (c) = 5 ମିଟର ।
(i) ଆୟତଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2 (ab + bc + ca) = 2 (12 × 8 + 8 × 5 + 5 × 12) 
= 2 (96 + 40 + 60) = 2 × 196 = 392 ବ. ମିଟର ।
(ii) ଆୟତଘନର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2(a + b) c = 2 × (12 +8) × 5 = 200 ବର୍ଗ ମିଟର ।
(iii) ଆୟତଘନର ଆୟତନ = a × b × c = 12 ମିଟର × 8 ମିଟର × 5 ମିଟର = 480 ବର୍ଗ ମିଟର ।

Question 4.
ଗୋଟିଏ ଆୟତଘନର ଦୈର୍ଘ୍ୟ, ପ୍ରସ୍ତର ଦୁଇଗୁଣ ଓ ଉଚ୍ଚତାର 3 ଗୁଣ । ଉଚ୍ଚତା 6 ସେ.ମି. ହେଲେ, ଏହାର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ଆୟତଘନର ଦୈର୍ଘ୍ୟ ପ୍ରସ୍ଥର ଦୁଇଗୁଣ ଓ ଉଚ୍ଚତାର 3 ଗୁଣ ।
ଉଚ୍ଚତା (c) = 6 ସେ.ମି., ଦୈର୍ଘ୍ୟ (a) = ଉଚ୍ଚତା × 3 = 6 × 3 = 18 ସେ.ମି.
ପ୍ରସ୍ଥ (b) = \(\frac{1}{2}\) (ଦୈର୍ଘ୍ୟ) = \(\frac{1}{2}\) × 18 = 9 ସେ.ମି. ।
ଆୟତଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2 (ab + bc + ca) = 2 (18 × 9 + 9 × 6 + 6 × 18)
= 2 (162 + 54 + 108) = 2 × 324 = 648 ବ. ସେ.ମି. ।

Question 5.
ଗୋଟିଏ ବନ୍ଦଥ‌ିବା ବାକ୍ସର ଦୈର୍ଘ୍ୟ, ପ୍ରସ୍ଥ ଓ ଉଚ୍ଚତା ଯଥାକ୍ରମେ 18 ସେ.ମି., 12 ସେ.ମି. ଓ 8 ସେ.ମି. ହେଲେ, ଏହାର ବାହାର ପାଖକୁ ରଙ୍ଗ କରିବାରେ ପ୍ରତି ବର୍ଗ ସେ.ମି.କୁ 50 ପଇସା ହିସାବରେ କେତେ ଖର୍ଚ୍ଚ ହେବ ?
ସମାଧାନ:
ବନ୍ଦ ଥିବା କାଠବାକ୍ସର ଦୈର୍ଘ୍ୟ (a) = 18 ସେ.ମି., ପ୍ରସ୍ଥ (b) = 12 ସେ.ମି. ଓ ଉଚ୍ଚତା (c) = 8 ସେ.ମି. ।
କାଠବାକ୍ସର ସମଗ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2 (ab + bc + ca) = 2 (18 × 12 + 12 × 8 + 8 × 18)
= 2 (216 + 96 + 144) ବ. ସେ.ମି.= 2 × 456 ବ. ସେ.ମି. = 912 ବ. ସେ.ମି. ।
1 ବର୍ଗ ସେ.ମି. ରଙ୍ଗ କରିବାକୁ ଖର୍ଚ୍ଚ ହୁଏ = 50 ପଇସା ବା \(\frac{1}{2}\) ଟଙ୍କା
912 ବର୍ଗ ସେ.ମି. ରଙ୍ଗ କରିବାକୁ ଖର୍ଚ୍ଚ ହୁଏ = \(\frac{1}{2}\) × 912 = 456 ଟଙ୍କା 
∴ ବନ୍ଦଥ‌ିବା ବାକ୍ସର ବାହାର ପାଖକୁ ରଙ୍ଗ କରିବା ପାଇଁ 456 ଟଙ୍କା ଖର୍ଚ୍ଚ ହୁଏ ।

Question 6.
ଏକ ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 264 ବର୍ଗ ମି. ହେଲେ, ଏହାର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ କେତେ ?
ସମାଧାନ:
ମନେକର ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = a ମି.
∴ ସମଘନର ସମଗ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 6a² ବ.ମି.
ପ୍ରଶ୍ବାନୁସାରେ 6a² = 264 ବ.ମି.
⇒ a² = \(\frac{264}{6}\) = 44
∴ ସମଘନର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 4a² = 4 × 44 = 176 ବର୍ଗ ମି.
∴ ସମଘନର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 176 ବର୍ଗ ମିଟର ।

Question 7.
ଗୋଟିଏ ସମଘନାକାର ଖୋଲା ପାଣିଟାଙ୍କିର ଭିତର ପାଖ ରଙ୍ଗ କରିବାରେ ପ୍ରତି ବର୍ଗ ସେ.ମି.କୁ 50 ପଇସା ହିସାବରେ 90 ଟଙ୍କା ଖର୍ଚ୍ଚ ହେଲା । ପାଣି ଟାଙ୍କିର ଭିତର ପାଖର ଉଚ୍ଚତା କେତେ ?
ସମାଧାନ: 
ବର୍ଗ ସେ.ମି.କୁ 50 ପଇସା ବା \(\frac{1}{2}\) ଟଙ୍କା ଖର୍ଚ୍ଚ ହେଲେ 90 ଟଙ୍କା ଖର୍ଚ୍ଚ ହେବ = \(\frac{90}{1/2}\) = 180 ବର୍ଗ ସେ.ମି.କୁ ।
ଅର୍ଥାତ୍ ସମଘନାକାର ଖୋଲା ପାଣିଟାଙ୍କିର ଭିତର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 180 ବର୍ଗ ସେ.ମି.
ମନେକର ସମଘନାକାର ଖୋଲା ପାଣିଟାଙ୍କିର ବାହୁର ଦୈର୍ଘ୍ୟ = a ସେ.ମି. ।
ମନେକର ପାଣିଟାଙ୍କିର ଉପର ଖୋଲା ହେତୁ ଏହାର ପାଞ୍ଚଗୋଟି ପୃଷ୍ଠତଳ ଅଛି । 
ଏହି ପାଞ୍ଚଗୋଟି ତଳର କ୍ଷେତ୍ରଫଳ = 5a² ବର୍ଗ ସେ.ମି. ।
ପ୍ରଶ୍ବାନୁସାରେ,  5a² = 180 ⇒ a² = \(\frac{180}{5}\) = 36
⇒ a = √36 = 6 ସେ.ମି.
∴ ପାଣିଟାଙ୍କିର ଭିତର ପାର୍ଶ୍ଵର ଉଚ୍ଚତା 6 ସେ.ମି. ।

Question 8.
ଗୋଟିଏ ଆୟତଘନର ଦୈର୍ଘ୍ୟ, ପ୍ରସ୍ଥ ଓ ଉଚ୍ଚତାର ଅନୁପାତ 6 : 5 : 4 ଏବଂ ଏହାର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 5328 ବର୍ଗ ମି. ହେଲେ, ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ଏବଂ ଆୟତନ କେତେ ?
ସମାଧାନ:
ମନେକର ଆୟତଘନର ଦୈର୍ଘ୍ୟ (a) = 6x ମି., ପ୍ରସ୍ଥ (b) = 5x ମି. ଓ ଉଚ୍ଚତା (c) = 4x ମି.
∴ ଆୟତଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2 (ab + bc + ca) =  2 (6x × 5x + 5x × 4x + 4x × 6x)
= 2 (30x² + 20x² + 24x²) = 2 × 74x² = 148 x²
ପ୍ରଶ୍ନନୁସାରେ 148x² = 5328 ବ. ମିଟର = x² = \(\frac{5328}{148}\) = 36 ⇒ x = 6 ମିଟର
∴ ଆୟତଘନର ଦୈର୍ଘ୍ୟ (a) = 6 × 6 = 36 ମି., ପ୍ରସ୍ଥ (b) = 5 × 6 = 30 ମି., ଓ ଉଚ୍ଚତା (c) = 4 × 6 = 24 ମି.
∴ ଆୟତଘନର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2c (a + b) = 2 x 24 (36 + 30)
= 48 x 66 = 3168 ବ. ମି.
ଆୟତଘନର ଘନଫଳ = a × b × c = 36 ମି. × 30 ମି. × 24 ମି. = 25,920 ଘନ ମି. ।
∴ ଆୟତଘନର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 3168 ବର୍ଗ ମି. ଓ ଘନଫଳ 25,920 ଘନ ମି. ।

Question 9.
ଗୋଟିଏ ଆୟତଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 1168 ବର୍ଗ ମିଟର, ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 720 ବର୍ଗ ମିଟର ଏବଂ ଉଚ୍ଚତା 12 ମି. ହେଲେ, ଦୈର୍ଘ୍ୟ ଓ ପ୍ରସ୍ଥ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଆୟତଘନର ଦୈର୍ଘ୍ୟ = a ମି., ପ୍ରସ୍ଥ = b ମି. ଓ ଉଚ୍ଚତା (c) = 12 ମି.
ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 1168 ବ.ମି. ଓ ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 720 ବ.ମି. ।
∴ ଆୟତଘନର ପାର୍ଶ୍ଵପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2c (a + b) = 2 × 12 (a + b) = 24 (a + b) ବ.ମି.
ପ୍ରଶ୍ବାନୁସାରେ, 24 (a + b) = 720 ବର୍ଗ ମି.
⇒ a + b = \(\frac{720}{24}\) = 30
∴ a + b = 30 … (i)
ଆୟତଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2 (ab + bc + ca) = 2ab + 2c (a + b)
ପ୍ରଶ୍ବାନୁସାରେ, 2ab + 2c (a + b) = 1168 ବ. ମିଟର ⇒ 2ab + 720 = 1168
⇒ 2ab = 1168 – 720
⇒ 2ab = 448
⇒ ab = \(\frac{448}{2}\) = 224
∴ ଆମେକାଣୁ (a – b)² = (a + b)² – 4ab = (30)² – 4 × 224 = 900 – 896 = 4
⇒ a – b = 2 … (ii)
a = \(\frac{({a}+{b})+({a}-{b})}{2}\) = \(\frac{30+2}{2}\) = \(\frac{32}{2}\) = 16 ଓ b = 30 – b = 30 – 16 = 14
∴ ଆୟତଘନର ଦୈର୍ଘ୍ୟ 16 ସେ.ମି., ଓ ପ୍ରସ୍ଥ 14 ସେ.ମି. ।

Question 10.
ଗୋଟିଏ ଆୟତଘନାକାର ପାଣିକୁଣ୍ଡର ଭିତର ପାଖର ଦୈର୍ଘ୍ୟ 10 ମି., ପ୍ରସ୍ଥ 8 ମି. ଏବଂ ଗଭୀରତା 3 ମି. ହେଲେ, ଏହାର ଭିତର ପାଖରେ ସିମେଣ୍ଟ ଦେବା ଖର୍ଜ ବର୍ଗ ମିଟରକୁ ଟ. 2.50 ଦରରେ କେତେ ଖର୍ଚ୍ଚ ହେବ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ଆୟତଘନାକାର ପାଣିକୁଣ୍ଡର ଭିତରପାଖର ଦୈର୍ଘ୍ୟ (a) = 10 ମି., ପ୍ରସ୍ଥ (b) = 8 ମି. ଓ ଗଭୀରତା (c) = 3 ମି. 
∴ ଆୟତଘନର ପାଣିଟାଙ୍କିରେ ସିମେଣ୍ଟ ଦିଆଯାଉଥିବା ଅଂଶର କ୍ଷେତ୍ରଫଳ = ପାର୍ଶ୍ଵ ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ + ଭୂମିର କ୍ଷେତ୍ରଫଳ
= 2c (a + b) + ab = 2 × 3 (10 + 8) + 10 × 8 = 108 + 80 = 188 ବର୍ଗ ମି. ।
1 ବର୍ଗ ମିଟରକୁ ଖର୍ଚ୍ଚ ହୁଏ = 2.50 ପଇସା
188 ବର୍ଗ ମିଟରକୁ ଖର୍ଚ୍ଚ ହୁଏ = 2.50 × 188 = 470 ଟଙ୍କା  ।
∴ ଆୟତ ଘନାକାର ପାଣିକୁଣ୍ଡର ଭିତର ପାଖରେ ସିମେଣ୍ଟ ଦେବାପାଇଁ 470 ଟଙ୍କା ଖର୍ଚ୍ଚ ହେବ ।

Question 11.
ଗୋଟିଏ ଆୟତଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 700 ବର୍ଗ ସେ.ମି., ଏହାର ଦୈର୍ଘ୍ୟ ପ୍ରସ୍ଥର ଦୁଇଗୁଣ ଓ ଉଚ୍ଚତା ପ୍ରସ୍ଥର ଅର୍ଦ୍ଧେକ ହେଲେ ଆୟତଘନର ଘନଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଆୟତଘନର ପ୍ରସ୍ଥ (b) = x ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, ଦୈର୍ଘ୍ୟ (a) = 2x ସେ.ମି. ଓ ଉଚ୍ଚତା (c) = \(\frac{x}{2}\) ସେ.ମି. ।
ଆୟତଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2(ab + bc + ca)

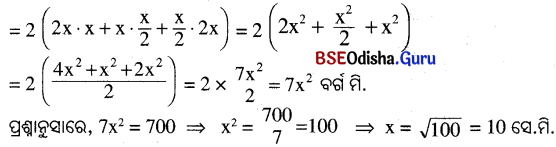
∴ ପ୍ରସ୍ଥ = x = 10 ସେ.ମି., ଦୈର୍ଘ୍ୟ = 2x = 2 × 10 = 20 ସେ.ମି. ଓ ଉଚ୍ଚତା = \(\frac{x}{2}\) = \(\frac{10}{2}\) 5 ସେ.ମି. ।
∴ ଆୟତଘନର ଘନଫଳ = abc = 20 ସେ.ମି. × 10 ସେ.ମି. × 5 ସେ.ମି. = 1000 ଘନ ମି. ।
∴ ଆୟତଘନର ଘନଫଳ = 1000 ଘନ ମି. ।

ବିକଳ୍ପ ସମାଧାନ:
ମନେକର ପ୍ରସ୍ଥ = 2x ସେ.ମି. ।
∴ ଉଚ୍ଚତା = x ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ ଦୈର୍ଘ୍ୟ = 4x ସେ.ମି.
ପ୍ରଶ୍ନନୁସାରେ 700 = 2 (4x · 2x + 2x . x + 4x . x) = 700 = 28x²
⇒ x² = 25
⇒ x = 5
ଦୈର୍ଘ୍ୟ = 20 ସେ.ମି., ପ୍ରସ୍ଥ = 10 ସେ.ମି. ଏବଂ ଉଚ୍ଚତା = 5 ସେ.ମି. 
ଘନଫଳ = (20 × 10 × 5) ଘ.ସେ.ମି. = 1000 ଘ.ସେ.ମି.

Question 12.
ଗୋଟିଏ ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ଅନ୍ୟ ଦୁଇଟି ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳର ସମଷ୍ଟି ସଙ୍ଗେ ସମାନ । ଯଦି ଏହି ଦୁଇ ସମଘନର ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 24 ମି. ଓ 32 ମି. ହୁଏ ତେବେ ପ୍ରଥମ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ଦ୍ବିତୀୟ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = a = 24 ମି.
∴ ଦ୍ଵିତୀୟ ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 6 × 24²
ତୃତୀୟ ସମଘନର ବାହୁ = 32 ମି.
∴ ତୃତୀୟ ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 6 × 32²
∴ ଦ୍ବିତୀୟ ଓ ତୃତୀୟ ସମଗ୍ରପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ସମଷ୍ଟି
= 6 × 24² + 6 × 32² = 6 (24² + 32²) ବର୍ଗ ମି. ।
ମନେକର ପ୍ରଥମ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ a ମି. ।
ପ୍ରଥମ ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 6a² ବର୍ଗ ମି.
ପ୍ରଶ୍ବାନୁସାରେ, 6a² = 6 (24² + 32²)
⇒ a² = 24² + 32²
⇒ a² = 576 + 1024
⇒ a² = 1600
⇒ a = √1600 = 40 ମି.
∴ ପ୍ରଥମ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ 40 ମି.

Question 13.
ଦୁଇଟି ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳର ଅନ୍ତର 1050 ବର୍ଗ ସେ.ମି. । ସମଘନ ଦ୍ଵୟର ବାହୁର ଦୈର୍ଘ୍ୟର ଅନୁପାତ 4 : 3 ହେଲେ, ପ୍ରତ୍ୟେକ ବାହୁର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ପ୍ରଥମ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = 4x ସେ.ମି. ଓ ଦ୍ୱିତୀୟ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = 3x ସେ.ମି. ।
ପ୍ରଥମ ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 6 × (4x)² ବ.ସେ.ମି. ।
ଓ ଦ୍ବିତୀୟ ସମଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 6 × (3x)² ବ. ସେ.ମି. । 
ପ୍ରଶ୍ନନୁସାରେ, 6 x (4x)² – 6 × (3x)² = 1050
⇒ 6 (16x² – 9x²) =1050
⇒ 7x² = \(\frac{1050}{6}\)
⇒ 7x² = 175
⇒ x² = \(\frac{175}{7}\) = 25
⇒ x = √25 = 5
ପ୍ରଥମ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = 4x = 4 × 5 = 20 ସେ.ମି. ।
ଦ୍ବିତୀୟ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = 3x = 3 × 5 = 15 ସେ.ମି. ।
∴ ସମଘନଦ୍ବୟର ବାହୁର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 20 ସେ.ମି. ଓ 15 ସେ.ମି. ।

Question 14.
ଗୋଟିଏ ଆୟତଘନର ଦୈର୍ଘ୍ୟ, ପ୍ରସ୍ଥ ଓ ଉଚ୍ଚତାର ଅନୁପାତ 6 : 5 : 4 ଏବଂ ଏହାର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 33300 ବର୍ଗ ସେ.ମି. ହେଲେ, ଏହାର ଘନଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଆୟତଘନର ଦୈର୍ଘ୍ୟ (a) = 6x ସେ.ମି., ପ୍ରସ୍ଥ (b) = 5x ସେ.ମି. ଓ ଉଚ୍ଚତା (c) = 4x ସେ.ମି.
∴ ଆୟତଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ = 2 (ab + bc + ca) =  2 (6x . 5x + 5x . 4x + 4x . 6x)
= 2 (30x² + 20x² + 24x²) = 2 × 74x² = 148x² ବର୍ଗ ସେ.ମି. ।
ପ୍ରଶ୍ବାନୁସାରେ, 148x² = 33300
⇒ x² = \(\frac{33300}{148}\) = 225
⇒ x = √225 = 15 ସେ.ମି.
∴ ଆୟତଘନର ଦୈର୍ଘ୍ୟ = 6x = 6 × 15 = 90 ସେ.ମି., ପ୍ରସ୍ଥ = 5x = 5 × 15 = 75 ସେ.ମି.
ଓ ଉଚ୍ଚତା = 4x = 4 × 15 = 60 ସେ.ମି.
∴ ଆୟତଘନର ଘନଫଳ = a × b × c
= 90 ସେ.ମି. × 75ସେ.ମି. × 60 ସେ.ମି. = 405000 ଘନ ସେ.ମି. ।

Question 15.
20 ମିଟର ଦୈର୍ଘ୍ୟ, 16 ମିଟର ପ୍ରସ୍ଥ ଓ 12 ମିଟର ଉଚ୍ଚତା ବିଶିଷ୍ଟ ଏକ କୋଠରୀରେ ରଖାଯାଇଥ‌ିବା ଦୀର୍ଘତମ ଲୁହାଛଡ଼ର ଦୈର୍ଘ୍ୟ କେତେ ?
ସମାଧାନ:
କୋଠରୀର ଦୈର୍ଘ୍ୟ (l) = 20 ମି., ପ୍ରସ୍ଥ (b) = 16 ମି. ଓ ଉଚ୍ଚତା (c) = 6 ସେ.ମି.

କୋଠରୀରେ ରଖାଯାଇଥ‌ିବା ଲୁହାଛଡ଼ର ଦୈର୍ଘ୍ୟ 20√2 ମିଟର ।

Question 16.
ଗୋଟିଏ ଆୟତଘନର ଦୈର୍ଘ୍ୟ, ପ୍ରସ୍ଥ ଓ ଉଚ୍ଚତାର ସମଷ୍ଟି 19 ସେ.ମି. ଏବଂ ଏହାର କର୍ଷ 5√5 ସେ.ମି. ହେଲେ, ଏହାର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
ମନେକର ଆୟତଘନର ଦୈର୍ଘ୍ୟ = a ସେ.ମି., ପ୍ରସ୍ଥ = b ସେ.ମି., ଉଚ୍ଚତା =  c ସେ.ମି. ।
ପ୍ରଶ୍ବାନୁସାରେ, a + b + c = 19 ସେ.ମି. ଓ କର୍ଣ୍ଣର ଦୈର୍ଘ୍ୟ = 5√5 ସେ.ମି.

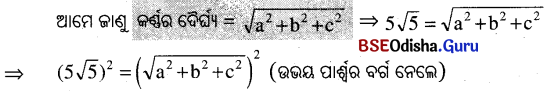
⇒ a² + b² + c² = 125 (a + b + c)² – 2 (ab + bc + ca) = 125
⇒ 19² – 2 (ab + bc + ca) = 125
⇒ 2 (ab + bc + ca) = 361 – 125 = 236
∴ ଆୟତଘନର ସମଗ୍ର ପୃଷ୍ଠତଳର କ୍ଷେତ୍ରଫଳ 236 ବର୍ଗ ସେ.ମି. । 

Question 17.
ଦୁଇଟି ସମଘନର ଘନଫଳର ସମଷ୍ଟି 5824 ଘନ ସେ.ମି. । ସେମାନଙ୍କର ବାହୁଦ୍ୱୟର ଦୈର୍ଘ୍ୟର ଅନୁପାତ 3 : 4 ହେଲେ ପ୍ରତ୍ୟେକର ବାହୁର ଦୈର୍ଘ୍ୟ ସ୍ଥିର କର ।
ସମାଧାନ:
ମନେକର 1ମ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = 3x ସେ.ମି. ଓ 2ୟ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = 4x ସେ.ମି. ।
1ମ ସମଘନର ଘନଫଳ = (3x)³ ଘ. ସେ.ମି. ଓ ଦ୍ୱିତୀୟ ସମଘନର ଘନଫଳ = (4x)³ ଘ. ସେ.ମି. ।
ପ୍ରଶ୍ନନୁସାରେ, (3x)³ + (4x)³ = 5824 
⇒ 27x³ + 64x³ = 5824
⇒ 91x³ = 5824
⇒ x³ = \(\frac{5824}{91}\) = 64
⇒ x = \(\sqrt[3]{64}\) = 4 ସେ.ମି.
∴ 1ମ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = 3x = 3 × 4 = 12 ସେ.ମି.
ଓ ଦ୍ୱିତୀୟ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = 4x = 4 × 4 = 16 ସେ.ମି. । 
∴ ସମଘନ ଦୁଇଟିର ବାହୁର ଦୈର୍ଘ୍ୟ ଯଥାକ୍ରମେ 12 ସେ.ମି. ଓ 16 ସେ.ମି. ।

Question 18.
ତିନୋଟି ସମଘନର ଭୂମିର କ୍ଷେତ୍ରଫଳ ଯଥାକ୍ରମେ 9 ବ. ମି., 16 ବ. ମି. ଓ 25 ବ. ମି. । ଏହି ସମଘନତ୍ରୟର ଘନଫଳର ସମଷ୍ଟି ସଙ୍ଗେ ସମାନ ଘନଫଳ ବିଶିଷ୍ଟ ଅନ୍ୟ ଏକ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ ନିର୍ଣ୍ଣୟ କର ।
ସମାଧାନ:
1ମ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = √9 ମି. = 3 ମି., 2ୟ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = √16 ମି. = 4 ମି.
ଓ 3ୟ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = √25 = 5 ମି. ।
ସମଘନ ତ୍ରୟର ଘନଫଳର ସମଷ୍ଟି = (3)³ + (4)³ + (5)³ ଘ.ମି. 
= (27 + 64 + 125) ଘ.ମି.  = 216 ଘ.ମି. ।
ନୂତନ ସମଘନର ଘନଫଳ = 216 ଘ.ମି.
∴ ନୂତନ ସମଘନର ବାହୁର ଦୈର୍ଘ୍ୟ = \(\sqrt[3]{216}\) ମି. = 6 ମି.