BSE Odisha 9th Class Maths Solutions Geometry Chapter 6 ଅଙ୍କନ Ex 6(k)

Odisha State Board BSE Odisha 9th Class Maths Solutions Geometry Chapter 6 ଅଙ୍କନ Ex 6(k) Textbook Exercise Questions and Answers.

BSE Odisha Class 9 Maths Solutions Geometry Chapter 6 ଅଙ୍କନ Ex 6(k)

Question 1.
11 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ AB ରେଖାଖଣ୍ଡ ଟାଣି ତାକୁ 5ଟି ସର୍ବସମ ଅଂଶରେ ବିଭକ୍ତ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :

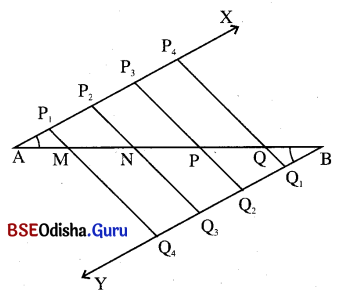
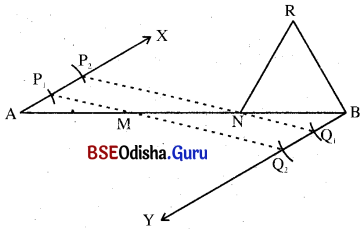
(a) 11 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ A͞B ର A ଓ B ବିନ୍ଦୁରେ ଦୁଇଟି ସମାନ ପରିମାଣ ବିଶିଷ୍ଟ କୋଣ ଯଥାକ୍ରମେ ∠XAB ଏବଂ ∠YBA ଅଙ୍କନ କର ।
(b) \(\overrightarrow{\mathrm{AX}}\) ରୁ A ଠାରୁ ଆରମ୍ଭକରି ଚାରିଗୋଟି ସର୍ବସମ ଅଂଶ ଏବଂ ସେହିପରି \(\overrightarrow{\mathrm{BY}}\) ରୁ B ଠାରୁ ଆରମ୍ଭକରି ପୂର୍ବ ଅଂଶ ସହ ସମାନ କରି ଚାରିଗୋଟି ସର୍ବସମ ଅଂଶରେ ବିଭକ୍ତ କର ।
ଏଠାରେ AP₁ = P₁P₂ = P₂P₃ = P₃P₄ = BQ₁ = Q₁Q₂ = Q₂Q₃ = Q₃Q₄ ହେବ ।
(c) ବର୍ତ୍ତମାନ P₁Q₄, P₂Q₃, P₃Q₂ ଏବଂ P₄Q₁ ଅଙ୍କନ କର । ଯାହାଦ୍ୱାରା A͞B ରେଖାଖଣ୍ଡଟି ପାଞ୍ଚଗୋଟି ସର୍ବସମ ଅଂଶରେ ବିଭକ୍ତ ହେଲା ।

Question 2.
10 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ A͞B ରେଖାଖଣ୍ଡ ଟାଣି X ବିନ୍ଦୁରେ ଏପରି ଭାବେ ଦୁଇଖଣ୍ଡ କର ଯେପରିକି AX = 2BX ହେବ ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :

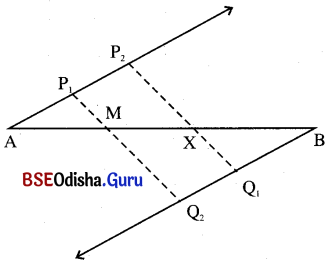
(a) 10 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ABକୁ ସମାନ ତିନି ସର୍ବସମ ଅଂଶରେ ବିଭକ୍ତ କର ।
(b) P₁Q₂ ଏବଂ P₂Q₁ ଅଙ୍କନ କରି M ଓ X କୁ AB ଉପରେ ଚିହ୍ନଟ କର ।
(c) ବର୍ତ୍ତମାନ AX = 2 BX ।

Question 3.
8 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ ଏକ ରେଖାଖଣ୍ଡ AB ଅଙ୍କନ କରି ଏହା ଉପରେ C ବିନ୍ଦୁ ଚିହ୍ନଟ କର ଯେପରିକି, AC : CB = 2 : 1 ହେବ ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :

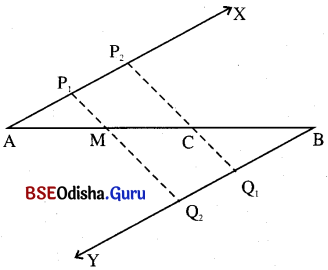
(a) 8 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ A͞B କୁ ତିନୋଟି ସର୍ବସମ ଅଂଶରେ ବିଭକ୍ତ କର ।
(b) A͞B ଉପରେ M ଓ C ବିନ୍ଦୁ ଚିହ୍ନଟ କର ।
(c) ବର୍ତ୍ତମାନ AC : BC = 2 : 1 ।

Question 4.
12.5 ସେ.ମି. ପରିସୀମା ବିଶିଷ୍ଟ ଏକ ତ୍ରିଭୁଜ ଅଙ୍କନ କର ଯାହାର ବାହୁମାନଙ୍କର ଦୈର୍ଘ୍ୟର ଅନୁପାତ 2 : 3 : 4 ହେବ ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :

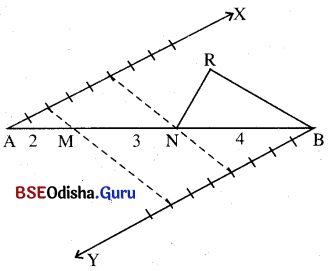
(a) 12.5 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ AB ଅଙ୍କନ କରି ଏହାକୁ 9 ସମାନ ଭାଗରେ ବିଭକ୍ତ କର ।
(b) ଆବଶ୍ୟକ ଭାଗକୁ ନିରୀକ୍ଷଣ କରି M ଓ N ବିନ୍ଦୁକୁ AB ଉପରେ ଚିହ୍ନଟ କର ।
(c) Δ RNB ଅଙ୍କନ କର ଯାହାର ବାହୁତ୍ରୟର ଦୈର୍ଘ୍ୟ NB, NR ଏବଂ RB ହେବ ।
(d) Δ RNB ସମ୍ପୂର୍ଣ କର । (ଏଠାରେ AM = BR ଓ MN = NR)

Question 5.
ଗୋଟିଏ ସମବାହୁ ତ୍ରିଭୁଜ ଅଙ୍କନ କର ଯାହାର ପରିସୀମା 13.5 ସେମି. ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :

(a) 13.5 ସେ.ମି. ଦୈର୍ଘ୍ୟ ବିଶିଷ୍ଟ AB ଅଙ୍କନ କର ।
(b) AB କୁ ତିନୋଟି ସର୍ବସମ ଅଂଶରେ ବିଭକ୍ତ କର ।
(c) AB ଉପରିସ୍ଥ M ଓ N ବିନ୍ଦୁ ଚିହ୍ନଟ କର ।
(d) Δ RNB ସମବାହୁ ତ୍ରିଭୁଜ ଅଙ୍କନ କର ଯାହାର ବାହୁର ଦୈର୍ଘ୍ୟ NB ହେବ ।

Question 6.
9 ସେ.ମି. ରେଖାଖଣ୍ଡ ଅଙ୍କନ କରି ଏହି ରେଖାଖଣ୍ଡରେ 3 ସେ.ମି.କୁ ଏକ ଏକକ ନେଇ 2\(\frac{1}{3}\), 2√2, 2 + \(\frac{\sqrt{3}}{2}\) ସଂଖ୍ୟାଗୁଡ଼ିକ କେଉଁ ବିନ୍ଦୁଦ୍ୱାରା ସୂଚିତ ସେଗୁଡ଼ିକୁ ନିରୂପଣ କର ।
ସମାଧାନ:
ଅଙ୍କନ ପ୍ରଣାଳୀ :

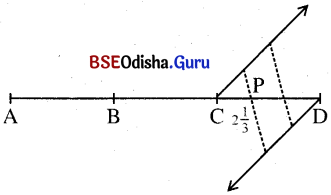
(a) A͞D ଅଙ୍କନ କର ଯାହାର ଦୈର୍ଘ୍ୟ 9 ସେ.ମି. ।
(b) AD ଉପରେ B ଓ C ବିନ୍ଦୁ ନିଅ ଯେପରିକି AB = BC = CD = 3 ସେ.ମି. ।
(c) CD କୁ ସମତ୍ରିଖଣ୍ଡ କରି P ବିନ୍ଦୁ ନିର୍ଣ୍ଣୟ କର । ଏଠାରେ P ବିନ୍ଦୁର ସ୍ଥାନାଙ୍କ 2\(\frac{1}{3}\) ।
(d) C ବିନ୍ଦୁରେ CR ଲମ୍ବ ଅଙ୍କନ କର ଯେପରିକି AC = CR ହେବ ।
(e) AR ବ୍ୟାସାର୍ଦ୍ଧ ପରିମିତ ଚାପ A͞D କୁ E ବିନ୍ଦୁରେ ଛେଦ କରୁ । ଏଠାରେ E ବିନ୍ଦୁରେ ସ୍ଥାନାଙ୍କ 2√2 ହେବ ।

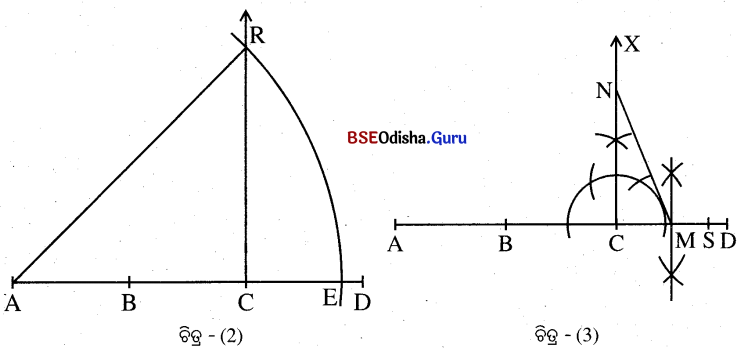
(f) C ବିନ୍ଦୁରେ \(\overrightarrow{\mathrm{CX}}\) ଲମ୍ବ ଅଙ୍କନ କର ।
(g) CD ର ମଧ୍ୟବିନ୍ଦୁ M ସ୍ଥିର କରି Δ CNM ଅଙ୍କନ କର ଯାହାର MN = CD (1 ଏକକ) ଏବଂ CM = \(\frac{1}{2}\) ଏକକ ହେବ ।
(h) CD ଉପରେ S ବିନ୍ଦୁ ଚିହ୍ନଟି କର ଯେପରିକି CN = CS ହେବ ।
(i) S ବିନ୍ଦୁଟି 2 + \(\frac{\sqrt{3}}{2}\) ଏକକର ସୂଚକ ବିନ୍ଦୁ ହେବ ।