Class 7

Odisha State Board BSE Odisha 7th Class Sanskrit Solutions Chapter 6 ପୂରଣବାଚକଶବ୍ଦାଃ Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Sanskrit Solutions Chapter 6 ପୂରଣବାଚକଶବ୍ଦାଃ

४. शून्यस्थानं पूरयतु
(ଶୂନ୍ୟସ୍ଥାନଂ ପୂରୟତୁ) ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର :

(क) ______ बालकः ।

(କ) _______ବାଳକଃ ।

उत्तर :
(क) चतुर्थः बालकः ।
(କ) ଚତୁର୍ଥୀ ବାଳକଃ ।

(ख) ________ शुकः ।

(ଖ) _______ ଶୁକଃ ।

उत्तर :
(ख) नवमः शुकः ।
(ଖ) ନବମଃ ଶୁକଃ ।

(ग) ________ बालिका: ।

(ଗ) _____ ବାଳିକା ।

उत्तर :
(ग) सप्तमी बालिका ।
(ଗ) ସପ୍ତମୀ ବାଳିକା ।

(घ) _______ माला ।

(ଘ) _________ ମାଳା

उत्तर :
(घ) तृतीया माला ।
(ଘ) ତୃତୀୟା ମାଳା।

२. किं समीचीनम् (✓) किम् असमीचीनम् (✗)
କିଂ ସମୀଚୀନମ୍ (✓) ଅସମୀଚୀନମ୍ (✗) କେଉଁଟି ଠିକ୍ କେଉଁଟି ଭୁଲ୍

यथा
(क) प्रथमा फलम् [ ]
(ख) पञ्चमी बालिका [ ]
(ग) पञ्चमः बालिका [ ]
(घ) द्वितीयं पुष्पम् [ ]
(ङ) द्वितीय: पुष्पम् [ ]
(च) चतुर्थः मार्जार: [ ]
(छ) तृतीया लता [ ]
(ज) चतुर्थं मार्जारः [ ]
(झ) तृतीयः लता [ ]
(ज) प्रथमं फलम् [ ]
उत्तर :
(क) प्रथमा फलम् [✗]
(ख) पञ्चमी बालिका [✓]
(ग) पञ्चमः बालिका [✗]
(घ) द्वितीयं पुष्पम् [✓]
(ङ) द्वितीय: पुष्पम् [✗]
(च) चतुर्थः मार्जार: [✓]
(छ) तृतीया लता [✓]
(ज) चतुर्थं मार्जारः [✗]
(झ) तृतीयः लता [✗]
(ज) प्रथमं फलम् [✓]

३. स्तम्भं योजयतु
(ସ୍ତମଂ ଯୋଜୟତୁ) ସ୍ତମ୍ଭ ମିଳନ କର:

पश्रम:	यानम्
सप्तमी	बालक:
दशमम्	भाषा
द्वितीया	स्थानम्
तृतीयम्	कक्षा

उत्तर :

अतिरिक्त प्रश्नोत्तरम्
(ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातृभाषया अनुवादं कुरुत ।

(क) रवि : प्रथमः सोमः द्वितीयः ।
उत्तर :
ରବିବାର ପ୍ରଥମ ସୋମବାର ଦ୍ଵିତୀୟ।

(ख) स एव छात्रोत्तमः ।
उत्तर :
ସେ ହିଁ ଉତ୍ତମ ଛାତ୍ର ।

(ग) एवं क्रमेण सप्ताहः वारक्रमः ।
उत्तर :
ଏହିପରି ସପ୍ତାହର ବାରକ୍ରମ।

(घ) छात्र सुखी परिश्रमी ।
उत्तर :
ଛାତ୍ର ସୁଖୀ ପରିଶ୍ରମୀ।

(ङ) विभक्तिगणनं जानाति क्रमशः ।
उत्तर :
କ୍ରମେ ବିଭକ୍ତି ଗଣନା ଜାଣେ ।

२. एकपदेन उत्तरं लिखत ।

(क) प्रथमं श्रवणं द्वितीयं किम् ?
उत्तर :
ମନନମ୍

(ख) द्वितीयं मननं तृतीयं किम् ?
उत्तर :
ସ୍ମରଣମ୍

(ग) तृतीयं स्मरणं चतुर्थं किम् ?
उत्तर :
ଭାଷଣମ୍

(घ) पंचमं पठनं षष्ठं किम् ?
उत्तर :
ଲେଖନମ୍

(ङ) षष्ठं लेखनं सप्तमं किम् ?
उत्तर :
ଗାୟନମ୍

३. शून्यस्थानं पूरयत ।

(क) नवमं ______ दशमं कीर्त्तनम् ।
उत्तर :
ନର୍ଭନମ୍

(ख) भाषाप्रशिक्षणं सामान्यं _____।
उत्तर :
ସୋପାନମ୍

(ग) प्रथमं ______ द्वितीयं मननम् ।
उत्तर :
ଶ୍ରବଣମ୍

(घ) अष्टमं ______
उत्तर :
ବୋଧନମ୍

ङ ______ सामान्यं सोपानम्।
उत्तर :
ଭାଷା ପ୍ରଶିକ୍ଷଣମ୍

४. विक्षिप्तवर्णाना मेलनेन शुद्धपदं रचयत ।

(क) ष्ट अम्न।
उत्तर :
ଅଷ୍ଟମମ୍

(ख) प्रमः थ।
उत्तर :
ପ୍ରଥମଃ

(ग) पासो म्म ।
उत्तर :
ସୋପାନମ୍

(घ) या द्विती।
उत्तर :
ଦ୍ଵିତୀୟା

(ङ) मी प
उत्तर :
ପଞ୍ଚମୀ

५. स्तम्भमेलनं’ कुरूत ।

उत्तर :

६. मातृभाषया अर्थं लिखत ।

(क) मननम्
उत्तर :
ମନନକରିବା

(ख) सोपानम्
उत्तर :
ପାହାଚ

(ग) वोधनम्
उत्तर :
ବୋଧନ

(घ) माला
उत्तर :
ମାଳ

(ङ) शुकः
उत्तर :
ଶୁଆ

७. उत्तर चयनं कुरूत ।

(क) भौमवार:
(a) सोमवार :
(b) मंगलवार
(c) बुधवार
(d) गुरुवारः
उत्तर :
(b) मंगलवार

(ख) कः षष्ठवार ?
(a) वुधवार :
(b ) भौमवार
(c) शुक्रवार :
(d) रविवार :
उत्तर :
(c) शुक्रवार :

(ग) कः विभक्तिगणना जानाति ?
(a) परिश्रमी
(b) दृष्ट:
(c) सुखी
(d) सुखी परिश्रमी
उत्तर :
(d) ସୁଖୀ ପରିଶ୍ରମୀ

(घ) प्रथमं किम् ?
(a) पठनम्
(b) श्रवणम्
(c) लेखनम्
(d) मननम्
उत्तर :
(b) श्रवणम्

(ङ) भाषा प्रशिक्षणश्च नवमं स्थानं किम् ?
(a) कीर्त्तनम्
(b) नर्त्तनम्
(c) गायनम्
(d ) श्रवणम्-
उत्तर :
(b) नर्त्तनम्

८. संशोधन कुरूत ।

(क) तृतीय स्थानम् ।
उत्तर :
ତୃତୀୟଂ ସ୍ଥାନମ୍ ।

(ख) चतुर्थं मार्जारः ।
उत्तर :
ଚତୁର୍ଥୀ ମାର୍ଜାରଃ ।

(ग) तृतीय : लता ।
उत्तर :
ତୃତୀୟା ଲତା।

(घ) सप्तमी वालकः ।
उत्तर :
ସପ୍ତମଃ ବାଳକଃ ।

(ङ) प्रथमा फलम् ।
उत्तर :
ପ୍ରଥମଂ ଫଳମ୍ ।

पूरणवाचकशब्दाः
ପୂରଣବାଚକଶବ୍ଦ (ପୂରଣବାଚକ ଶବ୍ଦ)

१. प्रथमः बालक:

ପ୍ରଥମଃ ବାଳକଃ ( ପ୍ରଥମ ବାଳକ)

द्वितीय: बालक:

ଦ୍ଵିତୀୟ ବାଳକଃ (ଦ୍ଵିତୀୟ ବାଳକ)

तृतीय: बालक:

ତୃତୀୟ ବାଳକ (ତୃତୀୟ ବାଳକ)

चतुर्थः बालक:

ଚତୁର୍ଥୀ ବାଳକଃ (ଚତୁର୍ଥ ବାଳକ)

पश्च्रम: बालक:

ପଞ୍ଚମଃ ବାଳକଃ (ପଞ୍ଚମ ବାଳକ)

षष्ठः बालक:

ଷଷ୍ଠୀ ବାଳକଃ (ଷଷ୍ଠୀ ବାଳକ)

सप्तमः बालक:

ସପ୍ତମଃ ବାଳକଃ (ସପ୍ତମ ବାଳକ)

अष्टम: बालक :

ଅଷ୍ଟମୀ ବାଳକଃ (ଅଷ୍ଟମ ବାଳକ)

नवम: बालक:

ନବମଃ ବାଳକଃ (ନବମ ବାଳକ)

दशम: बालक:

ଦଶମଃ ବାଳକଃ (ଦଶମ ବାଳକ)

प्रथमा बालिका

ପ୍ରଥମା ବାଳିକା (ପ୍ରଥମ ଝିଅ)

द्वितीया बालिका

ଦ୍ଵିତୀୟା ବାଳିକା (ଦ୍ଵିତୀୟ ଝିଅ)

तृतीया बालिका

ତୃତୀୟା ବାଳିକା (ତୃତୀୟ ଝିଅ)

चतुर्थी बालिका

ଚତୁର୍ଥୀ ବାଳିକା (ଚତୁର୍ଥ ଝିଅ)

पश्चमी बालिका

ପଞ୍ଚମୀ ବାଳିକା (ପଞ୍ଚମ ଝିଅ)

षष्ठी बालिका

ଷଷ୍ଠୀ ବାଳିକା (ଷଷ୍ଠ ଝିଅ)

सप्तमी बालिका

ସପ୍ତମୀ ବାଳିକା (ସପ୍ତମ ଝିଅ)

अष्टमी बालिका

ଅଷ୍ଟମୀ ବାଳିକା (ଅଷ୍ଟମ ଝିଅ)

नवमी बालिका

ନବମୀ ବାଳିକା (ନବମ ଝିଅ)

दशमी बालिका

ଦଶମୀ ବାଳିକା (ଦଶମ ଝିଅ)

प्रथमं फलम्

ପ୍ରଥମ ଫଳମ୍ (ପ୍ରଥମ ଫଳ)

द्वितीयं फलम्

ଦ୍ଵିତୀୟଂ ଫଳମ୍ (ଦ୍ଵିତୀୟ ଫଳ)

तृतीयं फलम्

ତୃତୀୟଂ ଫଳମ୍ (ତୃତୀୟ ଫଳ)

चतुर्थं फलम्

ଚତୁର୍ବିଂ ଫଳମ୍ (ଚତୁର୍ଥ ଫଳ)

पश्च्रमं फलम्

ପଞ୍ଚମ ଫଳମ୍ (ପଞ୍ଚମ ଫଳ)

षष्ठं फलम्

ଷବଂ ଫଳମ୍ (ଷଷ୍ଠ ଫଳ)

सप्तमं फलम्

ସପ୍ତମଂ ଫଳମ୍ (ସପ୍ତମ ଫଳ)

अष्टमं फलम्

ଅଷ୍ଟମ ଫଳମ୍ (ଅଷ୍ଟମ ଫଳ)

नवमं फलम्

ନବମଂ ଫଳମ୍ (ନବମ ଫଳ)

दशमं फलम्

ଦଶମାଂ ଫଳମ୍ (ଚତୁର୍ଥ ଫଳ)

प्रथमं श्रवणं द्वितीयं मननम्
तृतीयं स्मरणं चतुर्थं भाषणम् ।
पश्चमं पठनं षष्ठं च लेखनम्
सप्तमं गायनम् अष्टमं बोधनम् ।
नवमं नर्त्तनं दशमं कीर्त्तनम्
भाषाप्रशिक्षणं सामान्यं सोपानम् ।

ପ୍ରଥମଂ ଶ୍ରବଣଂ ଦ୍ଵିତୀୟଂ ମନନମ୍
ତୃତୀୟଂ ସ୍ମରଣଂ ଚତୁର୍ଥୀ ଭାଷଣମ୍ ।
ପଞ୍ଚମାଂ ପଠନଂ ଷଶଂ ଚ ଲେଖନମ୍
ସପ୍ତମଂ ଗାୟନମ୍ ଅଷ୍ଟମଂ ବୋଧନମ୍ ।
ନବମଂ ନର୍ତ୍ତନଂ ଦଶମ କୀର୍ତ୍ତନମ୍
ଭାଷାପ୍ରଶିକ୍ଷଣଂ ସାମାନ୍ୟ ସୋପାନମ୍ ।

Odisha State Board BSE Odisha 7th Class Sanskrit Solutions Chapter 14 ପଞ୍ଚମୀବିଭକ୍ତିପ୍ରୟୋଗଃ Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Sanskrit Solutions Chapter 14 ପଞ୍ଚମୀବିଭକ୍ତିପ୍ରୟୋଗଃ

१. पठतु (ପଞ୍ଚମୀବିଭକ୍ତିରୂପାଣି ଲିଖତୁ) ପଞ୍ଚମୀ ବିଭକ୍ତି ରୂପ ଲେଖ :

ଉତ୍ତରମ୍:

२. कोष्ठकस्थानां शब्दानां साहाय्येन वाक्यानि लिखतु-
(କୋଷ୍ଠକସ୍ମାନାଂ ଶବ୍ଦାନାଂ ସାହାଯ୍ୟନ ବାକ୍ୟାନି ଲିଖନ୍ତୁ।) କୋଠରି ମଧ୍ୟରେ ଥ‌ିବା ଶବ୍ଦଗୁଡ଼ିକ ସାହାଯ୍ୟରେ ବାକ୍ୟ ରଚନା କର ।

ଉତ୍ତରମ୍:
(क) अश्च: ग्रामात् आगच्छति ।
ଅଶ୍ଵ ଗ୍ରାମାତ୍ ଆଗଛତି। (ଘୋଡ଼ା ଗ୍ରାମରୁ ଆସୁଛି) ।

(ख) कङ्फणं हस्तात् पतति।
କଙ୍କଣଂ ହସ୍ତାତ୍ ପତତି। (କଙ୍କଣ ହାତରୁ ପଡ଼ୁଛି)

(ग) हारः कण्ठात् पतति ।
ହାରଃ କଣ୍ଠାତ୍ ପତତି । (ହାର କଣ୍ଠରୁ ପଡୁଛି।)

(घ) वृष्टिः आकाशात् पतति।
ବୃଷ୍ଟି ଆକାଶାତ୍ ପତତି । (ବୃଷ୍ଟି ଆକାଶରୁ ପଡ଼ୁଛି ।)

(ङ) नदी गिरे: प्रवहति।
ନଦୀ ଗିରେ ପ୍ରବହତି। (ନଈ ପାହାଡ଼ରୁ ପ୍ରବାହିତ ହେଉଛି ।)

(च) जलं द्रोण्याः पतति ।
ଦ୍ରୋଣ୍ୟା ପତତି। (ପାଣି ବାଲ୍ମିରୁ ପଡୁଛି।)

(छ) प्रकाशः भानो : आगच्छति ।
ପ୍ରକାଶଃ ଭାନୋ ଆଗଚ୍ଛତି । (ସୂର୍ଯ୍ୟଙ୍କଠାରୁ ଆଲୋକ ଆସେ)

(ज) तैलं वाहनात् पतति  ।
ତୈଳଂ ବାହନାତ୍ ପତତି। (ଗାଡ଼ିରୁ ତେଲ ବାହାରୁଛି ।)

(झ) फलं वृक्षात् पतति ।
ଫଳ ବୃକ୍ଷାତ୍ ପତତି। (ଗଛରୁ ଫଳ ଝଡୁଛି।)

३. चित्रं पश्यतु, बालक: कस्मात् किं स्वीकरोति इति लिखतु ।
ଚିତ୍ର ପଶ୍ୟତୁ ବାଳକଃ କସ୍ମାତ୍ କିଂ ସ୍ୱୀକରୋତି ଇତି ଲିଖନ୍ତୁ । ଚିତ୍ର ଦେଖ୍ ପିଲାଟି କାହାଠାରୁ କ’ଣ ନେଉଛି ଲେଖନ୍ତୁ ।)

यथा – बालक: मित्रात् वाहनं स्वीकरोति ।

(क) ब़ालक: मित्रांतु वाहनं स्वीकरोति ।
ବାଳକ ମିତ୍ରାତ୍ ବାହନଂ ସ୍ଵୀକରୋତି।
(ପିଲାଟି ବନ୍ଧୁଙ୍କଠାରୁ ଗାଡ଼ି ନେଉଛି।)

(ख) बालक: पाचकात् भोजनं स्वीकरोति।
ବାଳକଃ ପାଚକାତ୍ର ଭୋଜନଂ ସ୍ଵୀକରୋତି।
(ପିଲାଟି ପାଚକଠାରୁ ଖାଦ୍ୟ ଗ୍ରହଣ କରୁଛି।)

(ग) बालकः पितुः वस्त्रं स्वीकरोति।
ବାଳକଃ ପିତୁଃ ବରଂ ସ୍ଵୀକରୋତି।
(ପିଲାଟି ବାପାଙ୍କଠାରୁ ଲୁଗା ଗ୍ରହଣ କରୁଛି ।)

(घ) बालक: धेनो: क्षीरं स्वीकरोति।
ବାଳକ ଧେନଃ କ୍ଷୀରଂ ସ୍ଵୀକରୋତି।
(ବାଳକଟି ଗାଈଠାରୁ କ୍ଷୀର ନେଉଛି।)

(ङ) बालक: नद्या: जलं स्वीकरोति ।
ବାଳକଃ ନଦ୍ୟା ଜଳଂ ସ୍ଵୀକରୋତି।
(ପିଲାଟି ନଈରୁ ପାଣି ନେଉଛି।)

(च) बालक: वैद्याया: ओषधं स्वीकरोति।
ବାଳକଃ ବୈଦ୍ୟାୟା ଔଷଧୀ ସ୍ଵୀକରୋତି।
(ପିଲାଟି ଡାକ୍ତରଙ୍କଠାରୁ ଔଷଧ ନେଉଛି।)

(छ) बालकः क्षेत्रात् शस्यं स्वीकरोति ।
ବାଳକ କ୍ଷେତ୍ରାତ୍ର ଶସ୍ୟ ସ୍ଵୀକରୋତି।
(ପିଲାଟି ବିଲରୁ ଶସ୍ୟ ନେଉଛି।)

(ज) बालक: गुरो: पुस्तकं स्वीकरोति।
ବାଳକଃ ଗୁରୋ ପୁସ୍ତକଂ ସ୍ଵୀକରୋତି।
(ପିଲାଟି ଶିକ୍ଷକଙ୍କଠାରୁ ବହି ନେଉଛି।)

४. शून्यस्थाने उचितं पदं लिखतु ।
(ଶୂନ୍ୟସ୍ଥାନେ ଉଚିତଂ ପଦଂ ଲିଖନ୍ତୁ।) (ଶୂନ୍ୟସ୍ଥାନରେ ଠିକ୍ ପଦଟି ଲେଖନ୍ତୁ।)

…………… जना: भारतम् आगच्छन्ति ।
पक्षिण: …………… सरोवरम् आगच्छन्ति ।
…………… प्रकाशः आगच्छति ।
महान् वृक्ष: …………… उद्भवति ।
(बीजात्, लताभ्यः सवितु …………… विदेशात्, दूरात्)
ଉତ୍ତରମ୍:
विदेशात् जना: भारतम् आगच्छन्ति ।
ବିଦେଶାତ୍ ଜନାଃ ଭାରତମ୍ ଆଗଛନ୍ତି।

पक्षिण: दूरात् सरोवरम् आगच्छन्ति
ପକ୍ଷିତଃ ଦୂରାତ୍ର ସରୋବରମ୍ ଆଗଛନ୍ତି।

लताभ्य: पर्णानि पतन्ति ।
ଲତାଭ୍ୟ ପର୍ଣାନି ପତନ୍ତି ।

सवितु: प्रकाशः आगच्छति ।
ସବିତଃ ପ୍ରକାଶଃ ଆଗଛନ୍ତି ।

महान् वृक्ष: वीजातु उद्भवति ।
ମହାନ୍ ବୃକ୍ଷୀ ବୀଜାତ୍ର ଉଦ୍ଭବତି।

अतिरिक्त प्रश्नोत्तरम्
(ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातृभाषया अनुवादं कुरुत।
(क) बालः बाहनात् अवतरति।
उत्तर :
ପିଲାଟି ଗାଡିରୁ ଓହ୍ଲାଉଛି ।

(ख) अभिनेता विदेशात् आगच्छति।
उत्तर :
ଅଭିନେତା ବିଦେଶରୁ ଆସୁଛି।

(ग) वृक्षात् फलानि पतन्ति।
उत्तर :
ଋଛରୁ ଫଳ ପଡୁଛି।

(घ) पर्वतेभ्य: नद्य: प्रवहन्ति।
उत्तर :
ପର୍ବତମାନଙ୍କରୁ ନଈଗୁଡ଼ିକ ବହୁଛନ୍ତି ।

(ङ) शब्द: वाहनात् भवति।
उत्तर :
ଗାଡିରୁ ଶବ୍ଦ ହେଉଛି।

(च) नलिक्राया: जलं निपतति।
उत्तर :
ନଳରୁ ପାଣି ପଡୁଛି ।

(छ) फलेभ्य: बीजानि प्राप्नुम:।
उत्तर :
ନଳରୁ ପାଣି ପଡୁଛି ।

२. एकपदेन उत्तरं लिखत।

(क) क़: वनात् आगच्छति ?
उत्तर :
ବାନରଃ

(ख) पुत्राः जनकेभ्यः किं प्राप्नुवन्ति ?
उत्तर :
ସ୍ନେହ

(ग) जनकः कया अवतरति ?
उत्तर :
ନୌକାୟଃ

(घ) महिला कस्या: जलम् आनयति ?
उत्तर :
ନମଃ

(ङ) काआकाशात् पतति ?
उत्तर :
ବୃଷ୍ଟି

(च) कार्यालये काभ्य: शब्द: भवति ?
उत्तर :
ଦୂରବାଣୀଭ୍ୟ

(छ) तरोः किं पतति ?
उत्तर :
ପୁଙ୍ଖ

३. शून्यस्थानं पूरयत।

(क) मुद्रिका …………. पतति।
उत्तर :
ଅଙ୍ଗୁଲ୍ୟା

(ख) नेत्राभ्याम् …………. पतन्ति।
उत्तर :
ଅଶୁଣି

(ग) …………. फलानि पतन्ति।
उत्तर :
ବୃକ୍ଷାତ୍

(घ) तैलं कुप्या: …………. |
उत्तर :
ସ୍ରବତି

(ङ) सा हस्ताभ्यां …………. निष्कासयति।
उत्तर :
କଙ୍କଣାନି

(च) फलेभ्य： …………….. प्राप्नुमः ।
उत्तर :
ବୀଜାନି

४．विक्षिप्तवर्णानां मेलनेन शुद्धपदं रचयत।

(क) म् ति म भ्या
उत्तर :
ମତିଭ୍ଯାମ୍

(ख) क：च पा
उत्तर :
ପାଚକ

(ग) ह ति व प्र
उत्तर :
ପ୍ରବହତି

(घ) ते：सं स्कृ
उत्तर :
ସଂସ୍କୃତଃ

(ङ) का त् शा आ
उत्तर :
ଆକାଶାତ୍

५．स्तम्भमेलनं कुरूत।
‘क’ स्मम्भ： — ‘ख’ स्तम्भ：
घट：– मते：
मति：– मधुन：
मधु — वनात्
लेखनी — घटात्
वनम् — लेखन्या：
उत्तर :
‘କ’ ସ୍ତମ୍ଭ — ‘ଖ’ ସ୍ତମ୍ଭ
ଘଟ — ଘଟାତ୍
ମତିଃ — ମତଃ
ମଧୁ — ମଧୁନଃ
ଲେଖନୀ — ଲେଖନ୍ଯା
ବନମ୍ — ବନାତ୍

६. मातृभाषया अर्थं प्रकाशयत।
(क) वाहनात्
उत्तर :
ବାହନରୁ

(ख) वनात्
उत्तर :
ବଣରୁ

(ग) भानुः
उत्तर :
ସୂର୍ଯ୍ୟ

(घ) अवतरति
उत्तर :
ଓହ୍ଲାଉଛି

(ङ) प्रवहति
उत्तर :
ପ୍ରବାହିତ ହେଉଛି

७. रेखाड्कितपदानां भ्रमसंशोधनं कुरुत।
(क) फलं वृक्षांत् पतन्ति।
उत्तर :
ଫଳ ବୃକ୍ଷାତ୍ ପତତି।

(ख) द्रोणीया: जलं पतति।
उत्तर :
ଦ୍ରୋଣ୍ୟା ଜଳ ପତତି ।

(ग) वानरः वनस्य आगच्छति।
उत्तर :
ବାନରଃ ବନାତ୍ ଆଗଚ୍ଛତି ।

(घ) तैल: कुप्या: स्रवति।
उत्तर :
ତୈଳଂ କୁପ୍ୟା ସୁବତି ।

(ङ) वृक्षा: बीजात् उद्भवति।
उत्तर :
ବୃକ୍ଷ ବୀଜାତ୍ ଉଦ୍‌ଭବତି ।

८. उत्तर चयनं कुरूत।
(क) वृष्टिः कस्मात् पतति ?
(a) आकाशात्
(b) भूमे:
(c) वायो:
(d) जलात्
उत्तर :
(a) ଆକାଶାତ୍

(ख) बालः कस्मात् अवतरति ?
(a) द्विचक्रिकाया:
(b) यानात्
(c) वाहनात्
(d) गृहात्
उत्तर :
(c) ବାହନାତ୍

(ग) वेेभ्य: नद्य: प्रवहन्ति ?
(a) जलेभ्य:
(b) वृक्षेभ्य:
(c) गृहेभ्य:
(d) पर्वतेभ्य:
उत्तर :
(d) ପର୍ବତେଭ୍ୟ

(घ) तरो: किं पतति ?
(a) फलं
(b) पुष्पं
(c) जलं
(d) दलं
उत्तर :
(b) ପୁଙ୍ଖ

(ङ) वाहनात् किं भवति ?
(a) यानं
(b) शब्द:
(c) अब्द:
(d) तैलं
उत्तर :
(b) ଶବ୍ଦ

पश्यतु वदतु
(ପଶ୍ୟତୁ, ଉଚ୍ଚୈଃ ପଠତୁ) :

→ वृक्षात् फलानि पतन्ति ।
(ବୃକ୍ଷାତ୍ ଫଳାନି ପତନ୍ତି।)
ଗଛରୁ ଫଳ ପଡୁଛି।

→ बालः वाहनानात् अवतरति ।
(ବାଳ ବାହାନାତ୍ ଅବତରତି।)
ପିଲାଟି ଗାଡ଼ିରୁ ଓହ୍ଲାଉଛି।

→ नलिकायाः जलं निपतति ।
(ନଳିକାୟା ଜଳଂ ନିପତତି।)
ନଳରୁ ପାଣି ପଡୁଛି ।

→ महिला: नद्या: जलम् आनयति ।
(ମହିଳା ନଦ୍ୟା ଜଳମ୍ ଆନୟତି)
ନାରୀଟି ନଈରୁ ପାଣି ଆଣୁଛି।

उच्चै : पठतु जानातु च
(ଉଚ୍ଚୈଃ ପଠତୁ ଜାନାଡ଼ୁ ଚ) ବଡ଼ପାଟିରେ ପଢ଼ନ୍ତୁ ଏବଂ ଜାଣନ୍ତୁ :

→ अभिनेता विदेशात् आगच्छति ।
(ଅଭିନେତା ବିଦେଶାତ୍ମ ଆଗଚ୍ଛତି।)
ଅଭିନେତା ବିଦେଶରୁ ଆସୁଛି ।

→ वृष्टिः आकाशात् पतति ।
(ବୃଷ୍ଟି ଆକାଶାତ୍ ପତତି।)
ବୃଷ୍ଟି ଆକାଶରୁ ପଡ଼ୁଛି ।

→ वानरः वनात् आगच्छति ।
(ବାନରଃ ବନାତ୍ ଆଗଚ୍ଛତି ।)
ମାଙ୍କଡ଼ ବଣରୁ ଆସୁଛି ।

→ शब्द：वाहनात् भवति ।
(ଶବ୍ଦ ବାହନାତ୍ ଭବତି।)
ଗାଡ଼ିରୁ ଶବ୍ଦ ହେଉଛି ।

→ जनक：नौकाया：अवतरति ।
(ଜନମଃ ନୌକାୟଃ ଅବତରତି।)
ବାପା ଡଙ୍ଗାରୁ ଓହ୍ଲାଉଛନ୍ତି ।

→ पुष्पं तरो: पतति ।
(ପୁଙ୍ଖ ତରୋ ପତତି।)
ଗଛରୁ ଫୁଲ ଝଡ଼ୁଛି ।

→ तैलं कुप्या: स्रवति ।
(ତୈଳଂ କୁପ୍ୟା ସୁବତି।)
ବୋତଲରୁ ତେଲ ବୋହୁଛି ।

→ मुद्रिका अङुगुल्या: पतति ।
(ମୁଦ୍ରିକା ଅଙ୍ଗୁଲ୍ୟା ପତତି।)
ଅଙ୍ଗୁଳିରୁ ମୁଦି ପଡ଼ିଯାଉଛି ।

→ पर्वतेभ्य: नद्य：प्रवहन्ति ।
(ପର୍ବତେଭ୍ୟ ନମଃ ପ୍ରବହନ୍ତି ।)
(ନଈଗୁଡ଼ିକ ପର୍ବତମାନଙ୍କରୁ ବହୁଛନ୍ତି।)

अवधेयम् :

Odisha State Board BSE Odisha 7th Class Sanskrit Solutions Chapter 15 ଷଷ୍ଠୀବିଭକ୍ତି ପ୍ରୟୋଗଃ Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Sanskrit Solutions Chapter 15 ଷଷ୍ଠୀବିଭକ୍ତି ପ୍ରୟୋଗଃ

१. वन्धनीमध्यस्थस्य शब्दस्य यथार्थरूपं शून्यस्थाने पूरयतु
(ବନ୍ଧନୀମଧ୍ଯସ୍ପୃସ୍ୟ ଶବ୍ଦସ୍ୟ ଯଥାର୍ଥରୂପଂ ଶୂନ୍ୟସ୍ଥାନେ ପୂରୟତ୍ବ।) ବନ୍ଧନୀ ମଧ୍ଯରେ ଥ‌ିବା ଶବ୍ଦର ଯଥାର୍ଥ ରୂପ କରି ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

• ___ राजधानी भुवनेश्वरम् । (ओड़िशा)
• ___ राजधानी श्रीनगरम् । (काश्मीरम्)
• ___ राजधानी गान्धिनगरम् । (गुजरात्)
• ___ मुखं प्रशान्तं भवति । (मुनिः)
• ___ वाक्यानि स्मरामि । (गुरुः)
• ___ चपलतां पश्यामि । (कपिः)
• ___ध्वनिः मंधुरः। (वीणा)
• ___ गतिः वक्रा। (नदी)
• बालक: ___ प्रिय:। (पिता)
• मूल्यम् अधिकम् । (वस्तु)

ଉତ୍ତରମ୍:
ओड़िशायाः राजधानी भुवनेश्वरम् ।
ଓଡ଼ିଶାୟା ରାଜଧାନୀ ଭୁବନେଶ୍ଵରମ୍ ।
(ଓଡ଼ିଶାର ରାଜଧାନୀ ଭୁବନେଶ୍ଵର।)

काश्मीस्स्य राजधानी श्रीनगरम्।
କାଶ୍ମୀରସ୍ୟ ରାଜଧାନୀ ଶ୍ରୀନଗରମ୍।
କାଶ୍ମୀରର ରାଜଧାନୀ ଶ୍ରୀନଗର।

गुजरातस्य राजधानी गान्धिनगरम्।
ଗୁଜରାତସ୍ୟ ରାଜଧାନୀ ଗାନ୍ଧିନଗରମ୍।
(ଗୁଜରାତର ରାଜଧାନୀ ଗାନ୍ଧିନଗର ।)

मुनेः मुखं प्रशान्तं भवति ।
ମୁନେ ମୁଖ୍ୟ ପ୍ରଶାନ୍ତ ଭବତି ।
(ମୁନିଙ୍କ ମୁଖ ପ୍ରଶାନ୍ତ ଅଟେ।)

गुरो: वाक्यानि स्मरामि ।
ଗୁରୋ ବାକ୍ୟାନି ସ୍ମରାମି |
(ଗୁରୁଙ୍କ ବାକ୍ୟ ମନେରଖୁଛି।)

कपे: चपलतां पश्यामि ।
କପେ ଚପଳତାଂ ପଶ୍ୟାମି ।
(ମାଙ୍କଡ଼ର ଚପଳତା ଦେଖୁଛି ।)

वीणाया: ध्वनिः मधुरः।
ବୀଣାୟା ଧ୍ଵନିଃ ମଧୁରଃ ।
(ବୀଣାର ଧ୍ବନି ମଧୁର।)

नद्या: गति: वक्रा ।
ନଦ୍ୟା ଗତିଃ ବକ୍ରା।
(ନଈର ଗତି ବଙ୍କା ।)

बालक: पितु: प्रिय:।
ବାଳକଃ ପିତୁଃ ପ୍ରିୟଃ ।
(ବାଳକ ପିତାଙ୍କର ପ୍ରିୟ ।)

वस्तुनः मूल्यम् अधिकम् ।
ବସ୍ତୁନଃ ମୂଲ୍ୟମ ଅଧ୍ଵକମ୍ ।
(ଜିନିଷର ଦର ଅଧ୍ବକ ।)

उदाहरणानु सारं वावन्यानि रचयतु
(ଉଦାହରଣାନୁସାରଂ ବାକ୍ୟାନି ରଚୟତୁ।)

हिमालय ← गिरि：→ कपिलास：
कुमारसम्भवम् ← ग्रन्थ：→ हर्षचरितम्
सुधर्मा ← पत्रिका → चन्दमामा
ऋषिकुल्या ← नदी → महानदी
जगन्नाथ：← देव：→लिङ्गराज：
ଉତ୍ତରମ୍:
(क) गिरे：नाम हिमालय：।
ଗିରଃ ନାମ ହିମାଳୟ ।
(ପର୍ବତର ନାମ ହିମାଳୟ ।)

(ख) गिरे: नंम कपिलासः।
ଗିରଃ ନାମ କପିଳାମଃ ।
( ପର୍ବତର ନାମ କପିଳାସ।)

(ग) ग्रन्थस्य नाम कुमारसम्भवम् ।
ଗ୍ରନ୍ଥସ୍ୟ ନାମ କୁମାରସମ୍ଭବମ୍ ।
(ଗ୍ରନ୍ଥର ନାମ କୁମାରସମ୍ଭବମ୍ ।)

(घ) ग्रन्थस्य नाम हर्षचरित्रम् ।
ଗ୍ରନ୍ଥସ୍ୟ ନାମ ହର୍ଷଚରିତ୍ରମ୍ ।
(ଗ୍ରନ୍ଥର ନାମ ହର୍ଷଚରିତ୍ର।)

(ङ) पत्रिकाया: नाम सुधर्मा।
ପତ୍ରିକାୟା ନାମ ସୁଧର୍ମା।
(ପତ୍ରିକାର ନାମ ସୁଧର୍ମା ।)

(च) पत्रिकाया: नाम चन्दामामा।
ପତ୍ରିକାୟଃ ନାମ ଚନ୍ଦାମାମା।
(ପତ୍ରିକାର ନାମ ଚନ୍ଦାମାମା।)

(छ) नद्या: नाम महानदी।
ନଦ୍ୟା ନାମ ମହାନଦୀ ।
(ନଦୀର ନାମ ମହାନଦୀ।)

(ज) नद्या: नाम ऋषिकूल्या।
ନଦ୍ୟା ନାମ ଋଷିକୂଲ୍ୟା ।)
(ନଦୀର ନାମ ଋଷିକୂଲ୍ୟା ।)

(झ) देवस्य नाम जगन्नाथः।
ଦେବସ୍ୟ ନାମ ଜଗନ୍ନାଥ ।
(ଦେବତାଙ୍କ ନାମ ଜଗନ୍ନାଥ।)

(ज) देवस्य नाम लिङ्नराज:।
ଦେବସ୍ୟ ନାମ ଲିଙ୍ଗରାଜଃ ।
(ଦେବତାଙ୍କ ନାମ ଲିଙ୍ଗରାଜଃ ।

३. उदाहरणं पश्यतु शुन्यस्थानं पूरयतु ।
(ଉଦାହରଣଂ ପଶ୍ୟତୁ ଶୂନ୍ୟସ୍ଥାନଂ ପୂରୟତୁ।)

ଉଦାହରଣ ଦେଖ ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
उदाहरणम् – देशयो : मध्ये युद्धं भवति । (देशौ)
स: …………. आशीर्वादं प्राप्नोति । (गुरू)

• …………. संयोजनेन अक्षलि: भवति । (हस्तौ)
• अद्य (कवी) …………. सम्मानकार्यक्रम: अस्ति ।
• (वाहने) …………. घट्टनेन दुर्घटना भवति ।
• (भातरौ) …………. कलहेन पिता खित्र: भवति ।
• मम (भगिन्यौ) …………. निवास: ग्रामे अस्ति ।

ଉତ୍ତରମ୍:
(क) देशयो: मध्ये युद्धं भवति ।
ଦେଶ ମଧ୍ୟ ଯୁଦ୍ଧ ଭବତି ।
(ଦୁଇଦେଶ ମଧ୍ୟରେ ଯୁଦ୍ଧ ହେଉଛି।)

(ख) स：गुरो: आशीर्वादं प्राप्नोति ।
ଡଃ ଗୁରୋ ଆଶୀର୍ବାଦଂ ପ୍ରାୟୋତି ।
(ସେ ଗୁରୁଙ୍କ ଆଶୀର୍ବାଦ ପାଉଛି।)

(ग) हस्तयो: संयोजनेन अज्जलिः भवति ।
ହସ୍ତୟୋ ସଂଯୋଜନେନ ଅଞ୍ଜଳି ଭବତି ।
(ଦୁଇହାତର ମିଳନରେ ଅଞ୍ଜଳି ହୁଏ।)

(घ) अद्य कव्यो: सम्मानकार्यक्रम：अस्ति ।
ଅଦ୍ୟ କବୟୋ ସମ୍ମାନକାର୍ଯ୍ୟକ୍ରମ ଅସ୍ତି ।
(ଆଜି ଦୁଇଜଣ କବିଙ୍କର ସମ୍ମାନ କାର୍ଯ୍ୟକ୍ରମ ରହିଛି ।)

(ङ) वाहनयो: घट्टनेन दुर्घटना भवति।
ଘଟନେନ ଦୁର୍ଘଟନା ଭବତି ।
( ଦୁଇଟି ଗାଡ଼ିର ଧକ୍କାରେ ଦୁର୍ଘଟଣା ହୁଏ।)

(च) भ्रात्रो: कलहेन पिता खिन्न：भवति ।
ଭ୍ରାତ୍ରୀ କଳହେନ ପିତା ଖୁନଃ ଭବତି।
(ଦୁଇଭାଇଙ୍କ କଳିରେ ବାପା ଦୁଃଖତ ଅଟନ୍ତି ।)

(छ) मम भगिन्यो: निवास：ग्रामे अस्ति ।
ମମ ଭଗିନ୍ୟା ନିବାସ ଗ୍ରାମେ ଅସ୍ତି।
(ମୋ ଦୁଇଭଉଣୀ ଗ୍ରାମରେ ରହୁଛନ୍ତି।)

४. उदाहरणं पश्यतु शब्दस्य यथार्थरूपेण शून्यस्थानं

यथा－भारतीयाः－संस्कृति प्राचीना－
भारतीयानां संस्कृति ：प्राचीना ।

• वयम्－भाषा－संस्कृतम्
  ……… ……….. ………
• भाषा – उपादानं संस्कृतम्
  ……… ……….. ………
• नेतार: – जीवनं – परोपकायाय
  ……… ……….. ………
• नद्य: – जलं – परोपकारार्थम्
  ……… ……….. ………

ଉତ୍ତରମ୍:
यथा－भारतीयाः－संस्कृति－प्राचीना
ଭାରତୀୟ – ସଂସ୍କୃତି ପ୍ରାଚୀନା।

भारतीयानां संस्कृति：प्राचीना ।
ଭାରତୀୟାନାଂ ସଂସ୍କୃତିଃ ପ୍ରାଚୀନା ।

वयम्－भाषां－संस्कृतम्
ବୟଂ ଭାଷା – ସଂସ୍କୃତମ୍
उत्तर :
वयं－भाषा－संस्कृतम्
ଅସ୍ଵାକଂ ଭାଷା ସଂସ୍କୃତମ୍ ।
(ଆମ ଭାଷା ସଂସ୍କୃତ)

नेतार：－जीवनं－परोपकायाय
ନେତାରଃ – ଜୀବନଂ – ପରୋପକାରାୟ
उत्तर :
नेतृणां जीवनं परोपकायाय
ନେତୃ ମାଂ ଜୀବନଂ ପରୋପକାରାୟ।
(ନେତାମାନଙ୍କର ଜୀବନ ପରର ଉପକାର ପାଇଁ)

भाषा－उपादान－संस्कृतम्
ଭାଷା – ଉପାଦାନଂ – ସଂସ୍କୃତମ୍
उत्तर :
भाषयाः उपादानं सस्कृतम्।
ଭାଷୟ ଉପାଦାନଂ ସଂସ୍କୃତମ୍ ।
(ଭାଷାର ଉପାଦାନ ସଂସ୍କୃତ ।)

नद्य：－जलं－परोपकारार्थम्
ଜଳଂ –ନମଃ – ପରୋପକାରାର୍ଥମ୍
उत्तर :
नदीनां जलं परोपकारार्थम्।
ନଦୀନାଂ ଜଳଂ ପରୋପକାରାର୍ଥମ୍।
( ନଈମାନଙ୍କ ପାଣି ପର ଉପକାର ପାଇଁ।)

५. बन्धनीमध्यस्थस्य शब्दस्य यथार्थरूपेण रिक्तस्थानं
(ବନ୍ଧନୀମଧ୍ଯସ୍ପୃସ୍ୟ ଶବ୍ଦସ୍ୟ ଯଥାର୍ଥରୂପେଣ ରିକ୍ତସ୍ନାନଂ ପୂରୟତୁ)

यथा – मयूरा: मेघानां गर्जनम् इच्छन्ति । (मेघा:)

• बृहस्पति: …………. गुरुः अस्ति । (देवाः)
• कवि: …………. रचनां करोति । (काव्यानि)
• वयं …………. वचनं पालयामः।
• पिता …………. गणनां करोति ।
• सभायां …………. ध्वनिः अधिक: अस्ति । (वाद्यानि)
• अहं …………. सेवां करोमि । (अतिथ्य:)
• गोपालक: …………. पालनं करोति । (धेनव:)
• सज्जना: …………. स्मरणं कुर्वन्ति । (सुभाषितानि)

ଉତ୍ତରମ୍:
यथा – मयूरा: मेघानां गर्जनम् इच्छन्ति ।
ମୟୂରା ମେଘାନାଂ ଗର୍ଜନମ୍ ଇଛନ୍ତି।

(क) बृहस्पति: देवानां गुरुः अस्ति।
ବୃହସ୍ପତିଃ ଦେବାନାଂ ଗୁରୁ ଅସ୍ତି ।
କବି କାବ୍ୟାନାଂ ରଚନାଂ କରୋତି।

(ख) कवि: काव्यानां रचनां करोति।
ବୟଂ ଗୁରୁମାଂ ବଚନଂ ପାଳୟାମଃ ।

(ग) वयं गुरूणां वचनं पालयामः।
ପିତା ବସ୍ତୁନାଂ ଗଣନାଂ କରୋତି ।

(घ) पिता वस्तूनां गणनां करोति।
ପିତା ବସ୍ତୁନାଂ ଗଣନାଂ କରୋତି ।

(ङ) सभायां वाद्यानां ध्वनिः अधिकः अस्ति ।
ସଭାୟାଂ ବାଦ୍ୟାନାଂ ଧ୍ଵନିଂ ଅଧ୍ଵତଃ ଅସ୍ତି

(च) अहं अतिथीनां सेवां करोमि ।
ଅହଂ ଅତିଥୀନାଂ ସେବାଂ କରୋମି।

(छ) गोपालक: धेनूनां पालनं करोति ।
ଗୋପାଳକ ଧେନୁନାଂ ପାଳନଂ କରୋତି।

(ज) सज्जना: सुभाषितानां स्मरणं कुर्वन्ति ।
ସଜନାଃ ସୁଭାଷିତାନାଂ ସ୍ମରଣଂ କୁର୍ବନ୍ତି।

६. उचितपदै: रिक्तस्थानं पूरयतु ।
(ଉଚତି ପଦଃ ରିକ୍ତସ୍ନାନଂ ପୂରୟତୁ।)

यथा – वयं प्रतिदिनं महापुरूषाणां जीवनचरितं पठाम:।

• गोपालक: …………. पालनं करोति ।
• तेषां …………. कविताः रमणीयाः सन्ति ।
• …………. आज्ञा पालनीया।
•  विवेकानन्दस्य …………. पठनेन शान्ति: भवति।
• ………… जलं कलुषितं भवति ।
  (उपदेशानां नदीनां, महापुरुषाणां, कविनां, धेनूनां, गुरूणां)

ଉତ୍ତରମ୍:
(क) वयं प्रतिदिनं महापुरूषाणां जीवनचरितं पठामः।
ବୟଂ ପ୍ରତିଦିନଂ ମହାପୁରୁଷାନାଂ ଜୀବନଚରିତଂ ପଠାମଃ ।

(ख) गोपालक: धेनूनां पालनं करोति।
ଗୋପାଳକଃ ଧେନୁନାଂ ପାଳନଂ କରୋତି।

(ग) तेषां कवीनां कविताः रमणीयाः सन्ति ।
ତେଷା କବୀନାଂ କବିତା ରମଣୀୟା ସନ୍ତି ।

(घ) गुरूणां आज्ञा पालनीया।
ଗୁରୁଣା ଆଜ୍ଞା ପାଳନୀୟା।

(ङ) विवेकानन्दस्य उपदेशानां पठनेन शान्ति: भवति।
ବିବେକାନନ୍ଦସ୍ୟ ଉପଦେଶାନାଂ ପଠନେନ ଶାନ୍ତଃ ଭବତି ।

(च) नदीनां जलं कलुषितं भवति ।
ନଦୀନାଂ ଜଳଂ କଳୁଷିତଂ ଭବତି।

अतिरिक्त प्रश्नोत्तरम्
(ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातृभाषया अनुवादं कुरुत।
(क) रामायणस्य कर्त्ता बाल्मीकि:।
उत्तर :
ରାମାୟଣର କର୍ତ୍ତା ବାଲ୍ମୀକି ।

(ख) विवेकानन्द: रामकृष्णस्य शिष्य:।
उत्तर :
ବିବେକାନନ୍ଦ ରାମକୃଷ୍ଣଙ୍କ ଶିଷ୍ୟ ।

(ग) पुस्तकस्य नाम कलिका।
उत्तर :
ପୁସ୍ତକର ନାମ କଳିକା ।

(घ) वेदस्य नाम यजुः।
उत्तर :
ବେଦର ନାମ ଯଜୁ।

(ङ) नद्या: नाम गङ्न।
उत्तर :
ନଦୀର ନାମ ଗଙ୍ଗା ।

(च) गृहस्य नाम श्रीकुटीरम्।
उत्तर :
ଘରର ନାମ ଶ୍ରୀକୁଟୀର।

(छ) श्रीकृष्ण: अर्जुनस्य मित्रम्।
उत्तर :
ଶ୍ରୀକୃଷ୍ଣ ଅର୍ଜୁନଙ୍କ ବନ୍ଧୁ।

२. एकपदेन उत्तरं लिखत।
(क) ओडिशाया: राजधानी किम् ?
उत्तर :
ଭୁବନେଶ୍ବରମ୍

(ख) देशस्य नाम किम् ?
उत्तर :
ଭାରତମ୍

(ग) कस्य कर्त्ता बाल्मीकि: ?
उत्तर :
ରାମାୟଣସ୍ୟ

(घ) कस्याः लेखक: बाणभट्टः ?
उत्तर :
କାଦମ୍ବର୍ଯ୍ୟା

(ङ) रामकृष्णस्य शिष्य: क: ?
उत्तर :
ବିବେକାନନ୍ଦ

(च) गणेशः कस्य पुत्र: ?
उत्तर :
ଶିବସ୍ଯ

(छ) उत्कलप्रशङ्क कस्याः नाम ?
उत्तर :
ପତ୍ରିକାୟଃ

३. शून्यस्थानं पूरयत।
(क) …………. नाम कलिका।
उत्तर : ପୁସ୍ତକସ୍ଯ

(ख) बेदस्य नाम …………. |
उत्तर :
ଯନୁଃ

(ग) अर्जुनस्य …………. श्रीकृष्णः।
उत्तर :
ମିତ୍ର

(घ) देशस्य नाम …………. |
उत्तर :
ଭାରତମ୍

(ङ) कादम्बर्या: लेखक: …………. ।
उत्तर :
ବାଣଭରଃ

(च) …………. नाम गङ्ग़।।
उत्तर :
ନଦ୍ଯା

४. विक्षिप्तवर्णानां मेलनेन शुद्धपदं रचयत।
(क) न का वे न्द: वि
उत्तर :
ବିବେକାନନ୍ଦ

(ख) त्रिया: का प
उत्तर :
ପତ୍ରିକାୟଃ

(ग) गु णा रू म्
उत्तर :
ଗୁରୂଣାମ୍

(घ) धा रा ज नी
उत्तर :
ରାଜଧାନୀ

(ङ) ग त्रा ज थः
उत्तर :
ଜଗନ୍ନାଥ

५. स्तम्भमेलनं कुरूत।

‘क’ स्मम्भ: — ‘ख’ स्तम्भ:
शिवस्य — भरत:
वसुदेवस्य — श्रीराम:
दशरथस्य — अर्जुनः
पण्डो: — श्रीकृष्ण:
शकुन्तलाया: — गणेश:
उत्तर :
‘କ’ ସ୍ତମ୍ଭ — ‘ଖ’ ସ୍ତମ୍ଭ
ଶିବସ୍ଯ — ଗଣେଶଃ
ବସୁଦେବସ୍ଯ — ଶ୍ରୀକୃଷ୍ଣ
ଦଶରଥସ୍ଯ — ଶ୍ରୀରାମ
ପଣ୍ଡା — ଅର୍ଜୁନଃ
ଶକୁନ୍ତଳାୟା — ଭରତଃ

६. मातृभाषया अर्थं प्रकाशयत।
(क) धेनुः
उत्तर :
ଗାଈ

(ख) नगरस्य
उत्तर :
ନଗରର

(ग) वेदानाम्
उत्तर :
ବେଦଗୁଡ଼ିକର

(घ) वीणाया:
उत्तर :
ବୀଣାର

(ङ) पत्रिकाया:
उत्तर :
ପତ୍ରିକାର

७. रेखाङ्कितपदानां भ्रमसंशोधनं कुरुत।
(क) कपयाः चपलतां पश्यामि।
उत्तर :
କପେ ଚପଳ ତାଂ ପଶ୍ୟାମି ।

(ख) अस्माकं भाषा संस्कृतः।
उत्तर :
ଅସ୍ମାକଂ ଭାଷା ସଂସ୍କୃତମ୍ ।

(ग) देशय: मध्ये युद्धं भवति।
उत्तर :
ଦେଶ ମଧ୍ୟ ଯୁଦ୍ଧ ଭବତି।

(घ) नदीनां जलं कलुषितं भवन्ति।
उत्तर :
ନଦୀନାଂ ଜଳଂ କଳୁଷିତଂ ଭବତି ।

(ङ) कवि: काव्याना: रचनां करोति।
उत्तर :
କବି କାବ୍ୟାନାଂ ରଚନା କରୋତି।

८. उत्तर चयनं कुरूत।
(क) काश्मीरस्य राजधानी किम् ?
(a) श्रीनगरम्
(b) भुवनेश्वरम्
(c) गान्धिनगरम्
(d) इटानगरम्
उत्तर :
(a) ଶ୍ରୀନଗରମ୍

(ख) वीणायाः ध्वनिः कीदृशः ?
(a) मधुरा
(b) मधुरम्
(c) मधुरः
(d) मधुराणि
उत्तर :
(c) ମଧୁରଃ

(ग) कस्या: नाम चन्दमामा ?
(a) पुस्तकस्य
(b) पत्रिकाया:
(c) मम
(d) तस्या:
उत्तर :
(b) ପତ୍ରିକାୟଃ

(घ) वयं केषां वचनं पालयाम: ?
(a) गुरूणाम्
(b) गुरुणाम्
(c) गुरुषु
(d) गुरो:
उत्तर :
(a) ଗୁରୁଣାମ୍

(ङ) कस्या: गति: वक्रा ?
(a) नदी
(b) नदीम्
(c) नदिना
(d) नद्या:
उत्तर :
(d) ନମଃ

पश्यतु, उच्चै: पठतु (ପଶ୍ୟତୁ, ଉଚ୍ଚୈଃ ପଠତୁ) ଦେଖନ୍ତୁ ବଡ଼ପାଟିରେ ପଢ଼ନ୍ତୁ :

→ देशस्य नाम भारतम् ।
(ଦେଶସ୍ୟ ନାମ ଭାରତମ୍ ।)
ଦେଶର ନାମ ଭାରତ।

→ शिवस्य पुत्र: गणेशः।
(ଶିବସ୍ୟ ପୁନଃ ଗଣେଶଃ ।)
ଗଣେଶ ଶିବଙ୍କ ପୁଅ।

→ पत्रिकाया: नाम उत्कलप्रसङ्मः।
(ପତ୍ରିକାୟଃ ନାମ ଉତ୍କଳପ୍ରସଙ୍ଗ ।)
ପତ୍ରିକାର ନାମ ଉତ୍କଳ ପ୍ରସଙ୍ଗ।

→ नद्या: नामं गड्ग़।
(ନଦ୍ୟା ନାମ ଗଙ୍ଗା ।)
ନଈର ନାମ ଗଙ୍ଗା ।

→ कादम्बर्या：लेखक：वाणभट्टः।
(କାଦମ୍ବର୍ଯ୍ୟା ଲେଖକଃ ବାଣଭଟ୍ଟ ।)
କାଦମ୍ବରୀର ଲେଖକ ବାଣଭଟ୍ଟ ।

→ पुस्तकस्य नाम कलिका।
(ପୁସ୍ତକସ୍ୟ ନାମ କଳିକା ।)
ବହିର ନାମ କଳିକା ।

→ रामायणस्य कर्त्ता बाल्मीकिः।
(ରାମାୟଣସ୍ୟ କର୍ତ୍ତା ବାଲ୍ମୀକି ।)
ରାମାୟଣର କର୍ତ୍ତା ବାଲ୍ମୀକି ।

→ गृहस्य नाम श्रीकुटीरम् ।
(ଗୃହସ୍ୟ ନାମ ଶ୍ରୀକୁଟୀରମ୍ ।)
ଘରର ନାମ ଶ୍ରୀକୁଟୀର।

→ अर्जुनस्य मित्रं श्रीकृष्णः।
(ଅର୍ଜୁନସ୍ୟ ମିତ୍ର ଶ୍ରୀକୃଷ୍ଣ ।)
ଅର୍ଜୁନଙ୍କ ବନ୍ଧୁ ଶ୍ରୀକୃଷ୍ଣ।

→ वेदस्य नाम यजुः।
(ବେଦସ୍ୟ ନାମ ଯଜଃ ।)
ବେଦର ନାମ ଯଜୁ।

उच्चै : पठतु (ଉଚ୍ଚୈଃ ପଠତୁ) ବଡ଼ ପାଟିରେ ପଢ଼ନ୍ତୁ

Odisha State Board BSE Odisha 7th Class Sanskrit Solutions Chapter 16 ସପ୍ତମୀବିଭକ୍ତିପ୍ରୟୋଗଃ Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Sanskrit Solutions Chapter 16 ସପ୍ତମୀବିଭକ୍ତିପ୍ରୟୋଗଃ

उच्चैः पठतु (ଉଚ୍ଚୈଃ ପଠତୁ) ବଡ଼ ପାଟିରେ ପଢ଼ନ୍ତୁ :

१. वन्धनीमध्यस्थस्य शब्दस्य यथार्थरूपं शून्यस्थाने पूरयतु
(ବନ୍ଧନୀମଧ୍ଯସ୍ପୃସ୍ୟ ଶବ୍ଦସ୍ୟ ଯଥାର୍ଥ ରୂପଂ ଶୂନ୍ୟସ୍ଥାନେ ପୂରୟତୁ।) ବନ୍ଧନୀ ମଧ୍ଯରେ ଥିବା ଯଥାର୍ଥ ରୂପ ନେଇ ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।

यथा – सन्यासी कुटीरे कटं प्रसारयति । (कुटीरः)

• सर्प: ………… दशति । (पादौ)
• धान्यं ………… शुष्यति । (छदि:)
• कथा: ………… सन्ति। (पुराणानि)
• सौन्दर्यं ………… अस्ति। (मूर्त्ति:)
• जगन्नाथमन्दिरं’ ………… अस्ति। (पुरी)
• सैनिका: ………… गच्छन्ति। (पर्वता:)
• पक्षिण: ………… उपविशन्ति। (शाखा:)
• सिंहा: ………… वसन्ति। (गुहाः)
• छात्रा: ………… नृत्यन्ति। (पङ्न्तिः)
• गृहिणी ………… धान्यं कुट्टयति। (उलूखलम्)
• विमानानि ………… सक्चरति। (गगनम्)
• शिशु: ………… मुद्रे स्थापयति। (मुष्टिः)
• जना ………… तिलकं धरन्ति। (ललाट:)
• रस: ………… भवति । (इक्षु:)

ଉତ୍ତରମ୍

यथा- सन्यासी कुटीरे कटं प्रसारयति ।
ସନ୍ୟାସୀ କୁଟୀରେ କରଂ ପ୍ରସାରୟତି ।

(क) सर्प: पादौ दशति ।
ସପଃ ପାଦୟୋ ଦଶତି ।

(ख) धान्यं छदौ शुष्यति ।
ଧାନ୍ୟ ଛଦୌ ଶୁଷ୍ଯତି ।

(ग) कथाः पुराणेषु सन्ति।
କଥା ପୁରାଣେଷୁ ସନ୍ତି |

(घ) सौन्दर्य मूत्तौ अस्ति।
ସୌନ୍ଦର୍ଯ୍ୟ ମୂଭୌ ଅସ୍ତ ।

(ङ) जगन्नाथमन्दिरं पूर्याम् अस्ति।
ଜଗନ୍ନାଥମନ୍ଦିରଂ ପୂର୍ଜ୍ୟମ୍ ଅଛି।

(च) सैनिकाः पर्वतेषु गच्छन्ति।
ସୈନିକା ପର୍ବତେଷୁ ଗଛନ୍ତି ।

(छ) पक्षिण: शाखासु उपविशन्ति।
ପକ୍ଷିଣ ଶାଖାସୁ ଉପବିଶନ୍ତି ।

(ज) सिंहाः गुहासु वसन्ति।
ସିଂହା ଗୁହାସୁ ବସନ୍ତି ।

(झ) छात्रा: पङ्क्तिषु नृत्यन्ति।
ଛାତ୍ରା ପଚ୍ଛିଶୁ ନୃତ୍ୟନ୍ତି।

(অ) गृहिणी उलूखले धान्यं कुट्टयति।
ଗୃହିଣୀ ଉଲ୍ଲେଖଳେ ଧାନ୍ୟ କୁଟ୍ଟୟତି ।

(ट) विमानानि गगने सश्चरन्ति।
ବିମାନାନି ଗଗନେ ସଞ୍ଚରନ୍ତି ।

(ठ) शिशुः मुष्टौ मुद्रे स्थापयति।
ଶିଶୁ ମୁଷ୍ଟି ମୁଦ୍ରେ ସ୍ଥାପୟତି।

(ढ) जना: ललाटे तिलकं धरन्ति।
ଜନଃ ଲଲାଟେ ତିଳକଂ ଧରନ୍ତି।

(ण) रस: इक्षै भवति ।
ରସ ଇକ୍ଷୌ ଭବତି ।

२. कोष्ठक-साहाय्येन उदाहरणानुसारं वाक्यानि लिखतु ।
(ବନ୍ଧନୀମଧ୍ଯସ୍ପୃସ୍ୟ ଶବ୍ଦସ୍ୟ ଯଥାର୍ଥ ରୂପଂ ଶୂନ୍ୟସ୍ଥାନେ ପୂରୟତୁ।) ବନ୍ଧନୀ ମଧ୍ଯରେ ଥ‌ିବା ଶବ୍ଦର ଯଥାର୍ଥ ରୂପ ନେଇ ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର ।
उदाहरणम् :
प्रकाशः दीपे भवति ।
………………………………………………
………………………………………………
………………………………………………
………………………………………………

………………………………………………
………………………………………………
………………………………………………

(क) प्रकाशः दीपे भवति ।
ପ୍ରକାଶଃ ଦୀପେ ଭବତି।

(ख) कोलाहल：मेलायां भवति ।
କୋଳାହଳ ମେଳାୟାଂ ଭବତି

(ग) श्य्या पर्यङ्के भवति।
ଶଯ୍ୟା ପର୍ଯଙ୍କ ଭବତି ।

(घ) व्याधिः शरीरे भवति।
ବ୍ୟାଧ୍ୱ ଶରୀରେ ଭବତି ।

(ङ) पक्षी नीडे उपविशति।
ପକ୍ଷୀ ନୀଡ଼େ ଉପବିଶତି ।

(च) वानरः वृक्षे उपविशति।
ବାନରଃ ବୃକ୍ଷେ ଉପବିଶତି ।

(छ) मनुष्य：वीथौ गच्छति ।
ମନୁଷ୍ୟ ବୀର୍ଥେ ଗଛନ୍ତି ।

(ज) विमानं आकाशे गच्छति।
ବିମାନଂ ଆକାଶେ ଗଛନ୍ତି ।

(झ) भ्रमरः पुष्पे उपविशति ।
ଭ୍ରମରଃ ପୁଷ୍ପ ଉପବିଶତି।

३. चित्रं पश्यतु वाक्यानि लिखतु ।
(ଚିତ୍ର ପଶ୍ୟତୁ ବାକ୍ୟାନି ଲିଖନ୍ତୁ।)

उदाहरणम् :
सर्प: विलेषु सश्चरति ।
१. ………………………………………………
२. ………………………………………………
३.  ………………………………………………
४. ………………………………………………
………………………………………………
………………………………………………
………………………………………………

१. सर्प: विलेषु सश्चरति।
ସର୍ପ ବିଳେଷୁ ସଞ୍ଚରତି।

२. सर्प: लतायां संचरति।
ସର୍ପ ଲତାୟାଂ ସଞ୍ଚରତି ।

३. सर्पः तरुषु संचरति।
ସର୍ପ ତରୁଷୁ ସଞ୍ଚରତି।

४. सर्प: वल्मीकेषु संचरति ।
ସର୍ପ ବଲ୍ଲୀକେଷୁ ସଞ୍ଚରତି।

५. सर्प: गुहासु संचरति।
ସର୍ପ ଗୁହାସୁ ସଞ୍ଚରତି।

६. सर्प: गुल्मेषु संचरति।
ସର୍ପ ଗୁଳ୍ମଷୁ ସଞ୍ଚରତି।

७. सर्प: कन्दरायां संचरति।
ସର୍ପ କନ୍ଦରାୟାଂ ସଞ୍ଚରତି ।

८. सर्प: गिरिषु संचरति।
ସର୍ପ ଗିରିଶୁ ସଞ୍ଚରତି।

४. कोष्ठक-साहाय्येन वाक्यानि रचयुत
(କୋଷ୍ଠକ-ସାହାଯ୍ୟନ ବାକ୍ୟାନି ରଚୟତୁ।)

उदाहरणम् :
कन्दुके सूतयो : स्त:।
………………………………………….
………………………………………….
………………………………………….
उदाहरणम् :
जना: वाटिकयो : सन्ति ।
………………………………………….
………………………………………….
………………………………………….
उत्तर :
(क) कन्दुके स्यूतयो ：स्तः।
କନ୍ଦୁକେ ସୂତୟୋ ୟଃ |

(ख) कङ़्मेणे हस्तयो ：स्तः।
କଙ୍କଣେ ହସ୍ତୟୋ ସ୍ତ୍ରୀ ।

(ग) कर्णाभरणे कर्णयो ：स्तः।
କଣ୍ଟାଭରଣେ କଣ୍ଠୀୟୋ ୟଃ ।

(घ) नूपुरे पादयो ：सन्ति ।
ନୂପୁରେ ପାଦୟୋ ୟଃ |

(ङ) जना：वाटिकयो：सन्ति ।
ଜନଃ ବାଟିକୟୋ ସନ୍ତି ।

(च) आभूषणानि पेटिकयो：सन्ति ।
ଆଭୂଷଣାନି ପେଟିକ ସନ୍ତି ।

(छ) कागदानि सश्चिकयो ：सन्ति ।
କାଗଦାନି ସଞ୍ଚୟୋ ସନ୍ତି।

(ज) चित्राणि शाटिकयो ：सन्ति ।
ଚିତ୍ରାଣି ଶାଟିକୟୋ ସନ୍ତି ।

५. उदाहरणानुसारम् एतै : पदै: वाक्यानि रचयतु
(ଉଦାହରଣାନୁସାରମ୍ ଏତୌ ପଦଃ ବାକ୍ୟାନି ରଚୟତୁ।) :

१. जना: आपणेषु उपविशन्ति ।
ଜନଃ ଆପଣେଷୁ ଉପବିଶନ୍ତି ।

२. जना: मार्गेषु भ्रमन्ति ।
ଜନଃ ମାର୍ଗେଷୁ ଭ୍ରମନ୍ତି।

३. जना: कार्यालयेषु उपविशन्ति ।
ଜନଃ କାର୍ଯ୍ୟାଳୟେଷୁ ଭ୍ରମନ୍ତି।

४. जना: उद्यानेषु भ्रमन्ति ।
ଜନଃ ଉଦ୍ୟାନେଷୁ ଭ୍ରମନ୍ତି।

५. जना: यानेषु उपविशन्ति ।
ଜନଃ ଯନେଷୁ ଉପବିଶନ୍ତି ।

६. जना: पर्यटनस्थलेषु भ्रमन्ति ।
ଜନଃ ପର୍ଯ୍ୟଟନସ୍ଥଳେଷୁ ଭ୍ରମନ୍ତି |

७. जना: गृहेषु उपविशन्ति ।
ଜନଃ ଗୃହେତୁ ଉପବିଶନ୍ତି ।

८. जना: महानगरेषु भ्रमन्ति ।
ଜନଃ ମହାନଗରେଷୁ ଭ୍ରମନ୍ତି।

९. जना: सभासु उपविशन्ति ।
ଜନଃ ସଭାସୁ ଉପବିଶନ୍ତି ।

१०. जना: वीथिषु भ्रमन्ति ।
ଜନଃ ବୀଥ୍ଷୁ ଭ୍ରମନ୍ତି।

११. जना: गोष्ठीषु उपविशन्ति ।
ଜନଃ ଗୋଷ୍ଠୀଷୁ ଉପବିଶନ୍ତି ।

१२. जना: प्रदर्शनीषु भ्रमन्ति ।
ଜନଃ ପ୍ରଦର୍ଶନୀଷୁ ଭ୍ରମନ୍ତି।

अतिरिक्त प्रश्नोत्तरम्
(ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातृभाषया अनुवादं कुरुत।

(क) बालक：पलङ्के निद्राति।
उत्तर :
ପିଲାଟି ପଲଙ୍କରେ ଶୋଇଛି।

(ख) जलं कुप्याम् अस्ति।
उत्तर :
ପାଣି ବୋତଲରେ ଅଛି।

(ग) जननी पाकशालायां पचति।
उत्तर :
ମାଆ ରୋଷଶାଳାରେ ରାନ୍ଧୁଛନ୍ତି ।

(घ) मीना：जले सन्तरन्ति।
उत्तर :
ମାଛମାନେ ଜଳରେ ପହଁରନ୍ତି।

(ङ) वेदना कर्णयो ：अस्ति।
उत्तर :
ଦୁଇ କାନରେ ଯନ୍ତ୍ରଣା ଅଛି ।

(च) श्लोकाः ग्रेन्थेषु सन्ति।
उत्तर :
ଗ୍ରନ୍ଥମାନଙ୍କରେ ଶ୍ଳୋକ ଅଛି ।

(छ) जानयो ：चक्राणि सन्ति।
उत्तर :
ଗାଡ଼ି ଦୁଇଟିରେ ଚକ ରହିଛି।

२. एकपदेन उत्तरं लिखत।
(क) जना：केषु भ्रमन्ति ？
उत्तर :
ମାର୍ଗେଷୁ

(ख) धनं कुत्र अस्ति ?
उत्तर :
କୋଷ

(ग) नद्यां का चलति ?
उत्तर :
ନୌକା

(घ) सिंहा: कुत्र गर्जन्ति ?
उत्तर :
ପର୍ବତେ

(ङ) पुस्तकेषु कानि सन्ति ?
उत्तर :
ଚିତ୍ରାଣି

(च) के वीथिषु सश्चरन्ति ?
उत्तर :
ଜନାଃ

(छ) दण्ड: कयो : अस्ति ?
उत्तर :
ସ୍ତମ୍ଭୟୋ

३. शून्यस्थानं पूरयत।
(क) शिशु: …………. अस्ति।
उत्तर :
ଦୋଳାୟାମ୍

(ख) पशव: …………. विहरन्ति।
उत्तर :
ବନେ

(ग) …………. पेटिकायो : सन्ति।
उत्तर :
ଭୂଷଣାନି

(घ) वार्त्ता: …………. सान्ति।
उत्तर :
ପତ୍ରିକାସୁ

(ङ) अश्रूणि …………. सन्ति।
उत्तर :
ନେତ୍ରୟୋ

(च) पुष्पाणि लतयो: …………. |
उत्तर :
ବିକସନ୍ତି

४. विक्षिप्तवर्णानां मेलनेन शुद्धपदं रचयत।
(क) च षु के ष
उत्तर :
ଚଷକେଷୁ

(ख) म ला क नि
उत्तर :
କମଳାନି

(ग) पा रा ज्य ल:
उत्तर :
ରାଜ୍ୟପାଳୀ

(घ) स यो गा नं
उत्तर :

(ङ) क: च वा
उत्तर :

५. स्तम्भमेलनं कुरूत।

‘क’ स्मम्भ: — ‘ख’ स्तम्भ:
पादे — कर्त्तुषु
नीति: — गृहेषु
वटु: — पादेषु
गृहे — नीतिषु
कर्त्ता — वटुषु
उत्तर :
‘କ’ ସ୍ତମ୍ଭ — ‘ଖ’ ସ୍ତମ୍ଭ
ପାଦେ — ପାଦେଷୁ
ନୀତିଃ — ନୀତିଷୁ
ବଟୁ — ବଟୁଷୁ
ଗୃହେ — ଗୃହେଷୁ
କର୍ତ୍ତା — କର୍ତ୍ତୃଷୁ

६. मातृभाषया अर्थं प्रकाशयत ।
(क) कण्डोलयो: ଝୁଡି ଦୁଇଟିରେ
(ख) वीधिषु ରାସ୍ତାରେ
(ग) वेदना ଯନ୍ତ୍ରଣା
(घ) कटे ମଶିଣାରେ
(ङ) हस्तयो: ହାତ ଦୁଇଟିରେ

७. रेखाङ्कितपदानां भ्रमसंशोधनं कुरुत ।

(क) सिंहा: गुहासु वसति।
ସିଂହା ଗୁହାସୁ ବସନ୍ତି

(ख) छात्र: विद्यालये पठन्ति।
ଛାତ୍ରା ବିଦ୍ୟାଳୟ ପଠନ୍ତି ।

(ग) जना: मार्गेसु भ्रमन्ति।
ଜନାଃ ମାର୍ଗେଷୁ ଭ୍ରମନ୍ତି।

(घ) क्षीरः चषकेषु अस्ति।
କ୍ଷୀରଂ ଚଷକେଷୁ ଅଛି ।

(ङ) बालकाः सोपानेशु क्रीडन्ति।
ବାଳକା ସୋପା ନେଷୁ କ୍ରୀଡ଼ନ୍ତି।

८. उत्तर चयनं कुरूत।
(क) कमलामि केषु विकसन्ति ?
(a) नदीषु
(b) जलेषु
(c) सागरेषु
(d) सरोवरेषु
उत्तर :
(d) ସରୋବରେଷୁ

(ख) पक्षिणः कुत्र तिष्ठन्ति ?
(a) शाखायाम्
(b) शाखायु:
(c) शाखासु
(d) शाखाभ्यै
उत्तर :
(a) ଶାଖାସୁ

(ग) ध्वनिमुद्रिकयो: कानि सान्ति ?
(a) भीतानि
(b) प्रीतानि
(c) गीतानि
(d) मित्राणि
उत्तर :
(c) ଗୀତାଳି

(घ) का: वाटिकायां भ्रमन्ति ?
(a) बालिका
(b) बालिका:
(c) बालिके
(d) बालिकाया:
उत्तर :
(b) ବାଳିକା

(ङ) जले के सन्तरन्ति ?
(a) कच्छपा:
(b) मकरा:
(c) वानरा:
(d) मीना:
उत्तर :
(d) ମୀନା:

पश्यतु, उच्चै: पठतु च (ପଶ୍ୟତୁ, ଉଚ୍ଚୈଃ ପଠତୁ ଚ)
ଦେଖନ୍ତୁ ବଡ଼ପାଟିରେ ପଢ଼ନ୍ତୁ :

नर्तकी मश्रे नृत्यति ।
(ନର୍ତକୀ ମଞ୍ଚେ ନୃତ୍ୟତି।)
ନର୍ତକୀ ମଞ୍ଚରେ ନାଚୁଛି।

युवक: कटे योगासनं करोति ।
(ଯୁବକଃ କଟେ ଯୋଗାସନଂ କରୋତି।)
ଯୁବକଟି ମଶିଣାରେ ଯୋଗାସନ କରୁଛି ।

धनं कोषे अस्ति ।
(ଧନଂ କୋଷେ ଅଛି।)
ଟଙ୍କା ପକେଟରେ ଅଛି ।

छात्रा: विद्यालये पठन्ति ।
(ଛାତ୍ରୀ ବିଦ୍ୟାଳୟ ପଠନ୍ତି।)
ଛାତ୍ରମାନେ ସ୍କୁଲରେ ପଢୁଛନ୍ତି ।

बालिका: वाटिकायां भ्रमन्ति ।
(ବାଳିକା ବାଟିକାୟାଂ ଭ୍ରମନ୍ତି।)
ଝିଅଟି ବଗିରରେ ବୁଲୁଛନ୍ତି ।

भगिनी स्थालिकायां भोजनम् आनयति ।
(ଭଗିନୀ ସ୍ଲାଳିକାୟାଂ ଭୋଜନମ୍ ଆନୟତି।)
ଭଉଣୀ ଥାଳିରେ ଖାଦ୍ୟ ଆଣୁଛି ।

शिशु : दोलायाम् अस्ति ।
(ଶିଶୁ ଦୋଳାୟାମ୍ ଅସ୍ଥି ।)
ଶିଶୁଟି ଦୋଳିରେ ଅଛି।

जननी पाकशालायां पचति ।
(ଜନନୀ ପାକଶାଳାୟଃ ପଚତି।)
ମାଆ ରୋଷଶାଳରେ ରୋଷେଇ କରୁଛି।

वाचक: सभायां बदति ।
(ବାଚକ ସଭାୟାଂ ବଦତି।)
ପ୍ରବଚକ ସଭାରେ କହୁଛନ୍ତି ।

नौका नद्यां चलति ।
(ନୌକା ନଦ୍ୟା ଚଳତି।)
ନଈରେ ଡଙ୍ଗା ଗଲେ ।

राज्यपाल: राजधान्यां तिष्ठति ।
(ରାଜ୍ୟପାଳ ରାଜଧାନ୍ୟ ତିଷ୍ଠତି।)
ରାଜ୍ୟପାଳ ରାଜଧାନୀରେ ରୁହନ୍ତି।

जलं कुप्याम् अस्ति ।
(ଜଳଂ କୁପ୍ୟାମ୍ ଅଛି।)
ପାଣି ବୋତଲରେ ଅଛି ।

मीना: जले सन्तरन्ति
(ମୀନାଃ ଜଳେ ସନ୍ତରନ୍ତି।)
ମାଛମାନେ ପାଣିରେ ପହଁରନ୍ତି।

पशव: वने विहरन्ति ।
(ପଶତଃ ବନେ ବିହରନ୍ତି।)
‘ପଶୁମାନେ ବଣରେ ବିହାର କରନ୍ତି।

सिंह़ाः पर्वते गर्जन्ति ।
(ସିଂହାଃ ପର୍ବତେ ଗର୍ଜନ୍ତି।)
ସିଂହମାନେ ପର୍ବତରେ ଗର୍ଜନ କରନ୍ତି।

फलानि कण्डोलयो: सन्ति ।
(ଫଳାନି କଣ୍ଡୋଳୟୋ ସନ୍ତି ।)
ଦୁଇଟି ଝୁଡ଼ିରେ ଫଳଗୁଡ଼ିକ ଅଛି।

वेदना कर्णयो : अस्ति ।
(ବେଦନା କୟୋ ଅସ୍ଥି ।)
ଦୁଇକାନରେ ଯନ୍ତ୍ରଣା ଅଛି।

पुस्तकानि निधिानिकयो : सन्ति ।
(ପୁସ୍ତକାନି ନିଧାନିକୟୋ ସନ୍ତି ।)
ବହିଗୁଡ଼ିକ ଦୁଇ ଥାକରେ ରହିଛି।

भूषणानि पेटिकयो : सन्ति ।
(ଭୂଷଣାନି ପେଟିକ ସନ୍ତୋ ।)
ଅଳଙ୍କାରଗୁଡ଼ିକ ବାକ୍ସଦୁଇଟିରେ ରହିଛି।

पुष्पाणि हस्तयो : सन्ति ।
(ପୁଷ୍ପାଣି ହସ୍ତୟୋ ସନ୍ତୋ ।)
ଦୁଇହାତରେ ଫୁଲଗୁଡ଼ିଏ ଅଛି।

दण्ड: स्तम्भयो : अस्ति ।
(ଦଣ୍ଡ ସ୍ତମ୍ଭୟୋ ଅସ୍ଥି ।)
ବାଡ଼ି ଦୁଇଖୁଣ୍ଟ ଉପରେ ଅଛି।

पुष्पाणि लतयो : विकसन्ति ।
(ପୁଷ୍ପାଣି ଲତ ବିକସନ୍ତି ।)
ଫୁଲଗୁଡ଼ିକ ଦୁଇଲତାରେ  ଫୁଟିଛି।

गीतानि ध्वनिमुद्रिकयो : सन्ति ।
(ଗୀତାନି ଧ୍ଵନିମୁଦ୍ରିକୟୋ ସନ୍ତୋ।)
ଦୁଇଟି କ୍ୟାସେଟରେ ସବୁଗୀତ ଅଛି।

जलं द्रोणयो : निपतिति ।
(ଜଳଂ ଦ୍ରୋଣେ ନିପତତି।)
ଦୁଇ ବାଲ୍ଟିରେ ପାଣି ପଡୁଛି ।

तैलं दर्व्यो : अस्ति ।
(ତୈଳ ଦ୍ରବ୍ୟ ଅସ୍ଥି ।)
ଦୁଇଟି ଡଙ୍କିରେ ତେଲ ଅଛି।

मसी पुनः पूरणयो : अस्ति ।
(ମସୀ ପୁନଃ ପୂରଣ୍ୟା ଅସ୍ତି।)
ରିଫଲ୍ ଦୁଇଟିରେ କାଳି ଅଛି ।

मीना: नद्यो : सन्ति ।
(ମୀନାଃ ନଦ୍ୟୋ ସନ୍ତୋ।)
ନଈ ଦୁଇଟିରେ ମାଛ ଅଛନ୍ତି ।

यानयो : चक्राणि सन्ति ।
(ଯାନ ଚକ୍ରାଣି ସନ୍ତ।)
ଗାଡ଼ିଦୁଇଟିରେ ଚକ ରହିଛି ।

अश्रूणि नेत्र्यो : सन्ति ।
(ଆଶୁଣି ନେତ୍ର ସନ୍ତ।)
ଦୁଇଆଖରେ ଲୋତକ ଅଛି ।

अलङ्कारा: कर्णयो : भान्ति ।
(ଅଳଙ୍କାରଃ କର୍ଷ ଭାନ୍ତି।)
କାନଦୁଇଟିରେ ଅଳଙ୍କାର ଶୋଭାପାଉଛି।

बालका: आसनयो : उपविशन्ति ।
(ବାଳକା ଆସନୟୋ ଉପବିଶକ୍ତି।)
ପିଲାମାନେ ଦୁଇଟି ଆସନରେ ବସିଛନ୍ତି।

जना: मार्गेषु भ्रमन्ति ।
(ଜନା ମାର୍ଗେଷୁ ଭ୍ରମନ୍ତି।)
ଲୋକମାନେ ରାସ୍ତାରେ ବୁଲୁଛନ୍ତି ।

फलानि वृक्षेषु सन्ति ।
(ଫଳାନି ବୃକ୍ଷେଷୁ ସନ୍ତି ।)
ଗଛମାନଙ୍କରେ ଫଳ ଅଛି।

क्षीरं चषकेषु अस्ति ।
(କ୍ଷୀରଂ ଚଷକେଷୁ ଅସ୍ତି।)
ଗ୍ଲାସ୍‌ରେ କ୍ଷୀର ଅଛି ।

श्लोकाः ग्रन्थेषु सन्ति ।
(ଶ୍ଳୋକା ଗ୍ରନ୍ମେଷୁ ସଜ୍ଜି ।)
ଗ୍ରନ୍ଥମାନଙ୍କରେ ଶ୍ଳୋକ ଅଛି ।

वार्त्ता : पत्रिकासु सन्ति ।
(ବାର୍ତ୍ତା ପତ୍ରିକାସୁ ସନ୍ତ।)
ପତ୍ରିକାମାନଙ୍କରେ ଖବର ଅଛି ।

कागदानि सन्त्रिकासु सन्ति ।
(କାଗଦାନି ସଞ୍ଚକାସୁ ସଜ୍ଜି ।)
ଫାଇଲମାନଙ୍କରେ କାଗଜ ଅଛି।

पक्षिण：शाखासु तिष्ठन्ति ।
(ପକ୍ଷିତଃ ଶାଖାସୁ ତିଷ୍ଠନ୍ତି।)
ପକ୍ଷୀମାନେ ଡାଳମାନଙ୍କରେ ବସିଛନ୍ତି।

सिंहा：गुहासु वसन्ति ।
(ସିଂହା ଗ୍ରହାସୁ ବସନ୍ତି।)
ସିଂହମାନେ ଗୁମ୍ଫାମାନଙ୍କରେ ବାସକରନ୍ତି।

चित्राणि पुस्तकेषु सन्ति ।
(ଚିତ୍ରାଣି ପୁସ୍ତକେଖୁ ସନ୍ତି ।)
ବହିମାନଙ୍କରେ ଛବି ଅଛି।

जलं कूपीषु अस्ति।
(ଜଳଂ କୃପୀଷୁ ଅସ୍ତି।)
ବୋତଲମାନଙ୍କରେ ପାଣି ଅଛି।

कर्मकारा：यन्त्रागारेषु कार्य कुर्वन्ति ।
(କର୍ମକାରଃ ଯନ୍ତ୍ରାଗାରେଷୁ କାର୍ଯ୍ୟ କୁର୍ବନ୍ତି।)
କର୍ମରରୀମାନେ ଯନ୍ତ୍ରାଗାରରେ କାର୍ଯ୍ୟ କରୁଛନ୍ତି।

बालका：सोपानेषु क्रीड़न्ति ।
(ବାଳକା ସୋପାନେଷୁ କ୍ରୀଡ଼ନ୍ତି।)
ବାଳକମାନେ ପାହାଚମାନଙ୍କରେ ଖେଳୁଛନ୍ତି।

कमलानि सरोवरेषु विकसन्ति ।
(କମଳାନି ସରୋବରେଷୁ ବିକସନ୍ତି ।)
ପୋଖରୀମାନଙ୍କରେ ପଦ୍ମ ଫୁଟିଛି ।

जना：वीथिषु सक्षरान्ति ।
(ଜନଃ ବୀଥୁଷୁ ସଞ୍ଚରନ୍ତି।)
ଲୋକମାନେ ରାସ୍ତାରେ ବୁଲୁଛନ୍ତି ।

टिप्पणी (ଟିପ୍ପଣୀ) :

• कण्डोलयो :  (କଣ୍ଡଳ) – ଝୁଡ଼ି ଦୁଇଟିରେ
• कण्डोल (କଣ୍ଡୋଳୀ) – ଝୁଡ଼ି
• दर्व्यो : (ଦର୍ଯ୍ୟା) – ପଳା ଦୁଇଟିରେ
• दर्वी (ଦର୍ବୀ) – ଡଙ୍କା, ତେଲ ମପାଯାଉଥିବା ପାତ୍ର
• मसी (ମସୀ) – କାଳି । ସ୍ୟାହି
• पुनः पूरणयो : (ପୁନଃ ପୂରଣ୍ୟା) – ରିଫଲ୍ ଦୁଇଟିରେ
• पुनः पूरणी (ପୁନଃ ପୂରଣୀ) – ରିଫଲ
• कटे (କଟେ) – ସପରେ । ମସିଣାରେ
• पयङ्के (ପର୍ଯ୍ୟଙ୍କେ) – ପଲଙ୍କରେ
• निधानिकयो : (ନିଧାନିକୟୋ) – ଥାକ ଦୁଇଟିରେ
• ध्वनिमुद्रिकयो :(ଧ୍ୱନିମୁଦ୍ରିକୟୋ) – କ୍ୟାସେଟ୍ଦୁଇଟିରେ

Odisha State Board BSE Odisha 7th Class Sanskrit Solutions Chapter 17 ଆତ୍ମ-ନ-ବା ପ୍ରୟୋଗଃ Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Sanskrit Solutions Chapter 17 ଆତ୍ମ-ନ-ବା ପ୍ରୟୋଗଃ

१. कोष्ठकस्थं चिह्नं पश्यतु, उचितवाक्यानि लिखतु।
(କୋଷ୍ଠକରଂ ଚିହ୍ନ ପଶ୍ୟତୁ, ଉଚିତବାକ୍ୟାନି ଲିଖନ୍ତୁ।)

उदाहरण –
१. गोपबन्धु: देशभक्त: वा ? आम् स: देशभक्त:। स: सत्र्यासी न ।

ଉତ୍ତରମ୍

१. गोपबन्धुः देशभक्त: वा ? आम् स: देशभक्तः। स: सन्य्यासी न ।
ଗୋପବନ୍ଧୁ ଦେଶଭକ୍ତ ବା ? ଆମ୍, ଡଃ ଦେଶଭକ୍ତ । ଡଃ ସନ୍ନ୍ୟାସୀ ନ ।

२. श्रीधर: छात्र: वा ? आम् स: छात्र:। स: वैद्य: न ।
ଶ୍ରୀଧରଃ ଛାତ୍ରୀ ବା ? ଆମ୍ ସ ଛାତ୍ରୀ। ଡଃ ବୈଦ୍ୟ ନ ।

३. प्रतिमा समाजसेविका वा ? न, सा समाजसेविका न । सा शिक्षिका ।
ପ୍ରତିମା ସମାଜସେବିକା ବା ? ନ, ସା ସମାଜସେବିକା ନ। ସା ଶିକ୍ଷିକା।

४. सुरेश: चित्रकार: वा ? आम्, स: चित्रकार:। स: कर्मकार: न।
ସୁରେଶଃ ଚିତ୍ରକାରଃ ବା ? ଆମ୍, ଡଃ ଚିତ୍ରକାରଃ । ଡଃ କର୍ମକାରଃ ନ ।

५. नरेन्द्र: शिक्षक: वा ? न, स: शिक्षक: न। स: सेवक:।
ନରେନ୍ଦ୍ର ଶିକ୍ଷକ ବା ? ନ, ଡଃ ଶିକ୍ଷକ ନ । ୟଃ ସେବକଃ ।

६. अबदुलकालाम वैज्ञानिक: वा ? आम्, स: वैज्ञानिक:। स: सैनिक: न।
ଅବଦୁଲକାଲାମ ବୈଜ୍ଞାନିକ ବା ? ଆମ୍, ଡଃ ବୈଜ୍ଞାନିକ । ଡଃ ସୈନିକଃ ନ ।

अतिरिक्त प्रश्नोत्तरम्
(ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१．मातृभाषया अनुवादं कुरुत।
(क) स：गज：वा ？
उत्तर :
ସେ ହାତୀ କି ?

(ख) आम्，एतानि पुष्पाणि।
उत्तर :
ହଁ, ଏଗୁଡ଼ିକ ଫୁଲ ।

(ग) ते वृक्षा：वा ？
उत्तर :
ସେଗୁଡ଼ିକ ଗଛ କି ?

(घ) एतत्मुष्पं वा ？
उत्तर :
ଏହା ଫୁଲ କି ?

(ङ) न，तत् विमानम्।
उत्तर :
ନା, ତାହା ଉଡାଜାହାଜ ।

(च) आम्，छात्र：पठति।
उत्तर :
ହଁ, ଛାତ୍ର ପଢୁଛି ।

(छ) बालिका नृत्यति।
उत्तर :
ବାଳିକା ନାଚୁଛି ।

२. विक्षिप्तवर्णानां मेलनेन शुद्धपदं रचयत।

(क) मा न वि म्
उत्तर :
ବିମାନମ୍

(ख) ज：ग
उत्तर :
ଗଜଃ

(ग) नि ता ए
उत्तर :
ଏତାନି

(घ) र्म का क र：
उत्तर :
କର୍ମକାରଃ

(ङ) क ला नि म
उत्तर :
କମଳାନି

३. स्तम्भमेलनं कुरूत।

‘क’ स्मम्भः — ‘ख’ स्तम्भ:
एष: — पुष्पाणि
स: — विमानम्
एषा — बालक:
तत् — गज:
एतानि — धेनु:
उत्तर :

४. मातृभाषया अर्थं प्रकाशयत।
(क) गज:
उत्तर :
ହାତୀ

(ख) कैरवम्
उत्तर :
କଇଁ

(ग) कमलानि
उत्तर :
ପଦ୍ମଗୁଡ଼ିକ

(घ) नृत्यति
उत्तर :
ନାଚୁଛି

(ङ) पठति
उत्तर :
ପଢୁଛି

आम्-न-वा प्रयोग:
ଆମ୍ବ-ନ-ବା ପ୍ରୟୋଗ (ବ୍ୟବହାର)

एषः बालक: वा ?
(ଏଷ ବାଳକଃ ବା ?)
ଇଏ ବାଳକ କି ?
आम्, एष: बालक:।
(ଆମ୍, ଏଷୀ ବାଳକଃ ।)
ହଁ ଇଏ ବାଳକ।

स: गज: वा ?
(ସ୍ୱ ଗଜଃ ବା ?)
ସେ ହାତୀ କି ?
आम्, स: गज:।
(ଆମ୍, ଡଃ ଗଜଃ । )
ହଁ ସେ ହାତୀ।

एषा अजा वा ?
(ଏଷା ଅଜା ବା ?)
ଇଏ ମାଈଛେଳି କି ?
न एषा धेनु : ।
(ନ, ଏଷା ଧେନୁଃ ।)
ନା, ଏଇ ଗାଈ ।

तत् लोकयानं वा ?
ତାହା ବସ୍ କି ?
न, तत् विमानम् ।
(ନ, ତତ୍ ବିମାନମ୍ ।)
ନା, ତାହା ଉଡ଼ାଜାହଜ।

एतत् पुष्पं वा ?
(ଏତତ୍ ପୁଷ୍ପ ବା ?)
ଏହା ଫୁଲ କି ?
न, एतत् पत्रम् ।
(ନ, ଏତତ୍ ପତ୍ରମ୍ ।)
ନା, ଏହା ପତ୍ର।

एते गजा: वा ?
(ଏତେ ଗଜାଃ ବା ? )
ଏଗୁଡ଼ିକ ଛେଳି କି ?
न, एते अश्वा: ।
(ନ, ଏତେ ଅଶ୍ଵ।)
ନା, ଏଗୁଡ଼ିକ ଘୋଡ଼ା।

ते वृक्षाः वा ?
(ତେ ବୃକ୍ଷା ବା ?)
ସେଗୁଡ଼ିକ ଗଛ କି ?
आम्, ते वृक्षा:।
(ଆମ୍, ତେ ବୃକ୍ଷା ।)
ହଁ, ସେଗୁଡ଼ିକ ଗଛ।

एता: माला: वा?
(ଏତା ମାଳା ବା ?)
ଏଗୁଡ଼ିକ ମାଳ କି ?

आम्, एता: माला:।
(ଆମ୍, ତେ ବୃକ୍ଷା ।)
ହଁ, ସେଗୁଡ଼ିକ ଗଛ।

ता: गदा: वा ?
(ତାଃ ଗଦା ବା ?)
ସେଗୁଡ଼ାକ ଗଦା କି ?
आम्, ता गदाः।
(ଆମ୍, ତାଃ ଗଦା ।)
ହଁ, ସେଗୁଡ଼ିକ ଗଦା।

एतानि पुष्पाणि वा ?
(ଏତାନି ପୁଷ୍ପାଣି ବା ?)
ଏଗୁଡ଼ିକ ଫୁଲ କି ?
आम्, एतानि पुष्पाणि ।
(ଆମ୍ବ, ଏତାନି ପୁଷ୍ପାଣି।)
ହଁ, ଏଗୁଡ଼ିକ ଫୁଲ। ।

तानि कैरवाणि वा ?
(ବାଳକ ନ୍ୟତ୍ୟତି ବା ?)
ବାଳକଟି ନାଚୁଛି କି ?
न, तानि कमलानि ।
(ତାନି କୈରବାଣି ବା ?)
ସେଗୁଡ଼ିକ କଇଁଫୁଲ କି ?

बालक: नृत्यति वा ?
(ନ, ବାଳକଃ ନ ନୃତ୍ୟତି।)
ନା, ବାଳକ ନାଚୁ ନାହିଁ।
न, बालक: न नृत्यति ।
(ନ, ତାନି କମଳାନି।)
ନା,ସେଗୁଡ଼ିକ ପଦ୍ମଫୁଲ।

बालिंका नृत्यति ।
(ବାଳିକା ନୃତ୍ୟତି।)
ବାଳିକା ନାଚୁଛି।

छात्र: पठति वा ?
(ଛାତ୍ରୀ ପଠତି ବା ?)
ଛାତ୍ରଟି ପଢ଼ୁଛି କି ?
आम्, छात्र: पठति ।
(ଆମ୍, ଛାତ୍ରୀ ପଠତି।)
ହଁ, ଛାତ୍ର ପଢୁଛି।

 

Odisha State Board BSE Odisha 7th Class Sanskrit Solutions Chapter 18 ଲଙ୍ଲକାର ପ୍ରୟୋଗଃ Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Sanskrit Solutions Chapter 18 ଲଙ୍ଲକାର ପ୍ରୟୋଗଃ

१. उत्तराणि लिखतु
(ଉତ୍ତରାଣି ଲିଖତୁ) ଉତ୍ତର ଲେଖନ୍ତୁ:

(क) जम्बुवृक्षे कः अवसत् ？
ଜମ୍ବୁବୃକ୍ଷେ ଡଃ ଅବସତ୍ ?
(ଜାମୁ ଗଛରେ କିଏ ବାସ କରୁଥିଲା।)
उत्तर :
जम्बुवृक्षे वानरः अवसत्।
ଜମ୍ବୁବୃକ୍ଷେ ବାନରଃ ଅବସତ୍।

(ख) वानरः जम्बुफलानि कस्य कृते अददात् ？
ବାନରଃ ଜମ୍ବୁଫଳାନି କସ୍ୟ କୃତେ ଅଦଦାତ୍ ?
(ମାଙ୍କଡ଼ ଜାମୁକୋଳି କାହାକୁ ଦେଲା ?)
उत्तर :
वानरः जम्बुफलानि मकरस्य कृते अददात्।
ବାନରଃ ଜମ୍ବୁ ଫଳାନି ମକରସ୍ୟ କୃତେ ଅଦଦାତ୍।

(ग) कानि फलानि मधुराणि ？
କାନି ଫଳାନି ମଧୁରାଣି ?
(କେଉଁ ଫଳସବୁ ମଧୁର ?)
उत्तर :
जम्बुफलानि मधुराणि।
ଜମ୍ବୁ ଫଳାନି ମଧୁରାଣି।

(घ) वानर：किम् आरोहत् ？
ବାନରଃ କିମ୍ ଆରୋହତ୍ ?
(ମାଙ୍କଡ଼ କ’ଣ ଚଢ଼ିଲା ?)
उत्तर :
वानर：मकरस्य पृष्ठम् आरोहत्।
ବାନରଃ ମକରସ୍ୟ ପୃଷ୍ଠମ୍ ଆରୋହତ୍।

(ङ) क：निराशः अभवत् ？
କଃ ନିରାଶଃ ଅଭବତ୍ ?
କିଏ ହତାଶ ହେଲା ?
उत्तर :
मकर：निराश：अभवत्।
ମକରଃ ନିରାଶଃ ଅଭବତ୍ ।

२. शून्यस्थानानि पूरयतु (ଶୂନ୍ୟସ୍ଥାନାନି ପୂରୟତୁ)
ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର :
(क) एक： ……………. अवसत्।
(अहम्，वानरः，त्वम्)

(ख) मधुराणि ………… खादति ।
(फलं, फले, फलानि)

(ग) ………… ! सत्यं वदामि ।
(मित्रः, मित्रे, मित्र)

(घ) स: वानरं प्रति …………
(अकथय :, अकथयत्, अकथयम्)

(ङ) वानर: ………… अभवत् ।
(चकितः, चकितौ, चकिताः)
उत्तर :
(क) वानरः ବାନରଃ
(ख) फलानि ଫଳାନି
(ग) मित्र ମିତ୍ର
(घ) अकथयत् ଅକଥୟତ୍
(ङ) चकितः ଚକିତଃ

३. रेखाङ्कितपदानां संशोधनं करोतु।
(ରେଖାଙ୍କିତପଦାନାଂ ସଂଶୋଧନଂ କରୋତୁ।)
(क) अहं तत्र त्वं नयामि ।
(ख) अपरस्या दिवसे मकरः पुनः आगच्छत्।
(ग) एकस्मिन् नद्याः तीरे जम्बुवृक्षः आसीत्।
(घ) स: प्रक्वफलानि भक्षणम् अकरोत् ।
(ङं) मम भार्या तव हृदयम् इच्छामि ।
उत्तर :
(क) त्वां ନାଂ
(ख) अपरस्मिन् ଅପରସ୍କ୍ରିନ୍
(ग) एकस्या: ଏକସ୍ଯ
(घ) पक्वफलानां ପକ୍ବଫଳାନାଂ
(ङ) इच्छति ଇଚ୍ଛତି

४. चित्रं पश्यतु नाम लिखतु
(ଚିତ୍ର ପଶ୍ୟତୁ ନାମ ଲିଖନ୍ତୁ ।)

उत्तर :
(क) वानरः ବାନରଃ
(ख) वृक्ष: ବୃକ୍ଷ :
(ग) मकरः ମକରଃ
(घ) गज:  ଗଜଃ

अतिरिक्त प्रश्नोत्तरम्
(ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातृभाषया अनुवादं कुरुत।

(क) वृक्षस्य शाखायाम् एक: वानरः अवसत्।
ଗଛ ଡାଳରେ ଗୋଟିଏ ମାଙ୍କଡ ବାସ କରୁଥିଲା ।

(ख) स: मकरः कानिचन फलानि अखादत्।
ସେ କୁମ୍ଭୀର କେତେକ ଫଳ ଖାଇଲା ।

(ग) अहं तस्य वानरस्य हृदयम् इच्छामि।
ମୁଁ ସେହି ମାଙ୍କଡର ହୃଦୟ ଇଚ୍ଛା କରୁଛି ।

(घ) आगच्छ मम पृष्ठदेशे उपविश।
ଆସ ମୋ ପିଠିରେ ବସ ।

(ङ) मित्र ! सत्यं वदामि।
ବନ୍ଧୁ ! ସତ କହୁଛି ।

(च) हृदयं वृक्षस्य कोटरे अस्ति।
ହୃଦୟ ଗଛ କୋରଡରେ ଅଛି ।

(छ) मूर्ख: मकरः निराशः अभवत्।
ମୂର୍ଖ କୁମ୍ଭୀର ନିରାଶ ହେଲା ।

२. विक्षिप्तवर्णानां मेलनेन शुद्धपदं रचयत।

(क) या शा खा म्
उत्तर :
ଶାଖାୟାମ୍

(ख) णा स्व प्रा न्
उत्तर :
ସପ୍ରାଣାନ୍

(ग) तः किच
उत्तर :
ଚକିତଃ

(घ) या आ मि न
उत्तर :
ଆନୟାମି

(ङ) से व दि
उत्तर :
ଦିବସେ

३. स्तम्भमेलनं कुरूत।

‘क’ समम्भ: — ‘ख’ स्तम्भ:
एक: — हृदयम्
नद्या: — शाखायाम्
वृक्षस्य — चकित:
तव — मकर:
वानर: — तीरे
उत्तर :
‘କ’ ସ୍ତମ୍ଭ — ‘ଖ’ ସ୍ତମ୍ଭ
ଏକଃ — ମକରଃ
ନମଃ — ତୀରେ
ବୃକ୍ଷସ୍ଯ — ଶାଖାୟାମ୍
ତବ — ହୃଦୟମ୍
ବାନରଃ — ଚକିତଃ

४. मातृभाषया अर्थं प्रकाशयत।

(क) अधुना
उत्तर :
ବଧିମାନ

(ख) अवसत्
उत्तर :
ବାସ କରୁଥିଲା

(ग) अरक्षत्
उत्तर :
ରକ୍ଷା କଲା

(घ) मकरः
उत्तर :
କୁମ୍ଭୀର

(ङ) झटिति
उत्तर :
ଶୀଘ୍ର

८. उत्तर चयनं कुरूत।

(क) नद्याः तीरे क: वृक्ष: आसीत् ?
(a) जम्बु वृक्ष:
(b) आम्र वृक्ष:
(c) पनस वृक्ष:
(d) कदली वृक्ष:
उत्तर :
(a) ଜମ୍ବୁବୃକ୍ଷ

(ख) क: पक्वफलानां भक्षणम् अकरोत् ?
(a) मकर:
(b) शृगाल:
(c) वानर:
(d) कच्छपः
उत्तर :
(c) ବାନରଃ

(ग) क: पुन: वृक्षमूलम् आगच्छत् ?
(a) शृगाल:
(b) वानरः
(c) मूषिक:
(d) मकर:
उत्तर :
(d) ମକରଃ

(घ) हृदयं कस्य कोटरे अस्ति इति वानरः अवदत् ?
(a) नद्या:
(b) वृक्षस्य
(c) जलस्य
(d) लताया:
उत्तर :
(b) ବୃକ୍ଷସ୍ଯ

(ङ) वानरः केन स्वप्राणान् अरक्षत् ?
(a) कौशलेन
(b) सूत्रेण
(c) बलेन
(d) अस्रेण
उत्तर :
(a) କୌଶଳେନ

चतुरः वानरः
(ଚତୁରଃ ବାନରଃ) ଚତୁର ମାଙ୍କଡ଼

एकस्या: नद्या: तीरे एक: जम्बुवृक्ष: आसीत्। वृक्षस्य शाखायाम् एक: वानर: अवसत् । सः पक्वफलानां भक्षणम् अकरोत् ।
ଏକସ୍ୟା ନଦ୍ୟା ତୀରେ ଏକଃ ଜମ୍ବୁବୃକ୍ଷୀ ଆସୀତ୍ । ବୃକ୍ଷସ୍ୟ ଶାଖାୟାମ୍ ଏକଃବାନରଃ ଅବସତ୍ । ଡଃ ପକ୍ବଫଳାନାଂ ଭକ୍ଷଣମ୍ ଅକରୋତ୍।

ଶବ୍ଦାର୍ଥୀ :

• ତୀରେ – କୂଳେ କୂଳରେ।
• ଜମ୍ବୁବୃକ୍ଷ – ଜାମୁକୋଳି ଗଛ।
• ଆସୀତ୍ – ଥିଲା।
• ଶାଖାୟାମ୍ – ଡାଳରେ।
• ବାନରଃ – ମାଙ୍କଡ଼ ।
• ଅବସତ୍ – ବାସ କରୁଥିଲା ।
• ପଦ୍ମଫଳାନାଂ – ପାଚିଲା ଫଳ।
• ଅକରୋତ୍ – କରୁଥିଲା।

ଅର୍ଥ :
ଗୋଟିଏ ନଈ କୂଳରେ ଏକ ଜାମୁଗଛ ଥିଲା। ଗଛ ଡାଳରେ ଗୋଟିଏ ମାଙ୍କଡ଼ ବାସକରୁଥିଲା। ସେ ପାଚିଲାଫଳ ଖାଉଥିଲା।

एकदा एक: मकरः वृक्षमूलम् आगच्छत्। वानर: मकरस्य कृते पक्वानि फलानि अददात् । सः मकरः कानिचन फलानि अखादत् । कानिचन भार्याया: कृते गृहम् अनयत्। तस्य भार्या मकरं प्रति अकथयत् – “अहो जम्बुफलानि मधुराणि । य: प्रतिदिनं मधुराणि फलानि खादति तस्य हृदयम् अवश्यं मधुरम् । भो पतिदेव ! अहं तस्य वानरस्य हृदयम् इच्छामि।’’

ଶବ୍ଦାର୍ଥୀ :

• ଏକଦା – ଥରେ।
• ମକରଃ – କୁମ୍ଭୀର।
• ଆଗଚ୍ଛତ୍ – ଆସିଲା।
• ମକରସ୍ୟ କୃତେ – କୁମ୍ଭୀର ପାଇଁ।
• ପକ୍ବାନି ଫଳାନି – ପାଚିଲା ଫଳ ।
• ଅଦଦାତ୍ – ଦେଉଥିଲେ।
• କାନିଚନ – କେତେକ ।
• ଭାର୍ଯ୍ୟାୟା-କୃତେ – ସ୍ତ୍ରୀ ପାଇଁ ।
• ଅନୟତ୍ – ନେଇଥିଲା।
• ପ୍ରତି – ଆଡ଼କୁ।
• ଅହୋ ! – ଆହେ ।
• ପ୍ରତିଦିନଂ – ନିତିଦିନ ।
• ଅବଶ୍ୟମ୍ – ନିଶ୍ଚୟ ।

ଅର୍ଥ :
ଥରେ ଗୋଟିଏ କୁମ୍ଭୀର ଗଛମୂଳକୁ ଆସିଲା। ମାଙ୍କଡ଼ କୁମ୍ଭୀର ପାଚିଲା ଫଳ ଦେଲା। ସେ କୁମ୍ଭୀର କେତେକ ଫଳ ଖାଇଲା। କେତେକ ଫଳ ସ୍ତ୍ରୀ ପାଇଁ ଘରକୁ ନେଲା। ତା’ର ସ୍ତ୍ରୀ କୁମ୍ଭୀରକୁ କହିଲା – ‘ ଆହେ ଜାମୁକୋଳି କେତେ ମିଠା। ଯିଏ ପ୍ରତିଦିନ ମିଠା ଫଳ ଖାଏ ତା’ର ହୃଦୟ ନିଶ୍ଚୟ ମଧୁର । ହେ ସ୍ଵାମୀ ! ମୁଁ ସେହି ମାଙ୍କଡ଼ର ହୃଦୟ ଇଚ୍ଛାକରୁଛି।

अपरस्मिन् दिवेसे मकरः पुनः वृक्षमूलम् आगच्छत्। स: वानरं प्रति अकथयत् – “मित्र ! मम भार्या तव निमन्त्रणम् अकरोत्। आगच्छ मम पृष्ठदेशे उपविश। अहं तत्र त्वां नयामि ।

ଶବ୍ଦାର୍ଥୀ :

• ପୁନଃ – ପୁଣି।
• ବାନରଂ – ମାଙ୍କଡ଼କୁ।
• ତବ – ତୁମର।
• ପୃଷ୍ଠଦେଶେ – ପିଠିରେ।
• ଉପବିଶ – ବସ ।
• ତତ୍ର – ସେଠାକୁ
• ବଂ – ତୁମକୁ।

ଅର୍ଥ :
ଅନ୍ୟ ଏକ ଦିନ କୁମ୍ଭୀର ପୁନଶ୍ଚ ଗଛମୂଳକୁ ଆସିଲା। ସେ ମାଙ୍କଡ଼କୁ କହିଲା – ‘ ବନ୍ଧୁ ! ମୋ ଭାର୍ଯ୍ୟା ତୁମକୁ ନିମନ୍ତ୍ରଣ କରିଛି । ଆସ ମୋର ପିଠିରେ ବସ । ମୁଁ ତୁମକୁ ସେଠାକୁ ନେଇଯିବି।

वानरः मकरपृष्ठम् आरोहत्। नदीमध्ये मकर: अवदत् – “मित्र ! सत्यं वदामि । मम भार्या तव हृदयम् इच्छति ।”
ବାନରଃ ମକରପୃଷ୍ଠମ୍ ଆରୋହିତ୍। ନଦୀମଧେ ମକରଃ ଓଁ ଅବଦତ୍ – ‘ ମିତ୍ର ! ସତ୍ୟ ବଦାମି। ମମ ଭାର୍ଯ୍ୟା ତବ ହୃଦୟମ୍ ଇଚ୍ଛତି।’’

ଶବ୍ଦାର୍ଥୀ :

• ଆରୋହତ୍ – ଚଢ଼ିଲା।
• ଅବଦତ୍ – କହିଲା।
• ବଦାମି – କହୁଛି ।
• ଇଚ୍ଛତି – ଚାହୁଁଛି।

ଅର୍ଥ :
ମାଙ୍କଡ଼ କୁମ୍ଭୀର ପିଠିରେ ଚଢ଼ିଲା। ନଈ ମଝିରେ କୁମ୍ଭୀର କହିଲା – ‘ ବନ୍ଧୁ ! ସତ କହୁଛି । ମୋ ସ୍ତ୍ରୀ ତୁମ ହୃଦୟ ଚାହୁଁଛି।

वानर: चकित: अभवत्, इष्टम् अस्मरत्। विचारम् अकरोत् । पुनः अकथयत् – ‘‘मम प्रिय मित्र ! पूर्वं कथं न अवदत् ? हृदयं वृक्षस्य कोटरे अस्ति। अधुना तत्र मां नय । तत् आनयामि । अत्र पुनः आगच्छाव:।’

ବାନରଃ ଚକିତଃ ଅଭବତ୍, ଇଷ୍ଟମ୍ ଅସ୍ମରତ୍। ବିଚାରମ୍ ଅକରୋତ୍ । ପୁନଃ ଅକଥୟତ୍ – ‘ମମ ପ୍ରିୟ ମିତ୍ର ! ପୂର୍ବ କରଂ
ନ ଅବଦତ୍ ? ହୃଦୟଂ ବୃକ୍ଷସ୍ୟ କୋଟରେ ଅସ୍ତି। ଅଧୁନା ତତ୍ର ମାଂ ନୟ। ତତ୍ ଆନୟାମି। ଅତ୍ର ପୁନଃ ଆଗଚ୍ଛାମଃ।

ଶବ୍ଦାର୍ଥୀ :

• ଚକିତଃ ଅଭବତ୍ – ଚମକି ପଡ଼ିଲା।
• ଇଷ୍ଟମ୍ – କୁଳଦେବତାଙ୍କୁ।
• ଅକଥୟତ୍ – କହିଲା ।
• କର୍ଡିଂ – କାହିଁକି ।
• କୋଟରେ – କୋରଡ଼ରେ।
• ଅଧୁନା – ବର୍ତ୍ତମାନ।
• ନୟ – ନିଅ।
• ତତ୍ – ତାହା।
• ଆଗଚ୍ଛାବ – ଆସିବା।

ଅର୍ଥ :
ମାଙ୍କଡ଼ ଚମକି ପଡ଼ିଲା, କୁଳଦେବତାଙ୍କୁ ସ୍ମରଣ କଲା। ବିଚାର କଲା। ପୁଣି କହିଲା – ‘‘ମୋର ପ୍ରିୟ ସାଙ୍ଗ ! ପୂର୍ବରୁ କାହିଁକି କହିଲୁ ନାହିଁ । ହୃଦୟ ଗଛ କୋରଡ଼ରେ ଅଛି। ବର୍ତ୍ତମାନ ମୁଁ ସେଠାକୁ ମୋତେ ନେଇଚାଲ । ତାହା ଆଣିବି । ଏଠାକୁ ପୁଣି ଆସିବା।
ततः मकरः वानरं वृक्षमूलम् अनयत् । झटिति वानरः वृक्षस्य उपरि आगच्छत् । मूर्ख : मकरः निराशः अभवत्। वानरः कौशलेन स्वप्राणान् अरक्षत् ।
ତତଃ ମକରଃ ବାନରଂ ବୃକ୍ଷମୂଳମ୍ ଅନୟତ୍। ଝଟିତି ବାନରଃ ବୃକ୍ଷସ୍ୟ ଉପରି ଆଗଚ୍ଛତ୍ । ମୂର୍ଖ ମକରଃ ନିରାଶଃ ଅଭବତ୍। ବାନରଃ କୌଶଳେନ ସ୍ଵପ୍ରାଣାନ୍ ଅରକ୍ଷତ୍ ।

ଶବ୍ଦାର୍ଥୀ :

• ତତଃ – ତାପରେ।
• ଅନୟତ୍ – ନେଲା।
• ଝଟିତି – ଶୀଘ୍ର ।
• ଉପରି – ଉପରକୁ।
• ନିରାଶଃ – ହତାଶଃ – ହତାଶ।
• ସ୍ଵପ୍ରାଣାନ୍ – ନିଜ ଜୀବନକୁ।
• ଅରକ୍ଷତ – ରକ୍ଷାକଲା।

ଅର୍ଥ :
ତା’ପରେ କୁମ୍ଭୀର ମାଙ୍କଡ଼କୁ ଗଛମୂଳକୁ ଆଣିଲା। ମାଙ୍କଡ଼ ଝିଅଟି ଗଛ ଉପରକୁ ଋଲିଗଲା। ମୂର୍ଖ କୁମ୍ଭୀର ହତାଶ ହେଲା । ମାଙ୍କଡ଼ କୌଶଳରେ ନିଜ ଜୀବନ ରକ୍ଷାକଲା।

शब्दार्थ (ଶବ୍ଦାର୍ଥ) :

Odisha State Board BSE Odisha 7th Class Sanskrit Solutions Chapter 19 ବିଦ୍ୟାଳୟଃ Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Sanskrit Solutions Chapter 19 ବିଦ୍ୟାଳୟଃ

१. उत्तराणि लिखतु
(ଉତ୍ତରାଣି ଲିଖତୁ) ଉତ୍ତର ଲେଖନ୍ତୁ:

(क) विद्यालयम् अभितः कः गच्छति ?
ବିଦ୍ୟାଳୟମ୍ ଅଭିତଃ କଃ ଗଚ୍ଛତି ?
(ସ୍କୁଲ ଆଗରେ କିଏ ଯାଉଛି ?)
उत्तर:
विद्यालयम् अभित: छात्र: गच्छति ।
ବିଦ୍ୟାଳୟମ୍ ଅଭିତଃ ଛାତ୍ରୀ ଗଚ୍ଛତି।

(ख) प्राचीरं कुत्र अस्ति ?
ପ୍ରାଚୀରଂ କୁତ୍ର ଅସ୍ତି ?
(ପାଚେରୀ କେଉଁଠାରେ ଅଛି ? )
उत्तर:
विद्यालयं परितः प्राचीरम् अस्ति ।
ବିଦ୍ୟାଳୟଂ ପରିତଃ ପ୍ରାଚୀରମ୍ ଅସ୍ଥି।

(ग) पुष्पवाटिका कुत्र अस्ति ?
ପୁଷ୍ପବାଟିକା କୁତ୍ର ଅସ୍ତି ?
(ଫୁଲବଗିର କେଉଁଠି ଅଛି ?)
उत्तर:
विद्यालयम् उभयतः पुष्पवाटिकाअस्ति।
ବିଦ୍ୟାଳୟମ୍ ଉଭୟତଃ ପୁଷ୍ପବାଟିକା ଅସ୍ତି।

(घ) वाटिकां सर्वतः के सन्ति ?
ବାଟିକାଂ ସର୍ବତଃ କେ ସନ୍ତି ?
(ବଗିପ୍ଟର ସବୁଆଡ଼େ କ’ଣ ଅଛି ?)
उत्तर:
वाटिकां सर्वतः वृक्षाः सन्ति ।
ବାଟିକାଂ ସର୍ବତଃ ବୃକ୍ଷା ସନ୍ତି।

(ङ) बालक: कुत्र उपविष्ट:?
ବାଳକଃ କୁତ୍ର ଉପବିଷ୍ଟ ?
(ବାଳକ କେଉଁଠି ବସିଛି ?)
उत्तर:
बालक: वृक्षस्य अध: उपविष्टः।
ବାଳକ ବୃକ୍ଷସ୍ୟ ଅଧଃ ଉପବିଷ୍ଟ ।

२. कोष्ठकस्थपदै: वाक्यानि रचयतु ।
(କୋଷ୍ଠକସୁପଦଃ ବାକ୍ୟାନି ରଚୟତୁ।)

(क) विद्यालयम् अभितः छात्रः गच्छति।
ବିଦ୍ୟାଳୟମ୍ ଅଭିତଃ ଛାତ୍ରୀ ଗଛତି।

(ख) विद्यालयम् उभयतः पुष्पवाटिका।
ବିଦ୍ୟାଳୟମ୍ ଉଭୟତଃ ପୁଷ୍ପବାଟିକା।

(ग) विद्यालयं परितः प्राचीरम् अस्ति ।
ବିଦ୍ୟାଳୟଂ ପରିତଃ ପ୍ରାଚୀରମ୍ ଅସ୍ତି।

३. वाक्यानि रचयतु।
(ବାକ୍ୟାନି ରଚୟତୁ।)

उच्चै :, पुनः, तूष्पीम्, परितः, अभितः
उत्तर:
उच्चै: (ଉଚ୍ଚୈଃ) – उच्चै: पाठस्य अभ्यासं करोतु ।
ଉଚ୍ଚୈଃ ପାଠସ୍ୟ ଅଭ୍ୟାସଂ କରୋତୁ।

पुनः (ପୁନଃ) – पुनः विषयं पठतु।
ପୁନଃ ବିଷୟଂ ପଠତୁ।

तूष्णीम् (ତୂଷ୍ଣୀମ୍)- श्रेण्याः अन्तः तूष्णीं तिष्ठतु ।
ଶ୍ରେଣ୍ୟା ଅନ୍ତଃ ତୂଷ୍ଣୀ ତିଷ୍ଠତୁ।

परितः (ପରିତଃ) – विद्यालयं परितः प्राचीरम् अस्ति।
ବିଦ୍ୟାଳୟଂ ପରିତଃ ପ୍ରାଚୀରମ୍ ଅସ୍ତି।

अभितः (ଅଭିତଃ) – विद्यालयम् अभितः छात्र: गच्छति।
ବିଦ୍ୟାଳୟମ୍ ଅଭିତଃ ଛାତ୍ର ଗଚ୍ଛତି।

४. अव्ययपदानि निर्वाचयतु ।
(ଅବ୍ୟୟପଦାନି ନିର୍ବାଚୟତୁ।)

पठतु, नमः, अधः, पुनः, तिष्ठतु, तूष्णीम्
उत्तर:
अधः ( ଅଧଃ), पुनः (ପୁନଃ), तूष्पीम् (ତୂଷ୍ଣୀମ୍)

अतिरिक्त प्रश्नोत्तरम्
(ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातृभाषया अनुवादं कुरुत।

(क) विद्यालयः ज्ञानमन्दिरं भवति।
उत्तर:
ବିଦ୍ୟାଳୟ ଜ୍ଞାନର ମନ୍ଦିର ଅଟେ ।

(ख) स: भगिन्या सह गच्छति।
उत्तर:
ସେ ଭଉଣୀ ସହିତ ଯାଉଛି ।

(ग) विद्यालयम् उभयतः पुष्पवाटिका।
उत्तर:
ବିଦ୍ୟାଳୟ ଦୁଇ ପଟେ ଫୁଲବଗିଚା ।

(घ) विद्यालये गुरुः अस्ति।
उत्तर:
ବିଦ୍ୟାଳୟରେ ଗୁରୁ ଅଛନ୍ତି |

(ङ) कक्षायां नीचै: वदतु।
उत्तर:
ଶ୍ରେଣୀରେ ଧୀରେ ଧୀରେ କୁହନ୍ତୁ ।

(च) कदापि मिथ्या मा वदतु ।
उत्तर:
କେବେହେଲେ ମିଛ କୁହ ନାହିଁ ।

(छ) वृक्षस्य उपरि वानराः कूर्दन्ति।
उत्तर:
ଗଛ ଉପରେ ମାଙ୍କଡ଼ମାନେ କୂଦୁଛନ୍ତି ।

२. शून्यस्थानं पूरयत।

(क) ………… अभित: छात्र: गच्छति।
उत्तर: ବିଦ୍ୟାଳୟମ୍

(ख) विद्यालयं परितः ………… अस्ति।
उत्तर: ପ୍ରାଚୀରମ୍

(ग) ………… नम:।
उत्तर: ଗୁରବେ

(घ) अलं ………… |
उत्तर: ବିବାଦେନ

(ङ) श्रेण्या: अन्त: ………… तिष्ठतु।
उत्तर: ତୂଷ୍ଣୀ

(च) ………… अध: बालक: उपविष्ट:।
उत्तर : ବୃକ୍ଷସ୍ଯ

३. विक्षिप्तवर्णानां मेलनेन शुद्धपदं रचयत।

(क) तः भि अ
उत्तर: ଅଭିତଃ

(ख) न वा वि दे
उत्तर: ବିବାଦେନ

(ग) ल या द्या वि त्
उत्तर:  ବିଦ୍ୟାଳୟାତ୍

(घ) दि प श उ ति
उत्तर:  ଉପଦିଶତି

(ङ) तः भ य उ
उत्तर:  ଉଭୟତଃ

४. स्तम्भमेलनं कुरूत।

‘क’ स्मम्भः — ‘ख’ स्तम्भः
विद्यालयम् — नम:
भगिन्या — उपरि
गुरवे — अलम्
विवादेन — अभितः
वृक्षस्य — सह
उत्तर:
‘କ’ ସ୍ତମ୍ଭ — ‘ଖ’ ସ୍ତମ୍ଭ
ବିଦ୍ୟାଳୟମ୍ — ଅଭିତଃ
ଭଗିନ୍ଯା — ସହ
ଗୁରବେ — ନମଃ
ବିବାଦେନ — ବୃକ୍ଷସ୍ଯ
ଅଳମ୍ — ଉପରି

६. मातृभाषया अर्थं प्रकाशयत।

(क) प्राचीरम्
उत्तर:
ପାଚେରୀ

(ख) सर्वतः
उत्तर:
ସବୁଆଡେ

(ग) अधः
उत्तर:
ତଳେ

(घ) परितः
उत्तर:
ଚାରିପଟେ

(ङ) अस्ति
उत्तर:
ଅଛି

६. रेखाड्कितपदानां भ्रमसंशोधनं कुरुत।

(क) कदापि मिथ्यां मा वदतु।
उत्तर:
କଦାପି ମିଥ୍ୟା ମା ବଦତୁ ।

(ख) विद्यालयस्य वहि: मा भ्रमतु।
उत्तर:
ବିଦ୍ୟାଳୟାତ୍ ବହିଃ ମା ଭ୍ରମତୁ ।

(ग) पुष्पवाटिकां सर्वतः वृक्षाः अस्ति।
उत्तर:
ପୁଷ୍ପ ବାଟିକାଂ ସର୍ବତଃ ବୃକ୍ଷା ସନ୍ତି ।

(घ) विवादं अलम्।
उत्तर:
ବିବାଦେନ ଅଳମ୍ ।

(घ) गुरूणा नमः।
उत्तर:
ଗୁରବେ ନମଃ ।

 ८. उत्तर चयनं कुरूत। 

(क) क: ज्ञानमन्दिरं भवति ?
(a) गृहम्
(b) कार्यालय:
(c) विद्यालय:
(d) देवालय:
उत्तर:
(c) ବିଦ୍ୟାଳୟ

(ख) उच्चै: कस्य अभ्यासं करोतु ?
(a) पाठस्य
(b) गीतस्य
(c) नृत्यस्य
(d) पुस्तकस्य
उत्तर:
(a) ପାଠସ୍ଯ

(ग) गुरुः किं करोति ?
(a) उपविशति
(b) उपदिशति
(c) उपदिशन्ति
(d) उपदिशतः
उत्तर:
(b) ଉପଦିଶନ୍ତି

(घ) वृक्षस्य अधः कया उपविष्ट: ?
(a) चालक:
(b) सर्प:
(c) बालक:
(d) गोपालक:
उत्तर:
(c) ବାଳକଃ

(ङ) स: क्या सह गच्छति ?
(a) लतया
(b) गीतया
(c) सीतया
(d) भगिन्या
उत्तर:
(d) ଭଗିନ୍ୟା

उपपदविभक्तिप्रयोगः :
(ଉପପଦବିଭନ୍ତଃ ପ୍ରୟୋଗ ଅବ୍ୟୟପ୍ରୟୋଗଶ୍ଚ)

ସଦୃଶଂ ତ୍ରିଶୁ ଲିଙ୍ଗେଷୁ ସର୍ବାସୁ ଚ଼ ବିଭଭିକ୍ଷୁ
ବଚନେଷୁ ତ୍ବ ସର୍ବେଷୁ ଯତ୍ନ ବେତି ତଦବ୍ୟୟମ୍ ।
ସୂଚନା : ଶବ୍ଦ ଯୋଗରେ ଯେଉଁ ବିଭକ୍ତି ହୁଏ, ତାହା ଉପପଦ ବିଭକ୍ତି ଏବଂ ଯେଉଁ ପଦର ତିନି ଲିଙ୍ଗ, ସାତ ବିଭକ୍ତି ଓ ତିନି ବଚନରେ ସମାନ ରୂପ ହୁଏ, ତାହା ଅବ୍ୟୟ ପଦ।

विद्यालयः (ବିଦ୍ୟାଳୟ) ବିଦ୍ୟାଳୟ

उपपदविभक्तिप्रयोगः (ଉପପଦବିଭକ୍ତିପ୍ରୟୋଗ)

• उभयतः (ଉଭୟତଃ) ଉଭୟପଟେ
• परितः (ପରିତଃ) ଋରିପଟେ
• सर्वतः (ପରିତଃ) ଋରିପଟେ
• नम: (ନମଃ) ନମସ୍କାର
• उपरि (ଉପରି) ଉପରେ

अव्ययप्रयोग: (ଅବ୍ୟୟପ୍ରୟୋଗ)

• अलम् (ଅଳମ୍) ବୃଥା
• अन्तः (ଅନ୍ତଃ) ଭିତରେ
• वहि: (ବହିଃ) ବାହାରେ
• अधः (ଅଧଃ) ତଳେ
• उच्चै: (ଉଚ୍ଚୈଃ) ବଡ଼ ପାଟିରେ
• नीच्चै: (ନୀଚ୍ଚି) ଧୀରେ ତଳେ
• कदापि (କଦାପି) କେବେହେଲେ
• पुनः (ପୁନଃ) ପୁଣି

विद्यलायः ज्ञानमन्दिरं भवति। विद्यालयम् अभितः छात्रः गच्छति। स: भगिन्या सह गच्छति। विद्यालयं परितः प्राचीरम् अस्ति। विद्यालयम् उभयतः पुष्पवाटिका। पुष्पवाटिकां सर्वतः वृक्षाः सन्ति। विद्यालये गुरुः अस्ति। गुरवे नमः गुरुः उपदिशति – अलं विवादेन। श्रेण्याः अन्तः तूष्णीं तिष्ठतु । विद्यालयात् वहि: मा भ्रमतु । उच्चै : पाठस्य अभ्यासं करोतु। कक्षायां नीचै: वदतु। कदापि मिश्या मा वदतु । पुनः विषयं पठतु । वृक्षस्य अधः बालक: उपविष्टः। वृक्षस्य उपरि वानराः कूर्दन्ति ।

ବିଦ୍ୟାଳୟ ଜ୍ଞାନମନ୍ଦିରଂ ଭବତି । ବିଦ୍ୟାଳୟମ୍ ଅଭିତଃ ଛାତ୍ରୀ ଗଚ୍ଛତି । ଡଃ ଭଗିନ୍ୟା ସହ ଗଛତି । ବିଦ୍ୟାଳୟ ପରିତଃ ପ୍ରାଚୀରମ୍ ଅଛି। ବିଦ୍ୟାଳୟମ୍ ଉଭୟତଃ ପୁଷ୍ପବାଟିକା । ପୁଷ୍ପବାଟିକାଂ ସର୍ବତଃ ବୃକ୍ଷା ସନ୍ତି । ବିଦ୍ୟାଳୟେ ଗୁରୁ ଅସ୍ତି । ଗୁରବେ ନମଃ। ଗୁରୁ ଉପଦିଶତି – ଅଳଂ ବିବାଦେନ । ଶ୍ରେଣ୍ୟା ଅନ୍ତଃ ତୂଷ୍ଣୀ ତିଷ୍ଠତି । ବିଦ୍ୟାଳୟାତ୍ ବହିଃ ମା ଭ୍ରମତୁ। ଉଚ୍ଚୈଃ ପାଠସ୍ୟ ଅଭ୍ୟାସଂ କରୋତୁ। କକ୍ଷାୟା ନୀତିଃ ବଦତୁ। କଦାପି ମିଥ୍ୟା ମା ବଦତୁ। ପୁନଃ ବିଷୟଂ ପଠତୁ। ବୃକ୍ଷସ୍ୟ ଅଧଃ ବାଳକଃ ଉପବିଷ୍ଟ । ବୃକ୍ଷସ୍ୟ ଉପରି ବାନରାଃ କୂର୍ଦନ୍ତି

ଅର୍ଥ :
ବିଦ୍ୟାଳୟ ଜ୍ଞାନର ମନ୍ଦିର ଅଟେ। ବିଦ୍ୟାଳୟ ଆଗରେ ଛାତ୍ରଟି ଯାଉଛି। ସେ ଭଉଣୀ ସହିତ ଯାଉଛି। ବିଦ୍ୟାଳୟ ଋରିପଟେ ପାଚେରୀ ଅଛି । ବିଦ୍ୟାଳୟ ଦୁଇପଟେ ଫୁଲବଗିର । ଫୁଲବଗିରର ସବୁଆଡ଼େ ଗଛ ରହିଛି। ବିଦ୍ୟାଳୟରେ ଶିକ୍ଷକ ଅଛନ୍ତି। ଗୁରୁଙ୍କୁ

ନମସ୍କାର, ଗୁରୁ ଉପଦେଶ ଦିଅନ୍ତି – କଳି କର ନାହିଁ । ଶ୍ରେଣୀରେ ନୀରବ ରୁହ। ବିଦ୍ୟାଳୟ ବାହାରେ ବୁଲ ନାହିଁ । ବଡ଼ ପାଟିରେ ପାଠ ଅଭ୍ୟାସ କର। ଶ୍ରେଣୀରେ ଧୀରେ ଧୀରେ କୁହନ୍ତୁ। କେବେହେଲେ ମିଛ କୁହନ୍ତୁ ନାହିଁ। ବିଷୟକୁ ବାରମ୍ବାର ପଢ଼ନ୍ତୁ। । ଗଛତଳେ ପିଲାଟି ବସିଥିଲା। ଗଛ ଉପରେ ମାଙ୍କଡ଼ମାନେ କୂଦୁଛନ୍ତି ।

शब्दार्थ (ଶବ୍ଦାର୍ଥ) :

Odisha State Board BSE Odisha 7th Class Sanskrit Solutions Chapter 20 ସମ୍ଭାଷଣମ୍ Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Sanskrit Solutions Chapter 20 ସମ୍ଭାଷଣମ୍

१. उत्तराणि लिखतु ‍
(ଉତ୍ତରାଣି ଲିଖତୁ) ଉତ୍ତର ଲେଖନ୍ତୁ:

(क) विवेकानन्दः बाल्ये कीदृशः आसीत् ?
ବିବେକାନନ୍ଦ ବାଲ୍ୟ କୀଦୃଶୀ ଆସୀତ୍ ?
(ପିଲାଦିନେ ବିବେକାନନ୍ଦ କିପରି ଥିଲେ ?)
उत्तर :
विवेकानन्द: बाल्ये साहसी आसीत्।
ବିବେକାନନ୍ଦ ବାଲ୍ୟ ସାହସୀ ଆସୀତ୍ଵ ।

(ख) प्रतिदिनं विवेकाननदः किं खादति स्म ?
ପ୍ରତିଦିନଂ ବିବେକାନନ୍ଦ କିଂ ଖାଦତି ସ୍ମ ?
(ପ୍ରତିଦିନ ବିବେକାନନ୍ଦ କ’ଣ ଖାଉଥିଲେ ?)
उत्तर :
प्रतिदिनं विवेकानन्द: निरामिषं खादति स्म ।
ପ୍ରତିଦିନଂ ବିବେକାନନ୍ଦ ନିରାମିଶଂ ଖାଦତି ସ୍ଵ।

(ग) विवेकानन्दः कं गुरुरूपेण स्वीकरोति स्म?
ବିବେକାନନ୍ଦ କଂ ଗୁରୁରୂପେଣ ସ୍ଵୀକରୋତି ସ୍ମ ?
(ବିବେକାନନ୍ଦ କାହାକୁ ଗୁରୁଭାବରେ ଗ୍ରହଣ କରିଥିଲେ।)
उत्तर :
विवेकानन्द: रामकृष्णदेवं गुरुरूपेण स्वीकरोति स्म।
ବିବେକାନନ୍ଦ ରାମକୃ ଷ୍ଣଦେବଂ ଗୁରୁରୂପେଣ ସ୍ତ୍ରୀକରୋତି ସ୍ଵ।

(घ) क्विकानन्दस्य बाल्यनाम किं भवति स्म ?
ବିବେକାନନ୍ଦସ୍ୟ ବାଲ୍ୟନାମ କିଂ ଭବତି ସ୍ମ ?
(ବିବେକାନନ୍ଦଙ୍କ ପିଲାଦିନର ନାମ କ’ଣ ଥୁଲା ? )
उत्तर :
विवेकानन्दस्य बाल्यनाम नरेन्द्र: भवति स्म ।
ବିବେକାନନ୍ଦସ୍ୟ ବାଲ୍ୟନାମ ନରେନ୍ଦ୍ର ଭବତି ସ୍ଵ।

(ङ) क: भारतीयसंस्कृतिम् उपदिशति स्म ?
କଃ ଭାରତୀୟସଂସ୍କୃତିମ୍ ଉପଦିଶତ ସ୍ଵ ?
(କି ଏ ଭାରତୀୟ ସଂସ୍କୃତି ଉପଦେଶ ଦେଉଥିଲେ ? )
उत्तर :
विवेकानन्द: भारतीयसंस्कृतिम् उपदिशति स्म।
ବିବେକାନନ୍ଦ ଭାରତୀୟ ସଂସ୍କୃତିମ୍ ଉପଦିଶତ ସ୍ଵ।

२. उचितपदेन शून्यस्थानं पूरयतु ।
(ଉଚିତପଦେନ ଶୂନ୍ୟସ୍ଥାନଂ ପୂରୟ।)

(क) ………… विषये अन्यः कोऽपि विशेषः
(ख) विवेकानन्दः ………… करोति स्म ।
(ग) धर्मविषये ………… पृच्छति स्म ।
(घ) नूतनं विषयं ………… |
(ङ) वयं विवेकानन्दविषये ………… इच्छामः।
(जनसेवां, तस्य, ज्ञास्यामः, ज्ञातुम्, गुरुजनान्)
उत्तर :
(क) तस्य (ତଥ୍ୟ)
(ख) जनसेवां (ଜନସେବାଂ)
(ग) गरुरजनान् ( ଗୁରୁଜନାନ୍)
(घ) ज्ञास्याम: (ଜ୍ଞାସ୍ୟାମ)
(ङ) ज्ञातुम् (ଜ୍ଞାତୁମ୍)

३. स्तम्भं मलेयतु (…….)

‘क’ स्तम्भ: — ‘ख’ स्तम्भ:
माता — गच्छति स्म
दक्षिणेश्वरं — खादति स्म
निरामिषं — वदति स्म
विश्ववविख्यातः — इच्छति स्म
संहतिम् — भवति स्म
उत्तर :
‘क’ स्तम्भ:  — ‘ख’ स्तम्भ:
माता — वदति स्म
(ମାତା) — (ବଦତି ସ୍କ)
दक्षिणेश्वर — गच्छति स्म
(ଦକ୍ଷିଣେଶ୍ଵରଂ) — (ଗଚ୍ଛତି ସ୍କ)
निरामिषं — खादति स्म
(ନିରାମିଶଂ) — (ଖାଦତି ସ୍କ)
विश्वविख्यात: — भवति स्म
(ବିଶ୍ୱବିଖ୍ୟାତଃ) — (ଭବତି ସ୍କ)
संहतिम् — इच्छति स्म
(ସଂହତିମ୍ ) — (ଇଚ୍ଛତି ସ୍କ)

शिक्षकड्क प्रति (ଶିକ୍ଷକଙ୍କ ପ୍ରତି) ଶିକ୍ଷକଙ୍କ ଉଦ୍ଦେଶ୍ୟରେ:

• ସମ୍ଭାଷଣଟିକୁ କେତେକ ଛାତ୍ର ମିଶି ବିଭିନ୍ନ ଭୂମିକାରେ ଅଭିନୟ କରିପାରିବେ ।
• ଶିକ୍ଷକ ଛାତ୍ରମାନଙ୍କଦ୍ଵାରା ଅନ୍ୟ କିଛି ବର୍ତ୍ତମାନକାଳୀନ କ୍ରିୟା ପଦରେ ‘ସ୍ମ’ ଯୋଗକରି ଅତୀତକାଳ ବୋଧକ କ୍ରିୟା ସଂଗ୍ରହ କରିପାରିବେ ।

ଯଥା :

• पठति स्म (ପଠତି ସୁ) ପଢୁଥିଲା
• लिखति स्म (ଲିଖତି ସ୍ଵ) ଲେଖୁଥିଲା
• पश्यति स्म (ପଶ୍ୟତି ସ୍ଵ) ଦେଖୁଥିଲା
• खादति स्म (ଖାଦତି ସୁ) ଖାଉଥିଲା
• हसति स्म (ହସତି ସ୍ଵ) ହସୁଥିଲା
• क्रन्दति स्म (କ୍ରନ୍ଦତି ସ୍କ) କାନ୍ଦୁଥିଲା
• ददाति स्म (ଦଦାତି ସ୍ଵ) ଦେଉଥ୍ଲା
• धावति स्म (ଧାବତି ସ୍ଵ) ଧାଉଁଥୁଲା
• नयति स्म (ନୟତି ସ୍ଵ) ନେଉଥୁଲା
• स्मरति स्म (ସ୍ମରତି ସ୍କ) ମନେରଖୁଥିଲା
• गायति स्म (ଗାୟତି ସ୍ମ) ଗାନ କରୁଥିଲା
• वहति स्म (ବହତି ସ୍ଵ) ବହନ କରୁଥିଲା
• आयाति स्म (ଆୟାତି ସ୍ଵ) ଆସୁଥୁଲା
• विभेति स्म (ବିଭେତି ସ୍ମ) ଭୟ କରୁଥିଲା
• लभते स्म (ଲଭତେ ସ୍ଵ) ଲାଭ କରୁଥିଲା

अतिरिक्त प्रश्नोत्तरम्
(ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातृभाषया अनुवादं कुरुत।
(क) विवेकानन्दः बाल्ये साहसी आसीत्।
उत्तर :
ବିବେକାନନ୍ଦ ପିଲାଦିନେ ସାହସୀ ଥିଲେ ।

(ख) स: प्रतिदिनं निरामिषं खादति स्म।
उत्तर :
ସେ ପ୍ରତିଦିନ ନିରାମିଷ ଖାଉଥିଲେ ।

(ग) रामकृष्णदेवं गुरुरूपेण स्वीकरोति स्म।
उत्तर :
ରାମକୃଷ୍ଣ ଦେବଙ୍କୁ ଗୁରୁ ଭାବରେ ଗ୍ରହଣ କଲେ ।

(घ) सः सर्वदा संहतिम् इच्छति स्म।
उत्तर :
ସେ ସବୁବେଳେ ଏକତା ଇଚ୍ଛା କରୁଥିଲେ ।

(ङ) तस्य बाल्यनाम नरेन्द्र: भवति स्म।
उत्तर :
ତାଙ୍କ ପିଲାଦିନର ନାମ ନରେନ୍ଦ୍ର ଥିଲା ।

(च) स: देशे विदेशे भ्रमति स्म।
उत्तर :
ସେ ଦେଶ ବିଦେଶରେ ବୁଲୁଥିଲେ ।

(छ) विवेकानन्द: जनसेवा करोति स्म।
उत्तर :
ବିବେକାନନ୍ଦ ଲୋକମାନଙ୍କ ସେବା କରୁଥିଲେ ।

२. विक्षिप्तवर्णानां मेलनेन शुद्धपदं रचयत।
(क) त् आ सी
उत्तर :
ଆସୀତ୍

(ख) भाण प्र वे
उत्तर :
ପ୍ରଭାବେଣ

(ग) दि प्र ति नं
उत्तर :
ପ୍ରତିଦିନଂ

(घ) वे न्द：का वि न
उत्तर :
ବିବେକାନନ୍ଦ

(ङ) य र भा ती
उत्तर :
ଭାରତୀୟ

३. मातृभाषया अर्थं प्रकाशयत।
(क) अद्य
उत्तर :
ଆଜି

(ख) क्रीडतीस्म
उत्तर : ଖେଳୁଥିଲା

(ग) संहतिम्
उत्तर : ଏକତା

(घ) गुरुजनान्
उत्तर : ଗୁରୁଜନମାନଙ୍କୁ

(ङ) कालान्तरे
उत्तर : ପରବର୍ତ୍ତୀ ସମୟରେ

४. रेखाड़ितपदानां भ्रमसंशोधनं कुरुत।
(क) स：बहु क्रीडन्ति स्म।
उत्तर :
ଧଃ ବହୁ କ୍ରୀଡତି ସ୍ମ ।

(ख) मम माताः वदति स्म।
उत्तर :
ମମ ମାତା ବଦତି ସ୍ମ ।

(ग) विवेकानन्द：जनसेवया करोति स्म।
उत्तर :
ବବକୋନନ୍ଦ ଜନସେବାଂ କରୋତି ସ୍ମ ।

(घ) तस्य प्रभावेण युवकाः संघटितः।
उत्तर :
ତସ୍ୟ ପ୍ରଭାବେଣ ଯୁବକା ସଂଘଟିତାଃ ।

(ङ) तस्या: बाल्यनाम नरेन्द्र：।
उत्तर :
ତସ୍ୟ ବାଲ୍ୟନାମ ନରେନ୍ଦ୍ର ।

५. उत्तर चयनं कुरूत।
(क) क: बहु क्रीडति स्म ?
(a) विवेकानन्द:
(b) आनन्द:
(c) विवेक:
(d) सुनन्द:
उत्तर :
(a) ବିବେକାନନ୍ଦ

(ख) कस्मिन् विषये गुरुजनान् पृच्छति ?
(a) कर्मविषये
(b) धर्मविषये
(c) मर्मविषये
(d) श्रमविषये
उत्तर :
(b) ଧର୍ମବିଷୟ

(ग) विवेकानन्दः किंकरोति स्म ?
(a) मनसेवा
(b) धनसेवा
(c) वनसेवां
(d) जनसेवां
उत्तर :
(d) ଜନସେବାଂ

(घ) स: सर्वदा किम् इच्छति स्म ?
(a) बलम्
(b) जलम्
(c) संहतिम्
(d) अहिंसाम्
उत्तर :
(c) ସଂହତିମ୍

(ङ) तस्य प्रभावेण के संघटिता: भवन्ति स्म ?
(a) युवका:
(b) जना:
(c) मूर्खा:
(d) वृद्धा:
उत्तर :
(a) ଯୁବକା

विद्यालय: (ସମ୍ଭାଷଣମ୍) ବାର୍ତ୍ତାଳାପ

शिक्षक: – भो छात्रा:! अद्य किम् इच्छन्ति ?
ଶିକ୍ଷକଃ – ଭୋ ଛାତ୍ର ! ଅଦ୍ୟ କିମ୍ ଇଚ୍ଛନ୍ତି ?
ଅନୁବାଦ – ହେ ଛାତ୍ରମାନେ ! ଆଜି କ’ଣ ଋହୁଁଛନ୍ତି ?

छात्रा: – श्रीमन् ! अद्य वयं विवेकानन्दविषये ज्ञातुम् इच्छामः।
ଛାତ୍ରା – ଶ୍ରୀମନ୍ ! ଅଦ୍ୟ ବୟଂ ବିବେକାନନ୍ଦବିଷୟେ ଜ୍ଞାତୁମ୍ ଇଚ୍ଛାମଃ ।
ଅନୁବାଦ – ସାର୍ ! ଆଜି ଆମେ ବିବେକାନନ୍ଦଙ୍କ ପିଲାଦିନ ବିଷୟରେ ଜାଣିବାକୁ ଚାହୁଁ।

शिक्षक: – उत्तमम् । विवेकानन्दस्य बाल्यकालविषये जानन्ति वा ?
ଶିକ୍ଷକଃ – ଉତ୍ତମମ୍ । ବିବେକାନନ୍ଦସ୍ୟ ବାଲ୍ୟକାଳବିଷୟେ ଜାଣନ୍ତି ବା ?
ଅନୁବାଦ – ଭଲ କଥା । ବିବେକାନନ୍ଦଙ୍କ ପିଲାଦିନ ବିଷୟରେ ଜାଣିଛ କି ?

मानसः – विवेकानन्द: बाल्ये कीदृशः आसीत् ? स: किं किं करोति स्म ?
ମାନମଃ – ବିବେକାନନ୍ଦ ବାଲ୍ୟ କୀଦୃଶୀ ଆସୀତ୍ ? ସ୍ୱ କିଂ କିଂ କରୋତି ସ୍ମ ?
ଅନୁବାଦ – ବିବେକାନ୍ଦ ପିଲାଦିନେ କିପରି ଥିଲେ ? ସେ କ’ଣ କ’ଣ କରୁଥିଲେ ?

शिक्षक: – विवेकानन्द: बाल्ये साहसी आसीत्। सः बहु क्रीड़ति स्म ।
प्रतिदिनं देवालयं गच्छति स्म। धर्मविषये गुरुजनान् पृच्छति स्म ।
ଶିକ୍ଷକଃ – ବିବେକାନନ୍ଦ ବାଲ୍ୟ ସାହସୀ ଆସୀତ୍ । ଡଃ ବହୁ କ୍ରୀଡ଼ତି ସୃ । ପ୍ରତିଦିନଂ ଦେବାଳୟଂ ଗଛତି ସ୍ମ। ଧର୍ମବିଷୟ ଗୁରୁଜନାନ୍ ପୃଚ୍ଛତି ସ୍ଵ।
ଅନୁବାଦ – ବିବେକାନନ୍ଦ ବାଲ୍ୟକାଳରେ ସାହସୀ ଥିଲେ । ସେ ବହୁତ ଖେଳୁଥିଲେ। ପ୍ରତିଦିନ ଦେଉଳକୁ ଯାଉଥଲେ। ଧର୍ମ ବିଷୟରେ ଗୁରୁଜନଙ୍କୁ ପଚାରୁଥିଲେ।

लता – सः अन्यत् किं करोति स्म ?
ଲତା – ଧଃ ଅନ୍ୟତ୍ କିଂ କରୋତି ସ୍ମ ?
ଅନୁବାଦ – ସେ ଅନ୍ୟ କ’ଣ କରୁଥିଲେ ?

शिक्षक: – विवेकानन्द: जनसेवां करोति स्म।
स: प्रतिदिनं निरामिषं खादति स्म ।
ଶିକ୍ଷକଃ — ବିବେକାନନ୍ଦ ଜନସେବାଂ କରୋତି ସ୍ଵ। ସ୍ୱ ପ୍ରତିଦିନଂ ନିରାମିଷ ଖାଦତି ସ୍ମ ।
ଅନୁବାଦ – ବିବେକାନନ୍ଦ ଲୋକମାନଙ୍କ ସେବା କରୁଥିଲେ। ସେ ନିତିଦିନ ନିରାମିଷ ଖାଦ୍ୟ ଖାଉଥିଲେ।

उमेशः – श्रीमन् ! मम माता वदति स्म – यत्
विवेकानन्द्: दक्षिणेश्वरमन्दिरं गच्छति स्म।

शिक्षक: – आम् । स प्रतिदिनं दक्षिणेश्वरं गच्छति स्म।
रामकृष्णदेवं गुरुरूपेण स्वीकरोति स्म ।

ଶିକ୍ଷକଃ – ଶ୍ରୀମନ୍ ! ମମ ମାତା ବଦତି ସ୍କୃ – ଯତ୍ ବିବେକାନନ୍ଦ ଦକ୍ଷିଣେଶ୍ଵରମନ୍ଦିରଂ ଗଚ୍ଛତି ସ୍ଵ।
ଅନୁବାଦ – ଆଜ୍ଞା ! ମୋର ମାଆ କହୁଥିଲେ ଯେ ବିବେକାନନ୍ଦ ଦକ୍ଷିଣେଶ୍ଵର ମନ୍ଦିରକୁ ଯାଉଥିଲେ।

शिक्षक: – आम् । स प्रतिदिनं दक्षिणेश्वरं गच्छति स्म।
रामकृष्णदेवं गुरुरूपेण स्वीकरोति स्म ।
ଶିକ୍ଷକଃ – ଆମ୍ବ । ଡଃ ପ୍ରତିଦିନଂ ଦକ୍ଷିଣେଶ୍ଵରଂ ଗଚ୍ଛତି ସ୍ମ। ରାମକୃଷ୍ଣଦେବଂ ଗୁରୁରୂପେଣ ସ୍ଵୀକରୋତି ସୃ।
ଅନୁବାଦ – ହଁ। ସେ ପ୍ରତିଦିନ ଦକ୍ଷିଣେଶ୍ଵର ଯାଉଥିଲେ। ରାମକୃଷ୍ଣଦେବଙ୍କୁ ଗୁରୁଭାବରେ ଗ୍ରହଣ କରୁଥିଲେ।

गीता – तस्य विषये अन्य: कोऽपि विशेष: ?
ଗୀତା – ତସ୍ୟ ବିଷୟେ ଅନ୍ୟ କୋଽପି ବିଶେଷ ?
ଅନୁବାଦ – ତାଙ୍କ ବିଷୟରେ ଅନ୍ୟ କିଛି ବିଶେଷ ବର୍ଣନା ଅଛି କି ?

शिक्षक: – स: सर्वदा संहतिम् इच्छति स्म। तस्य प्रभावेण युवकाः संघटिता: भवन्ति स्म। तस्य बाल्यनाम नरेन्द्र: भवति स्म । कालान्तरे सः विश्वविख्यातः भवति स्म। स: देशे विदेशे भ्रमति स्म । भारतीयसंस्कृतिम् उपदिशति स्म ।

ଶିକ୍ଷକଃ – ଡଃ ସର୍ବଦା ସଂହତିମ୍ ଇଚ୍ଛତି ସ୍ମ। ତଥ୍ୟ ପ୍ରଭାବେଣ ଯୁବକାଂ ସଂଘଟିତଃ ଭବନ୍ତି ସ୍ଵ। ତସ୍ୟ ବାଲ୍ୟନାମ ନରେନ୍ଦ୍ର ଭବତି ସ୍ଵ। କାଳାନ୍ତରେ ଡଃ ବିଶ୍ୱବିଖ୍ୟାତଃ ଭବତି ସ୍ମ । ସ୍ୱ ଦେଶ ବିଦେଶେ ଭ୍ରମତି ସ୍ମ। ଭାରତୀୟ- ସଂସ୍କୃତିମ୍ ଉପଦିଶତି ସ୍ମ ।

ଅନୁବାଦ – ସେ ସବୁବେଳେ ସଂହତି ଇଚ୍ଛା କରୁଥିଲେ। ତାଙ୍କ ପ୍ରଭାବରେ ଯୁବକମାନେ ସଂଘଟିତ ହେଉଥିଲେ। ତାଙ୍କ ପିଲାଦିନର ନାମ ନରେନ୍ଦ୍ର ଥିଲା। ପରବର୍ତ୍ତୀ ସମୟରେ ସେ ବିଶ୍ଵପ୍ରସିଦ୍ଧ ହୋଇଥିଲେ । ସେ ଦେଶ ଓ ବିଦେଶରେ ବୁଲୁଥିଲେ। ଭାରତୀୟ ସଂସ୍କୃତିର ଉପଦେଶ ଦେଉଥିଲେ । ହେଉ ଆଜି ଯଥେଷ୍ଟ ହେଲାଣି । ଆସନ୍ତା କାଲି ପୁଣି ନୂଆ ବିଷୟ ଜାଣିବା ।

शब्दार्थ (ଶବ୍ଦାର୍ଥ) :

Odisha State Board BSE Odisha 7th Class Sanskrit Solutions Chapter 5 ସଂଖ୍ୟା Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Sanskrit Solutions Chapter 5 ସଂଖ୍ୟା

१. कति सन्ति अक्षरेण लिखतु
କତି ସନ୍ତା ଅକ୍ଷରେଣ ଲିଖନ୍ତୁ (କେତୋଟି ଅଛି ଅକ୍ଷରରେ ଲେଖନ୍ତୁ)

(१) मस्तकम्
(୧) ମସ୍ତକମ୍ ।
उत्तर :
एकं मस्तकम् ।
ଏବଂ ମସ୍ତକମ୍ ।

(२) फले
(୨) ଫଳେ ।
उत्तर :
द्वे फले ।
ସ୍ଵେ ଫଳେ ।

(३) पुस्तकानि
(୩) ପୁସ୍ତକାନି ।
उत्तर :
त्रीणि पुस्तकानि ।
ତ୍ରୀଣି ପୁସ୍ତକାନି ।

(५) अङुलय:
(୫) ଅଙ୍ଗୁଳୟଃ
उत्तर :
पश्च अड्गुलयः ।
ପଞ୍ଚ ଅଙ୍ଗୁଳୟ ।

(६) ग्रहा:
(୬) ଗ୍ରହ
उत्तर :
षट् ग्रहा:।
ଷଟ୍ ଗ୍ରହଃ ।

(७) दिवसा:
(୭) ଦିବସା ।
उत्तर :
सप्त दिवसा:
ସପ୍ତ ଦିବସା ।

(३ २) दन्ता:
(୩୨) ଦନ୍ତା
उत्तर :
द्वात्रिंशत् दन्ताः।
ଦ୍ବାତ୍ରିଂଶତ୍ ଦନ୍ତୀ ।

(१०) अवतारा:
(୧୦) ଅବତାରାଃ ।
उत्तर :
दश अवतारा:।
ଦଶ ଅବତାରାଃ ।

(१ २) मासा:
(୧୨) ମାସା
उत्तर :
द्वादश मासाः।
ଦ୍ବାଦଶ ମାସ ।

(२४) सोपानानि
(୨୪) ସୋପାନାନି ।
उत्तर :
चतुर्विंशतिः सोपानानि।
‘ଚତୁର୍ବିଂଶତିଃ ସୋପାନାନି।

(२८) वानरा;
(୨୮) ବାନରଃ ।
उत्तर :
अष्टविंशति वानराः।
ଅଷ୍ଟାବିଂଶତିଃ ବାନରଃ ।

(३५) पत्राणि
(୩୫) ପତ୍ରାଣି ।
उत्तर :
पश्चत्रिंशत् पत्राणि:
ପଞ୍ଚତ୍ରିଂଶତ୍ ପତ୍ରାଣି ।

(४०) बालिका:
(୪୦) ବାଳିକା ।
उत्तर :
चत्वारिंशत् बालिकाः।
ଚତ୍ୱାରିଂଶତ୍ ବାଳିକା ।

(૪६) पुत्तलिका:
(୪୬) ପୁତ୍ତଳିକା ।
उत्तर :
षड्चत्वारिंशत् पुत्तलिका:।
ଷଡ଼ଚତ୍ବାରିଂଶତ୍ ପୁତ୍ତଳିକା ।

(५ २) स्तम्भा:
(୫୨) ସ୍ତମ୍ଭ ।
उत्तर :
द्विपश्चाशत् स्तम्भाः।
ଦ୍ବିପଞ୍ଚାଶତ୍ ସ୍ତମ୍ଭା ।

(४८) करवस्त्राणि
(୪୮) କରବସ୍ତ୍ରାଣି ।
उत्तर :
अष्टपञ्चाशत् करवस्त्राणि।
ଅଷ୍ଟପଞ୍ଚାଶତ୍ କରବସ୍ତାଣି ।

(६४) कला:
(୬୪) କଳା ।
उत्तर :
चतुषष्टि: कला:।
ଚତୁଷଷ୍ଟି କଳା ।

(६५) घट:
(୬୫) ଘଟା ।
उत्तर :
पञ्चषष्टि: घटाः।
ପଞ୍ଚଷଷ୍ଟି ଘଟା ।

(७ १) द्रोण्य:
(୭୧) ଦ୍ରୋଣ୍ୟ ।
उत्तर :
एकसप्तति: द्रोण्य:।
ଏକସପ୍ତତଃ ଦ୍ରୋଣଂ ।

(७५) व्याघ्रा:
(୭୫) ବ୍ୟାଘ୍ରା
उत्तर :
पंचसप्तति: व्याघ्राः।
ପଞ୍ଚସପ୍ତତଃ ବ୍ୟାଘ୍ରା ।

(७८) शिक्षिका:
(୭୮) ଶିକ୍ଷିକାଂ
उत्तर :
अष्टसप्ततिः शिक्षिका:।
ଅଷ୍ଟସପ୍ତତଃ ଶିକ୍ଷିକା ।

(२४) पत्रिका:
(୨୪) ପତ୍ରିକା
उत्तर :
चतुर्विंशतिः पत्रिकाः।
ଚତୁର୍ବିଂଶତିଃ ପତ୍ରିକା ।

(२ २) पिपीलिका:
(୨୨) ପିପୀଲିକା
उत्तर :
द्वाविंशतिः पिपीलिकाः।
ଦ୍ୱାବିଂଶତିଃ ପିପୀଳିକା ।

(६ १) इष्टिका:
(୬୧) ଇଷ୍ଟିକା
उत्तर :
एकषष्टि: इष्टिकाः।
ଏକଷଷ୍ଟି ଇଷ୍ଟିକା ।

(६७) दीपा:
(୬୭) ଦୀପା
उत्तर :
सप्तषष्टि: दीपाः।
ସପ୍ତଷଷ୍ଟି ଦୀପା ।

(१००) लोकयानानि
(୧୦୦) ଲୋକଯାନାନି
उत्तर :
शतं लोकयानानि
ଶତଂ ଲୋକଯାନାନି ।

२. अड्केन लिखतु
(ଅଙ୍କନ ଲିଖତୁ) ସଂଖ୍ୟାରେ ଲେଖନ୍ତୁ:

एकादश – ________.
अष्टादश – ________.
विंशति: – ________.
चतुर्विशति: – ________.
सप्तविंशति: – ________.
द्वाविंशत् – ________.
पत्रत्रिंशत् – ________.
चत्वारिंशत् – ________.
त्रिचत्वारिंशत् – ________.
नवचत्वारिंशत् – ________.
एकपत्राशत् – ________.
द्विषष्टि: – ________.
सप्तषष्टि: – ________.
पश्चसप्ततिः – ________.
द्वयशीति – ________.
चतुर्नवतिः – ________.
उत्तर :

३. स्तम्भं योजयतु –
(ସ୍ତମଂ ଯୋଜୟତୁ) ସ୍ତମ୍ଭ ମିଳନ କର :

अष्टादश २२
द्वाविंशतिः २५
त्रयस्त्रिंशत् ३७
पश्चविंशतिः १८
सप्तत्रिंशत् ३३
उत्तर :

अतिरिक्त प्रश्नोत्तरम्
(ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातृभाषया अनुवादं कुरुत

(क) अप्यविंशति: व्याघा:।
उत्तर :
ଅଠାଇଶ ବାଘ

(ख) अष्टाविंशतिः छात्रा
उत्तर :
ଏକତିରିଶ ଛାତ୍ର

(ग) द्वाविंशतिः दीपा:
उत्तर :
ବାଇଶ ଦୀପ

(घ) नवतिः फलानि
उत्तर :
ନବେ ଫଳ

(ङ) सप्ततिः दिवसा:
उत्तर :
ସତୁରୀ ଦିନ

(च) अशीतिः दन्ता:
उत्तर :
ଅଶୀ ଦାନ୍ତ

(छ) पंचअझुलयः
उत्तर :
ପଞ୍ଚ ଆଙ୍ଗୁଳି

२. एकपदेन उत्तरं लिखत।

(क) पंचविंशतिः पदस्य कोऽर्थः
उत्तर :
୨୫

(ख) विंशतिः पदस्य कोऽर्थः ?
उत्तर :
୨୦

(ग) अशीति पदस्य कोऽर्थ: ?
उत्तर :
୮୦

(घ) नवतिः पदस्य कोर्शः ?
उत्तर :
୯୦

(ङ) सप्तत्रिंशत् पदस्य कोऽर्थ: ?
उत्तर :
୩୭

(च) अष्टादश पदस्य कोऽर्थः ?
उत्तर :
୧୮

(छ) द्वाविंशतिः पदस्य कोऽर्थः ?
उत्तर :
୨୨

३. शून्यस्थानं पूरयत।

(क) सहस्तमयुतं ______।
उत्तर :
ତଥା

(ख) पद्मश्च सागरं।
उत्तर :
ଣଙ୍

(ग) एकं _____ शतं चैव।
उत्तर :
ଦଶ

(घ) कोटिर्र्वुदमेव ______।
उत्तर :
ବ

(ङ) अन्त्यं ______ पदार्यं चं।
उत्तर :
ମଧ୍ଯ

५. स्तम्भमेलनं कुरूत।

उत्तर :

७. मातृभाषया अर्थं लिखत।

(क) एकादश
उत्तर :
ଏଗାର

(ख) सप्त
उत्तर :
ସାତ

(ग) पंचदश
उत्तर :
ପନ୍ଦର

(घ) द्वात्रिंशत्
उत्तर :
ବତୀଶ

(ङ) पंचाशत्
उत्तर :
ପାଚାଶ

८. उत्तर चयनं कुरूत।

(क) षष्टि:
(a) ୧୦
(b) ୨୦
(c) ୪୦
(d) ୬୦
उत्तर :
(d) ୬୦

(ख) पंचाशत्
(a) ୪୦
(b) ୫୦
(c) ୬୦
(d) ୭୦
उत्तर :
(b) 80

(ग) सप्ततिः
(a) ୬୦
(b) ୭୦
(c) ୮୦
(d) ୯୦
उत्तर :
(b) ୭୦

(घ) एकविंशत्
(a) ୨୧
(b)୨୨
(c) ୩୧
(d) ୩୨
उत्तर :
(d) ୬୦

(ङ) नवविंशति:
(a) ୯୦
(b) ୮୦
(c) ୨୯
(d) ୬୦
(c) ୨୯

९. संशोधनं कुरुत ।

(क) विंशतय: छात्राः।
उत्तर :
ବିଂଶତିଃ ଛାତ୍ରା ।

(ख) एकादशाः जनाः।
उत्तर :
ଏକାଦଶ ଜନାଃ ।

(ग) अष्टविंशतिः कलानि।
उत्तर :
ଅଷ୍ଟାବିଂଶତିଃ ଫଳାନି।

(घ) सप्ततयः अश्वा:
उत्तर :
ସପ୍ତତଃ ଅଶ୍ବାସ

(ङ) पंचवींशतिः अजाः।
उत्तर :
ପଞ୍ଚ ବିଂଶତିଃ ଅଜାଃ ।

पठतु जानातु
(ପଠତୁ ଜାନାତୁ) ପଢ଼ନ୍ତୁ ଜାଣନ୍ତୁ :

पठतु अवगच्छतु
(ପଠତୁ ଅବଗଛତୁ) ପଢ଼ି ବୁଝ :

श्लोकं पठतु स्मरतु
(ଶ୍ଳୋକଂ ପଠତୁ ସ୍ମରତୁ) ଶ୍ଳୋକ ପଢ଼ନ୍ତୁ ଓ ମନେରଖନ୍ତୁ :

एकं दश शत चैव सहस्रमयुतं तथा
लक्षं च नियुतं चैव कोटिर्र्बुदमेव च
वृन्दं खर्वो निखर्वश्च शङ्छः पद्मश्च सागरः
अन्त्यं मध्यं परार्धं च दश वृद्ध्या यथा क्रमम्।

ଏବଂ ଦଶ ଶତଂ ଚୈବ ସହସ୍ରମୟୁତଂ ତଥା
ଲକ୍ଷ୍ୟ ଚ ନିୟୁତଂ ଚୈବ କୋଟିରର୍ବୁଦମେବ ଡ଼
ବୃନ୍ଦ ଖର୍ବୋ ନିଖର୍ବଶ୍ଚ ଶଙ୍ଖ ପଦ୍ମଶ୍ଚ ସାଗରଃ
ଅନ୍ତ୍ଯ ମଧ୍ଯ ପରାଶଂ ଡ଼ ଦଶ ବୃଦ୍ଧା ଯଥାକ୍ରମମ୍ ।।

शिक्षकं प्रति :

ପଦର ଶେଷରେ, ବାକ୍ୟର ଶେଷରେ ଏବଂ ସ୍ଵରବର୍ଷ ପୂର୍ବରୁ ‘ମ୍’ ରହିବ । ବ୍ୟଞ୍ଜନବର୍ଷ ପୂର୍ବରୁ ଅନୁ ସ୍କା ର (°) ରହିବ । ବିଦ୍ୟାର୍ଥୀମାନଙ୍କୁ ଏହି ବିଷୟରେ ଉଦାହରଣ ଦେଇ ବୁଝାଇ ଦେବେ ଯଥା- ମଧୁରମ୍, ଏକମ୍, ଏବଂ ଫଳମ୍ବ, ଫଳମ୍ ଆନୟ, ଜଳଂ ପିବାମି ।

Odisha State Board BSE Odisha 7th Class Sanskrit Solutions Chapter 21 ଶିଶୁଗୀତମ ଭାରତଭକ୍ତାଃ Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Sanskrit Solutions Chapter 21 ଶିଶୁଗୀତମ ଭାରତଭକ୍ତାଃ

भारतभक्ता:
(ଭାରତଭକ୍ତା) ଭାରତ ଭକ୍ତମାନେ

वयं बालका: भारतभक्ता:
ବୟଂ ବାଳକା ଭାରତଭକ୍ତା

वयं बालिका: भारतभक्ता:
ବୟଂ ବାଳିକା ଭାରତଭକ୍ତା

वयं हि सर्वे भारतभक्ता:
ବୟଂ ହି ସର୍ବେ ଭାରତଭକ୍ତା

भुवनत्रयं विजेतुं शक्ताः । वयम् …
ଭୁବନତ୍ରୟଂ ବିଜେପୁଂ ଶକ୍ତା । ବୟମ୍ …

वयं सुधीरा: वयं सुवीरा:
ବୟଂ ସୁଧୀରଃ ବୟଂ ସୁବୀରା

हृष्टमानसाः पुष्टशरीरा:
ହୃଷ୍ଟମାନସ ପୁଷ୍ଟଶରୀରା

सम्यक् पठाम: सम्यक् लिखाम:
ସମ୍ୟକ୍ ପଠାମଃ ସମ୍ୟକ୍ ଲିଖାମ

लोकसेवायां युक्ता: भवामः। वयम् …
ସମ୍ୟକ୍ ପଠାମଃ ସମ୍ୟକ୍ ଲିଖାମ

जातिधर्ममतभेदं त्यक्त्वा
ଜାତିଧର୍ମମତଭେଦଂ ତ୍ୟକ୍ସା

भारतवर्षं पूज्यं मत्वा
ଭାରତବର୍ଷ ପୂଜ୍ୟ ମତ୍ସ୍ୟ

ऐक्यभावं हृदये धृत्वा
ଐକ୍ୟଭାବଂ ହୃଦୟେ ଧୃତ୍ଵ

देशसेवायामनुरक्ता ….. । वयम् ।
ଦେଶସେବାଯାମନୁରକ୍ତା … । ବୟମ୍ ।

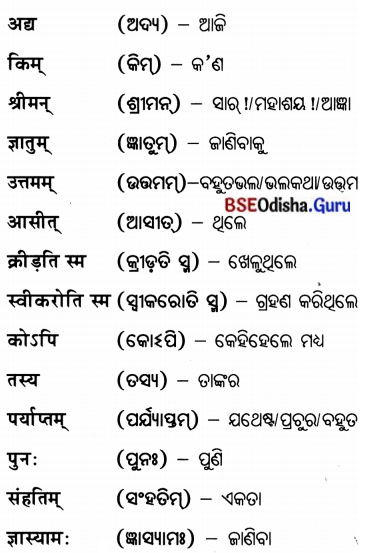
शब्दार्थ (ଶବ୍ଦାର୍ଥ) :

अतिरिक्त प्रश्नोत्तरम् (ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातृभाषया अर्थं प्रकाशयत।
(क) वयं
उत्तर : ଆମେମାନେ

(ख) जेतुम्
उत्तर : ଜୟ କରିବାକୁ

(ग) सम्यक्
उत्तर : ଭଲ

(घ) ऐक्यभावम्
उत्तर :ଏକତାଭାବ

(ङ) मत्वा
उत्तर : ମନେକରି

२. उत्तर चयनं कुरूत।
(क) के भारतभक्ता：？
(a) वालका：
(b) शालका：
(c) कृषकाः
(d) कारकाः
उत्तर :
(a) ବାଳକା

(ख) कस्यां युक्ता：भवामः ？
(a) सेवायां
(b) कार्ये
(c) लोकसेवाया
(d) पशुसेवायां
उत्तर :
(c) ଲୋକସେବାୟଂ

(ग) जातिधर्ममतभेदं किं कुर्मः ?
(a) जानीम:
(b) पश्याम:
(c) कुर्म:
(d) त्यजाम:
उत्तर :
(d) ତ୍ୟଜାମ

(ग) जातिधर्ममतभेदं किं कुर्मः ?
(a) जानीम:
(b) पश्याम:
(c) कुर्म:
(d) त्यजाम:
उत्तर :
(b) ଏକ୍ୟ

(ङ) वयं कस्याम् अनुरक्ता: भवाम: ?
(a) देशसेवाया
(b) वृक्षसेवाया
(c) पशुसेवायां
(d) मत्स्यसेवायां
उत्तर :
(b) ଏକ୍ୟ

प्रहेलिका (उत्तरं वदतु) ପ୍ରହେଳିକା (ଉତ୍ତର କୁହ)

कस्तुरी जायते कस्मात् ？
କସ୍ତୁରୀ ଜାୟତେ କସ୍ମାତ୍ ?

को हन्ति करिणां कुलम् ？
କୋ ହନ୍ତି କରିବାଂ କୁଳମ୍ ?

किं कुर्यात् कातरो युद्धे ？
କିଂ କୁର୍ଯ୍ୟାତ୍ କାତରୋ ଯୁଦ୍ଧେ ?

मृगात् सिंहः पलायते ।
ମୃଗାତ୍ ସିଂହଃ ପଳାୟତେ

वृक्षाग्रवासी न च पक्षिराज：
ବୃକ୍ଷାଗ୍ରବାସୀ ନ ଚ଼ ପକ୍ଷିରାଜଃ

त्रिनेत्रधारी न च शूलपाणिः।
ତ୍ରିନେତ୍ରଧାରୀ ନ ଚ଼ ଶୂଳପାଣି

त्वग्वस्त्रधारी न च सिद्धयोगी
ତ୍ବଗୁଧାରୀ ନ ବୃ ସିଦ୍ଧଯୋଗୀ ।

जलं च बिभ्रन्न घटो न मेघः।
ଜଳଂ ବୃ ବିଭ୍ରନ୍ନ ଘଟୋ ନ ମେଘ ।

कं संजधान कृष्णः
କଂ ସଂଜଧାନ କୃଷ୍ଣ

का शीतलवाहिनी गड्गा
କା ଶୀତଳବାହିନୀ ଗଙ୍ଗା

के दारपोषणरता:
କେ ଦାରପୋଷଣରତଃ

कं वलवन्तं न वाधते शीतम् ।
କଂ ବଳବନ୍ତ ନ ବାଧତେ ଶୀତମ୍ ।

अपदो दूरगामी च साक्षरो न च पणिडतः।
ଅପଦୋ ଦୂରଗାମୀ ଚ ସାକ୍ଷରେ ନ ଚ ପଣ୍ଡିତଃ ।

अमुखः स्कुटवक्ता च यो जानाति स पण्डितः ।।
ଅମୁଖ ସ୍କୁଟବକ୍ତା ଚ ୟୋ ଜାନାତି ସ ପଣ୍ଡିତଃ ||

न तस्यादिर्न तस्यान्तः मध्ये यस्तस्य तिष्ठति ।
ନ ତସ୍ୟାଦିର୍ନ ତସ୍ୟାନ୍ତଃ ମଧ୍ଯ ଯସ୍ତସ୍ୟ ତିଷ୍ଠତି ।

तवाप्यस्ति ममाप्यस्ति यदि जानासि तद् वद ।।
ତବାପ୍ୟସ୍ତି ମମାଧ୍ୟସ୍ଥି ଯଦି ଜାନାସି ତଦ୍ ବଦ ।।

कठिनशब्दार्थः  (କଠିନଶବ୍ଦ) କଠିନ ଶବ୍ଦ :

• जायते (ଜାୟତେ) – ଜାତ ହୁଏ
• हन्ति (ହନ୍ତି) – ହତ୍ୟା କରେ
• करिणाम् (କରିଣାମ୍) – ହାତୀମାନଙ୍କର
• कातरः (କାତରଃ) – ଭୀରୁ
• शूलपाणि: (ଶୂନଃପାଣି) – ଶିବା ଶଙ୍କର
• विभ्रन् ଭଗବାନ (ବିଭ୍ରନ୍) – ଧାରଣ କରୁଥିବା
• जघान (ଜଘାନ) – ମାରିଥିଲେ
• पोषणरता: (ପୋଷଣରତାଃ) – ପୋଷଣକାରୀ
• स्कुटवक्ता (ସ୍ଫୁଟବକ୍ତା) – ଯଥାର୍ଥ ବକ୍ତା
• त्वग्वस्त्रधारी (ଦ୍ବିଗବସ୍ତ୍ରଧାରୀ) – ବକଳ ବସ୍ତ୍ରଧାରୀ
• वाधते (ବାଧତେ) – ବାଧାଦିଏ
• वृक्षाग्रवासी (ବୃକ୍ଷାଗ୍ରବାସୀ) – ବୃକ୍ଷ ଅଗ୍ରଭାଗରେ ଯିଏ ବାସକରେ।
• दूरगामी (ଦୂରଗାମୀ) – ଦୂରସ୍ଥାନକୁ ଯାତ୍ରାକରେ ଯେ
• पणिडत: (ପଣ୍ଡିତଃ) – ବିଦ୍ବାନ୍
• अमुख: (ଅମୁଖ) – ମୁଖ ନାହିଁ ଯାହାର
• तद् (ତଦ୍) – ତାହା

सन्धि (ସନ୍ଧି):

तस्य + आदि + न = तस्यादिर्न
ତଥ୍ୟ + ଆଦି + ନ = ତସ୍ୟାଦିର୍ନ

य: + तस्य = यतस्य
ଯଃ + ତଥ୍ୟ = ଯତସ୍ୟ

मम + अपि + अस्ति = ममाप्यस्ति
ମମ + ଅପି + ଅସ୍ଥି = ମମାପ୍ୟସ୍ତ

तस्य + अन्त: = तस्यान्त:
ତସ୍ୟ + ଅନ୍ତଃ = ତସ୍ୟାନ୍ତଃ

अतिरिक्त प्रश्नोत्तरम् (ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातृभाषया अर्थं प्रकाशयत।
(क) जायते
उत्तर : ଜାତହୁଏ

(ख) कातरः
उत्तर : ଭୀରୁ

(ग) वाधते
उत्तर : ବାଧାଦିଏ

(घ) विभ्रन्
उत्तर : ଧାରଣ କରୁଥିବା

(ङ) पण्डितः
उत्तर : ବିଦ୍ବାନ୍

२. उत्तर चयनं कुरूत।
(क) मृगात्क：पलायते ？
(a) सिंह：
(b) मार्जार：
(c) शृगाल：
(d) मृग：
उत्तर :
(a) ସିଂହ

(ख) वृक्षाग्रवासी न च …………
(a) राज：
(b) पक्षीराज：
(c) पशुराज：
(d) स्वराज：
उत्तर :
(b) ପକ୍ଷୀରାଜଃ

(ग) ……………. न च पण्डितः।
(a) अक्षरो
(b) प्रक्षरो
(c) साक्षरो
(d) चक्षरो
उत्तर :
(c) ସାକ୍ଷରୋ

(घ) य: जानाति स: ……………. |
(a) मूर्ख:
(b) वाचाल:
(c) गुणी
(d) पण्डित:
उत्तर :
(d) ପଣ୍ଡିତଃ

(ङ) त्रिनेत्रधारी न च ………. पाणि:।
(a) शूल
(b) तिल
(c) निल
(d) नील
उत्तर :
(a) ଶୂଳ

सुभाषितानि ସୁଭାଷିତାନି (ସୁଭାଷିତ)

माता शत्रु : पिता वैरी येन बालो न पाठितः ।
न शोभते सभामध्ये हंसमध्ये बको यथा ।।१।।
ମାତା ଶତ୍ରୁ ପିତା ବୈରୀ ଯେନ ବାଳୋ ନ ପାଠିତଃ
ନ ଶୋଭତେ ସଭାମଧେ ହଂସମସ୍ତେ ବକୋ ଯଥା ।।୧।।

अर्थः (ଅର୍ଥ)
या माता बालं न पाठयति सा माता शत्रु भवति।
यः पिता न पाठयति । सः पिता वैरी भवति ।
हंसमध्ये वक: यथा न शोभते तथा अयं
मूर्ख: बाल: सभामध्ये न शोभते ।
ଯା ମାତା ବାଳଂ ନ ପାଠୟତି ସା ମାତା ଶତଃ ଭବତି।
ଯଃ ପିତା ନ ପାଠୟତି। ଡଃ ପିତା ବୈରୀ ଭବତି।
ହଂସମସ୍ତେ ବୟଃ ଯଥା ନ ଶୋଭତେ ତଥା
ଅୟଂ ମୂର୍ଖ ବାନଃ ସଭାମଧେ ନ ଶୋଭିତେ।

शब्दार्थ (ଶବ୍ଦାର୍ଥ) :

• पाठयति (ପାଠୟତି) – ପଢ଼ାଏ
• स: (ନଃ) – ସେହି
• सा (ସା) – ସେହି
• वैरी (ବୈରୀ) – ଶତ୍ରୁ
• यथा (ଯଥା) – ଯେପରି
• तथा (ତଥା) – ଯେପରି
• शोभते (ଶୋଭତେ) – ଶୋଭାପାଏ

ଅର୍ଥ :
ଯେଉଁ ମାଆ ପିଲାକୁ ପଢ଼ାଏ ନାହିଁ । ସେ ମାଆ ଶତ୍ରୁ ଅଟେ । ଯେଉଁ ପିତା ପାଠ ପଢ଼ାଏ ନାହିଁ। ସେ ପିତା ଶତ୍ରୁ ଅଟେ । ହଂସ ମଧ୍ୟରେ ବଗ ଯେପରି ଶୋଭା ପାଏ ନାହିଁ । ସେହିପରି ଏହି ମୂର୍ଖ ବାଳକ ସଭା ମଧ୍ଯରେ ଶୋଭା ପାଏ ନାହିଁ।

पठतो नास्ति मूर्खत्वं जपतो नास्ति पातकम् ।
मौनिनः कलहः नास्ति न भयं चास्ति जाग्रतः।।२।।
ପଠତୋ ନାସ୍ତି ମୂର୍ଖତଂ ଜପତୋ ନାସ୍ତି ପାତକମ୍ ।
ମୌନିନଃ କଳହୋ ନାସ୍ତି ନ ଭୟଂ ଚାସ୍ତି ଜାଗ୍ରତଃ

अर्थः (ଅର୍ଥ)

पठत: जनस्य मूर्खत्वं नास्ति ।
जपत: लोकस्य पातकं नास्ति ।
मौनिजनस्य कलह: नास्ति ।
जाग्रत: जनस्य भय: नास्ति ।
ପଠତଃ ଜନସ୍ୟ ମୂର୍ଖତଂ ନାସ୍ତି ।
ଜପତଃ ଲୋକସ୍ୟ ପାତକଂ ନାସ୍ତି।
ମୌନିଜନସ୍ୟ କଳହ ନାସ୍ତି।
ଜାଗ୍ରତଃ ଜନସ୍ୟ ଭୟ ନାସ୍ତି।

शब्दार्थ (ଶବ୍ଦାର୍ଥ) :

• पठतः (ପଠତଃ) – ପଢୁଥ‌ିବା
• नास्ति (ନାସ୍ତି) – ନାହିଁ
• जपतः (ଜପତଃ) – ଜପ କରୁଥିବା
• पातकं (ପାତକଂ) – ପାପ
• मौनिजनस्य (ମୌନିଜନସ୍ୟ )–ନୀରବ ଥିବା ଲୋକର
• कलहः(କଳହଃ) – ବିବାଦ
• जाग्रतः (ଜାଗ୍ରତଃ) – ଜାଗ୍ରତ ଥିବା

ଅର୍ଥ :
ପାଠ ପଢ଼ୁଥିବା ଲୋକର ମୂର୍ଖତ୍ଵ ରହେ ନାହିଁ । ଜପ କରୁଥିବା ଲୋକର ପାପ ରହେ ନାହିଁ । ନୀରବ ରହୁଥିବା ଲୋକର ବିବାଦ ଉପୁଜେ ନାହିଁ । ଜାଗ୍ରତ ଥିବା ଲୋକର ଭୟ ରହେ ନାହିଁ ।

विद्या ददाति विनयं विनयाद् याति पात्रताम् ।
पात्रत्वाद् धनम् आप्नोति धनाद्वर्मं ततः सुखम् ।।३ ।।
ବିଦ୍ୟା ଦଦାତି ବିନୟଂ ବିନୟାଦ୍ ଯାତି ପାତ୍ରତାମ୍
ପାତ୍ରତ୍ବାଦ୍ ଧନମ୍ ଆପ୍ଳୁତି ଧନାଦ୍ ଧର୍ମ ତତଃ ସୁଖମ୍ ।।୩ । ।

अर्थः (ଅର୍ଥ)
विद्या विनयं ददाति । विनयात् पात्रतां याति ।
पात्रत्वात् धनम् आप्नोति । धनात् धर्मं ततः सुखम् आप्नोति।
ବିଦ୍ୟା ବିନୟଂ ଦଦାତି । ବିନୟାଦ୍ ପାତ୍ରତାଂ ଯାତି।
ପାତ୍ରତ୍ୱାତ୍ ଧନମ୍ ଆପ୍ଳୁତି।
ଧନାତ୍ ଧର୍ମ ତତଃ ସୁଖମ୍ ଆଷ୍ଟୋତି।

शब्दार्थ (ଶବ୍ଦାର୍ଥ) :

• ददाति (ଦଦାତି) – ଦାନକରେ
• विनयं (ବିନୟଂ) – ନମ୍ରତା
• विनयात् (ବିନୟାତ୍) – ନମ୍ରତାରୁ
• पात्रताम् (ପାତ୍ରତାମ୍) – ଯୋଗ୍ୟତାକୁ
• आप्नोति (ଆପ୍ଳୁତି) – ଲାଭ କରେ
• ततः (ତତଃ ) – ସେଥୁରୁ
• सुखम् (ସୁଖମ୍ ) – ସୁଖ

ଅର୍ଥ :
ବିଦ୍ୟା ନମ୍ରତା ଦାନ କରେ। ନମ୍ରତାରୁ ଯୋଗ୍ୟତା ଜାତ ହୁଏ। ଯୋଗ୍ୟତାରୁ ଧନ ପ୍ରାପ୍ତି ହୁଏ। ଧନରୁ ଧର୍ମ ଏବଂ ସେଥୁରୁ ସୁଖ ମିଳେ।

वृक्षः पुष्पाणि शाकं सस्यं फलानि प्राणवायुं
(अम्लजानं) छायां च ददाति। अतः वृक्षस्य रोपणं कुरु ।
ବୃକ୍ଷେ ଦଦାତି ପୁଷ୍ପାଣି ଶାକଂ ସସ୍ୟ ଫଳାନି ତୁ ।
ପ୍ରାଣବାୟୁ ଚ ଛାୟାଂ ବୈ କୁରୁ ବୃକ୍ଷସ୍ୟ ରୋପଣମ୍ ।।୪।।

अर्थः (ଅର୍ଥ )
वृक्षः पुष्पाणि शाकं सस्यं फलानि प्राणवायुं (अम्लजानं)
छायां च ददाति। अतः वृक्षस्य रोपणं कुरु ।
ବୃକ୍ଷ ପୁଷ୍ପାଣି ଶାକଂ ସସ୍ୟ ଫଳାନି
ପ୍ରାଣବାୟୁ ଚ ଦଦାତି । ଅତଃ ବୃକ୍ଷସ୍ୟ ରୋପଣଂ କୁରୁ।

शब्दार्थ  (ଶବ୍ଦାର୍ଥ) :

• पुष्पाणि (ପୁଷ୍ପାଣି) – ଫୁଲଗୁଡ଼ିକ
• शाकं (ଶାକଂ) – ଶାଗ
• सस्यं (ସସ୍ଯ) – ଶସ୍ୟ
• प्राणवायुं (ପ୍ରାଣବାୟୁ) – ଅମ୍ଳଜାନ
• छायां (ଛାୟା) – ଛାଇ
• अतः (ଅତଃ) – ଏଣୁ
• रोपणं कुरु (ରୋପଣଂ କୁରୁ) – ରୋପଣ କରା ଲଗାଅ

ଅର୍ଥ :
ଗଛ, ଫୁଲ, ଶାଗ, ଶସ୍ୟ, ଫଳ ଓ ପ୍ରାଣବାୟୁ ପ୍ରଦାନ କରେ। ଏଣୁ ବୃକ୍ଷ ରୋପଣ କର।

अर्थः (ଅର୍ଥ)
अयं निजः परो वेति गणना लघुचेतसाम् ।
उदारचरितानां तु वसुधैव कुटुम्बकम् ।।५।।
ଅୟଂ ନିଜଃ ପରେ ବେତି ଗଣନା ଲଘୁଚେତସାମ୍ ।
ଉଦାରଚରିତାନାଂ ତୁ ବସୁଧୈବ କୁଟୁମ୍ବକମ୍ ।।୫।।

शब्दार्थ  (ଶବ୍ଦାର୍ଥ) :

• निज: (ନିଜଃ) – ନିଜର ଆପଣାର
• परः (ପରଃ) – ଶତ୍ରୁ
• इति (ଇତି) – ବୋଲି ବି କିମ୍ବା
• गणना (ଗଣନା) – ବିଚାର
• लघुचेतसाम् (ଲଘୁଚେତସାମ) – ନୀଜମନା ଲୋକଙ୍କର
• उदारचरितानां (ଉଦାରଚରିତାନାଂ) – ଉଦାରମନା ଲୋକଙ୍କର
• तु (ତୁ) – କିନ୍ତୁ
• वसुधा (ବସୁଧା) – ପୃଥ‌ିବୀ
• कुटुम्बकम् (କୁଟୁମ୍ବକମ୍) – ପରିବାର/ କୁଟୁମ୍ବ

ଅର୍ଥୀ :
ଏହା ନିଜର କିମ୍ବା ଶତ୍ରୁର ଏହିପରି ବିଚାର ନୀଚ୍ଚମନା ଲୋକଙ୍କର ଥାଏ। ମାତ୍ର ଉଦାରହୃଦୟ ଲୋକଙ୍କ ବିଚାର ସାରା ସଂସାର ହିଁ ଏକ ପରିବାର।

पृथिव्यां त्रीणि रत्नानि जलम अन्त्रं सुभाषितम् ।
मूढै: पाषाणखण्डेषु रत्नसंज्ञा विधीयते ।।६।।
ପୃଥବ୍ୟା ତ୍ରୀଣି ରତ୍ନାନି ଜଳମ୍ ଅନଂ ସୁଭାଷିତମ୍ ।
ମୂଜଃ ପାଷାଣଖଣ୍ଡେଷୁ ରତ୍ନସଂଜ୍ଞା ବିଧୀୟତେ ।।୬।।

अर्थः (ଅର୍ଥ)
जलम् अन्नं सुभाषितम् इति त्रीणि रत्नानि पृथिव्यां सन्ति।
मूढा: जना: पाषाणखण्डेषु रत्नम् इति विचारयन्ति ।
ଜଳମ୍ ଅନଂ ସୁଭାଷିତମ୍ ଇତି ତ୍ରୀଣି ରତ୍ନାନି ପୃଥବ୍ୟା ସନ୍ତି ।
ମୂଢା ଜନଃ ପାଷାଣଖଣ୍ଡେଷୁ ରତ୍ନମ୍ ଇତି ବିଚାରୟନ୍ତି।

शब्दार्थ  (ଶବ୍ଦାର୍ଥ) :

• जलम् (ଜଳମୂ) – ପାଣି
• अन्नं (ଅନଂ) – ଖାଦ୍ୟ
• पृथिव्यां (ପୃଥୁବ୍ୟା) – ପୃଥ‌ିବୀରେ
• मूढा: (ମୂଢା) – ମୂର୍ଖମାନେ
• पाषाणखण्डेषु (ପାଷାଣଖଣ୍ଡେଷୁ)—ପଥରଖଣ୍ଡମାନଙ୍କରେ
• संज्ञा (ସଂଜ୍ଞା) – ନାମ
• विधीयते (ବିଧୀୟତେ) – ବିଧାନ କରନ୍ତି

ଅର୍ଥୀ :
ଜଳ ଅନ୍ନ ଏବଂ ସୁଭାଷିତ ତିନିଗୋଟି ରତ୍ନ ପୃଥ‌ିବୀରେ ରହିଛି । ମୂର୍ଖମାନେ ପାଷାଣଖଣ୍ଡମାନଙ୍କରେ ରତ୍ନ ବୋଲି ନାମକରଣ କରନ୍ତି ।

हस्तस्य भूषणं दानं सत्यं कण्ठस्य भूषणम् ।
श्रोत्रस्य भूषणं शास्त्रं भूषणै : किं प्रयोजनम् ।।७।।
ହସ୍ତସ୍ୟ ଭୂଷଣଂ ଦାନଂ ସତ୍ୟ କଣ୍ଠସ୍ୟ ଭୂଷଣମ୍
ଶ୍ରୋତ୍ରସ୍ୟ ଭୂଷଣଂ ଶାସ୍ତ୍ର ଭୂଷଣି କିଂ ପ୍ରୟୋଜନମ୍ ||୭||

अर्थः (ଅର୍ଥ)
ଦାନଂ ହସ୍ତସ୍ୟ ଭୂଷଣମ୍। ସତ୍ୟ କଣ୍ଠସ୍ୟ ଭୂଷଣମ୍ । ଶାସ୍ତ୍ର ଶ୍ରୋତ୍ରସ୍ୟ ଭୂଷଣମ୍। ଅତଃ ଭୂଷଣି କିଂ ବା
ପ୍ରୟୋଜନମ୍ ।

शब्दार्थ  (ଶବ୍ଦାର୍ଥ) :

• भूषणम् (ଭୂଷଣମ୍) – ଅଳଙ୍କାର
• कण्ठस्य (କଣ୍ଠସ୍ୟ) – କଣ୍ଠର
• श्रोत्रस्य (ଶ୍ରୋତ୍ରସ୍ୟ) – କାନର
• अतः (ଅତଃ) – ଏଣୁ
• किं (କିଂ) – କ’ଣ
• प्रयोजनं (ପ୍ରୟୋଜନଂ) ଆବଶ୍ୟକ

ଅର୍ଥ :
ଦାନ ହାତର ଅଳଙ୍କାର । ସତ୍ୟ କଣ୍ଠର ଭୂଷଣ। ଶାସ୍ତ୍ର କଣ୍ଠିର ଭୂଷଣ। ଏଣୁ ଅନ୍ୟ ଭୂଷଣରେ କ’ଣ ବା ପ୍ରୟୋଜନ।

अतिरिक्त प्रश्नोत्तरम्
(ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातृभाषया अर्थं प्रकाशयत।
(क) शोभते
उत्तर :
ଶୋଭାପାଏ

(ख) कलहः
उत्तर :
ବିବାଦ

(ग) भूषणम्
उत्तर :
ଅଳଙ୍କାର

(घ) वर्तुधा
उत्तर :
ପୃଥ୍ବୀ

(ङ) ददाति
उत्तर :
ଦାନ କରେ

२. उत्तर चयनं कुरूत।
(क) जपतः किं नास्ति ?
(a) पातकं
(b) जातकं
(c) शतकं
(d) नतकं
उत्तर :
(a) ପାତଙ୍କ

(ख) पात्रत्वात् किम् आप्नोति ?
(a) जनम्
(b) धनम्
(c) मानम्
(d) ध्यानम्
उत्तर :
(b) ଧନମ୍

(ग) हस्तस्य भूषणं किम् ?
(a) कङ्कणम्
(b) सुवर्णम्
(c) दानम्
(d) चन्दनम्
उत्तर :
(c) ଦାନମ୍

(घ) अयं निजः परो वेति केषा गणना ?
(a) मानवाना
(b) जनाना
(c) मूर्खाणां
(d) लघुचेतसा
उत्तर :
(d) ଲଘୁଚେତସାଂ

(ङ) वृक्षः कानि ददाति ?
(a) पुष्पाणि
(b) जलानि
(c) मलानि
(d) क्रीडनकानि
उत्तर :
(a) ପୁଷ୍ପାଣି

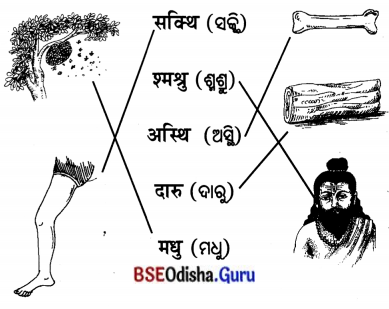
के च ते (କେ ବୃ ତେ) ସେମାନେ କିଏ ?

बानुरः
पश्यत वानरराजं दक्षम्
कूर्दति वृक्षादन्यं वृक्षम् ।

ବାନରଃ
ପଶ୍ୟତ ବାନରାଜଂ ଦକ୍ଷମ୍
କୃର୍ଦତି ବୃକ୍ଷାଦନ୍ୟ ବୃକ୍ଷମ୍ ।

कुक्कुरः
दृष्ट्वा रात्रौ एकं चौरम्
भषति कुक्कुरो वारं वारम् ।

କୁକ୍କୁର
ଦୃଷ୍ଟା ରାତ୍ରି ଏକଂ ଚୌରମ୍
ଭଷତି କୁକୁରେ ବାରଂ ବାରମ୍ ।

मार्जारी
माजारीयं खादति मीनम्
पिबति च दुग्धं तिष्ठति म़ौनम् ।

ମାର୍ଜାରୀ
ମାକାରୀୟଂ ଖାଦିତ ମୀନମ୍
ପିବତି ବୃ ଦୁଗ୍ଧ ତିଷ୍ଠତି ମୌନମ୍ ।

मधुपः
मधुपोऽयं विहरति सानन्दम्
पायं पायं मधुमकरन्दम्

ମଧୁପଃ
ମଧୁପୋଽୟଂ ବିହରତି ସାନନ୍ଦମ୍
ପାୟଂ ପାରଂ ମଧୁମକନ୍ଦମ୍ ।

हस्ती
हस्ती गच्छति मन्दं सुमन्दम्
जनयति चासौ नयनानन्दम् ।

ହସ୍ତୀ
ହସ୍ତୀ ଗଳ୍ପତି ମୟଂ ସୁମନ୍ଦମ୍
ଜନୟତି ଚାସୌ ନୟନାନନ୍ଦମ୍ ।

शशक:
शशकः सततं कुरुते क्रीडाम्
ततः परमनुभवति पीडाम् ।

ଶଶକଃ
ଶଶକଃ ସତତଂ କୁରୁତେ କ୍ରୀଡ଼ାମ୍
ତତଃ ପରମନୁଭବତି ପୀଡ଼ାମ୍ ।

सन्धिविच्छदः (ସନ୍ଧିବିଚ୍ଛେଦଃ )

शब्दार्थ  (ଶବ୍ଦାର୍ଥ) :

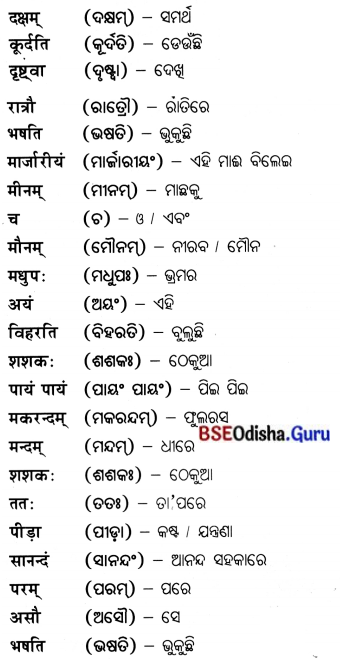
श्लोकार्था :

१. यूयं दक्षं वानरराजं पश्यत ।
असौ वृक्षात् अन्यं वृक्षं कूर्दति ।
ଯୂୟଂ ଦକ୍ଷୀ ବାନରରାଜ୍ୟ ପଶ୍ୟତ।
ଅସୌ ବୃକ୍ଷାତ୍ ଅନ୍ୟ ବକ୍ଷ କତି ।

२. रात्रौ एकं चौरं दृष्ट्ववा कुक्कुरः वारं वारं भषति।
ରାତ୍ରି ଏବଂ ଚୌରଂ ଦୃଷ୍ଟା କୁକୁରଃ ବାରଂ ବାରଂ ଭଷତି।

३. इयं मार्जारी मीनं खादति ।
दुग्धं पिबति । मौनं च तिष्ठति ।
ଇୟଂ ମାର୍ଜାରୀ ମୀନଂ ଖାଦତି।
ଦୁଗ୍ଧ ପିବତି । ମୌନଂ ଚ ତିଷ୍ଠତି।

४. अयं मधुप: मधुमकरन्दं पायं पायं सानन्दं विहरति।
ଅୟଂ ମଧୁରଃ ମଧୁମକରଣଂ ପାୟଂ ପାୟଂ ସାନନ୍ଦ ବିହରତି ।

५. हस्ती मन्दं सुमन्दं गच्छति ।
नयनानन्दं च असौ जनयति ।
ହସ୍ତୀ ମନଂ ସୁମନଂ ଗଚ୍ଛତି ।
ନୟନାନନ୍ଦ ଚ ଅସୌ ଜନୟତି ।

६. शशक: सततं क्रीड़ां कुरुते ।
ततः परं पीडाम् अनुभवति ।
ଶଶକଃ ସତତଂ କ୍ରୀଡ଼ା କୁରୁତେ ।
ତତଃ ପରଂ ପୀଡ଼ାମ୍ ଅନୁଭବତି ।

अतिरिक्त प्रश्नोत्तरम्
(ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातूभाषया अर्थं प्रकाशयत।
(क) कूर्दति
उत्तर : ଡେଉଛି

(ख) रात्रौ
उत्तर :
ରାତିରେ

(ग) मीनम्
उत्तर :
ମାଛକୁ

(घ) मधुपः
उत्तर :
ଭ୍ରମର

(ङ) शशक：
उत्तर :
ଠେକୁଆ

२. उत्तर चयनं कुरूत।
(क) क：वृक्षादन्यं वृक्षं कूर्दति ？
(a) वानरराज：
(b) मकरः
(c) शशक：
(d) मानव：
उत्तर :
(a) ବାନରରାଜଃ

(ख) रात्रौ कं दृष्ट्वा कुक्कुरः भषति ？
(a) जनं
(b) चौरं
(c) सर्पं
(d) कीटं
उत्तर :
(b) ଚୌରଂ

(ग) मधुपः किं पिबति ?
(a) रसं
(b) मधुं
(c) मधुमकरन्दं
(d) पुष्परसं
उत्तर :
(c) ମଧୁମକରଫ

(घ) का मीनं खादति ?
(a) कच्छप:
(b) बक:
(c) कुलीरक:
(d) मार्जारी
उत्तर :
(d) ମାର୍କାରୀ

(ङ) हस्ती कथं गच्छति ?
(a) सुमन्दं
(b) द्रुतं
(c) क्षिप्रं
(d) सत्वरं
उत्तर :
(a) ସୁମଙ୍ଘ

सुप्रभातम्  (ସୁପ୍ରଭାତମ୍) ସୁପ୍ରଭାତ

उदिते सूर्ये धरणी विहसति ।
ଉଦିତେ ସୂର୍ଯ୍ୟ ଧରଣୀ ବିହସତି ।

पक्षी कूजति कमलं विकसति ॥ १ ॥
ପକ୍ଷୀ କୂଜତି କମଳଂ ବିକସତି ।। ୧ ।।

नदति मन्दिरे उच्चै : ढक्का ।
ନଦତି ମନ୍ଦିରେ ଉଚ୍ଚି ଢକ୍କା ।

सरितः सलिले चलति नौका ।। २ ।।
ସରିତଃ ସଲିଳେ ଚଳତି ନୌକା ।। ୨||

पुष्पे पुष्पे नानारङ्गः ।
ପୁଷ୍ପ ପୁଷ୍ପ ନାନାରଙ୍ଗା ।

तेषु डयते चित्रविहझुगः।। ३ ।।
ତେଷୁ ଜୟତେ ଚିତ୍ରବିହଙ୍ଗା ।। ୩ ।।

वृक्षे वृक्षे नूतनपत्रम् ।
ବୃକ୍ଷେ ବୃକ୍ଷେ ନୂତନପତ୍ରମ୍ ।

विविधै : वर्णं: विभाति चित्रम् ॥
ବିବିଧଃ ବହିଃ ବିଭାତି ଚିତ୍ରମ୍ ।। ୪ ।।

गहने विपिने व्याघ्रो गर्जति ।
ଗହନେ ବିପିନେ ବ୍ୟାଘ୍ର ଗର୍ଜତି ।

उच्चै : तत्र सिंहः क्रोशति ।। ५ ।।
ଉଚ୍ଚୈଃ ତତ୍ର ସିଂହଃ କ୍ରୋଶତି ।। ୫ ।।

हरिणोऽयं खादति नवघासम् ।
ହରିଣୋଽୟଂ ଖାଦତି ନବଘାସମ୍ ।

सर्वत्र च पश्यति सविलासम् ।। ६ ।।
ସର୍ବତ୍ର ବୃ ପଶ୍ୟତି ସବିଳାସମ୍ || ୬ ||

घोटकराज : क्षिप्रं धावति ।
ଘୋଟକରାଜଃ କ୍ଷିପୁଂ ଧାବତି ।

धावनकाले किमपि न खादति ।। ७ ।।
ଧାବନକାଳେ କିମପି ନ ଖାଦତି || ୭ ||

पश्यत भल्लुकमिमं करालम्
ପଶ୍ୟତ ଭଲୁକମଂ କରାଲମ୍

नृत्यति थर्थधै कुरु करातालम् ।। ८।।
ନୃତ୍ୟତି ଥଥଥୈ କୁରୁ କରାତାଳମ୍ ।। ୮ ।।

सन्धिविच्छदः (ସନ୍ଧିବିଚ୍ଛେଦ) :

शब्दार्थ  (ଶବ୍ଦାର୍ଥ) :

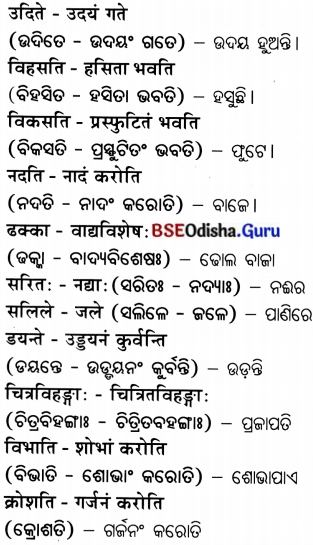
अतिरिक्त प्रश्नोत्तरम्
(ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातृभाषया अर्थं प्रकाशयत।
(क) कूजति
उत्तर :
ଭାବୁଛି

(ख) नूतनपत्रम्
उत्तर :
ନୂଆପତ୍ର

(ग) विपिने
उत्तर :
ବଣରେ

(घ) खादति
उत्तर :
ଖାଉଛି

(ङ) भल्लुक:
उत्तर :
ଭାଲୁ

२. उत्तर चयनं कुरूत।
(क) सूर्ये उदिते का विहसति ?
(a) लता
(b) माला
(c) धरणी
(d) जननी
उत्तर :
(c) ଧରଣୀ

(ख) ढक्का कुत्र उच्चै: नदति ?
(a) मन्दिरे
(b) गृहे
(c) प्रान्तरे
(d) मार्गे
उत्तर :
(a) ମନ୍ଦିରେ

(ग) कः क्षिप्रं धावति ?
(a) पशुराज:
(b) घोटकराज:
(c) शशक:
(d) व्याघ्र:
उत्तर :
(b) ଘୋଟକରାଜଃ

(घ) व्याघ्र: कुत्र गर्जति ?
(a) गुहाया
(b) वने
(c) विपिने
(d) गृहे
उत्तर :
(c) ବିପିନେ

(ङ) सिंहः किं करोति ?
(a) चलति
(b) निद्राति
(c) पश्यति
(d) क्रोशति
उत्तर :
(d) କ୍ରୋଶତି

रक्ष रक्ष काननम्
(ରକ୍ଷ ରକ୍ଷ କାନନମ୍) ଅରଣ୍ୟ ରକ୍ଷା କର

रक्ष रक्ष काननम्
ରକ୍ଷ ରକ୍ଷ କାନନମ୍

वृक्षराशिशोभनम् ।
ବୃକ୍ଷରାଶିଶୋଭନମ୍ ।

काले वृष्टिकारकम्
କାଳେ ବୃଷ୍ଟିକାରକମ୍

शुद्धवायुदायकम् ।। १ ।।
ଶୁଦ୍ଧବାୟୁଦାୟକମ୍ || ୧ ||

रोगवारणोचिता
ରୋଗବାରଣୋଚିତା

मूलिका वने स्थिता ।
ମୂଳିକା ବନେ ସ୍ଥିତା ।

सम्पदां हि सम्पदं
ସମ୍ପଦା ହି ସମ୍ପଦଂ

काननं विचिन्तय ।। २ ।।
କାନନଂ ବିଚିନ୍ତୟ || ୨ ||

काननं हि जीवनं
କାନନଂ ହି ଜୀବନଂ

रक्ष रक्ष तद् धनम् ।
ରକ୍ଷ ରକ୍ଷ ତଦ୍ ଧନମ୍ ।

काननस्य नाशनं
କାନନସ୍ୟ ନାଶନଂ

स्वस्य विधिनाशनम् ।। ३ ।।
ସ୍ଵସ୍ୟ ବିଦ୍ଧିନାଶନମ୍ ।। ୩ ।।

काननस्य वर्धने
କାନନସ୍ଯ ବର୍ଧନେ

निरतः सत्यरक्षणे ।
ନିରତଃ ସତ୍ୟରକ୍ଷଣେ ।

त्वं भविष्यचिन्तने
ତଂ ଭବିଷ୍ୟଚିନ୍ତନେ

युक्तमानसो भव ।। ४ ।।
ଯୁକ୍ତମାନସୋ ଭବ ।। ୪ ।।

शब्दार्थ  (ଶବ୍ଦାର୍ଥ) :

अतिरिक्त प्रश्नोत्तरम्
(ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातृभाषया अर्थं प्रकाशयत।
(क) काननम्
उत्तर :
ବଣ

(ख) राशि：
उत्तर :
ସମଷ୍ଟି

(ग) भव
उत्तर :
ହୁଅ

(घ) रक्ष
उत्तर :
ରକ୍ଷାକର

(ङ) काले
उत्तर :
ଉପଯୁକ୍ତ ସମୟରେ

२. उत्तर चयनं कुरूत।
(क) रक्ष रक्ष
(a) मातरम्
(b) भ्रातरम्
(c) काननम्
(d) मानवम्
उत्तर :
(c) କାନନମ୍

(ख) काले ……………. कारकम्।
(a) जल
(b) वृष्टि
(c) मेघ
(d) शीत
उत्तर :
(b) ବୃଷ୍ଟି

(ग) किंहि जीवनम् ?
(a) वृक्ष:
(b) वायु:
(c) यानं
(d) काननं
उत्तर :
(d) କାନନଂ

(घ) काननस्य नाशनं कस्य विधिनाशनम् ?
(a) स्वस्य
(b) तस्य
(c) यस्य
(d) मानवस्य
उत्तर :
(a) ସସ୍ୟ

(ङ) …………….. वर्धने निरतः सत्यरक्षणे।
(a) मृगस्य
(b) वृक्षस्य
(c) काननस्य
(d) जनस्य
उत्तर :
(c) କାନନସ୍ଯ

सर्वं नयामि विद्यालयम् 

पुत्री – अम्ब ! न यामि विद्यालयम् ।
ପୁତ୍ରୀ – ଅମ୍ବ ! ନ ଯାମି ବିଦ୍ୟାଳୟମ୍ ।

अम्ब : न यामि विद्यालयम् ।
ଅମ୍ବ ! ନ ଯାମି ବିଦ୍ୟାଳୟମ୍ ।

माता – किं प्रवृत्तं वद वत्से !
ମାତା – କିଂ ପ୍ରବୃତ୍ତ ବଦ ବତ୍ସ !

येनैवं त्वं नोत्सहसे ।
ଯେନୈବଂ ତଂ ନୋତ୍ସହସେ ।

पुत्री – चिनु-मिनु-पिनु-प्रमिला ।
ପୁତ୍ରୀ – ଚିନୁ-ମିନୁ-ପିନୁ-ପ୍ରମିଳା ।

सुरेश – गौरीश – गोपाल:
ସୁରେଶ-ଗୌରୀଶ-ଗୋପାନଃ

न केडपि मामभिभाषन्ते
ନ କେଽପି ମାମଭିଭାଷନ୍ତେ

न मया साकं मोदन्ते ।
ନ ମୟା ସାକଂ ମୋଦନ୍ତେ ।

जननी – अहो धृष्टता ईदृशी
ଜନନୀ – ଅହୋ ଧୃଷ୍ଟତା ଈଦୃଶୀ

बालानां किं भो : जल्पसि ?
ବାଳାନାଂ କିଂ ଭୋ ଜସି ?

अधुना यामि विद्यालयम्
ଅଧୁନା ଯାମି ବିଦ୍ୟାଳୟମ୍

वदामि सर्वम् आचार्यम् ।।
ବଦାମି ସର୍ବମ୍ ଆଚାର୍ଯ୍ୟମ୍ ।।

पुत्री – न तथा करोतु मे जननि !
ପୁତ୍ରୀ – ନ ତଥା କରୋତୁ ମ ଜନନି

नितरां कुप्यन्ति मित्राणि ।
ନିତରାଂ କୁପ୍ୟନ୍ତ ମିତ୍ରାଣି ।

जननी – अधुना किं वा करवाणि ?
ଜନନୀ– ଅଧୁନା କିଂ ବା କରବାଣି ?

ददाति किं ते मधुराणि ?
ଦଦାତି କିଂ ତେ ମଧୁରାଣି ?

पुत्री – अहो चतुरा मे जननी
ପୁତ୍ରୀ – ଅହୋ ଚତୁରା ମ ଜନନୀ

इटिति मदाशयग्राहिणी
ଝଟିତି ମଦାଶୟଗ୍ରାହିଣୀ

प्रेषय सर्वाणि मधुराणि
ପ୍ରେଷୟ ସର୍ବାଣି ମଧୁରାଣି

तोषय मम मित्राणि ।
ତୋଷୟ ମମ ମିତ୍ରାଣି ।

अधुना गच्छामि विद्यालयम्
ଅଧୁନା ଗଚ୍ଛାମି ବିଦ୍ୟାଳୟମ୍

देहि मधुरं सातिशयम्
ଦେହି ମଧୁରଂ ସାତିଶୟମ୍

अम्ब ! नयामि विद्यालयम्
ଅନ୍ତଃ ନୟାମି ବିଦ୍ୟାଳୟମ୍

सर्वं नयामि विद्यालयम् ।।
ସର୍ବଂ ନୟାମି ବିଦ୍ୟାଳୟମ୍ ।।

सन्धिविच्छद: (ସନ୍ଧିବିଚ୍ଛେଦଃ ) :

शब्दार्थ  (ଶବ୍ଦାର୍ଥ) :

अतिरिक्त प्रश्नोत्तरम्
(ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातृभाषया अर्थं प्रकाशयत।
(क) अम्ब
उत्तर : ହେ ମାଆ !

(ख) साकम्
उत्तर : ସାଙ୍ଗରେ

(ग) देहि
उत्तर : ଦିଅ

(घ) तथा
उत्तर : ସେପରି

(ङ) कुप्यन्ति
उत्तर : ରାଗିଛନ୍ତି

२. उत्तर चयनं कुरूत।
(क) अम्ब ! न यामि विद्यालयम् इति का वदति ?
(a) पुत्री
(b) पुत्र:
(c) लता
(d) गीता
उत्तर :
(a) ପୁତ୍ରୀ

(ख) न मया सांकं …………..
(a) खेलन्ति
(b) वदन्ति
(c) मोदन्ते
(d) हसन्ति
उत्तर :
(c) ମୋଦନ୍ତେ

(ग) …………… यामि विद्यालयम्।
(a) अधुना
(b) तदा
(c) सर्वदा
(d) अद्य
उत्तर :
(a) ଅଧୁନା

(घ) अहो चतुरा मे……………
(a) मित्रम्
(b)आचार्य:
(c) पिता
(d) जननी
उत्तर :
(d) ଜନନୀ

(ङ) …………… मम मित्राणि।
(a) प्रेषय
(b) भक्षय
(c) तोषय
(d) मार्जय
उत्तर :
(c) ତୋଷୟ

उपदेशः (ଉପଦେଶଃ) ଉପଦେଶ

प्रत्युषकाले उच्तिष्ठतु
ପ୍ରତ୍ୟୁଷକାଳେ ଉତ୍ତିଷ୍ଠତୁ

स्वकीयं कर्म विदधातु
ସ୍ଵକୀୟଂ କର୍ମ ବିଦଧାତୁ

अल्पामाहारं स्वीकरोतु
ଅଳ୍ପାମାହାରଂ ସ୍ଵୀକରୋତୁ

गृहपठनम् आचरतु ।।
ଗୃହପଠନମ୍ ଆଚରତୁ ।

पौष्टिकं भोजनं खादतु
ପୌଷ୍ଟିକଂ ଭୋଜନଂ ଖାଦତୁ

विशुद्धं पानीयं पिबतु ।
ବିଶୁଦ୍ଧ ପାନୀ ପିବତୁ

हितोपदेशं पालयतु
ହିତୋପଦେଶଂ ପାଳୟତୁ

परोपकारं साधयतु ।।
ପରୋପକାରଂ ସାଧୟତୁ ।।

विद्यामन्दिरम् आगच्छतु
ବିଦ୍ୟାମନ୍ଦିରମ୍ ଆଗଚ୍ଛତୁ

तत्र नियमान् पालयतु ।
ତତ୍ର ନିୟମାନ୍ ପାଳଋତୁ ।

शृणोतु पठतु लिखतु
ଶୃଣୋତୁ ପଠତୁ ଲିଖନ୍ତୁ

क्रीडतु सत्यं कथयतु ।।
କ୍ରୀଡ଼ତୁ ସତ୍ୟ କଥୟତୁ ।।

आलस्यभावं वर्जयतु
ଆଳସ୍ୟଭାବଂ ବର୍ଜୟତୁ

मातापितरौ तोषयतु
ମାତାପିତରୌ ତୋଷୟତୁ

देशसेवकान् पूजयतु
ଦେଶସେବକାନ୍ ପୂଜୟତୁ

समाजे आदरमाप्नोतु ।।
ସମାଜେ ଆଦରମାପ୍ଳୁତୁ ।।

देशगौरवं बोधयतु
ଦେଶଗୌରବଂ ବୋଧୟତୁ

अनुजान् नित्यं मोदयतु
ଅନୁଜାନ୍ ନିତ୍ୟ ମୋଦୟତୁ

गुरुजनान् सम्मानयतु
ଗୁରୁଜନାନ୍ ସମ୍ମାନୟତୁ

विश्वबन्धुत्वं स्थापयतु ।।
ବିଶ୍ୱବନ୍ଧୁତ୍ୱ ସ୍ଥାପୟତୁ ।।

कठिनशब्दा: (କଠିନଶବ୍ଦା) :

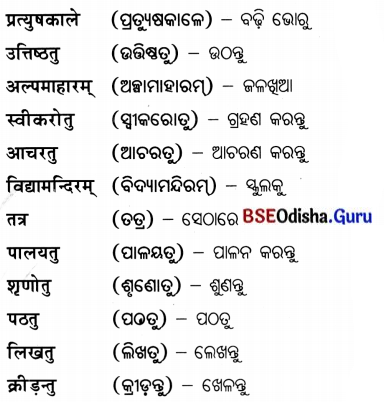
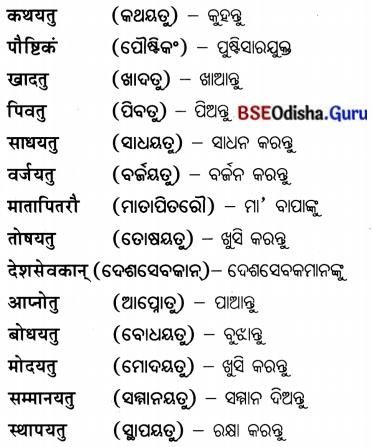
अतिरिक्त प्रश्नोत्तरम्
(ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातृभाषया अर्थं प्रकाशयत।
(क) पालयतु
उत्तर :
ପାଳନ କର

(ख) नियमान्
उत्तर :
ନିୟମଗୁଡ଼ିକୁ

(ग) बोधयतु
उत्तर :
ବୁଝାଅ

(घ) स्वकीयं
उत्तर :
ନିଜର

(ङ) कथयतु
उत्तर :
କୁହନ୍ତୁ

२. उत्तर चयनं कुरूत।
(क) किंस्वीकरोतु ?
(a) धनं
(b)अल्पमाहारं
(c) जनं
(d) फलं
उत्तर :
(b) ଅଳ୍ପମାହାରଂ

(ख) समाजे किम् आप्नोतु ?
(a) आदरम्
(b) सम्मानम्
(c) विद्याम्
(d) धनम्
उत्तर :
(a) ଆଦରମ୍

(ग) तत्र कान् पालयतु ?
(a) सर्वान्
(b) जनान्
(c) नियमान्
(d) कर्माण्
उत्तर :
(c) ନିୟମାନ୍

(घ) किं बोधयतु ?
(a) मानं
(b) पाठं
(c) ज्ञानं
(d) देशगौरवं
उत्तर :
(d) ଦେଶଗୌରବଂ

(ङ) कौ तोषयतु ?
(a) मातपितरौ
(b) गुरुजनौ
(c) देवौ
(d) पितरौ
उत्तर :
(a) ମାତାପିତରେ

Odisha State Board BSE Odisha 7th Class Sanskrit Solutions Chapter 4 ‘ଇ’ କାରାନ୍ତନପୁଂସକଲିଙ୍ଗଃ Textbook Exercise Questions and Answers.

BSE Odisha Class 7 Sanskrit Solutions Chapter 4 ‘ଇ’ କାରାନ୍ତନପୁଂସକଲିଙ୍ଗଃ

१. योजयतु
(ଯୋଜୟତୁ) ଯୋଗ କରନ୍ତୁ :

उत्तर :

२. परिचयं ददातु
(ପରିଚୟଂ ଦଦାତୁ) ପରିଚୟ ଦିଅନ୍ତୁ:

उत्तर :
(क) दधि
(କ) ଦଧ୍

(ख) अश्रु
(ଖ) ଅଶ୍ରୁ

(ग) दारु
(ଗ) ଦାରୁ

(घ) अस्थि
(ଘ) ଅସ୍ଥି

३. शून्यस्थानं पूरयतु
(ଶୂନ୍ୟସ୍ଥାନଂ ପୂରୟତୁ) ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର :

(क) ______ धि ।
(କ) ______ ଧୂ।
उत्तर :
(କ) ଦଧଃ ।

(ख) ______ रि ।
(ଖ) ______ ରି ।
उत्तर :
(ଖ) ବାରି ।

(ग) स ______ ।
(ଗ) ସ ______ ।
उत्तर :
(ଗ) ସନ୍ଧି ।

(घ) ______ रु ।
(ଘ) ରୁ _________ ।
उत्तर :
(ଘ) ଦାରୁ ।

(ङ) अ ______ ।
(ଙ) ଅ ________ ।
उत्तर :
(ଙ) ଅଶ୍ରୁ ।

(च) श्म ______ ।
(ଚ) ଶ୍ମ ________ ।
उत्तर :
(ଚ) ଶୁଶ୍ରୁ ।

अतिरिक्त प्रश्नोत्तरम्
(ଅତିରିକ୍ତ ପ୍ରଶ୍ନୋତ୍ତରମ୍)

१. मातूभाषया अनुवादं कुरुत।

(क) दधि
उत्तर :
ଦହି

(ख) अश्रु
उत्तर :
ଲୋତକ

(ग) दारू
उत्तर :
କାଠ

(घ) अस्थि
उत्तर :
ହାଡ଼

(ङ) श्मश्रु
उत्तर :
ଦାଢ଼ି

(च) वारि
उत्तर :
ପାଣି

२. स्तम्भमेलनं कुरूत।

उत्तर :

३. संसोधन कुरुत।

(क) दधि:
उत्तर :
ଦଧୂ

(ख) अश्रु
उत्तर :
ଅଶୁ

(ग) दारू
उत्तर :
ଦାରୁ

(घ) अस्थी
उत्तर :
ଅସ୍ଥି

(ङ) वारी
उत्तर :
ବାରି

‘इ’ कारान्त-नपुंसकलिङ्गः
‘ଇ’ କାରାନ୍ତ-ନପୁଂସକଲିଙ୍ଗ (‘ଇ’କାରାନ୍ତ ନପୁଂସକପୁଲିଙ୍ଗ)

वारि
(ବାରି) ପାଣି

अस्थि
(ଅସ୍ଥି) ହାଡ଼

दधि
(ଦଧୂ) ଦହି

सक्शि
(ସକ୍ତି) ଜଙ୍ଘ

‘उ’ कारान्ती-नपुंसकलिङ्गः
‘ଉ’ କାରାନ୍ତ-ନପୁଂସକଲିଙ୍ଗ(‘ଉ’କାରାନ୍ତ ନପୁଂସକପୁଲିଙ୍ଗ)

मघु
(ମଧୁ) ମହୁ

श्मश्रु
(ଶ୍ମଶ୍ରୂ) ଦାଢ଼ି

दारु
(ଦାରୁ) କାଠଗଡ଼

अश्रु
(ଅଶ୍ରୁ) ଲୋତକ