Odisha State Board CHSE Odisha Class 11 Economics Solutions Chapter 18 ତଥ୍ୟାବଳୀର ଉପସ୍ଥାପନା Questions and Answers.
CHSE Odisha 11th Class Economics Solutions Chapter 18 ତଥ୍ୟାବଳୀର ଉପସ୍ଥାପନା
ବସ୍ତୁନିଷ୍ଠ ଓ ଅତିସଂକ୍ଷିପ୍ତ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
A. ପ୍ରତ୍ୟେକ ପ୍ରଶ୍ନରେ ପ୍ରଦତ୍ତ ବିକଳ୍ପଉତ୍ତରମାନଙ୍କ ମଧ୍ୟରୁ ସଠିକ୍ ଉତ୍ତରଟି ବାଛି ଲେଖ।
୧। ଯେଉଁ ସ୍ତମ୍ଭ ଚିତ୍ରରେ ସ୍ତମ୍ଭମାନଙ୍କର କ୍ଷେତ୍ରଫଳ ଶ୍ରେଣୀ ବାରମ୍ବାରତା ସହ ସମାନୁପାତୀ ତାହା
(i) ଲେଖଚିତ୍ର
(ii) ହିଷ୍ଟୋଗ୍ରାମ
(iii) ବାରମ୍ବାରତା
(iv) ଓଜିଭ୍
Answer:
(ii) ହିଷ୍ଟୋଗ୍ରାମ୍
୨। କ୍ଷୁଦ୍ରତର (less than) ଓଜାଇଭ୍
(i) ନିମ୍ନଗାମୀ ହୋଇଥାଏ
(ii) ଉର୍ଦ୍ଧ୍ୱଗାମୀ ହୋଇଥାଏ
(iii) ସମାନ୍ତରାଳ ହୋଇଥାଏ
(iv) ଉଲ୍ମ୍ ହୋଇଥାଏ
Answer:
(ii) ଉର୍ଦ୍ଧ୍ୱଗାମୀ ହୋଇଥାଏ।
୩ । ସଞ୍ଚୟୀ ବାରମ୍ବାରତା ପରିବଣ୍ଟନର ରେଖାଚିତ୍ରକୁ କ’ଣ କୁହାଯାଏ ?
(i) ଲରେଞ୍ଜ ବକ୍ର
(ii) ଓଜାଇଭ୍
(iii) ହିଷ୍ଟୋଗ୍ରାମ୍
(iv) ଉପରୋକ୍ତ କୌଣସିଟି ନୁହେଁ
Answer:
(ii) ଓଜାଇଭ୍
୪। ଆୟତ ଚିତ୍ର ଅଙ୍କନ ସମୟରେ
(i) ଶ୍ରେଣୀ ସଂଭାଗର ବିସ୍ତାରକୁ ଆୟତ ଚିତ୍ରର ଆଧାର ରୂପେ ଗ୍ରହଣ କରାଯାଏ
(ii) ଆୟତଚିତ୍ରର ଉଚ୍ଚତା ସଂଭାଗର ବାରମ୍ବାରତା ସହ ସମାନୁପାତୀ ହୋଇଥାଏ
(iii) ସଂଭାଗ Y ଅକ୍ଷରେ ଦର୍ଶାଯାଇଥାଏ
(iv) ଉପରୋକ୍ତ ସମସ୍ତ ଉତ୍ତର ଠିକ୍ ଅଟେ।
Answer:
(iv) ଉପରୋକ୍ତ ସମସ୍ତ ଉତ୍ତର ଠିକ୍ ଅଟେ
୫। ନିମ୍ନୋକ୍ତ ମଧ୍ୟରୁ କେଉଁଟି ବାରମ୍ବାରତା ପରିବଣ୍ଟନର ରେଖାଚିତ୍ର ଅଟେ ।
(i) ପାଇ ଚିତ୍ର
(ii) ଆୟତ ଚିତ୍ର
(iii) ଚିତ୍ରଲେଖ
(iv) ସ୍ତମ୍ଭ ଚିତ୍ର
Answer:
(ii) ଆୟତ ଚିତ୍ର
୬। କେଉଁଟି ଏକ ମସୃଣ ରେଖା ଅଟେ ?
(i) ହିଷ୍ମେ।ଗ୍ରମ୍
(ii) ବାରମ୍ବାରତା ବହୁଭୂଜ
(iii) ବାରମ୍ବାରତା ବକ୍ରରେଖା
(iv) ଉପରୋକ୍ତ ସମସ୍ତ
Answer:
(iii) ବାରମ୍ବାରତା ବକ୍ରରେଖା
![]()
୭। କେଉଁ ରେଖା ଇଂରାଜୀ ଅକ୍ଷର ‘S’ ଆକୃତି ବିଶିଷ୍ଟ ଅଟେ ?
(i) ବାରମ୍ବାରତା ନିଦ୍ଦେଶକ ରେଖା
(ii) ବାରମ୍ବାରତା ବକ୍ରରେଖା
(iii) ପୂର୍ବାପେକ୍ଷା କମ୍ ଓଜିଭ୍
(iv) ପୂର୍ବାପେକ୍ଷା ଅଧିକ ଓଜିଭ୍
Answer:
(iii) ପୂର୍ବାପେକ୍ଷା କମ୍ ଓଜିଭ୍
୮। କେଉଁଟି ଏକ ଆୟତନ ବିଶିଷ୍ଟ ରେଖାଚିତ୍ର ଅଟେ ?
(i) ସରଳ ସ୍ତମ୍ଭଚିତ୍ର
(ii) ହିଷ୍ଟୋଗ୍ରାମ୍
(iii) ଓଜିଭ୍
(iv) ଉପରୋକ୍ତ ସମସ୍ତ
Answer:
(ii) ହିଷ୍ଟୋଗ୍ରାମ୍
୯। ଗୋଟିଏ ଶ୍ରେଣୀର ଊର୍ଦ୍ଧ୍ୱସୀମା ଓ ନିମ୍ନସୀମାର ଯୋଗଫଳକୁ 2ରେ ବିଭକ୍ତ କଲେ କ’ଣ ମିଳିଥାଏ ?
(i) ମାଧ୍ୟମାନ
(ii) ଗରିଷ୍ଠକ
(iii) ମଧ୍ୟବିନ୍ଦୁ
(iv) ସହସମ୍ବନ୍ଧ
Answer:
(iii) ମଧ୍ୟବିନ୍ଦୁ
୧୦। ବୃତ୍ତ ଲେଖରେ ଅଂଶଗୁଡ଼ିକ କେତେ ଡିଗ୍ରୀକୁ ଭାଗକରି ସମାନୁପାତି ହୋଇଥାଏ ?
(i) 90°
(ii) 180°
(iii) 220°
(iv) 360°
Answer:
(iv) 360°
B. ଶୂନ୍ୟସ୍ଥାନ ପୂରଣ କର :
୧। ଅଶୋଧୂତ ସାଂଖ୍ୟକ ତଥ୍ୟାବଳୀର __________________ ଧର୍ମ ଗୁଡ଼ିକ ସହଜରେ ପ୍ରକାଶ ଲାଭ କରନ୍ତି ନାହିଁ।
Answer:
ମୌଳିକ
୨। ତଥ୍ୟାବଳୀକୁ ବାରମ୍ବାରତା ପରିବଣ୍ଟନ ସାରଣୀ ମାଧ୍ୟମରେ ପ୍ରଦର୍ଶନ କଲେ, ତାହାର __________________ ରୈଶୈଷ୍ମ୍ୟ ମାନଙ୍କର ପରିପ୍ରକାଶ ଘଟିଥାଏ।
Answer:
ଅନ୍ତର୍ନିହିତ
୩। ଲବ୍ଧାଙ୍କ ଗୁଡ଼ିକୁ ଗୋଟିଏ ସ୍ତମ୍ଭରେ ଓ ସେମାନଙ୍କର ବାରମ୍ବାରତା ଗୁଡ଼ିକୁ ଅନ୍ୟ ଏକ ସ୍ତମ୍ଭରେ ଲେଖୁ ଯେଉଁ ସାରଣୀ ___________________ ସାରଣୀ କୁହାଯାଏ ।
Answer:
ବାରମ୍ବାରତା ପରିବଣ୍ଟନ
![]()
୪। ତଥ୍ୟାବଳୀର ପ୍ରତ୍ୟେକ ଲବ୍ଧାଙ୍କ ଲାଗି ଲବ୍ଧାଙ୍କ ତାଲିକାରେ ସଂପୃକ୍ତ ଲବ୍ଧାଙ୍କ ଡାହାଣରେ ଗୋଟିଏ ଗୋଟିଏ ଗାର (/) ସାମାନ୍ୟ ତିର୍ଯ୍ୟକ୍ ଭାବେ ଅଙ୍କନ କରାଯାଏ, ଏହି ଗାରକୁ ____________________ ରେଖା କୁହାଯାଏ ।
Answer:
ଅନୁମେଳକ
୫। ତଥ୍ୟାବଳୀକୁ ଅଳ୍ପ ସ୍ଥାନରେ ଓ ସଂକ୍ଷିପ୍ତରେ ଦର୍ଶାଇବା ନିମିତ୍ତ ଲବ୍ଧାଙ୍କ ଗୁଡ଼ିକୁ କେତେକ ସଂଭାଗରେ ବିଭକ୍ତ କରାଯାଇଥାଏ, ଏହି ପ୍ରକ୍ରିୟାକୁ _______________________ କୁହାଯାଏ ।
Answer:
ସଂଭାଗୀକରଣ
୬। ବାରମ୍ବାରତା ବିତରଣର __________________ ମାଧ୍ୟମରେ ଉପସ୍ଥାପନାର ବାରମ୍ବାରତା ବିତରଣ ଚିତ୍ରଲେଖ ରୂପେ ଅଭିହିତ କରାଯାଏ।
Answer:
ଚିତ୍ରଲେଖ
୭। ନିରବଚ୍ଛିନ୍ନ ମାଳାର ବାରମ୍ବାରତା ବିତରଣର ଚିତ୍ର ଲେଖକ ଉପସ୍ଥାପନାକୁ __________________ କୁହାଯାଏ ।
Answer:
ହିଷ୍ଟୋଗ୍ରାମ୍
୮। ହିଷ୍ଟୋଗ୍ରାମ୍ ହେଉଛି କେତେ ଗୁଡ଼ିଏ ଉଲ୍ଲମ୍ବ ସ୍ତମ୍ଭଚିତ୍ରର ସେଟ୍, ଯାହାର କ୍ଷେତ୍ରଫଳ ପ୍ରତିନିଧ୍ଵ କରୁଥିବା ବାରମ୍ବାରତା ସହିତ ।
Answer:
ସମାନୁପାତୀ
୯। ହିଷ୍ଟୋଗ୍ରାମ୍ ଅଙ୍କନ କରିବାବେଳେ ଲବ୍ଧଙ୍କକୁ ସର୍ବଦା ______________________ ଅକ୍ଷରେ ନିଆଯାଏ।
Answer:
ଆନୁଭୂମିକ,
୧୦। ହିଷ୍ଟୋଗ୍ରାମ୍ ଅଙ୍କନ କରିବାବେଳେ ବାରମ୍ବାରତା __________________ ଅକ୍ଷରେ ନିଆଯାଏ।
Answer:
ଉଲ୍ଲମ୍ବ
୧୧। ହିଷ୍ଟୋଗ୍ରାମ୍ର କ୍ଷେତ୍ରଫଳ ସମସ୍ତ ସଂଭାଗ ଗୁଡ଼ିକରେ ଆବଣ୍ଟନ ହୋଇଥିବା ସମୁଦାୟ __________________ କୁ ପ୍ରତିନିଧୂତ୍ବ କରିଥାଏ ।
Answer:
ବାରମ୍ବାରତା
୧୨। ଯଦିଓ ହିଷ୍ଟୋଗ୍ରାମ୍ ବାରମ୍ବାରତା ବିତରଣର ଚିତ୍ରଲେଖକ ଉପସ୍ଥାପନା ପାଇଁ ବିସ୍ତୃତ ଭାବରେ ବ୍ୟବହୃତ ହୁଏ, ତଥାପି ଏହା ବାରମ୍ବାରତା ବିତରଣର _______________ ସଂଭାଗ ପାଇଁ ଅନୁପଯୁକ୍ତ।
Answer:
ପ୍ରକାଶ୍ୟଅନ୍ତ
୧୩। ଗୋଟିଏ ସମୟ ପର୍ଯ୍ୟାୟ ଲେଖଚିତ୍ରରେ _____________________ ଉପାଦାନ y- ଅକ୍ଷରେ ଦର୍ଶାଯାଏ ।
Answer:
ନିର୍ଭରଶୀଳ
![]()
୧୪। ଯେତେବେଳେ ସଂଭାଗ ଗୁଡ଼ିକର ସଂଖ୍ୟା ____________________ ହୋଇଥାଏ, ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ର ପ୍ରସନ୍ଦନୀୟ।
Answer:
ଅନେକ
୧୫। ବାରମ୍ବାରତା ରେଖାଚିତ୍ର _____________________ ମାଧ୍ୟମରେ ଅଙ୍କନ କରାଯାଏ।
Answer:
ହିଷ୍ଟୋଗ୍ରାମ୍
୧୬। ଗୋଟିଏ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ରର ବିଭିନ୍ନ ବିନ୍ଦୁ ଗୁଡ଼ିକୁ ସରଳରେଖା ଦ୍ଵାରା ସଂଯୋଗ ନ କରି ଯଦି ମୁକ୍ତ ହସ୍ତରେ ସଂଯୋଗ କରାଯାଏ, ତାହାକୁ _____________________ କୁହାଯାଏ ।
Answer:
ବାରମ୍ବାରତା ବକ୍ରରେଖା
୧୭। ଯେତେବେଳେ ସଂଭାଗ ବିସ୍ତାରର ପରିମାଣ ___________________ ହୋଇଥାଏ, ବାରମ୍ବାରତା ବକ୍ରରେଖାର ଶୀର୍ଷବିନ୍ଦୁ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ରର ଶୀର୍ଷବିନ୍ଦୁରୁ ମସୃଣ କରି ମୁକ୍ତ ହସ୍ତରେ ଅଙ୍କନ କରାଯାଏ।
Answer:
ବୃହତ
୧୮। ବକ୍ରରେଖାର ମସୃଶୀକରଣ _____________________ ଓ __________________ ଉପରେ ନିର୍ଭରଶୀଳ ।
Answer:
ପ୍ରକୃତି ଓ ଲକ୍ଷଣ
୧୯। ଗୋଟିଏ ______________________ ହେଉଛି ପରିସଂଖ୍ୟାନ ତଥ୍ୟ ଧାଡ଼ି ଏବଂ ସ୍ତମ୍ଭର ପଦ୍ଧତିଗତ ସଜ୍ଜୀକରଣ ।
Answer:
ସାରଣୀ
୨୦। ମୁଖ୍ୟଶ _____________________ ଆକାରରେ ସାରଣୀ ତଳେ ଲେଖା ଯାଇଥାଏ ।
Answer:
ଶୀର୍ଷକ
୨୧। ପଦଟୀକାଟି ସାରଣୀର ______________________ ରଖାଯାଇଥାଏ ।
Answer:
ଷ୍ଟବ/ମୁଖ୍ୟଅଂଶର ତଳେ
![]()
୨୨। ପାଇ ରେଖାଚିତ୍ରକୁ _______________ ରେଖାଚିତ୍ର ମଧ୍ୟ କୁହାଯାଏ ।
Answer:
କୌଣିକ
୨୩।
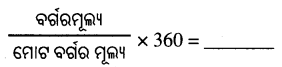
Answer:
ବର୍ଗର କୋଣ
୨୪। ଗୋଟିଏ _________________________ ଲେଖଚିତ୍ର ଦୁଇଟି ଉପାଦାନ ମଧ୍ୟରେ ସମ୍ପର୍କକୁ ଦର୍ଶାଇପାରେ ।
Answer:
ରେଖା
୨୫। ଲେଖଚିତ୍ରର ଗୋଟିଏ ଉପାଦାନ ଯଦି ______________________ ହୁଏ, ଏହାକୁ ସମୟ ପର୍ଯ୍ୟାୟ ଲେଖଚିତ୍ର କୁହାଯାଏ ।
Answer:
ସମୟ
୨୬। ଗୋଟିଏ ସମୟ ପର୍ଯ୍ୟାୟ ଲେଖଚିତ୍ରରେ _____________________ ହେଉଛି ସ୍ବାଧୀନ ଉପାଦାନ ।
Answer:
ସମୟ
C. ଗୋଟିଏ ବାକ୍ୟରେ ଉତ୍ତର ଦିଅ ।
୧। ଓଜିଭ୍ କ’ଣ ?
Answer:
ଲବ୍ଧାଙ୍କ ଓ ତା’ର ରାଶିକୃତ ବାରମ୍ବାରତାର କ୍ରମିକ ଯୋଡ଼ିକୁ ନେଇ ବିନ୍ଦୁମାନଙ୍କୁ ରେଖାଦ୍ଵାରା ଯୋଗ କଲେ ଯେଉଁ ରେଖାଚିତ୍ର ଅଙ୍କିତ ହୁଏ ତାହାକୁ ଓଜିଭ କୁହାଯାଏ।
୨। କେଉଁ ହାରାହାରି ଓଜିଭ ସାହାଯ୍ୟରେ ଦର୍ଶାଯାଇ ପାରିବ ।
Answer:
ମଧ୍ଯମା
![]()
୩। ବାରମ୍ବାରତା ବିତରଣ ଚିତ୍ରଲେଖ କ’ଣ ?
Answer:
ବାରମ୍ବାରତା ବିତରଣ ଚିତ୍ରଲେଖ ମାଧ୍ୟମରେ ଉପସ୍ଥାପନାକୁ ବାରମ୍ବାରତା ବିତରଣ ଚିତ୍ରଲେଖ ରୂପେ ଅଭିହିତ କରାଯାଏ।
୪। ହିଷ୍ଟୋଗ୍ରାମ୍ କ’ଣ ?
Answer:
ନିରବଚ୍ଛିନ୍ନ ମାଳାର ବାରମ୍ବାରତା ବିତରଣର ଚିତ୍ରଲେଖକ ଉପସ୍ଥାପନାକୁ ହିଷ୍ଟୋଗ୍ରାମ୍ କୁହାଯାଏ।
୫। ରାଶିକୃତ ବାରମ୍ବାରତା କ’ଣ ?
Answer:
ଯେତେବେଳେ ଗୋଟିଏ ସଂଭାଗର ବାରମ୍ବାରତା ସହିତ ପରବର୍ତୀ ସଂଭାଗର ବାରମ୍ବାରତାକୁ ଯୋଗ କରାଯାଇଥାଏ ଏବଂ ଯୋଗଫଳକୁ ପରବର୍ତ୍ତୀ ସଂଭାଗର ବାରମ୍ବାରତା ସହିତ ଯୋଗ କରାଯାଏ, ଇତ୍ୟାଦି, ଏହି ରାଶିକୃତ ବାରମ୍ବାରତା କୁହାଯାଏ।
୬। ରାଶିକୃତ ବାରମ୍ବାରତା ବକ୍ରରେଖା କ’ଣ ?
Answer:
ଲଜ୍ଜାଙ୍କକୁ ଉଲ୍ଲମ୍ବ ଅକ୍ଷରେ ଓ ରାଶିକୃତ ବାରମ୍ବାରତାକୁ ଅନୁଲମ୍ବ ଅକ୍ଷରେ ନେଇ ଯେଉଁ ବକ୍ରରେଖା ପାଇଥାଉ, ତାହାକୁ ରାଶିକୃତ ବାରମ୍ବାରତା ବକ୍ରରେଖା ରୂପେ ଅଭିହିତ କରାଯାଏ।
୭। ଓଜିଭର ମୂଳ ଆଭିମୁଖ୍ୟ କ’ଣ ?
Answer:
କୌଣସି ଦତ୍ତ ମୂଲ୍ୟର ତଳ ପାର୍ଶ୍ଵ ବା ଉପର ପାର୍ଶ୍ଵରେ ରାଶିଗୁଡ଼ିକର ସଂଖ୍ୟାକୁ ସ୍ଥିର କରିବା ଓ ଦର୍ଶାଇବା, ଦୁଇ ବା ତତୋଽଧୂକ ବାରମ୍ବାରତା ବିତରଣ ଗୁଡ଼ିକୁ ତୁଳନା କରିବା ଇତ୍ୟାଦି ଓଜିଭର ମୂଳ ଆଭିମୁଖ୍ୟ।
୮। ବାରମ୍ବାରତା ବକ୍ରରେଖା କ’ଣ ?
Answer:
ଗୋଟିଏ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ରର ବିଭିନ୍ନ ବିନ୍ଦୁ ଗୁଡ଼ିକୁ ସରଳରେଖା ଦ୍ଵାରା ସଂଯୋଗ ନ କରି ଯଦି ହସ୍ତରେ ସଂଯୋଗ କରାଯାଏ, ତାହାକୁ ବାରମ୍ବାରତା ବକ୍ରରେଖା କୁହାଯାଏ।
୯। କେଉଁ ସଂଭାଗ ଥିବା ବାରମ୍ବାରତା ପରିବଣ୍ଟନର ହିଷ୍ଟୋଗ୍ରାମ୍ ଅଙ୍କନ ସମ୍ଭବ ହୋଇ ନ ଥାଏ ?
Answer:
ଅବାଧ ସଂଭାଗ
୧୦। ରାଶିକୃତ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ପରିବଣ୍ଟନର ଜ୍ୟାମିତିକ ଚିତ୍ରକୁ କ’ଣ କହନ୍ତି ?
Answer:
ଓଜିଭ୍
୧୧। ଆୟତ କ୍ଷେତ୍ରମାନଙ୍କ ଦ୍ବାରା ପ୍ରଦର୍ଶିତ ବାରମ୍ବାରତା ପରିବଣ୍ଟନକୁ କ’ଣ କହନ୍ତି ?
Answer:
ହିଷ୍ଟୋଗ୍ରାମ୍
![]()
୧୨। ସଂଭାଗର ବାରମ୍ବାରତାକୁ ସେହି ସଂଭାଗର ବିସ୍ତାରରେ ଭାଗ କଲେ କ’ଣ ମିଳିଥାଏ ?
Answer:
ସମନ୍ବିତ ବାରମ୍ବାରତା
D. ନିମ୍ନଲିଖ ଉକ୍ତିଗୁଡ଼ିକ ଭୁଲ କି ଠିକ୍ ଲେଖ । ରେଖାଙ୍କିତ ଅଂଶର ପରିବର୍ତ୍ତନ ନ କରି ଆବଶ୍ୟକ ସ୍ଥଳେ ସଂଶୋଧନ କର ।
୧। ପୂର୍ବାପେକ୍ଷା କମ୍ ଓଜିଭ୍ ଏକ ନିମ୍ନଗାମୀ ବକ୍ର ଅଟେ ।
Answer:
ପୂର୍ବାପେକ୍ଷା କମ୍ ଓଜିଭ୍ ଏକ ଉର୍ଦ୍ଧ୍ୱଗାମୀ ବକ୍ର ଅଟେ ।
୨। ହିଷ୍ଟୋଗ୍ରାମ୍ ଅଙ୍କନ କରି ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ଲେଖଚିତ୍ର ଅଙ୍କନ କରାଯାଇପାରେ।
Answer:
ହିଷ୍ଟୋଗ୍ରାମ୍ ଅଙ୍କନ କରି ବା ନ କରି ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ଲେଖଚିତ୍ର ଅଙ୍କନ କରାଯାଇପାରେ।
୩। ଅସମାନ ଶ୍ରେଣୀ ଅନ୍ତରାଳ ଥିବା ବିତରଣର ହିଷ୍ଟୋଗ୍ରାମ୍ ଅଙ୍କନ କରାଯାଇପାରେ ନାହିଁ ।
Answer:
ଅସମାନ ଶ୍ରେଣୀ ଅନ୍ତରାଳ ଥିବା ବିତରଣର ହିଷ୍ଟୋଗ୍ରାମ୍ ଅଙ୍କନ କରାଯାଇପାରେ ।
୪। ଓଜିଭ ସାହାଯ୍ୟରେ ମାଧମାନ ନିର୍ଣ୍ଣୟ କରାଯାଇପାରେ ।
Answer:
ଓଭିଜ୍ ସାହାଯ୍ୟରେ ମଧ୍ୟମା ନିର୍ଣ୍ଣୟ କରାଯାଇପାରେ ।
୫। ହିଷ୍ଟୋଗ୍ରାମ୍ ହେଉଛି ଏକ-ଆୟତନ ବିଶିଷ୍ଟ କ୍ଷେତ୍ର ।
Answer:
ହିଷ୍ଟୋଗ୍ରାମ୍ ହେଉଛି ଦୁଇ -ଆୟତନ ବିଶିଷ୍ଟ କ୍ଷେତ୍ର ।
୬। ବାରମ୍ବାରତା ବକ୍ରରେଖା ଏକ ମସୃଣ ରେଖା।
Answer:
ଠିକ୍
୭। ପୂର୍ବାପେକ୍ଷା ଅଧିକ ଓଜିଭ ‘S’ ଆକୃତିର।
Answer:
ପୂର୍ବାପେକ୍ଷା ଅଧିକ ଓଜିଭ୍ ଓଲଟା ‘s’ ଆକୃତିର।
![]()
୮। ହିଷ୍ଟୋଗ୍ରାମ୍ ହେଉଛି ପରସ୍ପର ସଂଯୁକ୍ତ କେତୋଟି ଉଲ୍ଲମ୍ବ ରେଖାର ସମାହାର।
Answer:
ହିଷ୍ଟୋଗ୍ରାମ୍ ହେଉଛି ପରସ୍ପର ସଂଯୁକ୍ତ କେତୋଟି ଉଲ୍ଲମ୍ବ ସ୍ତମ୍ବଚିତ୍ରର ସମାହାର ।
୯। ମେଳକ ରେଖା ସାହାଯ୍ୟରେ ହିଷ୍ଟୋଗ୍ରାମ୍ ଅଙ୍କନ ହୁଏ।
Answer:
ଆୟତକାର କ୍ଷେତ୍ର ସାହାଯ୍ୟରେ ହିଷ୍ଟୋଗ୍ରାମ୍ ଅଙ୍କନ ହୁଏ ।
୧୦। ନିରବଚ୍ଛିନ୍ନ ସଂଭାଗ ପାଇଁ ହିଷ୍ଟୋଗ୍ରାମ୍ ଅନୁପଯୁକ୍ତ।
Answer:
ପ୍ରକାଶ୍ୟ ଅନ୍ତ ସଂଭାଗ ପାଇଁ ହିଷ୍ଟୋଗ୍ରାମ୍ ଅନୁପଯୁକ୍ତ ।
E. ନିମ୍ନଲିଖ ପ୍ରଶ୍ନମାନଙ୍କର ଉତ୍ତର ଦିଅ ।
୧। ସାରଣୀ ମାଧ୍ୟମରେ ତଥ୍ୟାବଳୀର ଉପସ୍ଥାପନା କହିଲେ କ’ଣ ବୁଝ ?
Answer:
ସାରଣୀ ମାଧ୍ୟମରେ ତଥ୍ୟାବଳୀର ଉପସ୍ଥାପନା କହିଲେ ତଥ୍ୟାବଳୀର ଲବ୍ଧଅଙ୍କଗୁଡ଼ିକୁ ସୁବ୍ୟସ୍ଥିତ ପଦ୍ଧତିରେ ସାରଣୀ ବା ତାଲିକା ମଧ୍ୟରେ ପଙକ୍ତି ଓ ସ୍ତମ୍ଭ ଆକାରରେ ସଜାଇ ଲେଖୁବାକୁ ହିଁ ବୁଝାଇଥାଏ । ସାରଣୀରେ ତଥ୍ୟାବଳୀ ପ୍ରଦର୍ଶିତ ହେଲେ ପର୍ଯ୍ୟବେକ୍ଷକ ବା ପାଠକମାନଙ୍କୁ କୌଣସି ଏକ ନିଦ୍ଧିଷ୍ଟ ଲବ୍ଧାଙ୍କ ଖୋଜି ବାହାର କରିବା ବା ଦୁଇଟି ଲବ୍ଧାଙ୍କ ମଧ୍ୟରେ ତୁଳନା କରିବା ସହଜ ହୋଇଥାଏ ।
୨। ସାରଣୀର ଆବଶ୍ୟକୀୟ ଅଂଶଗୁଡ଼ିକ କ’ଣ ?
Answer:
ସାରଣୀର, ଆବଶ୍ୟକୀୟ ଅଂଶଗୁଡ଼ିକ ତଳେ ଦିଆଗଲା। (କ) ସାରଣୀ ସଂଖ୍ୟା, (ଖ) ଶୀର୍ଷକ, (ଗ) ଶୀର୍ଷଟୀକା, (ଘ) ପଙକ୍ତିନାମା (ଙ) ଶିରୋନାମା (ଚ) କ୍ଷେତ୍ର (ଛ) ପାଦଟୀକା (ଜ) ଉତ୍ସଟୀକା ଇତ୍ୟାଦି
![]()
୩। ସାରଣୀ ମାଧ୍ୟମରେ ତଥ୍ୟାବଳୀର ଉପସ୍ଥାପନା ଲକ୍ଷ୍ୟ କ’ଣ ?
Answer:
ସାରଣୀ ମାଧ୍ୟମରେ ତଥ୍ୟାବଳୀର ଉପସ୍ଥାପନାର ମୁଖ୍ୟ ଲକ୍ଷ୍ୟଗୁଡ଼ିକ ହେଲା –
- ସାରଣୀର ମୁଖ୍ୟ ଲକ୍ଷ୍ୟ ହେଲା ତାହା ବିଭିନ୍ନ ଅଂଶକୁ ତୁଳନା କରିବାରେ ସାହାଯ୍ୟ କରେ ।
- ତଥ୍ୟାଳୀକୁ ସରଳୀକରଣ କରି ଉପସ୍ଥାପିତ କରିଥାଏ ଯାହାଦ୍ୱାରା ସମସ୍ତେ ସହଜରେ ବୁଝିପାରନ୍ତି ।
- ପ୍ରତ୍ୟେକ ସାରଣୀର ପରିଚୟ ତାହାର ଶୀଷକରୁ ଜଣାପଡ଼ିଥାଏ ।
- ଏହା ତଥ୍ୟାବଳୀକୁ ନିର୍ଭୁଲ ଭାବରେ ଉପସ୍ଥାପିତ କରିବାରେ ସାହାଯ୍ୟ କରେ ।
- ଏହା ଆକର୍ଷଣୀୟ ଦେଖାଯାଏ ।
- ଏହାଦ୍ଵାରା କଥ୍ୟାବଳୀରେ ଭୁଲ ବାଛିବା ସହଜ ହୋଇଥାଏ ।
- ତଥ୍ୟାମଳୀକୁ ସଂକ୍ଷିପ୍ତରେ ପ୍ରକାଶ କରିବା ପାଇଁ ଏହା ସାହାଯ୍ୟ କରିଥାଏ ।
- ପର୍ଯ୍ୟାଲୋଚନା କରିବାରେ ସାରଣୀ ସାହାଯ୍ୟ କରିଥାଏ ।
୪। ସାରଣୀର ଶିରୋନାମା କହିଲେ କ’ଣ ବୁଝ ?
Answer:
ଶିରୋନାମା ସାରଣୀର ଅନ୍ତର୍ଭୁକ୍ତ ସ୍ତମ୍ଭଗୁଡ଼ିକ ସମ୍ବନ୍ଧୀୟ ତଥ୍ୟାବଳୀର ସୂଚନା ପ୍ରଦାନ କରେ । ମୁଖ୍ୟ ଶିରୋନାମାକୁ କେତେକ ଉପଶିରୋନାମା ବା ସ୍ତମ୍ଭ ଶୀର୍ଷକରେ ପ୍ରକାଶ କରାଯାଇପାରେ । ତଥ୍ୟାବଳୀର ବିଭିନ୍ନ ଆଭିମୁଖ୍ୟକୁ ଆଖ୍ ଆଗରେ ରଖ୍ ଏହା କରାଯାଇଥାଏ । ଫଳରେ ତଥ୍ୟାବଳୀର ବିଶ୍ଳେଷଣ ସହଜ ଓ ଉପାଦେୟ ହୋଇଥାଏ ।
୫। ସ୍ତମ୍ଭ ଚିତ୍ର କାହାକୁ କୁହାଯାଏ ?
Answer:
ଏହି ଚିତ୍ରଗୁଡ଼ିକ ଆନୁଭୂମିକ ବା ଉଲମ୍ବ ସ୍ତମ୍ଭ ଆକାରରେ ପ୍ରଦର୍ଶିତ ହୋଇଥାଆନ୍ତି । ସ୍ତମ୍ଭଗୁଡ଼ିକର ପ୍ରସ୍ଥ ସମାନ ରହି ସେମାନଙ୍କର ଦୈର୍ଘ୍ୟ ଲବ୍ଧାଙ୍କମାନଙ୍କ ସହ ସମାନୁପାତରେ ପରିବର୍ତ୍ତନ ହୋଇଥାଆନ୍ତି ।ସ୍ତମ୍ଭଗୁଡ଼ିକୁ ସହଜରେ ଚିହ୍ନଟ କରିବା ପାଇଁ ଦୁଇଟି ସହ୍ନିହିତ ସ୍ତମ୍ଭ ମଧ୍ଯରେ ବ୍ୟବଧାନ ରଖାଯାଇଥାଏ ।
୬। ଅଂଶକ ସ୍ତମ୍ଭଚିତ୍ର କାହାକୁ କୁହାଯାଏ ?
Answer:
ଅନେକ ସମୟରେ ଆମେ ତଥ୍ୟାବଳୀର ଲବ୍ଧାଙ୍କଗୁଡ଼ିକ ସହ ସେମାନଙ୍କର ବିଭିନ୍ନ ଅଂଶକୁ ପ୍ରଦର୍ଶନ କରିବା ପାଇଁ ଆଗ୍ରହୀ ହୋଇଥାଉ । ଏ ସ୍ଥଳରେ ଅଂଶକୁ ପ୍ରଦର୍ଶନ କରିବା ପାଇଁ ଆଗ୍ରହୀ ହୋଇଥାଉ । ଏ ସ୍ଥଳରେ ଅଂଶକ ସ୍ତମ୍ଭଚିତ୍ର ବେଶ୍ ଉପଯୋଗୀ ହୋଇଥାଏ । ଉଦାହରରସ୍ୱରୂପ ଏକ ବର୍ଷରେ ଗୋଟିଏ ଶ୍ରେଣୀର ଛାତ୍ର ସଂଖ୍ୟା 150 ଅଟନ୍ତି ।
ସେମାନଙ୍କ ମଧ୍ୟରୁ ଅନୁସୂଚିତ ଜାତି 55 ଜଣ ଅଟନ୍ତି । ଏହି ତଥ୍ୟରେ ଆମେ ମୋଟ୍ ଛାତ୍ରଛାତ୍ରୀମାନଙ୍କୁ ଏକସ୍ତମ୍ଭରେ ପ୍ରକାଶ କର ସ୍ତମ୍ଭକୁ ବିଭିନ୍ନ ଅଂଶ ଯଥା ଅନୁସୂଚିତ ଜାତି, ଉପଜାତି, ସାଧାରଣ ବର୍ଗରେ ପ୍ରକାଶ କରିପାରିବ । ଏହାକୁ ଅଂଶକ ସ୍ତମ୍ଭଚିତ୍ର କୁହାଯିବ ।
୭। ବୃତ୍ତ ଲେଖ କାହାକୁ କୁହାଯାଏ?
Answer:
ସଂଗୃହୀତ ତଥ୍ୟକୁ ଅନେକ ସମୟରେ ଏକ ବୃତ୍ତାକାର କ୍ଷେତ୍ରରେ ଆନୁପାତିକ ଅଂଶ ରୂପେ ପ୍ରକା କରାଯାଇ ଚିତ୍ର ଅଙ୍କନ କରାଯାଇଥାଏ । ଏହାକୁ ବୃତ୍ତଲେଖ କୁହାଯାଏ । ସାଧାରଣତଃ ତଥ୍ୟର ବିଭିନ୍ନ ଅଂଶକୁ ବୃତ୍ତର ମଧ୍ୟାହ୍ନ ସମୟ ଚିହ୍ନଠାରୁ ଘଣ୍ଟା କଣ୍ଟା ଘୂରୁଥିବା ଦିଗରେ ବଡ଼ରୁ ସାନ କ୍ରମରେ ଏପରି ପ୍ରଦର୍ଶନ କରାଯାଏ । ଯେପରିକି ଏହାର ପ୍ରତ୍ୟେକ ଅଂଶ ବୃତ୍ତକଳାର କେନ୍ଦ୍ରୀୟ କୋଣମାନଙ୍କ ସହ ସମାନୁପାତିକ ହେବ ।
![]()
୮। ଛବି ଚିତ୍ର କାହାକୁ କୁହାଯାଏ ?
Answer:
ଛବି ବା ଚିତ୍ର ସାହାଯ୍ୟରେ ତଥ୍ୟାବଳୀର ପ୍ରଦର୍ଶନ କରାଗଲେ ତାହାକୁ ଛବି ଲେଖ କୁହାଯାଏ । ତଥ୍ୟାବଳୀର ବିସ୍ତାର ଛବିର ଅକୃତି ସହ ସମ୍ବନ୍ଧିତ ହୋଇଥାଏ । ବରଂ ଛବିଗୁଡ଼ିକର ସଂଖ୍ୟାରୁ ତଥ୍ୟାବଳୀର ଆକାର ବିଷୟରେ ଧାରଣା କରାଯାଇଥାଏ । ଅନେକ ସମୟରେ ଛବିକୁଡ଼ିକୁ ବିଭିନ୍ନ ରଙ୍ଗ ବା ରେଖାଦ୍ୱାରା ସୂଚିତ କରାଯାଇ ତଥ୍ୟାବଳୀର ବିଭିନ୍ନ ଭାଗର ପରିମାଣ ନିର୍ଣ୍ଣୟ କରାଯାଇଥାଏ ।
୯। ପାଦଟୀକା କାହାକୁ କୁହାଯାଏ ?
Answer:
ସାରଣୀର କୌଣସି ନିଦ୍ଧିଷ୍ଟ ଉଲ୍ଲେଖ ବା ଅଂଶ ବିଷୟରେ ସ୍ପଷ୍ଟୀକରଣ ଦେବାକୁ ଥିଲେ ପାଦଟୀକାର ବ୍ୟବହାର କରାଯାଏ । ଏହା ଏକ ଖଣ୍ଡବାକ୍ୟ ହିସାବରେ ସାରଣୀର ନିମ୍ନରେ ବାମପାଖକୁ ଲେଖାଯାଇଥାଏ । ଏହା ପାଠକମାନଙ୍କ ମନରୁ ସଂଶୟ ଦୂର କରିବାରେ ସହାୟକ ହୋଇଥାଏ ।
୧୦। ଉତ୍ସଟୀକା କାହାକୁ କୁହାଯାଏ ?
Answer:
ତଥ୍ୟାବଳୀ କେଉଁ ଉତ୍ସ ବା ସୁତ୍ରରୁ ସଂଗୃହୀତ ହୋଇଛି ସେ ସମ୍ବନ୍ଧରେ ସର୍ବଶେଷ ତଥ୍ୟ ସାରଣୀ ନିମ୍ନରେ ପ୍ରଦାନ କରାଯାଏ । ତଥ୍ୟ କେବେ ପ୍ରକାଶିତ ହୋଇଛି ବା କେଉଁଠାରୁ ସଂଗୃହୀତ ହୋଇଛି ଜାଣିବା ଦ୍ଵରା ପର୍ଯ୍ୟବେକ୍ଷକ ବା ପାଠକମାନେ ପରବର୍ତୀ ଅନୁସନ୍ଧାନ ସମୟରେ ମୂଳ ଉତ୍ସରୁ ତଥ୍ୟ ସଂଗ୍ରହ କରିବାର ସୁଯୋଗ ଲାଭ କରିଥାନ୍ତି ।
୧୧। ସମୟାନୁକ୍ରମୀ ଶ୍ରେଣୀଲେଖ କାହାକୁ କୁହାଯାଏ ?
Answer:
ସମୟ ବା କାଳକୁ ସ୍ୱାଧୀନ ବା ଅନ୍ୟପକ୍ଷେ ଚଳ ଓ ତଥ୍ୟାବଳୀର ଲବ୍ଧାଙ୍କମାନଗୁଡ଼ିକୁ ସାପେକ୍ଷଚଳ ହିସାବରେ ଗ୍ରହର କରାଯାଇ ଯେଉଁ ରେଖା ଅଙ୍କନ କରାଯାଏ ତାହାକୁ ସମୟନୁକ୍ରମୀ ଶ୍ରେଣୀ ଲେଖ କୁହାଯାଏ ।
୧୨। ଓଜିଭ୍ କ’ଣ ?
Answer:
ରାଶିକୃତ ବାରମ୍ବାରତାକୁ ବ୍ୟବହାର କରି ଲେଖଚିତ୍ର ଅଙ୍କନ କଲେ ତାହାକୁ ଓଜିଭ୍ କୁହାଯାଏ ।
୧୩। ରେଖା ଲେଖଚିତ୍ର କହିଲେ କ’ଣ ବୁଝ ?
ସମୟ ଅନୁସାରେ ପରିବର୍ଭନ ହୋଇଥିବା ତଥ୍ୟ ଓ ସୂଚନାକୁ ଚିତ୍ର ମାଧ୍ୟମରେ ପ୍ରଦର୍ଶିତ କଲେ ତାହାକୁ ରେଖା ଲେଖଚିତ୍ର କୁହାଯାଏ ।
F. ନିମ୍ନଲିଖ ପ୍ରଶ୍ନମାନଙ୍କ ଉତ୍ତର ଦୁଇଟି / ତିନୋଟି ବାକ୍ୟ ମଧ୍ଯରେ ଦିଅ ।
୧। ହିଷ୍ଟୋଗ୍ରାମ୍ କ’ଣ ?
Answer:
ହିଷ୍ଟୋଗ୍ରାମ୍ ବାରମ୍ବାରତା ବିତରଣ ଚିତ୍ରଲେଖର ବିଭିନ୍ନ ପ୍ରଣାଳୀ ମଧ୍ୟରୁ ସବୁଠାରୁ ଅଧିକ ପ୍ରଚଳିତ ଚିତ୍ରଲେଖା । ତଥ୍ୟାବଳୀର ସଂଭାଗ ଗୁଡ଼ିକୁ ଆନୁଭୂମିକ ଅକ୍ଷ (ox-oxen)ରେ ଓ ସେହି ସଂଭାଗର ବାରମ୍ବାରତାଗୁଡ଼ିକୁ ଉଲ୍ଲମ୍ବ ଅକ୍ଷ (Y – oxen)ରେ ନେଇ ପାଖକୁ ପାଖ ଲାଗି ଯେଉଁ ଆୟତକ୍ଷେତ୍ର ଗୁଡ଼ିକ ଅଙ୍କନ କରାଯାଏ, ତାହାକୁ ହିଷ୍ଟୋଗ୍ରାମ୍ କହନ୍ତି। ଏହି ଆୟତକ୍ଷେତ୍ରର କ୍ଷେତ୍ରଫଳ ଗୁଡ଼ିକ ସଂଭାଗର ବାରମ୍ବାରତା ସହ ସମାନୁପାତୀ ଅଟନ୍ତି ।
ସଂଭାଗ ବିସ୍ତାରଗୁଡ଼ିକ ସମାନ ହୋଇଥିଲେ, ସମସ୍ତ ଆୟତକ୍ଷେତ୍ରର ଆଧାର (base) ସମାନ ହୋଇଥାଏ ଓ ଆୟତକ୍ଷେତ୍ରର ଉଚ୍ଚତା ସଂଭାଗ ଗୁଡ଼ିକର ବାରମ୍ବାରତା ସହ ମଧ୍ଯ ସମାନୁପାତୀ ହୋଇଥା’ନ୍ତି। ଯେତେବେଳେ ସଂଭାଗ ବିସ୍ତାର ଅସମାନ ହୁଏ, ଆୟତକାର କ୍ଷେତ୍ରର ପ୍ରସ୍ଥ ପରିବର୍ତ୍ତନ ହୁଏ ଓ ଆୟତକାର କ୍ଷେତ୍ରଗୁଡ଼ିକର ଉଚ୍ଚତା ସମନ୍ବିତ ବାରମ୍ବାରତା ସହିତ ସମାନୁପାତୀ ହୋଇଥାଏ।
![]()
୨। ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ର କ’ଣ ?
Answer:
ହିଷ୍ଟୋଗ୍ରାମିଂରେ ଆୟତକ୍ଷେତ୍ରମାନଙ୍କର ଶୀର୍ଷ ଆନୁଭୂମିକ ରେଖାମାନଙ୍କର ମଧ୍ୟ ବିନ୍ଦୁ ଗୁଡ଼ିକୁ ସରଳ ରେଖାଖଣ୍ଡମାନଙ୍କ ଦ୍ଵାରା ସଂଯୋଗ କଲେ ଯେଉଁ ରେଖା ଅଙ୍କିତ ହୁଏ ତାହାକୁ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ର କୁହାଯାଏ। ହିଷ୍ଟୋଗ୍ରାମ୍ର ସାହାଯ୍ୟ ନ ନେଇ ମଧ୍ୟ ଏହା ସ୍ଵାଧୀନ ଭାବରେ ଅଙ୍କନ କରାଯାଇପାରେ ।
ଯଦି ଲଜ୍ଜାଙ୍କ ଓ ତାହାର ବାରମ୍ବାରତାର କ୍ରମିକ ଯୋଡ଼ିମାନଙ୍କୁ ନେଇ ଗ୍ରାଫ୍ କାଗଜରେ ବିନ୍ଦୁମାନ ସ୍ଥାପନ କରି ସେଗୁଡ଼ିକୁ ରେଖାଦ୍ଵାରା ସଂଯୋଗ କରାଯାଏ, ତାହାହେଲେ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ ଅଙ୍କିତ ହୋଇଥାଏ। ଭାଗବିଭକ୍ତ ବାରମ୍ବାରତା ବିତରଣ କ୍ଷେତ୍ରରେ ଲବ୍ଧଙ୍କ ସ୍ଥାନରେ ସଂଭାଗର ମଧ୍ୟବିନ୍ଦୁ ମାନଙ୍କୁ ନିଆଯାଇଥାଏ ।
୩। ବାରମ୍ବାରତା ବକ୍ର କାହାକୁ କୁହାଯାଏ ?
Answer:
ବାରମ୍ବାରତା ବକ୍ର ଏକ ସଦୃଶ ବକ୍ର (smooth caive) ବାରମ୍ବାରତା ବକ୍ର ଓ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ରର ଅଙ୍କନ ପ୍ରଣାଳୀ ଏକ ପ୍ରକାର । ଲବ୍ଧଙ୍କ (ବା ସଂଭାଗର ମଧ୍ୟବିନ୍ଦୁ) ଓ ତା’ର ବାରମ୍ବାରତାର କ୍ରମିକ ଯୋଡ଼ି ଗୁଡ଼ିକ ନେଇ ଗ୍ରାଫ୍ କାଗଜରେ ବିନ୍ଦୁମାନ ସ୍ଥାପନ କରାଯାଏ। କିନ୍ତୁ ବାରମ୍ବାରତା ବକ୍ରରେ ବିନ୍ଦୁମାନଙ୍କୁ ସ୍ଵଚ୍ଛନ୍ଦରେ ହସ୍ତୀଙ୍କିତ ରେଖାଦ୍ଵାରା ଯୋଗ କରାଯାଇ ଏକ ସଦୃଶ ବକ୍ର ଅଙ୍କନ କରାଯାଏ।
୪। ଓଜିଭ୍ କାହାକୁ କୁହାଯାଏ ?
Answer:
ଓଜିଭ୍ ବାରମ୍ବାରତା ବିତରଣ ଚିତ୍ରଲେଖର ଏକ ବହୁଳ ଭାବରେ ବ୍ୟବହୃତ ପ୍ରଣାଳୀ ଅଯେ । ଏଥିରେ ଲଜ୍ଜାଙ୍କମାନଙ୍କ ଓ ସେମାନଙ୍କର ରାଶିକୃତ ବାରମ୍ବାରତାର କ୍ରମିକ ଯୋଡ଼ିଦ୍ଵାରା ସ୍ଥାପିତ ବିନ୍ଦୁମାନଙ୍କ ରେଖାଦ୍ଵାରା ଯୋଗକଲେ ରାଶିକୃତ ବାରମ୍ବାରତା ରେଖାଚିତ୍ର ବା ଓଜିଭ୍ ଗଠନ ହୁଏ।
ଏହା ଦୁଇଟି ଉପାୟରେ ଗଠନ କରାଯାଏ, ଯଥା – (i) ଲଜ୍ଜାଙ୍କଠାରୁ ସାନ ପଦ୍ଧତି (less than method), (ii) ଲଜ୍ଜାଙ୍କଠାରୁ ବଡ଼ ପଦ୍ଧତି (more than method). ଲଜ୍ଜାଙ୍କଠାରୁ ସାନ ପଦ୍ଧତିରେ ସଂଭାଗର ଉର୍ଦ୍ଧ୍ୱସୀମାକୁ ଆଧାର କରାଗଲାବେଳେ, ବଡ଼ ପଦ୍ଧତିରେ ସଂଭାଗର ନିମ୍ନସୀମାକୁ ଆଧାର ଆକାରରେ ଗ୍ରହଣ କରାଯାଇଥାଏ। ଓଜିଭରୁ ମଧ୍ୟମା ଓ ଚତୁର୍ଥାଂଶକୁ ନିର୍ଣ୍ଣୟ କରାଯାଇପାରିବ ।
G. ପାଞ୍ଚଟି / ଛଅଟି ବାକ୍ୟରେ ସୀମିତ ରଖ୍ ପାର୍ଥକ୍ୟ ଦର୍ଶାଅ ।
୧। ପୂର୍ବାପେକ୍ଷା ସାନ ଓ ପୂର୍ବପେକ୍ଷା ବଡ଼ ଓଜିଭ୍
Answer:
ପୂର୍ବାପେକ୍ଷା ସାନ ପ୍ରଣାଳୀରେ ସଂଭାଗ ଗୁଡ଼ିକର ଉର୍ଦ୍ଧ୍ୱସୀମାରୁ ଆରମ୍ଭ କରାଯାଏ ଓ ବାରମ୍ବାରତା ଗୁଡ଼ିକୁ ଯୋଗ କରାଯାଏ। ଏହି କ୍ରମବର୍ଦ୍ଧିଷ୍ଣୁ ବାରମ୍ବାରତାକୁ ତତ୍ ସଂଲଗ୍ନ ସଂଭାଗ ଗୁଡ଼ିକ ସହିତ ଚିତ୍ରଲେଖରେ ଚିହ୍ନିତ କଲେ ଆମେ ଗୋଟିଏ ବକ୍ରରେଖା ପାଇବା ଯାହାକୁ ଓଜିଭ୍ କିମ୍ବା ରାଶିକୃତ ବାରମ୍ବାରତା କୁହାଯାଏ। ଏହି ବକ୍ରରେଖା ବାମ ପାର୍ଶ୍ଵରୁ ଦକ୍ଷିଣ ପାର୍ଶ୍ଵକୁ ଉର୍ଦ୍ଧ୍ବ ଆଡ଼କୁ ବୃଦ୍ଧି ହୁଏ ଓ S ଆକୃତିର ହୋଇଥାଏ।
ପୂର୍ବାପେକ୍ଷା ଅଧିକ ପ୍ରଣାଳୀରେ ଆମେ ସଂଭାଗଗୁଡ଼ିକର ନିମ୍ନସୀମାରୁ ଆରମ୍ଭ କରିଥାଉ ଓ ସମୁଦାୟ ବା ମୋଟ ବାରମ୍ବାରତାରୁ ପ୍ରତ୍ୟେକ ସଂଭାଗର ବାରମ୍ବାରତାକୁ ଅନ୍ତର କରିଥାଉ । ଯେତେବେଳେ ଏହି ବାରମ୍ବାରତାଗୁଡ଼ିକୁ ରେଖା ଚିତ୍ରରେ ଚିହ୍ନିତ କରାଯାଏ, ଆମେ ଏକ ବକ୍ରରେଖା ପାଇଥାଉ ଯାହା ବାମରୁ ଦକ୍ଷିଣକୁ ନିମ୍ନଗାମୀ ହୋଇଥାଏ। ଏହି ରେଖାକୁ ରାଶିକୃତ ବାରମ୍ବାରତା ବକ୍ରରେଖା କିମ୍ବା ଓଜିଭ୍ କୁହାଯାଏ। ଏହା ଓଲଟା ‘s’ ଆକୃତିର।
![]()
୨। ହିଷ୍ଟୋଗ୍ରାମ୍ ଓ ବାରମ୍ବାରତା ବକ୍ର
Answer:
ନିରବଚ୍ଛିନ୍ନ ମାଳାର ବାରମ୍ବାରତା ବିତରଣର ଚିତ୍ରଲେଖକ ଉପସ୍ଥାପନାକୁ ହିଷ୍ଟାଗ୍ରାମ୍ କୁହାଯାଏ। ହିଷ୍ଟୋଗ୍ରାମ୍ ହେଉଛି କେତେଗୁଡ଼ିଏ ଉଲ୍ଲମ୍ବ ସ୍ତମ୍ଭଚିତ୍ରର ସେଟ୍, ଯାହାର କ୍ଷେତ୍ରଫଳ ପ୍ରତିନିଧ୍ଵ କରୁଥିବା ବାରମ୍ବାରତା ସହିତ ସମାନୁପାତୀ। ହିଷ୍ଟୋଗ୍ରାମ୍ ଅଙ୍କନ କରିବାବେଳେ ଲଜ୍ଜାଙ୍କକୁ ସର୍ବଦା ଆନୁଭୂମିକ ଅକ୍ଷରେ ଓ ବାରମ୍ବାରତାକୁ ଉଲ୍ଲମ୍ବ ଅକ୍ଷରେ ନିଆଯାଏ। ହିଷ୍ଟୋଗ୍ରାମ୍ ଏକ ଦୁଇ ଆୟତନ ବିଶିଷ୍ଟ କ୍ଷେତ୍ର ଯାହାର ଲମ୍ବ ଓ ପ୍ରସ୍ଥ ଦ୍ଵୟର ପ୍ରାଧାନ୍ୟ ଥାଏ। ଏହା ବାରମ୍ବାରତା ବିତରଣର ପ୍ରକାଶ୍ୟ ଅନତ ସଂଭାଗ ପାଇଁ ଅନୁପଯୁକ୍ତ ।
ଗୋଟିଏ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ରର ବିଭିନ୍ନ ବିନ୍ଦୁଗୁଡ଼ିକୁ ସରଳରେଖା ଦ୍ଵାରା ସଂଯୋଗ ନ କରି ଯଦି ମୁକ୍ତ ହସ୍ତରେ ସଂଯୋଗ କରାଯାଏ, ତାହାକୁ ବାରମ୍ବାରତା ବକ୍ରରେଖା କୁହାଯାଏ। ଅର୍ଥାତ୍ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ରକୁ ମସୃଣ କରି ବାରମ୍ବାରତା ବକ୍ରରେଖା ଅଙ୍କନ କରାଯାଇଥାଏ। ବାରମ୍ବାରତା ବକ୍ରରେଖା ଏଭଳି ମୁକ୍ତ ହସ୍ତରେ ଅଙ୍କନ କରାଯାଏ ଯେ ବାରମ୍ବାରତା ବକ୍ରରେକାର କ୍ଷେତ୍ରଫଳ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ରର କ୍ଷେତ୍ରଫଳ ସହିତ ପ୍ରାୟ ସମାନ ହୋଇଥାଏ।
୩। ହିଷ୍ଟୋଗ୍ରାମ୍ ଓ ବାରମ୍ବାରତା ବହୁଭୂଜ
Answer:
ନିରବଚ୍ଛିନ୍ନ ମାଳାର ବାରମ୍ବାରତା ବିତରଣର ଚିତ୍ରଲେଖକ ଉପସ୍ଥାପନାକୁ ହିଷ୍ଟୋଗ୍ରାମ୍ କୁହାଯାଏ। ହିଷ୍ଟୋଗ୍ରାମ୍ ହେଉଛ କେତେଗୁଡ଼ିଏ ଉଲ୍ଲମ୍ବ ସ୍ତମ୍ଭଚିତ୍ରର ସେଟ୍, ଯାହାର କ୍ଷେତ୍ରଫଳ ପ୍ରତିନିଧ୍ଵ କରୁଥିବା ବାରମ୍ବାରତା ସହିତ ସମାନୁପାତୀ। ହିଷ୍ଟାଗ୍ରାମ୍ ଅଙ୍କନ କରିବାବେଳେ ଲବ୍ଧଙ୍କକୁ ସର୍ବଦା ଆନୁଭୂମିକ ଅକ୍ଷରେ ଓ ବାରମ୍ବାରତାକୁ ଉଲ୍ଲମ୍ବ ଅକ୍ଷରେ ନିଆଯାଏ । ହିଷ୍ଟୋଗ୍ରାମ୍ ଏକ ଦୁଇ-ଆୟତନ ବିଶିଷ୍ଟ କ୍ଷେତ୍ର ଯାହାର ଲମ୍ବ ଓ ପ୍ରସ୍ଥ ଦ୍ଵୟର ପ୍ରାଧାନ୍ୟ ଥାଏ। ଏହା ବାରମ୍ବାରତା ବିତରଣର ପ୍ରକାଶ୍ୟ ଅନ୍ତ ସଂଭାଗ ପାଇଁ ଅନୁପଯୁକ୍ତ ।
ବାରମ୍ବାରତା ବହୁଭୂଜ ହେଉଛି, ଅନ୍ୟ ଏକ ପ୍ରଣାଳୀ ଯହିଁରେ ଚିତ୍ରଲେଖ ମାଧ୍ଯମରେ ବାରମ୍ବାରତା ବିତରଣର ଉପସ୍ଥାପ କରାଯାଏ । ବିଭିନ୍ନ ପ୍ରକାରର ବାରମ୍ବାରତା ବିତରଣର ବାରମ୍ବାରତା ବହୁଭୂଜ ଗୋଟିଏ ଅକ୍ଷରେ ଦର୍ଶାଯାଇପାରିବ । ଯେତେବେଳେ ସଂଭାଗ ଗୁଡ଼ିକର ସଂଖ୍ୟା ଅନେକ ହୋଇଥାଏ, ବାରମ୍ବାରତା ବହୁଭୂଜ ପସନ୍ଦନୀୟ ହୋଇଥାଏ। କିନ୍ତୁ ବାରମ୍ବାରତା ବହୁଭୂଜ ପ୍ରକାଶ୍ୟ ଅନ୍ତ ସଂଭାଗ ଥବା ବାରମ୍ବାରତା ବିତରଣ କ୍ଷେତ୍ରରେ ବ୍ୟବହୃତ ହୋଇ ନଥାଏ।
ଦୀର୍ଘ ଉତ୍ତରମୂଳକ ପ୍ରଶ୍ନୋତ୍ତର
୧। ପରିସଂଖ୍ୟାନ ସାରଣୀ କ’ଣ ? ସାରଣୀ ବିନ୍ୟାସର ଗୁରୁତ୍ଵ ଆଲୋଚନା କର ।
Answer:
ତଥ୍ୟାବଳୀକୁ ସ୍ତମ୍ଭ ଓ ପକ୍ତି ମାଧ୍ୟମରେ ଯଥାଯଥ ବିନ୍ୟାସ କରିବାକୁ ପରିସଂଖ୍ୟାନ ସାରଣୀ କୁହାଯାଏ। ତେଣୁ ପରସ୍କର ସମ୍ପର୍କିତ ସାଂଖ୍ୟକ ଘଟଣାର ଉଲ୍ଲମ୍ବ ସ୍ତମ୍ଭ ଓ ଅନୁଲ୍ଲମ୍ବ ପକ୍ତିରେ ବିଭାଗିକରଣୁ ପରିସଂଖ୍ୟାନ ସାରଣୀ କୁହାଯାଏ । ଏଥୁରୁ ଜଣାଯାଏ ଯେ ସାରଣୀର ଉଲ୍ଲମ୍ବ ବ୍ୟବଚ୍ଛେଦକୁ ସ୍ତମ୍ଭ ଓ ଅନୁଲମ୍ବ ବ୍ୟବଚ୍ଛେଦକୁ ପକ୍ତି କୁହାଯାଏ। ସାରଣୀ ମାଧ୍ୟମରେ ତଥ୍ୟ ଉପସ୍ଥାପନା ପ୍ରକ୍ରିୟାକୁ ସାରଣୀ ବିନ୍ୟାସ କୁହାଯାଏ।
ସାରଣୀ ବିନ୍ୟାସର ଗୁରୁତ୍ଵ :
- ଅନୁସନ୍ଧାନର ଅଭିପ୍ରାୟକୁ ସ୍ପଷ୍ଟ କରିଥାଏ, ସାରଣୀ ମାଧ୍ୟମରେ ତଥ୍ୟ ଉପସ୍ଥାପନା ଅନୁସନ୍ଧାନରତ ସମସ୍ୟାକୁ ସରଳ ଓ ସ୍ପଷ୍ଟ କରିଥାଏ। ସାରଣୀରେ ପ୍ରଦତ୍ତ ଅନେକ ସମସ୍ୟାର ଉତ୍ତର ପ୍ରଦାନ କରିଥାଏ।
- ତଥ୍ୟର ବୈଶିଷ୍ଟ୍ୟକୁ ସ୍ପଷ୍ଟ ରୂପେ ପ୍ରକାଶ କରିଥାଏ – ଅନୁସନ୍ଧାନରତ ଘଟଣାବଳୀକୁ ସାରଣୀ ସରଳ, ସ୍ପଷ୍ଟ ଓ ଯଥାଯଥ ଭାବେ ଉପସ୍ଥାପନ କରିଥାଏ। ଏହା ତଥ୍ୟର ମୁଖ୍ୟ ବୈଶିଷ୍ଟ୍ୟଗୁଡ଼ିକୁ ଦର୍ଶାଇଥାଏ।
- ସର୍ବନିମ୍ନ ସ୍ଥାନରେ ଘଟଣାବଳୀକୁ ଉପସ୍ଥାପନ କରିଥାଏ – ସାରଣୀ ଘଟଣାବଳୀକୁ ସର୍ବନିମ୍ନ ସ୍ଥାନରେ ଉପସ୍ଥାପନ କରିବା ସହ ବୃତ୍ତାନ୍ତକୁ ମୂଳ ପାଠାନ୍ତର୍ଗତ ଉପକରଣ ଠାରୁ ଅଧିକ ଉନ୍ନତ ଢାଞ୍ଚାରେ ପ୍ରକାଶ କରିଥାଏ।
- ଏହା ପରିସଂଖ୍ୟାନ ପ୍ରକ୍ରିୟାକୁ ସୁଗମ କରେ – ଏହା ତଥ୍ୟକୁ ସରଳ କରେ, ତୁଳନାତ୍ମକ ବିଶ୍ଳେଷଣକୁ ତ୍ବରାନ୍ବିତ କରେ ଓ ଘଟଣାବଳୀକୁ ବ୍ୟାଖ୍ୟା କରିଥାଏ।
- ଏହା ତୁଳନାକୁ ସୁଗମ କରେ – ତଥ୍ୟର ବିଭିନ୍ନ ବିଭାଗିକରଣ କରି ଏହା ତାର ତୁଳନା କରିବା ସହାୟକ ହୋଇଥାଏ। ତେଣୁ ବିଭିନ୍ନ ଅଂଶର ସଂପର୍କକୁ ଏହାଦ୍ବାରା ସହଜରେ ଜାଣି ହୁଏ।
- ଅଶୁଦ୍ଧି ବାହାର କରେ – ସାରଣୀ ମାଧ୍ୟମରେ ଅଶୁଦ୍ଧି ଓ ଅବହେଳାକୁ ସହଜରେ ବାହାର କରାଯାଇପାରେ।
- ଏହା ଉତ୍ତମ ପ୍ରବଣତା ପ୍ରଦାନ କରେ – ସାରଣୀ ବିନ୍ୟାସ ଅଧ୍ୟୟନରତ ସମସ୍ୟାର ଉତ୍ତମ ପ୍ରବଣତା ଓ ପ୍ରବୃତ୍ତି ପ୍ରଦାନ କରିଥାଏ ।
- ଏହା ବ୍ୟୟ ସଂକୋଚ ଘଟାଇଥାଏ – ସାରଣୀ ବିନ୍ୟାସ ତଥ୍ୟ ଉପସ୍ଥାପନା ନିମିତ୍ତ ଏକ ସମୟ ଓ ସ୍ଥାନ ସଞ୍ଚୟ କରିଥାଏ। ସାରଣୀ ମଧ୍ଯରୁ ଗୁରୁତ୍ଵପୂର୍ଣ୍ଣ ସଂଖ୍ୟା ଗୁଡ଼ିକୁ ସହଜରେ ଚିହ୍ନଟ କରାଯାଇପାରେ ।
- ଏହା ସଂପର୍କ ସ୍ଥାପନରେ ସାହାଯ୍ୟ କରେ – ବୃହତ-ବିକ୍ଷିପ୍ତ ତଥ୍ୟ ଗୁନ୍ଥି ସଂକ୍ଷିପ୍ତ କରିବା ନିମିତ୍ତ ସାରଣୀ ବିନ୍ୟାସ ଏକ ଉତ୍ତମ ଅବଲମ୍ବନ ଅଟେ । ତେଣୁ ଏହାଦ୍ବାରା ସର୍ବାଧିକ ବୃତ୍ତାନ୍ତ ସଂଗ୍ରହ କରିବା ସହ ଏହି ସାରଣୀ ମାଧ୍ୟମରେ ଅଧୂକ ସଂପର୍କ ସ୍ଥାପନ କରାଯାଇପାରେ।
- ଏହା ପ୍ରତିପାଦନ କରିବାରେ ସାହାଯ୍ୟ କରେ – ଯେହେତୁ ତଥ୍ୟ ଗୁଡ଼ିକୁ ସାରଣୀରେ ସଂଜ୍ଞା ଓ ସଂଖ୍ୟାରେ ସଜାଇ ରଖାଯାଇ ଥାଏ, ସେଗୁଡ଼ିକୁ ସହଜରେ ପ୍ରତିପାଦନ କରିବା ସହ ଆବଶ୍ୟକୀୟ ଉଦ୍ଦେଶ୍ୟରେ ବ୍ୟବହାର କରାଯାଇଥାଏ।
![]()
୨। ତଥ୍ୟର ଉପସ୍ଥାପନା କ’ଣ ? ପରିସଂଖ୍ୟାନ ସାରଣୀର ଉପାଦାନଗୁଡ଼ିକ ଉଲ୍ଲେଖ କର ?
Answer:
ତଥ୍ୟକୁ ସ୍ପଷ୍ଟ ଓ ଆକର୍ଷଣୀୟ କରି ତାକୁ ସହଜ ବୋଧଗମ୍ୟ ତଥା ସାଂଖ୍ୟକ ବିଶ୍ଳେଷଣ ସୁବିଧା ପାଇଁ ପ୍ରଦର୍ଶିତ କରିବାକୁ ତଥ୍ୟର ଉପସ୍ଥାପନା କୁହାଯାଏ। ତଥ୍ୟ ସାରଣୀ ମାଧ୍ୟମରେ ଉପସ୍ଥାପନା କରାଯାଏ। ତଥ୍ୟାବଳୀକୁ ସ୍ତମ୍ଭ ଓ ପଡ୍କ୍ତି ମାଧ୍ୟମରେ ଯଥାଯଥ ବିନ୍ୟାସ କରିବାକୁ ପରିସଂଖ୍ୟାନ ସାରଣୀ କୁହାଯାଏ । ଏକ ଉତ୍ତମ ପରିସଂଖ୍ୟାନ ସାରଣୀ ଏକ କଳା। ତେଣୁ ଗୋଟିଏ ସାରଣୀ ଗଠନର ଅଧ୍ୟୟନ ଅତ୍ୟନ୍ତ ଜରୁରୀ। ଗୋଟିଏ ପରିସଂଖ୍ୟାନ ସାରଣୀର ଉପାଦାନ ଗୁଡ଼ିକ ହେଲା –
(i) ସାରଣୀ ସଂଖ୍ୟା – ସାରଣୀ ସଂଖ୍ୟାଦ୍ଵାରା ଚିହ୍ନିତ ହୋଇଥାଏ ଓ ଏହା ସାହାଯ୍ୟରେ ଜଣେ ସାରଣୀକୁ ଆବଶ୍ୟକ ସ୍ଥଳେ ଉଦ୍ଧାର କରିପାରନ୍ତି । ସୁବିଧା ଦୃଷ୍ଟିରୁ ସାରଣୀ ଗୁଡ଼ିକୁ ପାଠ୍ୟକ୍ରମର ବିଭିନ୍ନ ଅଧ୍ୟାୟରେ ସଂଖ୍ୟାକ୍ରମରେ ସଜ୍ଜିତ ହେବା ଆବଶ୍ୟକ। ଉଦାହରଣ ସ୍ୱରୂପ ସାରଣୀ ସଂଖ୍ୟା- ୭.୧, ସପ୍ତମ ଅଧ୍ୟାୟରେ ଥିବା ପ୍ରଥମ ସାରଣୀକୁ ସୂଚିତ କରିଥାଏ।
(ii) ଶୀର୍ଷକ – ସାରଣୀରେ ଥିବା ବିଷୟବସ୍ତୁକୁ ବର୍ଣ୍ଣନା କରିବା ନିମିତ୍ତ ଶୀର୍ଷକର ଆବଶ୍ୟକତା ଅନୁଭୂତ ହୁଏ। ଏହା ସାରଣୀ ସଂଖ୍ୟା ତଳକୁ ସ୍ଥାନିତ ହୋଇଥାଏ। ଶୀର୍ଷକର ନାମକରଣ ଏପରି କରାଯାଏ ଯେ ଏହା ସାରଣୀର ମୁଖପତ୍ର ରୂପେ କାର୍ଯ୍ୟ ରେ । ଶୀର୍ଷକର ନାମରୁ ସାରଣୀ ବିଷୟରେ ଧାରଣା ହୋଇଥାଏ। ଶୀର୍ଷକଟି ସଂକ୍ଷିପ୍ତ ପୂର୍ଣାଙ୍ଗ ଓ ସ୍ପଷ୍ଟ ହେବା ଆବଶ୍ୟକ।
(iii) ଶୀର୍ଷଟୀକା – ଶୀର୍ଷଟୀକା ଶୀର୍ଷକର ନିକଟରେ ଲେଖାଯାଇଥାଏ ଓ ଏହା ଶୀର୍ଷକ ସମ୍ବନ୍ଧରେ ଅତିରିକ୍ତ ତଥ୍ୟ ପ୍ରଦାନ କରିଥାଏ। ଏହା ସୂଚନାକୁ ଅଧିକ ରୁଦ୍ଧିମନ୍ତ କରିଥାଏ। ଏହା ସାଧାରଣତଃ ବନ୍ଧନୀ ମଧ୍ଯରେ ରଖାଯାଏ ଓ ଶୀର୍ଷକର ଠିକ୍ ତଳକୁ ଲେଖାଯାଏ ।
(iv) ପଙ୍କ୍ତିନାମା – ପକ୍ତିନାମା ଦୁଇ ଭାଗରେ ବିଭକ୍ତ ଯଥା – ପଂକ୍ତି ମସ୍ତକ ଓ ପଂକ୍ତି ଉଲ୍ଲେଖ । ପଂଡ୍ ମସ୍ତକ ସାରଣୀରେ ଅନ୍ତର୍ଭୁକ୍ତ ସ୍ତମ୍ଭରେ ଲିପିବଦ୍ଧ କରାଯାଇଥିବା ବିବରଣୀ ସମ୍ବନ୍ଧରେ ଧାରଣା ଦେଉଥିବାବେଳେ ପଙ୍କ୍ତି ଉଲ୍ଲେଖ ପଙ୍କ୍ତିରେ ଦିଆଯାଉଥବା ପ୍ରତ୍ୟେକ ତଥ୍ୟକୁ ବୁଝାଏ। ଉଦାହରଣ ସ୍ଵରୂପ ଗୋଟିଏ ସାରଣୀରେ ପମ୍ପୃକ୍ତ ମସ୍ତକରେ ବର୍ଷ ଲୋଯାଉଥିବା ବେଳେ ପଙ୍କ୍ତି ଉଲ୍ଲେଖରେ ନିର୍ଦ୍ଦିଷ୍ଟ ବର୍ଷମାନଙ୍କୁ ଉଲ୍ଲେଖ କରାଯାଏ। ପକ୍ତି ଉଲ୍ଲେଖ ପକ୍ତି ମସ୍ତକ ତଳେ ଲେଖାଯାଏ ।
(v) ଶିରୋନାମା – ସାରଣୀ ଅନ୍ତର୍ଗତ ସ୍ତମ୍ଭରେ ଲିପିବଦ୍ଧ କରାଯାଇଥିବା ବିବରଣୀ ସମ୍ବନ୍ଧରେ ଶିରୋନାମା ଧାରଣା ପ୍ରଦାନ କରେ। ଶିରୋନାମାରେ ଏକ ବା ତଦୁର୍ଣ ଉପଶିରୋନାମା ଥାଇପାରେ। ତଥ୍ୟାବଳୀର ବିଭିନ୍ନ ଉପବିଭାଗକୁ ଏଥରେ ଦରରେ ଜାତୀୟ ଆୟ ଉପଶିରୋନାମାର ଉଦାହରଣ। ବର୍ଣ୍ଣନା କରାଯାଇଥାଏ। କୌଣସି ସାରଣୀରେ ଥିବା ଜାତୀୟ ଆୟ ଶିରୋନାମା ହୋଇଥିବାବେଳେ ବର୍ତ୍ତମାନ ଓ ନିର୍ଦ୍ଦିଷ୍ଟ ଦରରେ ଜାତୀୟ ଆୟ ଉପଶିରୋନାମାର ଉଦାହରଣ।
(vi) କ୍ଷେତ୍ର – କ୍ଷେତ୍ରରେ ତଥ୍ୟାବଳୀର ନିର୍ଦ୍ଦିଷ୍ଟ ଲବ୍ଧଙ୍କ ଗୁଡ଼ିକ ଲିପିବଦ୍ଧ କରାଯାଏ, ପ୍ରତ୍ୟେକ ଲବ୍ଧାଙ୍କ ଗୋଟିଏ ଗୋଟିଏ କୋଷରେ ଲେଖାଯାଏ। ତେଣୁ ପ୍ରତ୍ୟେକ ଲବ୍ଧାଙ୍କ ପଡ୍କ୍ତି ଓ ସ୍ତମ୍ଭ ସହିତ ସମ୍ପର୍କିତ ।
(vii) ପାଦଟୀକା – ପାଦଟୀକାର ବ୍ୟବହାର ନିର୍ଦ୍ଦିଷ୍ଟ କ୍ଷେତ୍ରରେ କରାଯାଇଥାଏ । ଯଦି ସାରଣୀରେ ଉଲ୍ଲେଖୁତ ହୋଇଥିବା ତଥ୍ୟ ବିଷୟରେ ବିଶେଷ ଟୀକା ବା ସ୍ପଷ୍ଟୀକରଣ ଦେବା ଆବଶ୍ୟକ ଦେଖାଦିଏ ତେବେ ପାଦଟୀକାର ବ୍ୟବହାର କରାଯାଏ।
(viii) ଉତ୍ସଟୀକା – ସାରଣୀର ସର୍ବନିମ୍ନରେ ଉତ୍ସଟୀକା ଦିଆଯାଏ। ତଥ୍ୟ କେଉଁ ଉତ୍ସରୁ ଉଦ୍ଧୃତ ହୋଇଅଛି, କେବେ ସଂଗୃହୀତ ହୋଇଅଛି ଇତ୍ୟାଦି ବିଷୟବସ୍ତୁ ଉତ୍ସଟୀକାରେ ଉଲ୍ଲେଖ କରାଯାଏ।
୩। ସାରଣୀ କ’ଣ ? ସାରଣୀର ପ୍ରକାରଭେଦ ଆଲୋଚନା କର ?
Answer:
ତଥ୍ୟାବଳୀକୁ ସୁବ୍ୟବସ୍ଥିତ ପଂକ୍ତି ଓ ସ୍ତମ୍ଭ ଆକାରରେ ଉପସ୍ଥାପନା କରିବା ପରିସଂଖ୍ୟାନର ଏକ ଗୁରୁ ଦାୟିତ୍ଵ। ପରିସଂଖ୍ୟାନରେ ଏହି କାର୍ଯ୍ୟକୁ ବିଶେଷ ଭାବେ ସାରଣୀ ମାଧ୍ୟମରେ କରାଯାଇଥାଏ । ତେଣୁ ପରସ୍ପର ସମ୍ପର୍କିତ ସାଂଖ୍ୟକ ଘଟଣାର ଉଲମ୍ବ ସ୍ତମ୍ଭ ଓ ଅନୁଲ୍ଲମ୍ବ ପଙକ୍ତିରେ ବିଭାଗିକରଣକୁ ପରିସଂଖ୍ୟାନ ସାରଣୀ କୁହାଯାଏ।
ପରିସଂଖ୍ୟାନ ସାରଣୀକୁ ବିଭିନ୍ନ ବିଭାଗିକରଣ କରାଯାଇପାରେ । ସାରଣୀକୁ ତିନି ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି । ସେଗୁଡ଼ିକ ହେଲା – (କ) ଉଦ୍ଦେଶ୍ୟ ଭିଭିରେ, (ଖ) ମୌଳିକତା ଭିତ୍ତିରେ ଓ (ଗ) ଗଠନ ଭିଭିରେ।
![]()
(କ) ଉଦ୍ଦେଶ୍ୟ ଭିଭିରେ :
ଉଦ୍ଧେଶ୍ୟ ଭିତ୍ତିରେ ପରିସଂଖ୍ୟାନ ସାରଣୀକୁ ପୁନଶ୍ଚ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଅଛି । ସେଗୁଡ଼ିକ ହେଉଛି –
(i) ସାଧାରଣ ଉଦ୍ଦେଶ୍ୟ ସାରଣୀ ଓ
(ii) ସ୍ଵତନ୍ତ୍ର ଉଦ୍ଦେଶ୍ୟ ସାରଣୀ।
(i) ସାଧାରଣ ଉଦ୍ଦେଶ୍ୟ ସାରଣୀ – ଯେଉଁ ସାରଣୀ ସାଧାରଣ ବ୍ୟବହାର ପାଇଁ ଉଦ୍ଦିଷ୍ଟ, ତାହାକୁ ସାଧାରଣ ଉଦ୍ଦେଶ୍ୟ ସାରଣୀ ବୋଲି କୁହାଯାଏ। ଏହି ସାରଣୀରେ ସେପରି କିଛି ସ୍ଵତନ୍ତ୍ର ଆଭିମୁଖ୍ୟ ନଥାଏ। ଏହି ସାରଣୀ ସଂଗୃହୀତ ତଥ୍ୟ ପାଇଁ ଅନେକ ସୁବିଧା ଯୋଗାଇ ଥାଏ।
ସେଥିପାଇଁ ଏହି ସାରଣୀକୁ ସଂପର୍କିତ ସାରଣୀ ବା ବୃତ୍ତାନ୍ତ ସାରଣୀ ବୋଲି ମଧ୍ୟ କୁହାଯାଏ। ସାଧାରଣତଃ ଏହା କାଳାନୁକ୍ରମିକ କ୍ରମରେ ରହିଥାଏ। ସରକାରୀ ପ୍ରତିନିଧୂମାନେ ଏହି ପ୍ରକାର ସାରଣୀ ପ୍ରସ୍ତୁତ କରନ୍ତି । ଉଦାହରଣ ସ୍ଵରୂପ, ବୟସ ଓ ଲିଙ୍ଗାନୁଭିଭିରେ ଜନସଂଖ୍ୟା ବଣ୍ଟନ, ବ୍ୟବସାୟ ପ୍ରତିଷ୍ଠାନର ଦରମା ତାଲିକା, ବିଭିନ୍ନ ଉତ୍ପାଦର ବିକ୍ରୟ, ବୟସ ଓ ଲିଙ୍ଗାନୁପାତରେ ମହାବିଦ୍ୟାଳୟ ଛାତ୍ର ବିଭାଜନ ଇତ୍ୟାଦି।
(ii) ସ୍ଵତନ୍ତ୍ର ଉଦ୍ଦେଶ୍ୟ ସାରଣୀ – ଯେଉଁ ସାରଣୀ କୌଣସି ସ୍ଵତନ୍ତ୍ର ଉଦ୍ଦେଶ୍ୟ ନେଇ ପ୍ରସ୍ତୁତ କରାଯାଇଥାଏ, ତାହାକୁ ସ୍ଵତନ୍ତ୍ର ଉଦ୍ଦେଶ୍ୟ ସାରଣୀ ବୋଲି କୁହାଯାଏ। ଏହି ସାରଣୀକୁ ସାରଂଶ ସାରଣୀ, ବିଶ୍ଳେଷଣ ସାରଣୀ, ବ୍ୟୁପରି ସାରଣୀ, ମୂଳ ଗ୍ରନ୍ଥିଶ ସାରଣୀ ବୋଲି ମଧ୍ୟ କୁହାଯାଏ। ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ଘଟଣାବଳୀକୁ ଅଧିକ ଗୁରୁତ୍ଵ ସହ ସରଳ ରୂପରେ ପ୍ରକା କରିବା ପାଇଁ ଉଦ୍ଦିଷ୍ଟ । ଅନୁପାତ ଓ ଶତକଡ଼ଶ ଦ୍ଵାରା ତୁଳନା କରିବା କ୍ଷେତ୍ରରେ ଏହା ବିଶେଷ ଉପଯୋଗୀ।
(ଖ) ମୌଳିକ ଭିତ୍ତିରେ ସାରଣୀ :
ମୌଳିକତା ଭିତ୍ତିରେ ପରିସଂଖ୍ୟାନ ସାରଣୀ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି।
(i) ପ୍ରାଥମିକ ସାରଣୀ ଓ
(ii) ବ୍ୟୁତ୍ପରି ସାରଣୀ।
(i) ପ୍ରାଥମିକ ସାରଣୀ – ପ୍ରାଥମିକ ସାରଣୀ ହେଉଛି, ସେହି ସାରଣୀ ଯେଉଁ ସାରଣୀରେ ତଥ୍ୟକୁ ଅବିକଳ ସଂଗୃହୀତ ଆକାର ଓ ଢଙ୍ଗ ଦ୍ବାରା ଉପସ୍ଥାପନା କରାଯାଇଥାଏ। ଅର୍ଥାତ୍ ପରିସଂଖ୍ୟାନ ଆକାରକୁ ମୌଳିକ ଅବସ୍ଥାରେ ପ୍ରକାଶ କରାଯାଇଥାଏ। ଏହା ବାସ୍ତବ ଓ ନିର୍ବିକଳ୍ପ ସଂଖ୍ୟାରେ ରହିଯାଇଥାଏ ।
(ii) ବ୍ୟୁତ୍ପରି ସାରଣୀ – ବ୍ୟୁତ୍ପତ୍ତି ସାରଣୀ ହେଉଛି ସେହି ସାରଣୀ ଯହିଁରେ ସଂଗୃହୀତ ତାକୁ ଅବିକଳ ଆକାର ଓ ଢଙ୍ଗରେ ଉପସ୍ଥାପନା କରାଯାଇ ନ ଥଶଏ। ଅର୍ଥାତ୍ ସଂଗୃହୀତ ତଥ୍ୟକୁ ମୌଳିକ ଆକାରରେ ପ୍ରକାଶ କରାଯାଇ ନ ଥାଏ। ଏହି ସାରଣୀ ପ୍ରାଥମିକ ବା ମୌଳିକ ତଥ୍ୟରୁ ସଂଗୃହୀତ ମୋଟ, ଶତକଡ଼ା, ଅନୁପାତ, ହାରାହାରି, ବିଚ୍ଛୁରଣ ବିଚ୍ଛୁରଣ ଗୁଣାଙ୍କ ଇତ୍ୟାଦି ଆକାରରେ ଉପସ୍ଥାପନା କରିଥାଏ। ସେଥିପାଇଁ ଏହାକୁ ବ୍ୟୁତ୍ପତ୍ତି ସାରଣୀ ବୋଲି କୁହାଯାଏ।
(ଗ) ଗଠନ ଭିଭିରେ ସାରଣୀ :
ଗଠନ ଭିତ୍ତିରେ ପରିସଂଖ୍ୟାନ ସାରଣୀକୁ ଦୁଇ ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଅଛି। ସେଗୁଡ଼ିକ ହେଲା –
(i) ସରଳ ସାରଣୀ ଓ
(ii) ଜଟିଳ ସାରଣୀ।
![]()
(i) ସରଳ ସାରଣୀ – ଯେଉଁ ସାରଣୀରେ ତଥ୍ୟର କେବଳ ମାତ୍ର ଗୋଟିଏ ବୈଶିଷ୍ଟ୍ୟ ଦେଖା ଯାଇଥାଏ ତାହାକୁ ସରଳ ସାରଣୀ କୁହାଯାଏ । ଏହାକୁ ମଧ୍ୟ “ ପ୍ରଥମ କ୍ରମର ସାରଣୀ” ବୋଲି କୁହାଯାଏ। ଏହି ପ୍ରକାର ସାରଣୀକୁ ବୁଝିବା ଓ ଗଢ଼ିବା ସହଜ ଅଟେ । ଉଦାହରଣ ସ୍ଵରୂପ, ବିଭିନ୍ନ ବର୍ଷର ଭାରତର ଜନସଂଖ୍ୟା, ବିଭିନ୍ନ ରାଜ୍ୟର କୃଷି ଉତ୍ପାଦ, ଭାରତର ବିଭିନ୍ନ ରାଜ୍ୟର ଜନସଂଖ୍ୟାର ଘନତ୍ଵ ଇତ୍ୟାଦି।
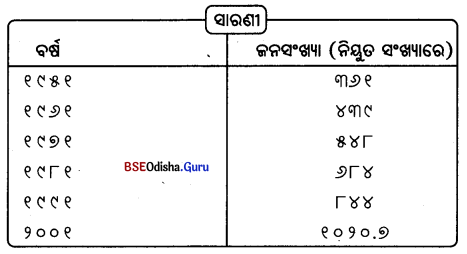
(ii) ଜଟିଳ ସାରଣୀ – ଯେଉଁ ସାରଣୀରେ ଏକ ସମୟ ତଥ୍ୟର ଏକାଧିକ ବୈଶିଷ୍ଟ୍ୟ ଦେଖାଯାଇଥାଏ, ତାହାକୁ ‘ଜଟିଳ ସାରଣୀ’ କୁହାଯାଏ। ଏହାକୁ ମଧ୍ୟ “ ବହୁବିଧ ସାରଣୀ” ବୋଲି କୁହାଯାଏ । ଏହି ସାରଣୀ ଅଧିକ ଜନପ୍ରିୟ ଅଟେ । କାରଣ ଏହା ସମସ୍ତ ସଂପୃକ୍ତ ଘଟଣାକୁ ବିଚାରକୁ ନେଇଥାଏ। ପରିସଂଖ୍ୟାନ ଘଟଣାବଳୀ ଏକାଧିକ ଶ୍ରେଣୀରେ ବିଭକ୍ତ ହୋଇଥାଏ। ଏହା ଦୁଇ-ପଥ ସାରଣୀ, ତିନି-ପଥ ସାରଣୀ ବା ବହୁବିଧ ସାରଣୀ ହୋଇପାରେ।
ଦୁଇ-ପଥ ସାରଣୀ – ଯେଉଁ ସାରଣୀରେ ତଥ୍ୟର ଦୁଇଟି ବୈଶିଷ୍ଟ୍ୟ ଦେଖାଯାଏ, ତାହାକୁ ଦୁଇ-ପଥ ସାରଣୀ କୁହାଯାଏ। ଅର୍ଥାତ୍ ଦୁଇ-ପଥ ସାରଣୀରେ ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ବ୍ୟାପାରର ପରସ୍ପର ସଂପୃକ୍ତ ଦୁଇ ବୈଶିଷ୍ଟ୍ୟ ବିଶିଷ୍ଟ ବୃତ୍ତାନ୍ତ ପ୍ରଦାନ କରାଯାଇଥାଏ। ଉଦାହରଣ ସ୍ଵରୂପ ଶ୍ରେଣୀ (ପ୍ରଥମ ବୈଶିଷ୍ଟ୍ୟ ଓ ଲିଙ୍ଗ (ଦ୍ଵିତୀୟ ବୈଶିଷ୍ଟ୍ୟ) ଭିଭିରେ ଏକ ମହାବିଦ୍ୟାଳୟର ଛାତ୍ରସଂଖ୍ୟାକୁ ବିଭାଜନ କରାଯାଇପାରେ ଯାହା ଦୁଇ-ପଥ ସାରଣୀ ସୂଚାଏ।
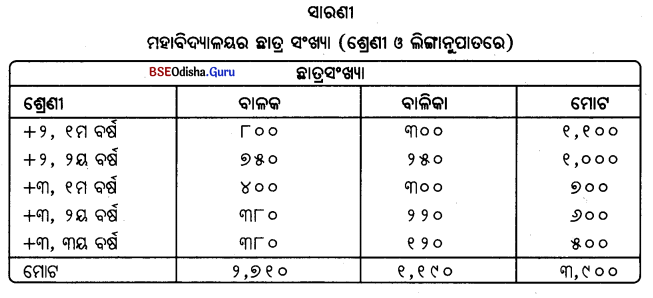
ତିନି-ପଥ ସାରଣୀ – ଯେଉଁ ସାରଣୀରେ ତଥ୍ୟର ତିନୋଟି ବୈଶିଷ୍ଟ୍ୟ ଦେଖାଯାଏ, ତାହାକୁ ତିନି-ପଥ ସାରଣୀ କୁହାଯାଏ। ଏହା ନିର୍ଦ୍ଦିଷ୍ଟ ବ୍ୟାପାରର ପରସ୍ପର ସଂପୃକ୍ତ ତିନୋଟି ବୈଶିଷ୍ଟ୍ୟ ବିଶିଷ୍ଟ ବୃତ୍ତାନ୍ତ ପ୍ରଦାନ କରିଥାଏ। ତେଣୁ ଏହାକୁ ତ୍ରିଗୁଣିତ ସାରଣୀ ବୋଲି ମଧ୍ୟ କୁହାଯାଏ। ଉଦାହାରଣ ସ୍ଵରୂପ, କୌଣସି ଏକ ଜନସଂଖ୍ୟାର ଶ୍ରେଣୀ, ଲିଙ୍ଗ ଓ ବସତିକୁ ନେଇ ବିଭାଗିକରଣ କରାଯାଇପାରେ।
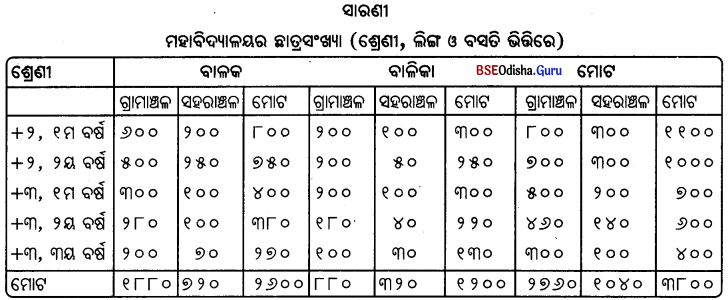
ବହୁବିଧ ସାରଣୀ – ଯେଉଁ ସାରଣୀରେ ତଥ୍ୟର ତିନିରୁ ଅଧିକ ବୈଶିଷ୍ଟ୍ୟ ଦେଖାଯାଏ, ତାହାକୁ ବହୁବିଧ ସାରଣୀ କୁହାଯାଏ। ଅର୍ଥାତ୍ ଗୋଟିଏ ସାରଣୀରେ ପରସ୍ପର ସଂପର୍କିତ ଅସଂଖ୍ୟ ବୈଶିଷ୍ଟ୍ୟ ବିଶିଷ୍ଟ ତଥ୍ୟାବଳୀ ଉପସୁନା କରାଯାଇ ଥାଏ। ଏହାକୁ ଉଚ୍ଚତର କ୍ରମ ସାରଣୀ ବୋଲି ମଧ୍ୟ କୁହାଯାଏ । ଉଦାହରଣ ସ୍ଵରୂପ କୌଣସି ଏକ ମହାବିଦ୍ୟାଳୟର ଛାତ୍ରମାନଙ୍କୁ ସେମାନଙ୍କର ଶ୍ରେଣୀ, ଲିଙ୍ଗ, ବସତି ଓ ବୈବାହିକ ସ୍ଥିତି ଭିତ୍ତିରେ ବହୁବିଧ ସାରଣୀ ମାଧ୍ୟମରେ ଉପସ୍ଥାପନା କରାଯାଇପାରେ।
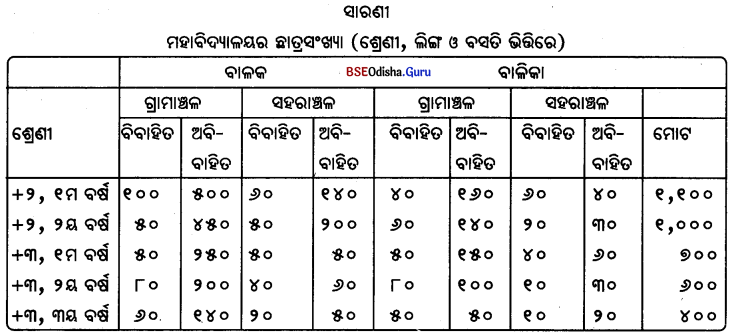
୪। ସମ୍ଭଚିତ୍ରର ଗଠନ ପ୍ରଣାଳୀ ସମ୍ବନ୍ଧରେ ଆଲୋକପାତ କର ।
Answer:
ସମ୍ଭଚିତ୍ର ଏକ ସହଜ ଓ ବହୁଆଦୃତ ତଥ୍ୟ ପ୍ରକାର ମାଧ୍ୟମ । ସମ୍ଭଚିତ୍ର ସାଧାରଣତଃ ଆନୁଭୂମିକ ବା ଉଲୁମ୍ବ ଆୟତକ୍ଷେତ୍ର ରୂପେ ପ୍ରଦର୍ଶିତ ହୋଇଥାଏ। ଏମାନଙ୍କ ସଂଖ୍ୟା ଏକାଧିକ ଓ ଏହା ଗାଢ଼ ରଙ୍ଗର ଲେଖାଦ୍ଵାରା ପ୍ରଦର୍ଶିତ ହୋଇଥାଏ। ସ୍ତମ୍ଭଚିତକୁ ଏକ ଆୟତନ ବିଶିଷ୍ଟ ରେଖାଚିତ୍ର ରୂପେ ଗ୍ରହଣ କରାଯାଏ କାରଣ ଏହାର ଦୈର୍ଘ୍ୟ ଲଜ୍ଜାଙ୍କମାନଙ୍କ ସହିତ ସମାନୁପାତ ଭାବରେ ପ୍ରଦର୍ଶିତ ହୋଇଥା’ନ୍ତି।
ଏହି ପ୍ରକାର ରେଖାଚିତ୍ରର ପ୍ରଭୁ ସମାନ ରେଖାଯାଇ ସମାନ ଦୂରତାରେ ସ୍ଥାପିତ କରାଯାଏ। ଫଳରେ ଦୁଇଟି ସନ୍ନିକଟ ସ୍ତମ୍ଭଚିତ୍ର ମଧ୍ୟରେ ତୁଳନା ସହଜ ହୋଇଥାଏ । ଏକ ସ୍ତମ୍ଭଚିତ୍ରକୁ ମଧ୍ୟ ବିଭିନ୍ନ ଭାଗରେ ବିଭକ୍ତ କରାଯାଇ ଏଥରେ ପ୍ରକାଶିତ ସମ୍ପୂର୍ଣ୍ଣ ତଥ୍ୟକୁ ବିଭିନ୍ନ ଉପବିଭାଗରେ ପ୍ରଦର୍ଶିତ କରାଯାଇଥାଏ।
ସମ୍ଭଚିତ୍ରକୁ ସାଧାରଣତଃ ୫ ଭାଗରେ ବିଭକ୍ତ କରାଯାଇ ଅଛି; ଯଥା –
(କ) ସରଳ ସ୍ତମ୍ଭଚିତ୍ର
(ଖ) ଯୌଗିକ ବା ଗଠନକାରୀ ସ୍ତମ୍ଭଚିତ୍ର
(ଗ) ଶତାଂଶ ସ୍ତମ୍ଭଚିତ୍ର
(ଘ) ବହୁବିଧ ସ୍ତମ୍ଭଚିତ୍ର
(ଙ) ବିଚଳନ ବା ପଥଚ୍ୟୁତ ସ୍ତମ୍ଭଚିତ୍ର
![]()
(କ) ସରଳ ସ୍ତମ୍ଭଚିତ୍ର :
ଏହା ବାସ୍ତବ କ୍ଷେତ୍ରରେ ବହୁ ଆଦୃତ । ଏଥିରେ କେବଳ ଗୋଟିଏ ମାତ୍ର ପରିବର୍ତ୍ତନଶୀଳ ଉପାଦାନକୁ ପ୍ରଦର୍ଶିତ କରାଯାଏ। ଯଥା – ବିଭିନ୍ନ ବର୍ଷମାନଙ୍କର ଲୋକସଂଖ୍ୟା, ବିକ୍ରୟ ବା ଉତ୍ପାଦନ ପରିମାଣ ଇତ୍ୟାଦି । ଉଦାହରଣ ସ୍ୱରୂପ – ବିଭିନ୍ନ ଜନଗଣନାରେ ଓଡ଼ିଶାର ଲୋକସଂଖ୍ୟା ପ୍ରଦତ୍ତ ଅଛି ଓ ଏହା ଏକ ସରଳ ସ୍ତମ୍ଭଚିତ୍ର ମାଧ୍ୟମରେ ପ୍ରଦର୍ଶିତ ହୋଇପାରେ।
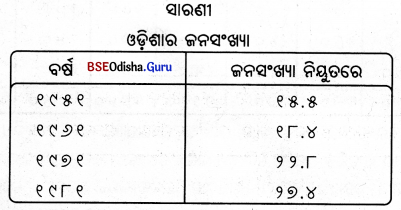
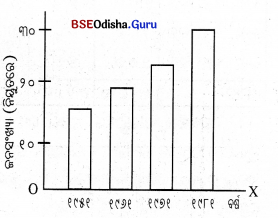
(ଖ) ଯୌଗିକ ସ୍ତମ୍ଭଚିତ୍ର :
ଯୌଗିକ ସ୍ତମ୍ଭଚିତ୍ର ମାଧ୍ୟମରେ କୌଣସି ଉପାଦାନର ଆୟତନ ପ୍ରଦର୍ଶିତ ହୋଇଥାଏ। ଏହା ମଧ୍ୟ ବିଭିନ୍ନ ଗଠନକାରୀ ଅଂଶ ଅନୁସାରେ ବିଭକ୍ତ ହୋଇଥାଏ। ଏହାର ପ୍ରତ୍ୟେକ ଅଂଶ ପୁରା ସ୍ତମ୍ଭର ଏକ ସମାନୁପାତିକ ଅଂଶ। ଯୌଗିକ ସ୍ତମ୍ଭଚିତ୍ର କୌଣସି ବିଷୟରେ ସାଂଖ୍ୟକ ସୂଚନାକୁ ସମାନୁପାତିକ ଭିଭିରେ ଚିତ୍ର ମାଧ୍ୟମରେ ପ୍ରଦର୍ଶିତ କରିବାର ଏକ ଉତ୍ତମ ମାଧ୍ୟମ।
ଉଦାହରଣ – ସାରଣୀରେ କଟକରେ ଥିବା ୩ ଗୋଟି ମହାବିଦ୍ୟାଳୟରେ ଅଧ୍ୟୟନ କରୁଥିବା ଛାତ୍ରଛାତ୍ରୀଙ୍କ ସଂଖ୍ୟା ଦିଆଯାଇଅଛି। ତାହାକୁ ଏକ ଯୌଗିକ ସ୍ତମ୍ଭଚିତ୍ର ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଯାଇଛି। କଟକରେ ଥିବା ବିଭିନ୍ନ ମହାବିଦ୍ୟାଳୟରେ ଥିବା ଛାତ୍ରଛାତ୍ରୀଙ୍କ ସଂଖ୍ୟା –
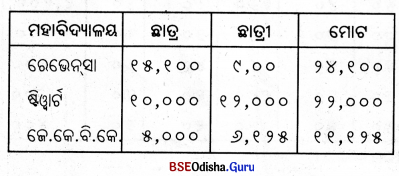
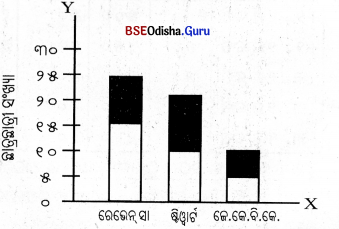
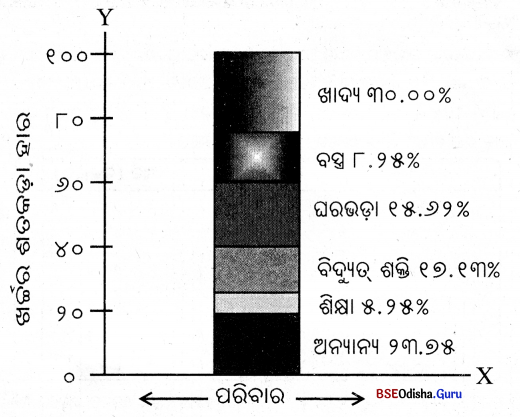
(ଗ) ଶତାଂଶ ସମ୍ଭଚିତ୍ର
ପରିସଂଖ୍ୟାନ ସମ୍ବନ୍ଧୀୟ କାର୍ଯ୍ୟରେ ତଥ୍ୟର ଆପେକ୍ଷିକ ପରିବର୍ତ୍ତନର ପ୍ରଦର୍ଶନ ନିମିତ୍ତ ଶତାଂଶ ସ୍ତମ୍ଭଚିତ୍ର ଅତି ଉପଯୋଗୀ। ଏଥୁଷର ପ୍ରତ୍ୟେକ ଗଠନକାରୀ ଅଂଶକୁ ସମ୍ପୂର୍ଣ୍ଣ ସ୍ତମ୍ଭଚିତ୍ରର ଶତକଡ଼ା ହାରରେ ପ୍ରକାଶ କରାଯାଇଥାଏ।
ଉଦାହରଣ – କୌଣସି ଏକ ପରିବାରର ବିଭିନ୍ନ ଆବଶ୍ୟକୀୟ ଦ୍ରବ୍ୟ ଉପରେ ମାସିକ ଖର୍ଚ୍ଚର ବିବରଣୀ ପ୍ରଦାନ କରାଯାଇଛି । ଏହାକୁ ଶତାଂଶ ସ୍ତମ୍ଭଚିତ୍ର ମାଧ୍ୟମରେ ପ୍ରକାଶ କରାଯାଇପାରେ।
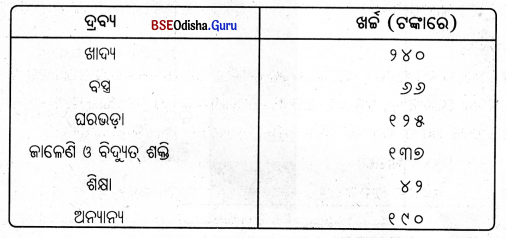
ସମାଧାନ – ପ୍ରଥମେ ଆମକୁ ପ୍ରତ୍ୟେକ ବସ୍ତୁ ଉପରେ ହେଉଥିବା ଖର୍ଚ୍ଚକୁ ମୋଟ ଖର୍ଚ୍ଚର ଶତକଡ଼ା ହାରରେ ପ୍ରକାଶିତ କରିବାକୁ ହେବ।
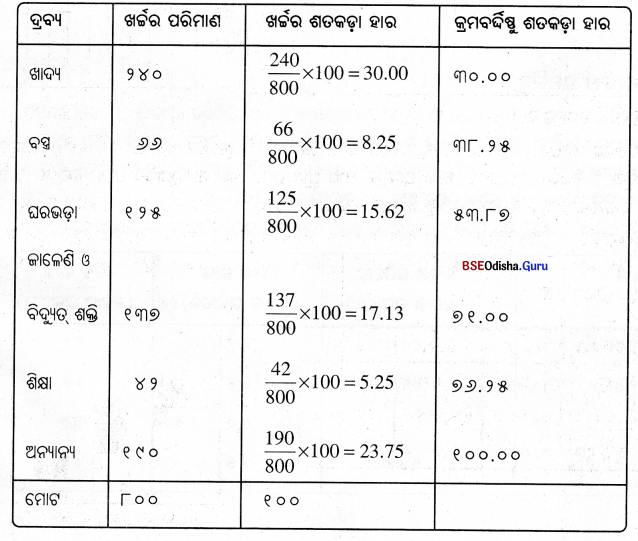
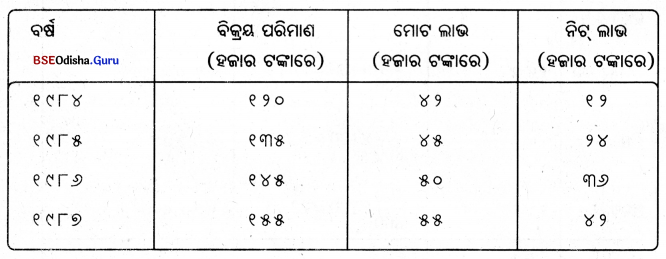
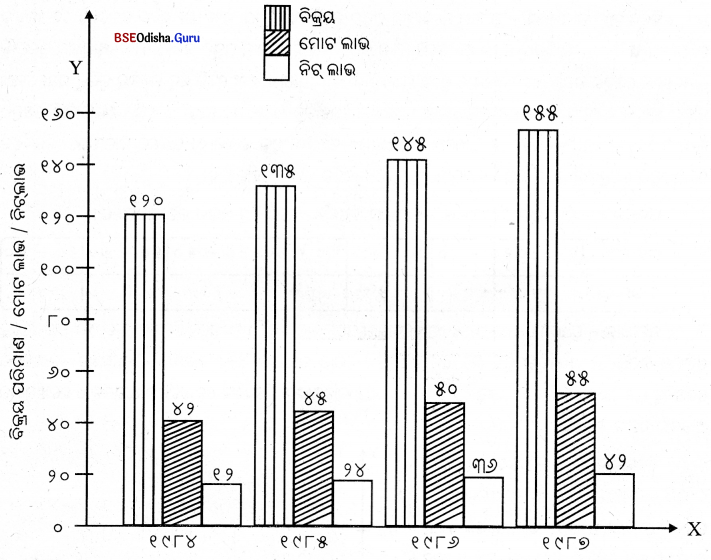
(ଘ) ବହୁବିଧ ସ୍ତମ୍ଭଚିତ୍ର
ବହୁବିଧ ସ୍ତମ୍ଭଚିତ୍ର ମାଧ୍ୟମରେ ଦୁଇ ବା ତଦୁର୍ଘ ପରସ୍ପର ସମ୍ପର୍କ ତ ତଥ୍ୟ ପ୍ରଦର୍ଶିତ ହୋଇଥାଏ। ସରଳ ସ୍ତମ୍ଭଚିତ୍ର ଗଠନ ପାଇଁ ଉପଯୋଗ ହେଉଥିବା ପ୍ରୟୋଗ କୌଶଳ ବ୍ୟବହାର କରି ବହୁବିଧ ସ୍ତମ୍ଭଚିତ୍ର ଗଠନ କରାଯାଏ। କିନ୍ତୁ ଏଥରେ ଗୋଟିଏ ପାର୍ଥକ୍ୟ ଦୃଷ୍ଟିଗୋଚର ହୁଏ, ଏହା ମାଧ୍ୟମରେ ଅନେକ ଗୁଡ଼ିଏ ସୂଚନା ସନ୍ନିବେଶିତ ହୋଇ ପ୍ରଦର୍ଶିତ ହେଉଥିବାରୁ ପ୍ରତ୍ୟେକ ତଥ୍ୟ ପାଇଁ ପୃଥକ୍ ରଙ୍ଗ, ରେଖା ଏବଂ ରେଖା ରହିତ ଅଂଶ ବ୍ୟବହାର କରାଯାଇଥାଏ।
![]()
ଉଦାହରଣ – ସାରଣୀରେ ପ୍ରଦତ୍ତ ତଥ୍ୟାନୁସାରେ ଗୋଟିଏ ବହୁବିଧ ସ୍ତମ୍ଭଚିତ୍ର ଅଙ୍କନ କରାଯାଇପାରେ।
(ଙ) ବିଚଳନ ବା ପଥଚ୍ୟୁତ ସ୍ତମ୍ଭଚିତ୍ର
ନିଟ୍ ପରିମାଣ ଯଥା – ନିଟ୍ ଲାଭ, ନିଟ୍ କ୍ଷତି, ନିଟ୍ ରପ୍ତାନି ଇତ୍ୟାଦି ପ୍ରଦର୍ଶନ ନିମିତ୍ତ ବିଚଳନ ସ୍ତମ୍ଭଚିତ୍ର ସାଧାରଣତଃ ବ୍ୟବହୃତ ହୋଇଥାଏ। ଏହି ସ୍ତମ୍ଭରେ ଯୁକ୍ତାତ୍ମକ ବା ଧନାତ୍ମକ ପରିମାଣ ସୂଚୀତ କରାଯାଇପାରେ। ଧନାତ୍ମକ ପରିମାଣ ଭୂମିରୁ ଉର୍ଦ୍ଧ୍ବରେ ରହିବାବେଳେ ଋଣାତ୍ମକ ଭୂମିରୁ ନିମ୍ନକୁ ପ୍ରଦର୍ଶିତ ହୋଇଥାଏ।
୫। ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ରର ଗଠନ ପ୍ରଣାଳୀ ଆଲୋଚନା କର ।
Answer:
ହିଷ୍ଟାଗ୍ରାମରେ ଥିବା ସମସ୍ତ ଆୟତକ୍ଷେତ୍ରର ଉପରିସ୍ଥିତ ମଧ୍ୟ ବିନ୍ଦୁଗୁଡ଼ିକୁ ଯୋଗ କରି ଯେଉଁ ରେଖା ଅଙ୍କନ କରାଯାଏ, ତାହାକୁ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ର ବୋଲି କୁହାଯାଏ। ଏହା ସମସ୍ତ ପ୍ରକାର ମାଳା ଯଥା ନିରବିଚ୍ଛିନ୍ନ, ଭାଗ ବିଭକ୍ତ ବା ବାରମ୍ବାରତା ବିତରଣକୁ ଚିତ୍ର ଆକାରରେ ପ୍ରକାଶ କରିବାରେ ସାହାଯ୍ୟ କର ।
ସାଧାରଣତଃ ସଂଭାଗ ଗୁଡ଼ିକର ସଂଖ୍ୟା କମ୍ ଥିବାବେଳେ ହିଷ୍ଟୋଗ୍ରାମ ପସନ୍ଦନୀୟ ମାତ୍ର ଯେତେବେଳେ ସଂଭାଗ ଗୁଡ଼ିକର ସଂଖ୍ୟା ଅନେକ ହୋଇଥାଏ, ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ର ପସନ୍ଦନୀୟ ହୋଇଥାଏ। ହିଷ୍ଟୋଗ୍ରାମ ଭଳି ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ର ପ୍ରକାଶ୍ୟ ଅନ୍ତ ସଂଭାଗ ଥିବା ବାରମ୍ବାରତା ବିତରଣ କ୍ଷେତ୍ରରେ ବ୍ୟବହୃତ ହୋଇ ନ ଥାଏ । ସାଧାରଣତଃ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ର ଦୁଇଟି ଉପାୟରେ ଅଙ୍କନ କରାଯାଏ; ଯଥା – ହିଷ୍ଟୋଗ୍ରାମ୍ ମାଧ୍ଯମରେ ଏବଂ ବିନା ହିଷ୍ଟୋଗ୍ରାମରେ।
![]()
ହିଷ୍ଟୋଗ୍ରାମ୍ ମାଧ୍ଯମରେ – ପ୍ରଥମେ ହିଷ୍ଟୋଗ୍ରାମ୍ ପ୍ରସ୍ତୁତ କରାଯାଏ। ଶ୍ରେଣୀ ବ୍ୟବଧାନ ସହିତ ଉଚ୍ଚତା ଓ ସେମାନଙ୍କର ଶ୍ରେଣୀ ଆନୁପାତିକ ବାରମ୍ବାରତାକୁ ନେଇ ଆୟତକ୍ଷେତ୍ରମାନ ଗଠନ କରି ହିଷ୍ଟୋଗ୍ରାମ୍ ପ୍ରସ୍ତୁତ କରାଯାଏ। ହିଷ୍ଟୋଗ୍ରାମର ପ୍ରତ୍ୟେକ ଆୟତାକାର କ୍ଷେତ୍ରର ଉପରିଭାଗ ଅନୁଲମ୍ବ ପାର୍ଶ୍ଵରେ ମଧ୍ୟବିନ୍ଦୁ ନିର୍ଣ୍ଣୟ କରାଯାଏ ଏବଂ ସେହି ସବୁ ମଧ୍ୟବିନ୍ଦୁ ଗୁଡ଼ିକୁ ସରଳରେଖା ସାହାଯ୍ୟରେ ସଂଯୋଗ କଲେ ଆମେ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ର ପାଇଥାଉ।
ପ୍ରଥମ ଓ ଅନ୍ତିମ ଆୟତକାର କ୍ଷେତ୍ରର ଉପରପାର୍ଶ୍ଵ ଅନୁଲମ୍ବର ମଧ୍ୟବିନ୍ଦୁକୁ ନିମ୍ନ ପାର୍ଶ୍ଵରେ ଥିବା ଅନୁଲମ୍ବ ସହିତ ସଂଯୁକ୍ତ କରାଯାଏ। ଫଳରେ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ରର କ୍ଷେତ୍ରଫଳ ତତ୍ସଂଲଗ୍ନ ହିଷ୍ଟୋଗ୍ରାମ୍ର କ୍ଷେତ୍ରଫଳ ସହିତ ସମାନ ହୋଇଥାଏ।
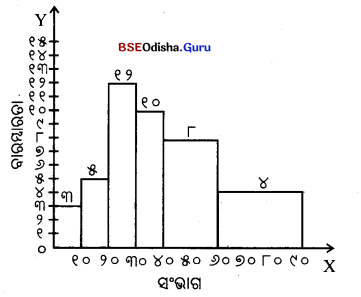
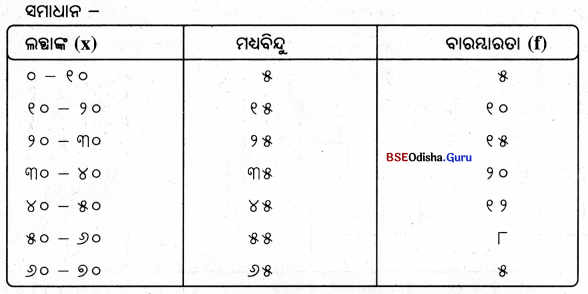
ଉଦାହରଣ – ନିମ୍ନଲିଖତ ତଥ୍ୟାବଳୀରୁ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ର ଅଙ୍କନ କରାଯାଇପାରେ।

ସମାଧାନ – ପ୍ରଥମେ ତଥ୍ୟାବଳୀକୁ ନେଇ ହିଷ୍ଟୋଗ୍ରାମ୍ ଗଠନ କରାଯାଇଚି। ତା’ପରେ ହିଷ୍ଟୋଗ୍ରାମରେ ଥିବା ଆୟତକ୍ଷେତ୍ର ଗୁଡ଼ିକର ଉପରିଭାଗ ମଧ୍ୟବିନ୍ଦୁକୁ ସ୍ଥିର କରି ସ୍ଲୋ ମାଧ୍ୟମରେ ଯୋଗ କରାଯାଇ ଅଛି। ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶିତ ରେଖାଚିତ୍ରର ଶେଷବିନ୍ଦୁ ମୂଳ ଆଧାର ରେଖାସହ ଯୋଗ ହୋଇଅଛି । ଫଳରେ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶିକ ରେଖାଚିତ୍ରର ଆୟତନ ଓ ହିଷ୍ଟୋଗ୍ରାମ୍ର ଆୟତନ ସମାନ ହୋଇଛି ।
ହିଷ୍ଟୋଗ୍ରାମ୍ ବିନା – ହିଷ୍ଟୋଗ୍ରାମ୍ ଅଙ୍କନ ନ କରି ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ର ଅଙ୍କନ କରିବା ଅନ୍ୟ ଏକ ପ୍ରଣାଳୀ। ଏହି କ୍ଷେତ୍ରରେ ବିଭିନ୍ନ ସଂଭାଗର ମଧ୍ୟବିନ୍ଦୁ ଗୁଡ଼ିକୁ ନିର୍ଣ୍ଣୟ କରାଯାଏ ଓ ସେହି ଅନୁଯାୟୀ ସେହି ସଂଭାଗରେ ଚିହ୍ନିତ କରାଯାଏ ଏବଂ ସେହି ସବୁ ବିନ୍ଦୁଗୁଡ଼ିକୁ ସରଳରେଖା ଗୁଡ଼ିକ ଦ୍ଵାରା ସଂଯୁକ୍ତ କରାଯାଏ। ଏହି ପ୍ରକାରରେ ଯେଉଁ ରେଖାଚିତ୍ର ମିଳେ ତାହାକୁ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ର କୁହାଯାଏ ଓ ଏହି ପ୍ରକାରରେ ଅଙ୍କିତ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ର ପୂର୍ବ ପ୍ରଣାଳୀରେ ଅଙ୍କିତ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ର ସହିତ ଠିକ୍ ସମାନ ହୋଇଥାଏ।
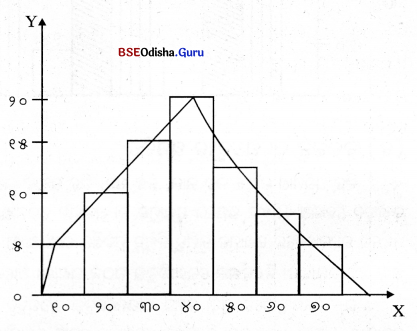
ନିମ୍ନଲିଖତ ତଥ୍ୟାବଳୀରୁ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ର ଅଙ୍କନ କରାଯାଇପାରେ।

୬। ବାରମ୍ବାରତା ବକ୍ରରେଖାର ଗଠନ ପ୍ରଣାଳୀ ସମ୍ବନ୍ଧରେ ଆଲୋଚନା କର ।
Answer:
ବାରମ୍ବାରତା ବକ୍ରରେଖା ଓ ବାରମ୍ବାରତା ବହୁଭୁଜର ଗଠନ ପ୍ରଣାଳୀ ପ୍ରାୟ ସମାନ। ବାରମ୍ବାରତା ବହୁଭୁଜ ଅଙ୍କନରେ ସ୍ଥାପିତ ବିନ୍ଦୁମାନଙ୍କୁ ସରଳରେଖା ଦ୍ଵାରା ସଂଯୋଗ କରାଯାଇଥାଏ। କିନ୍ତୁ ବାରମ୍ବାରତା ବକ୍ରରେ ବିନ୍ଦୁମାନଙ୍କୁ ସ୍ଵଚ୍ଛନ୍ଦରେ ହସ୍ତୀଙ୍କିତ ରେଖାଦ୍ଵାରା ସଂଯୋଗ କରାଯାଇ ଏକ ମସୃଣ ବକ୍ରରେଖଶ ଅଙ୍କନ କରାଯାଏ।
ତେଣୁ ଗୋଟିଏ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ରର ବିଭିନ୍ନ ବିନ୍ଦୁଗୁଡ଼ିକୁ ସରଳରେଖା ଦ୍ଵାରା ସଂଯୋଗ ନ କରି ଯଦି ମୁକ୍ତ ହସ୍ତରେ ସଂଯୋଗ କରାଯାଏ, ତାହାକୁ ବାରମ୍ବାରତା ବକ୍ରରେଖା କୁହାଯାଏ। ଅର୍ଥାତ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ରକୁ ମସୃଣ କରି ବାରମ୍ବାରତା ବକ୍ରରେଖା ଅଙ୍କନ କରାଯାଇଥାଏ। ବାରମ୍ବାରତା ବକ୍ରରେଖା ଏଭଳି ମୁକ୍ତ ହସ୍ତରେ ଅଙ୍କନ କରାଯାଏ ଯେ ବାରମ୍ବାରତା ବକ୍ରରେଖାର କ୍ଷେତ୍ରଫଳ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ରର କ୍ଷେତ୍ରଫଳ ସହିତ ପ୍ରାୟ ସମାନ ହୋଇଥାଏ।
ତଥ୍ୟାବଳୀର ଥବା ଅନିୟମିତ ଗତିକୁ ବାଦ୍ ଦେବା ହେଉଚି ବାରମ୍ବାରତା ବକ୍ରରେଖା ଅଙ୍କନ କରିବାର ମୁଖ୍ୟ ଅଭିପ୍ରାୟ। ଯେତେବେଳେ ସଂଭାଗ ବିସ୍ତାରର ପରିମାଣ ବୃହତ୍ ହୋଇଥାଏ, ବାରମ୍ବାରତା ବକ୍ରରେଖାର ଶୀର୍ଷବିନ୍ଦୁ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ରର ଶୀର୍ଷବିନ୍ଦୁରୁ ମସୃଣ କରି ମୁକ୍ତ ହସ୍ତରେ ଘଟଣା ହୋଇଥାଏ, ମୁକ୍ତ ହସ୍ତରେ ଅଙ୍କିତ ମସୃଣ ବକ୍ରରେଖା ଏକ ପ୍ରତିସମ ବକ୍ରରେଖା କିମ୍ବା ଏକ ଘଣ୍ଟାକୃତି ବକ୍ରରେଖା ସୃଷ୍ଟି କରିଥାଏ ।
![]()
ଯଦି ଘଟଣାଟି ସାମାଜିକ କିମ୍ବା ଅର୍ଥନୈତିକ ହୋଇଥାଏ, ବକ୍ରରେଖା ସାଧାରଣତଃ ଅପ୍ରତିସମ ହୋଇଥାଏ। ଯାହାହେଉ, ମସୃଣ ବାରମ୍ବାରତା ବକ୍ରରେଖାର ଅଙ୍କନ ପାଇଁ ହିଷ୍ଟୋଗ୍ରାମ୍ ଅଙ୍କନ କରି ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ର ଅଙ୍କନ କରିବା ଆବଶ୍ୟକ ଓ ପରେ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ରକୁ ମୁକ୍ତ ହସ୍ତରେ ମସୃଣ କରାଯାଏ ।
ତେଣୁ ମସୃଣ ବାରମ୍ବାରତା ବକ୍ରରେଖାର ଅଙ୍କନ ପାଇଁ ପ୍ରଥମେ ହିଷ୍ଟୋଗ୍ରାମ ଅଙ୍କନ କରାଯାଏ, ତା’ପରେ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ର ଅଙ୍କନ କରାଯାଏ ଓ ଶେଷରେ ବାରମ୍ବାରତା ନିର୍ଦ୍ଦେଶକ ରେଖାଚିତ୍ରକୁ ମୁକ୍ତ ହସ୍ତରେ ମସୃଣ କରାଯାଇ ବାରମ୍ବାରତା ବକ୍ରରେଖା ଅଙ୍କନ କରାଯାଏ। ଫଳରେ ବାରମ୍ବାରତା ବକ୍ରରେଖାର କ୍ଷେତ୍ରଫଳ ବାରମ୍ବାରତା ବିତରଣରେ ସମୁଦାୟ ବାରମ୍ବାରତାକୁ ପ୍ରତିନିଧୃତ୍ଵ କରିଥାଏ।
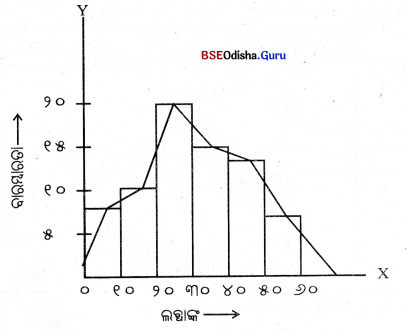
ଉଦାହରଣ – ନିମ୍ନୋକ୍ତ ସାରଣୀ ପ୍ରଦତ୍ତ ତଥ୍ୟାବଳୀର ବାରମ୍ବାରତା ବକ୍ରରେଖା ଅଙ୍କନ କରାଯାଇପାରେ –

୭। କାଳାନୁସାରୀ ଚିତ୍ରଲେଖର ଗଠନ ପ୍ରଣାଳୀ ସମ୍ବନ୍ଧରେ ଆଲୋଚନା କର ।
Answer:
କାଳାନୁସାରୀ ଚିତ୍ର ଲେଖକୁ ମଧ୍ଯ ହିଷ୍ଟୋରିଗ୍ରାମ୍ ବୋଲି କୁହାଯାଏ। ପରିସଂଖ୍ୟାନ ତଥ୍ୟାବଳୀ କାଳାନୁକ୍ରମିକ କ୍ରମରେ ଅର୍ଥାତ୍ ଏହାର ଉତ୍ପତ୍ତି ସମୟ କ୍ରମରେ ବ୍ୟବସ୍ଥା ସିଦ୍ଧ ହେଲେ ତାହାକୁ କାଳାନୁସାରୀ ବୋଲି କୁହାଯାଏ । ସମୟ କହିଲେ ଗୋଟିଏ ବର୍ଷ, ତିନିମାସ, ଏକମାସ, ଏକ ସପ୍ତାହ, ଦିନ, ଘଣ୍ଟା ଇତ୍ୟାଦିକୁ ବୁଝାଇଥାଏ।
ଅର୍ଥନୀତି ଓ ବ୍ୟବସାୟ କ୍ଷେତ୍ରରେ ବ୍ୟବହୃତ ଅଧିକାଂଶ ତଥ୍ୟ ଏହି କାଳାନୁସାରୀ ଅଟେ । ଏହି କାଳାନୁସାରୀ ମଧ୍ୟରେ ଦେଶର ଜନସଂଖ୍ୟା, ବ୍ୟାଙ୍କଜମା, ଦ୍ରବ୍ୟର ଦାମ, ଆମଦାନୀ, ରପ୍ତାନୀ ଇତ୍ୟାଦି ଅନ୍ତର୍ଭୁକ୍ତ ।
କାଳାନୁସାରୀ ତଥ୍ୟର ଲେଖଚିତ୍ର ଉପସ୍ଥାପନାକୁ ହିଷ୍ଟୋରିଗ୍ରାମ୍ କୁହାଯାଏ। ସ୍ଵାଧୀନ ଉପାଦାନ ‘ସମୟ’କୁ X ଅକ୍ଷରେ ଓ ନିର୍ଭରଶୀଳ ଉପାଦାନକୁ Y ଅକ୍ଷରେ ନେଇ ହିଷ୍ଟୋରିଗ୍ରାମ୍ ଅଙ୍କନ କରାଯାଇପାରେ।
ହିଷ୍ଟୋରିଗ୍ରାମ୍ ଦୁଇ ପ୍ରକାରର। ନିରଙ୍କୁଶ ହିଷ୍ଟୋରିଗ୍ରାମ୍ ଓ ସୂଚକ ହିଷ୍ଟୋରିଗ୍ରାମ୍।
(i) ନିରୁଙ୍କୁଶ ହିଷ୍ଟୋରିଗ୍ରାମ୍
କାଳାନୁସାରୀ ଲେଖଚିତ୍ରକୁ ଗାଣିତିକ ସ୍କେଲରେ ଗୋଟିଏ ସମୟରୁ ଅନ୍ୟ ଏକ ସମୟକୁ ନିରଙ୍କୁଶ ପରିବର୍ତ୍ତନର ପ୍ରତିଫଳନ କରିବାକୁ ନିରଙ୍କୁଶ ବା ବିଶୁଦ୍ଧ ହିଷ୍ଟୋରିଗ୍ରାମ୍ କୁହାଯାଏ। ଏହି କ୍ଷେତ୍ରରେ ବଣ୍ଟନ ମାଳାର ବାସ୍ତବ ମୂଲ୍ୟକୁ ବିଚାରକୁ ନିଆଯାଇ ଗ୍ରାଫ୍ କାଗଜରେ ସ୍କଟ କରାଯାଏ। ଏଠାରେ କେବଳ ମାତ୍ର ଗୋଟିଏ ପରିବର୍ଭନୀୟ ମୂଲ୍ୟ ନିଆଯାଇଥାଏ। ସେଥିପାଇଁ ଏହାକୁ ମଧ୍ଯ ଏକ ପରିବର୍ତ୍ତନୀୟ ଚିତ୍ରଲେଖ ବୋଲି କୁହାଯାଏ।
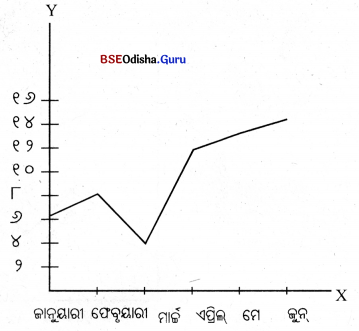
ଉଦାହରଣ – ନିମ୍ନ ସାରଣୀରେ ଗୋଟିଏ କାରଖାନାର ଜାନୁୟାରୀରୁ ଜୁନ୍ ମଧ୍ଯରେ ଉତ୍ପାଦନ ଦର୍ଶାଯାଇଛି ।

X ଅକ୍ଷରେ ସମୟ ଓ Y ଅକ୍ଷରେ ଉତ୍ପାଦନ ନେଇ ଗ୍ରାଫ୍ କାଗଜରେ ବିଶୁଦ୍ଧ ହିଷ୍ଟୋରିଗ୍ରାମ୍ ଅଙ୍କନ କରାଯାଇପାରେ ।
ମିଥ୍ୟା ଆଧାର ରେଖାର ବ୍ୟବହାର – କାଳାନୁସାରୀ ତଥ୍ୟରେ ମିଥ୍ୟା ଆଧାର ରେଖାର ବ୍ୟବହାର ଅତି ସାଧାରଣ। ଲବ୍ଧଙ୍କ ଗୁଡ଼ିକ ମୂଲ୍ୟର ପରିବର୍ତ୍ତନକୁ Y ଅକ୍ଷରେ ଦର୍ଶାଇଲା ବେଳେ, ଲବ୍ଧାଙ୍କର ସର୍ବନିମ୍ନ ମୂଲ୍ୟ ଶୂନ୍ୟଠାରୁ ବେଶୀ ଦୂର ହୋଇଥିଲେ, ଏହି ମିଥା ଆଧାର ରେଖାର ପ୍ରୟୋଗ କରାଯାଇଥାଏ।
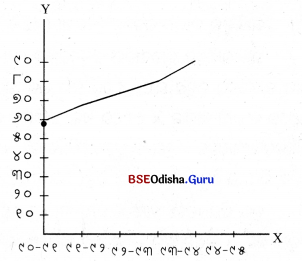
ଉଦାହରଣ – ୧୯୯୦-୯୧ ଠାରୁ ୧୯୯୪- ୯୫ ମଧ୍ୟରେ ଭାରତର ରପ୍ତାନୀକୁ ନିମ୍ନ ସାରଣୀରେ ଦର୍ଶାଯାଇ ଅଛି। ଏହି ତଥ୍ୟକୁ ଉପଯୁକ୍ତ ଚିତ୍ରଲେଖରେ ଉପସ୍ଥାପାନ କରାଯାଇଛି।

ସମାଧାନ – ଏହି କ୍ଷେତ୍ରରେ ମିଥ୍ୟା ଆଧାର ରେଖାର ଅଙ୍କନ ଆବଶ୍ୟକ ହୋଇଅଛି। କାରଣ ସର୍ବନିମ୍ନ ରପ୍ତାନୀ ଏବଂ ୦ (ଶୂନ) ମଧ୍ୟରେ ବ୍ୟବଧାନ ଖୁବ୍ ବେଶୀ। ଦ୍ଵିତୀୟତଃ ବିଭିନ୍ନ ନିମ୍ନଲିଖତ ଚିତ୍ରରେ ମିଥ୍ୟା ଆଧାର ରେଖା ଅଙ୍କନ କରାଯାଇ ଅଛି।
(ii) ସୂଚକ ହିଷ୍ଟୋରିଗ୍ରାମ୍
ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ମୂଲ୍ୟର ସୂଚକ ସଂଖ୍ୟା ନେଇ କାଳାନୁସାରୀ ଚିତ୍ରଲେଖ ପ୍ରସ୍ତୁତ କଲେ ତାହାକୁ ସୂଚକ ହିଷ୍ଟୋରିଗ୍ରାମ୍ ବୋଲି କୁହାଯାଏ। ଏକ ନିର୍ଦ୍ଦିଷ୍ଟ ସ୍ଥିର ମୂଳ ସମୟ ତୁଳନାରେ କୌଣସି ଏକ ବ୍ୟାପାରର ମୂଲ୍ୟରେ ଶତକଡ଼ା ପରିବର୍ତ୍ତନ ହେଲେ ଏହା ସୂଚନା ଯୋଗାଇ ଥାଏ। ସେମାନଙଙ୍କର ବାସ୍ତବ ମୂଲ୍ୟ ପରିବର୍ତ୍ତେ ସଂପର୍କିତ ମୂଲ୍ୟକୁ ନେଇ ଗ୍ରାଫ୍ କାଗଜରେ ଚିତ୍ରଲେଖ ଅଙ୍କନ କରାଯାଏ। ସେହି ଗୋଟିଏ ଚିତ୍ରଲେଖରେ ଦୁଇ ବା ତତୋଽଧିକ ଲଜ୍ଜାଙ୍କର ମୂଲ୍ୟର ତୁଳନା କରାଯାଇପାରେ।
![]()
ଉଦାହରଣ – ସାରଣୀରେ ଗୋଟିଏ କାରଖାନାର ଉତ୍ପାଦନ ଓ ବିକ୍ରୟ ଜାନୁୟାରୀରୁ ଜୁନ୍ ମଧ୍ଯରେ ଦିଆଯାଇଛି।
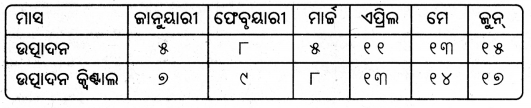
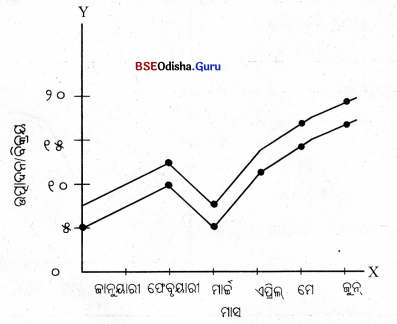
ଉଭୟ ଉତ୍ପାଦନ ଓ ବିକ୍ରୟକୁ Y ଅକ୍ଷରେ ଏବଂ ମାସକୁ X ଅକ୍ଷରେ ନିଆଯାଇ ଅଛି । ଏଠାରେ ଦୁଇଟି ଚିତ୍ରଲେଖ ଅଙ୍କିତ ହୋଇଛି।
୮। ରାଶିକୃତ ବାରମ୍ବାରତା ବକ୍ରରେଖା (ଓଜିଭ୍) କ’ଣ ? ଏହାର ବ୍ୟବହାରିକ ଗୁଣମାନ ଆଲୋଚନା କର ।
Answer:
ରାଶିକୃତ ବାରମ୍ବାରତା ବକ୍ରରେଖାକୁ ମଧ୍ୟ ‘ଓଜିଭ’ ବକ୍ରରେଖା କୁହାଯାଏ। ରାଶିକୃତ ବାରମ୍ବାରତା ତଥ୍ୟକୁ ନେଇ ଗ୍ରାଫ୍ କାଗଜରେ ମସୃଣ ଭାବେ ଯେଉଁ ବକ୍ରରେଖା ଗଠନ କରାଯାଏ, ତାହାକୁ ରାଶିକୃତ ବାରମ୍ବାରତା ବକ୍ରରେଖା କୁହାଯାଏ। ଏଥିରେ ସଂଭାଗ ସୀମାକୁ X ଅକ୍ଷରେ ଏବଂ ରାଶିକୃତ ବାରମ୍ବାରତାକୁ Y ଅକ୍ଷରେ ନେଇ ଯେଉଁ ବକ୍ରରେକା ପାଇଥାଉ, ତାହାକୁ ରାଶିକୃତ ବାରମ୍ବାରତା ବକ୍ରରେଖା ରୂପେ ଅଭିହିତ କରାଯାଏ। ସୁତରାଂ ରାଶିକୃତ ବାରମ୍ବାରତା ବିତରଣର ଚିତ୍ରଲେଖକ ଉପସ୍ଥାପନାକୁ ଓଜିଭ୍ କିମ୍ବା ରାଶିକୃତ ବାରମ୍ବାରତା ବକ୍ରରେଖା କୁହାଯାଏ।
ଦୁଇ କିମ୍ବା ତତୋଽଧୂକ ବାରମ୍ବାରତା ବିତରଣ ଗୁଡ଼ିକୁ ତୁଳନା କରିବା ଇତ୍ୟାଦି ଓଜିଭର ମୂଳ ଆଭିମୁଖ୍ୟ। ମଧ୍ୟମା, ଓ ଦଶମାଂଶକ ଓ ଶତାଂଶ ଭଳି ଅବସ୍ଥାପିତ ହାରାହାରି ସଂଖ୍ୟାକୁ ନିର୍ଣ୍ଣୟ କରିବାପାଇଁ ରାଶିକୃତ ବାରମ୍ବାରତା ବକ୍ରରେଖା ବ୍ୟବହୃତ ହୁଏ । ସଂଭାଗ ବିସ୍ତାର ଅସମାନ ଥିବା ସତ୍ତ୍ବେ ଚିତ୍ରଲେଖ ମାଧ୍ୟମରେ ତଥ୍ୟାବଳୀର ଉପସ୍ଥାପନା କରିବାରେ ଏହା କୌଣସି ପ୍ରତିବନ୍ଧକ ସୃଷ୍ଟି କରେ ନାହିଁ। ପୁନଶ୍ଚ, ପ୍ରକାଶ୍ୟ ଅନ୍ତ ସଂଭାଗ କ୍ଷେତ୍ରରେ ଏହା ସହଜ ଓ ସୁବିଧାରେ ଚିତ୍ରଲେଖ ମାଧ୍ୟମରେ ତଥ୍ୟାବଳୀକୁ ଉପସ୍ଥାପନ କରିଥାଏ।
ଦୁଇଟି ପ୍ରଣାଳୀରେ ଓଜିଭ୍ ଅଙ୍କନ କରାଯାଇପାରେ; ଯଥା – ପୂର୍ବାପେକ୍ଷା କମ୍ ପ୍ରଣାଳୀ (less than Method) ଓ (More than Method) ପୂର୍ବାପେକ୍ଷା କମ୍ ପ୍ରଣାଳୀ (Less than Method) ଏହି ପ୍ରଣାଳୀରେ ସଂଭାଗ ଗୁଡ଼ିକର ଉର୍ଦ୍ଧ୍ୱସୀମାରୁ ଆରମ୍ଭ କରାଯାଏ ଓ ବାରମ୍ବାରତାଗୁଡ଼ିକୁ ଯୋଗ କରାଯାଏ। ଏହି ରାଶିକୃତ ବାରମ୍ବାରତାକୁ ତତ୍ ସଂଲଗ୍ନ ସଂଭାଗ ଗୁଡ଼ିକ ସହିତ ଚିତ୍ରଲେଖରେ ଚିହ୍ନିତ କଲେ ଗୋଟିଏ ବକ୍ରରେଖା ମିଳେ, ଯାହାକୁ ଓଜିଭ ବା ରାଶିକୃତ ବାରମ୍ବାରତା ବକ୍ରରେଖା କୁହାଯାଏ। ଏହି ବକ୍ରରେ ବାମ ପାର୍ଶ୍ଵରୁ ଦକ୍ଷିଣ ପାର୍ଶ୍ଵକୁ ଉର୍ଦ୍ଧ୍ଵ ଆଡ଼କୁ ବୃଦ୍ଧି ହୁଏ ଓ S ଆକୃତିର ହୋଇଥାଏ।

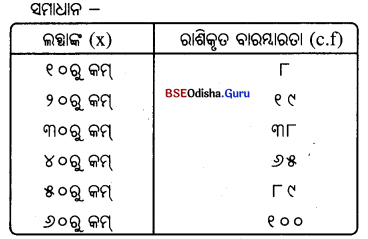
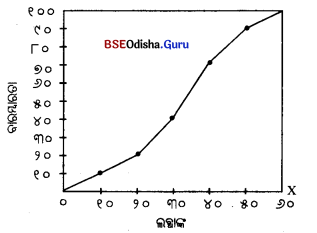
ଚିତ୍ରରେ ବିନ୍ଦୁ ଦ୍ଵାରା ଚିହ୍ନିତ ରେଖାକୁ ଓଜିଭ୍ କିମ୍ବା ରାଶିକୃତ ବାରମ୍ବାରତା ବକ୍ରରେଖା କୁହାଯାଏ। ଏହା ବାମରୁ ଦକ୍ଷିଣକୁ ଉର୍ଦ୍ଧ୍ୱଗାମୀ ହୋଇଛି । ଏହି କ୍ଷେତ୍ରରେ ଲବ୍ଧଶଙ୍କ ସଂଲଗ୍ନ ରାଶିକୃତ ବାରମ୍ବାରତା ଚିତ୍ରଲେଖ ମାଧ୍ୟମରେ ଉପସ୍ଥାପନା କରାଯାଇଛି।
ପୂର୍ବାପେକ୍ଷା ଅଧିକ ପ୍ରଣାଳୀ (More than Method) – ପୂର୍ବାପେକ୍ଷା ଅଧିକ ପ୍ରଣାଳୀରେ ଆମେ ସଂଭାଗ ଗୁଡ଼ିକର ନିମ୍ନସୀମାରୁ ଆରମ୍ଭ କରାଯାଏ। ଏବଂ ମୋଟ ବାରମ୍ବାରତାରୁ ପ୍ରତ୍ୟେକ ସଂଭାଗର ବାରମ୍ବାରତାକୁ ଅନ୍ତର କରାଯାଏ। ଯେତେବେଳେ ଏହି ବାରମ୍ବାରତା ଗୁଡ଼ିକୁ ରେଖା ଚିତ୍ରରେ ଚିହ୍ନିତ କରାଯାଏ, ଆମେ ଏକ ବକ୍ରରେଖା ପାଇଥାଉ ଯାହା ବାମରୁ ଦକ୍ଷିଣକୁ ନିମ୍ନଗାମୀ ହୋଇଥାଏ। ଏହି ରେଖାକୁ ରାଶିକୃତ ବାରମ୍ବାରତା ବକ୍ରରେଖା କିମ୍ବା ଓଜିଭ୍ କୁହାଯାଏ।
ପୂର୍ବ ଉଦାହରଣରୁ ପୂର୍ବାପେକ୍ଷା ଅଧିକ ପ୍ରଣାଳୀ ରାଶିକୃତ ବାରମ୍ବାରତା ବକ୍ରରେଖା ଦର୍ଶାଯାଇ ପାରିବ।
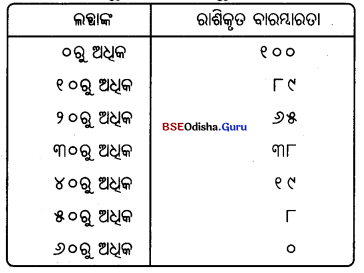
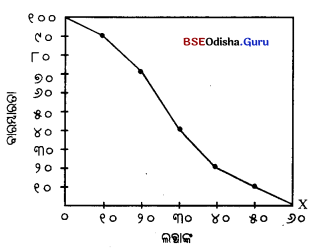
ଚିତ୍ରରେ ବିନ୍ଦୁ ଗୁଡ଼ିକ ଦ୍ଵାରା ସୂଚୀତ ରେଖାକୁ ଓଜିଭ୍ କିମ୍ବା ରାଶିକୃତ ବାରମ୍ବାରତା ବକ୍ରରେଖା କୁହାଯାଏ। ଏହା ବାମରୁ ଦକ୍ଷିଣକୁ ନିମ୍ନଗାମୀ। ଏହି ବକ୍ରରେଖା ଲବ୍ଧଶଙ୍କ ସଂଲଗ୍ନ ରାଶିକୃତ ବାରମ୍ବାରତା ଭିଭିରେ ଅଙ୍କନ କରାଯାଇଥିବା ହେତୁ ତାହାକୁ ରାଶିକୃତ ବାରମ୍ବାରତା ବକ୍ରରେଖା ଅଭିହିତ କରାଯାଏ। ଏହା ଓଲଟା ‘S’ ଆକୃତିର।
![]()
୯। ବୃତ୍ତଲେଖ ବା ବୃତ୍ତରେଖାଚିତ୍ର ପ୍ରସ୍ତୁତି ପାଇଁ ମୌଳିକ ନିୟମଗୁଡ଼ିକ ବର୍ଣ୍ଣନା କର ।
Answer:
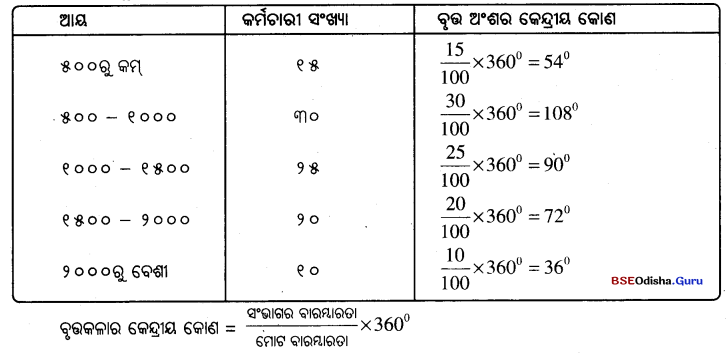
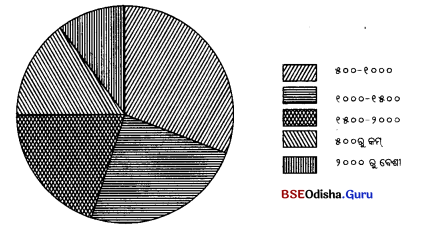
ଗୋଟିଏ ବୃତ୍ତକୁ ଆୟତକ୍ଷେତ୍ରରେ ବିଭକ୍ତ କରି ଯେଉଁ ରେଖାଚିତ୍ର ଗଠନ କରାଯାଏ, ତାହାକୁ ବୃତ୍ତଳେଖ କୁହାଯାଏ। ସଂଗୃହୀତ ତଥ୍ୟକୁ ଅନେକ ସମୟରେ ଏକ ବୃତ୍ତାକାର କ୍ଷେତ୍ରର ଆନୁପାତିକ ଅଂଶରୂପେ ପ୍ରକାଶ କରାଯାଇ ଚିତ୍ର ଅଙ୍କନ କରାଯାଇଥାଏ। ଏହାକୁ ବୃତ୍ତ ଲେଖ କୁହାଯାଏ। ସାଧାରଣତଃ ତଥ୍ୟର ବିଭିନ୍ନ ଅଂଶକୁ ବୃତ୍ତର ମଧ୍ୟାହ୍ନ ସମୟ ଚିହ୍ନଠାରୁ ଘଣ୍ଟାକଣ୍ଟା ଘୁରୁଥୁବା ଦିଗରେ ବଡ଼ରୁ ସାନ କ୍ରମରେ ଏପରି ପ୍ରଦର୍ଶନ କରାଯାଏ ଯେପରିକି ଏହାର ପ୍ରତ୍ୟେକ ଅଂଶ ବୃତ୍ତକଳାର କେନ୍ଦ୍ରୀୟ କୋଣମାନଙ୍କ ସହ ସମାନୁପାତୀ ହେବ। ବିମିନ୍ନ ଅଂଶକୁ ବିଭିନ୍ନ ରଙ୍ଗ ବା ରେଖା ଦ୍ଵାରା ସୂଚୀତ କରାଯାଇଥାଏ ।
ଉଦାହରଣ – କୌଣସି ଏକ କାରଖାନାରେ କାମ କରୁଥିବା ୧୦୦ ଜଣ କର୍ମଚାରୀମାନଙ୍କୁ ସେମାନଙ୍କ ଆୟ ସ୍ତର ଅନୁସାରେ ୫ଟି ଶ୍ରେଣୀରେ ବିଭକ୍ତ କରାଯାଇଛି।

କର୍ମଚାରୀମାନଙ୍କୁ ସେମାନଙ୍କର ଆୟ ଭିତ୍ତିରେ ୫ଟି ଭାଗରେ ବିଭକ୍ତ କରାଯାଇଛି । ତେଣୁ ଏହି ତଥ୍ୟାବଳୀକୁ ବୃତ୍ତଲେଖରେ ପ୍ରକାଶ କରିବାକୁ ହେଲେ, ବୃତ୍ତର ୫ଟି ଅଂଶକୁ ଏପରି ସୂଚୀତ କରିବାକୁ ହେବ ଯେପରି ବୃତ୍ତର ୫ଟି ଅଂଶର କେନ୍ଦ୍ରୀୟ କୋଣମାନଙ୍କର ଅନୁପାତ ବିଭିନ୍ନ ଭାଗରେ ଥିବା କର୍ମଚାରୀମାନଙ୍କ ଅନୁପାତ ସହ ସମାନ ହେବ।
୧୦ । ହିଷ୍ଟୋଗ୍ରାମ୍ର ଗଠନ ପ୍ରଣାଳୀ ସମ୍ବନ୍ଧରେ ଆଲୋଚନା କର।
Answer:
ନିରବଚ୍ଛିନ୍ନ ମାଳାର ବାରମ୍ବାରତା ବିତରଣର ଚିତ୍ରଲେଖକ ଉପସ୍ଥାପନାକୁ ହିଷ୍ଟୋଗ୍ରାମ୍ କୁହାଯାଏ। ହିଷ୍ଟୋଗ୍ରାମ୍ ହେଉଛି କେତେଗୁଡ଼ିଏ ଉଲ୍ଲମ୍ବ ସ୍ତମ୍ଭଚିତ୍ରର ସେଟ୍, ଯାହାର କ୍ଷେତ୍ରଫଳ ପ୍ରତିନିଧ୍ଵ କରୁଥିବା ବାରମ୍ବାରତା ସହିତ ସମାନୁପାତୀ।
ହିଷ୍ଟୋଗ୍ରାମ୍ ଏକ ଗ୍ରାଫ୍ କାଗଜରେ ଅଙ୍କନ କରାଯାଏ। ହିଷ୍ଟାଗ୍ରାମ୍ ଅଙ୍କନ କରିବାବେଳେ ଲଚ୍ଛାଙ୍କକୁ ସର୍ବଦା ଆନୁଭୂମିକ ଅକ୍ଷରେ ନିଆଯାଏ ଏବଂ ଏହା ସହିତ ସଂଶ୍ଳିଷ୍ଟ ହୋଇଥିବା ବାରମ୍ବାରତା ଉଲ୍ଲମ୍ବ ଅକ୍ଷରେ ନିଆଯାଏ। ପ୍ରତ୍ୟେକ ସଂଭାଗକୁ ସ୍କେଲ ଭିଭିରେ ଦୂରତା ଦ୍ଵାରା ପ୍ରତିନିଧୁତ୍ଵ କରାଯାଇଥାଏ ଯାହା ସଂଭାଗ ବିସ୍ତାର ସହିତ ସମାନୁପାତୀ ହୋଇଥାଏ।
ଆନୁଭୂମିକ ଅକ୍ଷରେ ପ୍ରତ୍ୟେକ ଆୟତାକାର କ୍ଷେତ୍ରର ଦୂରତା ସମାନ ରହିବା ଉଚିତ୍, ଯଦି ସଂଭାଗ ବିସ୍ତାର ସମାଜ ବା ସମଜାତୀୟ ହୋଇଥାଏ। ଯଦି ସଂଭାଗ ପାଇଥାଉ ଓ ପ୍ରତ୍ୟେକ ଆୟତକାର କ୍ଷେତ୍ରର ସଂଭାଗ ବିସ୍ତାରର ଦୂରତାକୁ ପ୍ରସ୍ଥ ଆକାରରେ ନିଆଯାଏ ଓ ବାରମ୍ବାରତାର ଦୂରତାକୁ ଲମ୍ବ ବା ଉଚ୍ଚତା ଆକାରରେ ନିଆଯାଏ।
ସୁତରାଂ ହିଷ୍ଟୋଗ୍ରାମ୍ର କ୍ଷେତ୍ରଫଳ ସମସ୍ତ ସଂଭାଗ ଗୁଡ଼ିକରେ ଆବଣ୍ଟନ ହୋଇଥିବା ଲମ୍ବ ବା ଉଚ୍ଚତା ଆକାରରେ ନିଆଯାଏ। ସୁତରାଂ ହି ସମୁଦାୟ ବାରମ୍ବାରତାକୁ ପ୍ରତିନିଧୂତ୍ବ କରିଥାଏ।
![]()
ହିଷ୍ଟୋଗ୍ରାମ୍ ସ୍ତମ୍ଭଚିତ୍ରଠାରୁ ଭିନ୍ନ, କାରଣ ହିଷ୍ଟୋଗ୍ରାମ୍ ଏକ ଦୁଇ ଆୟତନ ବିଶିଷ୍ଟ କ୍ଷେତ୍ର ଯାହାର ଲମ୍ବ ଓ ପ୍ରସ୍ଥ ଦ୍ଵୟର ପ୍ରାଧାନ୍ୟ ଥାଏ; ମାତ୍ର ସ୍ତମ୍ଭଚିତ୍ର ଗୋଟିଏ ଏକ ଆୟତନ ବିଶିଷ୍ଟ କ୍ଷେତ୍ର ଯାହାର ଲମ୍ବର ପ୍ରାଧାନ୍ୟ ଥାଏ। ଯଦିଓ ହିଷ୍ଟୋଗ୍ରାମ୍ ବାରମ୍ବାରତା ବିତରଣର ଚିତ୍ରଲେଖକ ଉପସ୍ଥାନା ପାଇଁ ବିସ୍ତୃତଭାବରେ ବ୍ୟବହୃତ ହୁଏ, ତଥାପି ଏହା ବାରମ୍ବାରତା ବିତରଣର ପ୍ରକାଶ୍ୟ ଅନ୍ତ ସଂଭାଗ ପାଇଁ ଅନୁପଯୁକ୍ତ ।
ସଂଭାଗ ବିସ୍ତାର ସମାନ ଥିବାବେଳେ ହିଷ୍ଟୋଗ୍ରାମ୍ର ଅଙ୍କନ – ଯେତେବେଳେ ସଂଭାଗ ବିସ୍ତାର ସମାନ ରହେ, ଆୟତକାର କ୍ଷେତ୍ରର ପ୍ରସୂ ସମାନ ରହେ ଓ ଲମ୍ବ ପରିବର୍ତ୍ତନ ହୋଇଥାଏ। ଆୟତକାର କ୍ଷେତ୍ରର ଲମ୍ବ ବା ଉଚ୍ଚତା ବାରମ୍ବାରତା ସହିତ ସମାନୁପାତୀ ହୋଇଥାଏ।

ସଂଭାଗ ବି ସ୍ତାର ଅସମାନ ଥିବାବେଳେ ହିଷ୍ଟୋଗ୍ରାମ୍ ଅଙ୍କନ ଯେତେବେଳେ ସଂଭାଗ ବିସ୍ତ।ର ଅସମାନ ହୁଏ, ଆୟତକାର କ୍ଷେତ୍ରର ପ୍ରସ୍ଥ ପରିବର୍ତ୍ତନ ହୁଏ ଓ ଆୟତକାର କ୍ଷେତ୍ରଗୁଡ଼ିକର ଲମ୍ବ ବା ଉଚ୍ଚତା ସମନ୍ବିତ ବାରମ୍ବାରତା ସହିତ ସମାନୁପାତୀ ହୋଇଥାଏ ।


ସମାଧାନ – ଯେହେତୁ ସଂଭାଗ ବିସ୍ତାର ଗୁଡ଼ିକ ଅସମାନ, ତେଣୁ ସମନ୍ବିତ ବାରମ୍ବାରତା ନିର୍ଣ୍ଣୟ କରିବାକୁ ହେବ ନଚେତ୍ ହିଷ୍ଟୋଗ୍ରାମ୍ ଭ୍ରମାତ୍ମକ ଧାରଣା ଦେବ ।
ପରିକଳ୍ପିତ ସମାନ ସଂଭାଗ ବିସ୍ତାର = ୧୦
ପ୍ରକୃତ ସଂଭାଗ = ୪୦ – ୬୦
ଏବଂ ପ୍ରକୃତ ସଂଭାଗ ବିସ୍ତାର ୬୦ – ୪୦ = ୨୦
ସଂଭାଗର ବାରମ୍ବାରତା = ୧୬
ସମନ୍ବିତ ବାରମ୍ବାରତା = \(\frac{16 \times 10}{20}=8\)
ପୁନଶ୍ଚ, ପରିକଳ୍ପିତ ସମାନ ସଂଭାଗ ବିସ୍ତାର = ୧୦
ପ୍ରକୃତ ସଂଭାଗ ୬୦ – ୯୦ ଏବଂ ପ୍ରକୃତ ସଂଭାଗ ବିସ୍ତାର = ୯୦ – ୬୦ = ୩୦ ସଂଭାଗର ବାରମ୍ବାରତା = ୧୨
ସମନ୍ବିତ ବାରମ୍ବାରତା = \(\frac{12 \times 10}{30}=4\)