Odisha State Board CHSE Odisha Class 11 Math Notes Chapter 12 Conic Sections will enable students to study smartly.
CHSE Odisha 11th Class Math Notes Chapter 12 Conic Sections
When a plane cuts a cone in various angles the figure obtained are called conic sections. The conic sections are point, line, circle, parabola, hyperbola, ellipse etc.
Circle: A circle is the locus of all points in a plane that are equidistant from a given point.
- The given point is called the centre.
- The constant distance is called the radius.
(a) Equation of a circle:
(i) Equation of a circle with a given centre and radius:
The equation of a circle with centre at (h, k) and radius ‘r’ is (x – h)2 + (y – k)2 = r2
Note:
If the centre is at the origin the equation is: x2 + y2 = r2
(ii) Equation of a circle with given two ends of a diameter:
If A(x1, y2) and B(x2, y2) are two ends of diameter then the equation of the circle is (x – x1)(x – x2) + (y – y1)(y – y2) = 0
(iii) General form of the equation of a circle:
The general form of equation of a circle is: x2 + y2 + 2gx + 2fy + c = 0
![]()
Note:
1. The above equation is the equation of circle if g2 + f2 – c > 0.
2. If g2 + f2 – c = 0 the circle reduces to a point called point circle.
3. Centre of the circle is at (-g, -f) and radius is r = \(\sqrt{g^2+f^2-c}\).
(b) Position of a point with respect to a circle:
If C is the centre, r is the radius of a circle and S is any point on that plane.
- CS = r ⇒ S lies on the circle.
- CS > r ⇒ S lies outside the circle.
- CS < r ⇒ S lies inside the circle.
(c) Length of intercept on axes:
The length of intersepts made by the circle x2 + y2 + 2gx + 2fy + c = 0
⇒ x-intercept = 2\(\sqrt{\mathrm{g}^2-\mathrm{c}}\), y-intercept = 2\(\sqrt{\mathrm{f}^2-\mathrm{c}}\)
(d) Tangents and normals to a circle:
(1) Equation of the tangent to the circle:
x2 + y2 + 2gx + 2fy + c = 0 at A(x1, y1) is xx1 + yy1 + g(x + x1) +f(y + y1) + c = 0
In particular the equation of tangent to x2 + y2 = r2 at A(x1, y1) is xx1 + yy1 = r2.
(2) Equation of normal to a circle:
Equation of the normal to the circle x2 + y2 + 2gx + 2fy + c = 0 at A(x1, y1) is : \(\frac{x-x_1}{x_1+g}=\frac{y-y_1}{y_1+f}\)
(3) Length of tangent:
Length of tangent from an external point A(x1, y1) to the circle x2 + y2 + 2gx + 2fy + c = 0 is \(A_m=\sqrt{x_1^2+y_1^2+2 g x_1+2 f y_1+c}\)
Condition of tangency:
The line y = mx + c will be a tangent to the circle x2 + y2 = a2 if c2 = a2(1 + m2)
Note:
(a) If c2 < a2(1 + m2) the line is a secant.
(b) If c2 > a2(1 + m2) the line does not intersect the line.
(c) The line y = mx ± a\(\sqrt{1+\mathrm{m}^2}\) is always a tangent to the circle x2 + y2 = a2
(d) The line lx + my + n = 0 is a tangent to the circle x2 + y2 + 2gx + 2fy + c = 0 if (lg + mf – n)2 = (l2 + m2)(g2 + f2 – c)
(e) Intersection of two circle:
Let two circle are
S1 = x2 + y2 + 2g1x + 2f1y + c1 = 0 ….(1)
S2 = x2 + y2 + 2g2x + 2f2y + c2 = 0 ….(2)
Two circles will touch each other
(i) internally if C1C2 = |r1 – r2|
(ii) Externally if C1C2 = |r1 + r2|
where C1 = Centre of first circle
C2 = Centre of second circle
r1 = Centre of first circle
r2 = Centre of second circle
⇒ Two circles intersect each other if C1C2 < r1 + r2.
⇒ Two circles do not intersect or touch each other if C1C2 > r1 + r2.
(f) Angle between two circles:
If two circle
S1 = x2 + y2 + 2g1x + 2f1y + c1 = 0
S2 = x2 + y2 + 2g2x + 2f2y + c2 = 0 intersect each other at ‘P’ the angle between them
(1) The angle between their tangents at P.
(2) The angle between their normals at P.
(3) Angle between C1P and C2P.
∴ The angle ‘θ’ between two intersecting circles is given by
cos θ = \(\frac{\left(C_1 P\right)^2+\left(C_2 P\right)^2-\left(C_1 C_2\right)^2}{2\left(C_1 P\right) \cdot\left(C_2 P\right)}\)
= \(\frac{2\left(\mathrm{~g}_1 \mathrm{~g}_2+\mathrm{f}_1 \mathrm{f}_2\right)-\mathrm{C}_1-\mathrm{C}_2}{2 \sqrt{\mathrm{g}_1^2+\mathrm{f}_1^2-\mathrm{C}_1} \sqrt{\mathrm{g}_2^2+\mathrm{f}_2^2-\mathrm{C}_2}}\)
![]()
Note:
Two circle are orthogonal if θ = \(\frac{\pi}{2}\) i,.e 2(g1g2 + f1f2) – c1 – c2 =0
(g) Family of circles:
Let S1 and S2 are two circles. The equation of all circles passing through the points of intersection of two circles is given by S1 + λS2 = 0 where λ ≠ -1 i,e., the equation of all circles passing through the intersection of two circles
x2 + y2 + 2g1x + 2f1y + c1 = 0 and x2 + y2 + 2g2x + 2f2y + c2 = 0 is given by (x2 + y2 + 2g1x + 2f1y +c1) + λ(x2 + y2 + 2g2x + 2f2y + c2)
(h) Radical axis:
The radical axis of two circles is the locus of point which moves so that the length of tangents drawn from it to two circles are equal.
(i) If two circles are
S1 = x2 + y2 + 2g1x + 2f1y + c1 = 0
S2 = x2 + y2 + 2g2x + 2f2y + c2 = 0 the equation of radical axis of S1 and S2 is: S1 – S2 = 0
⇒ 2(g1 – g2)x + 2(f1 – f2)y + (c1 – c2) = 0
(ii) Properties of radical axis:
- The radical axis of two circle is perpendicular to the line joining their centres.
- If two circles touch each other then their common tangent is the radical axis.
- If two circles intersect each other the line passing through their point of intersection is the radical axis.
- If two circles neither touch nor intersect then the radical axis is the perpendicular bisector of the line segment joining two centres.
- The radical axis of three circles taken in pairs are concurrent that point of concurrency is known as Radical centre of three circles.
(i) Co-axial system of circles:
A system of circles is said to be coaxial if each pair of circles have same radical axis.
(i) Equation of co-axial system of circles:
- If the radical axis is y-axis i.e x = 0 and the line containing the centres is x-axis i.e y = 0 then the equation of the co-axial system of the circle is x2 + y2 + 2gx + 2fy + c = 0, g2 > c …(1) hence g is the parameter and c is a constant.
- If the radical axis is x-axis i.e y = 0 and the line containing centres is y-axis i.e x = 0 then the equation of co-axial system of circles is x2 + y2 + 2gx + 2fy + c = 0, f2 > c …(1)
- The equation of the family of circles co-axial with S1 and S2 = 0 is S1 + λS2 = 0.
(ii) Limiting points of a co-axial system:
The limiting points of the co-axial system (1) are at (±√c, 0) for c > 0 and for (2) the limiting points are (0 ± √c)
(iii) Intersecting and non-intersecting system of co-axial circles:
If the co-axial system of circles intersects the radical axis then it is an intersecting co-axial system. Otherwise, the system is a non-intersecting co-axial system.
(j) Parametric form of the equation of a circle:
The parametric equation of the (x – h)2 + (y – k)2 = r2 is x = h + r cos θ, y = k + r sin θ.
![]()
Parabola:
A parabola is the locus of all points in a plane such that the distance of every point from a fixed point is equal to its distance from a fixed-line.
- The fixed point is the focus.
- The fixed line is the Directrix.
- The line through focus and perpendicular to the directrix is the Axis.
- The point where the parabola intersects axis is its Vertex.
- Any chord passing through focus is the focal chord.
- The focal chord perpendicular to axis is called the Latusrectum.
(a) Equation of parabola.
(i) Equation of a parabola with vertex at (0, 0) axis along x-axis, with focus at (a, 0) is y2 = 4ax
(ii) Equation of parabola with vertex at (0, 0) and axis along y-axis with focus (0, a) is: x2 = 4ay
(iii) Equation of the parabola with vertex at (h, k) and axis parallel to x-axis is: (y – k)2 = 4a(x – h)
(iv) Equation of the parabola with vertex at (h, k) and axis parallel to y-axis is: (x – h)2 = 4a(y – k)
(v) parametric form of the equation of parabola y2 = 4ax is: x = at2, y = 2at
Some Information About Parabola:
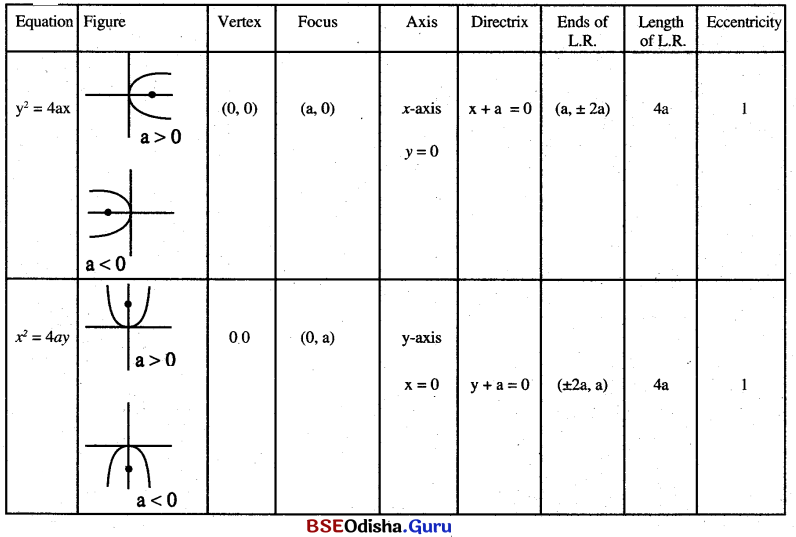
(b) Tangents and normals to parabola
(i) Equation of tangent to the parabola y2 = 4ax at (x, y1) is: yy1 = 2a(x + x1)
(ii) Equation of tangent to the parabola y2 = 4ay at (x1, y1) is: xx1 = 2a(y + y1)
(iii) Equation of normal to y2 = 4ax at (x1, y1) is: 2ax – yy1 + 2ax1 = 0
(iv) y = mx + c will be a tangent to y2 = 4ax if c = \(\frac{\mathrm{a}}{\mathrm{m}}\)
(v) y = mx + c will be a tangent to x2 = 4ax if c = -am2
Ellipse:
An ellipse is the locus of all points in a plane such that the sum of the distances of any point on it form two fixed points in the plane is a constant.
- The fixed points are foci.
- Mid point of the line segment joining two foci is the centre
- The line joining two foci is the major axis
- The line perpendicular to the transverse axis at the centre is the minor axis
- The points at which the ellipse intersect the major axis are the vertices.
Equation of ellipse:
Equations of ellipse in standard form is:

Some Information About Ellipse:
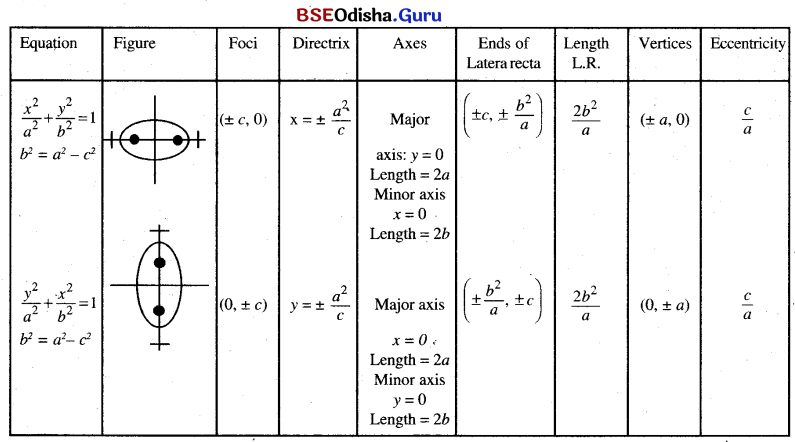
(b) Tangents and normals to ellipse:
- Equation of tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 at (x1, y1) is \(\frac{x x_1}{a^2}+\frac{y y_1}{b^2}\) = 1
- The line y = mx + c will be a tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 if c2 = a2m2 + b2
- Parameteric form of equation of ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 is x = a cos θ, y = b sin θ.
Hyperbola:
A hyperbola is the locus of all points in a plane such that the difference of distances of any point on it from two fixed points is constant.
- The fixed points are foci.
- Mid point of the line segment joining two foci is the centre.
- The line joining two foci is the transverse axis.
- The line perpendicular to transverse axis and passing through the centre is the conjugate axis.
![]()
Some Information About Hyperbola:
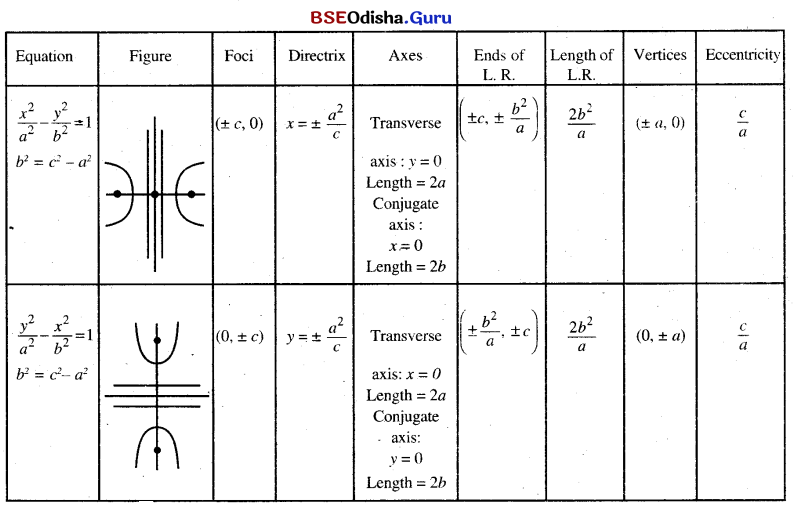
(a) Equation of hyperbola

x = h + a sec θ, y = k + b tan θ.
(b) Tangents and normals to hyperbola:
(i) Equation of a tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 at (x1, y1) is \(\frac{x x_1}{a^2}-\frac{y y_1}{b^2}\) = 1
(ii) y = mx + c is a tangent to the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 if c2 = a2m2 – b2.
