Odisha State Board CHSE Odisha Class 11 Math Notes Chapter 13 Introduction To Three-Dimensional Geometry will enable students to study smartly.
CHSE Odisha 11th Class Math Notes Chapter 13 Introduction To Three-Dimensional Geometry
Coordinates Of A Point In Space:
In three-dimensional geometry three mutually perpendicular planes divide the space into eight equal parts. Each equal part is an octant.
(i) Sign of coordinate of a point in various octants.
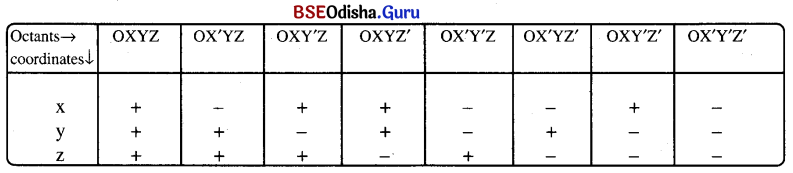
(ii) Location of a point at 3D
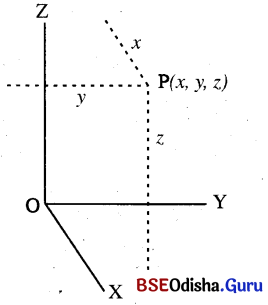
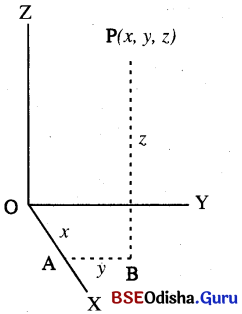
Note:
(1) Coordinate of a point on x-axis is (x, 0, 0).
(2) Coordinate of a point on y-axis is (y, 0, 0).
(3) Coordinate of a point on z-axis is (y, 0, 0).
(4) Distance of a point (a, b, c) from x-axis = \(\sqrt{\mathrm{b}^2+\mathrm{c}^2}\)
(5) Distance of a point (a, b, c) from y-axis = \(\sqrt{\mathrm{a}^2+\mathrm{c}^2}\)
(6) Distance of a point (a, b, c) from z-axis = \(\sqrt{\mathrm{a}^2+\mathrm{b}^2}\)
Distance formula:
Distance between two points A(x1, y1, z1) and B(x2, y2, z2) = \(\sqrt{\left(\mathrm{x}_2-\mathrm{x}_1\right)^2+\left(\mathrm{y}_2-\mathrm{y}_1\right)^2+\left(\mathrm{z}_2-\mathrm{z}_1\right)^2}\)
![]()
Division Formula (Section Formula):
(i) Internal division:
If R(x, y, z) divides the join of A(x1, y1, z1) and B(x2, y2, z2) in ratio m: n internally then
\(\mathrm{x}=\frac{\mathrm{mx} \mathrm{x}_2+\mathrm{nx} \mathrm{x}_1}{\mathrm{~m}+\mathrm{n}}, \mathrm{y}=\frac{\mathrm{my} \mathrm{y}_2+\mathrm{ny} \mathrm{y}_1}{\mathrm{~m}+\mathrm{n}}\), \(\mathrm{z}=\frac{\mathrm{mz} \mathrm{z}_2+\mathrm{nz} \mathrm{z}_1}{\mathrm{~m}+\mathrm{n}}\)
(ii) External division:
If R divides AB in ratio m: n externally then \(x=\frac{m x_2-n x_1}{m-n}\), \(y=\frac{m y_2-n y_1}{m-n}, \frac{m z_2-n z_1}{m-n}\)
(iii) Midpoint formula:
If R is the midpoint of AB then

