Odisha State Board CHSE Odisha Class 11 Math Notes Chapter 4 Trigonometric Functions will enable students to study smartly.
CHSE Odisha 11th Class Math Notes Chapter 4 Trigonometric Functions
Angle:
If A, B, and C are three non-collinear points, then ∠ABC = \(\overrightarrow{\mathrm{BA}} \cup \overrightarrow{\mathrm{BC}}\)
\(\overrightarrow{\mathrm{BA}}\) is the initial side, \(\overrightarrow{\mathrm{BC}}\) is called the terminal side and B is called the vertex of the angle.
Positive and negative angles:
If the direction of rotation is anti-clockwise then the angle is positive and if the direction of rotation is clockwise then the angle is negative.
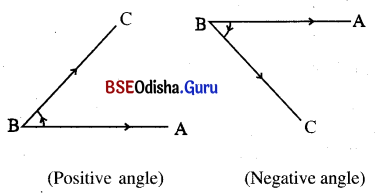
Measure of an angle:
(a) Sexagesimal system or English System (Degree measure):
1 degree = 1° = \(\left(\frac{1}{360}\right) \text { th }\) of revolution from initial side to terminal side.
- One revolution = 360°
- 1° = 60′ (sixty minute)
- 1′ = 60” (sixty seconds)
(b) Circular system(Radian measure):
One radian = 1c = The angle at the centre of the circle by an arc where the arc length equals to
Note:
(i) θ = \(\frac{l}{r}=\frac{\text { arc }}{\text { radius }}\) where θ is an radian.
(ii) θ in radian is created as a real number.
(c) Relation between Degree and radian measure:
- 2π radians = 360°
⇒ π radian = 180° - We can convert radian to degree or degree to radian by using the identity.
\(\frac{\mathrm{D}}{180}=\frac{\mathrm{R}}{\pi}\) where D is the degree measure and R is the radian measure of an angle.
![]()
Trigonometry Functions:

(i) Sign of trigonometry functions:
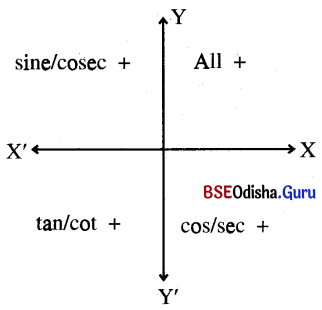
(ii) \(\begin{array}{cccc}
\text { Add } & \text { Sugar } & \text { To } & \text { Coffee } \\
\downarrow & \downarrow & \downarrow & \downarrow \\
\text { all }+ & \sin + & \tan + & \cos +
\end{array}\)
(iii) Periodicity of trigonometry functions:
| Trigonometric function | Period |
| sin x | 2π |
| cos x | 2π |
| tan x | π |
| cot x | π |
| sec x | 2π |
| cosec x | 2π |
| sin2 x or cos2 x | π |
| |sin x| or |cos x| | π |
Trigonometric functions of some standard angles
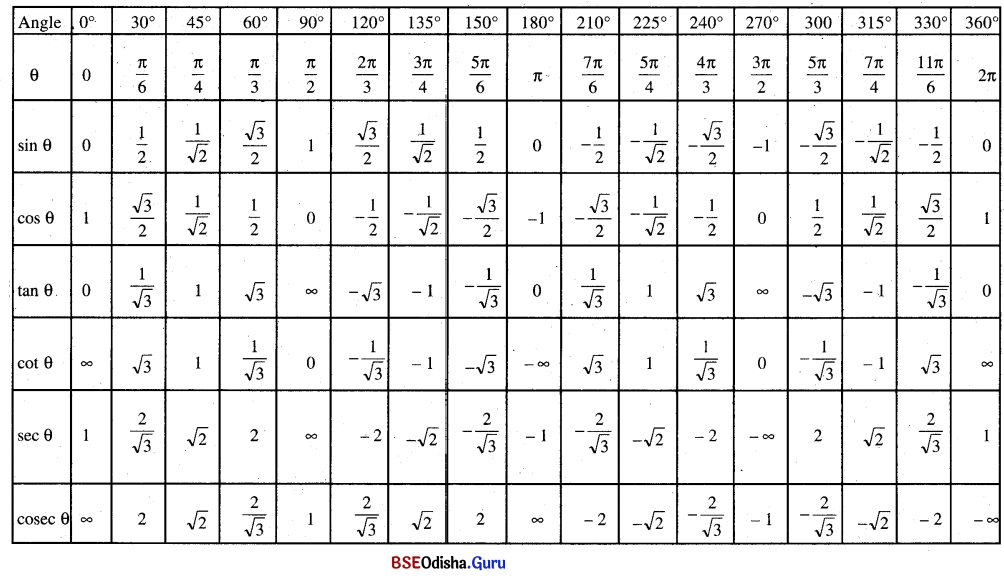
Fundamental trigonometric identities:
(a) sin θ = \(\frac{1}{{cosec} \theta}\)
(b) cos θ = \(\frac{1}{{sec} \theta}\)
(c) tan θ = \(\frac{1}{{cot} \theta}\)
(d) sin2 θ + cos2 θ = 1
(e) sec2 θ – tan2 θ = 1
(f) cosec2 θ – cot2 θ = 1
(g) sin (-θ) = -sin (θ)
(h) cos (-θ) = -cos (θ)
Trigonometric functions of allied angles:
(a) sin \(\left((2 n+1) \frac{\pi}{2} \pm \theta\right)\) = (±) cos θ choose + or – in (±) by using ASTC rule
(b) cos \(\left((2 n+1) \frac{\pi}{2} \pm \theta\right)\) = (±) sin θ choose + or – in (±) by using ASIC rule
Similar technique can be used for other trigonometric functions.
(c) sin (nπ ± θ) = (±) sin θ
cos (nπ ± θ) = (±) cos θ
tan (nπ ± θ) = (±) tan θ
choose + or – in (±) by using ASTC rule.
Sum And Difference Formulae:
(a) sin(A + B) = sin A . cos b + cos A . sin B
(b) sin(A – B) = sin A . cos B – cos A . sin B
(c) cos(A + B) = sin A . cos B – cos A . sin B
(d) cos(A – B) = sin A . cos B + cos A . sin B
(e) tan(A + B) = \(\frac{\tan A+\tan B}{1-\tan A \cdot \tan B}\)
(f) tan(A – B) = \(\frac{\tan A-\tan B}{1+\tan A \cdot \tan B}\)
(g) cot(A + B) = \(\frac{\cot A \cdot \cot B-1}{\cot A+\cot B}\)
(h) cot(A – B) = \(\frac{\cot A \cdot \cot B+1}{\cot A-\cot B}\)
(i) sin(A + B) + sin (A – B) = 2 sin A . cos B
(j) sin (A + B) – sin(A – B) = 2 cos A . sin B
(k) cos(A + B) + cos(A – B) = 2 cos A . cos B
(l) cos(A + B) – cos(A – B) = -2sin A . sin B
(m) sin(A + B) sin(A – B) = sin2 A – sin2 B = cos2 B – cos2 A
(n) cos(A + B) cos(A – B) = cos2 A – sin2 B = cos2 B – sin2 A
(o) sin 2A = 2 sin A cos A = \(\frac{2 \tan \mathrm{A}}{1+\tan ^2 \mathrm{~A}}\)
(p) cos 2A = cos2 A – sin2 A
= 2 cos2 A – 1
= 1 – 2 sin2 A
= \(\frac{1-\tan ^2 \mathrm{~A}}{1+\tan ^2 \mathrm{~A}}\)
(q) tan 2A = \(\frac{2 \tan A}{1-\tan ^2 A}\)
(r) tan(A + B + C) = \(\frac{\tan A+\tan B+\tan C-\tan n A \cdot \tan B \cdot \tan C}{1-\tan A \cdot \tan B-\tan B \cdot \tan C-\tan C \cdot \tan A}\)
(s) sin 3A = 3 sin A – 4 sin3 A
= 4 sin A sin(\(\frac{\pi}{3}\) – A) sin(\(\frac{\pi}{3}\) + A)
(t) cos 3A = 4 cos3 A – 3 cos A
= 4 cos A cos(\(\frac{\pi}{3}\) – A) cos(\(\frac{\pi}{3}\) + A)
(u) tan 3A = \(\frac{3 \tan A-\tan ^3 A}{1-3 \tan ^2 A}\)
= tan A. tan(\(\frac{\pi}{3}\) – A) tan(\(\frac{\pi}{3}\) + A)
![]()
Sum or Difference → Product:
(a) sin A + sin B = 2 sin(\(\frac{A+B}{2}\)) cos(\(\frac{A-B}{2}\))
(b) sin A – sin B = 2 cos(\(\frac{A+B}{2}\)) cos(\(\frac{A-B}{2}\))
(c) cos A + cos B = 2 cos(\(\frac{A+B}{2}\)) cos(\(\frac{A-B}{2}\))
(d) cos A – cos B = -2 sin(\(\frac{A+B}{2}\)) sin(\(\frac{A-B}{2}\))
Submultiple Arguments:
(a)

(b) 2 sin2 \(\frac{\theta}{2}\) = 1 – cos θ
2 cos2 \(\frac{\theta}{2}\) = 1 + cos θ
(c) tan \(\frac{\theta}{2}\) = \(\frac{\sin \theta}{1+\cos \theta}=\frac{1-\cos \theta}{\sin \theta}\)
(d) sin θ = 3 sin \(\frac{\theta}{2}\) – 4 sin3 \(\frac{\theta}{2}\)
cos θ = 4 cos3 \(\frac{\theta}{2}\) – 3 cos \(\frac{\theta}{2}\)
(e) tan θ = \(\frac{3 \tan \frac{\theta}{2}-\tan ^3 \frac{\theta}{2}}{1-3 \tan ^2 \frac{\theta}{2}}\)
Trigonometric Equations:
(a) Equation involving trigonometric equations of unknown angles are called trigonometric function.
(b) Principle solution: The solution ‘x’ of a trigonometric equation is said to be a principle solution if x ∈ (0, 2π)
(c) The solution considered over the entire set R are called the general solution.
(d) General solution of some standard trigonometric equations.
- sin x = 0 ⇒ x = nπ, n ∈ Z
- cos x = 0 ⇒ x = (2n + 1) \(\frac{\pi}{2}\), n ∈ Z
- tan x = 0 ⇒ x = nπ, n ∈ Z
- sin x = sin α ⇒ x = nπ + (-1)n, n ∈ Z
- cos x = cos α ⇒ x = 2nπ ± α, n ∈ Z
- tan x = tan α ⇒ x = nπ + α, n ∈ Z
- \(\left.\begin{array}{l}
\sin ^2 x=\sin ^2 \alpha \\
\cos ^2 x=\cos ^2 \alpha \\
\tan ^2 x=\tan ^2 \alpha
\end{array}\right]\) ⇒ x = nπ ± α - \(\left.\begin{array}{l}
\cos x=\cos \alpha \\
\text { and } \sin x=\sin \alpha
\end{array}\right]\) ⇒ x = nπ ± α, n ∈ Z
Sine Formula:
In any Δ ABC, \(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\) or, \(\frac{\sin \mathrm{A}}{a}=\frac{\sin \mathrm{B}}{b}=\frac{\sin \mathrm{C}}{c}\) = 2R
∴ a = 2R sin A, b = 2R sin B and c = 2R sin C
Also, sin A = \(\frac{a}{2R}\), sin B = \(\frac{b}{2R}\) and sin c = \(\frac{c}{2R}\)
Cosine fromulae:
In any Δ ABC,
(i) a2 = b2 + c2 – 2bc cos A
(ii) b2 = c2 + a2 – 2ca cos B
(iii) c2 = a2 + b2 – 2ab cos C
or, → cos A = \(\frac{b^2+c^2-a^2}{2 b c}\)
→ cos B = \(\frac{c^2+a^2-a^2}{2 c a}\)
→ cos C = \(\frac{a^2+b^2-c^2}{2 a b}\)
Projection formulae:
In any Δ ABC,
(i) a = b sin C + c sin B
(ii) b = c cos A + a cos C
(iii) c = a cos B + b cos A
Tangent formulae (Napier’s Analogy);
In any Δ ABC

Area of Triangle (Heron’s formulae):
(i) Area of triangle ABC
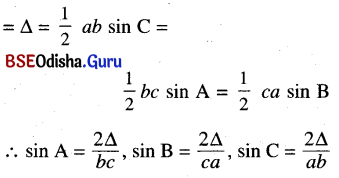
(ii) Heron’s formulae:
In any Δ ABC Let 2S = a + b + c
Area of Δ ABC = Δ = \(\sqrt{s(s-a)(s-b)(s-c)}\)
Δ = \(\frac{1}{2}\) bc sin A = \(\frac{1}{2}\) ca sin B
= \(\frac{1}{2}\) ab sin C, Δ = \(\frac{abc}{4R}\)
![]()
Semi-Angle Formulae:

