Odisha State Board Elements of Mathematics Class 11 CHSE Odisha Solutions Chapter 1 Mathematical Reasoning Ex 1(a) Textbook Exercise Questions and Answers.
CHSE Odisha Class 11 Math Solutions Chapter 1 Mathematical Reasoning Exercise 1(a)
Question 1.
Choose the correct answer from the given choices:
(i) Negation of ‘Paris is in France and London is in England’ is :
(A) Paris is in England and London is in France.
(B) Paris is not in France or Landon is not in England.
(C) Paris is in England or London is in France.
(D) Paris is not in France and London is not in England.
Solution:
(A) Paris is in England and London is in France.
(ii) The conditional (p ∧ q) → p is :
(A) a tautology
(B) a contradiction
(C) neither a tautology nor a contradiction
(D) none of these
Solution:
(A) a tautology
(iii) Which of the following is a contradiction?
(A) (p ∧ q) ∧ ~ (p ∧ q)
(B) p ∨ (~ p ∧ q)
(C) (p → q) → p
(D) None of these
Solution:
(A) (p ∧ q) ∧ ~ (p ∧ q)
![]()
(iv) Which of the following is logically equivalent to ~ (~ p → q)?
(A) p ∧ q
(B) p ∧ ~ q
(C) ~ p ∧ q
(D) ~ p ∧ ~ q
Solution:
(D) ~ p ∧ ~ q
(v) (~(~p) ∧ q) is equivalent to
(A) ~ p ∧ q
(B) p ∧ q
(C) p ∧ ~ q
(D) ~ p ∧ ~ q
Solution:
(B) p ∧ q
(vi) If p: It rains today, q: I go to school, r: I shall meet any friend, and s’: I shall go to a movie, then which of the following is the proposition.
If it does not rain or if I do not go to school, then I shall meet a friend and go to a movie.
(A) ∼ (p ∧ q) → (r ∧ s)
(B) ~ (p ∧ q) → (r ∧ s)
(C) ~ (p ∧ q) → (r ∨ s)
(D) None of these
Solution:
(A) ~ (p ∧ q) → (r ∧ s)
(vii) Which of the following is true?
(A) p → q ≡ (~p → ~q)
(B) ~ (p → ~ q) ≡ (~ p ∧ q)
(C) ~ (~p ~ q) ≡ (~ p ∧ q)
(D) ~ (p ↔ q) ≡ [~(p → q)∧~(q → p)]
Solution:
(C) ~ (~p ~ q) ≡ (~ p ∧ q)
(viii)The Inverse of the proposition p ∧ ~ q) → r is:
(A) ~ r (~ p ∨ q)
(B) ~ p ∨ q → ~ r
(C) r → (p ∧ ~q)
(D) None of these
Solution:
(B) ~p ∨ q → ~ r
(ix) The contrapositive of (p ∨ q) → r is
(A) r → (p ∨ q)
(B ) ~r → (p ∨ q)
(C) ~ r → (~p ∧ ~q)
(D) p → (q ∨ r)
Solution:
(C) ~ r → (~p ∧ ~q)
(x) Which of the following is inverse of the proposition: “If a number is a prime, then it is odd.
(A) if a number is not prime, then it is odd.
(B) if a number is not a prime, then it is not odd.
(C) if a number is not odd then it is not a prime.
(D) if a number is not odd, then it is a prime.
Solution:
(B) if a number is not a prime, then it is not odd.
Question 2.
Give examples, five in each case, of , sentences that are
(i) propositions
Solution :
Examples of a proposition:
(a) Rama is a boy.
(b) He is ten years old.
(c) He is reading in class six.
(d) He has 2 brothers and 3 sisters.
(e) 2 + 3 ≥ 5
![]()
(ii) not-propositions
Solution:
Examples of not-proposition:
(a) How old are you?
(b) What is he to you?
(c) Read mindfully.
(d) What a beautiful girl!
(e) May God offer you long life.
Question 3.
Illustrate the use of all connectives and the modified ‘not’ in five separate examples of propositions.
Solution:
Conjunction: Hari and Madhu are two friends.
Disjunction: Hari or Madhu stand first in their class.
Implication: If I will be the king, then I will make you my queen.
Double Implication: I will love you if you will love me.
Negation: I don’t like her.
Question 4.
Try to construct an example of a proposition involving all connectives and also the modifier ‘not’.
Solutions:
If she do not come and take my help, then she neither understands the problem nor solves them but she can create other problems.
Question 5.
Which of the following sentences are propositions and which are not? Write with reasons :
(i) 2 < 5.
(ii) Is 9 < 3?
(iii) x is greater than 100.
(iv) Why are you crying?
(v) May God grant you long life.
(vi) Cuttack is a big city.
(vii) It is possible that there is life on Mars.
(viii)Ram is a friend of Hari.
(ix) x2 – x + 1=0
(x) Oh! What scenery!
(xi) You must go to school every day.
(xii) It was raining yesterday.
Solution:
(i) 2 < 5 is a proposition, as it is true.
(ii) Is 9 < 3? Is not a proposition, as it is neither true nor false.
(iii) “x is greater than 100” is not a statement as x is not defined.
(iv) Why are you crying? Is not a statement as it is neither true nor false.
(v) “May God grant you long life” is not a statement as it is neither true nor false.
(vi) “Cuttack is a big city” is not a statement, as it contains the word ‘big’ (not defined).
(vii) “It is possible that there is life on Mars” is not a proposition. (To date it is not confirmed)
(viii)Ram is a friend of Hari. It is a statement as it is true or false.
(ix) “x2 – x + 1 = 0” is not a statement as ‘x’ is not defined.
(x) Oh! What scenery! It is not a statement as it is neither true nor false.
(xi) You must go to school every day. It is not a statement as it is neither true nor false.
(xii) It was raining yesterday. It is not a proposition as it is not known to which day yesterday means.
Question 6.
Write down negations of each of the following.
(i) If you read, you will pass.
(ii) John is a friend of Thomas.
(iii) Fifteen is greater than five.
(iv) Either Pramod is clever or he is laborious.
(v) Money is necessary for happiness.
(vi) It is raining and Mahanadi is flooded.
(vii) Pen is might than a sword.
(viii) |x| is equal to either x or – x.
(ix) It is raining and it is cool.
(x) 3 + 6 > 8 and 2 + 3 < 6.
Solution:
(i) It is not true that if you read, you will pass.
(ii) John is not a friend of Thomas.
(iii) Fifteen is not greater than five.
(iv) Pramod is not clever and also not laborious.
(v) Money is not necessary for happiness.
(vi) It is neither raining nor Mahanadi is flooded.
(vii) Pen is not more mighty than a sword.
(viii) |x| is neither x nor – x
(ix) It is not raining or it is not cool.
(x) 3 + 6 ≤ 8 or 2+ 3 ≥ 6.
![]()
Question 7.
Translate the following propositions into symbolic form, stating the prime components in each case.
(i) If you do not work hard, you will repent.
(ii) Jamini will be rewarded if and only if he is punctual.
(iii) If there is a will, there is a way.
(iv) Time and tide wait for none.
(v) 29 is a prime number which is a sum of two squares.
(vi) Life is short, but virtue is lasting.
(vii) If the boy is poor, then he will be hungry and if he is hungry, then he cannot be honest.
(viii) A year consists of twelve months while a month does not consist of more than thirty-one days.
(ix) If the government cannot solve the unemployment problem, then public opinion will rise against it which will lead to a strengthening
of opposition.
(x) Chinu and Minu went to Calcutta, but Minu came back earlier since she lost all her money
Solution:
(i) Let p: You work hard, q: you will repent. Then the given statement is ~ p → q.
(ii) Let p: Jamini will be rewarded, q: He is punctual. The given statement is p ↔ q.
(iii) Let p: There is a will, q: There is a way.
∴ The given statement is p → q.
(iv) Let p: Time waits for none. q: Tide waits for none.
∴ Solution is p ∧ q.
(v) Let p: 29 be a prime number. q: It is a sum erf two squares
∴ Solution is p ∧ q.
(vi) Let p: Life is short. q: Virtue is lasting.
Solution is q ∧ q.
(vii) Let p: The boy is poor. q: He will be hungry. r: He can be honest.
Solution is (p → q) ∧ (q → ~r)
(viii) Let p: A year consists of twelve 9. months. q: A month consists of more than 31 days.
∴ Solution is p ∧ ~ q.
(ix) Let p: The Government can solve the unemployment problem. q: Public opinion will rise against it. r: It will lead to a strengthening
of opposition.
∴ Solution is (p → q) → r.
(x) Let p: Chinu went to Calcutta. q: Minu went to Calcutta. r: Minu came back earlier. s: She lost all her money.
Solution is (p ∧ q) ∧ (s → r).
Question 8.
Let p, q, and r denote respectively the statements: “you are honest”, “you are laborious” and “you will receive a promotion”, Translate the following statements into English language :
(i) (p ∨ q) → r
(ii) ~ r → ~ p
(iii) ~ (p ∨ q) → ~ r
(iv) |r ∨ (~ p)| → ~ q
(v) p ∧ q ∧ r
Solution:
Let p: You are honest. q: You are laborious. r: You will receive a promotion.
(i) (p ∨ q) → r. It’s the English language is “If you are honest or laborious then you will receive a promotion.”
(ii) If you will not receive a promotion, then you are not honest.
(iii) If you are neither honest nor laborious then you will not receive a promotion.
(iv) If you will receive a promotion or you are not honest then you are not, laborious.
(v) You are honest and laborious and you will receive a promotion.
![]()
Question 9.
Construct truth tables for the following and indicate which of these are tautologies :
Solution:
(i) p ∧ q → p ∨ q
| p | q | p ∧ q | p ∨ q | p ∧ q ∧ p ∨ q |
| T | T | T | T | T |
| T | F | F | T | T |
| F | T | F | T | T |
| F | F | F | F | T |
∴ It is a tautology.
(ii) p ∧ q → p
Solution:
| p | q | p ∧ q | p ∧ q → p |
| T | T | T | T |
| T | F | F | T |
| F | T | F | T |
| F | F | F | T |
∴ It is a tautology.
(iii) p ∧ (p → q) → q
Solution:
| p | q | p → q | p ∧ (p → q) | p ∧ (p → q) → q |
| T | T | T | T | T |
| F | T | T | F | T |
| T | F | F | F | T |
| F | F | T | F | T |
∴ It is a tautology.
(iv) p → p ∧ q
Solution:
| p | q | p ∧ q | p → (p ∧ q) |
| T | T | T | T |
| T | F | F | F |
| F | T | F | T |
| F | F | F | T |
∴ It is a not tautology.
(v) p → (~p → q)
Solution:
| p | q | ~p | ~p → q | p → (~p → q) |
| T | T | F | T | T |
| T | F | F | T | T |
| F | T | T | T | T |
| F | F | T | F | T |
∴ It is a tautology.
(vi) ~p ∧ (p ∧ q) → q
Solution:

∴ It is a tautology.
(vii) (p ∨ ~q) ∧ (q ∨ ~p)
Solution:
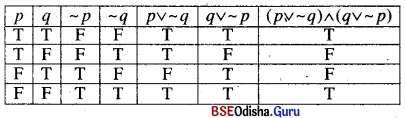
∴ It is a not tautology.
(viii) p → (~ q ∧ r)
Solution:
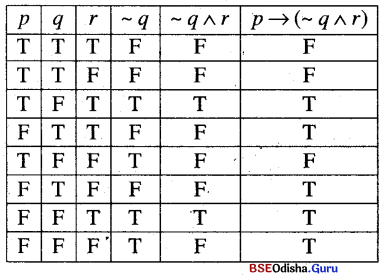
∴ It is a not tautology.
(ix) (p → q) → [(q → r) → (p → r)]
Solution:
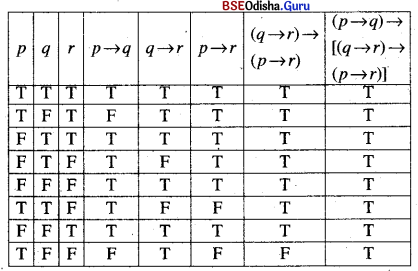
∴ It is a tautology.
(x) p ∨ → ~(p ∧ q)
Solution:
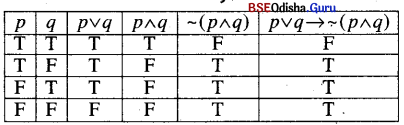
∴ It is a not tautology.
(xi) (p → ~p) → ~p
Solution:
| P | ~p | p → ~p | (p → ~p) → ~p |
| T | F | F | T |
| F | T | T | T |
∴ It is a tautology.
(xii) (~ p ∨ p) → (~ q ∨ q)
Solution:
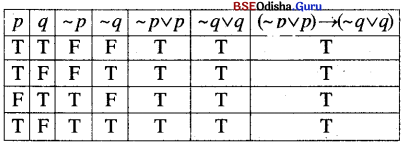
∴ It is a tautology.
(xiii) (p ∧ q) → p) → q
Solution:
| p | q | p ∧ q | (p ∧ q) → p | ((p → q) → p) → q |
| T | T | T | T | T |
| T | F | F | T | F |
| F | T | F | T | T |
| F | F | F | T | F |
∴ It is a not tautology.
(xiv) (p ↔ q) ∧ (q ↔ r) → (p ↔ r)
Solution:

∴ It is a tautology.
(xv) [p → (p ∨ q)] → [q → (p ∧ q)]
Solution:

Question 10.
If p has truth value T, what can be said about the truth values of
(i) ~p ∧ q → p ∨ q
Solution:
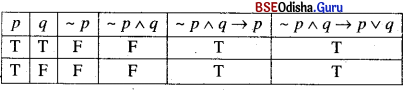
∴ ~p ∧ q → p v q is always true if p is true.
(ii) p ∨ q → ~p ∧ q
Solution:

∴ p ∨ q → ~ p ∧ q is always false it is true.
![]()
Question 11.
Determine the truth values of p ↔ ~ q when the biconditional p ↔ q has truth value (i) F, (ii) T.
Solution:
| p | q | -q | p ↔ q | p ↔ ~q |
| T | T | F | T | F |
| T | F | T | F | T |
| F | T | F | F | T |
| F | F | T | T | F |
(i) When p ↔ q is False, p ↔ ~ q is True.
(ii) ∴ When p ↔ q is True, p ↔ ~q is False.
Question 12.
State the converse, inverse and contra-positive of each of the following propositions. Stating it as a conditional, wherever necessary.
(i) If A ABC is equilateral, then its three angles are congruent.
Solution:
If A ABC is equilateral, then its three angles are congruent.
Converse: If the three angles of the A ABC are congruent, then it is equilateral.
Inverse: If A ABC is not equilateral, then its three angles are not congruent.
Contrapositive: If the three angles of the A ABC are not congruent, then it is not equilateral.
(ii) If Gopal is clever, then he is rich.
Solution:
Con: If Gopal is rich, then he is clever.
Inv.: If Gopal is not clever, then he is not rich.
Cont: If Gopal is not rich, then he is not clever.
(iii) p → ~ q
Solution:
p → ~ q
Con: ~ q → p
Inv: ~ p → q
Cont: q → ~ p
(iv) Sum of two odd integers is even.
Solution:
If two integers are odd, then their sum is even.
Con: If the sum of two integers is even, then they are odd.
Inv: If two integers are not odd, then their sum is not even.
Cont: If the sum of two integers is not even then they are not odd.
(v) The square of an integer is a natural number.
Solution:
If a number is an integer, then its square is a natural number.
Con: If the square of a number is a natural number, then it is an integer.
Inv: If a number is not an integer, then its square is not a natural number.
Cont: If the square of a number is not a natural number then it is not an integer.
(vi) A parallelogram that is inscribed in a circle is a rectangle.
Solution:
If a parallelogram is inscribed in a circle, then it is a rectangle.
Con: If a parallelogram is a rectangle, then it is inscribed in a circle.
Inv: If a parallelogram is not inscribed in a circle then it is not a rectangle.
Cont: If a parallelogram is not a rectangle, then it is not inscribed in a circle.
(vii) The ground being wet, there has been rainfall at night.
Solution:
If the ground being wet then there has been rainfall at night.
Con: If there has been rainfall at night then the ground being wet,
Inv: If the ground is not wet then there has been no rainfall at night.
Con: If there has been no rainfall at night then the ground is not wet.
Question 13.
Are the following pair of statements negation of each other?
(i) The number π is not a rational number.
(ii) The number π is not an irrational number.
(iii) The number π is a rational number. The number π is an rational number.
Solution:
(i) No (ii) Yes
![]()
Question 14.
Write the component statement of the following compound statements and check whether the compound statement is true or false.
(i) 24 is a multiple of 4 and 6
(ii) The school is closed if there is a holiday or a Sunday.
(iii) 7 is a rational number or an irrational number.
(iv) 57 is divisible by 2 or 3.
(v) All things have two eyes and two legs.
(vi) 2 is an even number and a prime number.
(vii) Every parallelogram is a trapezium or a rhombus.
Solution:
(i) The component statement is
p: 24 is a multiple of 4
q: 24 is a multiple of 6
The truth value of the statement is ‘True’
(ii) The component statements are :
p: There is a holiday or a Sunday
q: The School is closed
The truth value of the compound statement is ‘True’.
(iii) The component statements are
p: 7 is a rational number
q: 7 is an irrational number
The truth value of the compound statement is ‘True’.
(iv) The component statements are
p: 57 is divisible by 2
q: 57 is divisible by 3
The truth value of the compound statement is ‘True’.
(v) The component statements are
p: All things have two eyes.
q: All things have two eyes
The truth value of the compound statement is ‘false’
(vi) The component statements are
p: 2 is an even number
q: 2 is a prime number
The truth value of the compound statement is ‘ True.
(vii) The component statements are
p: Every parallelogram is a trapezium
q: Every parallelogram is a rhombus.
The truth value of the compound statement is “false”.
Question 15.
Identify the Quantifiers of the following statements.
(i) There exists a number that is equal to its square.
(ii) For every real number x, x is less than x + 1.
(iii) There exists a capital for every state of India.
(iv) For all x ∈ R , sin2 x + cos2 x = 1
(v) There exists an even prime number other than 2.
(vi) For every negative integer x, x3 is also a negative integer.
(vii) For every real number x, x2 ≠ x.
Solution:
(i) There exists
(ii) for every
(iii) There exists
(iv) for all
(v) There exists
(vi) for every
(vii) for every
![]()
Question 16.
Write the negation of the following statement.
(i) Every living person is not 150 years old.
(ii) There exists x∈ N, x + 3 ≠ 10
(iii) All the students completed their homework.
(iv) There exists a number that is equal to its square.
(v) For every real number x, x + 4 is greater than x.
(vi) Everyone who lives in India is an Indian.
Solution:
(i) There exists a living person who is 150 years old.
(ii) for all x ∈ N, x + 3 ≠ 10
(iii) There exists a student who has not completed his homework.
(iv) Each number is not equal to its square.
(v) There exists a real number x, x + 4 is not greater than x.
(vi) There exists a person who lives in India but is not an Indian.
