Odisha State Board Elements of Mathematics Class 11 CHSE Odisha Solutions Chapter 1 Mathematical Reasoning Ex 1(b) Textbook Exercise Questions and Answers.
CHSE Odisha Class 11 Math Solutions Chapter 1 Mathematical Reasoning Exercise 1(b)
Question 1.
Check the validity of the following statements.
(i) p: 100 is a multiple of 5 and 4.
(ii) q: 125 is multiple of 5 and 7.
(iii) r: 60 is a multiple of 3 or 5.
Solution:
(i) Here the connective is ‘and’
Step -1: 100 is a multiple of 5 (True)
Step -2: 100 is a multiple of 4 (True)
∴ 100 is a multiple of 5 and 4 is true, i.e. the statement ‘p’ is valid.
(ii) Here the connective is ‘and’
Step – 1: 125 is a multiple of 5 (True)
Step – 2: 125 is a multiple of 7 (false)
∴ The statement ‘q’ is (false), i.e. the statement ‘q’ is not a valid statement
(iii) Here the connective is ‘or’
60 is a multiple of 3 (True)
60 is a multiple of 5 (True)
Thus the component statements are both true.
∴ The statement ‘r’: 60 is a multiple of 3 or is true, i.e. ‘r’ is a valid statement.
![]()
Question 2.
Check the validity of the statements given below by the method given against each.
(i) “The sum of an irrational number and a rational number is irrational’’ (by contradiction method).
(ii) “If n is a real number with n > 3, then n2 > 9 (by the method of contradiction).
(iii) ‘‘If x, y are integers such that xy is odd then both x and y are odd” (by the method of contrapositive)
(iv) “If x is an integer and x2 is even then x is also even” (method of contrapositive).
Solution:
(i) Let the given statement is false.
i.e. the sum of an irrational number and a rational number is rational.
⇒ An irrational number + a rational number = a rational number
⇒ An irrational number = A rational number + rational number = A rational number
Which is absurd.
We arrive at a contradiction.
This is due to our false assumption. Thus, the given statement is true.
(ii) Let the given statement is false.
i.e. for a natural number n > 3 n2 > 9
⇒ n2 ≤ 3 ⇒ n ≤ 3
(.’. n is a natural number which contradicts the fact that n > 3)
This contradiction is due to our false assumption.
Thus for any natural number
n > 3, n2 > 9.
(iii) Let p: x and y are integers such that xy is odd. and q: both x and y are odd. We shall prove the validity of p → q by using the method of contrapositive.
Now ~ q: It is not true that both x and y are odd, i.e. at least one of x (or y) is even.
Let ~ q is true.
Let x is even and x = 2n for some integer n.
⇒ xy = 2ny for some integer n.
⇒ xy is even (not odd)
⇒ ~ p is true.
Thus by the method of contrapositive, we proved ~ q ⇒ ~ p, i.e. p → q is true.
(iv) Let p: x is an integer and x2 is even
q : x is even.
Let ~ q is true
⇒ x is not an even integer
⇒ x is an odd integer
Let x = 2n + 1 for some integer ‘n ’
⇒ x2 = (2n + 1)2 = 4n2 + 4n + 1
= 2 (2n2 + 2n) + 1
which is odd.
⇒ p is false ⇒ ~ p is true
Thus ~ q ⇒ ~ p
∴ Thus the statement is true.
i.e x is even ⇒x is also even
Question 3.
By giving counter-examples, show that the following statements are not true:
(i) If measures of all the angles of a triangle are equal, then the triangle is an obtuse angled triangle.
(ii) For every real number x and y, x2 = y2 ⇒ x = y.
(iii) The equation x2 – 1 = 0 does not have any root lying between 0 and 2.
Solution:
(i) Let in ΔABC
∠A = ∠B = ∠C = 60°
Clearly, no angle is obtuse.
∴ The triangle is not obtuse-angled.
(ii) for x = – 2, y = 2
x2 = y2 = 4 but x ≠ y
∴ x2 = y2 ⇒ x = y
(iii) x = 1 is a root of x2 – 1=0
that lies between 0 and 2.
∴ The given statement is false.
![]()
Question 4.
Check the validity of “If I do not work, I sleep.
If I am worried, I will not sleep. Therefore, if I am worried, I will work”.
Solution:
Method-1:
Let p: I work
q: I sleep
r: I am worried
“If I do not work, I sleep” can be written as ~ p → q
“If I am worried, I will not sleep” can be written as r → ~ q
‘If I am worried, I will work’’ can be written as r → p
The given statement can be written as [(~ p → q) ∧ (r → ~ q)] → ( r → p)
Let us draw the truth table
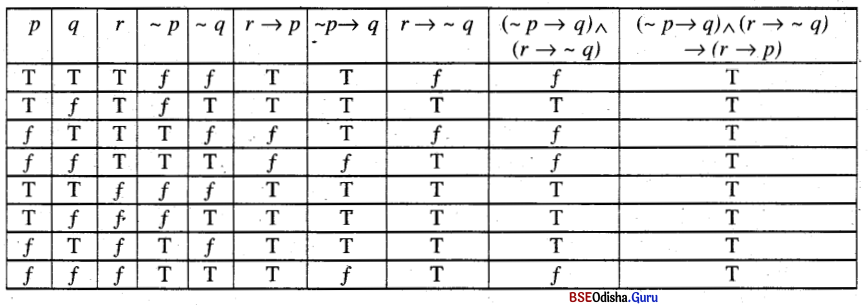
As [(~ p → q) ∧ (r → q)] → (r → p)
is a tautology the given statement is logically valid.
Method – 2:
Let p: I do work
q: I sleep
r: I am worried
“If I do not work, I sleep ” can be represented as ~ p → q
“If I am worried, I will not sleep” can be written as r → ~ q
Thus we can write the given statement as
[(~ p → q) ∧ (r → q)] → (r → p)
But a statement and its contrapositive are equivalent.
Thus this can be written as
[(r → ~ q) ∧ (~ q → p)] → (r → p)
By the principle of syllogism, the given statement is logically valid.
Question 5.
Let a and b be integers. By the law of contrapositive prove that if ab is even then either a is even or b is even:
Solution:
Let p: For integers ‘a and b’ ab is even q: a is even or b is even
we shall check the validity of p → q by the method of contrapositive Let ~ q is true.
⇒ Both a and b are odd
Let a = 2m + 1, b = 2n + 1
for some integers m and n
⇒ ab = (2m + 1) (2n + 1)
= 4mn + 2 (m + n ) + 1
= 2 [2mn + m + n) + 1
Which is odd
⇒ p is false
⇒ ~ p is true
Thus the method of contrapositive p → q is true.
i.e. The given statement is logically valid.
