CHSE Odisha Class 11 Math Solutions Chapter 11 Straight Lines Ex 11(b)

Odisha State Board Elements of Mathematics Class 11 Solutions CHSE Odisha Chapter 11 Straight Lines Ex 11(b) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 11 Straight Lines Exercise 11(b)

Question 1.
Fill in the blanks in each of the following, using the answers given against each of them :
(a) The slope and x-intercept of the line 3x – y + k = 0 are equal if k = _________ . (0, -1, 3, -9)
Solution:
-9

(b) The lines 2x – 3y + 1 = 0 and 3x + ky – 1=0 are perpendicular to each other if k = ___________ . (2, 3, -2, -3)
Solution:
2

(c) The lines 3x + ky – 4 = 0 and k – Ay – 3x = 0 are coincident if k = _____________. (1, -4, 4, -1)
Solution:
4

(d) The distance between the lines 3x – 1 = 0 and x + 3 = 0 is _________ units. (4, 2, \(\frac{8}{3}\), \(\frac{10}{3}\))
Solution:
\(\frac{10}{3}\)

(e) The angle between the lines x = 2 and x – √3y + 1 = 0 is _________. (30°, 60°, 120°, 150°)
Solution:
60°

Question 2.
State with reasons which of the following are true or false :
(a) The equation x = k represents a line parallel to x – axis for all real values of k.
Solution:
False. As the line x = k is parallel to y- axis for all values of k.

(b) The line, y + x + 1 = 0 makes an angle 45° with y – axis.
Solution:
y + x + 1 = 0
∴ Its slope = -1 = tan 135°
∴ It makes 45° with y – axis, as it makes 135° with x – axis. (True)

(c) The lines represented by 2x – 3y + 1 = 0 and 3x + 2y – k = 0 are perpendicular to each other for positive values of k only.
Solution:
2x – 3y + 1 = 0, 3x + 2y – k = 0
∴ \(m_1 m_2=\frac{2}{3} \times \frac{(-3)}{2}=-1\)
∴ The lines are perpendicular to each other for + ve values of k only. (False)

(d) The lines represented by px + 2y – 1 = 0 and 3x + py + 1 = 0 are not coincident for any value of ‘p’.
Solution:
px + 2y – 1 = 0, 3x + py + 1=0
∴ \(\frac{p}{3}=\frac{2}{p}=\frac{-1}{1} \Rightarrow p^2=6\)
and p = -3 or -2
There is no particular value of p for which \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\) (True)

(e) The equation of the line whose x and y – intercepts are 1 and -1 respectively is x – y + 1 = 0.
Solution:
Equation of the line whose intercepts 1 and -1 is \(\frac{x}{1}+\frac{y}{-1}\) = 1
or, x – y = 1 (False)

(f) The point (-1, 2) lies on the line 2x + 3y – 4 = 0.
Solution:
Putting x = – 1, y = 2
we have 2 (- 1) + 3 × 2 – 4
= -2 + 6 – 4 = 0
∴ The point (-1, 2) lies on the line 2x + 3 – 4 = 0 (True)

(g) The equation of a line through (1, 1) and (-2, -2) is y = – 2x.
Solution:
The equation of the line through (1, 1) and (-2, -2) is y – y₁ = \(\frac{y_2-y_1}{x_2-x_1}\) (x – x₁)
or, y – 1 = \(\frac{-2-1}{-2-1}\) (x – 1)
or, y – 1 = x – 1
or, x – y = 0 (False)

(h) The line through (1, 2) perpendicular to y = x is y + x – 2 =0.
Solution:
The slope of the line y = x is 1.
∴ The slope of the line perpendicular to the above line is -1.
∴ The equation of the line through (1, 2) having slope – 1 is y – y₁ = m(x – x₁)
or, y – 2 = -1 (x – 1)
or, y – 2= -x + 1
or, x + y = 3 (False)

(i) The lines \(\frac{x}{a}+\frac{y}{b}\) = 1 and \(\frac{y}{a}-\frac{x}{b}\) = 1 are intersecting but not perpendicular to each other.
Solution:
\(\frac{x}{a}+\frac{y}{b}\) = 1 and \(\frac{y}{a}-\frac{x}{b}\) = 1
∴ \(m_1 m_2=\frac{\left(-\frac{1}{a}\right)}{\frac{1}{b}} \times \frac{\left(-\frac{1}{b}\right)}{\left(-\frac{1}{a}\right)}=-1\)
∴ The lines intersect and are perpendicular to each other. (False)

(j) The points (1, 2) and (3, – 2) are on the opposite sides of the line 2x + y = 1.
Solution:
2x + y = 1
Putting x = 1, y = 2,
we have 2 × 1 + 2 = 4 > 1
Putting x – 3, y = -2,
we have 2 × 3 – 2 – 4 > 1
∴ Points (1, 2) and (3, – 2) lie on the same side of the line 2x + y = 1 (False)

Question 3.
A point P (x, y) is such that its distance from the fixed point (α, 0) is equal to its distance from the y – axis. Prove that the equation of the locus is given by, y² = α (2x – α).
Solution:

Question 4.
Find the locus of the point P (x, y) such that the area of the triangle PAB is 5, where A is the point (1, -1) and B is the tie point (5, 2).
Solution:

= \(\frac{1}{2}\) (-3x + 4y + 7) = 5
or, – 3x + 4y + 7 = 10
or, 3x – 4y + 3 =0 which is the locus of the point P (x, y).

Question 5.
A point is such that its distance from the point (3, 0) is twice its distance from the point (-3, 0). Find the equation of the locus.

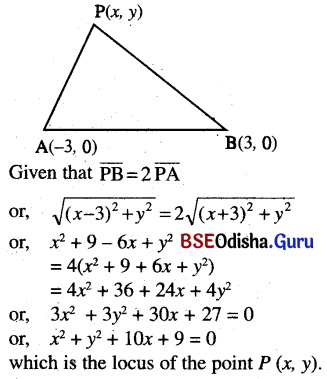
Question 6.
Obtain the equation of straight lines:
(a) Passing through (1, – 1) and making an angle 150°.
Solution:
The slope of the line
= tan 150° = –\(\frac{1}{\sqrt{3}}\)
∴ The equation of the line is y – y₁ = m(x – x₁)
or, y + 1 = –\(\frac{1}{\sqrt{3}}\) (x – 1)
or, y√3 + √3 = -x + 1
or, x + y√3 + √3 – 1 = 0

(b) Passing through (-1, 2) and making intercept 2 on the y-axis.
Solution:
Let the equation of the line be
y – mx + c or, y = mx + 2
∴ As the line passes through (-1, 2)
we have 2 = – m + 2, or, m = 0
∴ Equation of the line is y = 2.

(c) Passing through the points (2, 3) and (-4, 1).
Solution:
The equation of the line is

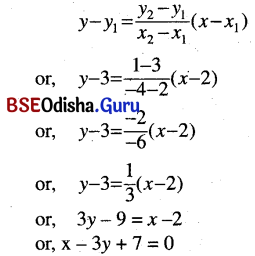
(d) Passing through (- 2, 3) and a sum of whose intercepts in 2.
Solution:
Let the equation of the line be \(\frac{x}{a}+\frac{y}{b}\) = 1 where a + b = 2     …….(1)
Again, as the line passes through the point (-2, 3), we have \(\frac{-2}{a}+\frac{3}{b}\) = 1      ………(2)
From (1), we have a= 2 – b
∴ From (2) \(\rightarrow \frac{-2}{2-b}+\frac{3}{b}=1\)
or, – 2b + 6 – 3b = (2 – b)b
or, 6 – 5b = 2b – b²
or, b² – 7b + 6 = 0
or, (b – 6)(b – 1) = 0
∴ b = 6, 1
∴ a =2 – b = 2 – 6 = -4
or, 2 – 1 = 1
∴ Equation of the lines are \(\frac{x}{-4}+\frac{y}{6}\) = 1 or \(\frac{x}{1}+\frac{y}{1}\) = 1
i, e. -3x + 2y = 12 or, x + y = 1

(e) Whose perpendicular distance from the origin is 2 such that the perpendicular from the origin has indication 150°.
Solution:
Here p = 2, α = 150°
The equation of the line in normal form is x cos α + y sin α = p
or, x cos 150° + y sin 150° = 2
or, \(\frac{-x \sqrt{3}}{2}+y \cdot \frac{1}{2}\) = 2
or, -x √3 + y = 4
or, x√3 – y + 4 = 0

(f) Bisecting the line segment joining (3, – 4) and (1, 2) at right angles.
Solution:
The slope of the line \(\overline{\mathrm{AB}}\) is

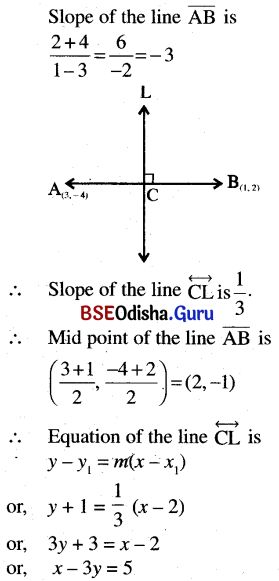
(g) Bisecting the line segment joining, (a, 0) and (0, b) at right angles.
Solution:
Refer to (f)

(h) Bisecting the line segments joining (a, b), (a’, b’) and (-a, b), (a’, -b’).
Solution:

(i) Passing through the origin and the points of trisection of the portion of the line 3x + y – 12 = 0 intercepted between the coordinate axes.
Solution:

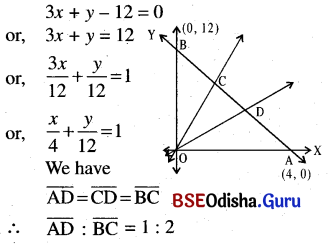
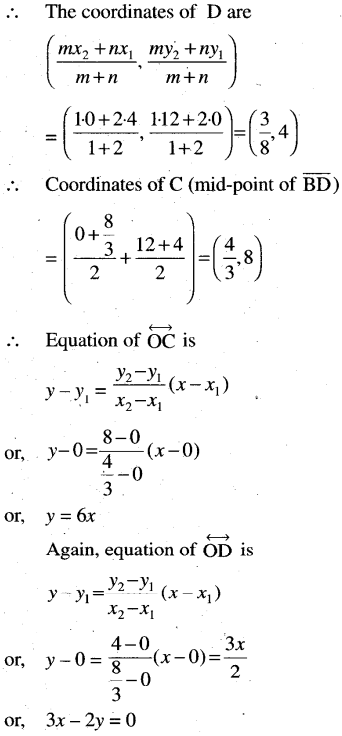
(j) Passing through (-4, 2) and parallel to the line 4x – 3y = 10.
Solution:
Slope of the line 4x – 3y = 10 is \(\frac{-4}{-3}=\frac{4}{3}\)
∴ The slope of the line parallel to the above line is \(\frac{4}{3}\).
∴ Equation of the line through (- 4, 2) and having slope \(\frac{4}{3}\) is y – y₁ = m(x – x₁)
or, y – 2 = \(\frac{4}{3}\) (x + 4)
or, 3y – 6 = 4x + 16
or, 4x – 3y + 22 = 0

(k) Passing through the point (a cos³ θ, a sin³ θ) and perpendicular to the straight line x sec θ + y cosec θ = α.
Solution:
The slope of the line x sec θ + y cosec θ = a is \(\frac{-\sec \theta}{{cosec} \theta}\) = -tanθ
∴ Slope of the required line  = cot θ
∴ Equation of the line through (a cos³ θ, a sin³ θ) is y – y₁ = m(x – x₁)
or, y – a sin³ θ = cot θ(x – a cos³ θ)
or, y – a sin³ θ = \(\frac{\cos \theta}{\sin \theta}\) (x – a cos³ θ)
or y sin θ – a sin⁴ θ = x cos  θ – a cos⁴ θ
or (x cos θ – y sin θ) + a(sin⁴ θ – cos⁴ θ) = 0

(l) Which passes through the point (3, -4) and is such that its portion between the axes is divided at this point internally in the ratio 2: 3.
Solution:

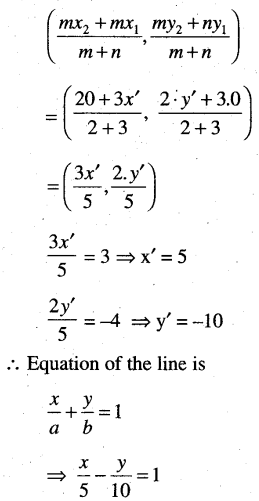
(m) which passes through the point (α, β) and is such that the given point bisects its portion between the coordinate axis.
Solution:

x = 2α , y = 2β
∴ Equation of the line \(\overleftrightarrow{\mathrm{AB}}\) is \(\frac{x}{2 \alpha}+\frac{y}{2 \beta}\) = 1(Intercept form)

Question 7.
(a) Find the equation of the lines that is parallel to the line 3x + 4y + 7 = 0 and is at a distance 2 from it.
Solution:
3x + 4y + 7 = 0
or, \(\frac{3 x}{5}+\frac{4 y}{5}+\frac{7}{5}\) = 0(Normal form)
∴ Equation of the lines parallel to the above line and 2 units away from it are \(\frac{3 x}{5}+\frac{4 y}{5}+\frac{7}{5}\) ± 2 = 0
or, 3x + 4y + 7 ± 10 = 0
∴ 3x + 4y + 17 = 0 and 3x + 4y – 3 = 0

(b) Find the equations of diagonals of the parallelogram formed by the lines ax + by = 0, ax + by + c = 0, lx + my = 0, and lx + my + n = 0. What is the condition that this will be a rhombus?
Solution:

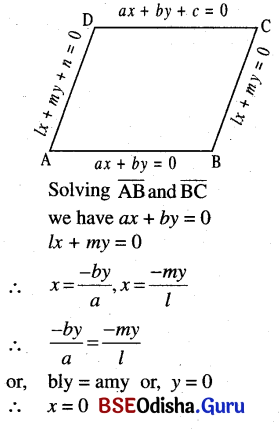
(c) Find the equation of the line passing through the intersection of 2x – y – 1 = 0 and 3x – 4y + 6 = 0 and parallel to the line x + y – 2 = 0.
Solution:
Let the equation of the required line be (2x – y – 1) + λ(3x – 4y + 6) = 0
or, x(2 + 3λ) + λ(-1 – Aλ) + 6λ – 1 = 0
As this line is parallel to the line x + y – 2 = 0
we have their slopes are equal.
∴ \(-\left(\frac{2+3 \lambda}{-1-4 \lambda}\right)=\frac{-1}{1}\)
or, 2 + 3λ = -1 – 4λ
or, 7λ = -3 or, λ = \(\frac{-3}{7}\)
∴ Equation of the line is (2x – y – 1) – \(\frac{3}{7}\) (3x – 4y + 6) = 0
or, 14x – 7y – 1 – 9x + 12y – 18 = 0
or, 5x + 5y – 25= 0
or, x + y = 5

(d) Find the equation of the line passing through the point of intersection of lines x + 3y + 2 = 0 and x – 2y – 4 = 0 and perpendicular to the line 2y + 5x – 9 = 0.
Solution:
Let the equation of the line be (x + 3y + 2) + λ(x – 2y – 4) = 0
or, x(1 + λ) + y(3 – 2λ) + 2 – 4λ = 0
As this line is perpendicular to the line 2y + 5x – 9 = 0.
We have the product of their slopes is -1.
∴ \(\frac{1+\lambda}{3-2 \lambda} \times \frac{5}{2}\) = -1
or, 5 + 5λ = – 6 + 4λ
or, λ = -6 – 5 = -11.
∴ Equation of the required line is (x + 3y + 2) – 11(x – 2y – 4) = 0
or, x + 3y + 2- 11x + 22y + 44 = 0
or, – 10x + 25y + 46 = 0
or, 10x – 25y – 46 = 0

(e) Find the equation of the line passing through the intersection of the lines x + 3y – 1 = 0 and 3x – y + 1 = 0 and the centroid of the triangle whose vertices are the points (3, -1) (1, 3) and (2, 4).
Solution:
Let the equation of the required line (x + 3y – 1) + λ(3x – y + 1) = 0   … (1)
Again, the centroid of the triangle with vertices (3, – 1), (1, 3), and (2, 4) is \(\left(\frac{3+1+2}{3}, \frac{-1+3+4}{3}\right)\) = (2, 2)
As line (1) passes through (2, 2), we have (2 + 6 – 1) +1(6 – 2 + 1) = 0
or, 7 + 5λ = 0 or, λ = \(\frac{-7}{5}\)
∴ Equation of the line (x + 3y – 1) – \(\frac{7}{5}\) (3x – y + 1) = 0
or, 5x + 15y – 5 – 21x + 7y – 7 = 0
or, 22y – 16x – 12 = 0
or, 11y – 8x – 6 = 0
or, 8x – 11y + 6 = 0

Question 8.
If lx + my + 3 = 0 and 3x – 2y – 1 = 0 represent the same line, find the values of l and m.
Solution:
lx + my + 3 = 0 and 3x – 2y – 1 = 0 represents the same line
∴ \(\frac{l}{3}=\frac{m}{-2}=\frac{3}{-1}\)
∴ l = -9, m = 6

Question 9.
Find the equation of sides of a triangle whose vertices are at (1, 2), (2, 3), and (-3, -5).
Solution:
Equation of \(\overline{\mathrm{AB}}\) is \(y-y_1=\frac{y_2-y_1}{x_2-x_1}\left(x-x_1\right)\)
\(y-2=\frac{3-2}{2-1}(x-1)\)
or, y – 2 = x – 1
or, x – y + 1 = 0

Question 10.
Show that origin is within the triangle whose sides are given by equations, 3x – 2y = 1, 5x + 3y + 11 = 0, and x – 7y + 25 = 0.
Solution:



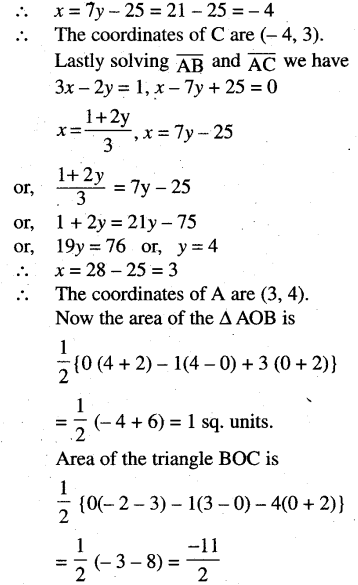
∴ The origin lies within the triangle ABC.

Question 11.
(a) Find the equations of straight lines passing through the point (3, -2) and making an angle 45° with the line 6x + 5y = 1.

or, 11x – y = 35, x + 11y + 19 = 0

(b) Two straight lines are drawn through the point (3, 4) inclined at an angle 45° to the line x – y – 2 = 0. Find their equations and obtain area included by the above three lines.
Solution:

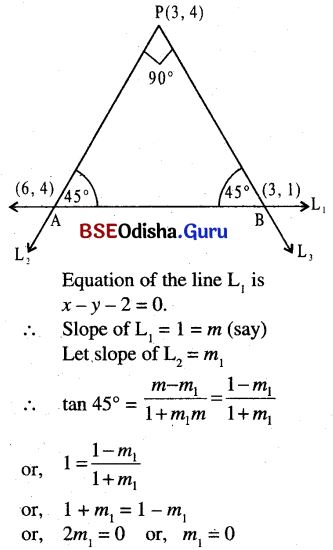
Slope of L₂ = 0
Then as L₂ ⊥ L₃
Slope of L₃ = ∞
∴ Equation of L₂ is
y – y₁ =m(x – x₁)
or, y – 4 = 0(x – 3) = 0
or, y = 4
∴ Equation of L₃ is y – 4 = ∞ (x – 3)
or, x – 3 = 0 or, x = 3
∴ Sloving L₁ and L₂, we have
x – y – 2 = 0, y = 4
or, x = 6
The coordinates of A are (6, 4).
Again solving L1 and L3, we have
x – y – 2 = 0, x = 3
or, y = x – 2 = 3 – 2 = 1
∴ The coordinates of B are (3, 1).
Area of the triangle PAB is

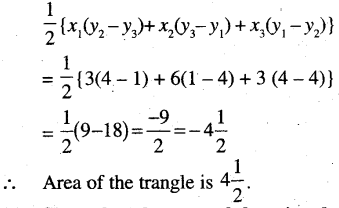
(c) Show that the area of the triangle formed by the lines given by the equations y = m₁x + c₁,y = m₂x + c_2, and x = 0 is \(\frac{1}{2} \frac{\left(c_1-c_2\right)^2}{\left[m_2-m_1\right]}\)
Solution:

Question 12.
Find the equation of lines passing through the origin and perpendicular to the lines 3x + 2y – 5 = 0 and 4x + 3y = 7. Obtain the coordinates of the points where these perpendiculars meet the given lines. Prove that the equation of a line passing through these two points is 23x + 11y – 35 = 0.
Solution:
The slopes of the line 3x + 2y – 5 = 0 and 4x + 3y = 7 are \(\frac{-3}{2}\) and \(\frac{-4}{3}\)
∴ Slopes of the lines perpendicular to the above lines are \(\frac{2}{3}\) and \(\frac{3}{4}\)
∴ Equation of the lines through the origin and having slopes \(\frac{2}{3}\) and \(\frac{3}{4}\)
y = \(\frac{2x}{3}\) and y = \(\frac{3x}{4}\)
Now solving 3x + 2y – 5 = 0 and y = \(\frac{2x}{3}\)
we have 3x + \(\frac{4x}{3}\) – 5 = 0
or, 9x + 4x – 15 = 0
or, x = \(\frac{15}{13}\)
∴ y = \(\frac{2 x}{3}=\frac{2}{3} \times \frac{15}{13}=\frac{10}{13}\)
∴ The perpendicular y = \(\frac{2 x}{3}\) meets the line 3x + 2y – 5 = 0 at \(\left(\frac{15}{13}, \frac{10}{13}\right)\)
Again, solving 4x + 3y = 7 and y = \(\frac{3 x}{4}\)
we have 4x + 3 × \(\frac{3 x}{4}\) = 7
or, 16x + 9x = 28 or, x = \(\frac{28}{25}\)

Question 13.
(a) Find the length of a perpendicular drawn from the point (-3, -4) to the straight line whose equation is 12x – 5y + 65 = 0.
Solution:
The length of the perpendicular drawn from the point (- 3, -4) to the straight line 12x – 5y + 65 = 0 is

(b) Find the perpendicular distances of the point (2, 1) from the parallel lines 3x – 4y + 4 = 0 and 4y – 3x + 5 = 0. Hence find the distance between them.
Solution:
The distance of the point (2, 1) from the line 3x – 4y + 4 = 0 is \(\left|\frac{3 \times 2-4 \times 1+4}{\sqrt{9+16}}\right|=\frac{6}{5}\)
Again distance of the point (2, 1) from the line 4y – 3x + 5 = 0 is

(c) Find the distance of the point (3, 2) from, the line x + 3y – 1 = 0, measured parallel to the line 3x – 4y + 1 = 0
Solution:

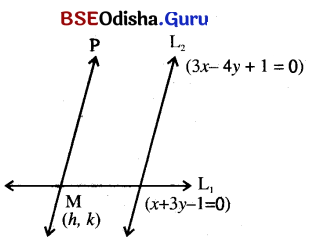
Let the coordinates of M be (h, k).
As \(\overline{\mathrm{PM}} \| \mathrm{L}_1\), We have their slopes are equal.

(d) Find the distance of the point (-1, -2) from the line x + 3y – 7 = 0, measured parallel to the line 3x + 2y – 5 = 0
Solution:
Slope of the line 3x + 2y – 5 = 0 is \(\left(-\frac{3}{2}\right)\)
Equation of the line through (-1, -2) and parallel to this line is y + 2 = – \(\frac{3}{2}\) (x + 1)
⇒ 2y + 4 = -3x – 3
⇒ 3x + 2y + 7 = 0 …(1)
Given line is : x + 3y – 7 = 0    ….(2)
from (1) and (2) we get 7y – 28 = 0 Py = 4 and x = \(-\frac{35}{7}\) = -5
Thus the required distance is \(\sqrt{(-1+5)^2+(-2-4)^2} \quad=\sqrt{16+36}\)
= √52 = 2√3 units.

(e) Fine the distance of the line passing through the points (a cos α, a sin α) and (a cos β, a sin β) from the origin.
Solution:
The equation of the line passing through the points (a cos α, a sin α) and (a cos β, a sin β) is y – y₁ = \(\frac{y_2-y_1}{x_2-x_1}\) x – x₁
or, y – a sin α

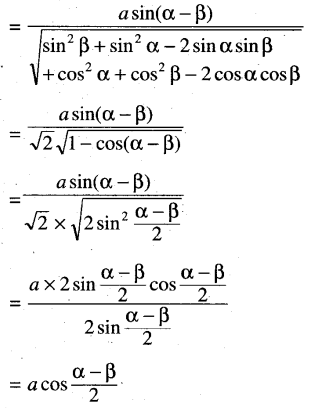
Question 14.
Find the length of perpendiculars drawn from the origin on the sides of the triangle whose vertices are A( 2, 1), B (3, 2), and C (- 1, -1).
Solution:

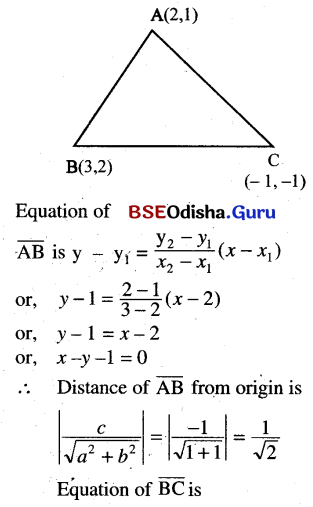
Question 15.
Show that the product of perpendicular from the points \(\left(\pm \sqrt{a^2-b^2}, 0\right)\) upon the straight line \(\frac{x}{a}\) cos θ + \(\frac{y}{b}\) sin θ = 1 is b²
Solution:

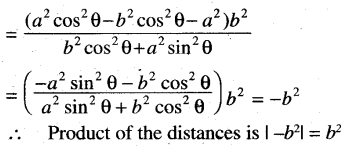
Question 16.
Show that the lengths of perpendiculars drawn from any point of the straight line 2x + 11y – 5 = 0 on the lines 24x + 7y – 20 = 0 and 4x – 3y – 2 = 0 are equal to each other.
Solution:
Let P(h, k) is any point on the line
2k + 11y – 5 = 0
∴ 2h + 11k – 5 = 0
Now the length of the perpendicular from P on the line 24x + 7y – 20 = 0 is

Clearly d₁ = d₂

Question 17.
If p and p’ are the length of perpendiculars drawn from the origin upon the lines x sec α + y cosec α = 0 and x cos α – y sin α – a cos 2α = 0
Prove that 4p² + p’² = a²
Solution:

Question 18.
Obtain the equation of the lines passing through the foot of the perpendicular from (h, k) on the line Ax + By + C = 0 and bisect the angle between the perpendicular and the given line.
Solution:

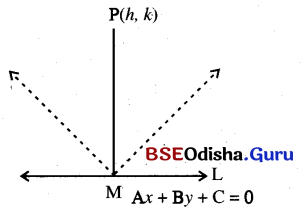
Slope of the line L is \(\frac{-\mathrm{A}}{\mathrm{B}}\)
∴ Slope of the line \(\overline{\mathrm{PM}} \text { is } \frac{\mathrm{B}}{\mathrm{A}}\)
∴ Equation of the line \(\overline{\mathrm{PM}}\) is y – y₁ = m(x – x₁)
or, y – k = \(\frac{\mathrm{B}}{\mathrm{A}}\) (x – h)
or, Ay – Ak =Bx – Bh
or, Bx – Ay + Ak – Bh = 0
∴ Equation of the bisectors of the angles between the lines L and \(\overline{\mathrm{PM}}\) is
\(\frac{\mathrm{A} x+\mathrm{B} y+\mathrm{C}}{\sqrt{\mathrm{A}^2+\mathrm{B}^2}}=\pm \frac{\mathrm{B} x-\mathrm{A} y+\mathrm{A} k-\mathrm{B} h}{\sqrt{\mathrm{B}^2+\mathrm{A}^2}}\)
or, Ax + By + C = ± (Bx – Ay +Ak – Bh)

Question 19.
Find the direction in which a straight line must be drawn through the point(1, 2) such that its point of intersection with the line x + y – 4 = 0 is at a distant \(\frac{1}{3} \sqrt{6}\) from this point.
Solution:

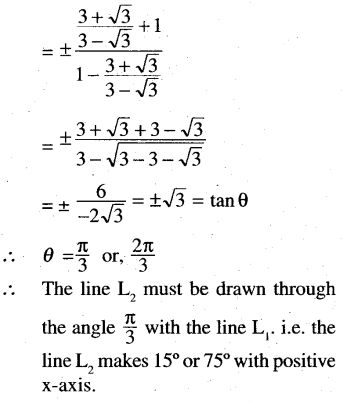
Question 20.
A triangle has its three sides formed by the lines x + y = 3, x + 3y = 3, and 3x + 2y = 6. Without solving for the vertices, find the equation of its altitudes and also calculate the angles of the triangle.
Solution:

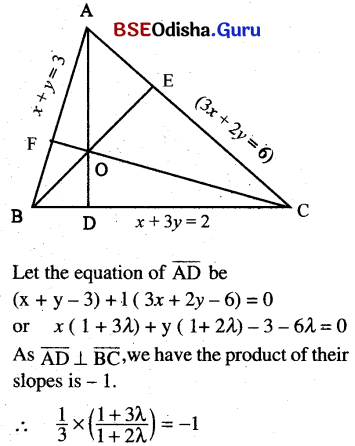
or 1 + 3λ = – 3 – 6λ
or 9λ = – 4 or , λ = \(\frac{-4}{9}\)
∴ Equation of \(\overline{\mathrm{AD}}\) is (x + y – 3) – \(\frac{4}{9}\) (3x + 2y – 6) = 0
or, 9x + 9y – 27 – 12x – 8y + 24 = 0
or, -3x + y – 3 = 0
or, 3x – y + 3 = 0
Let the equation of \(\overline{\mathrm{BE}}\) be (x + y – 3) + 1(x + 3y – 3) = 0
or, x(1 + λ) + y( 1 + 3λ) – 3 – 3λ = 0
As \(\overline{\mathrm{BE}} \perp \overline{\mathrm{AC}}\)
we have \(\frac{1+\lambda}{1+3 \lambda} \times \frac{3}{2}\) = -1
or, 3 + 3λ = -2 – 6λ
or, 9λ = – 5 or λ = \(\frac{-5}{9}\)
∴ Equation of \(\overline{\mathrm{BE}}\) is (x + y – 3) – \(\frac{5}{9}\) (x + 3y – 3) = 0
or 9x + 9y – 27 – 5x – 15y + 15 = 0
or, 4x – 6y – 12 = 0
or, 2x – 3y – 6 = 0
Let the equation of \(\overline{\mathrm{CE}}\) be (3x + 2y – 6) + λ (x + 3y – 3) = 0
x(3 + λ) + y (x + 3λ) – 6 – 3λ = 0
As \(\overline{\mathrm{CF}} \perp \overline{\mathrm{AB}} .\)
we have \(\frac{3+\lambda}{2+3 \lambda}\) × 1 = -1
or, 3 + λ = -2 – 3λ
or, 4λ = -2 – 3 = -5
or, λ = \(\frac{-5}{4}\)
∴ Equation of is \(\overline{\mathrm{CF}}\) (3x + 2y – 6) \(\frac{-5}{4}\) (x + 3y – 3) = 0
or, 12x + 8y – 24 – 5x – 15y + 15 =0
or, 7x – 7y – 9 = 0

Question 21.
A triangle has its vertices at P(1, -1), Q(3, 4) and R(2, 5). Find the equation of altitudes through P and Q and obtain the coordinates of their point of intersection. (This point is called the ortho-center of the triangle.)
Solution:

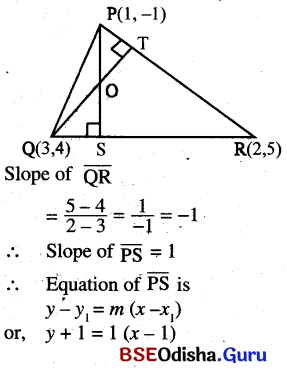
Question 22.
(a) Show that the line passing through (6, 0) and (-2, -4) is concurrent with the lines
2x – 3y – 11 = 0 and 3x – 4y = 16
Solution:
The equation of the line through (6,0) and (-2, -4) is

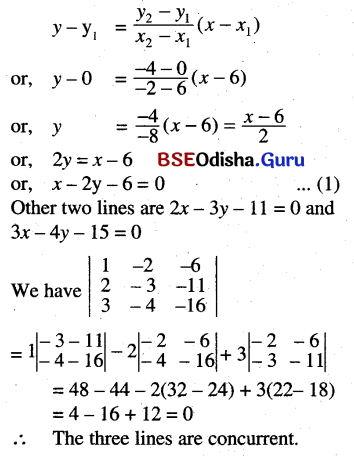
(b) Show that the lines lx + my + n = 0 mx + ny + 1 = 0 and nx + ly + m = 0 are concurrent, l + m + n = 0
Solution:
As the lines
lx + my + n = 0
mx + ny + 1 = 0
and nx + ly + m = 0 are concurrent.

Question 23.
Obtain the equation of the bisector of the acute angle between the pair of lines.
(a) x + 2y = 1, 2x + y + 3 = 0
Solution:
Equation ofthe bisectors ofthe angles between the lines x + 2y – 1 = 0 and 2x + y + 3 = 0 are \(\frac{x+2 y-1}{\sqrt{1^2+2^2}}=\pm \frac{2 x+y+3}{\sqrt{2^2+1^2}}\)
or, x + 2y – 1 = ± (2x + y + 3)
∴ x + 2y – 1 = 2x + y + 3 and
x + 2y – 1= -2x – y – 3
∴ x – y + 4 = 0 and 3x + 3y + 2 = 0
Let θ be the angle between x + 2y – 1 = 0 and x – y + 4 = 0
∴ tan θ = \(\frac{a_1 b_2-a_2 b_1}{a_1 a_2+b_1 b_2}\)
\(=\frac{1 \cdot(-1)-(+1) \cdot 2}{1 \cdot 1+2(-1)}\)
\(=\frac{-1-2}{1-2}=\frac{-3}{-1}=3\)
sec² θ = 1 + tan² θ = 1 + 9 = 10
cos² θ = 1/10
cos θ = \(\frac{1}{\sqrt{10}}<\frac{1}{\sqrt{2}}\) ⇒ θ > 45°
∴ x – y + 4 = 0 is the obtuse angle bisector.
⇒ 3x + 3y + 2 = 0 is acute angle bisector.

(b) 3x – 4y = 5, 12y – 5x = 2
Solution:
Given equation of lines are
3x – 4y – 5 = 0    …..(1) and  5x – 12y + 2 = 0     ……(2)
Equation of bisectors of angles between these Unes are:

Question 24.
(a) Find the coordinates of the center of the inscribed circle of the triangle formed by the line x cos α + y sin α = p with the coordinate axes.
Solution:


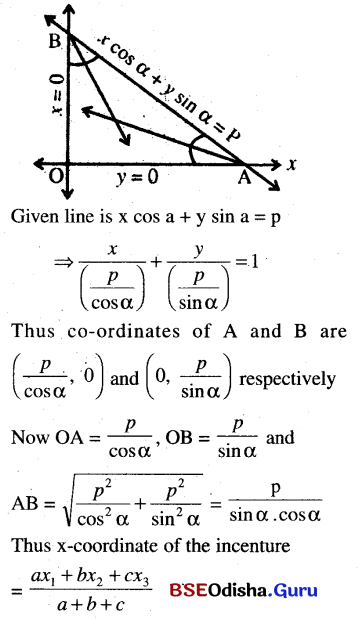
\(\left(\frac{p}{\sin \alpha+\cos \alpha+1}, \frac{p}{\sin \alpha+\cos \alpha+1}\right)\)

(b) Find the coordinates of the circumcentre and incentre of the triangle formed by the lines 3x – y = 5, x + 2y = 4, and 5x + 3y + 1 = 0.
Solution:

Question 25.
The vertices B, and C of a triangle ABC lie on the lines 3y = 4x and y = 0 respectively, and the side \(\overline{\mathbf{B C}}\) passes through the point (2/3, 2/3). If ABOC is a rhombus, where O is the origin, find the equation of \(\overline{\mathbf{B C}}\) and also the coordinates of A.
Answer:
Let the coordinates of C be (a, 0) so that the length of the side of the rhombus is ‘a’

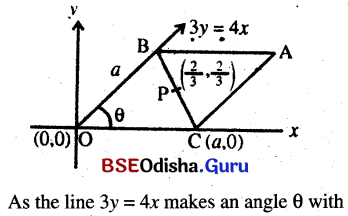
Question 26.
Find the equation of the lines represented by the following equations.
(a) 4x² – y² = 0
Solution:
4x² – y² = 0
or, (2x + y)(2x – y) = 0
∴ 2x + y = 0 and 2x – y = 0 are the two separate lines.

(b) 2x² – 5xy – 3y²
Solution:
2x² – 5xy – 3y²
or, 2x² – 6xy + xy – 3y² = 0
or, 2x(x – 3y) + y(x – 3y) = 0
or, (x – 3y)(2x + y) = 0
∴ x – 3y = 0 and 2x + y = 0 are the two separate lines.

(c) x² + 2xy sec θ + y² = 0
Solution:
x² + 2xy sec θ + y² = 0
∴ a = 1, b = 2y sec θ, c = y²
x = \(\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)
= \(\frac{2 y \sec \theta \pm \sqrt{4 y^2 \sec ^2 \theta-4 y^2}}{2}\)
= \(\frac{-2 y \sec \theta \pm 2 y \tan \theta}{2}\)
= y (- sec θ ± tan θ)
∴ x = y (- sec θ + tan θ) and x – y (- sec θ – tan θ) are the two separate lines.

(d) 3x² + 4xy = 0
Solution:
3x² + 4xy = 0
or x (3x + 4y) = 0
∴ x = 0 and 3x + 4y = 0 are the two separate lines.

Question 27.
From the equations which represent the following pair of lines.
(a) y = mx; y = nx
Solution:
y – mx = 0, y – nx = 0
or (y – mx) (y – nx) = 0
or, y² – nxy – mxy + mnx² = 0
or, y² – xy (m + n) + mnc² = 0 which is the equation of a pair of lines.

(b) y – 3x = 0 ; y + 3x = 0
Solution:
y – 3x = 0, y + 3x = 0
∴ (y – 3x) (y + 3x) = 0
or, y² – 9x² = 0 which is the equation of a pair of lines.

(c) 2x – 3y + 1 = 0 ; 2x + 3y + 1 = 0
Solution:
2x – 3y + 1 = 0; 2x + 3y + 1 =0
or, (2x – 3y + 1)(2x + 3y + 1) = 0
or, (2x + 1)² – 9y² = 0
or, 4x² + 1 + 4x – 9y² = 0
or, 4x² – 9y² + 4x + 1= 0 which represents a pair of lines.

(d) x = y. x + 2y + 5 = 0
Solution:
x = y, x + 2y + 5 = 0
∴ (x – y) (x + 2y + 5) = 0
or, x² + 2xy + 5x – xy – 2y² – 5y =0
or, x² – 2y² + xy + 5x – 5y = 0 which represents a pair of lines.

Question 28.
Which of the following equations represents a pair of lines?
(a) 2x² – 6y² + 3x +  y + 1 = 0
Solution:
a = 2, b = -6, 2g = 3
2f = 1, c = 1
∴ g = \(\frac{3}{2}\), f = \(\frac{1}{2}\), h = 0
∴ abc + 2fgh – ah² – bg² – ch²
= 2(-6). 1 + 2 × \(\frac{1}{2}\) × \(\frac{3}{2}\) – 0 – (-6) × \(\frac{9}{4}\) – 1 × 0
= -12 + \(\frac{3}{2}\) + \(\frac{27}{2}\) = \(\frac{6}{2}\) = 3 ≠ 0
∴ The given equation does not represent a pair or lines.

(b) 10x² – xy – 6y² – x + 5y – 1 = 0
Solution:
a = 10. 2h = 1
B = -6, 2g = -1
2f = 5. C= -1
∴ h = –\(\frac{1}{2}\), g = –\(\frac{1}{2}\) , f = \(\frac{5}{2}\)
∴ abc + 2fgh – ah² – bg² – ch²
= 10(-6)(-1) + 2 × \(\frac{5}{2}\) × (-\(\frac{1}{2}\)) × (-\(\frac{5}{2}\)) – 10 × \(\frac{2.5}{4}\) – (-6)\(\frac{1}{4}\) – (-1)\(\frac{1}{4}\)
= 60 + \(\frac{5}{4}\) – \(\frac{250}{4}\) + \(\frac{6}{4}\) + \(\frac{1}{4}\)
= \(\frac{240+5+6-250+1}{4}=\frac{2}{4}\)
∴ The given equation does not represent a pair of lines.

(c) xy + x + y + 1 = 0
Solution:
xy + x + y + 1= 0
or, x(y + 1) + 1(y + 1 ) = 0
or (y + 1 )(x + 1) =0
∴ x + 1 = 0
and y + 1 = 0 are the two separate lines,
∴ The given equation represents a pair of lines.

Question 29.
For what value of λ do the following equations represent pair of straight lines?
(a) λx² + 5xy – 2y² – 8x + 5y – λ = 0
Solution:
λx² + 5xy – 2y² – 8x + 5y – λ = 0
∴ a = λ, 2h = 5, b = -2, 2g = -8
2f = 5, c = -1
∴ h = \(\frac{5}{2}\), g = -4, f = \(\frac{5}{2}\)
As the given equation represent a pair of lines, we have abc + 2fgh – ah² – bg² – ch² = 0
or, λ(-2)(-λ) + 2. \(\frac{5}{2}\) (-4). \(\frac{5}{2}\) -λ × \(\frac{25}{4}\) – (-2) (-4)² – (-λ) × \(\frac{25}{4}\) = 0
or, 2λ² – 50 – \(\frac{25 λ }{4}\) + 32 + \(\frac{25 λ }{4}\) = 0
or, 2λ² = 18 or, λ² = 9
λ = ±3

(b) x² – 4xy – y² +6x + 8y + λ = 0
Solution:
Here a = 1, 2h = -1, b = -1, 2g = 6, 2f = 8, c = τ
As the given equation represent a pair of lines, we have
abc + 2fgh – af² – bg² – ch² = 0
⇒ (-1) τ + 2.4.3 (-2) – 1. 4² – (-1). ³2 – τ(-2)² = 0
⇒ -τ – 48 – 16 + 9 – 4τ = 0
⇒ -5τ – 55 = 0 ⇒ τ = -11

Question 30.
(a) Obtain the value of λ for which the pair of straight lines represented by 3x² – 8xy + λy² = 0 are perpendicular to each other.
Solution:
3x² – 8xy + λy² = 0
∴ a = 3. 2h = -8, b = λ
As the pair of lines are perpendicular to each other, we have a + b = 0.
or, 3 + λ = 0 – or, λ = -3

(b) Prove that a pair of lines through the origin perpendicular to the pair of lines represented by px² – 2qxy + ry² = 0 is given by rx² – 2qxy + py² = 0
Solution:
px² – 2qxy + ry² = 0
∴ a = p, b = 2qy, c = ry²

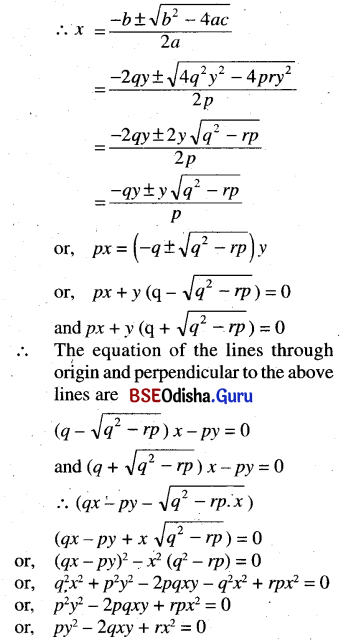
(c) Obtain the condition that a line of the pair of lines ax² + 2hxy + by² = 0,
(i) Coincides with
Solution:

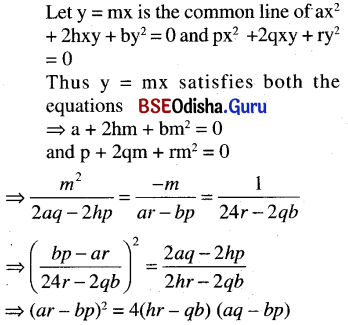
(ii) is perpendicular to, a line of the pair of lines px² + 2qxy + ry² = 0
Solution:

Question 31.
Find the acute angle between the pair of lines given by :
(a) x² + 2xy – 4y² = 0
Solution:
x² + 2xy – 4y² = 0
∴ a=1, 2h = 2, b = -4
∴ tan θ = \(\frac{\pm 2 \sqrt{h^2-a b}}{a+b}=\frac{\pm 2 \sqrt{1+4}}{1-4}\)
\(=\pm \frac{2 \sqrt{5}}{-3}=\mp \frac{2 \sqrt{5}}{3}\)
∴ The acute angle between the pair of lines is tan^-1 \(\frac{2 \sqrt{5}}{3}\)

(b) 2x² + xy – 3y² + 3x + 2y + 1 = 0
Solution:
2x² + xy – 3y² + 3x + 2y + 1 = 0
∴ a = 2, 2h = 1, b = -3, 2g = 3 2f= 2, c = 1.
tan θ = \(\frac{\pm 2 \sqrt{h^2-a b}}{a+b}\)
\(=\pm \frac{2 \sqrt{\frac{1}{4}+6}}{2-3}=\pm \frac{2 \times 5}{2(-1)}\) = ± 5
∴ The acute angle is tan^-1 5

(c) x² + xy – 6y² – x – 8y – 2 = 0
Solution:
Given Equation is x² + xy – 6y² – x – 8y – 2 = 0
here a = 1, 2h = 1, b = -6 thus if 0 is the acute angle between two lines then
tan θ = \(=\left|\frac{2 \sqrt{h^2-a b}}{a+b}\right|=\left|\frac{2 \sqrt{\frac{1}{4}+6}}{-5}\right|\)
= \(\left|\frac{2 \times 5}{-10}\right|\) = 1
∴ θ = 45°

Question: 32.
Write down the equation of the pair of bisectors of the following pair of lines :
(a) x² – y² = 0 ;
Solution:
x² – y² = 0
∴ a = 1, b = -1, h = 0
∴ The equation of the bisectors of the angles between the pair of lines are \(\frac{x^2-y^2}{a-b}=\frac{x y}{h}\)
or, \(\frac{x^2-y^2}{1+1}=\frac{x y}{0}\)
or, xy = 0

(b) 4x² – xy – 3y² = 0
Solution:
4x² – xy – 3y² = 0
∴ a = 4, 2h = -1, b = -3
∴ Equation of the pair of bisectors are \(\frac{x^2-y^2}{(a-b)}=\frac{x y}{h}\)
or, \(\frac{x^2-y^2}{7}=\frac{x y}{\left(-\frac{1}{2}\right)}\)
or, x² – y² = -14xy
or, x² + 14xy – y² = 0

(c) x² cos θ + 2xy – y² sin θ = 0
Solution:
x² cos θ + 2xy – y² sin θ = 0
∴ a = cos θ, 2h = 2, b = – sin θ
∴ Equation of the pair of bisectors are \(\frac{x^2-y^2}{a-b}=\frac{x y}{h}\)
or, \(\frac{x^2-y^2}{\cos \theta+\sin \theta}=\frac{x y}{1}\)
or, x² – y² = xy(cos θ + sin θ)

(d) x² – 2xy tan θ – y² = 0
Solution:
x² – 2xy tan θ – y² = 0
∴ a = 1, 2h = -2 tan θ, b = -1
∴ Equation of the pair of bisectors are \(\frac{x^2-y^2}{2}=\frac{x y}{-\tan \theta}\)
or, x² – y² = 2xy cot θ
or, x² + 2xy cot θ – y² = 0

Question 33.
If the pair of lines represented by x² – 2pxy – y² = 0 and x² – 2qxy – y² = 0 be such that each pair bisects the angle between the other pair, then prove that pq = -1.
Solution:

Question 34.
Transform the equation: x² + y² – 2x – 4y + 1 = 0 by shifting the origin to (1, 2) and keeping the axes parallel.
Solution:
x² + y² – 2x – 4y + 1 = 0     ……(1)
Let h = 1, k = 2
Taking x’ + h and y = y’ + k we have
(x’ + h)² + (y’ + k)² – 2(x’ + j) -4(y’ + k) + 1=0
or, (x + 1)² + (y’ + 2)² – 2(x’ + 1) – 4(y’+ 2) + 1=0
or, x^‘2 + 1 + 2x’ + y^‘2 + 4 – 4y’ – 2x’ – 2 – 4y’- 8 + 1 = 0
or, x^‘2 + y’² – 4 = 0
∴ The transformed equation is x² + y² = 4

Question 35.
Transform the equation: 2x² + 3y² + 4xy – 12x – 14y + 20 = 0. When referred to parallel axes through(2, 1).
Solution:
2x² + 3y² + 4xy – 12x – 14y + 20 = 0
Let h = 2, k = 1
Taking x = x’ + 1 and y = y’ + 1
we have
2(x’ + 2)² + 3(y’ + 1)² + 4(x’ + k)(y’ + 1) – 12 (x’ + 2)- 14 (y’ + 1) + 20 = 0
or, 2x^‘2 + 8 + 8x’ + 3 + 6y’ + 3y^’2 + 4x’y’ + 4x’ + 8y’ + 8 – 12x’ – 14y’ – 18 = 0
or, 2x^‘2 + 3y^’2 + 4x’y’ + 1=0
The transformed equation is
2x² + 3y² + 4xy + 1 = 0

Question 36.
Find the measure of rotation so that the equation x² – xy + y² = 5 when transformed does not contain xy- term.
Solution:
x² – xy + y² = 5
Taking x = x’ cos α – y’ sin α
y = x’ sin α – y’ cos α
We get (x’ cos α – y’ sin α)² – (x’ cos α – y’ cos α) (x’ sin α + y’ cos α) + (x’ sin α + y’ cos α)² = 5
⇒ x^‘2 cos² α + y^‘2 sin² α – 2x’y sin α.
cos α – x^‘2 sin α. cos α – x’y cos² α + x’y’ sin² α + y^‘2 sin α. cos α + x^‘2 sin² α + y^‘2 cos² α + 2x’y’ sin α cos α = 5
Given that the transformed equation does not xy term.
Hence the co-efficient of x’y’ is zero.
That is sin² α – cos² α = 0
⇒ sin² α = cos² α
⇒ tan² α = 1 ⇒ tan α = 1 ⇒ α= 45°

Question 37.
What does the equation x + 2y – 10 =0 become when the origin is changed to (4, 3)?
Solution:
x + 2y – 10 = 0
Let h = 4, k = 3
Taking x = x’ + 4, y = y’ + 3
we have x’ + 4 + 2 (y’ + 3) – 10 = 0
or, x + 2y’ = 0
∴ The transformed equation is x + 2y = 0.