Odisha State Board CHSE Odisha Class 11 Math Solutions Chapter 12 Conic Sections Ex 12(b) Textbook Exercise Questions and Answers.
CHSE Odisha Class 11 Math Solutions Chapter 12 Conic Sections Exercise 12(b)
Question 1.
Fill in the blanks by choosing the correct answer from the given ones :
(a) The equation of the directrix to the parabola x2 = -6y is _____________. [y + 6 = 0, 2y – 3 = 0, y – 6 = 0, 2y + 3 = 0]
Solution:
2y – 3 = 0
(b) The eccentricity of the parabola y2 = 8x is ____________. (2, 8, 0, 1)
Solution:
1
(c) The line y + x = k is tangent to the parabola y2 + 12x = 0 if k = ______________. (-3, 3, 6, -6)
Solution:
3
(d) The latus rectum of the parabola (y – 2)2 = 8(x + 3) is ______________. (2, 4, 8, 16)
Solution:
8
(e) The equation of tangent to the parabola x2 = 6y at vertex is _______________. (x = 0, y = 0, x = \(\frac{-3}{2}\), y = \(\frac{-3}{2}\))
Solution:
y = 0
(f) The equation of axis of the ellipse \(\frac{x^2}{16}+\frac{y^2}{9}\) = 1 is ___________. (x = 4, y = 3, x = 0, y = 0)
Solution:
y = 0
(g) The equation of the major axis of the ellipse \(\frac{(x+1)^2}{16}+\frac{(y-2)^2}{25}\) = 1 is __________. (x = 4, x = -1, y = 5, y = 2)
Solution:
x = -1
(h) The distance between the focii of the ellipse 3x2 + 4y2 = 1 is _____________. (1, \(\frac{1}{\sqrt{3}}\), \(\frac{2}{\sqrt{3}}\), \(\frac{1}{2 \sqrt{3}}\)
Solution:
\(\frac{1}{\sqrt{3}}\)
(i) The eccentricity of the ellipse \(\frac{x^2}{16}+\frac{y^2}{25}\) = 1 is _______________. (\(\frac{4}{5}, \frac{5}{4}, \frac{3}{5}, \frac{16}{25}\))
Solution:
\(\frac{3}{5}\)
(j) The line y = 2x + K is a tangent to the ellipse 5x2 + y2 = 5 if K = ______________. (2, 5, √3, √21)
Solution:
3
(k) The length of the latus rectum of the ellipse \(\frac{(x-2)^2}{4}+\frac{(y+3)^2}{25}\) = 1 is _______________. (\(\frac{4}{25}, \frac{2}{5}, \frac{5}{2}, \frac{8}{5}\))
Solution:
\(\frac{8}{5}\)
(l) The equation of the conjugate axis of the hyperbola \(\frac{x^2}{9}-\frac{(y+2)^2}{16}\) = 1 is ____________. (x = 0, x = 3, y = -3, y = 4)
Solution:
x = 0
(m) the hyperbola \(\frac{y^2}{16}-\frac{x^2}{12}\) = 1 intersects x – axis at ___________. [(0, ±4), (±2√3, 0), (2, 0), no where]
Solution:
no where
(n) The eccentricity of the hyperbola 4x2 – 3y2 = 1 is ____________. (\(\frac{4}{3}, \frac{3}{4}, \frac{\sqrt{21}}{3}, \frac{\sqrt{7}}{2 \sqrt{3}}\))
Solution:
\(\frac{\sqrt{21}}{3}\)
(o) The latus rectum of the hyperbola \(\frac{x^2}{9}-\frac{y^2}{16}\) = 1 is ___________. (\(\frac{16}{9}, \frac{9}{16}, \frac{1}{9}, \frac{32}{9}\))
Solution:
\(\frac{32}{9}\)
(p) The line y = 3x – k is a tangent to the hyperbola 6x2 – 9y2 = 1 if k ____________. (1, \(\frac{5}{3 \sqrt{2}}, \frac{1}{\sqrt{6}}, \frac{2}{3}\))
Solution:
\(\frac{5}{3 \sqrt{2}}\)
![]()
Question 2.
Mention which of the following statements are true (T) and false (F) :
(a) The equation y = x2 + 2x + 3 represents a parabola with its axis parallel to y – axis.
Solution:
True
(b) The latus rectum of the parabola y2 = -8x is 2.
Solution:
False
(c) The eccentricity of the parabola (y – 1)2 = 2(x + 3)2 is \(\frac{1}{3}\).
Solution:
False
(d) The line y = 3 is a tangent to the parabola (x + 2)2 = 6(y – 3).
Solution:
True
(e) The equation Ax2 + By2 = 1 represents an ellipse with its axis parallel to x – axis, if A > B > 0.
Solution:
False
(f) The focii of the ellipse \(\frac{x^2}{3}+\frac{y^2}{2}\) = 1 are the points (±1, 0).
Solution:
True
(g) The equation of the ellipse with focii at (0, ±4) and vertices (0, ±7) is \(\frac{x^2}{16}+\frac{y^2}{49}\) = 1.
Solution:
False
(h) The length of the latera recta of the ellipse \(\frac{x^2}{9}+\frac{y^2}{4}\) = 1 and \(\frac{(x+2)^2}{4}+\frac{(y-1)^2}{9}\) = 1 are equal.
Solution:
True
(i) The equation of the latera recta of the ellipse \(\frac{(x-4)^2}{16}+\frac{(y-1)^2}{9}\) = 1 are x = 4 ± √7.
Solution:
True
(j) The line y = x + 2 is a tangent to the ellipse \(\frac{x^2}{2}+\frac{y^2}{1}\) = 1.
Solution:
False
(k) The conjugate axis of the hyperbola, \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 meets the hyperbola at two points which are at distance 2b from each other.
Solution:
False
(l) The conjugate axis of the hyperbola, \(\frac{(y-3)^2}{9}+\frac{(x+2)^2}{3}\) = 1 is parallel to the line x = 4.
Solution:
False
(m) The length of the transverse axis of the hyperbola with focii at (±5, 0) and vertices at (±2, 0) is 10.
Solution:
False
(n) The latera recta of the ellipse \(\frac{x^2}{25}-\frac{y^2}{16}\) = 1 are same.
Solution:
True
(o) The y – axis is tangent to the hyperbola ay2 – bx2 = 1
Solution:
False
Question 3.
Find the equation of the parabola in each of the following cases :
(a) the vertex at (0, 0) and focus at (0, 3).
Solution:
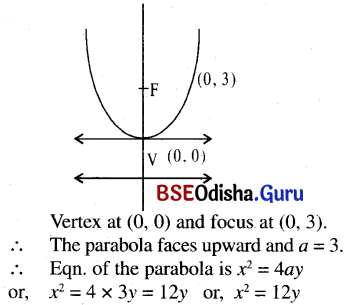
(b) the vertex at (0, 0) and directrix x – 2 = 0.
Solution:
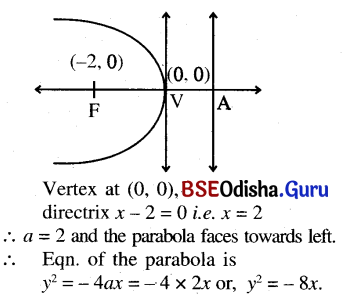
(c) the vertex at (6, -2) and focus at (-3, -2).
Solution:
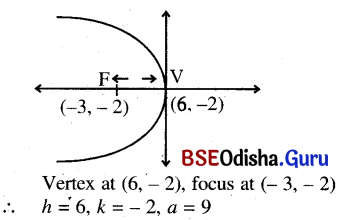
and the parabola facing towards left.
Eqn. of the parabola is (y – k)2 = -4a(x – h)
or, (y + 2)2 = -4 × 9(x – 6)
= -36(x + 6)
or, (y + 2)2 + 36(x – 6) = 0
(d) the vertex at (-2, 1) and focus at (-2, 4).
Solution:
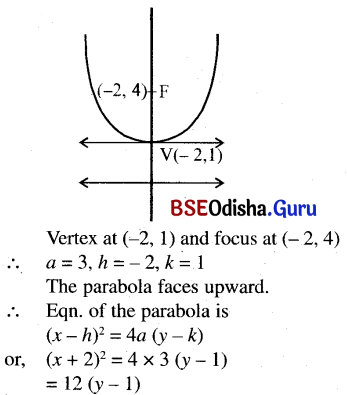
(e) the length of the latus rectum is 6. and the vertex is at (0, 0), the parabola opening to the right.
Solution:
The length of the latus rectum is 6
∴ 4a = 6
The parabola opens to right and vertex at (0, 0).
∴ Eqn. of the parabola is y2 = 4ax = 6x.
(f) the vertex is at (0, 0) the parabola opening to the left and passing through (-1, 2).
Solution:
Vertex at (0, 0), parabola opening to left, passing through (-1, 2).
∴ Let the eqn. of the parabola be y2 = -4ax
As it passes through (-1, 2),
we have 4 = -4a (-1) or, a = 1
∴ Eqn. of the parabola is y2 = 4x.
(g) the vertex at (0, 0) the parabola opens downwards, and the latus rectum of length 10.
Solution:
Vertex at (0, 0), the parabola opens downward, length of the latus rectum is 10.
∴ 4a = 10
∴ Eqn. of the parabola is
x2 = -4ay or, x2 = -10y.
(h) the axis is vertical and the parabola passes through the points (0, 2), (-1, 1), (2, 10).
Solution:
Axis is vertical, parabola passes through the points (0, 2), (-1, 1), and (2, 10).
Let the eqn. of the parabola be
x2 + 2gx + 2fy + c = 0. As it passes through the above points,
we have 0 + 0 + 2f . 2 + c = 0
⇒ c = -4f, 1 – 2g + 2f . 1 + c = 0
⇒ c = 2g – 2f – 1 and
4 + 2g . 2 + 2f . 10 + c = 0
⇒ c = -4g – 20f – 4
∴ -4f = 2g – 2g – 1

∴ Equation of the parabola is
x2 + 2gx + 2fy + c = 0
or, x2 + 2x – y + 2 = 0
or, y = x2 + 2x + 2
(i) the axis is horizontal and the parabola passes through the points (2, -1), (-2, -4), and (-1, 3).
Solution:
Le the eqn. of the parabola be
y2 + 2gx + 2fy + c = 0
As it passes through the points (2, -1), (-2, -4), and (-1, 3)
we have 1 + 2g . 2 +2f (-1) + c = 0 …(1)
16 + 2g (-2) + 2f (-4) + c = 0 …(2)
and 9 + 2g (-1) + 2f . 3 + c = 0 …(3)
∴ From eqn. (1) → 1 + 4g – 2f + c = 0
⇒ c = 2f – Ag – 1
Eqn. (2) → 16 – 4g – 8f + c = 0
⇒ c = 8f + 4g – 16
and eqn. (3) → 9 – 2g + 6f + c = 0
⇒ c = 2g – 6f – 9
∴ – 1 + 2f – 4g = 8f + 4g – 16
or, -6f = 8g – 15 or, f = \(\frac{8 g-15}{-6}\)
Again -1 + 2f – 4g = 2g – 6f – 9
or, 8f = 6g – 8 or, f = \(\frac{6 g-8}{8}\)
∴ \(\frac{8 g-15}{-6}=\frac{6 g-8}{8}\)
or, 32g – 60 = -18g + 24
or, 50g = 84

(j) Vertex at (1, 3) and the directrix, x + 3 = 0.
Solution:
Vertex at (1, 3), directrix x + 3 = 0
∴ h = 1, k = 3
We have the directrix is x = h – a
∴ h – a = -3
or, a = h + 3 = 4
∴ Eqn. of the parabola is
(y – k)2 = 4a(x – h)
or, (y – 3)2 = 16(x – 1)
![]()
(k) Vertex at (1, -1) and the directrix y – 2 = 0
Solution:
Vertex at (2, -1), directrix y – 2 = 0
∴ h = 1, k = -1
We have the directrix is y = k – a
∴ k – a = 2
or, a = k – 2 = -1 – 2 = – 3
∴ Eqn. of the parabola is
(x – h)2 = 4a(y – k)
⇒ (x – 1)2 = 4 (-3) (y + 1)
⇒ (x – 1)2 = -12 (y + 1)
⇒ (x – 1)2 + 12 (y + 1) = 0
(l) the focus at(-2, 3) and the directrix 3x + 4y – 2 = 0.
Solution:
Focus at (-2, 3),
directrix 3x + 4y – 2 = 0.

Question 4.
Find the equation of the ellipse in each of the following cases :
(a) center at (0, 0), one vertex at (0, -5) and one end of minor axis is (3, 0).
Solution:
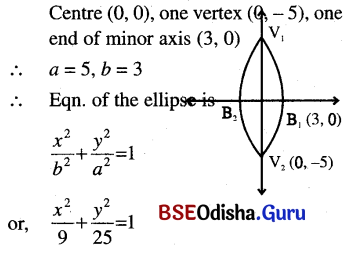
(d) centre at (0, 0), one vertex at (7, 0) and one end of the minor axis is (0, -5).
Solution:

(c) foci at (±5, 0), and the length of the major axis is 12.
Solution:
Foci at (±5, 0),
length of the major axis is 12
∴ c = 5, 2a = 12
∴ a = 6
∴ b2 = a2 – c2 = 36 – 25 = 11
Equ. of the ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 or, \(\frac{x^2}{25}+\frac{y^2}{4}\) = 1
(e) center at (5, 4) and the major axis, is of length 16 and the minor axis is of length 10.
Solution:
Centre at (5, 4), major axis 16, minor axis 10.
∴ h = 5, k = 4, 2a = 16, 2b = 10
∴ a = 8, b = 5
Eqn. of the ellipse is \(\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}\) = 1
or, \(\frac{(x-5)^2}{64}+\frac{(y-4)^2}{25}\) = 1
(f) Centre at (-3, 3), vertex at (-3, 6), and one end of minor axis at (0, 3).
Solution:
Centre at (-3, 3), vertex at (-3, 6),
one end of minor axis (0, 3).

(g) Centre at (0, 0), axes parallel to coordinate axes, eccentricity is \(\frac{1}{\sqrt{2}}\) and the minor axis is of length 5.
Solution:
(0, 0), axes parallel to coordinate axes, eccentricity is \(\frac{1}{\sqrt{2}}\), and the minor axis is 5.
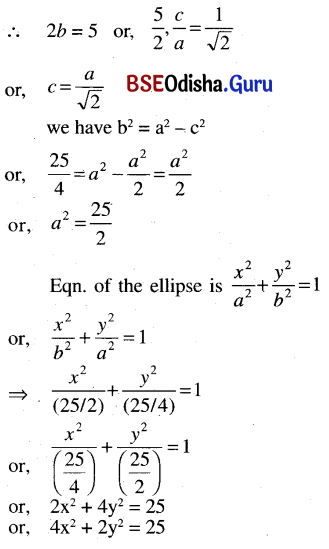
(h) centre at (0, 0) axes parallel to coordinate axes, eccentricity is \(\frac{\sqrt{3}}{2}\) and the ellipse passing through the point (√3, \(\frac{1}{2}\))
Solution:

we have 3 + 4 × \(\frac{1}{4}\) = a2 or, a2 = 4
∴ Eqn of the ellipse is x2 + 4y2 = 4
(i) centre at (0, 0), one end of the major axis is (-5, 0) and eccentricity \(\frac{3}{5}\)
Solution:
centre at (0, 0), one end of the major axis is (-5, 0), eccentricity \(\frac{3}{5}\)
∴ a = 5, \(\frac{c}{a}\) = \(\frac{3}{5}\) or, c = 3
∴ b2 = a2 – c2 = 25 – 9 = 16
∴ Eqn. of the ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 or, \(\frac{x^2}{25}+\frac{y^2}{16}\) = 1
![]()
(j) axis parallel to coordinate axes, the centre at (0, 0) and the ellipse passing through (3, -2) and (-1, 3).
Solution:
Axis parallel to coordinate axes, centre at (0, 0), ellipse passing through (3, -2) and (-1, 3).
Let the eqn. of the ellipse be

(k) centre at (3, 4), axis parallel to x – axis and passing through (6, 4) and (3, 6).
Solution:
Centre at (3, 4), axis parallel to x – axis, ellipse passing through (6, 4) and (3, 6).
Let the eqn. of the ellipse be

(l) Centre at (-2, 1) axis parallel to y – axis, eccentricity is \(\frac{\sqrt{7}}{4}\) and the ellipse passing through (-2, 5).
Solution:
Centre at (-2, 1), axis parallel to y – axis, eccentricity is \(\frac{\sqrt{7}}{4}\) passing through (-2, 5)

Question 5.
Obtain the equation of a hyperbola in each of the following cases :
(a) foci at (±4, 0) and vertices (±2, 0).
Solution:
Here c = 4, a = 2
∴ b2 = c2 – a2 = 16 – 4 = 12
∴ Eqn. of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 or, \(\frac{x^2}{4}-\frac{y^2}{12}\) = 1
(b) foci at (0, ±72) and vertices (0, ±1).
Solution:
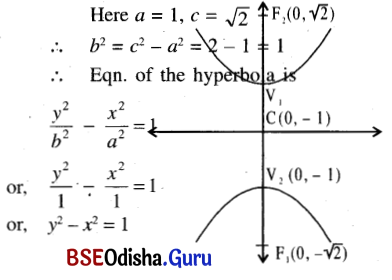
(c) centre at (0, 0) transverse axis along x – axis of length 4, and focus at (2√5,0).
Solution:
Here 2a = 4, c = 2√5
∴ a =2
∴ b2 = c2 – a2 = 20 – 4 = 16
∴ Eqn. of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 or, \(\frac{x^2}{4}-\frac{y^2}{16}\) = 1
(d) centre at (0, 0), the conjugate axis along x – axis of length 6 and eccentricity 2.
Solution:
Here 2b = 6 ⇒ b = 3, \(\frac{c}{a}\) = 2
or, c = 2a
We have a2 + b2 = c2
or, a2 + 9 = 4a2
or, 3a2 = 9 or, a2 = 3
∴ Eqn. of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 or, \(\frac{x^2}{3}-\frac{y^2}{9}\) = 1
(e) foci at (±2√3, 0) and eccentricity √3.
Solution:
Here c = 2√3, \(\frac{c}{a}\) = √3
or, a = \(\frac{c}{\sqrt{3}}\) = 2
∴ b2 = c2 – a2 = 12 – 4 = 8
∴ Eqn. of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 or, \(\frac{x^2}{4}-\frac{y^2}{8}\) = 1
(f) centre at (0, 0) transverse axis is along y – axis, the distance between the foci is 14 and the distance between the vertices is 12.
Solution:
Here 2c = 14, 2a = 12
∴ c = 7, a = 6
∴ b2 = c2 – a2 = 49 – 36 = 13
∴ Eqn. of the hyperbola is \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1 or, \(\frac{x^2}{36}-\frac{y^2}{13}\) = 1
(g) centre (1, -2), transverse axis parallel to the x-axis of length 6 and conjugate axis of length 10.
Solution:
Centre (1, -2), transverse axis parallel to x – axis of length 6, the conjugate axis of length 10.
∴ 2a = 6, 2b= 10
∴ a = 3, b = 5, h = 1, k = -2
∴ Eqn. of the hyperbola \(\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}\) = 1 or, \(\frac{(x-1)^2}{9}-\frac{(y-2)^2}{25}\) = 1
(h) Centre (2, -3), eccentricity \(\frac{5}{3}\) and hyperbola passing through (5, -3).
Solution:
Here h = 2, k = -3, \(\frac{c}{a}=\frac{5}{3}\) or, c = \(\frac{5 a}{3}\) we have c2 = a2 + b2

(i) centre at origin, axis perpendicular to y-axis and the hyperbola passes through the points (3, -2) and (5, -7).
Solution:
Let the eqn. of the hyperbola be \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1
As the hyperbola passes through the points (3, -2) and (5, -7)
we have \(\frac{9}{a^2}-\frac{4}{b^2}\) = 1 …..(1)

or, 45x2 – 16y2 = 341.
![]()
(j) The transverse axis parallel to the y-axis, the hyperbola passes through the points (\(\frac{11}{3}\), 0), (1, 2) and its centre is the intersection of the lines. x + y – 6 = 0, 4x – y + 1 = 0.
Solution:
Solving x + y – 6 = 0
\(\frac{4 x-y+1=0}{5 x=5 \quad \text { or, } x=0}\)
∴ y = 6 – x = 6 – 1 = 5
∴ Centre of the hyperbola is at (1, 5).

Question 6.
Reducing to standard form, obtain the coordinates of the vertex, focus, endpoints of the latus rectum, the length of latus return, the equation of axis and directrix of the following parabolas:
(a) y2 – 4x + 4y – 1 = 0
Solution:
y2 – 4x + 4y – 1 = 0
or, y2 + 4y = 4x + 1
or, y2 + 4y + 4 = 4x + 5
or, (y + 2)2 = 4(x + \(\frac{5}{4}\))
or, (y + 2)2 = 4 × 1 × (x + \(\frac{5}{4}\)) standard from

Length of the latus rectum
= 4a = 4 × 1 = 4
Eqn. of the axis is y = k or, y = -2
Eqn. of the directrix is x = h – a
or, \(\frac{-5}{4}\) – 1 \(\frac{-9}{4}\)
or, 4x + 9 = 0
(b) 2x2 – 4y + 6x – 3 = 0
Solution:
2x2 – 4y + 6x – 3 = 0
or, 2x2 + 6x = 4y + 3
or, 2(x2 + 3x) = 4(y + \(\frac{3}{4}\))


(c) x2 + x + y + 1 = 0
Solution:
x2 + x + y + 1 = 0

and (0, -1)
Length of the latus rectum = 4a = 1.
Eqn. of the axis x = h or x = –\(\frac{1}{2}\)
or, 2x + 1 = 0
Eqn. of the directrix is y = k – a or, y = \(\frac{-3}{4}+\frac{1}{4}\)
or, y = –\(\frac{1}{2}\) or, 2y + 1 = 0
(d) y2 + 14y – 3x + 1 = 0
Solution:
y2 + 14y – 3x + 1 = 0
or, y2 + 14y = 3x – 1
or, y2 + 2.y.1 + 49 = 3x – 1 + 49
or, (y + 7)2 = 3x + 48 = 3 (x + 16)
or, (y + 7)2 = 4 × \(\frac{3}{4}\) (x + 16)
This is the standard form

y = k or, y = -7
or, y + 7 = 0
Eqn of the directrix is x = h – a
or, x = -16 = \(\frac{3}{4}\) = \(\frac{-67}{4}\)
or, 4x + 67 = 0
![]()
Question 7.
Reducing to standard form, obtain the coordinates of the centre, the foci, the vertices, the endpoints of the minor axis, the endpoints of latera recta, the equation of the directrices and the eccentricity of the following ellipses :
(a) 3x2 + 4y2 + 6x + 8y – 5 = 0
Solution:
3x2 + 4y2 + 6x + 8y – 5 = 0
or, 3(x2 + 2y) + 4(y2 + 2y) = 5
or, 3(x2 + 2x + 1 – 1) + 4(y2 + 2y + 1 – 1) = 5
or, 3(x + 1)2 – 3 + 4(y + 1)2 – 4 = 5
or, 3(x + 1)2 + 4(y + 1)2 = 12
or, \(\frac{(x+1)^2}{4}+\frac{(y+1)^2}{3}\) = 1 is the standard form.
∴ h = -1, k = -1, a2 = 4, b2 = 3
∴ a = 2, b = √2, c = \(\sqrt{a^2-b^2}\) = 1
Centre at (h, k) = (-1, -1), the vertices of (h±a, k)
= (-1±2, -1) = (1, -1)
and (-3, -1) foci at (h±c, k)
= (-1±1, -1) = (-2, -1) and (0, -1)
The endpoints of minor axis are (h, k±b) = (-1, -1±√3)
Endpoints of latera recta are (h + c, k±\(\frac{b^2}{a}\)) and (h – c, k±\(\frac{b^2}{a}\))

(b) 4x2 + 8y2 + 4x + 24y – 13 = 0
Solution:
4x2 + 8y2 + 4x + 24y – 13 = 0
or, 4(x2 + x) + 8(y2 + 3y) = 13


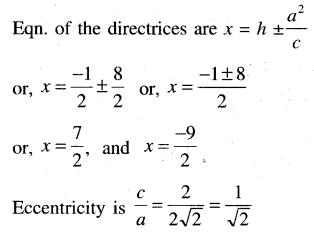
(c) 2x2 + 3y2 – 12x + 24y + 60 = 0
Solution:
2x2 + 3y2 – 12x + 24y + 60 = 0
or, 2(x2 – 6x) + 3(y2 + 8y) = -60
or, 2(x2 – 2.x.3 + 9 – 9) + 3(y2 + 2.y.4 + 16 – 16 = -60
or, 2(x – 3)2 – 18 + 3 (y + 4)2 – 48 = -60
or, 2 (x – 3)2 + 3 (y + 4)2 = 6
or, \(\frac{(x-3)^2}{3}+\frac{(y+4)^2}{2}\) = 1 is the standard form.
∴ h = 3, k = -4, a2 = 3, b2 = 2
∴ a = √3, b = √2, c = \(\sqrt{a^2-b^2}\) = 1
Centre at (h, k) = (3, -4),
Foci at (h±c, k)
= (3±1, -4) = (4, -4) and (2, -4)
Vertices at (h±a, k) = (3±√3, -4)
The endpoints of the minor axis are (h, k±b) = (3, -4±√2)

(d) 9x2 + 4y2 + 36x – 8y + 4 = 0
Solution:
9x2 + 4y2 + 36x – 8y + 4 = 0
or, 9(x2 + 4x) + 4(y2 – 2y) = -4
or, 9(x2 + 4x + 4 – 4) + 4(y2 – 2y + 1 – 1) = -4
or, 9(x + 2)2 – 36 + 4(y – 1)2 – 4 = -4
or, 9(x + 2)2 + 4(y – 1)2 = 36
or, \(\frac{(x+2)^2}{4}+\frac{(y-1)^2}{9}\) = 1, This is the standard form
∴ h = -2, k = 1, a2 = 9, b2 = 4
∴ a = 3, b = 2, c = \(\sqrt{a^2-b^2}\) = √5
∴ Centre at (h, k) = (-2, 1)
Foci at (h, k±c) = (-2, 1±√5)
Vertices at (h, k±a)
= (-2, 1±3)
Endpoints of minor axis are (h±b, k) = (-2±2, 1)
The endpoints of latera recta are (h ± \(\frac{b^2}{a}\), k ± c) = (-2 ± \(\frac{4}{3}\), 1 ± √5)
End of directrices arty = k ± \(\frac{a^2}{c}\)
or y = 1 ± \(\frac{9}{\sqrt{5}}\)
Eccentricity is \(\frac{c}{a}\) = \(\frac{\sqrt{5}}{3}\).
Question 8.
Reducing to standard form, obtain the coordinates of the centre, the vertices, the foci, the endpoints of the conjugate axis, the endpoints of latera recta, the equation of directrices and the eccentricity of the following hyperbola :
(a) x2 – 2y2 – 6x – 4y + 5 = 0
Solution:
x2 – 2y2 – 6x – 4y + 5 = 0
or, x2 – 6x – 2(y2 + 2y) =-5
or, x2 – 2.x.3 + 9 – 9 – 2(y2 + 2y + 1 – 1) = -5
or, (x – 3)2 – 2(y + 1)2 + 2 = 4
or, (x – 3)2 – 2(y + 1)2 = 2
or, \(\frac{(x-3)^2}{2}-\frac{(y+1)^2}{1}\) = 1 the standard form
∴ h = 3, k = -1, a2 = 2, b2 = 1
∴ a = √2 , b = 1, c \(\sqrt{a^2+b^2}\) = √3
∴Centre at (h, k) = (3, -1)
Vertices (h±a, k) = (3±√2, -1)
Foci at (h±c, k) = (3±√3 , -1)
The endpoints of a conjugate axis are (h, k±b) = (3, -1±1)
Endpoints of latera recta are (h ± c, k ± \(\frac{b^2}{a}\)) and (3±√3, -1 ± \(\frac{1}{\sqrt{2}}\))
Eqn. of directrices are x = h ± \(\frac{a^2}{c}\) = 3 ± \(\frac{2}{\sqrt{3}}\) or, x = 3 ± \(\frac{2}{\sqrt{3}}\)
Eccentricity = \(\frac{c}{a}=\frac{\sqrt{3}}{\sqrt{2}}\)
(b) 9y2 – 4x2 – 90y + 189 = 0
Solution:
9y2 – 4x2 – 90y + 189 = 0
or, 9(y2 – 10y) – 4x2 = -189 .
or, 9(y2 – 2.y.5 + 25 – 25) – 4x2 = -189
or, 9(y – 5)2 – 225 – 4x2 = -189
or, 9(y – 5)2 – 4x2 = 225 – 189 = 36
or, \(\frac{(y-5)^2}{4}-\frac{(x)^2}{9}\) = 1 the standard form
h = 0, k = 5, a2 = 4, b2 = 9
a = 2 , b = 3, c \(\sqrt{a^2+b^2}\) = √13
Centre at (h, k) = (0, 5)
Vertices (h, k±a) = (0, 5±2)
Foci at (h , k±c) = (0, 5±√13)
The endpoints of a conjugate axis are (h±a, k) = (0±2, 5) = (±2, 5)
Endpoints of latera recta are (h ± \(\frac{b^2}{a}\), k ± c) = (0 ± \(\frac{9}{2}\), 5 ± √13)
Eqn. of directrices are y = k ± \(\frac{a^2}{c}\) = 5 ± \(\frac{4}{\sqrt{13}}\)
Eccentricity = \(\frac{c}{a}\) = \(\frac{\sqrt{13}}{2}\)
(c) 49x2 – 4y2 – 98x + 48y – 291 = 0
Solution:
49x2 – 4y2 – 98x + 48y – 291 = 0
or, 49(x2 – 2x) – 4(y2 – 12y)= 291
or, 49(x2 – 2x + 1 – 1) – 4(y2 – 2.y.6 + 36 – 36) = 291
or, 49(x – 1 )2 – 49 – 4(y – 6)2 + 144 = 291
or, 49(x – 1)2 – 4(y – 6)2
= 291 – 144 + 49 = 196
or, \(\frac{(x-1)^2}{4}\) – \(\frac{(y-6)^2}{49}\) = 1
h= 1, k = 6, a2 = 4, b2 = 49
a = 2, b = 7, c = \(\sqrt{a^2+b^2}\) = √53
Centre at (h, k) = (1, 6)
Vertices at (h±a, k) = (1±2, 6)
Foci at (h±c, k) = (1±√53, 6)
Endpoints of latera recta are (h ± c, k ± \(\frac{b^2}{a}\)) = (1 ±√53, 6 ± \(\frac{49}{2}\))
Eccentricity = \(\frac{c}{a}=\frac{\sqrt{53}}{2}\)
Endpoints of conjugate axis are (h, k±b) = (1, 6±7) = (1, -1) and (1, 13)
![]()
(d) 3x2 – 2y2 – 4y – 26 = 0
Solution:
3x2 – 2y2 – 4y – 26 = 0
or, 3x2 – 2(y2 + 2y) = 26
or, 3x2 – 2(y2 + 2y + 1 – 1) = 26
or, 3x2 – 2(y + 1)2 + 2 = 26
or, 3x2 – 2(y + 1)2 = 24
or, \(\frac{x^2}{8}-\frac{(y+1)^2}{12}\) = 1 Standard form
h= 0, k = -1, a2 = 8, b2 = 12
a = 2√2, b = 2√3, c = \(\sqrt{a^2+b^2}\) = √20 = 2√3
Centre at (h, k) = (0, -1)
Vertices at (h±a, k) = (±2√2, -1)
Foci at (h±c, k) = (±2√5, -1)

Question 9.
Prove that the equation of the parabola whose vertex and focus are at distances α and β from the origin on the x-axis respectively is y2 = 4(β – α)(x – α)
Solution:

Question 10.
Find the locus of the point of trisection of a double ordinate of the parabola y2 = 4ax.
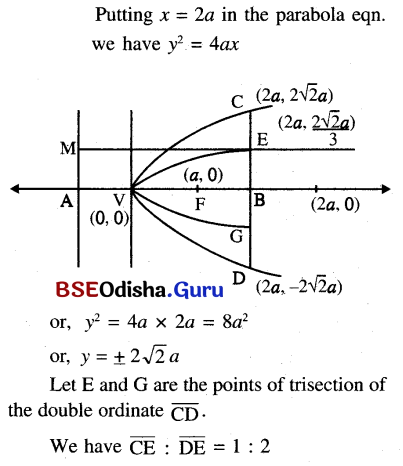
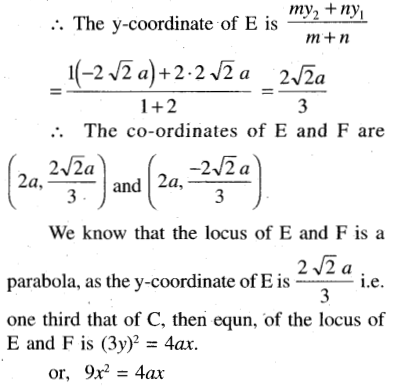
Question 11.
(a) Prove that a double ordinate of the parabola y2 = 4ax of length 8a subtends a right angle at its vertex.
Solution:

(b) Find the angle which a double ordinate of length 2a subtends at its vertex and focus.
Solution:
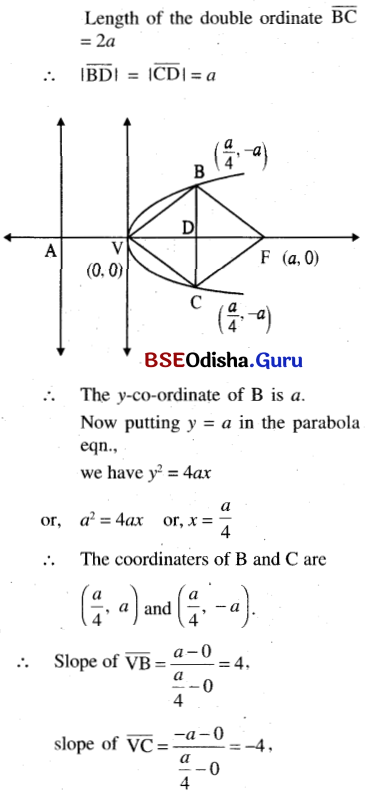
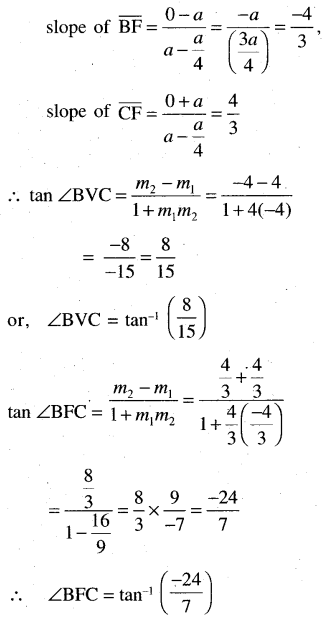
Question 12.
(a) Obtain the equations of the tangent and normal of the parabola y2 = 4ax at a point where the ordinate is equal to three times the abscissa.
Solution:
Putting y = 3x in the parabola equation.
we have y2 = 4ax
or, 9x2 = 4ax
or, x = \(\frac{4 a}{9}\)
∴ y = 3x = \(\frac{4 a}{3}\)
∴ The point of contact is (\(\frac{4 a}{9}\), \(\frac{4 a}{3}\))

(b) Find the equation of tangents and normals to the parabola y2 = 4ax at the ends of its latus rectum.
Solution:
The endpoints of the latus rectum of the parabola y2 = 4ax are (a, 2a) and (a, -2a).
∴ Eqn. of the tangent at (a, 2a) is yy1 = 2a (x + x1)
or, 2ay = 2a (x + a)
or, y = x + a
or, x – y + a = 0
Eqn. of the tangent at (a, -2a) is -2ay = 2a(x + a).
or, -y = x + a
or, x + y + a = 0
Eqn. of the normal at (a, 2a) is y – y1 = \(\frac{-y_1}{2 a}\) (x – x1)
or, y + 2a = \(\frac{+2 a}{2 a}\) (x – a)
or, y – 2a = -x + a
or, x – y – 3a = 0
![]()
(c) Find the equations of tangents and normals to the parabola y2 = 4ax at the points, where it is cut by the line y = 3x – a.
Solution:
Solving y = 3x – a, y2 = 4ax
∴ (3x – a)2 = 4ax
or, 9x2 + a2 – 6ax – 4ax = 0
or, 9x2 – 10ax + a2 = 0
or, 9x2 – 9ax – ax + a2 = 0
or, 9x(x – a) – a(x – a) = 0
or, (x – a) (9x – a) = 0
∴ x = a, x = \(\frac{a}{9}\)
∴ y = 3x – a = 3a – a = 2a

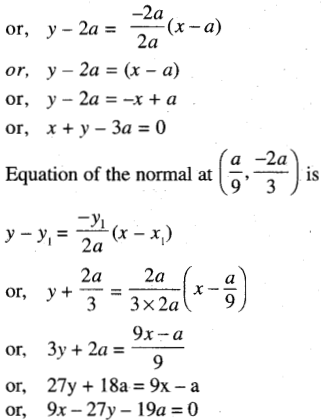
(d) Show that the tangent to the parabola y2 = 4ax at the point (a’, b’) is perpendicular to the tangent at the point (\(\frac{a^2}{a^{\prime}}, \frac{-4 a^2}{b^{\prime}}\)).
Solution:

∴ The product of their slopes = -1
∴ The two tangents are perpendicular to each other.
(e) A tangent to the parabola y2 = 8x makes an angle of 45° with the line 3x – y + 5 = 0. Find the equation and the point of contact.
Solution:

or, 4a + 2y + 2 = 0 or, 2x + y + 1 = 0
(f) Prove that, for all values of k, the line y = k(x + a) + \(\frac{a}{k}\) is a tangent to the parabola y2 = 4a(x + a).
Solution:

(g) Obtain the condition that the line lx + my + n = 0 will touch the parabola y2 = 4ax
Solution:
We have lx + my + n = 0
or, y = \(\frac{-l x-n}{m}\)
Now putting the value of y in the parabola Eqn., we have y2 = 4ax.
or, \(\frac{-l x-n}{m}\)2 = 4ax
or, l2x2 + n2 + 2lnx = 4am2x
or, l2x2 + x(2ln – 4am2) + n2 = 0
a’ = l2, b’ = 2ln – 4am2, c’ = n2
As the line is a tangent to the parabola,
we have b’2 – 4a’c’ = 0.
or, (2ln – 4am2)2 – 4l2x2 = 0
or, 4l2n2 + 16a2m4 – 16alnm2 – 4l2n2 = 0
or, 16am2(am2 – ln) = 0
or, am2 – ln = 0
or, am2 = ln
(h) Prove that the line 4x – 2y – 1 = 0 touches the parabola whose focus is at (0, 0) and the directrix is the line y = 2x – 1.
Solution:
According to the definition,


Question 13.
(a) If (-2, 0) and (2, 0) are the two vertices of a triangle with a perimeter of 16, then obtain the locus of the third vertex.
Solution:

or, 8x2 + 9y2 – 288 = 0
∴ This is the locus of the 3rd vertex of the triangle.
(b) A point in a plane is such that the sum of its distances from point (2, 2) and (6, 2) is 12. Find the locus of the point.
Solution:
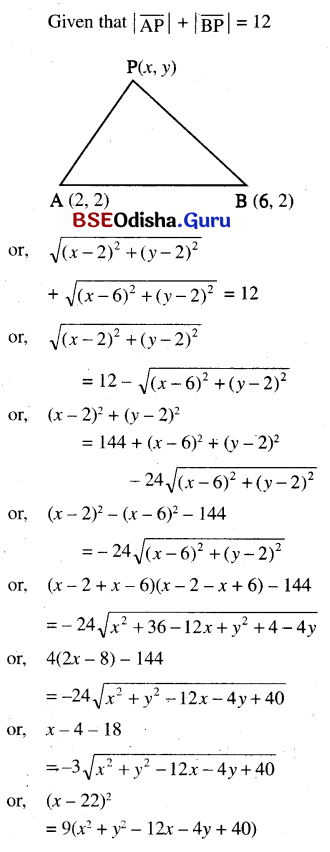
or, x2 + 484 – 44x
= 9x2 + 9y2 – 108x – 36y + 360
or, 8x2 + 9y2 – 64x – 36y – 124 – 0 which is the locus of the point P.
(c) Obtain the equation of the ellipse which has its centre at the origin, a focus at (2, 0) and the corresponding directrix is the line 2x = 7. Calculate the length of the latus rectum.
Solution:
Centre at (0, 0), focus at (2, 0),
directrix is 2x = 7

![]()
(d) Find the equation of the ellipse which has its centre at (-1, 4), eccentricity \(\frac{1}{\sqrt{3}}\) and the ellipse passes through the point (3, 2).
Solution:

Question 14.
(a) Find the equation of the tangent and normal to the ellipse \(\frac{x^2}{16}+\frac{y^2}{9}\) = 1 at the point (\(\frac{8}{3}\), √5)
Solution:
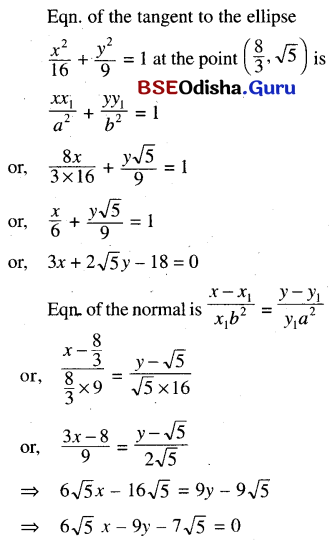
(b) Find the equation of the tangent and normals to the ellipse 2x2 + 3y2 = 6 at the endpoints of the latera recta.
Solution:
2x2 + 3y2 = 6


(c) Prove that the line y = 2x + 5 is a tangent to the ellipse 9x2 + 4y2 = 36 and find the point of contact.
Solution:
Putting y = 2x + 5 in the ellipse eqn.
we have 9x2 + 4y2 = 36
or, 9x2 + 4(2x + 5)2 = 36
or, 9x2 + 4(4x2 + 25 + 20x) = 36
or, 9x2 + 16x2 + 100 + 80x – 36 = 0
or, 25x2 + 80x + 64 = 0 …..(1)
∴ b2 – 4ac = (80)2 – 4 × 25 × 64
= 6400 – 6400 = 0
∴ The line y = 2x + 5
touches the ellipse 9x2 + 4y2 = 36.
Now from eqn. (1),
we have (5x + 8)2 = 0

(d) Find the equation of the tangent to the ellipse 4x2 + 5y2 = 20 which are parallel to the line x – y = 2
Solution:
4x2 + 5y2 = 20


(e) Find the equation of the tangent to the ellipse 4x2 + 9y2 = 1, which are perpendicular to 2ax + y – 1 = 0.
Solution:
4x2 + 9y2 = 1

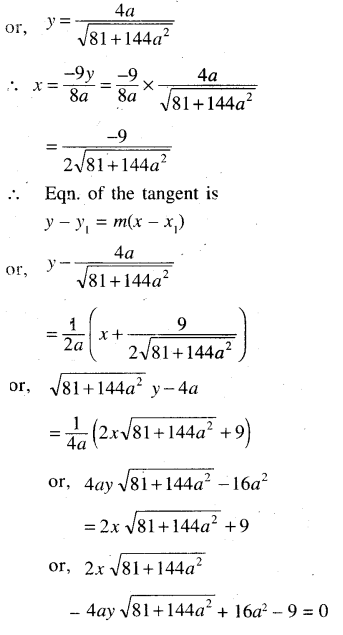
(f) Prove that the line x cos α + y sin α = p touches the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1, if p2 = a2 cos2 α + b2 sin2 α.
Solution:

(g) Prove that the product of the distances of the foci from any tangent to the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 is equal to b2
Solution:
The tangent at (x1, y1) to the ellipse
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \text { is } \frac{x x_1}{a^2}+\frac{y y_1}{b^2}=1\)

Question 15.
(a) Find the equation of the hyperbola which has it foci at (0, 0) and (0, 4) and which passes through the point (12, 9).
Solution:
Foci at (0, 0) and (0, 4)
∴ Centre at (0, 2)

(b) Find the equation of the hyperbola with foci at (±3, 0) and directrices x = ± 2.
Solution:
Foci at (±3, 0) and directrices x = ±2.
∴ c = 3, \(\frac{a^2}{c}\) = 2, a2 = 2c = 6
∴ b2 = c2 – a2 = 9 – 6 = 3
∴ Eqn. of the ellipse \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1
or, \(\frac{x^2}{6}-\frac{y^2}{3}\) = 1 or, x2 – 2y2 = 6
(c) Find the foci and latus rectum of the hyperbola whose transverse and conjugate axes are 6 and 4 and whose centre is at (0, 0).
Solution:
The transverse axis is 6, the conjugate axis is 4, the centre is at (0, 0).
∴ 2a = 6, 2b = 4
∴ a = 3, b = 2
∴ c = \(\sqrt{a^2+b^2}=\sqrt{9+4}=\sqrt{13}\)
The foci are (±c, 0) = (±√13 , 0)
∴ Length of the latus rectum = \(\frac{2 b^2}{a}=\frac{2 \times 4}{3}=\frac{8}{3}\)
![]()
Question 16.
(a) Find the equation of tangent and normal to the hyperbola x2 – 6y2 = 3 at the point (-3, -1).
Solution:
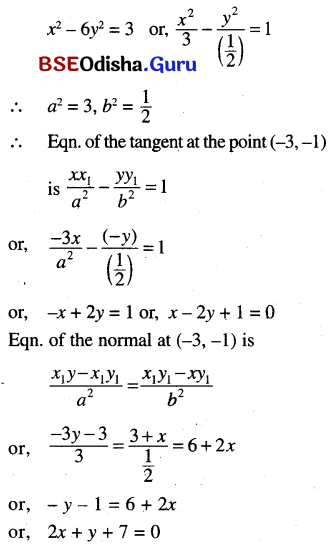
(b) Find the equation of the tangent to the hyperbola 4x2 – 11y2 = 1 which is parallel to the straight line 20x – 33y = 13.
Solution:

(c) Find the equation of tangent to hyperbola 9x2 – 16y2 = 144 which are perpendicular to the line 2x + 3y = 4.
Solution:
9x2 – 16y2 = 144
or, 18x – 32y\(\frac{d y}{d x}\) = 0

(d) Prove that the line x + y + 2 = 0 touches the hyperbola 3x2 – 5y2 = 30 and find the point of contact . Find also the equation of normal at the point.
Solution:
x + y + 2 = 0
or, y = -x – 2
putting y = -x – 2 in the hyperbola equation we have 3x2 – 5y2 = 30
or, 3x2 – 5 (-x – 2)2 = 30
or, 3x2 – 5 (x2 + 4 + 4x) = 30
or, 3x2 – 5x2 – 20 – 20x = 30
or, 2x2 + 20x + 50 = 30
or, x2 + 10x + 25 = 0
b2 – 4ac = 100 – 4 × 25 = 0
The line x + y + 2 = 0 touches the hyperbola 3x2 – 5y2 = 30
Now solving x2 + 10x + 25 = 0
we have x = – 5.
y = – x – 2 = 5 – 2 = 3
The point of contact is (-5, 3).
Eqn. of the normal is
y – y1 = m (x – x1)
or, y – 3 = 1 (x + 5)
or, x – y + 8 = 0
(e) Prove that the line x cos α + y sin α = p touches the hyperbola \(\frac{x^2}{a^2}-\frac{y^2}{b^2}\) = 1, if p2 = a2 cos2 α – b2 sin2 α.
Solution:
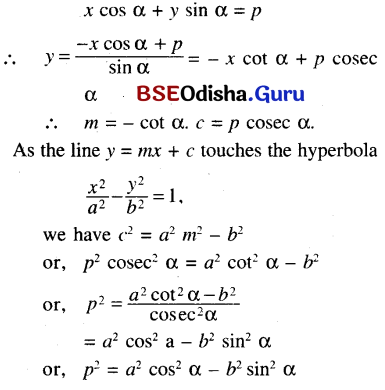
Must Read:
