Odisha State Board Elements of Mathematics Class 11 Solutions CHSE Odisha Chapter 14 Limit and Differentiation Ex 14(c) Textbook Exercise Questions and Answers.
CHSE Odisha Class 11 Math Solutions Chapter 14 Limit and Differentiation Exercise 14(c)
Question 1.
Evaluate the following limits :
(i) \(\lim _{x \rightarrow 0} \frac{x}{\sin 2 x}\)
Solution:
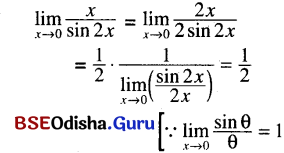
(ii) \(\lim _{x \rightarrow 0} \frac{\sin 3 x}{\sin 5 x}\)
Solution:
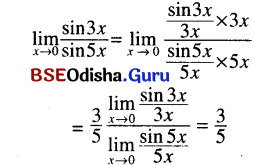
(iii) \(\lim _{x \rightarrow 0} \frac{\sin m x}{\sin n x}\)
Solution:
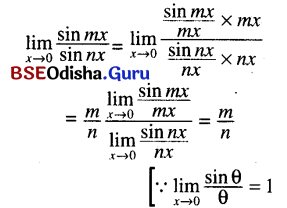
(iv) \(\lim _{x \rightarrow 0} \frac{\tan \alpha x}{x}\)
Solution:
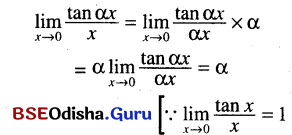
(v) \(\lim _{x \rightarrow 0} \frac{1-\cos x}{x^2}\)
Solution:

(vi) \(\lim _{x \rightarrow 0} \frac{\sin x^{\circ}}{x}\)
Solution:
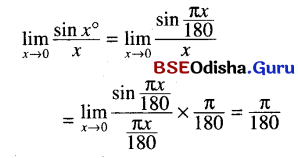
![]()
(vii) \(\lim _{x \rightarrow \pi} \frac{\sin x}{\pi-x}\)
Solution:
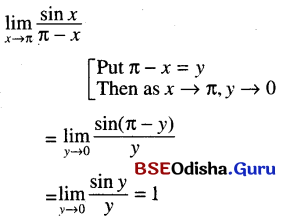
(viii) \(\lim _{x \rightarrow \frac{\pi}{2}} \frac{1-\sin x}{\left(\frac{\pi}{2}-x\right)^2}\)
Solution:
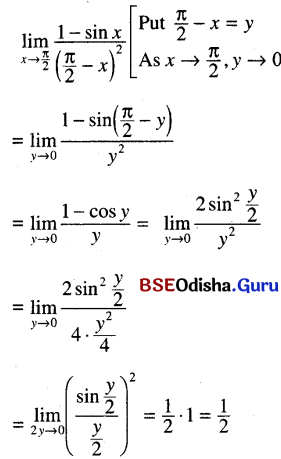
(ix) \(\lim _{x \rightarrow 0} \frac{1-\cos ^3 x}{x \sin 2 x}\)
Solution:
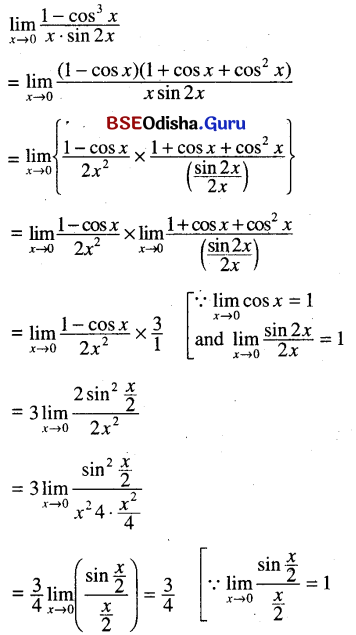
(x) \(\lim _{x \rightarrow 0} \frac{1+\sin x-\cos x}{1-\sin x-\cos x}\)
Solution:

(xi) \(\lim _{x \rightarrow 0} \frac{\tan x-\sin x}{x^3}\)
Solution:
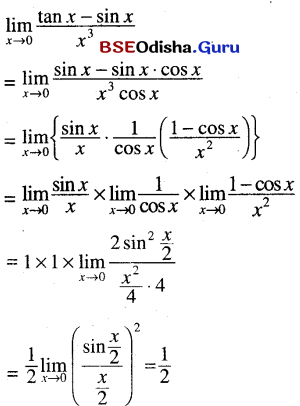
(xii) \(\lim _{x \rightarrow 0} \frac{(1-\cos x)^2}{\tan ^3 x-\sin ^3 x}\)
Solution:

(xiii) \(\lim _{x \rightarrow \frac{\pi}{2}}\left(\frac{\pi}{2}-x\right) \tan x\)
Solution:
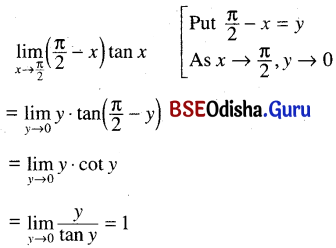
(xiv) \(\lim _{x \rightarrow \frac{\pi}{4}} \frac{\cos x-\sin x}{\cos 2 x}\)
Solution:
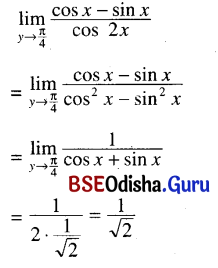
(xv) \(\lim _{x \rightarrow 0} \frac{x-x \cos 2 x}{\sin ^3 2 x}\)
Solution:
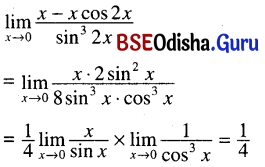
(xvi) \(\lim _{x \rightarrow 0} \frac{\sqrt{1+\sin x}-\sqrt{1-\sin x}}{\tan x}\)
Solution:

(xvii) \(\lim _{x \rightarrow 0} \frac{2 \sin x-\sin 2 x}{x^3}\)
Solution:

![]()
(xviii) \(\lim _{x \rightarrow 0} \frac{\cos x-\cos 5 x}{\cos 2 x-\cos 6 x}\)
Solution:

(xix) \(\lim _{x \rightarrow 0} \frac{\sin ^{-1} x}{x}\)
Solution:
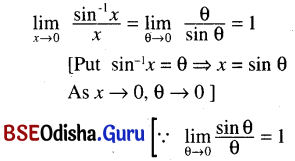
Question 2.
Evaluate
(i) \(\lim _{x \rightarrow \alpha} \frac{x \sin \alpha-\alpha \sin x}{x-\alpha}\)
Solution:
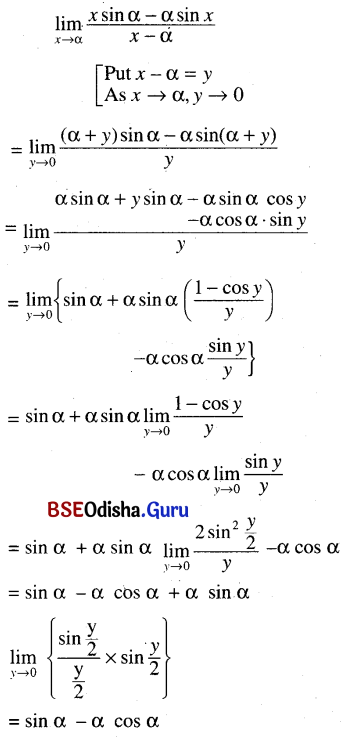
(ii) \(\lim _{x \rightarrow 0} x \sin \frac{1}{x}\)
Solution:
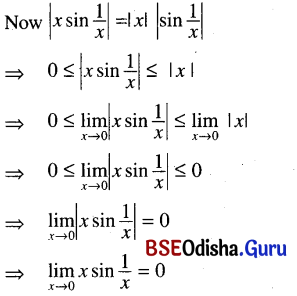
Question 3.
Evaluate the following limits :
(i) \(\lim _{h \rightarrow 0} \frac{\sin (x+h)-\sin x}{h}\)
Solution:
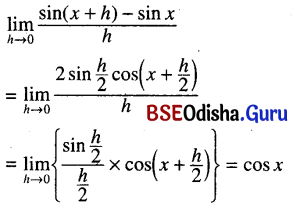
(ii) \(\lim _{h \rightarrow 0} \frac{\cos (x+h)-\cos x}{h}\)
Solution:
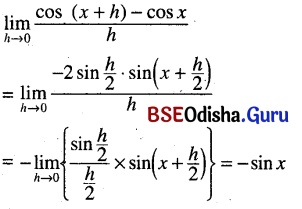
(iii) \(\lim _{h \rightarrow 0} \frac{\tan (x+h)-\tan x}{h}\)
Solution:
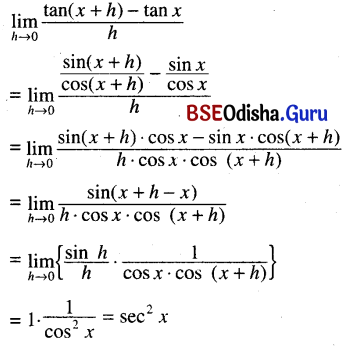
(iv) \(\lim _{h \rightarrow 0} \frac{{cosec}(x+h)-{cosec} x}{h}\)
Solution:
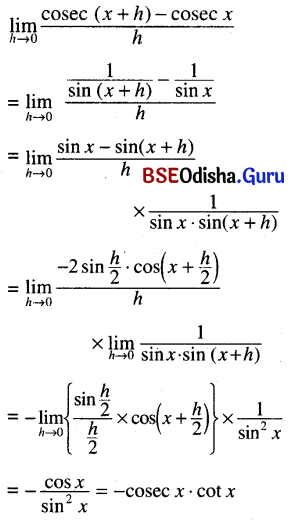
(v) \(\lim _{h \rightarrow 0} \frac{\sec (x+h)-\sec x}{h}\)
Solution:

(vi) \(\lim _{h \rightarrow 0} \frac{\cot (x+h)-\cot x}{h}\)
Solution:

(vii) \(\lim _{h \rightarrow 0} \frac{\sqrt{x+h}-\sqrt{x}}{h}\)
Solution:
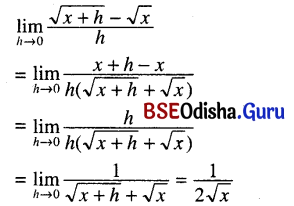
(viii) \(\lim _{h \rightarrow 0} \frac{\log _{\mathrm{a}}(x+h)-\log _a x}{h}\)
Solution:

(ix) \(\lim _{h \rightarrow 0} \frac{\ln (x+h)-\ln x}{h}\)
Solution:
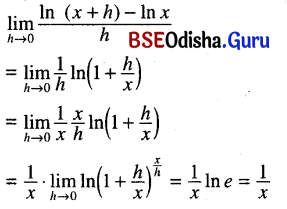
(x) \(\lim _{h \rightarrow 0} \frac{a^{x+h}-e^x}{h}\)
Solution:

(xi) \(\lim _{h \rightarrow 0} \frac{e^{x+h}-e^x}{h}\)
Solution:

![]()
(xii) \(\lim _{h \rightarrow 0}\left\{\frac{1}{(x+h)^3}-\frac{1}{x^3}\right\}\)
Solution:

(xiii) \(\lim _{h \rightarrow 0} \frac{\sin (x+h)-\sin (x-h)}{h}\)
Solution:
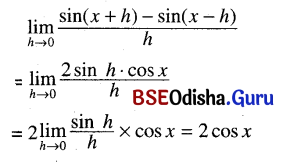
(xiv) \(\lim _{h \rightarrow 0} \frac{1}{h}\left\{\frac{1}{\sqrt{x+h}-\frac{1}{\sqrt{x}}}\right\}\)
Solution:

Question 4.
Evaluate the following :
(i) \(\lim _{x \rightarrow 0} \frac{\log _e\left(1+\frac{x}{2}\right)}{x}\)
Solution:
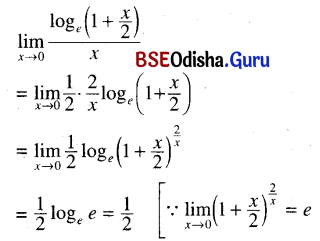
(ii) \(\lim _{x \rightarrow 1} \frac{x-1}{\log _e x}\)
Solution:

(iii) \(\lim _{x \rightarrow 1} \frac{\log _e(2 x-1)}{x-1}\)
Solution:

(iv) \(\lim _{x \rightarrow 0} \frac{\log _e(x+1)}{\sqrt{x+1}-1}\)
Solution:
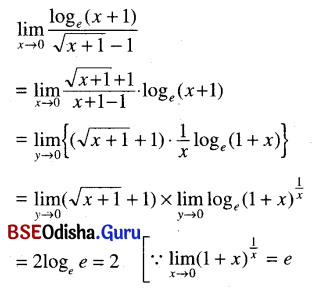
(v) \(\lim _{x \rightarrow 2} \frac{\log _e(x-1)}{x^2-3 x+2}\)
Solution:

(vi) \(\lim _{x \rightarrow 0} \frac{e^{a x}-1}{x}\)
Solution:
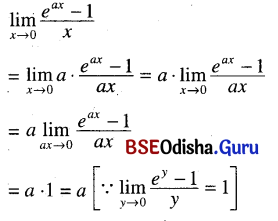
(vii) \(\lim _{x \rightarrow 0} \frac{e^{a x}-e^{-a x}}{x}\)
Solution:

(viii) \(\lim _{x \rightarrow 0} \frac{e^{3 x}-e^{2 x}}{e^{4 x}-e^{3 x}}\)
Solution:
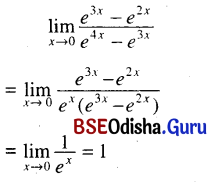
(ix) \(\lim _{x \rightarrow 0} \frac{a^{2 x}-1}{x}\)
Solution:
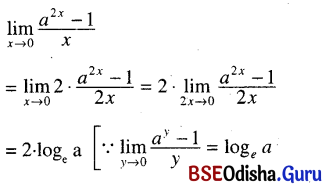
(x) \(\lim _{x \rightarrow 0} \frac{a^x-b^x}{x}\)
Solution:
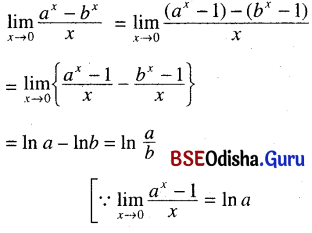
(xi) \(\lim _{x \rightarrow 1} \frac{2^{x-1}-1}{x-1}\)
Solution:
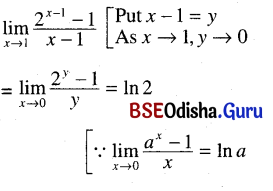
(xii) \(\lim _{x \rightarrow 0} \frac{a^x-a^{-x}}{x}\)
Solution:

(xiii) \(\lim _{x \rightarrow 1} \frac{3^x-3}{x-1}\)
Solution:
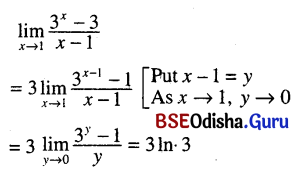
![]()
(xiv) \(\lim _{x \rightarrow 0} \frac{3^x-2^x}{4^x-3^x}\)
Solution:

(xv) \(\lim _{x \rightarrow 1} \frac{2^{x-1}-1}{\sqrt{x}-1}\)
Solution:

Question 5.
Evaluate the following :
(i) \(\lim _{x \rightarrow 0} \frac{\sqrt{x+1}-1}{x}\)
Solution:
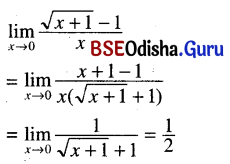
(ii) \(\lim _{x \rightarrow 0} \frac{\sqrt{x+2}-\sqrt{2}}{x}\)
Solution:

(iii) \(\lim _{x \rightarrow 0} \frac{\sqrt{x}-\sqrt{5}}{x-5}\)
Solution:
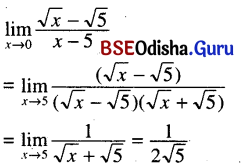
(iv) \(\lim _{x \rightarrow 0} \frac{\sqrt{3-2 x}-\sqrt{3}}{x}\)
Solution:

(v) \(\lim _{x \rightarrow 5} \frac{\sqrt{x-1}-2}{x-5}\)
Solution:

(vi) \(\lim _{x \rightarrow 1} \frac{x^2-\sqrt{x}}{\sqrt{x}-1}\)
Solution:
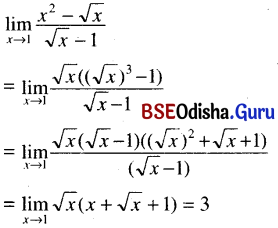
(vii) \(\lim _{x \rightarrow a} \frac{\sqrt{x-b}-\sqrt{a-b}}{x^2-a^2}\), (a > b)
Solution:

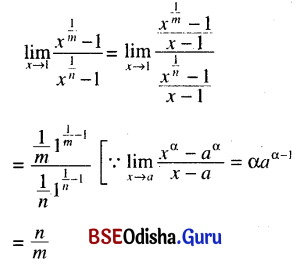
(viii) \(\lim _{x \rightarrow 1} \frac{x^{\frac{1}{m}}-1}{x^{\frac{1}{n}}-1}\) (m, n are integers)
Solution:
(ix) \(\lim _{x \rightarrow 0} \frac{\sqrt{x^2+1}-1}{\sqrt{x^2+4}-2}\)
Solution:
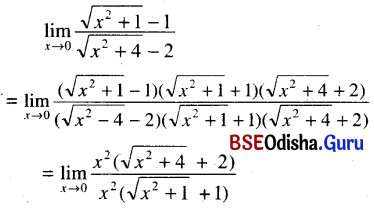
= \(\frac{2+2}{1+1}=\frac{4}{2}\) = 2
(x) \(\lim _{x \rightarrow \infty}(\sqrt{x+1}-\sqrt{x})\)
Solution:
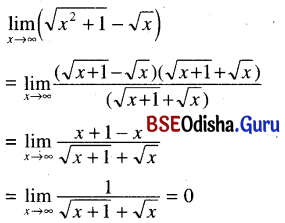
(xi) \(\lim _{x \rightarrow \infty}\left(\sqrt{x^2+1}-\sqrt{x^2-1}\right)\)
Solution:
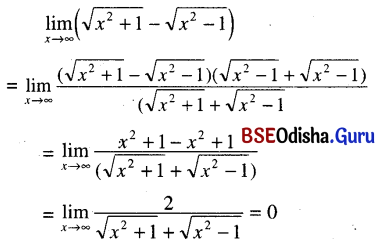
![]()
(xii) \(\lim _{x \rightarrow 0} \frac{\sqrt[3]{1+x}-\sqrt[3]{1-x}}{x}\)
Solution:

(xiii) \(\lim _{x \rightarrow 0} \frac{(x+9)^{\frac{3}{2}}-27}{x}\)
Solution:
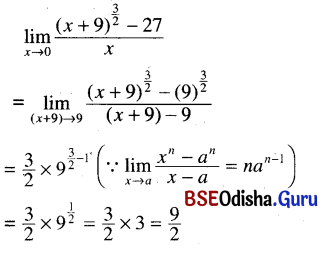
(xiv) \(\lim _{x \rightarrow 0} \frac{\sqrt{1+x}-\sqrt{1-x}}{\sqrt[3]{1+x}-\sqrt[3]{1-x}}\)
Solution:

(xv) \(\lim _{x \rightarrow \infty} \frac{a_0+a_1 x+a_2 x^2+\ldots+a_m x^m}{b_0+b_1 x+b_2 x^2+\ldots+b_n x^n}\)
Solution:
\(\lim _{x \rightarrow \infty} \frac{a_0+a_1 x+a_2 x^2+\ldots+a_m x^m}{b_0+b_1 x+b_2 x^2+\ldots+b_n x^n}\)
= \(\left\{\begin{array}{lll}
\infty & \text { if } & m>n \\
0 & \text { if } & m<n \\
\frac{a_m}{b_n} & \text { if } & m=n
\end{array}\right.\)
Question 6.
Evaluate the following :
(i) \(\lim _{x \rightarrow \infty} \frac{\sin x}{x}\)
Solution:
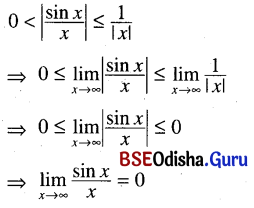
(ii) \(\lim _{x \rightarrow \infty} x\left(a^{\frac{1}{x}}-1\right)\), a > 0
Solution:
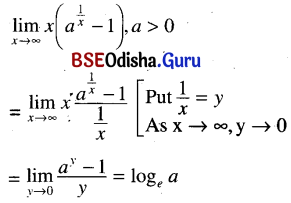
(iii) \(\lim _{x \rightarrow 0} \frac{x^{\frac{1}{2}}+2 x+3 x^{\frac{3}{2}}}{2 x^{\frac{1}{2}}-2 x^{\frac{5}{2}}+4 x^{\frac{7}{2}}}\)
Solution:
\(\lim _{x \rightarrow 0} \frac{x^{\frac{1}{2}}+2 x+3 x^{\frac{3}{2}}}{2 x^{\frac{1}{2}}-2 x^{\frac{5}{2}}+4 x^{\frac{7}{2}}}\)
= \(\lim _{x \rightarrow 0} \frac{1+2 \sqrt{x}+3 x}{2-2 x^2+4 x^3}=\frac{1}{2}\)
(iv) \(\lim _{x \rightarrow \infty} \sqrt{x}\{\sqrt{x+1}-\sqrt{x}\}\)
Solution:

(v) \(\lim _{x \rightarrow \infty} x^2\left\{\sqrt{x^4+a^2}-\sqrt{x^4-a^2}\right\}\)
Solution:

(vi) \(\lim _{x \rightarrow 0} \cos (\sin x)\)
Solution:
\(\lim _{x \rightarrow 0} \cos (\sin x)\)
= cos (sin 0) = cos 0 = 1
(vii) \(\lim _{x \rightarrow 0} \log _e \frac{\sqrt{1+x}-1}{x}\)
Solution:
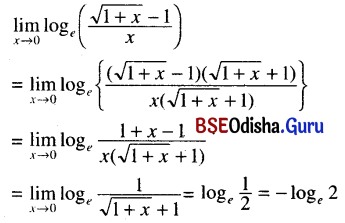
![]()
(viii) \(\lim _{x \rightarrow 2} \log _e \frac{x^2-4}{\sqrt{3 x-2}-\sqrt{x+2}}\)
Solution:

(ix) \(\lim _{x \rightarrow \infty} \log _e\left(1+\frac{a}{x}\right)^x\)
Solution:
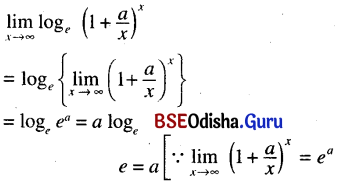
(x) \(\lim _{x \rightarrow 0} \log _e(1+b x)^{\frac{1}{x}}\)
Solution:
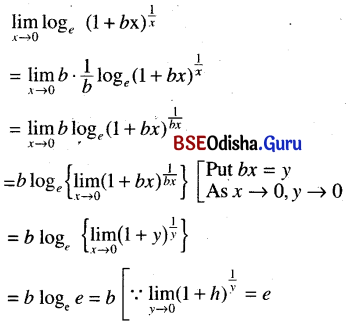
(xi) \(\lim _{x \rightarrow \frac{\pi}{4}} \frac{\sin \left(\frac{1-\tan x}{1+\tan x}\right)}{\frac{\pi}{4}-x}\)
Solution:

(xii) \(\lim _{x \rightarrow \frac{\pi}{2}} \log \frac{1-\sin ^3 x}{\cos ^2 x}\)
Solution:
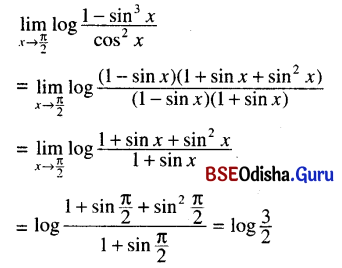
(xiii) \(\lim _{x \rightarrow \infty} e^x\left(a^{\frac{1}{x}}-1\right)\)
Solution:

(xiv) \(\lim _{x \rightarrow 0} \frac{x\left(e^{\frac{\sqrt{1+x^2+x^4-1}}{x}-1}\right)}{\sqrt{1+x^2+x^4}-1}\)
Solution:

(xv) \(\lim _{x \rightarrow 0+} \frac{b \tan x\left(e^{\sin \frac{a x}{b x}-\frac{a}{b}}\right)}{b \sin a x-a \tan b x}\)
Solution:

Question 7.
Examine the existence of the following limits :
(i) \(\lim _{x \rightarrow 0+} \log _a x\)
Solution:
\(\lim _{x \rightarrow 0+} \log _a x\)
= \(\lim _{h \rightarrow 0} \log _a h=-\infty\)
∴ The limit exists
(ii) \(\lim _{x \rightarrow \frac{\pi}{2}} \tan x\)
Solution:

(iii) \(\lim _{x \rightarrow 0}{cosec} x\)
Solution:
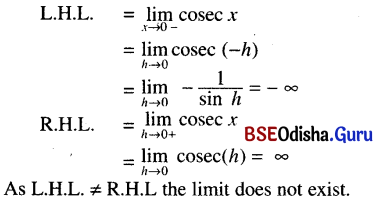
(iv) \(\lim _{x \rightarrow 0-} \frac{1}{e^x}\)
Solution:
\(\lim _{x \rightarrow 0-} \frac{1}{e^x}\) = 0 because as
x → 0, \(\frac{1}{x}\) → ∞
So \(e^{\frac{1}{x}}\) → 0
∴ The limit exists.
(v) \(\lim _{x \rightarrow 0+} \frac{1}{e^x}\)
Solution:
\(\lim _{x \rightarrow 0+} \frac{1}{e^x}\) = \(\lim _{h \rightarrow 0} e^{\frac{1}{h}}=e^{\infty}\) = ∞
The limit exists.
(vi) \(\lim _{x \rightarrow 0} \frac{1}{e^{\frac{1}{x}}-1}\)
Solution:
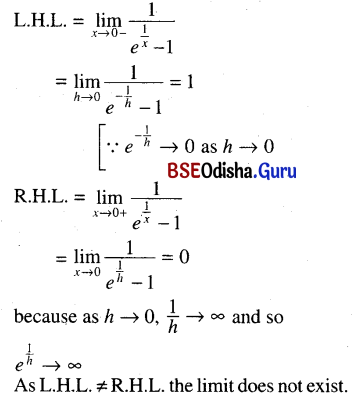
Question 8.
(i) \(\lim _{x \rightarrow \alpha} \frac{\tan a(x-\alpha)}{x-\alpha}=\frac{1}{2}\)
Solution:
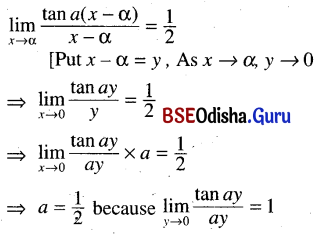
(ii) \(\lim _{x \rightarrow \alpha} \frac{\tan a x}{\sin 2 x}=1\)
Solution:
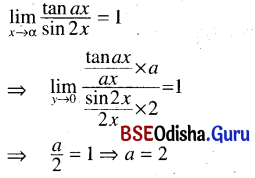
(iii) \(\lim _{x \rightarrow 0} \frac{e^{a x}-e^x}{x}\) = 2
Solution:
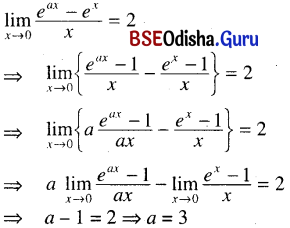
(iv) \(\lim _{x \rightarrow 1} \frac{5^x-5}{(x-1) \log _e a}\) = 5
Solution:

(v) \(\lim _{x \rightarrow 2} \frac{\log _e(2 x-3)}{a(x-2)}\) = 1
Solution:

