Odisha State Board Elements of Mathematics Class 11 Solutions CHSE Odisha Chapter 14 Limit and Differentiation Ex 14(e) Textbook Exercise Questions and Answers.
CHSE Odisha Class 11 Math Solutions Chapter 14 Limit and Differentiation Exercise 14(e)
Question 1.
Find derivatives of the following functions from the definition :
(i) 3x2 – \(\frac{4}{x}\)
Solution:
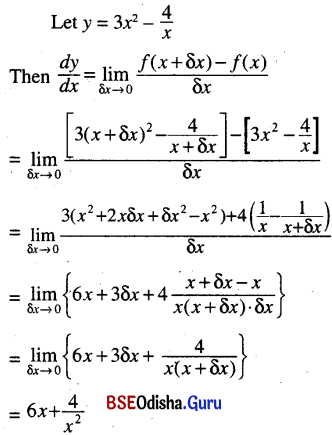
(ii) (4x – 1)2
Solution:

(iii) 2 + x + √x3
Solution:

![]()
(iv) x – \(\sqrt{x^2-1}\)
Solution:

(v) \(\frac{1}{x^{2 / 5}}\) + 1
Solution:

Question 2.
(i) cos (ax + b)
Solution:
Let y = cos (ax + b)
Then \(\frac{d y}{d x}\) = -sin (ax + b) × \(\frac{d}{d x}\) (ax + b) by chain rule.
= -sin(ax + b). a = -a sin (ax + b)
(ii) x2 sin x
Solution:
Let y = x2 sin x
Then \(\frac{d y}{d x}=\frac{d}{d x}\) (x2). sin x + x2 \(\frac{d}{d x}\)
[ ∴ \(\frac{\mathrm{d}}{\mathrm{dx}}(u \cdot v)=\frac{d u}{d x} \cdot v+u \cdot \frac{d v}{d x}\)
= 2x sin x + x2 cos x
(iii) \(\sqrt{\tan x}\)
Solution:
Ley y = \(\sqrt{\tan x}\) = \((\tan x)^{\frac{1}{2}}\)
Then \(\frac{d y}{d x}=\frac{1}{2}(\tan x)^{-\frac{1}{2}} \times \frac{d}{d x}\)(tan x)
= \(\frac{1}{2 \sqrt{\tan x}}\) sec2 x.
(iv) cot x2
Solution:
Let y = cot x2
Then \(\frac{d y}{d x}=-{cosec}^2 x^2 \times \frac{d}{d x}\left(x^2\right)\)
= – cosec2 x2. 2x
= -2x. cosec2 x2
(v) cosec 3x
Solution:
Let y = cosec 3x
Then \(\frac{d y}{d x}\) = -3 cosec 3x . cot 3x
![]()
Question 3.
(i) √x sin x
Solution:
Let y = √x sin x
Then \(\frac{d y}{d x}=\frac{d}{d x}\)(√x) sin x + √x. \(\frac{d}{d x}\)(sin x)
= \(\frac{1}{2 \sqrt{x}}\) sin x + √x. cos x
(ii) \(\sqrt{x^2+1}\)cos x
Solution:

(iii) tan x – x2 – 2x
Solution:
Let y = tan x – x2 – 2x
\(\frac{d y}{d x}\) = sec2 x – 2x – 2
