CHSE Odisha Class 11 Math Solutions Chapter 15 Statistics Ex 15

Odisha State Board CHSE Odisha Class 11 Math Solutions Chapter 15 Statistics Ex 15 Textbook Exercise Questions and Answers.

APOLLOTYRE Pivot Point Calculator

CHSE Odisha Class 11 Math Solutions Chapter 15 Statistics Exercise 15

Question 1.
If the values observed are 1, 2, …..,n each with frequency 1, find
(i) the mean value
Solution:
Mean of 1, 2, 3, ….. n
= \(\frac{1+2+3 \ldots . . .+n}{n}=\frac{n(n+1)}{2 n}=\frac{n+1}{2}\)

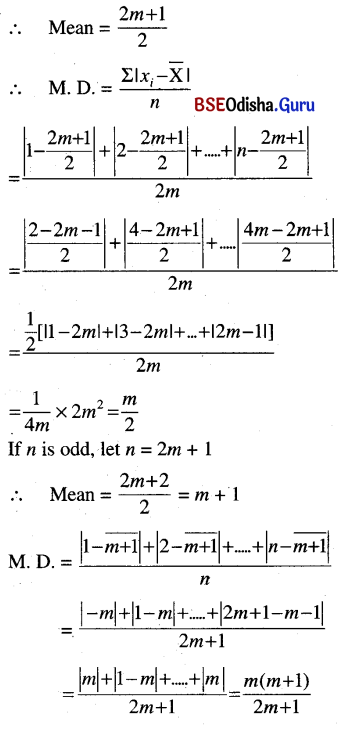
(ii) the mean deviation from the mean separately for two cases when n is odd and when n is even.
Solution:
If n is even, let n = 2m.

Question 2.
For the same set of values as in (1) above, find the variance and standard deviation.
Solution:
x: 1, 2, 3, ….., n

Question 3.
From the table below, find the mean value and the variance.
(a) Values: 1  2  3 ….. n
Frequency: 1  2  3 …. n
Solution:
x: 1  2  3 ….. n
y: 1  2  3 …. n

Question 4.
From the table below, find the mean and the variance.
Solution:
(a) Values: 1  2  5 ….. (2n – 1)
Frequency: 1  1  1        1

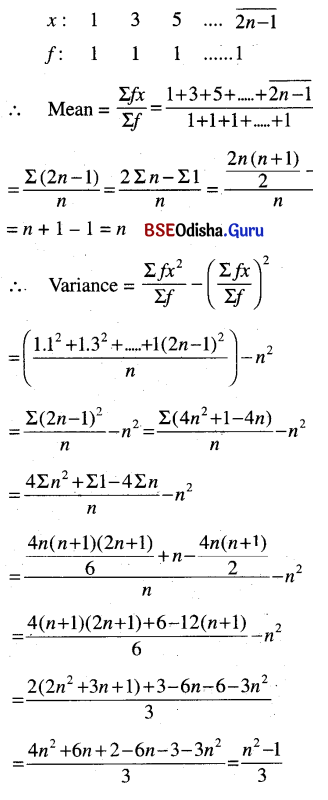
(b) Values: 2  4  6 …..2n
Frequency: 1  1  1      1

Question 5.
From the table below, calculate the mean and the variance
\(\text { Values } \quad \mathbf{0} \quad 1 \quad 2 \ldots \quad r \ldots n\)
\(\text { Frequency: } \quad{ }^n \mathbf{C}_0{ }^n \mathbf{C}_1{ }^n \mathbf{C}_2{ }^n \mathbf{C}_r \ldots . .{ }^n \mathbf{C}_n\)
Solution:

Question 6.
From the following table calculate the mean, mean deviation from the mean, and variance.

Marks	Number of students
30-35	5
35-40	7
40-45	8
45-50	20
50-55	16
55-60	12
60-65	7
65-70	5

Solution:

C. I	f	Mid value (x)	d = x – A
30-35	5	32.5	-15
35-40	7	37.5	-10
40-45	8	42.5	-5
45-50	20	47.5	0
50-55	16	52.5	5
55-60	12	57.5	10
60-65	7	62.5	15
65-70	5	67.5	20
	∑f = 80

Let A (working mean) = 47.5, i = 5

u = d/i	fu	u2	fu2
-3	-15	9	45
-2	-14	4	28
-1	-8	1	8
0	0	0	0
1	16	1	16
2	24	4	48
3	21	9	63
4	20	16	80
	∑fu = 44		∑fu2 = 44

Question 7.
In a soccer league, two teams A and B have the following records
A: Goals scored: 0  1  2  3  4
Number of matches: 11 18 8 6 2
B: Goals scored: 0  1  2  3  4  5
Number of matches: 5 20 10 6 3 1
Which team is more consistent? Which is a better team.
Solution:

∴ The mean of B is more than that of A, so B is the better team. A is more consistent as its variance is less than that of B.

Question 8.
The coefficient of variation is defined as \(\sigma / \bar{x}\), that is the standard deviation divided by the mean value. Find the coefficient of variation c.v. for each of the following sets of observations.
(i) 2, 3, 4, 2, 5, 7, 8, 9
Solution:

(ii) 5, 7, 9, 10, 7, 5, 8, 9, 3
Solution:

(iii) 3, 3, 3, 4, 4, 4, 5, 5, 5
Solution:

Question 9.
Suppose the values x₁, x₂, …. x_n having frequency f₁, f₂, …. f_n respectively having mean value x̄ and variance σ². Let a be a fixed real number
x₁ + a, x₂ + a, ….. , x_n + a with frequency f₁, f₂, ….. f_n respectively will have mean value x̄ + a and variance σ.
Solution:

Question 10.
Find the mean and deviation from the mean and the standard deviation of a, a + d, a + 2d, …. , a + 2nd assume that d > 0.
Solution:

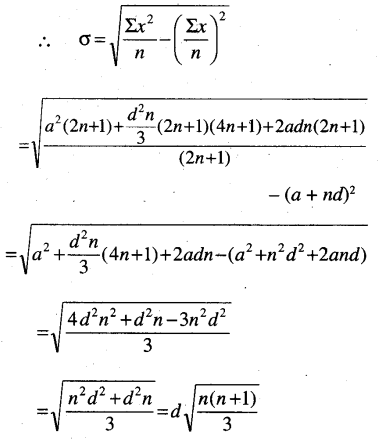
Question 11.
Let x₁, x₂, …. x_n be a set of observations with mean value 0 and variance σ²_x and y₁, y₂, …. y_m be another set of observations with mean value 0 and variance σ²_y. Find the mean value and variance of the set of observations x₁, x₂, …. x_n , y₁, y₂, …. y_m combined.
Solution:
x₁, x₂, …. x_n be a set of observations with mean value 0 and variance σ²_x and y₁, y₂, …. y_m be another set of observations with mean value 0 and variance σ²_y

Question 12.
Find which group of the following data is more dispersed :

Range	10-20	20-30	30-40	40-50	50-60
(Group A) Frequency	5	1	3	2	1
(Group A) Frequency	1	3	2	3	1

Solution:
Let us find the mean and standard deviation for the given two distributions.
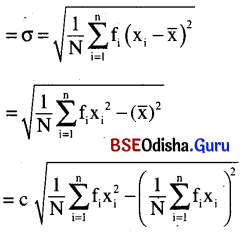
(i) Mean deviation about mean
M. D = \(\frac{1}{N} \sum_{i=1}^n f_i\left|x_i-\bar{x}\right|\)

(ii) Mean deviation about median
M. D = \(\frac{1}{N} \sum_{i=1}^n f_i\left|x_i-M\right|\)

(iii) variance
Variance is the mean of squared deviations from the mean.

(iv) Standard deviation
Standard deviation is the square root of the mean of squared deviations from the mean.
∴ Standard deviation

Question 13.
The price of land per square meter and that of gold per ten grams over five consecutive years is given below. Decide, which price maintains better stability. [Hint: Stability ⇔ Consistency]

Price of land/Sq.meter(₹)	1500	2500	2600	3000	4000
Price of gold/10 gms(₹)	2500	2600	2750	2900	2850

Solution: