Odisha State Board Elements of Mathematics Class 11 Solutions CHSE Odisha Chapter 2 Sets Ex 2(b) Textbook Exercise Questions and Answers.
CHSE Odisha Class 11 Math Solutions Chapter 2 Sets Exercise 2(b)
Question 1.
An examination was conducted in physics, chemistry, and mathematics. If P.C.M. denotes respectively the sets of students who passed in Physics, Chemistry, and Mathematics, express the following sets using union, intersection, and different symbols.
(a) Set of candidates who passed in Mathematics and Chemistry, but not in Physics.
(b) Set of candidates who passed in all three subjects.
(c) Set of candidates who passed in Mathematics only.
(d) Set of candidates who failed in Mathematics, but passed in at least one subject.
(e) Set of candidates who passed in at least two subjects.
(f) Set of candidates who failed in one subject only.
Solution:
An examination was conducted in Physics, Chemistry, and Mathematics. P, C, and M denoted the set of students who passed Physics, Chemistry, and Mathematics, respectively. Then.
(a) Set of candidates who passed in Mathematics and Chemistry, but not in Physics (M ∩ C) – P.
(b) Set of candidates who passed in all three subjects M ∩ C ∩ P.
(c) Set of candidates who passed in Mathematics only M – C – P.
(d) Set of candidates who failed in Mathematics, but passed in at least one subject (P ∪ C) – M.
(e) Set of candidates who passed in at least two subjects.
(f) Set of candidates who failed in one subject only.
(P ∩ C – M) ∪ (P ∩ M – C) ∪ (M ∩ C – P)
Question 2.
What can you say about sets A and B if
(i) A ∪ B= Φ
(ii) A Δ B = Φ
(iii) A \ B = Φ
(iv) A \ B = A
(v) A ∩ B= U, Where U is the Universal set, A \ B = U?
Solution:
(i) if A ∪ B = Φ then A = Φ =B
(ii) A Δ B = Φ ⇒ A = B
(iii) A – B = Φ ⇒ A ⊆ B
(iv) A – B = A ⇒ B = Φ
(v) A ∩ B = U ⇒ A = B = U
(vi) A – B = U ⇒ A = U and B = Φ
Question 3.
Are differences and symmetric commutative? Give reason.
Solution:
The difference of the two sets is not commutative but the symmetric of the two sets is commutative.
Reason:
Let x ∈ A – B ⇔ x ∈ A ∧ x ∉ B
≠ x ∈ B ∧ x ∉ A ⇔ x ∈ b – A
A- B ≠ B – A
But if y ∈ A Δ ⇔ y ∈ (A-B) ∪ (B – A)
⇒ y ∈ (B – A) ∪ (A – B) ⇔ y ∈ B Δ A
∴ A Δ B = B Δ A.
![]()
Question 4.
If B ⊂ C, prove that A/B = A/C. Is this result true when a difference is replaced by a symmetric difference? Give reason.
Solution:
If B ⊂ C, then x ∈ A ⇒ x ∈ C
Now x ∈ A – C ⇔ x: x ∈ A ∧ x ∉ C
⇔ {x: x ∈ A ∧ x ∉ B}
⇔ {x: x ∈ A – C}
∴ A – C = A – B
but, A Δ B ≠ A Δ C.
Question 5.
Prove the following :
(i) (A\B)\C = (A\C)\B = A\(B ∪ C)
(ii) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∪ B)
(iii) A Δ (B Δ C) = (A Δ B) Δ C
(iv) A ⊂ B ⇔ B’ ⊂ A’ A ⇔ A’ ∪ B = U
⇔ B’ ∩ A = Φ, where U is the universal set.
(v) A ∪ B = U and A ∩ B = Φ
⇒ B = A’
(iv) A ∪ B = A for all A ⇒ B = Φ
Solution:
(i) Let x ∈ (A – B) – C ……(1)
⇔ x ∈ A- B ∧ x ∉ C
⇔ (x ∈ A ∧ x ∉ B) ∧ x ∉ C ……(2)
⇔ (x ∈ A ∧ x ∉ C) ∧ x ∉ B
⇔ x ∈ A – C ∧ x ∉ B
⇔ x ∈ (A – C) – B ……(3)
∴ from (2), we have
x ∈ A ∧ ∉ B ∧ x ∉ C
⇔ x ∈ A ∧ (x ∉ B ∧ x ∉ C)
⇔ x ∈ A ∧ x ∉ B ∪ C
[∴ ~ (p ∨ q) = ~ p ∧ ~ q]
⇔ x ∈ A – (B ∪ C) …….(4)
∴ From (1), (3), and (4), we have
(A – B) – C = (A – C)-B = A – (B ∪ C)
(ii) Let x ∈ A ∩ (B ∪ C)
⇔ x ∈ A ∧ x ∈ B Δ C
⇔ x ∈ A ∧ (x ∈ B – C ∨ x ∉ C – B)
⇔ x ∈ A ∧ (x ∈ B ∧ x ∉ C ∨ x ∈ C ∧ x ∉ B)
⇔ x ∈ A ∧ (x ∈ B ∧ x ∈ A ∧ C) ∨ x ∈ A ∧ (x ∈ B ∧ x ∈ B ∧ x ∈ A ∧ x ∉ B)
⇔ (x ∈ A ∩ B ∧ x ∉ A ∩ C) ∨ (x ∈ A ∩ C ∨ x ∉ A ∩ B)
⇔ x ∈ (A ∩ B) – (A ∩ C) ∨ x ∈ (A ∩ C) – (A ∩ B)
⇔ x ∈ (A ∩ B) Δ (A ∩ C) ……(2)
∴ From (1) and (2), we have
A ∩ (B Δ C) = (A ∩ B) Δ (A ∩ C)
(iii) A Δ (B Δ C)
= A ∪ (B Δ C)- A ∩ (B Δ C)
= A Δ (B ∪ C)- A Δ (B ∩ C)
[ ∴ A ∪ (B Δ C) = A Δ (B ∪ C)]
and A n (B Δ C) = A Δ (B ∩ C)
= (A Δ B) ∪ C- (A Δ B) ∩ C
[∴ A Δ (B ∪ C) = (A Δ B) ∪ C and A Δ (B ∩ C) = (A Δ B) ∩ C
= (A Δ B) Δ C
∴ A Δ (B Δ C)= (A Δ B) Δ C
(Proved)
(iv) If A ⊂ B then x ∈ B’ or ⇒ x ∉ B
⇒ x ∉ B ⇒ x ∈ A’ (∴ A ⊂ B)
∴ B’ ⊂ A’
Again, let y ∈ A ⇒ y ∉ A’ ⇒ y ∈ B’
(∵ B’ ⊂ A’)
⇒ y ∈ B ∴ A ⊂ B
∴ A ⊂ B ⇔ B’ ⊂ A’
∴ Again as A ⊂ B, we have
U = A ∪ B = B = U, where U is the universal set of A and B.
∴ A’= B – A ⇒ A’ ∪ B
= (B – A) ∪ B = B = U
∴ A ⊂ B ⇒ A’ ∪ B = U
Again A’ ∪ B = U
⇒ A ∩ (A’ ∪ B) = A ∩ U = A
⇒ (A ∩ A’) ∪ (A ∩ B) = A
⇒ Φ ∪ (A ∩ B) = A
⇒ A ∩ B = A ⇒ A ⊂ B
Lastly, B’ = U’ = Φ
∴ B’ ∩ A = Φ
(v) Let A ∪ B = U and A ∩ B = Φ
∴ Let x ∈ B ⇔ x ∉ B’ ⇔ x ∉ U – B
⇔ x ∉ A ⇔ x ∉ A’
(vi) As A ∪ B = A for all A
we have B ⊂ A for all A
∴ B ⊂ A even for A = Φ Thus B = Φ
Question 6.
Prove all the results of sections 1.13 and 1.14 that are started without proof.
Solution:
(i) A ∪ B = B ∪ A
Let x ∈ A ∪ B ⇔ x ∈ A ∨ x ∈ B
⇔ x ∈ B ∨ x ∈ B ⇔ x ∈ B ∪ A
(ii) A ∩ B = B ∩ A
Let x ∈ A ∩ B ⇔ x ∈ A ∧ x ∈ B
∴ A ∩ B = B ∩ A
(iii) A ∩ (B ∪ C)
= (A ∩ B) ∪ (A ∩ C)
Let x ∈ A ∩ (B ∪ C)
⇔ x ∈ A ∧ x ∈ A ∪ C
⇔ x ∈ A ∧ (x ∈ A ∨ x ∈ C)
⇔ (x ∈ A ∩ B ∨ x ∈ A ∩ C)
⇔ (x ∈ A ∧ x ∈ B) ∨ (x ∈ A ∧ x ∈C)
⇔ x ∈ (A ∩ B) ∪ (A ∩ C)
∴ A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
Question 7.
Prove that
(i) \(\mathbf{A}-\bigcup_{i=1}^n \mathbf{B}_i=\bigcap_{i=1}^n\left(\mathbf{A}-\mathbf{B}_i\right)\)
Solution:
Let x ∈ \(A-\bigcup_{i=1}^n B_i \Rightarrow x \in A \wedge x \notin \bigcup_{i=1}^n B_i\)
⇔ x ∈ A ∧ x ∉(B1 ∪ B2 ∪….∪ Bn )
⇔ x ∈ A ∧ (x ∉ B1 ∧ x ∉ B2 ∧…..∧ x ∉ Bn )
⇔ (x ∈ A ∧ x ∉ B1 ) ∧ (x ∈ A ∧ x ∉ B2 ) ∧….∧ (x ∈ A ∧ x ∉ Bn )
⇔ x ∈ A – B1 ∧ x ∈ A – B2 ∧……..∧ x ∈ A – Bn
⇔ x ∈ (A – B1 ) ∩ (A – Bi ) ∩…..∩ (A – Bn )
⇔ \(x \in \bigcap_{i=1}^n\left(\mathrm{~A}-\mathrm{B}_{\mathrm{i}}\right)\)
∴ \(\mathrm{A}-\cup_{i=1}^n \mathrm{~B}_{\mathrm{i}}=\bigcap_{i=1}^n\left(\mathrm{~A}-\mathrm{B}_{\mathrm{i}}\right)\)
(ii) ∴ \(\mathbf{A}-\bigcap_{i=1}^n \mathbf{B}_i=\bigcup_{i=1}^n\left(\mathbf{A}-\mathbf{B}_i\right)\)
Solution:
Let x ∈ \(A-\bigcap_{i=1}^n B_i\)
⇔ x ∈ A ∧ x ∈ \(\bigcap_{i=1}^n \mathrm{~B}_{\mathrm{i}}\)
⇔ x ∈ A ∧ x ∉ (B1 ∩ B2 ∩….∩ Bn )
⇔ x ∈ A ∧ (x ∉ B1 ∨ x ∉ B2 ∨….∨ x ∉ Bn )
⇔ (x ∈ A ∧ x ∉ B1 ) ∨ (x ∈ A ∧ x ∉ B2 ) ∨….∨ (x ∈ A ∧ x ∉ Bn )
⇔ x ∈ A – B1 ∨ x ∈ A – B2 ∨……..∨ x ∈ A – Bn
⇔ x ∈ (A – B1 ) ∪ (A – B2 )……(A – Bn )
⇔ x ∈ \(\cup_{i=1}^n\left(\mathrm{~A}-\mathrm{B}_{\mathrm{i}}\right)\)
∴ \(\mathrm{A} \bigcap_{i=1}^n \mathrm{~B}_1=\bigcup_{u=1}^n\left(\mathrm{~A}-\mathrm{B}_i\right)\)
![]()
Question 8.
Prove that |A ∪ B ∪ C|
Solution:
= |A| + |B| + |C| + |A ∩ B ∩ C| – |A ∩ B| – |B ∩ C| – |C ∩ A|
L.H.S. =|A ∪ B ∪ C| = |A ∪ D|
where D = B ∪ C
= |A| + |D| – |A ∩ D|
( ∵ |A ∪ B| =|A| + |B| – |A ∩ B|)
= |A| + |B ∪ C| – | A ∩ (B ∪ C)|
= |A| + |B| + |C| – |B ∩ C| – |(A ∩ B) ∪ (A ∩ C)|
= |A| + |B| + | C |- |B ∩ C| – [|A ∩ B| + |A ∩ C| – |(A ∩ B) ∩ (A ∩ C)|]
= |A| + |B| + |C| – |B ∩ C| – |A∩ B| – |A ∩ C| + |A ∩ B ∩ Cl
= |A| + |B| + |C| – | A ∩ Bl – |B ∩ C| – |C ∩ A| + |A ∩ B ∩ Cl = R.H.S.
Question 9.
If X and Y are two sets such that X ∪ Y has 20 objects, X has 10 objects and Y has 15 objects; how many objects does X ∩ Y have?
Solution:
Given |X ∪ Y| = 20
|X| = 10
|Y| = 15
We know that |X ∪ Y|
= |X| + |Y| – |X ∩ Y|
⇒ 20 = 10 + 15 – |X ∩ Y|
⇒ |X ∩ Y| = 25 -20 = 5
∴ X ∩ Y has 5 elements.
Question 10.
In a group of 450 people, 300 can speak Hindi and 250 can speak English. How many people can speak both Hindi and English?
Solution:
Let H = The set of people who can speak Hindi
E = The set of people who can speak English.
According to the question we have
|H ∪ E| = 450, |H| = 300,
|E| = 250
We want to find 1 H ∩ E
|H ∩ E| = |H| + |E|- |H ∪ E|
= 300 + 250 – 450 = 100
∴ 100 people can speak both Hindi and English.
Question 11.
In a group of people,37 like coffee, 52 like tea and each person in the group likes at least one of the two drinks. 19 people like both tea and
coffee, how many people are in the group?
Solution:
Let T = The set of persons who like Tea. ,
C = The set of persons who like coffee According to the question
|C| = 37, |T| = 52 and |T ∩ C| = 19
Total number of persons in the group
= |T ∩ C| = |T| + |C| – |T ∩ C|
= 37 + 52 – 19 = 70
Question 12.
In a class of 35 students, each student likes to play either cricket or hockey. 24 students like to play cricket and 5 students like to play both games; how many students play hockey?
Solution:
Let C = Set of students like to play cricket
H = The set of students like to play Hockey.
According to the question
|C ∪ H| = 35
|C| = 24, |C ∩ H| = 5
Now |C ∪ H| = |C| + |H| – |C ∩ H|
⇒ 35 = 24 + |H| – 5
⇒ |H| = 16
16 students like to play Hockey.
Question 13.
In a class of 400 students, 100 were listed as taking apple juice, 150 as taking orange juice and 75 were listed as taking both apple as well as orange juice. Find how many students were taking neither apple juice or orange juice.
Solution:
Let A = The set of students take apple juice
O = The set of students take orange juice
According to the question
|A| = 100, |O| = 150 and
|A ∩ O| = 75
∴ Number of students take at least one of the juice = |A ∪ O|
= |A| + |O| – |A ∩ O|
= 100 + 150 – 75 = 175
Total number of students
= |U| = 400
Number of students taking neither of these juice
= |U| – |A ∪ O|
= 400 – 175 = 225
![]()
Question 14.
In a group of 65 people, 40 like cricket, and 10 like both cricket and tennis. How many like tennis only and not cricket? How many like tennis?
Solution:
Let C = The set of persons like cricket
T = The set of people who like tennis.
According to the question
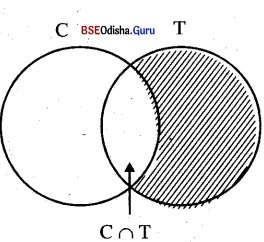
|C| = 40 , |C ∩ T| = 10 and
|C ∪ T| = 65
A number of people like tennis only but not cricket = |C ∪ T| – |C|
= 65 – 40 = 15
Number of persons like tennis
= |C ∩ T| – |C| + |C ∩ T|
= 65 – 40 + 10 = 25
Question 15.
In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12
people liked products C and A, 14 people liked products B and C and 8 liked all the three products, find how many liked products C only.
Solution:
Let E = Set of persons like product A
F = Set of persons like product B
G = Set of persons like product C
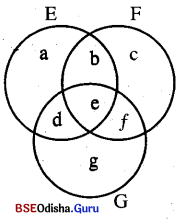
According to the question
a + b + d + e = 21
c + b + f + e = 26
g + f + d + e = 29
b + e = 14
f + e = 14
d + e = 12
e = 8
⇒ e = 8 g = 11
d = 4 c = 6
f = 6 a = 3
b = 6
Number of persons like product C only
O = g = 11
