CHSE Odisha Class 11 Math Solutions Chapter 4 Trigonometric Functions Ex 4(d)

Odisha State Board Elements of Mathematics Class 11 CHSE Odisha Solutions Chapter 4 Trigonometric Functions Ex 4(d) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 4 Trigonometric Functions Exercise 4(d)

Question 1.
Fill in the blanks choosing the correct answer from the brackets.

(i) In Δ ABC, b =____________. (b cos B + c cos C, a cos A + c cos C, c cos A + a cos C)
Solution:
c cos A + a cos C

(ii) If a cot A = b cot B then Δ ABC is__________. (isosceles, right-angled, equilateral)
Solution:
isosceles

(iii) In Δ ABC if b sin C = c sin B = 2 then b sin C = ___________. (0, 1, 2)
Solution:
1

(iv) In Δ ABC if \(\frac{\cos \mathrm{A}}{a}=\frac{\cos \mathrm{B}}{b}=\frac{\cos \mathrm{C}}{c}\) then the tringle is_________ (equilateral, isosceles, scalene)
Solution:
equilateral

(v) If sin A = sin B and b = 1/2, then a = _______________. (2, 1/2, 1)
Solution:
a = 1/2

(vi) In Δ ABC if A = 60°, B = 45° a : b = __________. ( √2 : √3, √6 : 2, √3 : 2)
Solution:
√6 : 2

(vii) In Δ ABC if b² + c² < a² , then _________ angle is obtuse. (A, B, C)
Solution:
A

(viii) If a cos B = b cos A. then cos B = _____________. \(\left(\frac{c}{a}, \frac{a}{2 c}, \frac{c}{2 a}\right)\)
Solution:
cos B = \(\frac{c}{2 a}\)

(ix) If a – b cos C, then __________ angle is a right angle. (A, B, C)
Solution:
∠B is a right angle

(x) If a = 12, b = 7, C = 30°, then Δ = ______________. (42, 84, 21)
Solution:
Δ = 21

Question 2.
Prove that
(i) a sin A – b sin B = c sin (A – B)
Solution:
R.H.S. = c sin (A – B)
= 2R sin C sin (A – B)
= 2R sin (A + B) sin (A – B)
[∴ A + B + C = π or, A + B = π – C
or sin (A + B) = sin (π – C) sin C]
= 2R (sin² A – sin²  B)
= 2R sin A sin A – 2R sin B sin B
= a sin A – b sin B = L.H.S.

(ii) b cos B + c cos C = a cos (B – C)
Solution:
R.H.S. = a cos (B – C)
= 2R sin A cos (B – C)
= 2R sin (B + C) cos (B – C)
= R sin (B + C + B – C) + sin (B + C – B + C)}
= R [(sin 2B + sin 2C)
= R(2sin B cos B + 2 sin C cos C)
= 2R sin B cos B + 2R sin C cos C
= b cos B + c cos C = L.H.S.

(iii) If (a + b + c)(b + c – a) = 3bc, then A = 60°
Solution:

(iv) If \(\frac{b+c}{5}=\frac{c+a}{6}=\frac{a+b}{7}\) then sin A : sin B : sin C = 4 : 3 : 2
Solution:

(v) If A: B: C = 1 : 2 : 3 then sin A: sin B: sin C = 1 : 2
Solution:

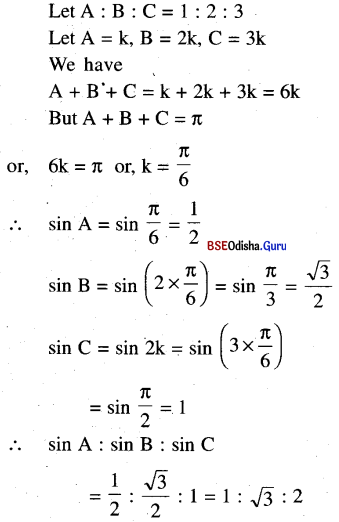
(vi) If b² + c² – a² = bc, then A = 60°
Solution:
If b² + c² – a² = bc, then A = 60°
or, \(\frac{b^2+c^2-a^2}{2 b c}\) = 1/2 or, cos A = 1/2
or, A = 60°

(vii) If A : B: C = 1 : 2 : 7, then c: a = (√5 + 1) : (√5 – 1)
Solution:

But we know that \(\frac{\sin C}{\sin A}=\frac{c}{a}\)
∴ \(\frac{c}{a}=\frac{\sqrt{5}+1}{\sqrt{5}-1}\)

Question 3.
(i) If cos A = \(\frac{12}{13}\), cos B = \(\frac{5}{13}\) then find a : b.
Solution:

(ii) If a = 7, b = 3, c = 5 then find A.
Solution:

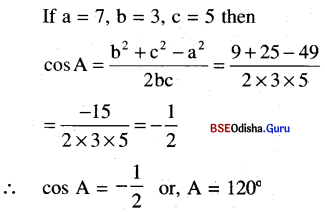
(iii) If a = 8, b = 6, c = 4 find tan \(\frac{B}{2}\)
Solution:

(iv) If \(\frac{a}{\sec A}=\frac{b}{\sec B}\) and a ≠ b then find C.
Solution:

(v) If a = 48, b = 35, ∠C = 60° then find c.
Solution:

In Δ ABC prove that (Q. 4 to Q. 26)

Question 4.
a sin (B – C) + b sin (C – A) + c sin (A – B) = 0
Solution:
a sin (B – C) + b sin (C – A) + c sin (A – B)
= 2R sin A sin (B – C) + 2R sin B sin (C – A) + 2R sin C sin (A – B)
= 2R [sin (B + C) sin (B – C) + sin (C + A) sin (C – A) + sin (A + B) sin (A – B)]
= 2R[sin² B – sin² C + sin² C – sin² A + sin² A – sin² A]
= 2R x 0 = 0

Question 5.
\(\frac{\sin (B-C)}{\sin (B+C)}=\frac{b \cos C-c \cos B}{b \cos C+c \cos B}\)
Solution:

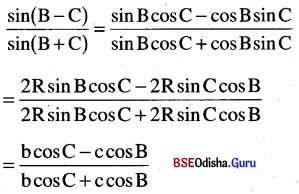
Question 6.
\(\sum \frac{a^2 \sin (B-C)}{\sin (B+C)}=0\)
Solution:

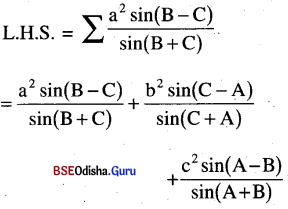
Question 7.
a²(cos² B – cos² C) + b²(cos² C – cos² A) + c²(cos² A – cos² B) = 0
Solution:

Question 8.
\(\frac{b^2-c^2}{a^2} \sin 2 A+\frac{c^2-a^2}{b^2} \sin 2 B\) \(+\frac{a^2-b^2}{c^2} \sin 2 \mathrm{C}=0\)
Solution:

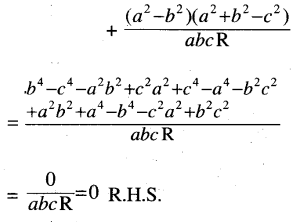
Question 9.
\(\frac{a^2\left(b^2+c^2-a^2\right)}{\sin 2 \mathrm{~A}}=\frac{b^2\left(c^2+a^2-b^2\right)}{\sin 2 \mathrm{~B}}\) \(=\frac{c^2\left(a^2+b^2-c^2\right)}{\sin 2 C}\)
Solution:

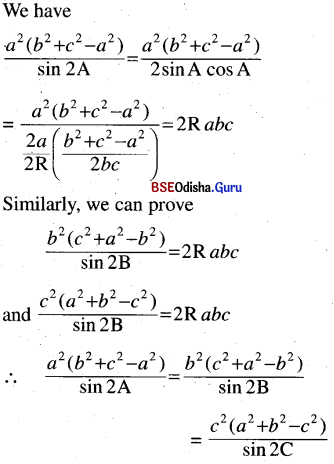
Question 10.
\(\Sigma \frac{\cos A}{\sin B \cdot \sin C}=2\)
Solution:

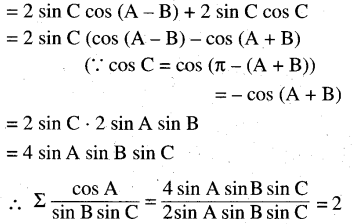
Question 11.
(a² – b² + c²) tan B = (a² + b² – c²) tan C
Solution:

Question 12.
(b² – c²) cot A + (c² – a²) cot B + (a² – b²) cot C = 0
Solution:

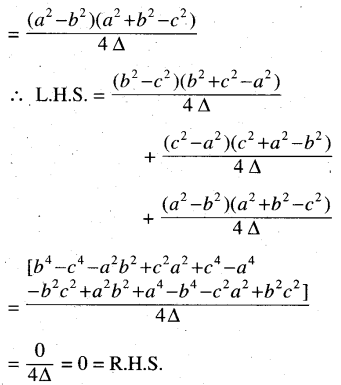
Question 13.
\(\frac{b+c}{a}=\frac{\cos \mathbf{B}+\cos C}{1-\cos A}\)
Solution:

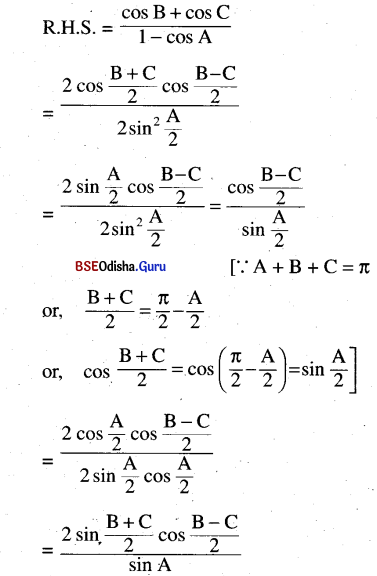
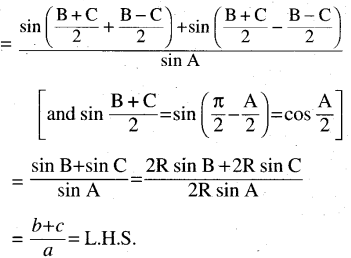
Question 14.
\(\sum a^3 \sin (B-C)=0\)
Solution:

Question 15.
(b + c) cos A + (c + a) cos B + (a + b) cos C = a + b + c
Solution:
L.H.S. = (b + c) cos A + (c + a) cos B + (a + b) cos C
= b cos A + c cos A + a cos B + c cos B + a cos C + b cos C
= (b cos C+ c cos B) +(c cos A + a cos C) + (a cos B + b cos A)
= a + b + c = R.H.S.

Question 16.
2 (bc cos A + ca cos B + ab cos C) = a² + b² + c²
Solution:
2 (bc cos A + ca cos B + ab cos C) = a² + b² + c²
\(=2\left(b c \times \frac{\left(b^2+c^2-a^2\right)}{2 b c}+c a \times \frac{c^2+a^2-b^2}{2 c a}\right.\) \(\left.+a b \times \frac{a^2+b^2-c^2}{2 a b}\right)\)
= b² + c² – a² + c² + a² – b² + a² + b²– c²
= a² + b² + c²

Question 17.
a (b² + c²) cos A + b (c² + a²) cos B + c(a² + b²) cos C = 3 abc.
Solution:
a (b² + c²) cos A + b (c² + a²) cos B + c(a² + b²) cos C
= ab² cos A + ac² cos A + bc² cos B + ba² cos B + ca² cos C + cb² cos C
= ab² cos A + ba² cos B + ac² cos A + ca² cos C + bc² cos B + cb² cos C
= ab (b cos A + a cos B) + ac (c cos A + a cos C) bc (c cos B + b cos C)
= abc = abc + abc = 3abc

Question 18.
a³ cos (B – C) + b³ cos (C – A) + c³ cos (A – B) = 3 abc
Solution:
1st term of L.H.S. = a³ cos (B – C)
= a² a cos (B – C)
= a² . 2R sin A cos (B – C)
= 2a²R sin (B + C) cos (B- C)
= a²R [sin (B + C + B – C) + sin (B + C – B + C)]
= a² R (sin 2B + sin 2C)
= a²R [2 sin B cos B + 2 sin C cos C]
= a² [2R sin B cos B + 2R sin C cos C]
= a² (b cos B + c cos C)
Similarly, 2nd term
= b² (c cos C + a cos A) and
3rd term = c² (a cos A + b cos B)
∴ L.H.S.= a²b cos B+a²c cos C+b²c cos C + b²a cos A + c²a cos A + c²b cos B
= ab (a cos B + b cos A) + bc (b cos C + c cos B) + ca (c cos A + a cos C)
= abc + bca + cab = 3abc = R.H.S.

Question 19.
a (cos B + cos C) = 2(b + c) sin² \(\frac{A}{2}\)
Solution:
Refer to Q. N. 13.

Question 20.
(b + c – a) tan \(\frac{A}{2}\) = (c + a – b) tan \(\frac{B}{2}\) = (a + b – c) tan \(\frac{C}{2}\)
Solution:

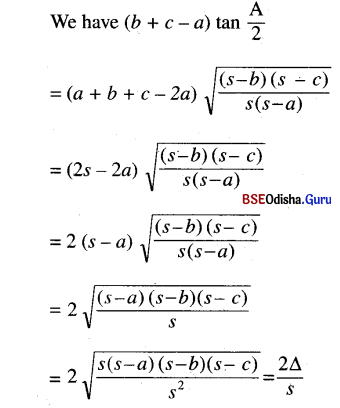
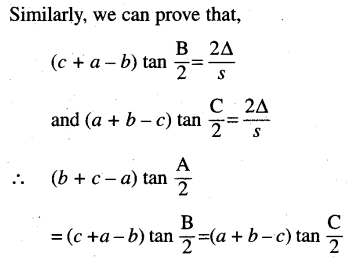
Question 21.
\((b+c-a)\left(\cot \frac{B}{2}+\cot \frac{C}{2}\right)\) \(=2 a \cot \frac{A}{2}\)
Solution:

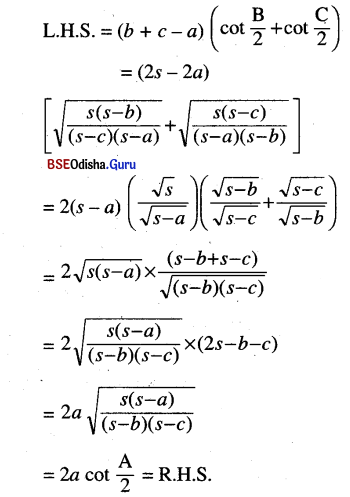
Question 22.
(a – b)² cos² \(\frac{C}{2}\) + (a + b)² sin² \(\frac{C}{2}\) = c²
Solution:
L.H.S = (a – b)² cos² \(\frac{C}{2}\) + (a + b)² sin² \(\frac{C}{2}\)

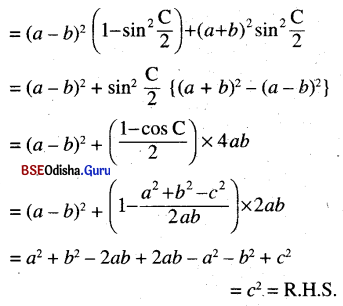
Question 23.
1 – tan \(\frac{A}{2}\) tan \(\frac{B}{2}\) = \(\frac{c}{2}\)
Solution:

Question 24.
(b – c) cot \(\frac{A}{2}\) + (c – a) cot \(\frac{B}{2}\) + (a – b) cot \(\frac{C}{2}\) = 0
Solution:

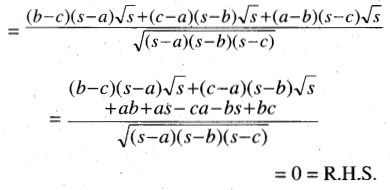
Question 25.
cot A + cot B + cot C = \(\frac{a^2+b^2+c^2}{4 \Delta}\)
Solution:

Question 26.
a² cot A + b² cot B + c² cot C = 4Δ
Solution:

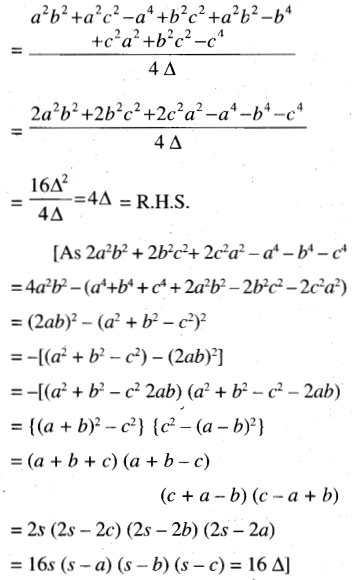
Question 27.
If \(\frac{1}{a+c}+\frac{1}{b+c}=\frac{3}{a+b+c}\) then prove C = 60°.
Solution:

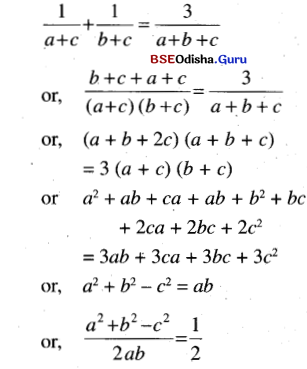
or, cos C = 1/2 or, ∠C = 60°

Question 28.
If a = 2b and A = 3B, find the measures of the angles of the triangle.
Solution:
If a = 2b and A = 3B, we have \(\frac{a}{b}\) = 2
or, \(\frac{\sin A}{\sin B}\) = 2
or, sin A = 2 sin B         …..(1)
Also  sin A = sin 3B (as a = 3B)    …..(2)
∴ From (1) and (2), we have
2 sin B = sin 3B = 3 sin B – 4 sin³ B
or, 4 sin³ B – sin B = 0
or, sin B(4 sin² B – 1) = 0
or, sin B = 0, 4 sin² B = 1
Now sin B = 0 ⇒ B = 0 (Impossible)
∴ sin² B = \(\frac{1}{2}\) or, sin B = ± \(\frac{1}{2}\)
If sin B = \(\frac{1}{2}\) then ∠B = 30°
∴ A = 3B = 3 x 30° = 90°
∠C = 60°

Question 29.
If a⁴ + b⁴ + c⁴ = 2c² (A² + b²), prove that m∠ACB = 45° or 135°.
Solution:
a⁴ + b⁴ + c⁴ = 2c² (a² + b²)
or, a⁴ + b⁴ + c⁴ + 2a²b² – 2b²c² – 2c²a² = 2a²b²
or, (a² + b² – c²)² = 2a²b²
or, a² + b² – c² = ± √2 ab
or, \(\frac{a^2+b^2-c^2}{2 a b}=\pm \frac{1}{\sqrt{2}}\)
or, cos C = ± \(\frac{1}{\sqrt{2}}\)
∴ ∠C = 45° or 135°.

Question 30.
If x² + x + 1, 2x + 1, and x² – 1 are lengths of sides of a triangle, then prove that the measure of the greatest angle is 120°.
Solution:

Question 31.
if cos B = \(\frac{\sin A}{2 \sin C}\), prove that the triangle is isosceles.
Solution:
cos B = \(\frac{\sin A}{2 \sin C}\)
⇒ \(\frac{c^2+a^2-b^2}{2 c a}=\frac{a}{2 c}\) ⇒ c² + a² – b² = a²
or, c² = b² or, c = b
∴ The triangle is isosceles.

Question 32.
If a tan A + b tan B = (a + b)tan \(\frac{1}{2}\) (A + B) prove that the triangle is isosceles.
Solution:

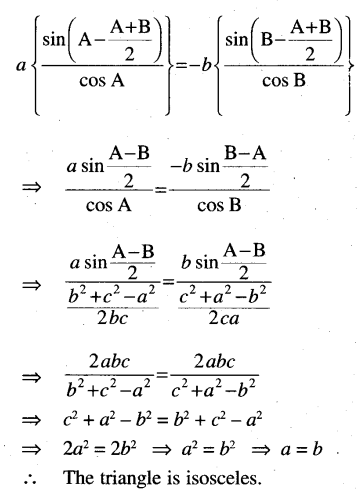
Question 33.
If (cos A + 2 cos C) : (cos A + 2 cos B) = sin B : sin C prove that the triangles are either isosceles or right-angled.
Solution:
\(\frac{\cos A+2 \cos C}{\cos A+2 \cos B}=\frac{\sin B}{\sin C}\)
⇒ cos A sin C = cos A sin B + 2 cos B sin B
⇒ cos A (sin B – sin C) + (sin 2B – sin 2c) = 0
⇒ cos A (sin B – sin C) + 2 cos (B + C) sin (B – C) = 0
⇒ cos A (sin B – sin C) – 2 cos A sin (B – C) = 0
(∴ cos (B + C) = cos (π – A) = – cos A)
⇒ cos A = 0 or sin B – sin C – 2 sin (B – C) = 0
cos A = 0 ⇒ A = 90°
i.e. the triangle is right-angled. sin B sin C – 2 sin (B – C) = 0

Question 34.
If cos A = sin B – cos C, prove that the triangle is right-angled.
Solution:
cos A = sin B – cos C
or, cos C + cos A = sin B

or, 2C = π
or, C = \(\frac{\pi}{2}\)

Question 35.
If a², b², c²  be in A.P., prove that cot A, cot B, cot C are also in A.P.
Solution:
If a², b², c²  be in A.P.
then b² – a² = c² – b²
or, 2b² = c² + a²
or, \(b^2=\frac{c^2+a^2}{2}\)
or, 2b² = c² + a² …..(1)
We have to prove that cot A, cot B, cot C are in A.P.
i.e. to prove cot B – cot A = cot C – cot B
i.e. 2 Cot B = cot C + cot A
∴ R.H.S. = cot C + cot A

Question 36.
If sin A: sin C = sin (A – B) : sin (B – C) prove that a², b², c² are in A.P.
Solution:
\(\frac{\sin A}{\sin C}=\frac{\sin (A-B)}{\sin (B-C)}\)
or, sin A sin (B – C) = sin C sin (A – B)
or, sin (B + C) sin (B – C) = sin (A + B) sin (A – B)
or, sin² B – sin² C = sin² A – sin² B
or, 2 sin² B = sin² C + sin² A
or, \(2 \frac{b^2}{4 \mathrm{R}^2}=\frac{c^2}{4 \mathrm{R}^2}+\frac{a^2}{4 \mathrm{R}^2}\)
or, 2b² = c² + a²
or, b² – a² = c² – b²
∴ a², b², c² are in A.P

Question 37.
If the side lengths a, b, and c are in A.P., then prove that cos \(\frac{1}{2}\) (A – C) = 2 sin \(\frac{1}{2}\) B.
Solution:
If a,b, and c are in A.P. then b – a – c – b or, 2b = c + a
We have to prove that

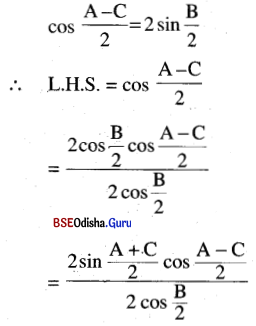
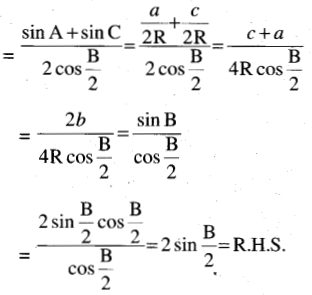
Question 38.
If the side lengths a, b, and c are in A.P., prove that cot \(\frac{1}{2}\) A, cot \(\frac{1}{2}\) B, cot \(\frac{1}{2}\) C are in A.P.
Solution: