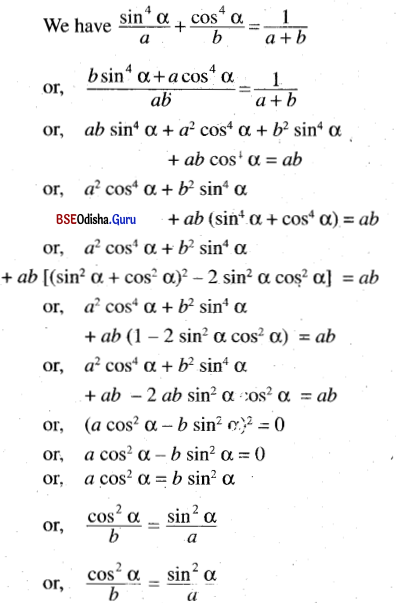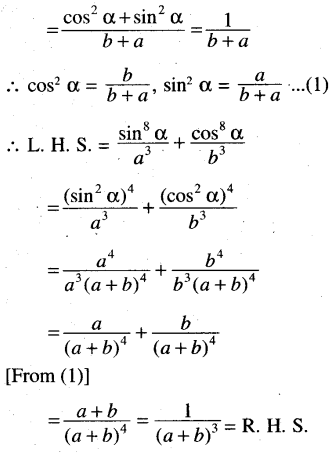Odisha State Board Elements of Mathematics Class 11 CHSE Odisha Solutions Chapter 4 Trigonometric Functions Ex 4(b) Textbook Exercise Questions and Answers.
CHSE Odisha Class 11 Math Solutions Chapter 4 Trigonometric Functions Exercise 4(b)
Question 1.
In the following questions, write ‘T’ for true and ‘F’ for false statements.
(i) If tan x + tan y = 5 and tan x, tan y = 1/2 then cot (x + y) = 10
Solution:
False
(ii) √3 (1 + tan 15°) = 1 – tan 15°
Solution:
False
(iii) If θ lies in 3rd quadrant, then cos \(\frac{\theta}{2}\) + sin \(\frac{\theta}{2}\) is positive.
Solution:
True
(iv) 2 sin 105°. sin 15° = 1/2.
Solution:
True
(v) If cos A = cos B = 1 then tan\(\frac{A+B}{2}\). tan\(\frac{A+B}{2}\) = 1
Solution:
False
(vi) cos 15° cos\(7 \frac{1}{2}^{\circ}\). sin \(7 \frac{1}{2}^{\circ}\) = 1
Solution:
False
(vii) sin 20° (3 – 4 cos2 70°) = \(\frac{\sqrt{3}}{2}\)
Solution:
True
(viii) √3 (3 tan 10° – tan3 10°) = 1 – 3tan2 10°
Solution:
True
(ix) \(\frac{2 \tan 7 \frac{1^{\circ}}{2}\left(1-\tan ^2 7 \frac{1^{\circ}}{2}\right)}{\left(1+\tan ^2 7 \frac{1^{\circ}}{2}\right)^2}\) = 1
Solution:
False
(x) The minimum value of sin θ. cos θ is (-1)2.
Solution:
False
![]()
Question 2.
In the following questions, fill in the gaps with correct answers choice from the brackets.
(i) If α and β lie in 1st and 2nd quadrants respectively, and if sin α = 1/2, sin β = 1/3, then sin (α + β) = _______. \(\left(\frac{1}{2 \sqrt{3}}+\frac{\sqrt{2}}{3}, \frac{1}{2 \sqrt{3}}-\frac{\sqrt{2}}{3}, \frac{-1}{2 \sqrt{3}}+\frac{\sqrt{2}}{3}\right)\)
Solution:
\(\frac{1}{2 \sqrt{3}}+\frac{\sqrt{2}}{3}\)
(ii) if tan α = 1/2, tan β = 1/3, then α + β = ______ \(\left(\frac{\pi}{2}, \frac{\pi}{4}, \frac{\pi}{3}\right)\)
Solution:
\(\frac{\pi}{4}\)
(iii) The value of \(\frac{\cos 15^{\circ}+\sin 15^{\circ}}{\cos 15^{\circ}-\sin 15^{\circ}}\) = ______ \(\left(\frac{\sqrt{3}}{2}, \sqrt{3}, \frac{1}{\sqrt{3}}\right)\)
Solution:
√3
(iv) if \(\frac{1+\sin A}{\cos A}\) = √2 + 1, then the value of \(\frac{1-\sin A}{\cos A}\) is_________, \(\left(\frac{1}{\sqrt{2}-1}, \sqrt{2}-1, \sqrt{2}+1\right)\)
Solution:
√2 – 1
(v) sin 105°. cos 105° = \(\left(\frac{1}{2},-\frac{1}{4},-\frac{1}{2}\right)\)
Solution:
– 1/4
(vi) 2 sin\(67 \frac{1}{2}^{\circ}\) cos\(22 \frac{1}{2}^{\circ}\) = ___ \(\left(1-\frac{1}{\sqrt{3}}, 1+\frac{1}{\sqrt{2}},-1+\frac{1}{\sqrt{2}}\right)\)
Solution:
1 + \(\frac{1}{\sqrt{2}}\)
(vii) sin 35° + cos 5° =____ (2 cos 25°, √3 cos 25°, √3 sin 25°)
Solution:
√3 cos 25°
(viii) sin2 24° – sin2 26° =_____ \(\left(\frac{\sqrt{5}+1}{8}, \frac{\sqrt{5}-1}{8}, \frac{\sqrt{5}-1}{4}\right)\)
Solution:
\(\frac{\sqrt{5}-1}{8}\)
(ix) sin 70° (4 cos2 20° – 3) =_____ \(\left(\frac{\sqrt{3}}{2}, \frac{1}{2}, \sqrt{3}\right)\)
Solution:
1/2
(x) cos 3θ + sin 3θ is maximum if θ =_____ (60°, 15°, 45°)
Solution:
15°
(xi) sin 15° – cos 15° = _____ (1/2, 0, positive, negative)
Solution:
Negative
(xii) If θ lies in the third quadrant and tan θ = 2, then the value of sin θ is ____. \(\left(\frac{1}{\sqrt{5}},-\frac{1}{\sqrt{5}}, \frac{2}{\sqrt{5}}, \frac{-2}{\sqrt{5}}\right)\)
Solution:
\(\frac{-2}{\sqrt{5}}\)
(xiii) The correct expression is. (sin 1° > sin 1, sin 1° < sin 1, sin 1° = sin 1, sin 1° = \(\frac{\pi}{180^{\circ}}\) sin 1)
Solution:
sin 1° < sin 1
(xiv) The correct expression is —. (tan 1 > tan 2, tan 1 < tan 2, tan 1 = 1/2 tan 2, tan 1 < 0)
Solution:
tan 1 > tan 2
Question 3.
Prove the following
(i) sin A. sin (B – C) + sin B sin (C – A) + sin C. sin(A – B) = 0
Solution:
L. H. S
= sin A sin (B – C) + sin B sin (C – A) + sin C sin (A – B)
= sin A (sin B cos C – cos B sin C) + sin B (sin C cos A – cos C sin A) + sin C (sin A cos B – cos A sin B)
= sin A sin B cos C – sin A cos B sin C + cos A sin B sin C – sin A sin B cos C + sin A cos B sin C – cos A sin B sin C
= 0 = R. H. S
(ii) cos A. sin (B – C) + sin B sin (C – A) + cos C. sin(A – B) = 0
Solution:
L.H.S.
= cos A sin (B – C) + cos B sin (C – A) + cos C sin (A – B)
= cos A (sin B cos C – cos B sin C) + cos B (sin C cos A – cos C sin A) + cos C (sin A cos B – cos A sin B)
= cos A sin B cos C – cos A cos B sin C + cos A cos B sin C- sin A cos B cos C + sin A cos B cos C – cos A sin B cos C = 0 = R. H. S.
(iii) \(\frac{\sin (B-C)}{\sin B \cdot \sin C}\) + \(\frac{\sin (C-A)}{\sin C \cdot \sin A}\) + \(\frac{\sin (A-B)}{\sin A \cdot \sin B}\) = 0
Solution:
L. H. S.
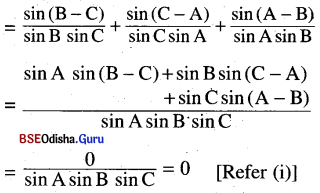
(iv) tan2 A – tan2 B = \(\frac{\sin (\mathbf{A}+\mathbf{B}) \cdot \sin (\mathbf{A}-\mathbf{B})}{\cos ^2 \mathbf{A} \cdot \cos ^2 \mathbf{B}}\)
Solution:
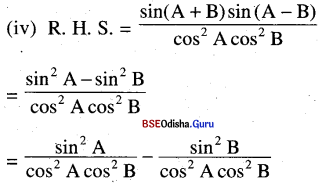
= tan2 A sec2 B – tan2 B sec2 A
= tan2 A (1 + tan2 B) – tan2 B (1 + tan2 A)
= tan2 A + tan2 A tan2 B – tan2 B tan2A tan2 B
= tan2 A – tan2 B = L. H. S
![]()
Question 4.
Prove the following :
Solution:
(i) tan 75° + cot 75° = 4
Solution:
L.H.S = tan 75° + cot 75° = tan 75° + \(\frac{1}{\tan 75^{\circ}}\)
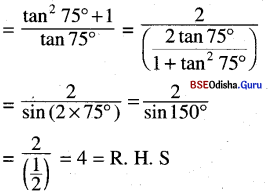
(ii) sin2 18° + cos2 36° = 3/4
Solution:
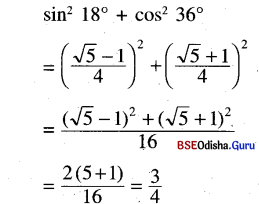
(iii) sin 18°. cos 36° = 1/4
Solution:
sin 18° cos 36°
\(=\left(\frac{\sqrt{5}-1}{4}\right)\left(\frac{\sqrt{5}+1}{4}\right)=\frac{5-1}{16}=\frac{1}{4}\)
(iv) sin 15° = \(\frac{\sqrt{3}-1}{2 \sqrt{2}}\)
Solution:
sin 15° = sin (45° – 30°)
= sin 45° cos 30° – cos 45° sin 30°
\(=\frac{1}{\sqrt{2}} \cdot \frac{\sqrt{3}}{2}-\frac{1}{\sqrt{2}} \cdot \frac{1}{2}=\frac{\sqrt{3}-1}{2 \sqrt{2}}\)
(v) cot \(\frac{\pi}{8}\) – tan \(\frac{\pi}{8}\) = 2
Solution:
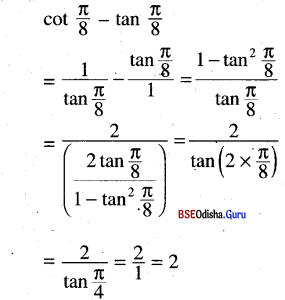
(vi) \(\frac{\cos 9^{\circ}+\sin 9^{\circ}}{\cos 9^{\circ}-\sin 9^{\circ}}\) = tan 54°
Solution:

(vii) tan 10° + tan 35° + tan 10°. tan 35 = 1
Solution:
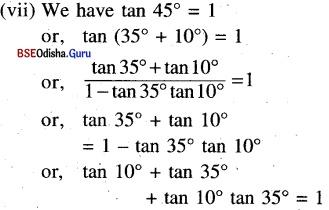
Question 5.
Prove the following:
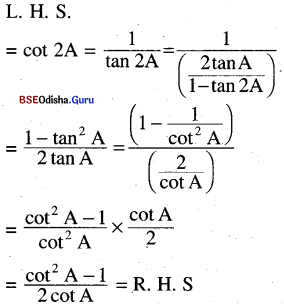
(i) cot 2A = \(\frac{\cot ^2 A-1}{2 \cot A}\)
Solution:
(ii) \(\frac{\sin B}{\sin A}=\frac{\sin (2 A+B)}{\sin A}\) – 2cos(A + B)
Solution:

= \(\frac{\sin B}{\sin A}\) = L.H.S
(iii) \(\frac{\sin 2 A+\sin 2 B}{\sin 2 A-\sin 2 B}=\frac{\tan (A+B)}{\tan (A-B)}\)
Solution:
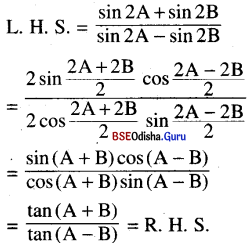
(iv) \(\frac{\cot A-\tan A}{\cot A+\tan A}\) = cos2A
Solution:

(v) \(\frac{\sin 2 A+\sin 5 A-\sin A}{\cos 2 A+\cos 5 A+\cos A}\) = tan 2A
Solution:

(vi) cot A – tan A = 2 cot 2A
Solution:
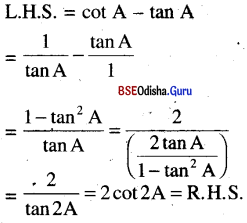
(vii) cot A – cosec 2A = cot 2A
Solution:

(viii) \(\frac{\cos A-\sin A}{\cos A+\sin A}\) = sec 2A – tan 2A
Solution:
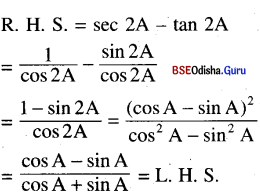
(ix) tan θ (1 + sec 2θ) = tan 2θ
Solution:
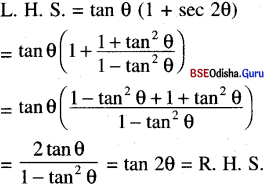
(x) \(\frac{\sin A+\sin B}{\sin A-\sin B}\) = tan \(\frac{A+B}{2}\) . cot \(\frac{A-B}{2}\)
Solution:
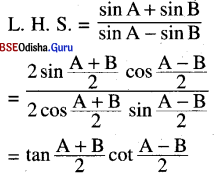
(xi) sin 50° – sin 70° + sin 10° = 0
Solution:
L. H. S. = sin 50° – sin 70° + sin 10°
= sin (60° – 10°) – sin (60° + 10°) + sin 10°
= – 2 cos 60° sin 10° + sin 10°
= – 2 × 1/2 sin 10° + sin 10°
= – sin 10° + sin 10° = 0 = R. H. S.
(xii) cos 80° + cos 40° – cos 20° = 0
Solution:
L. H. S. = cos 80° + cos 40° – cos 20°
= cos(60° + 20°) + cos (60° – 20°) – cos 20°
= 2 cos 60° cos 20° – cos 20° = 0
(xiii) 8 sin 10°. sin 50°. sin 70° = 1
Solution:
L. H. S. = 8 sin 10° sin 50° sin 70°
= 8 sin 10° sin (60° – 10°) sin (60° + 10°)
= 8 sin 10° (sin2 60° – sin2 10°)
= 8 sin 10°(3/4 – sin2 10°)
= 6 sin 10° – 8 sin3 10°)
= 2 (3 sin 10° – 4 sin3 10°)
= 2 sin (3 × 10°)
= 2 sin 30° = 2 × 1/2 = 1 = R.H.S
(xiv) 4 sin A sin (60° – A) sin (60° + A) – sin 3A = 0
Solution:
L. H. S. = 4 sin A sin (60° – A)
sin (60° + A) – sin 3A
= 4 sin A (sin2 60°- sin2 A) – sin 3A
= 4 sin A. 3/4 – 4 sin3 A – sin 3A
= (3 sin A – 4 sin3A) – sin 3A
= sin 3A – sin 3A = 0
(xv) tan 3A – tan 2A – tan A = tan 3A tan 2A tan A
Solution:
We have tan 3A = tan (2A + A)
or, tan 3A = \(\frac{\tan 2 A+\tan A}{1-\tan 2 A \tan A}\)
or, tan 3A (1 – tan 2A tan A) = tan 2A + tan A
or, tan 3A – tan 3A tan 2A tan A = tan 2A + tan A
or, tan 3A – tan 2A – tan A = tan 3A tan 2A tan A (Proved)
![]()
Question 6.
Prove the following
(i) tan\(\frac{A}{2}\) = \(\sqrt{\frac{1-\cos A}{1+\cos A}}\)
Solution:
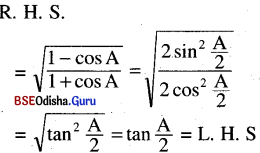
(ii) \(\sqrt{\frac{1+\sin A}{1-\sin A}}\) = tan\(\left(\frac{\pi}{4}+\frac{A}{2}\right)\)
Solution:

(iii) \(\frac{1+\tan \frac{A}{2}}{1-\tan \frac{A}{2}}\) = sec A + tan A
Solution:

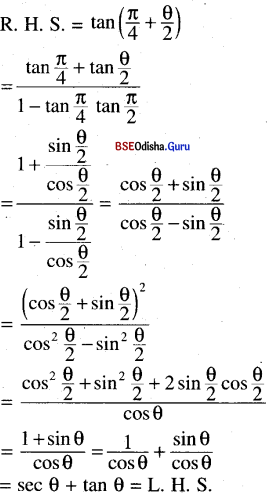
(iv) sec θ + tan θ = tan\(\left(\frac{\pi}{4}+\frac{θ}{2}\right)\)
Solution:
(v) cot\(\frac{A}{2}\) = \(\frac{\sin A}{1-\cos A}\)
Solution:
R.H.S = \(\frac{\sin A}{1-\cos A}=\frac{2 \sin \frac{A}{2} \cos \frac{A}{2}}{2 \sin ^2 \frac{A}{2}}\)
= cot\(\frac{A}{2}\) R.H.S
Question 7.
Find the maximum value of the following.
(i) 5 sin x + 12 cos x
Solution:
5 sin x + 12 cos x
Let 5 = r cos θ, 12 = r sin θ 52
∴ 52 = r2 cos2 θ, 122 = r2 sin2 θ
∴ 52 + 122 = r2 (cos2 θ + sin2 θ) = r2
∴ r = \(\sqrt{25+144}\) = 13
∴ The maximum value of 5 sin x + 12 cos x is 13.
(ii) 24 sin x – 7 cos x
Solution:
The maximum value of 24 sin x – 7 cos x is
\(\sqrt{(24)^2+(-7)^2}\)
= \(\sqrt{576+49}=\sqrt{625}\) = 25
(iii) 2 + 3 sin x + 4 cos x
Solution:
The maximum value of 3 sin x + 4 cos x is
\(\sqrt{3^2+4^2}\) = 5
∴ Maximum value of 2 + 3 sin x + 4 cos x is 2 + 5 = 7
(iv) 8 cos x – 15 sin x – 2
Solution:
Maximum value of 8 cos x- 15 sin x is \(\sqrt{(8)^2+(-15)^2}\)
= \(\sqrt{64+225}=\sqrt{289}\) = 17
∴ Maximum value of 8 cos x- 15 sin x – 2 is 17 – 2 = 15
Question 8.
Answer the following:
(i) If tan A = \(\frac{13}{27}\), tan B = \(\frac{7}{20}\) and A, B are acute, show that A + B = 45°.
Solution:

(ii) If tan θ = \(\frac{b}{a}\), find the value of a cos 2θ + b sin 2θ.
Solution:

(iii) If sec A – tan A = \(\frac{1}{2}\) and 0< A < 90° then show that sec A = \(\frac{5}{4}\)
Solution:
If sec A – tan A = \(\frac{1}{2}\), ….(1)
0< A < 90°
⇒ sec A – tan A = \(\frac{\sec ^2 A-\tan ^2 A}{2}\)
= \(\frac{(\sec \mathrm{A}+\tan \mathrm{A})(\sec \mathrm{A}-\tan \mathrm{A})}{2}\)
or, sec A + tan A = 2 ……(2)
Now adding eqn. (1) and (2), We have
2 sec A = \(\frac{1}{2}\) + 2 = \(\frac{5}{2}\)
or, sec A = \(\frac{5}{4}\)
(iv) If sin θ + sin Φ = a and cos θ + cos Φ = b the show that tan \(\frac{1}{2}\) (θ + Φ) \(\frac{a}{b}\)
Solution:
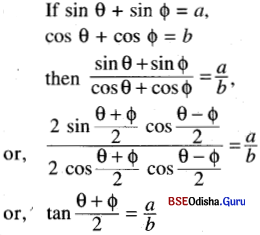
(v) If tan θ = \(\frac{a \sin x+b \sin y}{a \cos x+b \cos y}\) then show that a sin (θ – x) + b sin (θ – y) = 0
Solution:
tan θ = \(\frac{a \sin x+b \sin y}{a \cos x+b \cos y}\)
or, \(\frac{\sin \theta}{\cos \theta}=\frac{a \sin x+b \sin y}{a \cos x+b \cos y}\)
or, a sin θ cos x + b sin θ cos y = a cos θ sin x + b cos θ sin y
or, a (sin θ cos x – cos θ sin x) + b (sin θ cos y – cos θ sin y) = 0
or, a sin (θ – x) + b sin (θ – y) = 0
(vi) If A + C = B, show that tan A. tan B. tan C = tan B – tan A – tan C.
Solution:
A + C = B
or, tan (A + C) = tan B
or, \(\frac{\tan A+\tan C}{1-\tan A \tan C}\)
or, tan A + tan C = tan B – tan A tan B tan C
or, tan A tan B tan C = tan B – tan A – tan C
(vii) If tan A = \(\frac{1}{5}\), tan B = \(\frac{2}{3}\) then show that cos 2A = sin 2B.
Solution:
tan A = \(\frac{1}{5}\), tan B = \(\frac{2}{3}\)
∴ cos 2A = \(\frac{1-\tan ^2 \mathrm{~A}}{1+\tan ^2 \mathrm{~A}}\)
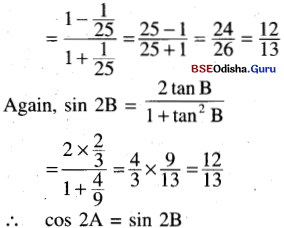
(viii) If cos 2A = tan2 B, then show that cos 2B = tan2 A In Δ ABC, prove that.
Solution:

(ix) tan\(\frac{B+C}{2}\) = cot\(\frac{A}{2}\)
Solution:
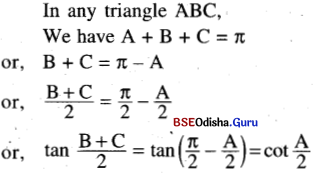
(x) cos (A + B) + sin C = sin (A + B) – cos C
If A + B + C = π and cos A = cos B. cos C show that (xi and xii)
Solution:
We have A + B = π – C or, cos (A + B)
or, cos (A + B)
= cos (π – C) = – cos C
and sin (A + B) = sin (π – C) = sin C
∴ cos (A + B) + sin C
= – cos C + sin (A + B)
= sin (A + B) – cos C.
(xi) tan B + tan C = tan A
Solution:
[∴ A + B + C = π ⇒ B + C = π – A
⇒ sin (B + C) = sin (π – A) = sin A]
L. H. S. = tan B + tan C
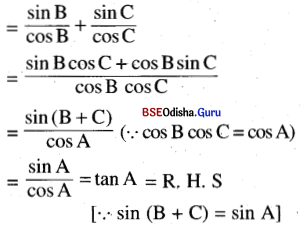
(xii) 2 cot B. cot C = 1
Solution:
We have A + B + C = π
⇒ B + C = π – A
⇒ cos (B + C) = cos (π – A) = – cosA
⇒ cos B cos C – sin B sin C = – cos B cos C
(∵ cos B cos C = cos A)
⇒ 2 cos B cos C = sin B sin C
⇒ \(\frac{2 \cos B \cos C}{\sin B \sin C}\) = 1
⇒ 2 cot B cot C = 1
![]()
Question 9.
Prove the following:
(i) cos (A – D) sin (B – C) + cos (B – D) sin (C – A) + cos (C- D) sin (A – B) = 0
Solution:
L. H. S. = cos (A – D) sin (B – C) + cos (B – D) sin (C – A) + cos (C – D) sin (A- B)
= \(\frac{1}{2}\) [2 cos (A- D) sin (B – C) + 2 cos (B – D) sin (C – A) + 2 cos (C – D) sin (A – B)]
= \(\frac{1}{2}\) [ sin (A- D + B – C) – sin (A – D – B + C) + sin (B – D + C – A)- sin (B- D- C + A) + sin ( C – D + A – B)- sin (C – D- A + B)]
= \(\frac{1}{2}\) × 0 = 0 = R.H.S
(ii) sin 2A + sin 2B + sin 2 (A – B) = 4 sin A. cos B. cos (A – B)
Solution:
L. H. S. = sin 2A + sin 2B + sin 2 (A – B)
= 2 sin \(\frac{2 A+2 B}{2}\) cos \(\frac{2 A-2 B}{2}\) + 2 sin (A – B) cos (A – B)
= 2 sin (A + B) cos (A- B) + 2 sin (A – B) cos (A – B)
= 2 cos (A – B)[ sin (A-+ B) + sin(A – B)]
= 2 cos (A – B) × 2 sin A cos B
= 4 sin A cos B cos (A – B) = R. H. S.
(iii) cos 2A + cos 2B + cos 2 (A – B) + 1 = 4 cos A. cos B. cos (A – B)
Solution:
cos 2A + cos 2B + cos 2 (A- B) + 1
= 2 cos \(\frac{2 A+2 B}{2}\) cos \(\frac{2 A-2 B}{2}\) + 2 cos2 (A – B)
= 2 cos (A + B) cos (A- B) + 2 cos2 (A – B)
= 2 cos (A – B) [cos (A + B) + cos (A – B)]
= 2 cos (A – B) x 2 cos A cos B
= 4 cos A cos B cos (A – B)
= R. H. S
(iv) sin 2A + sin 2B + sin 2C- sin 2 (A + B + C)
Solution:
L. H. S. = sin 2A + sin 2B + sin 2C- sin 2 (A + B + C)
= 2 sin \(\frac{2 A+2 B}{2}\) cos \(\frac{2 A-2 B}{2}\) = 2 cos \(\frac{2 \mathrm{C}+2(\mathrm{~A}+\mathrm{B}+\mathrm{C})}{2}\) × \(\frac{2 \mathrm{C}-2(\mathrm{~A}+\mathrm{B}+\mathrm{C})}{2}\)
= 2 sin (A + B) cos (A – B) + 2 cos (A + B + 2C) sin (A – B)
= 2 sin (A + B) [cos (A- B) – cos (A + B + 2C)]
= 2 sin (A + B) × 2 sin \(\frac{A-B+A+B+2 C}{2}\) sin \(\frac{A+B+2 C-A+B}{2}\)
= 4 sin (A + B) sin (C + A) sin (B + C) = R. H. S.
(v) sin A + sin 3A + sin 5A = sin 3A (1 + 2 cos 2A)
Solution:
L. H. S. = sin A + sin 3A + sin 5A
= sin 3A + sin 5A + sin A
= sin 3A + 2 sin \(\frac{5 \mathrm{~A}+\mathrm{A}}{2} cos \frac{5 \mathrm{~A}-\mathrm{A}}{2}\)
= sin 3A + 2 sin 3A cos 2A
= sin 3A (1 + 2 cos 2A) = R. H. S
(vi) sin A – sin 3A + sin 5A = sin 3A (2 cos 2A – 1)
Solution:
L. H. S. = sin A – sin 3A + sin 5A
= sin A + sin 5A – sin 3A
= sin 5A + sin A – sin 3A
= 2 sin \(\frac{5 \mathrm{~A}+\mathrm{A}}{2} cos \frac{5 \mathrm{~A}-\mathrm{A}}{2}\) – sin 3A
= 2 sin 3A cos 2A – sin 3A
= sin 3A (2 cos 2A – 1) = R. H. S.
(vii) cos (A + B) + sin (A – B) = 2 sin (45° + A) cos (45° + B)
Solution:
R. H. S. = 2 sin (45° + A) cos (45° + B)
= sin (45° + A + 45° + B) + sin (45° + A – 45° – B)
= sin (90° + A + B) sin (A – B)
= cos (A + B) sin (A – B) = L. H. S.
(viii) cos (120° + A) cos (120° – A) + cos (120° + A) cos A + cos A cos (120° – A) + \(\frac{3}{4}\) = 0
Solution:
L. H. S.
= cos (120° + A) cos (120° – A) + cos (120° + A) cos A + cos A cos (120° – A) + \(\frac{3}{4}\)
= cos2 A – sin2 120° + cos A [ cos (120° + A) + cos (120° – A)] + \(\frac{3}{4}\)
= cos2 A – \(\frac{3}{4}\) + cos A ( 2 cos 120°. cos A) + \(\frac{3}{4}\)
= cos2 A + 2 cos 120°. cos2 A
= cos2 A + 2 \(\left(-\frac{1}{2}\right)\) . cos2 A
= cos2 A – cos2 A = 0
(ix) cos 4A – cos 4B = 8 (cos A – cos B) (cos A + cos B) (cos A – sin B) (cos A + sin B)
Solution:
R. H. S. = 8 (cos A- cos B) (cos A + cos B)
(cos A – sin B) (cos A + sin B)
= 8 (cos2 A – cos2 B) (cos2 A – sin2 B)
= – 8(cos2 B – cos2 A)(cos2 A – sin2 B)
= – 8 sin (A +B) sin (A – B) cos (A + B) cos (A – B)
= – 2 x [ 2 sin (A + B) cos (A + B)] [2 sin (A – B) cos (A – B)]
= – 2 sin (2A + 2B) sin (2A – 2B)
= – [cos (2A + 2B – 2A + 2B) – cos (2A + 2B + 2A – 2B)]
= – cos 4B + cos 4A
= cos 4A – cos 4B = L. H. S.
Question 10.
Prove the following:
(i) \(\frac{1-\tan ^2\left(45^{\circ}-A\right)}{1+\tan ^2\left(45^{\circ}-A\right)}\) = sin 2A
Solution:
L.H.S \(\frac{1-\tan ^2\left(45^{\circ}-A\right)}{1+\tan ^2\left(45^{\circ}-A\right)}\) = sin 2A = cos 2(45° – A)
= cos (90° – 2A) = sin 2A = R. H. S.
(ii) \(\frac{\cos A+\sin A}{\cos A-\sin A}-\frac{\cos A-\sin A}{\cos A+\sin A}\) = 2 tan 2A
Solution:

(iii) \(\frac{1-\cos 2 A+\sin 2 A}{1+\cos 2 A+\sin 2 A}\) = tan A
Solution:

(iv) \(\frac{\sin (\mathbf{A}+\mathbf{B})+\cos (\mathbf{A}-\mathbf{B})}{\sin (\mathbf{A}-\mathbf{B})+\cos (\mathbf{A}+\mathbf{B})}\) = sec 2B + tan 2B
Solution:

(v) \(\frac{\cos 7 \alpha+\cos 3 \alpha-\cos 5 \alpha-\cos \alpha}{\sin 7 \alpha-\sin 3 \alpha-\sin 5 \alpha+\sin \alpha}\) = cot 2α
Solution:
L.H.S = \(\begin{array}{r}
\cos 7 \alpha+\cos 3 \alpha \\
-\cos 5 \alpha-\cos 3 \alpha \\
\hline \sin 7 \alpha-\sin 3 \alpha \\
-\sin 5 \alpha+\sin \alpha
\end{array}\)

(vi) \(\frac{\sin \theta+\sin 3 \theta+\sin 5 \theta+\sin 7 \theta}{\cos \theta+\cos 3 \theta+\cos 5 \theta+\cos 7 \theta}\) = tan 4θ
Solution:
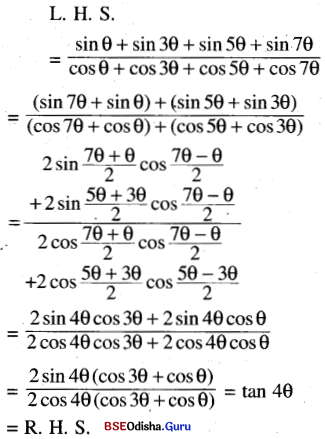
Question 11.
Prove the following:
(i) Express 4 cos A. cos B. cos C as the sum of four cosines.
Solution:
4 cos A cos B cos C
= 2 (2cos A cos B) cos C
= 2 [ cos (A + B) + cos (A – B)] cos C
= 2 cos (A + B) cos C + 2 cos (A – B) cos C
= cos (A + B + C) + cos (A + B – C) + cos (A – B + C) + cos (A – B – C)
(ii) Express cos 2A + cos 2B + cos 2C + cos 2 (A + B + C) as the product of three cosines.
Solution:
cos 2A + cos 2B + cos 2C + cos 2(A + B + C)
= 2 cos \(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\) cos \(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\) = 2 cos \(\frac{2 C+2(A+B+C)}{2}\) × cos \(\frac{2 C-2(A+B+C)}{2}\)
= 2 cos (A + B) cos (A- B) + 2 cos (A + B + 2C) cos (A + B)
= 2 cos (A + B) [cos (A- B) + cos (A + B + 2C)]
= 2 cos (A + B) × 2 cos \(\frac{(A-B+A+B+2 C)}{2}\) cos \(\frac{(A-B-A-B-2 C)}{2}\)
= 4 cos (A + B) cos (C + A) cos (B + C)
![]()
Question 12.
Prove the following:
(i) cos6 A – sin6 A = cos 2A(1 – \(\frac{1}{4}\) sin2 2A)
Solution:
L.H.S = cos6 A – sin6 A
= (cos2 A)3– (sin2 A)3 = (cos2 A – sin2 A)3 + 3 cos2 A sin2 A (cos2 A – sin2 A)
= cos3 2A + \(\frac{3}{4}\) sin2 2A cos 2A
= cos2 A (cos2 2A + \(\frac{3}{4}\) sin2 2A)
= cos 2A (1 – sin2 2A + \(\frac{3}{4}\) sin2 2A)
= cos 2A (1 – \(\frac{1}{4}\) sin2 2A) = R.H.S
(ii) cos6A + sin6 A = \(\frac{1}{4}\) (1 + 3 cos22A)
Solution:
L.H.S = cos6 A + sin6 A
= (cos2 A)3 + (sin2 A)3
= (cos2 A)3 + (sin2 A)3 – 3 cos2 A. sin2 A (cos2 A + sin2 A)
= 1 – \(\frac{3}{4}\) sin2 2A = 1 – \(\frac{3}{4}\) (1 – cos2 2A)
= 1 – \(\frac{3}{4}\) + \(\frac{3}{4}\) cos2 2A
= \(\frac{1}{4}\) + \(\frac{3}{4}\) cos2 2A = \(\frac{1}{4}\) (1 + 3cos2 2A) = R.H.S.
(iii) cos3 A. cos 3A + sin3 A sin3 A = cos3 2A
Solution:
L.H.S = cos3 A cos 3A + sin3 A sin 3A
= cos3 A (4 cos3 A- 3 cos A) + sin3 A (3 sin A- 4 sin3 A)
= 4 cos6A- 3 cos4A + 3 sin4A- 4 sin6A
= 4 (cos6A- sin6A) – 3(cos4A- sin4A)
= 4 {(cos2A)3– (sin2A)3} – 3 {(cos2A)2– (sin2A)2}
= 4 (cos2A- sin2A) {(cos2A)2 + cos2A sin2A + (sin2A)2} – 3 (cos2A- sin2A) (cos2A + sin2A)
= (cos2A- sin2A) [4 {(cos2A + sin2A)2-2 cos2A sin2A + cos2A sin2A} -3×1]
= cos 2A ( 4- 4 sin2A cos2A- 3)
= cos 2A ( 1 – 4 sin2A cos2A)
= cos 2A (1 – sin22A)
= cos 2A cos22A = cos32A = R. H. S.
(iv) sin4 θ = \(\frac{3}{8}\) – \(\frac{1}{2}\) cos 2θ + \(\frac{1}{8}\) cos 4θ
Solution:
R.H.S = \(\frac{3}{8}\) – \(\frac{1}{2}\) cos 2θ + \(\frac{1}{8}\) cos 4θ
= \(\frac{3}{8}\) – \(\frac{1}{2}\) (1 – 2 sin2 θ) + \(\frac{1}{8}\) (1 – 2 sin2 θ)
= \(\frac{3}{8}\) – \(\frac{1}{2}\) + sin2 θ + \(\frac{1}{8}\) – \(\frac{1}{4}\) sin2 2θ
= sin2 θ – \(\frac{1}{4}\) × 4 sin2 θ cos2 θ
= sin2 θ (1 – cos2 θ)
= sin2 θ sin2 θ = sin4 = L.H.S
(v) cot 3A = \(\frac{\cot ^3 A-3 \cot A}{3 \cot ^2 A-1}\)
Solution:
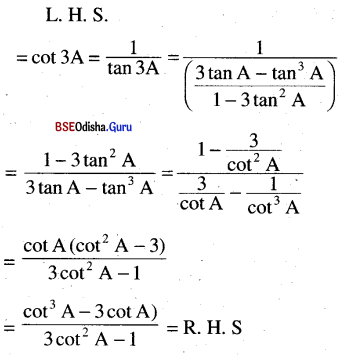
(vi) tan 4θ = \(\frac{4 \tan \theta-4 \tan ^3 \theta}{1-6 \tan ^2 \theta+\tan ^4 \theta}\)
Solution:

(vii) \(\frac{1}{\tan 3 A-\tan A}-\frac{1}{\cot 3 A-\cot A}\) = cot 2A
Solution:

(viii) \(\frac{\cot A}{\cot A-\cot 3 A}-\frac{\tan A}{\tan 3 A-\tan A}\) = 1
Solution:
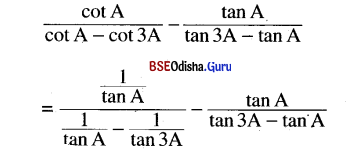
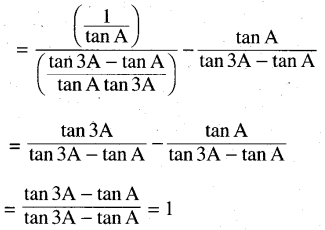
Question 13.
Find the value of
sin 3°,cos 3°, 2 sin \(\frac{\pi}{32}\)
Solution:
sin 3° = sin (18° – 15°)
= sin 18° cos 15° – cos 18° sin 15°


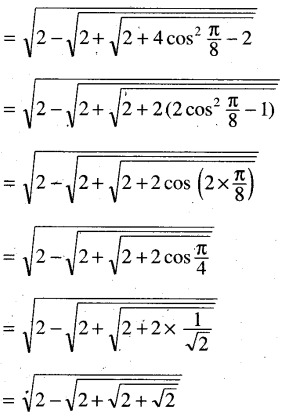
Question 14.
If sin A + sin B = a and cos A + cos B = b, then show that
(i) tan(A + B) = \(\frac{2 a b}{b^2-a^2}\)
Solution:

(ii) sin (A + B) = \(\frac{2 a b}{b^2-a^2}\)

(iii) cos (A + B) = \(\frac{b^2-a^2}{b^2+a^2}\)
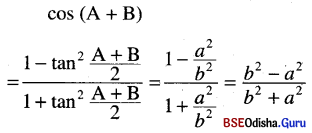
Question 15.
Prove the following:
(i) \(\frac{1+\sin A-\cos A}{1+\sin A+\cos A}\) = tan \(\frac{A}{2}\)
Solution:
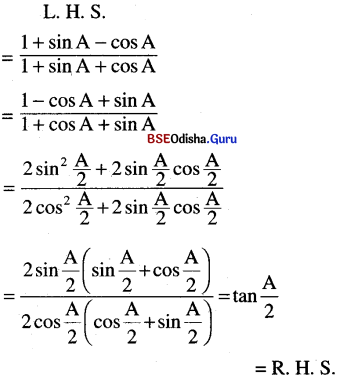
(ii) \(8 \sin ^4 \frac{1}{2} \theta-8 \sin ^2 \frac{1}{2} \theta\) + 1 = cos 2θ
Solution:
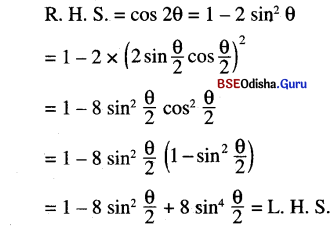
(iii) \(\cos ^4 \frac{\pi}{8}+\cos ^4 \frac{3 \pi}{8}+\cos ^4 \frac{5 \pi}{8}\) \(+\cos ^4 \frac{7 \pi}{8}=\frac{3}{2}\)
Solution:
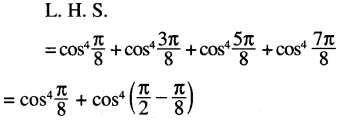

(iv) cos2 \(\frac{\alpha}{2}\) (1- 2cos α)2 + sin2 α(1+ 2 cos α)2 =1
Solution:
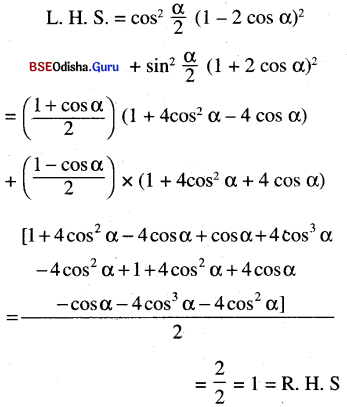
Question 16.
Prove the following:
(i) sin 20°. sin 40°. sin 60°. sin 80° = \(\frac{3}{16}\)
Solution:

(ii) cos 36°. cos 72°. cos 108°. cos144° = \(\frac{7}{16}\)
Solution:
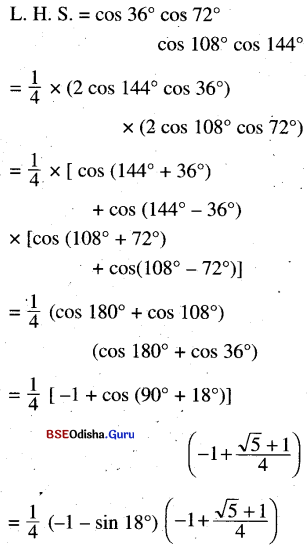
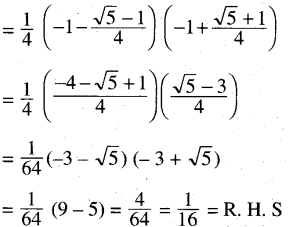
(iii) cos 10°. cos 30°. cos 50°. cos 70° = \(\frac{3}{16}\)
Solution:

(iv) cos 20°. cos 40°. cos 60°. cos 80° = \(\frac{1}{16}\)
Solution:

(v) tan 6°. tan 42°.tan 66°. tan 78° = 1 [Hints: Use the identity tan 3A = tan A tan (60° – A) tan (60° + A)]
Solution:
We have tan 3A
= tan A tan (60° – A) tan (60° + A)
Now putting A = 6° and 18°.
in (1) we have
tan 18° = tan 6° tan 54° tan 66° …(2)
and tan 54°
= tan 18° tan 42° tan 78° ……(3)
Multiplying (2) and (3) we have
tan 18° tan 54°
= tan 6° tan 54° tan 66° tan 18° . tan 42°. tan 78°
or, 1 = tan 6° tan 42° tan 66° tan 78°.
![]()
Question 17.
Prove the following:
(i) cos 7 \(\frac{1}{2}\)° = √6 + √3 + √2 + 2
Solution:

(ii) cot 22 \(\frac{1}{2}\)° = √2 + 1
Solution:
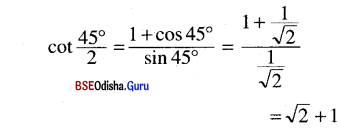
(iii) cot 37 \(\frac{1}{2}\)° = √6 – √3 – √2 + 2
Solution:

(iv) tan 37 \(\frac{1}{2}\)° = √6 + √3 – √2 + 2
Solution:
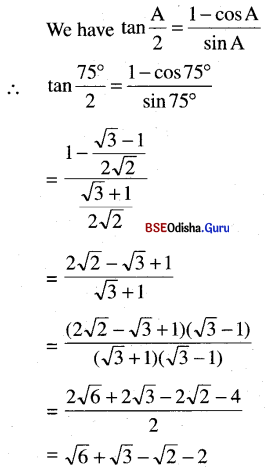
(v) cos \(\frac{\pi}{16}\) = 1/2 \(\sqrt{2+\sqrt{2+\sqrt{2}}}\)
∴ 2 cos \(\frac{\pi}{16}\)

Question 18.
(i) If sin A = K sin B, prove that tan 1/2(A – B) = \(\frac{K-1}{K+1}\) tan 1/2(A – B)
Solution:

(ii) Ifa cos (x + α) = b cos (x – α) show that (a + b) tan x = (a – b) cot α.
Solution:
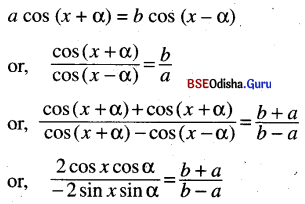
or, cot x cot α = \(\frac{a+b}{a-b}\)
or, (a – b) cot α = \(\frac{a+b}{\cot x}\) = (a + b) tan x
or, (a + b) tan x =(a-b) cot α
(iii) An angle 0 is divided into two parts α, β such that tan α: tan β = x : y.
Prove that sin (α – β) = \(\frac{x-y}{x+y}\) sin θ.
Solution:

(iv) If sin θ + sin Φ = a, cos θ + cos Φ = b, show that
\(\frac{\sin \frac{\theta+\phi}{2}}{a}=\frac{\cos \frac{\theta+\phi}{2}}{b}=2 \frac{\cos \frac{\theta-\phi}{2}}{a^2-b^2}\)
Solution:
sin θ + sin Φ = a
cos θ + cos Φ = b
We have
a2 + b2 = (sin θ + sin Φ)2 + (sin θ + sin Φ)2
= sin2 θ + sin2 Φ + 2 sin θ. sin Φ + cos2 θ +cos2 Φ + 2 cos θ. cos Φ
= 2 + 2 (cos θ cos Φ + sin θ sin Φ)
= 2 + 2 cos (θ – Φ)
= 2 [1+ cos (θ – Φ)]
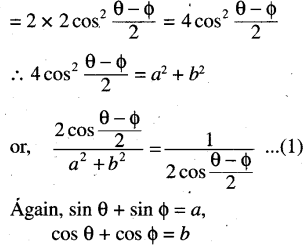

(v) If a cos α + b sin α = c = a cos β + b sin α then prove that
\(\frac{a}{\cos \frac{1}{2}(\alpha+\beta)}=\frac{b}{\sin \frac{1}{2}(\alpha+\beta)}\) \(=\frac{c}{\cos \frac{1}{2}(\alpha-\beta)}\)
Solution:

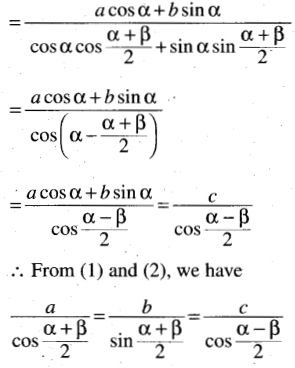
(vi) Prove that \(\left(\frac{\cos A+\cos B}{\sin A-\sin B}\right)^n+\left(\frac{\sin A+\sin B}{\cos A-\cos B}\right)^n\) = 2 cosn \(\frac{A-B}{2}\) or zero according as n is even or odd.
Solution:

Question 19.
(i) If (1 – e) tan2 \(\frac{\boldsymbol{\beta}}{2}\) = (1 + e) tan2 \(\frac{\boldsymbol{\alpha}}{2}\), prove that cos β = \(\frac{\cos \alpha-e}{1-e \cos \alpha}\)
Solution:
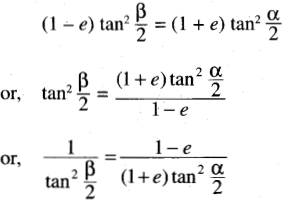
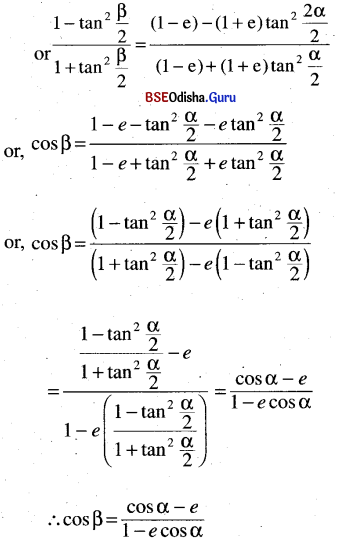
(ii) If cos θ = \(\frac{\cos \mathbf{A}-\cos \mathbf{B}}{1-\cos \mathbf{A} \cdot \cos \mathbf{B}}\) prove that one of the values of
tan \(\frac{θ}{2}\) is tan \(\frac{A}{2}\) . tan \(\frac{B}{2}\).
Solution:
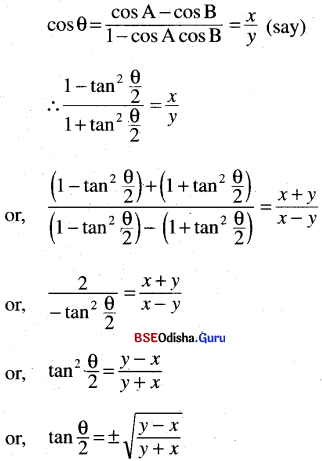
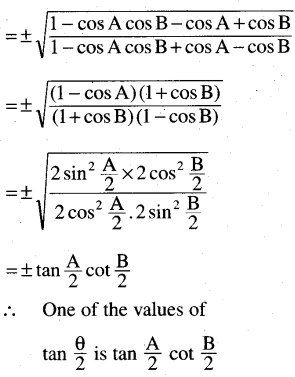
(iii) If tan θ = \(\frac{\sin x \cdot \sin y}{\cos x+\cos y}\) then prove that one of the values of tan \(\frac{1}{2}\) θ tan \(\frac{1}{2}\) x and tan \(\frac{1}{2}\) y.
Solution:

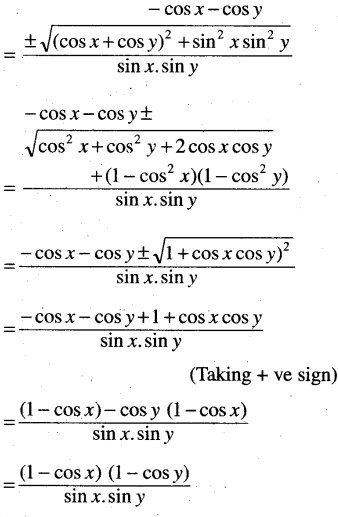
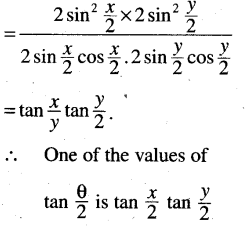
(iv) If sec (Φ + a) + sec (Φ – α) = 2 sec Φ. show that cos Φ = ± √2 cos \(\frac{α}{2}\)
Solution:
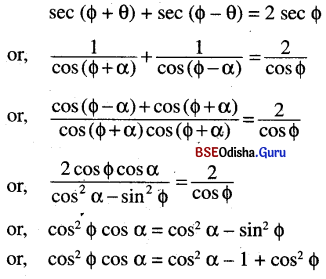
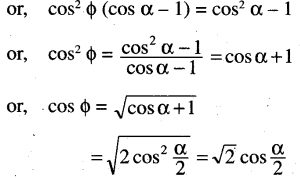
(v) If tan A + tan B = a and cot A + cot B = b. then show that cot (A + B) = \(\frac{1}{a}\) – \(\frac{1}{b}\).
Solution:
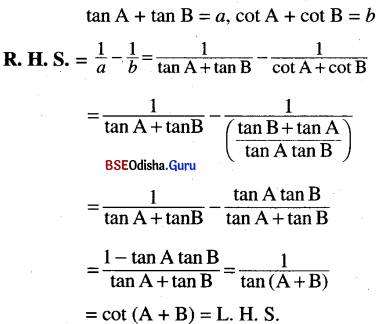
(vi) If cot θ = cos (x + y) and cot Φ = cos (x – y) show that tan (θ = Φ) = \(\frac{2 \sin x \cdot \sin y}{\cos ^2 x+\cos ^2 y}\)
Solution:

(vii) If tan β = \(\frac{n^2 \sin \alpha \cdot \cos \alpha}{1-n^2 \sin ^2 \alpha}\), then show that \(\frac{\tan (\alpha-\beta)}{\tan \alpha}\) = 1 – n2
Solution:
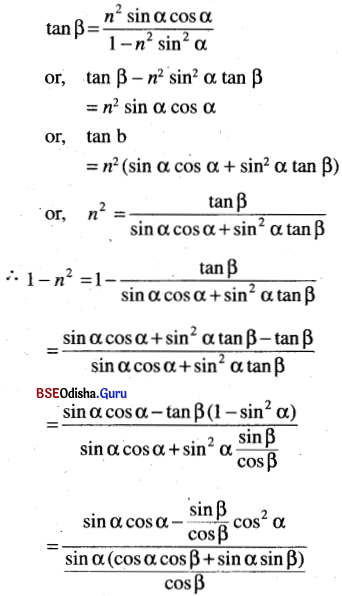
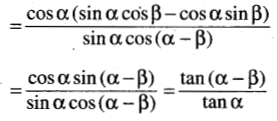
(viii)If 2 tan α = 3 tan β, then prove that tan(α – β) = \(\frac{\sin 2 \beta}{5-\cos 2 \beta}\)
Solution:

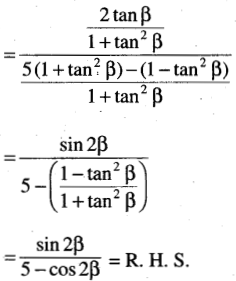
(ix) If α, β are acute angles and cos 2α = \(\frac{3 \cos 2 \beta-1}{3-\cos 2 \beta}\) then prove that tan α = √2 tan β.
Solution:

![]()
Question 20.
If A + B + C = π, then prove the following.
(i) cos 2A + cos 2B + cos 2C + 1 + 4 cos A. cos B. cos C = 0
Solution:
A + B + C = π or, A + B = π – C
or, cos (A + B) = cos (π – C) = – cos C
∴ cos 2A + cos 2B + cos 2C
= 2 cos \(\frac{2 \mathrm{~A}+2 \mathrm{~B}}{2}\) cos \(\frac{2 \mathrm{~A}-2 \mathrm{~B}}{2}\)
= 2 cos (A + B) cos (A- B) + 2 cos2 C – 1
= – 2 cos C cos (A – B) + 2 cos2 C – 1
= – 1 – 2 cos C cos (A – B) – cos C
= – 1 – 2 cos C [cos (A- B) + cos (A + B)]
= – 1 – 2 cos C × 2 cos A cos B
= – 1 – 4 cos A cos B cos C
∴ L. H. S. = cos 2A + cos 2B + cos 2C + 1 + 4 cos A cos B cos C
= – 1 – 4 cos A cos B cos C + 1 + 4 cos A cos B cos C = 0 = R. H. S.
(ii) sin 2A + sin 2B – sin 2C = 4 cos A. cos B. sin C
Solution:
L. H. S. = sin 2A + sin 2B – sin 2C
= 2 sin \(\frac{2 A+2 B}{2}\) cos \(\frac{2 A-2 B}{2}\) – sin 2C
= 2 sin(A + B) cos (A – B) -2 sinC cos C
= 2 sin C cos (A- B) – 2 sin C cos C [ ∵ A + B= π – C]
or, sin (A + B) = sin (n- C) = sin C]
= 2 sin C [cos (A – B)- cos C]
= 2 sin C [cos (A – B) – cos (A + B)]
= 2 sin C. 2 cos A. cos B
= 4 cos A cos B sin C = R. H. S.
(iii) cos A + cos B + cos C = 1 + 4 sin \(\frac{1}{2}\) A. sin \(\frac{1}{2}\) B. sin \(\frac{1}{2}\) C.
Solution:
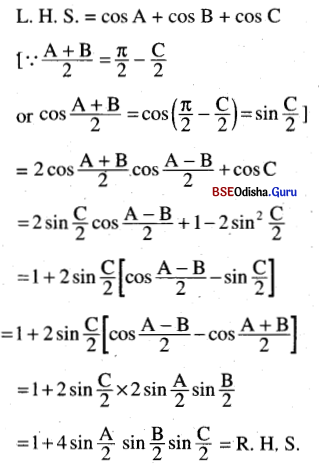
(iv) sin A + cos B- sin C = 4 sin \(\frac{1}{2}\) A. sin \(\frac{1}{2}\) B. cos \(\frac{1}{2}\) C.
Solution:

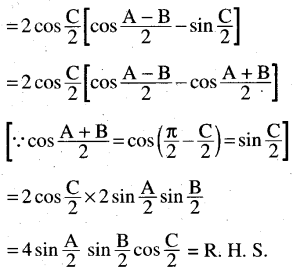
(v) cos2 A + cos2 B + 2cos A. cos B. cos C = sin2 C
Solution:
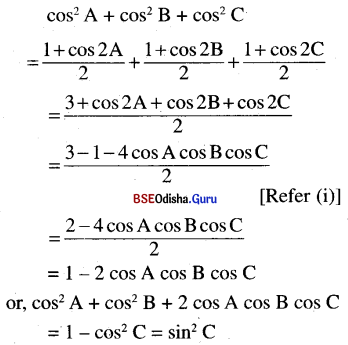
(vi) sin2 \(\frac{A}{2}\) + sin2 \(\frac{B}{2}\) + sin2 \(\frac{C}{2}\) = 1 – 2 sin \(\frac{A}{2}\). sin \(\frac{B}{2}\). sin \(\frac{C}{2}\)
Solution:
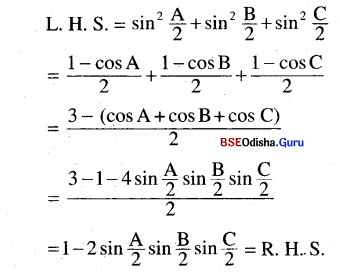
(vii) sin \(\frac{A}{2}\) + sin \(\frac{B}{2}\) + sin \(\frac{c}{2}\) = 4 sin \(\frac{\pi-A}{4}\) sin \(\frac{\pi-B}{4}\). sin \(\frac{\pi-C}{4}\) + 1
Solution:
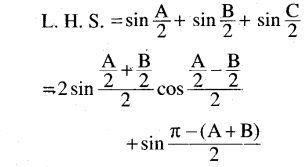

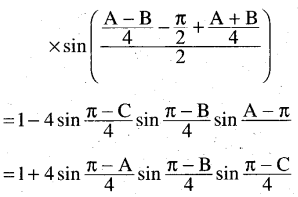
(viii) cos2 \(\frac{A}{2}\) + cos2 \(\frac{B}{2}\) – cos2 \(\frac{C}{2}\) = 2 cos \(\frac{A}{2}\). cos \(\frac{B}{2}\). sin \(\frac{C}{2}\)
Solution:
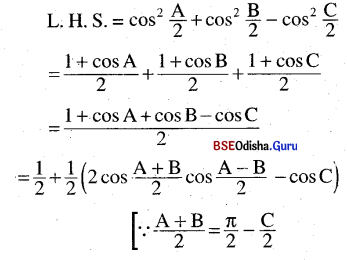
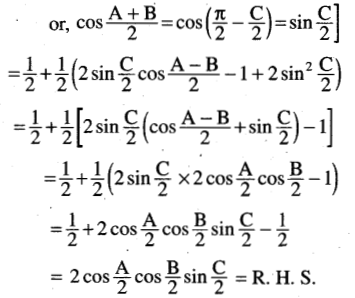
(ix) sin (B + 2C) + sin (C + 2A) + sin (A + 2B) = 4 sin \(\frac{B-C}{2}\). sin \(\frac{C-A}{2}\). sin \(\frac{A-B}{2}\)
Solution:

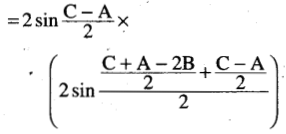
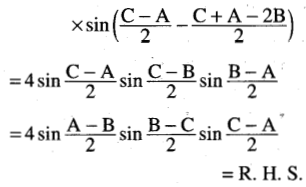
Question 21.
(i) Show that (2 cos θ – 1) (2 cos 2θ – 1) (2 cos2 2θ – 1) ….. (2 cos 2n-1 θ – 1) \(=\frac{2 \cos 2^n \theta+1}{2 \cos \theta+1}\)
Solution:
We have
(2 cos θ + 1) (2 cos θ – 1)
= 4 cos2 θ – 1=4 cos2 θ – 2+1
= 1 + 2(2 cos2 θ – 1)
= 1+2 cos 2θ = 2 cos 2θ+1
And, (2 cos 2θ + 1) (2 cos 2θ – 1)
= 4 cos2 2θ – 1 = 2 ( 2 cos2 2θ – 1) + 1
= 2 cos 4 θ + 1 = 2 cos 22 θ + 1
Similarly, we can prove,
( 2 cos 22 θ + 1) ( 2 cos 22 θ- 1)
= 2 cos 23 θ + 1
Proceeding in this way, we can prove,
(2 cos 2θ + 1) (2 cos 2θ – 1)
(2 cos 2θ- 1) (2 cos 22 θ – 1) …… (2 cos 2n-1 θ-1)
= 2 cos 2n θ + 1
or, (2 cos θ-1) (2 cos 2θ-1) (2 cos 22 θ- 1) (2 cos 2n-1 θ-1)
\(=\frac{2 \cos 2^n \theta+1}{2 \cos \theta+1}\)
(ii) Show that 2n cos θ. cos 2θ. cos22 θ ……… 2n-1 θ = 1 If θ = \(\frac{\pi}{2^n+1}\)
Solution:
we have, θ = \(\frac{\pi}{2^n+1}\)
or, 2n θ + θ = π
or, 2n θ = π – θ
or, 2n θ = sin (π – θ) = sin θ
or, \(\frac{\sin 2^n \theta}{\sin \theta}\) = 1 …….(1)
Again, sin 2n θ = 2 sin 2n-1 θ cos 2n-1 θ
= 2 × 2 sin 2n-2 θ cos 2n-2 θ cos 2n-1 θ
= 22 × 2 sin 2n-3 θ cos 2n-3 θ cos 2n-2 θ cos 2n-v θ
= 23 sin 2n-3 θ cos 2n-3 θ cos 2n-2 θ cos 2n-1 θ
………………………..
………………………..
………………………..
= 2n sin θ cos θ cos 2θ cos 22 θ …….. cos 2n-2 θ cos 2n-1 θ

or, 2n cos θ cos 2θ cos 22 θ …… cos 2n-1 θ = 1
(iii) Prove that \(\frac{\tan 2^n \theta}{\tan \theta}\) = = (1 + sec 2θ) (1 + sec22 θ) …. (1 + sec2n θ)
Solution:
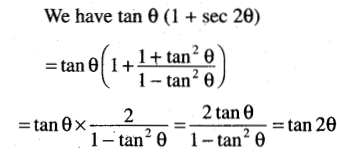

Question 22.
If x + y + z = xyz, prove that
(i) \(\frac{x}{1-x^2}+\frac{y}{1-y^2}+\frac{z}{1-z^2}\) = =\(\frac{4 x y z}{\left(1-x^2\right)\left(1-y^2\right)\left(1-z^2\right)}\)
Solution:
x + y + z = xyz (Given)
Let x = tan α, y = tan β, z = tan γ
∴ tan α + tan β + tan γ = tan α .tan β .tan γ or; tan α + tan β
= – tan γ + tan α tan β tan γ
= – tan γ(1 – tan α tan β)
or, \(\frac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\) = – tan γ
or, tan (α + β) = tan (π- γ)
or, α + β = π-γ
or, 2α + 2β = 2π- 2γ
or, tan (2α + 2β = tan (2π- 2γ)
or, tan (2α + 2β) = tan (2π- 2γ)

(ii) \(\frac{3 x-x^3}{1-3 x^2}+\frac{3 y-y^3}{1-3 y^2}+\frac{3 z-z^3}{1-3 z^2}\) = \(\frac{3 x-x^3}{1-3 x^2} \cdot \frac{3 y-y^3}{1-3 y^2} \cdot \frac{3 z-z^3}{1-3 z^2}\)
Solution:
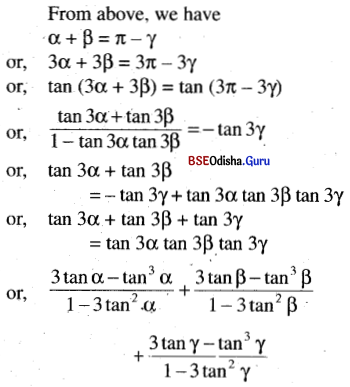
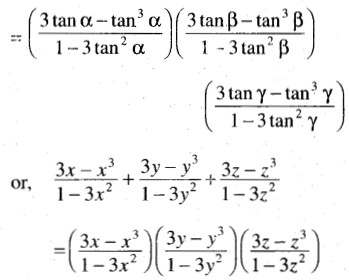
![]()
Question 23.
If \(\text { If } \frac{\sin ^4 \alpha}{a}+\frac{\cos ^4 \alpha}{b}=\frac{1}{a+b}\) show that \(\frac{\sin ^8 \alpha}{a^3}+\frac{\cos ^8 \alpha}{b^3}=\frac{1}{(a+b)^3}\)
Solution: