CHSE Odisha Class 11 Math Solutions Chapter 6 Complex Numbers and Quadratic Equations Ex 6(b)

Odisha State Board CHSE Odisha Class 11 Math Solutions Chapter 6 Complex Numbers and Quadratic Equations Ex 6(b) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 6 Complex Numbers and Quadratic Equations Exercise 6(b)

Question 1.
If Z₁ and Z₂ are two complex numbers then show that
\(\begin{aligned}
& \left|1-z_1 \overline{z_2}\right|^2-\left|z_1-z_2\right|^2 \\
& =\left(1-\left|z_1\right|^2\right)\left(1-\left|z_2\right|^2\right)
\end{aligned}\)
Solution:
Let z₁ and z₂ be two complex numbers.
Let z₁ = a + ib, z₂ = c + id

Question 2.
If a, b, c are complex numbers satisfying a + b + c = 0 and a² + b² + c² = 0 then show that |a| = |b| = |c|
Solution:
Let a + b + c = 0 and a² + b² + c² = 0
Then (a + b + c)² = 0
⇒ a² + b² + c² + 2ab + 2bc + 2ca = 0
⇒ 2(ab + bc + ca) = 0
⇒ ab + bc = – ca
⇒ b(a + c) = – ca
⇒ b(- b) = – ca [a + b + c = 0]
⇒ b² = ca
⇒ b³ = abc
Similarly it can be shown that a³ = abc and c³ = abc
Thus a³ = b³ = c³
⇒ |a³|= |b³| = |c³|
⇒ |a|³ = |b|³ = |c|³
⇒ |a| = |b| = |c|

Question 3.
What do the following represent?
(i) { z : |z – a| + |z + a| = 2c } where |a| < c
Solution:
{ z : |z – a| + |z + a| = 2c } where |a| < c    …….(1)
Here z is a complex number.
Let z = x + iy.
∴ (x, y) is the point corresponding to the complex number z?
Let ‘a’ and ‘ – a’ be two fixed points.
∴ Eqn. (1) implies that the sum of the distances of the point (x, y) from two points la and a’ is constant i.e. 2c
∴ The locus is an ellipse.

(ii) {z : |z – a| – |z + a| = c }
Solution:
Here {z : |z – a| – |z + a| = c } implies that, the difference of the distances of the point (x, y) from two fixed points ‘ – a’ and ‘a’ is a constant i.e. c.
So the locus is a hyperbola.

(iii) What happens in (i) |a| > c?
Solution:
In(i), if |a| > c. then there is no locus. But if |a| = c, then the locus reduces to a straight line.

Question 4.
Given cos α + cos β + cos γ = sin α + sin β + sin γ = 0 Show that cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ)
Solution:
Let a = cos α + i sin α,
b = cos β + i sin β
c = cos γ + i sin γ
∴ a + b + c = ( cos α + cos β + cos γ) + i ( sin α + sin β + sin γ)
= 0 + i0 = 0
∴ a³ + b³ + c³ – 3 abc
= (a + b + c )( a² + b² + c² – ab – bc – ca) = 0
or, a³ + b³ + c³ = 3 abc
or, ( cos α + i sin α)³ + (cos β + i sin β)³ + ( cos γ + i sin γ)³
= 3( cos α + i sin α) (cos β + i sin β) ( cos γ + i sin γ)
or, cos 3α + i sin 3α + cos 3β + i sin 3β + cos 3γ + i sin 3γ
= 3[cos (α + β + γ) + i sin (α + β + γ)]
or, (cos 3α + cos 3β + cos 3γ) + i (sin 3α + sin 3β + sin 3γ)
= 3 cos (α + β + γ) + i 3 sin (a + β + γ)
∴ cos 3α + cos 3β + cos 3γ
= 3 cos (α + β + γ) and sin 3α + sin 3β + sin 3γ
= 3 sin (α + β + γ)

Question 5.
Binomial theorem for complex numbers. Show that (a+b)ⁿ = a^{n n}C₁a^n-1b +  …..+ ⁿc_ra^n-rb^r + …..+ bⁿ where a,b ∈ C and n, rule of multiplication of complex numbers and the relation ⁿC_r + ⁿC_r-1 = ⁿ⁺¹C_r)
Solution:
Let a and b be two complex numbers
Let a = α₁ + iβ₁, b = α₂ + iβ₂
(a + b)¹ = (α₁ + iβ₁ + α₂ + iβ₂)¹
= α₁ + iβ₁ + α₂ + iβ₂
= (α₁ + iβ₁)¹ + ¹C₁(α₁ + iβ₁)^1-1(α₁ + iβ₁)¹
= a¹ + ¹C₁ a^1-1 b¹
∴ P₁ is true
Let P_k be true
i.e., (a + b)^k = a^k + ^kC₁ a^k-1 b¹ + … + b^k
where a.b ∈ C
Now ( a + b)^k+1 = (a + b)^k (a + b)¹
= (a^k + ^kC₁ a^k-1b¹ +…+ b^k) (a + b)
= a^k-1 + ba^k+ ^kC₁ a^kb + ^kC₁a^k-1b² + … + b^k+1
= a^k+1 + a^kb(^kC₁+ 1)+ …+ b^k+1
= a^k+1 + ^k+1C₁a^kb¹ + ^k+1 C₂a^k-1b² +… + b^k+1
∴ P_k+1 is true
∴ P_n is true for all values of n ∈ N

Question 6.
Use the Binomial theorem and De Moiver’s theorem to show
cos 3θ = 4 cos ³ θ – 3 cos θ,
sin 3θ = 3 sin θ – 4 sin ³ θ
Express cos nθ as a sum of the product of powers of sin θ and cos θ. Do the same thing for sin nθ.
Solution:
We have (cos θ + i sin θ)³
= cos 3θ + i sin 3θ       …..(1)
But by applying the Binomial theorem, we have
(cos θ + i sin θ)³
= cos ³ θ + ³C₁ (cos θ)^3-1 (i sin θ)¹ + ³C₂ (cos θ)^3-2  (i sin θ)² + (i sin θ)³
= cos3θ + 3i cos2θ sin θ + 3i² cos θ sin² θ + i³ sin³ θ
= (cos³ θ – 3 cos θ sin² θ) + i(3 cos² θ sin θ – sin³ θ)
∴ cos ³ θ =cos³ θ – 3 cos θ(1 – cos² θ)
= cos³ θ – 3 cos θ + 3 cos ³ θ
= 4 cos³ θ – 3 cos θ and
sin 3θ = 3 cos² θ sin³ θ – sin³ θ
= 3 (1 – sin² θ) sin θ – sin³ θ
= 3 sin θ – 3 sin³ θ – sin³ θ
= 3 sin θ – 4 sin³ θ (Proved)
Again, (cos θ + i sin θ)ⁿ
= cos nθ + i sin nθ         ….(3)
Also, (cos θ + i sin θ)ⁿ
= cosⁿ θ + ⁿC₁ cos^n-1 θ ( i sin θ) + ⁿc₂ cos ^n-2 θ (i sin θ)² + …+ (i sin θ)
= cosⁿ θ – ⁿC₂ cos^n-2 θ sin² θ + ⁿC₄ cos^n-4 θ sin⁴ θ – …) + i (ⁿC₁ cos^n-1 θ sin θ – ⁿC₃ cos^n-3 θ sin ³ θ) + ⁿC₅ cos^n-5 θ sin⁵ θ – …)    …..(4)
Equating real part and imaginary parts in (1) and (3), we have
cos nθ = cosⁿ θ – ⁿC₂ cos^n-2 θ × sin² θ + ⁿC₄ cos^n-4 θ sin⁴ θ …
and sin nθ = ⁿC₁ cos^n-1 θ sin θ – ⁿC₃ cos^n-3 θ sin³ θ + ⁿC₅ cos^n-5 θ sin⁵ θ…

Question 7.
Find the square root of
(i) – 5 + 12 √-1
Solution:

(ii) – 11 – 60 √-1
Solution:
Let \(\sqrt{-11-60 \sqrt{-1}}\) = x + iy
Squaring both sides we get
– 11 – 60i = (x + iy)²

(iii) – 47 + 8 √-1
Solution:

As 2ab = 8 > 0, a and b have the same sign.
∴ \(\sqrt{-47+8 i}\)
\(=\pm\left(\sqrt{\frac{\sqrt{2273}-47}{2}}+i \frac{\sqrt{2273}+47}{2}\right)\)

(iv) – 8 + √-1
Solution:

(v) a² – 1 +2a √-1
Solution:
a² – 1 + 2a √-1
= a² + i² + 2ai = (a + i)²
∴ \(\sqrt{a^2-1+2 a \sqrt{-1}}\) = ±(a + i)

(vi) 4ab – 2 (a² – b²) √-1
Solution:
4ab – 2 (a² – b²) √-1
= (a + b)² – (a – b)² – 2(a² – b²)i
= (a + b)² + (a – b)²i² – 2(a + b)(a – b)i
= (a + b) – i(a – b)²
∴ \(\sqrt{4 a b-2\left(a^2-b^2\right) \sqrt{-1}}\)
= ±[(a + b) – i (a – b)]

Question 8.
Find the values of cos72° ….
Solution:
Let 18° = θ then 5θ = 90°
⇒ 3θ = 9θ – 2θ
⇒ cos 3θ = cos (9θ – 2θ) = sin 2θ
⇒ 4 cos³ θ – 3 cos θ = 2 sin θ cos θ
⇒ 4 cos² 0 – 3 = 2 sin 0 (∴ cos θ = cos 18° ≠ 0)
⇒ 4(1 – sin² θ) – 3 = 2 sin θ
⇒ 4 sin² θ + 2 sin θ – 1 = 0
⇒ sin θ = \(\frac{-2 \pm \sqrt{4+16}}{2 \times 4}=\frac{-1 \pm \sqrt{5}}{4}\)
⇒ sin 18° = \(\frac{-1+\sqrt{5}}{4}=\frac{\sqrt{5}-1}{4}\)
(∴ 18° is a cut)
Now cos 72° = cos (90° – 18°)
= sin 18° = \(\frac{\sqrt{5}-1}{4}\)
For other methods refer 148 pages of the text book.

Question 9.
Find the value of cos 36°.
Solution:
We have 36° = \(\frac{\pi^0}{5}\)
∴ cos 36° = cos \(\frac{\pi}{5}\)
Let α = cos \(\frac{\pi}{5}\) + i sin \(\frac{\pi}{5}\)
be the root of the equation x⁵ + 1 = 0
Again, if x⁵ + 1 = 0
or, x⁵ = – 1 = cosπ + i sinπ
or, x = (cos π + i sin π )^1/5
= [cos (π + 2kπ)+ i sin (π + 2kπ)]^1/5
or, x = cos \(\frac{(2 k+1) \pi}{5}+i \sin \frac{(2 k+1) \pi}{5}\)
where 2kπ is the period of sine and cosine and k = 0, 1, 2, 3, 4
∴ The eqn x⁵ + 1 = 0 has 5 roots out of which -1 is one root which corresponds to k = 2
Again,
x⁵ + 1 = (x + 1)(x⁴ – x³ + x² – x + 1)
So their 4 roots will be obtained on solving the eqn.
x⁴ – x³ + x² – x + 1 = 0
we have, x⁴ – x³ + x² – x + 1 = 0
or, x² – x + 1 – \(\frac{1}{x}+\frac{1}{x^2}\) = 0
(Dividing both sides by x²)

Re α i.e. cos \(\frac{\pi}{5}=\frac{1+\sqrt{5}}{5}=\frac{\sqrt{5}+1}{4}\)
and cos.108° = \(\frac{1-\sqrt{5}}{4}\)

Question 10.
Evaluate cos \(\frac{2 \pi}{17}\) using the equation x¹⁷ – 1 = 0
Solution:
x¹⁷ – 1 = 0
or, x¹⁷ = 1 = cos 0° + i sin 0°
= cos (0 + 2kπ) + i sin (0 + 2kπ)
= cos 2kπ + i sin 2kπ
or x = (cos 2kπ + i sin 2kπ)^1/17
= cos \(\frac{2k \pi}{17}\) + i sin \(\frac{2k \pi}{17}\)
If k = 1, x = cos \(\frac{2 \pi}{17}\) + i sin \(\frac{2 \pi}{17}\)
If k = 0 , x = 1
As x¹⁷ – 1 = (x – 1) (x¹⁶ + x¹⁵ + …. +1)
So one root of the eqn. x¹⁷ – 1 = 0 is 1 and all other roots are the roots of the eqn.
x¹⁶ + x¹⁵ + ….+ 1 = 0
∴ The value of cos \(\frac{2 \pi}{17}\) can be found from the roots of the eqn.  (1)

Question 11.
Solve the equations.
(i) z⁷ = 1
Solution:
z⁷ = 1 = cos 0 + i sin 0
= cos (0 + 2kπ) + i sin (0 + 2kπ)
= cos 2kπ + i sin 2kπ
∴ z = (cos 2kπ + i sin 2kπ)^1/7
= cos \(\frac{2k \pi}{7}\) + i sin \(\frac{2k \pi}{7}\)
where k = 0, 1, 2, 3, 4, 5, 6

(ii) z³ = i
Solution:

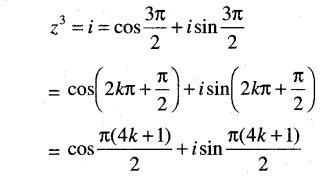
(iii) z⁶ = – i
Solution:

(iv) z³ = 1 + i
Solution:

Question 12.
If sin α + sin β + cos γ = 0
= cos α + cos β + cos γ = 0
Show that
(i) sin 3α + sin 3β + sin 3γ = 3 sin (α + β + γ)
Solution:
Refer to Q. No. 4

(ii) sin² α + sin² β + sin² γ = cos² α + cos² β + cos² γ =3/2
Solution:
Let x = cos α + i sin α,
y = cos β + i sin β
z = cos β + sin β
∴ x + y + z = (cos α + cos β + cos γ) + i ( sin α + sin β + sin γ) = 0 +i0= 0
∴ xy + yz + zx = xyz (\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\)) = 0
Since \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\) = cos α – i sin α + cos β – i sin β + cos γ – i sin γ
= (cos α + cos β + cos γ) – i (sin α + sin β + sin γ) = 0 – i0 =0
∴ (x + y + z)² = x ² + y² +z² + 2(xy + yz + zx)
= x² + y² + z² + 0 = x² + x² + z²
or 0 = x² + y² + z²
∴ x² +y² + z² =0
or, (cos α + i sin α)² + (cos β + i sin β)² + ( cos γ + i sin γ)² = 0
or, cos 2α + i sin 2α + cos 2β + i sin 2β + cos 2γ + i sin 2γ = 0
or, (cos 2α + cos 2β + cos 2γ) + i(sin 2α + sin 2β + sin 2γ) = 0
∴ cos 2α + cos 2β + cos 2γ = 0
or, cos² α – sin² α + cos² β – sin² β + cos² γ – sin² γ =0
or, (cos² α + cos² β + cos² γ) = (sin² α + sin² β + sin² γ)
But cos² α + sin² α + cos² β + sin² β + cos² γ + sin² γ = 1 + 1 + 1 = 3
∴ cos² α + cos² β + cos² γ = sin² α + sin² β + sin² γ = 3/2   (Proved)

Question 13.
If x + \(\frac{1}{x}\) = 2 cos θ
Show that \(x^n+\frac{1}{x^n}\) = 2 cos nθ

Question 14.
x_r = cos a^r + i sin a^r
r =1, 2, 3 and x₁ + x₂ + x₃ = 0 Show that \(\frac{1}{x_1}+\frac{1}{x_2}+\frac{1}{x_3}\) = 0
Solution:

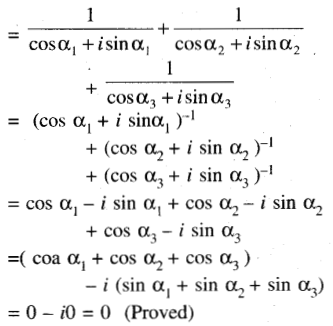
Question 15.
Show that \(\left(\frac{1+\sin \theta+i \cos \theta}{1+\sin \theta-i \cos \theta}\right)^n\) = \(\cos \left(\frac{n \pi}{2}-n \theta\right)+i \sin \left(\frac{n \pi}{2}-n \theta\right)\)
Solution:

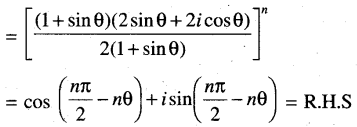
Question 16.
If α and β are roots x² – 2x + 4 = 0 then show that \(\alpha^n+\beta^n=2^{n+1} \cos \frac{n \pi}{3}\)
Solution:
we have x² – 2x + 4 = 0

= \(2^n \times 2 \cos \frac{n \pi}{3}=2^{n+1} \cos \frac{n \pi}{3}\)

Question 17.
For a positive integer n show that
(i) (1 + i)ⁿ + (1 – i)ⁿ = \(2^{\frac{n+2}{2}} \cos \frac{n \pi}{4}\)
Solution:

(ii) (1 + i√3)ⁿ + (1 – i√3)ⁿ = \(2^{n+1} \cos \frac{n \pi}{3}\)
Solution:

Question 18.
Let x + \(\frac{1}{x}\) = 2 cos α, y + \(\frac{1}{y}\) = 2 cos β, z + \(\frac{1}{z}\) = 2 cos γ. Show that
(i) 2 cos (α + β + γ) = xyz + \(\frac{1}{xyz}\)
Solution:
We can take x = cos α + i sin α
y = cos β + i sin β, z = cos γ + i sin γ
∴ xyz = (cos α + i sin α ) (cos β + i sin β ) (cos γ + i sin γ)
= cos (α + β + γ) – i sin (α + β + γ)
∴ \(\frac{1}{xyz}\) = cos (α + β + γ) – i sin(α + β + γ)
∴ xyz + \(\frac{1}{xyz}\) = 2 cos(α + β + γ)

(ii) 2 cos (pα + qβ + rγ) = \(x^p y^q z^r+\frac{1}{x^p y^q z^r}\)
Solution:

Question 19.
Solve x⁹ + x⁵ – x⁴ = 1
Solution:
x⁹ + x⁵ – x⁴ = 1
or, x⁵(x⁴ + 1) – (x⁴ + 1) = 0
or, (x⁵ – 1) (x⁴ + 1) = 0
x⁴ + 1 = 0 and x⁵ – 1 = 0
x⁴ = – 1 = cos π + i sin π
= cos (π + 2nπ) + i sin (π + 2nπ)
∴ x = [cos (2n + 1) π + 1 sin (2n + 1) π]^1/4
= \(\cos \frac{2 n+1 \pi}{4}+i \sin \frac{2 n+1 \pi}{4}\)
for n = 0, 1, 2, 3
Again, x⁵ – 1 = 0 or, x⁵ = 1
or, x⁵ = cos 0 + i sin 0
= cos 2nπ + i sin 2nπ
or, x = (cos 2nπ + i sin 2nπ)^1/5
= \(\cos \frac{2 n \pi}{5}+i \sin \frac{2 n \pi}{5}\)
Where n = 0, 1, 2, 3, 4.

Question 20.
Find the general value of θ if (cos θ + i sin θ) (cos 2θ + i sin 2θ),…..(cos nθ + i sin nθ) =1
Solution:

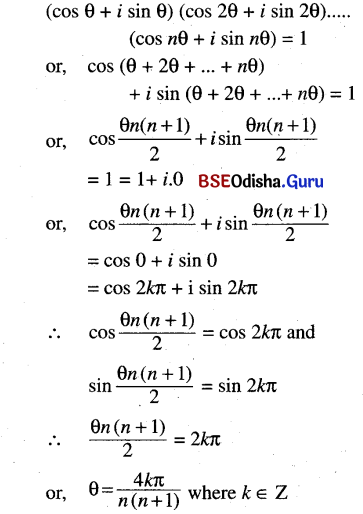
Question 21.
If z = x + iy show that |x| + |y| ≤ √2 |z|
Solution:
z = x + iy
∴ |z| = \(\sqrt{x^2+y^2}\)
∴ |z| = x² + y²
We have (|x| – |y|)² ≥ 0
⇒ |x|² + |y|² -2|x||y|> 0
⇒ 2(|x|² + |y|²) – 2|x||y| ≥ |x|² + |y|²
⇒ 2(|x|² + |y|²) ≥ |x|² + |y|² + 2|x||y|
⇒ 2|z|² ≥ (|x| + |y|)²
⇒ √2|z| ≥ |x| + |y|
⇒ |x| + |y| ≤ √2|z|

Question 22.
Show that
Re (Z₁Z₂) = Re z₁, Re z₂ – Im z₁, Im z₂
Im (Z₁Z₂) = Re z₁, Im z₂ + Re z₂ Im z₁
Solution:
Let z₁ = a + ib, z₂ = c + id
∴ z₁, z₂ = (a + ib) (c + id)
= ac + iad + ibc + i²bc
= (ac – bd) + i (ad + be)
∴ Re (z₁, z₂) = ac – bd – Re z₁. Re z₂
– Im z₁,. Im z₂
Again, Im z₁, z₂ = ad + be
= Re z₁. Im z₂ + Im z₁,. Re z₂

Question 23.
What is the value of arg ω + arg ω²?
Solution:
arg ω = arg ω² = arg (ω • ω²)
= arg (ω³) = arg (1) = 2nπ
∴ The principal agrument = 0.

Question 24.
If |z₁| ≤ 1, |z₂| ≤ 1 show that \(\left|1-z_1 \overline{z_2}\right|^2-\left|z_1-z_2\right|^2=\left(1-\left|z_1\right|^2\right)\left(1-\left|z_2\right|^2\right)\) Hence and otherwise show that. \(\left|\frac{z_1-z_2}{1-z_1 z_2}\right|<1 \text { if }\left|z_1\right|<1,\left|z_2\right|<1\)
Solution:

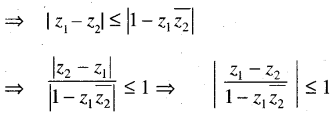
Question 25.
If z₁² + z₂² + z₃² – z₁z₂ – z₂z₃ – z₃z₄ = 0 Show that |z₁ – z₂| = |z₂ – z₃| = |z₃ – z₁|
Solution:
Let z₁² + z₂² + z₃² – z₁z₂ – z₂z₃ – z₃z₄ = 0
⇒ 2z₁² + 2z₂² + 2z₃² – 2z₁z₂ – 2z₂z₃ – 2z₃z₄ = 0
⇒ (z₁ – z₂)² + (z₂ – z₃)² + (z₃ – z₁)² = 0
Put a = z₁ – z₂, b = z₂ – z₃, c = z₃ – z₁
Then a + b + c = 0 and a² + b² + c² = 0 As in Q2 we can show that |a| = |b| = |c|
⇒ |z₁ – z₂| = |z₂ – z₃| = |z₃ – z₁|

Question 26.
If |a| < |c| show that there are complex numbers z satisfying |z – a| = |z + a| = 2|c|
Solution:
Let z = x + iy
∴ |z – a| + |z + a| = 2c
or, |x + iy – a| + |x + iy + a| = 2c

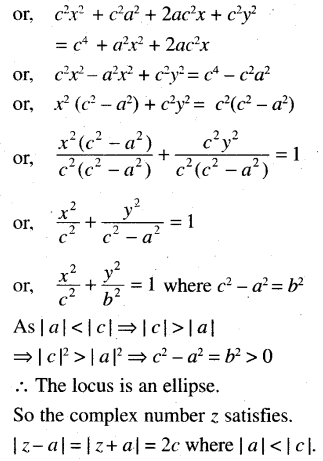
Question 27.
Solve \(\frac{(1-i) x+3 i}{2+i}+\frac{(3+2 i) y+i}{2-i}=-i\) where x, y, ∈ R.
Solution:

Question 28.
If (1 + x + x²)ⁿ = p₀ + p₁x + p₂x² + …..+ p_2nx²ⁿ, then prove that p₀ + p₃ + p₆ + …..+ 3^n-1
Solution:
Given, (1 + x + x²)ⁿ = p₀ + p₁x + p₂x² + …..+ p_2nx²ⁿ
putting x = ω we get

Question 29.
Find the region on the Argand plane on which z satisfying
[Hint Arg (x + iy) =\(\frac{\pi}{2}\) = 0, y>0]
(i) 1 < |z – 2i| < 3
Solution:
Let z = x + iy
The given inequality is
1 < |x + i(y – 2)| < 3
⇒ \(1<\sqrt{x^2+(y-2)^2}<3\)

(ii) arg \(\left(\frac{z}{z+i}\right)=\frac{\pi}{2}\)
Solution:

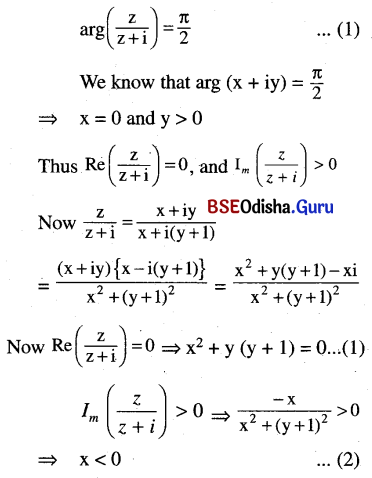
As all are +ve we have
1 < x² + (y – 2)² < 9
x² + (y – 2)² < 9 is the region inside the circle with center (0, 2) and radius 1.
x² + (y – 2)² > 1 is the region outside the circle with center (0, 2) and radius.
∴ 1 < |z – 2i| < 3 is the region between two concentric circles with center (0, 2) and radius 1 and 3 which is shows below.