CHSE Odisha Class 11 Math Solutions Chapter 9 Binomial Theorem Ex 9(a)

Odisha State Board CHSE Odisha Class 11 Math Solutions Chapter 9 Binomial Theorem Ex 9(a) Textbook Exercise Questions and Answers.

CHSE Odisha Class 11 Math Solutions Chapter 9 Binomial Theorem Exercise 9(a)

Question 1.
The rows n = 6 and n = 7 in the pascal triangle have been kept vacant. Fill in the gaps
Solution:

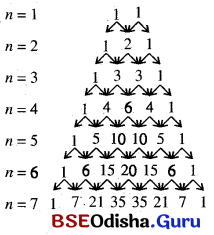
Question 2.
Write down the expansion of (a + b)⁸ using Pascal’s triangle.
Solution:
The row n = 8 in Pascal’s triangle is 1, 8, 28, 56, 70, 56, 28, 8, 1.
∴ (a + b)⁸ = a⁸ + 8a^8-1b¹ + 28a^8-2b² + 56a^8-3b³ + 70a^8-4b⁴ + 56a^8-5b⁵ + 28a^8-6b⁶ + 8a^8-7b⁷ + b⁸
= a⁸ + 8a⁷b + 28a⁶b² + 56a⁵b³ + 70a⁴b⁴ + 56a³b⁵ + 28a²b⁶ + 8ab⁷ + b⁸

Question 3.
Find the 3rd term in the expansion of \(\left(2 x^3-\frac{1}{x^6}\right)^4\) using rules of Pascal triangle.
Solution:

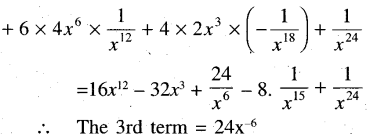
Question 4.
Expand the following :
(a) (7a + 3b)⁶
Solution:
(7a + 3b)⁶ = (7a)⁶ + ⁶C₁(7a)^6-1(3b)¹ + ⁶C₂(7a)^6-2(3b)² + ….. + (3b)⁶7⁶a⁶ + 6(7a)⁵(3b) + 15(7a⁴) × 9b² + …. + 3⁶b⁶
= 7a⁶ + 18 × 7⁵a⁵b + 135 × 7⁴a⁴b² + ….. + 3⁶b⁶

(b) \(\left(\frac{-9}{2} a+b\right)^7\)
Solution:

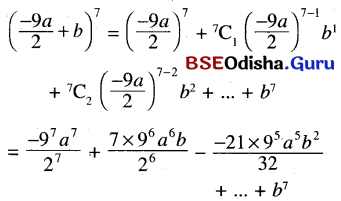
(c) \(\left(a-\frac{7}{3} c\right)^4\)
Solution:

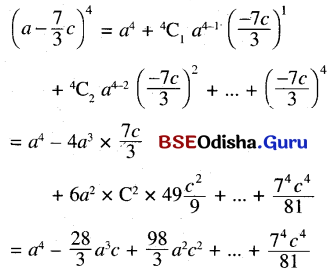
Question 5.
Apply Binominal Theorem to find the value of (1.01)⁵.
Solution:
= 1 + ⁵C₁(0.01)¹ + ⁵C₂(0.01)² + ⁵C₃(0.01)³ + ⁵C₄(0.01)⁴ + (0.01)⁵
= 1 + 5 × 0.01 + 10(0.0001) + 10(0.000001) + 5(0.00000001) + 0.0000000001
= 1 + 0.05 + 0.001 + 0.00001 + 0.00000005 + 0.000000001
= 1.0510100501

Question 6.
State true or false.
(a) The number of terms in the expansion of \(\left(x^2-2+\frac{1}{x^2}\right)^6\) is equal to 7.
Solution:
False

(b) There is a term independent of both x and y in the expansion of \(\left(x^2+\frac{1}{y^2}\right)^9\)
Solution:
False

(c) The highest power in the expansion of \(x^{40}\left(x^2+\frac{1}{x^2}\right)^{20}\) is equal to 40.
Solution:
False

(d) The product of K consecutive natural numbers is divisible by K!
Solution:
True

Question 7.
Answer the following :
(a) If the 6th term in the expansion of (x + *)ⁿ is equal to ⁿC₅x^n-10 find *
Solution:
Let the 6th term (x + y)ⁿ is ⁿC₅x^n-10
∴ ⁿC₅x^n-5y⁵ = ⁿC₅x^n-10 = ⁿC₅x^n-5.x^-5
⇒ y⁵ = x^-5 = \(\frac{1}{x^5}\)
∴ y = \(\frac{1}{x}\) . Hence * = \(\frac{1}{x}\)

(b) Find the number of terms in the expansion of (1 + x)ⁿ (1 – x)ⁿ.
Solution:
(1 + x)ⁿ (1 – x)ⁿ = (1 – x²)ⁿ
∴ The number of terms in this expansion is (n + 1)

(c) Find the value of \(\frac{{ }^n \mathrm{C}_{r-1}}{{ }^n \mathrm{C}_r}\)
Solution:

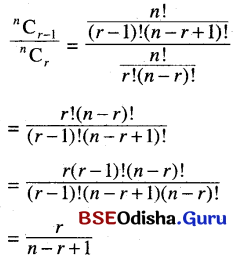
(d) How many terms in the expansion of \(\left(\frac{3}{a}+\frac{a}{3}\right)^{10}\) have positive powers of a? How many have negative powers of a?
Solution:

Question 8.
Find the middle term(s) in the expansion of the following.
(a) \(\left(\frac{a}{b}+\frac{b}{a}\right)^6\)
Solution:
Here there is only one middle term i.e. the 4th term.
∴ 4th term i.e. (3 + 1)th term in the expansion of

(b) \(\left(x+\frac{1}{x}\right)^9\)
Solution:
Here there are two middle terms i.e. 5th and 6th terms.
∴ 5th term in the above expansion is

(c) \(\left(x^{\frac{3}{2}}-y^{\frac{3}{2}}\right)^8\)
Solution:
Here there is only one middle term i.e. 5th term.
∴ 5th term i.e. (4 + 1)th term in the expansion of

Question 9.
Find the 6th term in the expansion of \(\left(x^2+\frac{a^4}{y^2}\right)^{10}\)
Solution:
6th term i.e. (5 + 1)th term in the expansion of
(x² + \(\frac{a^4}{y^2}\))¹⁰ is ¹⁰C₅(x²)^10-5 (\(\frac{a^4}{y^2}\))⁵

Question 10.
(a) Find the fifth term in the expansion of (6x – \(\frac{a^3}{x}\))¹⁰
Solution:

(b) Is there a term independent of x? If yes find it out.
Solution:
Let (r + 1)th term in the expansion of  (6x – \(\frac{a^3}{x}\))¹⁰ is independent of x.
∴ (r + 1)th term = ¹⁰C_r(6x)^10-r(\(\frac{-a^3}{x}\))^r
= ¹⁰C_r6^10-rx^10-r(-1)^ra^3rx^-r
= (-1)^{r 10}C_r6^10-ra^3rx^10-2r
∴ x^10-2r = 1 = x⁰
or, 10 – 2r = 0 or, r = 5
∴ 6th term is term independent of x in the above expansion and the term is (-1)^{5 10}C₅6^10-5a^3.5
= – ¹⁰C₅6⁵a¹⁵ = – 252 × 6⁵a¹⁵

Question 11.
(a) Find the coefficient of \(\frac{1}{y^{10}}\) in the expansion of \(\left(y^3+\frac{a^7}{y^5}\right)^{10}\)
Solution:

(b) Does there exist a term independent of y in the above expansion?
Solution:
Let (r + 1)th term is independent of y.
∴ y^30-8r = 1 = y⁰ or, 30 – 8r = 0
or, r = \(\frac{30}{8}\) = \(\frac{15}{4}\) which is not possible as r∈ N or zero.
∴ There is no term in the expansion of \(\left(y^3+\frac{a^7}{y^5}\right)^{10}\) which is independent of y.

Question 12.
(a) Find the coefficient of x⁴ in the expansion of (1 + 3x + 10x²)(x + \(\frac{1}{x}\))¹⁰
Solution:

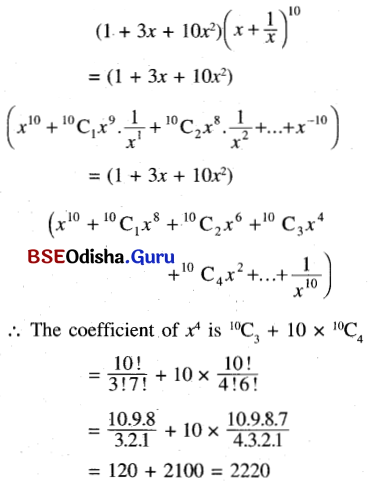
(b) Find the term independent of x in the above expansion.
Solution:

Question 13.
Show that the coefficient of a^m and aⁿ in expansion of (1 + a)^m+n are equal.
Solution:
(m + 1)th and (n + 1)th terms in the expansion of (1 + a)^m+n are ^m+nC_ma^m and ^m+nC_naⁿ
∴ The coefficient of a^m and aⁿ are ^m+nC_m and ^m+nC_n which are equal.

Question 14.
An expression of the form (a + b + c + d + …. ) consisting of a sum of many distinct symbols called a multinomial. Show that (a + b + c)ⁿ is
the sum of all terms of the form \(\frac{\boldsymbol{n} !}{\boldsymbol{p} ! \boldsymbol{q} ! \boldsymbol{r} !}\) a^pb^qc^r where p, q and r range over all positive triples of non-negative integers such that p + q + r = n.
Solution:

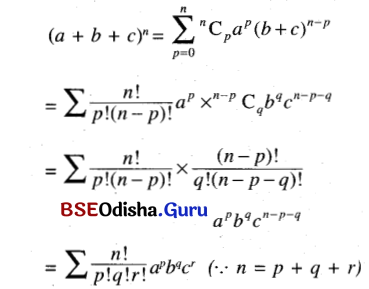
Question 15.
State and prove a multinominal Theorem.
Solution:
Multinominal Theorem:
(P₁ + P₂ + ……. + P_m)ⁿ
\(=\sum \frac{n !}{n_{1} ! n_{2} ! \ldots n_{m} !} p_1^{n_1} p_2^{n_2} \ldots p_m^{n_m}\)
where n₁ + n₂ + ……. + n_m = n
The proof of this theorem is beyond the syllabus.