CHSE Odisha Class 12 Logic Solutions Chapter 5 Symbolic Logic

Odisha State Board CHSE Odisha Class 12 Logic Solutions Chapter 5 Symbolic Logic Questions and Answers.

CHSE Odisha 12th Class Logic Chapter 5 Question Answer Symbolic Logic

Group – A

Short type Questions with Answers
I. Answer with in Two/Three sentence.

Question 1.
State the characteristics of symbolic logic.
Answer:
(i) It uses ideograms
(ii) It uses deductive method.
(iii) It uses constants and variables.

Question 2.
What is variable?
Answer:
(i) Variable means that varies or changes from time to time.
(ii) Variable is a symbol which has no fixed meaning.
(iii) Three types of variables are used in symbolic logic
Prepositional variables = p, q, r, s, t, etc. predicate variable f, g,h and individual variables, x, y, z etc

Question 3.
What, is called propositional variable?
Answer:
(i) The variable which is used in order to symbolise any prepositional that is called propositional variable.
(ii) Example : Ram is intelligent and A Hari is clever can be symbolised as p and q.

Question 4.
What do you mean by constant?
(i) Constant means which is not changeable. It meaning is always same and it has a fixed meaning.
(ii) Different logical constants are used in the symbolic logic. These are conjunction (.), Disjunction (v), alternation (∧), implication (>), equivalence (=), negation (~)

Question 5.
What is truth function?
(i) When the truth of falsity of a proposition depends upon the truth of falsify of another proposition, then the first one is called the truth function of the second one.

(ii) Example;
Madhavi is beauty = P
Madhavi is not beauty = ~P

Question 6.
What is called conjuctive function?
(i) When two propositions are joined together with the word and that is called conjunctive function.
(ii) Example; Mira is beauty and Sarita is clever can be symbolised p. q

Question 7.
What is tautology?
(i) In a truth table, if the main result is always truth that is called tautology,
(ii) Examples;

Question 8.
What is contradictory truth table?
Answer:
(i) In a truth table, if the main result is always false that is called contradictory truth table.
(ii) Example;

Question 9.
Construct the truth table of the following;
Answer:

Question 10.
What is ideogram?
Answer:
(i) The soundless symbols are called ideograms.
(ii) All the written symbols like +, -, × , √ etc are called ideograms.

Question 11.
Fallacy of ambiguous minor :
Answer:
When the minor term is used more than one sense in an argument that is called the fallacy of ambiguous minor.

Question 12.
Fallacy of amphiboly.
Answer:
(i) The fallacy of amphibody arises due to the wrong construction of a sentence.
(ii) He was given twice two amd three rupees. It may mean that he was given either seven or ten rupees.

Question 13.
Fallacy of Division.
Answer:
(i) When we pass from the collective use of term to its distributive use, that is called the fallacy of division.

(ii) Example; the students of this college are intelligent.
Rani is a student of this college.
∴ Rani is intelligent

Question 14.
What is the fallacy of composition?
Answer:
(i) This fallacy arises, when we pass from the distributive use to a collective use of a term in our argument.
(ii) Example; Nine and one are odd numbers
Ten is nine and one
∴ Ten is an odd number

Question 15.
What is a called the fallacy of accent ?
Answer:
(i) When the emphasis is given on a particular word in a sentence at that time we commit the fallacy of accent.
(ii) Example : Thou shalt not insult thy parents

Question 16.
Fallacy of post hoc ergo propter hoc.
Answer:

1. “Post hoc ergo propter hoc” literally means after this, therefore due to this.
2. It arises when we take any and every antecedent to be the cause :
3. Example; A crow sits on the palm tree and a palm falls down, so it is said that crow is the cause of the falling of the palm.

Question 17.
Fallacy of neglecting the negative condition.
Answer:
(i) When we take only positive conditions to be the cause and neglect the negative conditions then we commit this fallacy.
(ii) Example; Intelligence does not lead to success, as a large number or intelligent students are unemployed.

Question 18.
Fallacy of mistaking the co-effects of a cause and effect.
Answer:
(i) Cause is the antecedent and effect is the consequent. But if we take one of the coeffects of a common cause as the cause of its effect, we commit this fallacy.

(ii) Examples; Day invariably preceded night, so day is the cause of night.

Question 19.
Fallacy of undue assumption.
Answer:
(i) When we unduly assume a premise at that time we commit the fallacy of undue assumtpion.
(ii) Example; The people of America are wealthy, because they are industrious.

II. Answer within Five/Six sentence :

Question 1.
What are the main characteristics of symbolic Logic?
Answer:
The Logician C. I. Lews has suggested three different kinds of characteristics regarding the nature of symbolic Logic. These are;

1. Symbolic Logic uses ideograms not phonograms
2. It applies deductive method
3. It uses constant and variables.

Question 2.
What is variable?
Answer:
A variable in a symbol which can stand for any one of a given range of values. Three types of variables are used in Logic, such as :
Prepositional variables, P, q, r, s, t etc (stand for the symbols of propositions) predicate variables, f, g, h (stand for the symbols of predicate), Individual variables x, y, z, (stands for the symbols of any individual.

Question 3.
What is Logical constant?
Answer:
Logical constant is a symbol whose meaning is remains same in any Logical expression. Logical constants are also called Logical connectives, because they connect propositions and build compound ones. The Logical connectives or constants are; Conjunction (.), Alternation (v), implication (a), Equivalence (s), Negation (u).

Question 4.
What is truth function?
Answer:
Borrowing the term ‘function’ from Mathematics, any expression with Logical constants is said to be a truth function of its Propositional variables, because the truth value of that expression depends value 01 that expression depends on the truth value of the prepositional variables.
Example: up is a truth function, of P, because the truth or falsity of ~p depends on the truth or falsity of‘up’.

Question 5.
Briefly explain the truth table.
Answer:
Truth table is a convenient way to show the truth-value of a truth function, taking into consideration all possible truth-values of the prepositional variables involved in it. Every proposition in either true or false, so the truth value of every constituent propositional variable can be written as true (T/I) or False (F/O).

Question 6.
What is conjunctive function?
Answer:
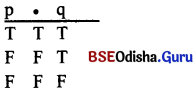
When two propositions are related with each other on the basis of conjuction or and (•) that is called conjunctive function. The conjunctive function will be true, when both antecedent and consequent are true together, otherwise if will be false.
Example:

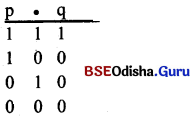
Question 7.
Construct the truth table of Alternative function.
Answer:

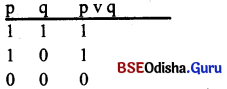
Question 8.
What is called tauto Logical truth table?
Answer:
A tautological truth table is that truth table where the main result in always true (T/I).
Example:

Question 9.
What is Tautology ? Give an example.
Answer:
In a truth table, if the main result is always true (T/I) that is called Tautology.
For examples;

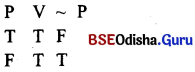
Question 10.
What is contingent truth table?
Answer:
In a truth table, if the result of many connective is mixed with true and false that is called contingent truth table For example:

Question 11.
What is contradictory Truth Table?
Answer:
In a truth table, if the main result is always false that is called contradictory truth table. For example, if we negate an affirmative proposition then we get its negative result. “Ram is a man” is a positive proposition but ‘Ram is not a man’ is a negative proposition. Let’s construct the truth false.

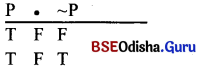
Question 12.
Fallacy of Equivocation.
Answer:
The fallacy of equivocation arises due to the use of ambiguous terms in an argument. A syllogism has three terms – the middle, the major and the minor. This fallacy arises if either the middle term or the major term or the minor term is used ambiguously or in more than one sense in the same argument.

Question 13.
Fallacy of Ambiguous middle :
Answer:
When the middle term is used more than one sense in an argument at that time the fallacy arises, Which is called the fallacy of Ambiguous middle.
Example : Light is pleasant
(Light = opposite of darkness) His injury is pleasant.

Question 14.
Ambiguous major :
Answer:
When the major term is used more than one sense in an argument at that time we commit the fallacy of ambugous major.
Example : No courageous creatures fly.
(Fly = run away)

Group – B

Long Type Questions With Answers

Question 1.
Explain the nature of symbolic Logic.
Or, State and explain the different characteristics of symbolic logic.
Or, What is symbolic Logic ? How it is different from classical or traditional Logic ? Explain.
Answer:
Symbolic logic is nothing but it is the recent or modem development of traditional logic. In otherwords we can say symbolic logic is called symbolic because certain symbols are used in it. We read symbolic logic because by the using of certain symbols. We simplety a great expression into a simple one within few minutes. That is why it is said that symbolic logic is very much necessary for us in modem age.

But the symbolic logic is definitely different from traditional or classical logic. Because in case of traditional logic we were using certain concrete examples but here in symbolic logic we are using certain symbolic examples. Aristotle is the father of traditional or classical logic. It is said that the foundation of logic were so brilliantly and thoroughly said by Aristotle in the 4th century B.C. That is seemed to most of Aristotle’s successors to be a finished science.

If we took out in the traditional logic then we can find out that he has given in syllogism certain premises and has drawn certain conclusion out of that premises. By this process he has proved that there are only 19 valid moods in syllogism. In this sense we can say Aristotles view carries only small branch of logic so it has a long history.

But latter on the great Mathematician and logicians like George Boole, Gowvon, Leibnitz, Basson and connor have proved there are 19 valid moods which have already seen given by Aristotle. According to them if we analyse Properly we will find actually there are not 19 valid moods but only 15 valid moods are there.

The main aim of philosophy is to know the idea of truth. As logic is the branch of philosophy so its business is to know whether an argument is valid or invalid. The logician have borrowed the idea of ‘truth’ from geometry and mathematics. As the conclusion of mathematics is always true in the similar way the conclusion of logic is always certain. As the structure traditional or classical logic is totally changed, then it is taken a new form which is known as symbolic logic. In this sense it is said that it has short history.

It is said that sometimes the traditional logicians have criticized the work at symbolic logician and vice-versa. But whatever may be now the logician are generally agree, that modern or symbolic logic is a development of concepts and techniques which were complicietely in the work of Aristotle. Thus according to Basson and connor, classical logic is related to symbolic logic as embryo to adult organism.

From this above discussion, it is said that tradition as or classical logical and symbolic logic are not differ in kind, yet the difference between them is only that of different stages of development. So symbolic logic is a developed stage of traditional of classical logic.

C.I. Lasisis a distinguished modern logician and a mathematician has cited three important characteristics regarding the nature of symbolic logic.

1. The use of ideogram.
2. The use of deductive method.
3. The use of constant and variable.

Let’s analyse the above three characteristics in details.
(1) The use of ideogram: Ideogram means the soundless symbols.
Example: All the written symbols like ? +, -, x, V etc. are called ideogram. But phonogram means soundful symbol. For example all the written words like question mark, plus, minus etc are called phonograms. So the ideogram directly stands for concept or symbols.

(2) The use of Deductive Method : In deductive method we clarify the complication. It is distributed in geometry. By the application of deductive method we can drawn a conclusion of out of premise. This method is used in case of symbolic logic and also in. traditional logic. But the difference is that in case of traditional logic we were used the concrete examples like. If there is sun then there is light.

(3) The use of constant and variable : A variable is different from constant. Constant is that which never changes. But variable means always changeable. It means we can take any variable for any proposition. The logician have borrowed this idea from geometry and mathematics. As we have seen in case of Geometry and mathematics. As we have seen in case of Geometry and mathematics, there are certain constant and variables are use such as x, y, z etc. are variables, But +,-,x, are constants like geometry and mathematics there are certain constants and variables used in case of symbolic logic.

Logical Constants:

1. Conjuctive (And) (.)
2. Disjuctive (either…or) (A) p,q,r,s,f etc.
3. Alternative (either …. or) (A.)
4. Equivalence (equalto) (‘=’)
5. Contradiction (Negation) (N)

Logical variables:

1. Prepositional variables
2. Predicate variables s, f, g, h etc.
3. Individual variable s, y, z etc.

Question 2.
What is Truth-function? Distinguish between variable and constant.
Answer:
All these concepts of truth-function, variable and constants are the concepts used is symbolic logic. The notion of function is very familiar in mathematics. Symbolic logic borrows this concept from Mathematics. An expression is said to be a function of a given variable or variables, if the value of the expression is uniquely determined when the variable or variables take a define value. The truth value of the expression is dependent on the truth value of the prepositional variables used in the expression. In Algebra, the formula ‘x – y + 5 ’ means the value of ‘x’ is dependent on the value of ‘y’. So ‘x’ is the function of‘y + 5′ If the value of ‘y’ is 3, then the value of x is (3 + 5) = 8. If the value of ‘y’ is 7, then the value of x is (7 + 5) 12. Similarly, the truth – value of ‘p⊃q’ is dependent on the truth – value of the variables ‘p’ and ‘q’. SO ‘p⊃q’ is the ‘truth – function’ of the prepositional variables p and q.

There is a lot of difference between variable and constant. A variable is a symbol which can stand for any one of a given range of values. Any letter of the alphabet may be taken as the symbol to represent any proposition, whatever may be its contents. Normally, ‘p’, ‘q’ ‘r’, etc. or p…p₂, p₃,, etc are used as prepositional variables. They constant for any proposition. These variables. They constant for any proposition. These variables are similar to the numerical variables are similar to the numerical variables x,y,z, etc of Algebra. Because they represent any number indifferently.

Logical constants are different from variables because the meaning oflogical constants always remains same in any logical expression. The symbol ‘V’ stands for ‘or’, stands for equivalence, etc. In the expression ‘pVq’ p and q are two variables standing for any two propositions. But the symbol ‘V’ stands for “either….. or…..” for example, if the variable ‘p’ stands for ‘Grass is green and ‘q’ stands for ‘Grass is red’ the ‘pVq’ will mean “Either grass is green or grass is red’. If ‘p’ stands for Grass is red and ‘q’ stands for “Birds are biped”, then the same expression ‘p v q’ stands for “Either grass is red or birds are biped”.

Question 3.
Draw the truth – tables of Negation, Conjuction Implication. Disjunction and Equivalence.
Answer:
Truth-Table of Negation or contradictory function: If the proposition ‘p’ is true, then its negation or contradiction ‘~p’ is false. Again, if ‘p’ is false, its negation ‘~p’ is true. The truth-table of negation or contradiction is given below, here ‘1’ means true and ‘o’ means false.

It is the truth-table of negation. Its matrix number is 01. Suppose, ‘p’ stands for ‘cat is white. If cat is white’ is true, then its negation ‘cat is not white’ is false. If cat is white is false, its hegation ‘cat is not white is true’.

Truth-Table of conjunctive Function:
Let ‘p’ and ‘q’ stand for two propositions ‘cat is white’ and ‘swan is white’ respectively. The conjunctive function ‘p q’ is true only when its constituent both propositions are true. In othe words, ‘p q’ is true only when ‘p’ is true and ‘q’ is true. If either of or both of them are false, the whole expression is false. Ther truth-table is

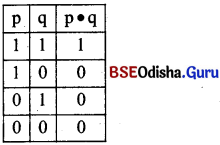
As we see in the above truth-table the conjuctive function is true only when both of the variables are true. Its matrix number is 1000.

Truth-Table of Disjunctive Function :
Let ‘p’ and ‘q’ be two propositions The truth-value of ‘p v q’ depends on the truth-value of ‘p’ and ‘q’. The symbol of disjunction is ‘v’ which means “either …. or ….” According to this function ‘p v q’ is true, when at least one of them is true. The function is false, when both of them are false. So the truth – table of disjunction is as below.

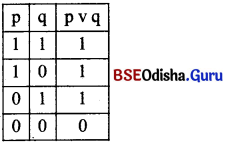
Disjunctive function is also called by some logicians as alternative function. The matrix – number of the truth table is 1110.

Truth – Table of Implicative function :
The symbol of implication is which stands for “If…. then….”. If‘p’ and ‘q’ are two variables stand for any two propositions, then ‘If p the q is symbolised as “P⊃q”, “P⊃q” is false only when p is true and q is thus.

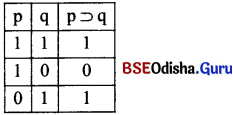
The matrix number of the function is 1011.

Truth table of equivalence :
If p and q stand for any two propositions, then p equivalent to q is symbolised as p….q. p….q is true when both the propositions are true or both are false. The truth-table of equivalence is—

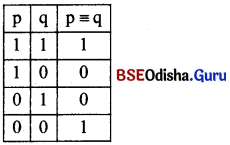
The matrix-number of equivalence is 1001. Two propositions are said to be equivalent when the meaning of both is same.

Question 4.
Determine the truth table of atternative function.
Answer:
When two propositions are related with each other on the basis of aftemative sign (A) that is called alternative function. It is always in the form of “either … or …. hot” both Here the word ‘or’ is used in the inclusive senser (weak sense).

For example:
Ramababu is either an M.L.A or an m.p but not both. Let’s take the symbol ‘p’ for the proposition Ramababu is an M.L.A. and the symbol ‘q’ for the proposition Ramababu is M.P.

Rule: When both antecedent and consequent are true together and false together at that time alternative function will be false, otherwise it will be true. Let’s construct the truth table of alternative function.

Question 5.
Explain the basic connectives of propositional logic.
Answer:
Propositional logic, also known as sentential logic, is a branch of formal logic that’deals with the manipulation and analysis of propositions. Propositions are declarative statements that are either true or false but not both. The language of propositional logic employs various logical connectives to form compound propositions from simpler ones. These basic connectives are fundamental building blocks in constructing logical expressions. Let’s explore the basic connectives of propositional logic:

1. Negation (~) : The negation connective, denoted by ~, is a unary operator that operates on a single proposition, changing its truth value. If P is a proposition, then ~P is the negation of P. The truth value of ~P is the opposite of the truth value of P.
For example, if P is “It is raining,” then ~P is “It is not raining.”

2 Conjunction (∧) : The conjunction connective, denoted by ∧, is a binary operator that combines two propositions, P and Q, to -form a compound proposition P ∧ Q. The compound proposition is true only when both P and Q are true; otherwise, it is false. For example, if P is “It is sunny” and Q is “It is warm,” then P ∧ Q is “It is sunny and warm.”

3. Disjunction (∨): The disjunction connective, denoted by (v is another binary operator that combines two propositions, P and Q, to form a compound proposition P ∨ Q. The compound proposition is true if at least one of P or Q is true. It is false only when both P and Q are false. For instance, if P is “It is a weekday” and Q is “It is a holiday,” then P ∨ Q is “It is either a weekday or a holiday.”

4. Implication (→) : The implication connective, denoted by →, is a binary operator that represents the relationship “if P, then Q.” The compound proposition P → Q is true unless P is true, and Q is false; in all other cases, it is true. It does not require P to cause Q, only that if P is true, then Q must also be true. For example, if P is “It is raining” and Q is “1 carry an umbrella,” then P → Q is “If it is raining, then I carry an umbrella.”

5. Biconditional (↔) : The biconditional connective, denoted by ↔, is a binary operator that represents the relationship “P if and only if Q.” The compound proposition P ↔ Q is true when both P and Q have the same truth value (either both true or both false). If they have different truth values, the compound proposition is false. For instance, if P is “It is noon” and Q is “The sun is at its zenith,” then P ↔ Q is “It is noon if and only if the sun is at its zenith.”

6. Exclusive Disjunction (XOR): While not always included in the basic set, the exclusive disjunction is a binary operator denoted by ⊕ or XOR. The compound proposition P ⊕ Q is true when either P or Q is true, but not both. It is false when both P and Q have the same truth value. For example, if P is “It is day” and Q is “It is night,” then P ⊕ Q is “It is either day or night, but not both.”

Understanding the properties and truth tables associated with these basic connectives is crucial for working with propositional logic. Truth tables provide a systematic way to evaluate the truth values of compound propositions based on the truth values of their constituent propositions. The logical connectives serve as tools for expressing relationships between propositions, and they play a fundamental role in various brandies of logic and computer science, including formal reasoning, artificial intelligence, and programming.

Question 6.
Distinguish between disjunction and alternation. Is alternation a basic connective? Discuss.
Answer:
In propositional logic, the terms “disjunction” and “alternation” are often used interchangeably, but it’s important to note that they can have nuanced meanings depending on the context. In this discussion, we will first distinguish between disjunction and alternation and then explore whether alternation can be considered a basic connective in propositional logic.

Distinguishing Disjunction and Alternation :
1. Disjunction (v) : Disjunction is a basic logical connective represented by the symbol ∨. In propositional logic, the disjunction of two propositions, P and Q, denoted as P ∨ Q, is true if at least one of P or Q is true. It is false only when both P and Q are false. Disjunction encompasses the idea of “or,” indicating that either P is true, or Q is true, or both. For example, if P is “It is sunny,” and Q is “It is warm,” then the disjunction P ∨ Q is true when either or both conditions are satisfied.

2. Alternation : The term “alternation” is more context-dependent and might not have a standardized symbol in propositional logic like disjunction. In some contexts, alternation refers to a similar concept as disjunction, indicating a choice between two options or the occurrence of either of two events. For instance, if P represents “Heads on a coin toss,” and Q represents “Tails on a coin toss,” then the alternation of P and Q could be seen as the concept of heads or tails.

In other contexts, “alternation” might be used to describe a more structured pattern of switching or oscillation between different states. This sense of alternation doesn’t necessarily align with the specific definition of disjunction in propositional logic but may have applications in ‘ other areas, such as temporal logic or automata theory.

Is Alternation a Basic Connective in Propositional Logic?
While disjunction is a recognized and well-defined basic connective in propositional logic, the term “alternation” itself is not typically considered a distinct basic connective within the formalism of propositional logic. Basic connectives in propositional logic are usually limited to a set that includes negation (~), conjunction (∧), disjunction (∨), implication (→), and biconditional (↔).

The absence of “alternation” as a basic connective does not diminish its significance in various logical discussions or applications. If alternation is used as a synonym for disjunction or is meant to convey a specific choice between alternatives, it aligns with the broader concept captured by the disjunction connective (v). However, if alternation is used in a more specialized context, such as temporal logic, it may involve different structures or operators beyond the basic connectives of propositional logic.

In certain logical systems, especially those dealing with temporal aspects or modalities, operators like “until” or “eventually” may be considered, but these go beyond the basic set of connectives in classical propositional logic.

Conclusion :
In summary, disjunction is a well-defined basic connective in propositional logic, represented by the symbol v, which captures the concept of “or.” On the other hand, “alternation” is a term that can be context-dependent and may be used to describe various patterns of choice or switching between alternatives. While “alternation” itself is not considered a basic connective in propositional
logic, it can be expressed using the disjunction connective when referring to a choice between two or more propositions. The specific interpretation of “alternation” may vary based on the context in which it is used, and it might, have specialized applications in specific logical systems.

Question 7.
Explain the indirect method of truth table decision.
Answer:
The indirect method of truth table decision, also known as the method of perfect induction or the method of exhaustion, is an approach used in propositional logic to determine the validity or satisfiability of logical formulas. This method involves constructing a truth table for a given formula and indirectly establishing its truth by showing that there are no cases where the formula is false. The indirect method is particularly useful when demonstrating the validity of logical arguments or proving the logical equivalence of two formulas. Let’s break down the steps involved in the indirect method of truth table decision :

1. Constructing the Truth Table : Start by constructing a truth table for the given logical formula. List all possible combinations of truth values for the atomic propositions involved in the formula. Each row in the truth table represents a unique combination of truth values.

Example :
Consider the formula (P → Q) ∧ (~ P ∨ Q). The truth table might look like this :

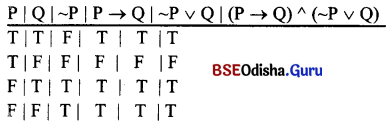
2. Identifying a Counterexample : A counterexample is a row in the truth table where the formula evaluates to false. In the indirect method, the goal is to show that no counterexample exists, indirectly establishing the truth of the formula.
Example:
In the truth table above, there is no row where (P ’! Q) ”'(¬p (“ Q) is false. Therefore, there is no counterexample, suggesting the formula is true in all cases.

3. Applying Perfect Induction: Perfect induction involves demonstrating that if the formula is true for a certain number of cases, it must be true for all cases. This is achieved by dividing the cases into subcases and showing that if the formula is true for each subcase, it is true for the entire set.
Example :
Subdivide the cases based on the truth values of P and Q :
Case 1: P is true.
Case 2: P is false.
Now, consider each subcase and verify that (P → Q) ∧ (~P ∨ Q) is true in each.
Subcase 1.1: P is true, Q is true. Formula is true.
Subcase 1.2: P is true, Q is false. Formula is true.
Subcase 2.1: P is false, Q is true. Formula is true.
Subcase 2.2: P is false, Q is false. Formula is true.
Since the formula is true for all subcases, it holds for all cases.

4. Generalizing for Ail Cases: Once it’s established that the formula is true for a set of cases, generalize the result to claim that the formula is true for all possible cases. This step involves making a general statement based on the perfect induction conducted in the previous step.
Example:
“Since (P → Q) ∨ (~P ∨ Q) is true for all possible combinations of truth values of P and Q, it is true for all cases.”

Advantages of the Indirect Method :
1. Simplicity and Systematic Approach : The indirect method provides a systematic and straightforward approach to proving the truth of a logical formula. By constructing a truth table and demonstrating the absence of counterexamples, it simplifies the process of establishing the validity or satisfiability of the formula.

2. General Applicability : The method of perfect induction is applicable to a wide range of logical formulas. It can be used to prove the validity of arguments, establish logical equivalence, or demonstrate the satisfiability of formulas in various contexts.

3. Rigorous Logical Analysis : The method encourages a rigorous analysis of all possible cases, ensuring that the formula is evaluated for every combination of truth values. This thorough examination contributes to a robust and convincing proof.

In conclusion, the indirect method of truth table decision is a valuable tool in propositional logic for proving the validity or satisfiability of logical formulas. By constructing a truth table, identifying counterexamples, applying perfect induction, and generalizing the result, one can establish the truth of a formula indirectly. This method provides a clear and systematic approach, contributing to a rigorous and convincing logical analysis.

Group – C

Objective type Questions with Answers
I. Multiple Choice Questions with Answers:

Question 1.
What is the truth value of p & q and if p = 0 and q = 1?
(i) 0
(ii) 1
(iii) undecided
(iv) None of these
Answer:
(i) 0

Question 2.
An argument is valid of the truth function corresponding to it is :
(i) A tautology
(ii) Contingent
(iii) Contradictory
(iv) None of these
Answer:
(i) A tautology

Question 3.
A disjunctive function in the exclusive sense (P k q) is true :
(i) When both p and q are true
(ii) When atleast one of them is true
(iii) When exactly one of them in true
(iv) All of these
Answer:
(iii) When exactly one of them in true

Question 4.
Symbolic logic is the developed stage of what?
(i) Deductive logic
(ii) Inductive logic
(iii) Traditional logic
(iv) Formal logic
Answer:
(iii) Traditional logic

Question 5.
Who has given the three important characteristics of symbolic logic?
(i) Aristotle
(ii) Plato
(iii) C.I. Lewis
(iv) J.S.Mill
Answer:
(iii) C.I. Lewis

Question 6.
Which of the following is the feature of Symbolic Logic?
(i) Use of ideogram
(ii) Use of variables
(iii) Application of the rules of deduction
(iv) All of these
Answer:
(i) All of these

Question 7.
Symbolic Logic builds?
(i) A deductive system
(ii) An inductive system
(iii) Both deductive and inductive system
(iv) Neither deductive nor inductive system
Answer:
(i) A deductive system

Question 8.
The soundless symbols are called what?
(i) Ideograms
(ii) Phonograms
(iii) Variables
(iv) Constants
Answer:
(i) Ideograms

Question 9.
The Letters like p,q,r, etc stand for :
(i) Prepositional variables
(ii) Logical constants
(iii) Truth function
(iv) All of these
Answer:
(i) Proposition variables

Question 10.
Variables are divided into
(i) Three types
(ii) Four types
(iii) Five types
(iv) Six types
Answer:
(i) Three Types

Question 11.
The letters like f, g, h etc stand for
(i) Prepositional variables
(ii) Predicate Variables
(iii) Individual variables
(iv) None of these
Answer:
(ii) Predicate Variables

Question 12.
The symbol ‘⊃’ stands for which of the following
(i) Conjunction
(iii) Implication
(ii) Disjunction
(iv) Equivalence
Answer:
(iii) Implication

Question 13.
The symbol ‘V’ stands for what?
(i) Conjuction
(ii) Disjunction
(iii) Alternation
(iv) Implication
Answer:
(iii) Alternation

Question 14.
The symbol ‘=’ stands for what?
(i) Conjunction
(ii) Equivalence
(iii) Alternation
(iv) Implication
Answer:
(ii) Equivalence

Question 15.
The symbol ‘A’ stands for what?
(i) Disjunction
(ii) Alternation
(iii) Disjunction
(iv) Alternative
Answer:
(i) Disjunction

Question 16.
The Symbol ‘•’ stands for what?
(i) Conjunction
(ii) Disjunction
(iii) Implication
(iv) Equivalence.
Answer:
(i) Conjuction
(ii) Disjunction
(iii) Alternation
(iv) Equivalence

Question 17.
The symbol stands for what?
(i) Conjuction
(ii) Alternation
(iii) Disjunction
Answer:
(iv) None of these

Question 18.
In which fruth tabular method, the main connective is always true? (iv) None of these
(i) Direct
(ii) Indirect
(iii) Tautology
(iv) Negation
Answer:
(iii) Tautology

II. Fill in the blanks:

Question 1.
Symbolic logic is the developmental stage of _____.
Answer:
Traditional logic

Question 2.
According to _____ there are three important characteristics of symbolic logic.
Answer:
C.I.Lewis

Question 3.
The three important characteristics of symbolic logic are _____,_____and _____.
Answer:
Use of ideogram, use of deductive method, use of constant and variable

Question 4.
The soundful symbols are called.
Answer:
Phonograms.

Question 5.
The soundless symbols are cal)ed _____.
Answer:
Ideograms:

Question 6.
Every talking word is called _____.
Answer:
Phonograms

Question 7.
If Aristotelian logic is a seed then symbolic logic is _____.
Answer:
Tree

Question 8.
Symbolic logic and traditional logic are related with each other just like embryo with
Answer:
Adult organism

Question 9.
The symbols that stand for proposition are called _____.
Answer:
Prepositional variables

Question 10.
The symbols that stand for relations of proposition are called _____.
Answer:
Logical constants

Question 11.
Variable is divided into _____ types.
Answer:
Three

Question 12.
The symbols like p,q,r,s,t etc are called _____.
Answer:
Prepositional variables

Question 13.
The symbols like f, g, h. etc are called _____.
Answer:
Predicate variables

Question 14.
The symbols like x,y,z are called _____.
Answer:
Individual variables

Question 15.
_____ stands for idea or concept directly.
Answer:
Ideogram

Question 16.
The symbol of contradiction or negation is _____.
Answer:
‘∼’

Question 17.
The symbol of conjunction is _____.
Answer:
‘•’

Question 18.
The symbol of disjunction is _____.
Answer:
‘∧’

Question 19.
The symbol of Alternation is _____.
Answer:
‘V’

Question 20.
The symbol of implication is_____
Answer:
‘⊃’

Question 21.
The symbol of equivalence is _____.
Answer:
‘s’

Question 22.
Symbolic logic uses _____ method.
Answer:
Deductive

Question 23.
Modem logicians are very much interested only for ideogram, not for .
Answer:
Phonogram

Question 24.
Truth tables are mainly divided into _____ types.
Answer:
Three

Question 25.
In a truth table, if the main result is always truth that is called _____ .
Answer:
Tautology

Question 26.
In a truth table, if the main result is always false that is called _____.
Answer:
Contradiction

Question 27.
In a truth table,-if the main result is mixed with truth and falsify (T/F) that is called
Answer:
contingent

Question 28.
Logical constants are also called as _____.
Answer:
Logical connectives

Question 29.
The truth values of an expression is a function of its constituent _____.
Answer:
Prepositional variables

Question 30.
PV~P is the example of _____ truth table.
Answer:
Tautological

Question 31.
P~P is the example of _____ truth table.
Answer:
Contradictory

Question 32.
The premises and the conclusion are connected by _____.
Answer:
Implication

Question 33.
Logical constants are _____ constants.
Answer:
Binary

Question 34.
When the truth value of a proposition is expressed in a tabular way then that is called _____.
Answer:
Truth table

Question 35.
The truth value of a proposition is _____ and _____.
Answer:
True or False

III. Correct the Sentences:

Question 1.
Symbolic makes the use of Phonograms.
Answer:
Symbolic makes the use of ideograms.

Question 2.
The letters like, p, q, r, s, t, etc are Logical constants.
Answer:
The letters like, p, q, r, s, t, etc are prepositional variables.

Question 3.
Aristotle has given three important characteristics of symbolic Logic.
Answer:
C.l. Lewis has given three important characteristics of symbolic Logic.

Question 4.
Ideograms are soundful symbols.
Answer:
Ideograms are soundless symbols.

Question 5.
Phonograms are soundless symbols.
Answer:
Phonogrmas are soundful symbols.

Question 6.
Symbolic Logic uses inductive method.
Answer:
Symbolic Logic uses deductive method.

Question 7.
The symbol stand for disjunction.
Answer:
The symbol V stands for conjunction.

Question 8.
The symbol‘V’stands for implication.
Answer:
The symbol ‘V’ stands for Alternation.

Question 9.
The symbol of implication is ____ .
Answer:
The symbol of implication is‘o’. .

Question 10.
When two propositions are related with each other in the form of if then that is called equivalence function.
Answer:
When two propositions are related with each other in the form of if then that is called implicative function.

Question 11.
When two propositions are related with each other in the form if “either… or” that is called _____ conjunctive function.
Answer:
When two propositions are related with each other in the form if “either… or” that is called alternative function.

Question 12.
A tautology is always false.
Answer:
A tautology is always true.

Question 13.
A contradictory function is sometimes true and sometimes false.
Answer:
A contingent function is sometimes true and sometimes false.

Question 14.
A contingent function is always false.
Answer:
A contradictory function is always false.

Question 15.
The letters like, f, g, g ete are called individual variables.
Answer:
The letters like f, g, h etc are called predicate variables.

IV. Answer the following questions in one word :

Question 1.
Which logic is called the development stage of traditional logic?
Answer:
Symbolic

Question 2.
The symbol which directly stands for idea or concept, it is called what?
Answer:
Ideogram

Question 3.
What is the symbol of Negative?
Answer:
‘−’

Question 4.
What is the symbol of Conjunction?
Answer:
‘•’

Question 5.
What is the symbol of Alternation?
Answer:
‘∨’

Question 6.
What is the symbol of Implication?
Answer:
‘⊃’

Question 7.
What is the symbol of equivalence?
Answer:
‘≡’

Question 8.
How many truth values are possible for a propositional variable, P?
Answer:
Two

Question 9.
If P = 1, what is the truth value of its contradictory function?
Answer:
Zero (0)

Question 10.
What is the truth value of ‘p≡q’ if p = 0 and q = 0?
Answer:
1

Question 11.
What is the truth function which is always true called?
Answer:
Tautology

Question 12.
Whether symbolic logic makes the use of ideograms or phonograms?
Answer:
Ideograms

Question 13.
How many truth combinations are possible if there are ‘n’ propositional variables in a truth function?
Answer:
2

Question 14.
What is the truth function which is always false called?
Answer:
Contradiction

Question 15.
What is truth function which is sometimes true and sometimes false called?
Answer:
Contigent

Question 16.
The letters like, p, q, r, s, t etc are coming under which variables?
Answer:
Propositional

Question 17.
The symbols like f, g, h etc. are coming under which variables?
Answer:
Predicate

Question 18.
When two propositions are related with each other in the form of if then that is called what?
Answer:
Implication