Odisha State Board Elements of Mathematics Class 12 Solutions CHSE Odisha Chapter 11 Differential Equations Ex 11(b) Textbook Exercise Questions and Answers.
CHSE Odisha Class 12 Math Solutions Chapter 11 Differential Equations Exercise 11(b)
Solve the following differential equations.
Question 1.
\(\frac{d y}{d x}\) + y = e-x
Solution:
Given equation is \(\frac{d y}{d x}\) + y = e-x … (1)
This is a linear differential equation.
Here P = 1, Q = e-x
So the integrating factor
I.F. = e∫P dx = e∫dx = ex
The solution of (1) is given by
yex = ∫e-x . ex dx = ∫dx = x + C
⇒ y – xe-x + Ce-x
Question 2.
(x2 – 1)\(\frac{d y}{d x}\) + 2xy = 1
Solution:
Given equation is (x2 – 1)\(\frac{d y}{d x}\) + 2xy = 1

![]()
Question 3.
(1 – x2)\(\frac{d y}{d x}\) + 2xy = x \(\sqrt{1-x^2}\)
Solution:
Given equation is

Question 4.
x log x \(\frac{d y}{d x}\) + y = 2 log x
Solution:
Given equation is

Question 5.
(1 + x2)\(\frac{d y}{d x}\) + 2xy = cos x
Solution:

Question 6.
\(\frac{d y}{d x}\) + y sec x = tan x
Solution:
Given equation is
\(\frac{d y}{d x}\) + y sec x = tan x
This is a linear equation where
P = sec x, Q = tan x
I.F. = e∫sec dx
= e(sec x + tan x) = sec x + tan x
The solution is y . (sec x + tan x)
= ∫(sec x + tan x) tan x dx
= ∫(sec x tan x + tan2 x) dx
= ∫(sec x . tan x + sec2 x – 1) dx
= ∫(sec x + tan x) – x + C
⇒ (y – 1) (sec x + tan x) + x = C
Question 7.
(x + tan y) dy = sin 2y dx
Given equation can be written as
Solution:

![]()
Question 8.
(x + 2y3)\(\frac{d y}{d x}\) = y
Solution:
Given equation can be written as

Question 9.
sin x\(\frac{d y}{d x}\)+ 3y = cos x
Solution:


Question 10.
(x + y + 1)\(\frac{d y}{d x}\) = 1
Solution:

Question 11.
(1 + y2) dx + (x – \(e^{-\tan ^{-1} y}\)) dy = 0
Solution:
Given equation can be written as

![]()
Question 12.
x\(\frac{d y}{d x}\) + y = xy2
Solution:
Given equation can be written as

⇒ z = -x ln x + Cx
⇒ \(\frac{1}{y}\) = -x ln x + Cx
⇒ 1 = -xy ln x + Cxy
∴ The solution is (C – ln x) xy = 1
Question 13.
\(\frac{d y}{d x}\) + y = y2 log x
Solution:
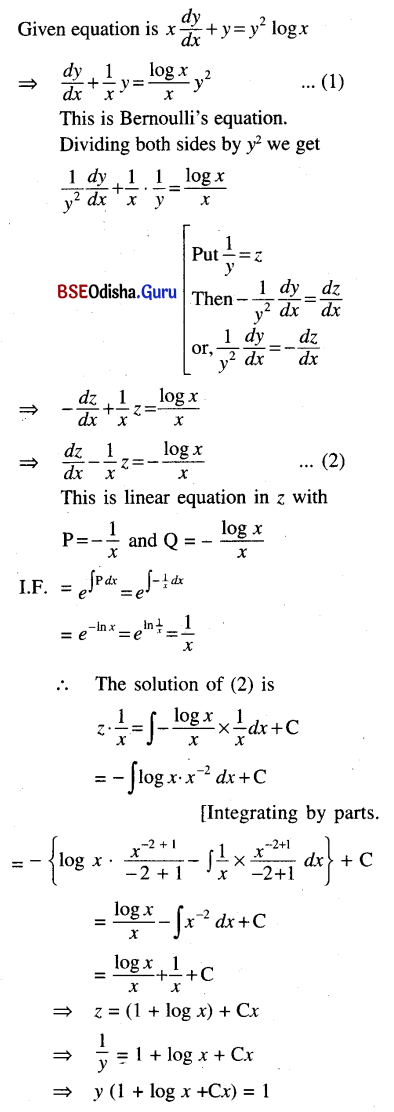
Question 14.
(1 + x2)\(\frac{d y}{d x}\) = xy – y2
Solution:
The given equation can be written as


Question 15.
\(\frac{d y}{d x}\) + \(\frac{y}{x-1}\) = \(x y^{\frac{1}{2}}\)
Solution:
The given equation can be written as

![]()
Question 16.
\(\frac{d y}{d x}\) + \(\frac{y}{x}\) = x2, y(1) = 1
Solution:
The given equation can be written as
\(\frac{d y}{d x}\) + \(\frac{y}{x}\) = x2, y(1) = 1 … (1)
This is a linear equation.

Question 17.
\(\frac{d y}{d x}\) + 2y tan x = sin x, y\(\left(\frac{\pi}{3}\right)\) = 0.
Solution:

