CHSE Odisha Class 12 Math Solutions Chapter 12 Vectors Ex 12(b)

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 12 Vectors Ex 12(b) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 12 Vectors Exercise 12(b)

Question 1.
Each question given below has four possible answers, out of which only one is correct. Choose the correct one.
(i) (2î – 4ĵ) . (î + ĵ + k̂) = _______.
(a) -3
(b) +2
(c) -1
(d) -2
Solution:
(d) -2

(ii) If a = î + 2ĵ – k̂, b = î + ĵ + 2k̂, c = 2î – ĵ; then
(a) \(\vec{a} \perp \vec{b}\)
(b) \(\vec{b} \perp \vec{c}\)
(c) \(\vec{a} \perp \vec{c}\)
(d) no pair of vectors are perpendicular.
Solution:
(c) \(\vec{a} \perp \vec{c}\)

(iii) (-3, λ, 1) ⊥ (1, 0, -3) ⇒ λ = _______.
(a) 0
(b) 1
(c) impossible to find
(d) any real number
Solution:
(c) impossible to find

(iv) If \(\vec{a} \cdot \vec{b}=\vec{c} \cdot \vec{a}\) for all vectors \(\vec{a}\), then
(a) \(\vec{a} \perp(\vec{b}-\vec{c})\)
(b) \(\vec{b}-\vec{c}\) = 0
(c) \(\vec{b} \neq \vec{c}\)
(d) \(\vec{b}+\vec{c}=\overrightarrow{0}\)
Solution:
(b) \(\vec{b}-\vec{c}\) = 0

Question 2.
Find the scalar product of the following pairs of vectors and the angle between them.
(i) 3î – 4ĵ and -2î + ĵ
Solution:

(ii) 2î – 3ĵ + 6k̂ and 2î – 3ĵ – 5k̂
Solution:

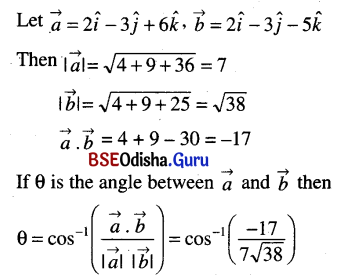
(iii) î – ĵ and ĵ + k̂
Solution:

(iv) \(\vec{a}\) = (2, -2, 1) and \(\vec{b}\) = (0, 2, 4)
Solution:

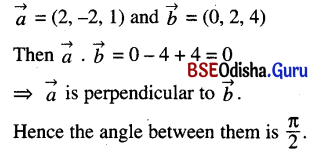
Question 3.
If A, B, C are the points (1, 0, 2), (0, 3, 1) and (5, 2, 0) respectively, find m∠ABC.
Solution:

Question 4.
Find the value of λ so that the vectors \(\vec{a}\) and \(\vec{b}\) are perpendicular to each other.
(i) \(\vec{a}\) = 3î + 4ĵ, \(\vec{b}\) = -5î + λĵ
Solution:
If \(\vec{a}\) and \(\vec{b}\) are perpendicular \(\vec{a} \cdot \vec{b}\) = 0
⇒ (3î + 4ĵ) . (-5î + λĵ) = 0
⇒ -15 + 4λ = 0
⇒ λ = \(\frac{15}{4}\)

(ii) \(\vec{a}\) = î + ĵ + λk̂, \(\vec{b}\) = 4î – 3k̂
Solution:
If \(\vec{a}\) and \(\vec{b}\) are perpendicular \(\vec{a} \cdot \vec{b}\) = 0
⇒ ( î + ĵ + λk̂) . (4î – 3k̂) = 0
⇒ 4 + 0 – 3λ = 0
⇒ λ = \(\frac{4}{3}\)

(iii) \(\vec{a}\) = 2î – ĵ – k̂, \(\vec{b}\) = λî + ĵ + 5k̂
Solution:
If \(\vec{a}\) and \(\vec{b}\) are perpendicular \(\vec{a} \cdot \vec{b}\) = 0
⇒ (2î – ĵ – k̂) . (λî + ĵ + 5k̂) = 0
⇒ 2λ – 1 – 5 = 0
⇒ 2λ = 6
⇒ λ = 3

(iv) \(\vec{a}\) = (6, 2, -3), \(\vec{b}\) = (1, -4, λ)
Solution:
If \(\vec{a}\) and \(\vec{b}\) are perpendicular \(\vec{a} \cdot \vec{b}\) = 0
⇒ (6, 2, -3) . (1, -4, λ) = 0
⇒ 6 – 8 – 3λ = 0
⇒ -2 – 3λ = 0
⇒ λ = –\(\frac{2}{3}\)

Question 5.
Find the scalar and vector projections of \(\vec{a}\) on \(\vec{b}\).
(i) \(\vec{a}\) = î, \(\vec{b}\) = ĵ
Solution:

(ii) \(\vec{a}\) = î + ĵ, \(\vec{b}\) = ĵ + k̂
Solution:

(iii) \(\vec{a}\) = î – ĵ – k̂, \(\vec{b}\) = 3î + ĵ + 3k̂
Solution:

Question 6.
In each of the problems given below, find the work done by a force \(\overrightarrow{F}\) acting on a particle, such that the particle is displaced from a point A to a point B.
(i) \(\overrightarrow{F}\) = 4î + 2ĵ + 3k̂
A (1, 2, 0), B (2, -1, 3)
Solution:
Displacement of the particle \(\overrightarrow{S}=\overrightarrow{AB}\)
= (2 – 1)î + (-1 – 2)ĵ + (3 – 0)k̂
=î – 3ĵ + 3k̂
Work done = \(\overrightarrow{F} \cdot \overrightarrow{S}\)
= (4î + 2ĵ + 3k̂) . (î – 3ĵ + 3k̂)
= 4 – 6 + 9
= 7 units.

(ii) \(\overrightarrow{F}\) = 2î + ĵ – k̂
A (0, 1, 2), B (-2, 3, 0)
Solution:
Displacement
\(\vec{S}\) = (-2 – 0)î + (3 – 1)ĵ + (0 – 2)k̂
= -2î + 2ĵ – 2k̂
Work done = \(\overrightarrow{F} \cdot \overrightarrow{S}\)
= (2î + ĵ – k̂) . (-2î + 2ĵ – 2k̂)
= -4 + 2 + 2
= 0 units.

(iii) \(\overrightarrow{F}\) = 4î – 3k̂
A (1, 2, 0), B (0, 2, 3)
Solution:
Displacement \(\vec{S}\) = -î + 3k̂
Work done = \(\overrightarrow{F} \cdot \overrightarrow{S}\)
= (4î – 3k̂) . (-î + 3k̂)
= -4 – 9
= -13 units.

(iv) \(\overrightarrow{F}\) = 3î – ĵ – 2k̂
A (-3, -4, 1), B (-1, -1, -2)
Solution:
Displacement \(\vec{S}\) = 2î + 3ĵ – 3k̂
Work done \(\overrightarrow{F} \cdot \overrightarrow{S}\)
= (3î – ĵ – 2k̂) . (2î + 3ĵ – 3k̂)
= 6 – 3 + 6
= 9 units.

Question 7.
If \((\vec{a}+\vec{b}) \cdot(\vec{a}-\vec{b})\) = 0 show that \(|\vec{a}|=|\vec{b}|\).
Solution:

Question 8.
(i) If a and b are perpendicular vectors show that

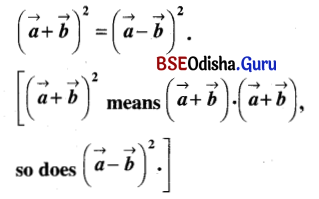
Solution:

(ii) Prove that two vectors are perpendicular iff \(|\vec{a}+\vec{b}|^2=|\vec{a}|^2+|\vec{b}|^2\)
Solution:

Question 9.
If \(\vec{a}, \vec{b}, \vec{c}\) are mutually perpendicular vectors of equal magnitude, show that \(\vec{a}+\vec{b}+\vec{c}\) is equally inclined to \(\vec{a} \cdot \vec{b} \cdot \vec{c}\)
Solution:

Question 10.
Prove the following by vector method.
(i) Altitudes of a triangle are concurrent;
Solution:
Let ABC be a triangle.

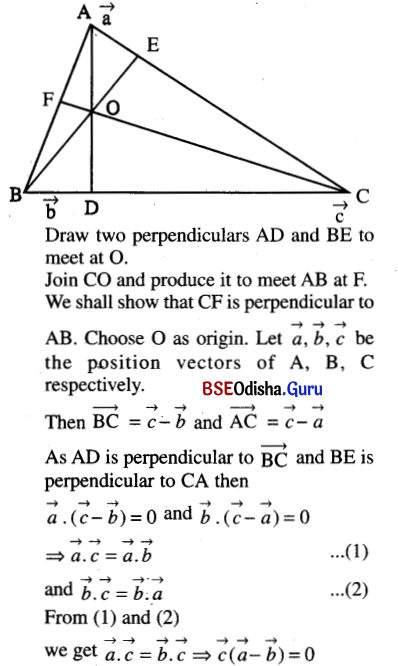
⇒ CF is perpendicular to AB.
Hence the altitudes of a triangle are concurrent.

(ii) Median to the base of an isosceles triangle is perpendicular to the base;
Solution:

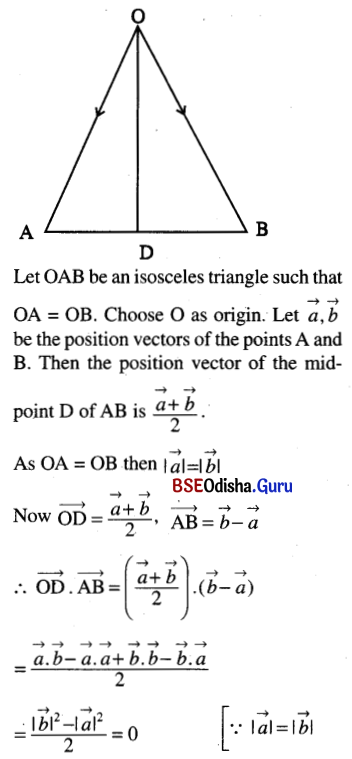
⇒ OD is perpendicular to the base AB.
Hence the median to the base of an isosceles triangle is perpendicular to the base. (Proved)

(iii) The parallelogram whose diagonals are equal is a rectangle;
Solution:

⇒ m∠COA = 90°
Hence OABC is a rectangle. (Proved)

(iv) The diagonals ofa rhombus are at right angles;
Solution:

Hence the diagonals of a rhombus are at right angles. (Proved)

(v) An angle inscribed in a semi-circle is a right angle;
Solution:

∴ m∠ABC = 90°
Hence the angle inscribed in a semi-circle is a right-angle. (Proved)

(vi) In any triangle ABC; a = b cos C + c cos B;
Solution:

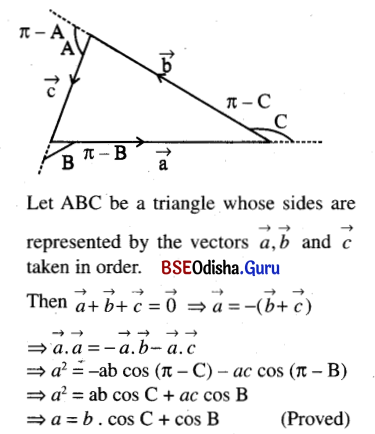
(vii) In a triangle AOB, m∠AOB = 90°. If P and Q are the points of trisection of AB, prove that OP2 + OQ2 = \(\frac{5}{9}\) AB2;
Solution:

(viii) Measure of the angle between two diagonals of a cube is cos-1\(\frac{1}{3}\).
Solution: