CHSE Odisha Class 12 Math Solutions Chapter 12 Vectors Ex 12(c)

Odisha State Board CHSE Odisha Class 12 Math Solutions Chapter 12 Vectors Ex 12(c) Textbook Exercise Questions and Answers.

CHSE Odisha Class 12 Math Solutions Chapter 12 Vectors Exercise 12(c)

Question 1.
Each question given below has four possible answers out of which only one is correct. Choose the correct one.
(i) (î + k̂) × (î + ĵ + k̂) = ______.
(a) î – k̂
(b) k̂ – î
(c) k̂ – 2î – ĵ
(d) 2
Solution:
(î + k̂) × (î + ĵ + k̂) = \(\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & 0 & 1 \\
1 & 1 & 1
\end{array}\right|\)
= î (0 – 1) – ĵ (1 – 1) + k̂ (1 – 0)
= -î + k̂ = k̂ – î

(ii) A vector perpendicular to the vectors î + ĵ and î + k̂ is ______.
(a) î – ĵ – k̂
(b) ĵ – k̂ + î
(c) k̂ – ĵ – î
(d) ĵ + k̂ + î
Solution:
A vector perpendicular to the vectors î + ĵ and î + k̂ is
(î + ĵ) × (î + k̂) = \(\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & 1 & 0 \\
1 & 0 & 1
\end{array}\right|\)
= î (1 – 0) – ĵ (1 – 0) + k̂ (0 – 1)
= î – ĵ – k̂

(iii) The area of the triangle with vertices (1, 0, 0), (0, 1, 0) and (0, 0, 1) is ______.
(a) \(\frac{1}{2}\)
(b) 1
(c) \(\frac{\sqrt{3}}{2}\)
(d) 2
Solution:

(iv) If â and b̂ are unit vectors such that â × b̂ is a unit vector, then the angle between â and b̂ is ______.
(a) of any measure
(b) \(\frac{\pi}{4}\)
(c) \(\frac{\pi}{2}\)
(d) π
Solution:
|a × b| = ab sin θ = sin θ
⇒ sin θ = 1
⇒ θ = \(\frac{\pi}{2}\)

(v) If \(\vec{a}, \vec{b} \text { and } \vec{c}\) are non-zero vectors, then \(\vec{a} \times \vec{b}=\vec{a} \times \vec{c}\) ______.
(a) \(\vec{b}=\vec{c}\)
(b) \(\vec{a} \|(\vec{b}-\vec{c})\)
(c) \(\vec{b} \| \vec{c}\)
(d) \(\vec{b} \perp \vec{c}\)
Solution:

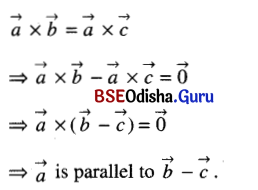
Question 2.
Let \(\vec{a}\) = 2î + ĵ, \(\vec{b}\) = -î + 3ĵ + k̂ and \(\vec{c}\) = î + 2ĵ + 5k̂ be three vectors. Find
(i) \(\vec{c} \times \vec{a}\)
Solution:

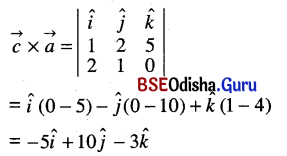
(ii) \(\vec{a} \times(-\vec{b})\)
Solution:

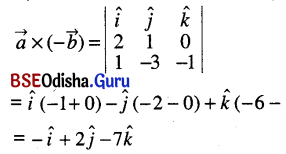
(iii) \((\vec{a}-2 \vec{b}) \times \vec{c}\)
Solution:

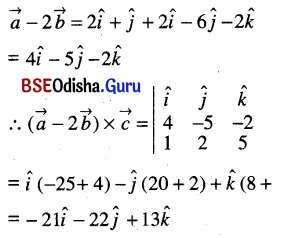
(iv) \((\vec{a}-\vec{c}) \times \vec{c}\)
Solution:

(v) \((\vec{a}-\vec{b}) \times(\vec{c}-\vec{a})\)
Solution:

Question 3.
Find the unit vectors perpendicular to the vectors
(i) î, k̂
Solution:

(ii) î + ĵ, î – k̂
Solution:

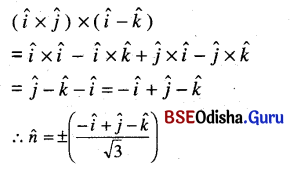
(iii) 2î + 3k̂, î – 2ĵ
Solution:

(iv) 2î – 3ĵ + k̂, -î + 2ĵ – k̂
Solution:

Question 4.
Determine the area of parallelogram whose adjacent sides are the vectors
(i) 2î, ĵ
Solution:

(ii) î + ĵ, -î + 2ĵ
Solution:

(iii) 2î + ĵ + 3k̂, î – ĵ
Solution:

(iv) (1, – 3, 1), (1, 1, 1).
Solution:

Question 5.
Calculate the area of the traingle ABC (by vector method) where
(i) A (1, 2, 4), B (3, 1, -2), C (4, 3, 1)
Solution:

(ii) A (1, 1, 2), B (2, 2, 3), C (3, -1, -1).
Solution:

Question 6.
Determine the sine of the angle between the vectors
(i) 5î – 3ĵ, 3î – 2k̂
Solution:

(ii) î – 3ĵ + k̂, î + ĵ + k̂
Solution:

Question 7.
Show that \((\vec{a} \times \vec{b})^2\) = a²b² – \((\vec{a}, \vec{b})^2\)
Solution:

Question 8.
If \(\vec{a} \times \vec{b}=\vec{b} \times \vec{c} \neq \overrightarrow{0}\), prove that \(\vec{a}+\vec{c}=m \vec{b}\), where m is a scalar.
Solution:

Question 9.
If \(\vec{a}\) = 2î + ĵ – k̂, \(\vec{b}\) = -î + 2ĵ – 4k̂, \(\vec{c}\) = î + ĵ + k̂, find \((\vec{a} \times \vec{b}) \cdot(\vec{a} \times \vec{c})\).
Solution:

Question 10.
If \(\vec{a}\) = 3î + ĵ – 2k̂, \(\vec{b}\) = 2î – 3ĵ + 4k̂ then verify that \(\vec{a} \times \vec{b}\) is perpendicular to both \(\vec{a}\) and \(\vec{b}\).
Solution:

Question 11.
Find the area of the parallelogram whose diagonals are vectors 3î + ĵ – 2k̂ and î – 3ĵ + 4k̂.
Solution:

Question 12.
Show that \((\vec{a}-\vec{b}) \times(\vec{a}+\vec{b})=2(\vec{a} \times \vec{b})\). Interpret this result geometrically.
Solution:

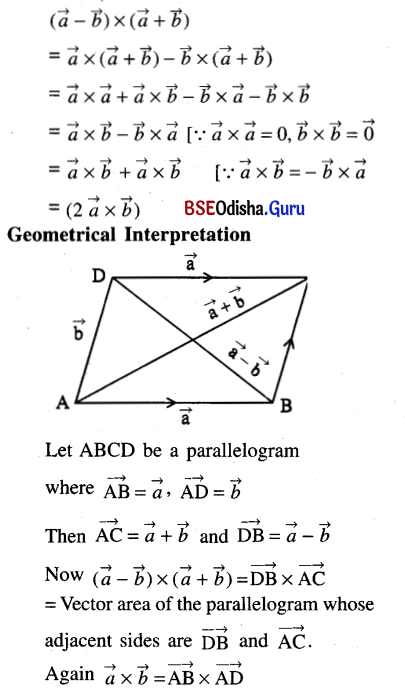
= Vector area of the parallelogram ABCD.
Hence twice the vector area of a parallelogram ABCD is equal to the vector area of the parallelogram whose adjacent sides are the diagonals of the parallelogram ABCD.